【摘 要】 我们提出了一种新的高斯过程 (GP) 回归模型，其协方差由 MM 个伪输入点的位置参数化，我们通过基于梯度的优化来学习该模型。我们采用 M<NM < N ，其中 NN 是真实数据点的数量，因此获得了每个测试用例具有 O(M2N)\mathcal{O}(M^2N) 训练成本和 O(M2)\mathcal{O}(M^2) 预测成本的稀疏回归方法。我们还在同一联合优化中找到协方差函数的超参数。该方法可以被视为具有特定输入相关噪声的贝叶斯回归模型。事实证明，该方法与其他几种稀疏高斯过程方法密切相关，我们将详细讨论这种关系。我们最终在一些大型数据集上展示了它的性能，并与其他稀疏高斯过程方法进行了直接比较。我们表明，我们的方法可以将完整的高斯过程性能与小 MM 相匹配，即非常稀疏的解决方案，并且它明显优于该方案中的其他方法。

【原 文】 Snelson, E. and Ghahramani, Z. (2005) ‘Sparse gaussian processes using pseudo-inputs’, in Y. Weiss, B. Schölkopf, and J. Platt (eds) Advances in neural information processing systems. MIT Press.

【难 度】 ⭐⭐⭐⭐⭐

1 简介

2 稀疏伪输入高斯过程 (SPGPs)

2.1 模型描述

为了推导出一个在计算上易于处理大数据集的稀疏模型，它仍然保留完整高斯过程的理想属性，我们详细检查了高斯过程预测分布 式 (3) 。将此分布的均值和方差视为新输入 xx 的函数。关于目前已知和固定的超参数，这些函数通过 NN 个训练输入和目标对 XX 和 yy 的位置有效地参数化。在本文中，我们考虑了一个模型，该模型具有由高斯过程预测分布给出的似然性，并由伪数据集参数化。模型中会出现稀疏性，因为我们通常会考虑大小为 M<NM < N 的伪数据集 Dˉ\bar{\mathcal{D}} ：伪输入 Xˉ={xˉm}m=1M\bar{\mathbf{X}} = \{\bar{\mathbf{x}}_m\}^{M}_{m=1} 和伪目标 fˉ={fˉm}m=1M\bar{\mathbf{f}} = \{\bar{f}_m\}^{M}_{m=1}。 我们将伪目标表示为 fˉ\bar{\mathbf{f}} 而不是 yˉ\bar{\mathbf{y}}，因为它们不是真实的观测结果，因此为它们包含噪声方差没有多大意义。因此，它们等同于隐函数值 f\mathbf{f} 。实际观测到的目标值当然会像以前一样假设有噪声。因此，这些假设导致以下单数据点似然：

p(y∣x,Xˉ,fˉ)=N(y∣kx⊤KM−1fˉ, Kxx−kx⊤KM−1kx+σ2)(4)p(y|\mathbf{x}, \bar{\mathbf{X}}, \bar{\mathbf{f}}) = \mathcal{N}(y \mid \mathbf{k}^{\top}_{\mathbf{x}} \mathbf{K}^{-1}_M \bar{\mathbf{f}}, \, \mathbf{K}_{\mathbf{xx}} − \mathbf{k}^{\top}_{\mathbf{x}} \mathbf{K}^{-1}_M \mathbf{k}_{\mathbf{x}} + \sigma^2) \tag{4}

其中 [KM]mm′=K(xˉm,xˉm′)[\mathbf{K}_M]_{mm'} = \mathbf{K}(\bar{\mathbf{x}}_m,\bar{\mathbf{x}}_{m'}) 和 [kx]m=K(xˉm,x)[\mathbf{k}_{\mathbf{x}}]_m = K(\bar{\mathbf{x}}_m, \mathbf{x})，对于 m=1,…,Mm = 1, \ldots , M。

这可以被视为具有特定形式的参数化均值函数和输入相关噪声模型的标准回归模型。目标数据是 i.i.d 生成的。给定输入，给出完整的数据似然：

p(y∣X,Xˉ,fˉ)=∏n=1Np(yn∣xn,Xˉ,fˉ)=N(y∣KNMKM−1fˉ,Λ+σ2I)(5)p(\mathbf{y|X}, \bar{\mathbf{X}}, \bar{\mathbf{f}}) = \prod^{N}_{n=1} p(y_n|\mathbf{x}_n, \bar{\mathbf{X}}, \bar{\mathbf{f}}) = \mathcal{N}(\mathbf{y}|\mathbf{K}_{NM} \mathbf{K}^{-1}_M \bar{\mathbf{f}}, \boldsymbol{\Lambda} + \sigma^2 \mathbf{I}) \tag{5}

其中 Λ=diag⁡(λ)\boldsymbol{\Lambda} = \operatorname{diag}(\boldsymbol{\lambda})，λn=Knn−kn⊤KM−1knλ_n = K_{nn} − \mathbf{k}^{\top}_n \mathbf{K}^{-1}_M \mathbf{k}_n，并且 [KNM]nm=K(xn,xˉm)[\mathbf{K}_{NM} ]_{nm} = K(\mathbf{x}_n,\bar{\mathbf{x}}_m)。

2.2 伪变量的先验和后验

在模型中学习涉及找到合适的参数设置，即找到一个可以很好地解释真实数据的伪数据集。但不是简单地最大化关于 Xˉ\bar{\mathbf{X}} 和 fˉ\bar{\mathbf{f}} 的似然，事实证明我们可以积分出伪目标 fˉ\bar{\mathbf{f}}。我们可以在伪目标上放置一个高斯先验：

p(fˉ∣Xˉ)=N(fˉ∣0,KM)(6)p(\bar{\mathbf{f}}| \bar{\mathbf{X}}) = \mathcal{N}(\bar{\mathbf{f}}| \mathbf{0}, \mathbf{K}_M) \tag{6}

这个先验很合理，因为我们希望伪数据与真实数据具有相同的分布。在伪输入上放置先验并保持易于处理的模型并不容易（即采用贝叶斯方法并不容易），因此可们通过最大似然 (ML) 找到伪输入的点估计。在继续讨论如何实施估计程序之前，我们暂时将伪输入视为已知。

我们使用 式 (5) 和 式 (6) 上的贝叶斯规则找到伪目标 fˉ\bar{\mathbf{f}} 的后验分布：

p(fˉ∣D,Xˉ)=N(fˉ∣KMQM−1KMN(Λ+σ2I)−1y, KMQM−1KM)(7)p(\bar{\mathbf{f}}|\mathcal{D}, \bar{\mathbf{X}}) = \mathcal{N}(\bar{\mathbf{f}}|\mathbf{K}_M \mathbf{Q}^{-1}_M \mathbf{K}_{MN}(\boldsymbol{\Lambda} + \sigma^2 \mathbf{I})^{-1} \mathbf{y},\, \mathbf{K}_M \mathbf{Q}^{-1}_M \mathbf{K}_M) \tag{7}

其中 QM=KM+KMN(Λ+σ2I)−1KNM\mathbf{Q}_M = \mathbf{K}_M + \mathbf{K}_{MN}(\boldsymbol{\Lambda} + \sigma^2 \mathbf{I})^{-1}\mathbf{K}_{NM} 。

2.3 预测

给定一个新的输入 x∗\mathbf{x_*}，然后通过将似然 式 (4) 与后验 式 (7) 相结合来获得预测分布：

p(y∗∣x∗,D,Xˉ)=∫p(y∗∣x∗,Xˉ,fˉ)p(fˉ∣D,Xˉ)dfˉ=N(y∗∣μ∗,σ∗2)(8)p(y_*|\mathbf{x_*}, \mathcal{D}, \bar{\mathbf{X}}) = \int p(y_*|\mathbf{x_*}, \bar{\mathbf{X}}, \bar{\mathbf{f}}) p(\bar{\mathbf{f}}| \mathcal{D}, \bar{\mathbf{X}}) d \bar{\mathbf{f}}= \mathcal{N}(y_*|\mu_*, \sigma^2_*) \tag{8}

其中

μ∗=k∗⊤QM−1KMN(Λ+σ2I)−1yσ∗2=K∗∗−k∗⊤(KM−1−QM−1)k∗+σ2\begin{align*} \mu_* &=\mathbf{k}^{\top}_* \mathbf{Q}^{-1}_M \mathbf{K}_{MN}(\boldsymbol{\Lambda} + \sigma^2 \mathbf{I})^{-1} \mathbf{y}\\ \sigma^2_* &= \mathbf{K}_{**} − \mathbf{k}^{\top}_* (\mathbf{K}^{-1}_M − \mathbf{Q}^{-1}_M)\mathbf{k}_* + \sigma^2 \end{align*}

请注意，矩阵 Λ+σ2I\boldsymbol{\Lambda} + \sigma^2 \mathbf{I} 的求逆不是问题，因为它是对角矩阵。在 QM\mathbf{Q}_M 的计算中，计算成本以矩阵乘法 KMN(Λ+σ2I)−1KNM\mathbf{K}_{MN}(\boldsymbol{\Lambda} + \sigma^2 \mathbf{I})^{-1} \mathbf{K}_{NM} 为主，为 O(M2N)\mathcal{O}(M^2N)。在各种预计算之后，然后可以在 O(M)\mathcal{O}(M) 中对每个测试用例的均值和 O(M2)\mathcal{O}(M^2) 的方差进行预测。

2.4 参数和伪输入的估计

我们剩下的问题是找到伪输入位置 Xˉ\bar{\mathbf{X}} 和超参数 Θ={θ,σ2}\boldsymbol{ \Theta} = \{ \boldsymbol{\theta}, \sigma^2 \}。我们可以通过计算 式 (5) 和 式 (6) 的边缘似然来做到这一点：

p(y∣X,Xˉ,Θ)=∫p(y∣X,Xˉ,fˉ))p(fˉ∣Xˉ)dfˉ=N(y∣0, KNMKM−1KMN+Λ+σ2I)\begin{align*} p(\mathbf{y} \mid \mathbf{X,\bar{X}, \boldsymbol{\Theta}}) &= \int p(\mathbf{y|X, \bar{X}, \bar{f})}) p(\mathbf{\bar{f}| \bar{X}}) d \bar{\mathbf{f}} \\ &=\mathcal{N}( \mathbf{y} \mid \mathbf{0}, \,\mathbf{K}_{NM} \mathbf{K}^{-1}_M \mathbf{K}_{MN} + \boldsymbol{\Lambda} + \sigma^2 \mathbf{I}) \tag{9} \end{align*}

然后可以通过梯度上升针对所有这些参数 {Xˉ,Θ}\{ \bar{\mathbf{X}}, \boldsymbol{\Theta} \} 最大化边缘似然。梯度计算的细节冗长乏味，因此为简洁起见，此处省略。他们密切遵循 Seeger 等人超参数梯度的推导[7]（另见第 3 节），并且可以使用 Cholesky 分解进行有效编码。请注意，KM\mathbf{K}_M 、KMN\mathbf{K}_{MN} 和 Λ\boldsymbol{\Lambda} 都是 MM 个伪输入 Xˉ\bar{\mathbf{X}} 和 θ\boldsymbol{\theta} 的函数。梯度的确切形式当然取决于所选协方差函数的函数形式，但我们的方法将适用于任何关于输入点可微的协方差函数。值得一提的是， SPGP 可以被视为一个标准高斯过程，只是其协方差函数是被伪输入参数化了的非平稳函数。

由于我们现在有 MD+∣Θ∣M D +|\boldsymbol{\Theta}| 个参数需要拟合，而不仅仅是完整高斯过程的 ∣Θ∣|\boldsymbol{\Theta}| 个参数，因此可能会担心过拟合。但如果考虑 M=NM = N 和 Xˉ=X\bar{\mathbf{X}}=\mathbf{X} （即伪输入与真实输入一致），则边缘似然等于完整高斯过程的边缘似然（ 式 (2) ）。这是因为 KMN=KM=KN\mathbf{K}_{MN} = \mathbf{K}_M = \mathbf{K}_N 和 Λ=0\boldsymbol{\Lambda} = \mathbf{0}。此外， 式 (8) 的预测分布也坍缩为完整高斯过程的预测分布 （ 式 (3)）。这些显然是模型的理想性质，它使我们相信当 M<NM < N 时会找到一个好的解。但超参数学习确实使事情变得复杂化，我们将在 第 4 节 中进一步讨论。

3 与其他方法的关系

事实证明，Seeger 的 PLV [7][8] 方法使用了非常相似的边缘似然近似和预测分布。如果您从所有 SPGP 方程中删除 Λ\boldsymbol{\Lambda}，您将精确地得到它们的表达式。特别是他们使用的边缘似然是：

p(y∣X,Xˉ,θ)=N(y∣0,KNMKM−1KMN+σ2I)(10)p(\mathbf{y}| \mathbf{X,\bar{X}}, \boldsymbol{\theta}) = \mathcal{N}(\mathbf{y}| \mathbf{0}, \mathbf{K}_{NM} \mathbf{K}^{−1}_M \mathbf{K}_{MN} + σ^2 I) \tag{10}

之前也曾在其他地方 [1][4][5] 使用过。他们从一种稍微不同的途径推导出这个表达式，作为对完整高斯过程边缘似然的直接近似。

如前所述，我们的方法与这些其他方法的主要区别在于，它们不使用这种边缘似然来学习活动集输入点的位置——仅从 式 (10) 中学习超参数。这就引出了一个问题，如果我们尝试使用它们的边缘似然近似 式 (10) 而不是 式 (9) 来尝试通过梯度上升来学习伪输入位置，会发生什么。我们表明出现在 SPGP 边缘似然 式 (9) 中的 Λ\boldsymbol{\Lambda} 对于通过梯度寻找伪输入点至关重要。

fig01

图 1：预测分布（均值和两条标准差线）：a) 完整高斯过程，b) 在式 (9) 上使用梯度上升训练的 SPGP，c) 在式 (10) 上使用梯度上升训练的 SPGP。初始伪点位置在顶部显示为红色十字；最终伪点位置在底部显示为蓝色十字（这些十字图上的 yy 值没有意义）

图 1 显示了当我们尝试在一个简单的一维数据集上使用关于伪输入的梯度上升来优化这两种似然时会发生什么。绘制的是预测分布、伪输入的初始和最终位置。在这个例子中，超参数被固定为它们的真实值。初始伪输入位置是对抗性选择的：全部朝向输入空间的左侧（红色十字）。使用 SPGP 似然，伪输入沿着训练数据的范围扩散，预测分布与完整高斯过程非常接近（ 图 1(b) ）。使用 PLV 似然，点开始扩散，但随着将点向右推的梯度变得很小，点很快就会卡住（ 图 1(c)）。

fig02

图 2：从不同边缘似然中提取的样本数据：a) 完整高斯过程，b) SPGP，c) PLV。对于 b) 和 c)，蓝色十字表示 10 个伪输入点的位置。

图 2 比较了在给定超参数的特定设置和少量伪输入点的情况下从边缘似然 式 (9) 和 式 (10) 采样的数据。两者之间的主要区别在于 SPGP 似然具有 Knn+σ2\mathbf{K}_{nn} + σ^2 的恒定边缘方差，而 PLV 降低到远离伪输入的 σ2\sigma^2。或者，PLV 似然的噪声分量是常数 σ2\sigma^2，而 SPGP 噪声在远离伪输入时增长到 Knn+σ2\mathbf{K}_{nn} + \sigma^2。如果处于 图 1(c) 的情况，在 SPGP 似然下，将最右边的伪输入稍微向右移动将立即开始减少该区域中的噪声，从 Knn+σ2\mathbf{K}_{nn} + \sigma^2 向 σ2\sigma^2 移动。因此会有一个很强的梯度将它拉到右边。对于 PLV 似然，噪声在任何地方都固定在 σ2\sigma^2，并且将点向右移动并不能充分提高局部均值函数的拟合质量以提供显着的梯度。因此，这些点变得卡住了，我们认为这种影响是 图 1(c) 中 PLV 似然失败的原因。

应该强调的是，PLV 似然 式 (10) 的全局最优值可能是一个很好的解决方案，但很难通过梯度找到。 SPGP 似然 式 (9) 当然也受到局部最优的影响，但没有那么灾难性。将来比较哪个在超参数优化方面表现更好可能会很有趣。

4 实验

在上一节中，我们展示了我们的梯度方法成功地学习了一维示例的伪输入。初始伪输入点是对抗性选择的，但在实际问题上，通过将它们随机放置在真实数据点上进行初始化是明智的，这就是我们为所有实验所做的。为了将我们的结果与其他方法进行比较，我们在与 Seeger 等人完全相同的数据集上进行了实验 [7]，精确地遵循他们的预处理和测试方法。在 图 3 中，我们重现了两个大型数据集 1 的学习曲线，叠加了我们的测试误差（均方）。

Seeger 等比较三种方法：random, info-gain 和 smo-bart。随机涉及从训练数据中随机选择一个大小为 MM 的活动集。 info-gain 是他们自己的贪心子集选择方法，训练起来非常便宜: 只比随机方法贵一点。 smo-bart 是 Smola 和 Bartlett [1]的更昂贵的贪心子集选择方法。还用水平线显示了在数据集 kin-40k 大小为 2000 和 pumadyn-32nm 大小为 1024 的数据子集上训练的完整高斯过程的测试误差。对于这些学习曲线，他们实际上并没有通过最大化边际似然 (10) 的近似来学习超参数。相反，他们将它们固定为从完整高斯过程获得的那些。

对于 kin-40k，我们遵循 Seeger 等在子集上从完整高斯过程设置超参数的过程。然后我们优化伪输入位置，并将结果绘制为红色方块。在 图 3 中，我们看到 SPGP 学习曲线明显低于所有其他三种方法。我们使用仅包含几百个点的伪集，快速接近在 2000 个点上训练的完整高斯过程的误差。然后，我们尝试更艰巨的任务，即在伪输入的同时找到超参数。结果绘制为蓝色圆圈。该方法对于小 MM 表现非常好，但我们看到大 MM 的一些过拟合行为，这似乎是由于噪声超参数被驱动得太小造成的（蓝色圆圈比它们下面的红色方块有更高的似然）。

对于数据集 pumadyn-32nm，我们再次尝试联合寻找超参数和伪输入。 图 3 再次显示了 SPGP 对于小的伪集大小具有极低的误差，只有 10 个伪输入，我们已经接近在 1024 个点上训练的完整高斯过程的误差。然而，在这种情况下，增加伪集大小并不会减少我们的错误。该问题中存在大量不相关的属性，需要通过ARD挑出相关的属性。尽管通过我们的方法学习到的超参数是合理的（找到了 4 个相关维度中的 2 个），但它们还不足以降低到完整高斯过程的误差。然而，如果我们用完整高斯过程的超参数初始化我们的梯度算法，我们得到的点被绘制为正方形（这次红色似然 > 蓝色似然，所以这是局部最优而不是过度拟合的问题）。现在只有一个大小为 25 的伪集，我们就达到了完整高斯过程的性能，并且明显优于其他方法（它们的超参数也来自完整高斯过程）。

这些方法之间的另一个主要区别在于训练时间。我们的方法在潜在的大参数空间上执行优化，因此训练起来相对昂贵。从表面上看，信息增益和随机等方法非常便宜。然而，所有这些方法都必须与以某种方式获得超参数相结合，要么通过子集上的完整高斯过程（通常很昂贵），要么通过对似然率的近似值进行梯度上升。当您考虑这个组合任务时，并且所有方法都涉及某种基于梯度的过程，那么没有一种方法特别便宜。我们相信，通过我们的方法获得的准确性增益通常值得在更大的参数空间中进行优化相关的额外训练时间。

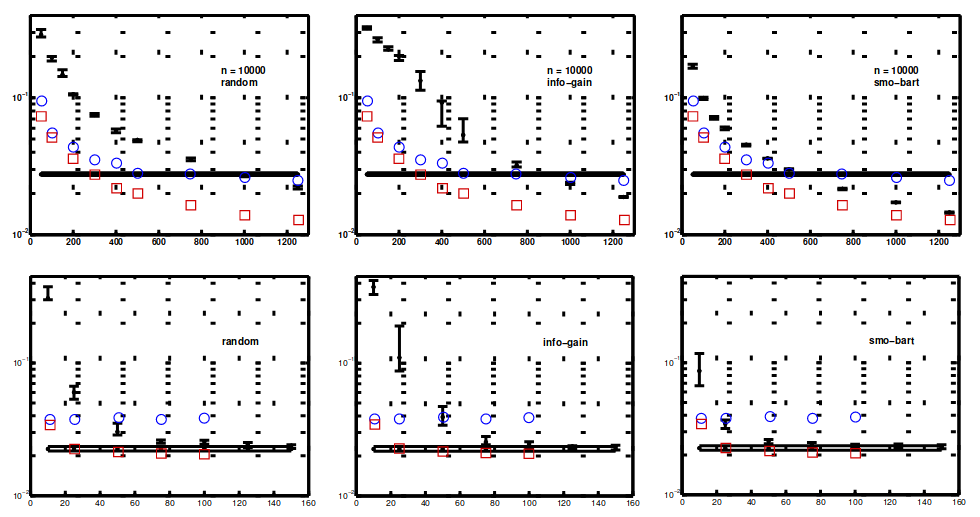
fig03

图 3：这些图显示均方检验误差作为活动/伪集大小 MM 的函数。顶行 - 数据集 kin-40k，底行 - pumadyn-32nm1。我们添加了圆圈，显示 SPGP 具有从随机初始化学习的超参数和伪输入。对于 kin-40k，方块显示 SPGP，其超参数从完整高斯过程获得并固定。对于 pumadyn-32nm，方块显示从完整高斯过程初始化的超参数。 random, info-gain 和 smo-bart 在文中有解释。水平线是在数据子集上训练的完整高斯过程。

fig04

图 4：对具有输入相关噪声的数据集进行回归。左：标准高斯过程。右：SPGP。显示了预测平均值和两条标准偏差线。十字显示 SPGP 的伪输入的最终位置。还学习了超参数。

5 结论、扩展和未来工作

尽管高斯过程是非常灵活的回归模型，但它们仍然受到协方差函数形式的限制。例如，很难用高斯过程对非平稳过程建模，因为很难构建合理的非平稳协方差函数。尽管 SPGP 并不是专门为非平稳性建模而设计的，但与移动伪输入相关的额外灵活性实际上可以在一定程度上实现这一点。 图 4 显示了 SPGP 适合某些具有输入相关噪声方差的数据。 SPGP 通过将几乎所有伪输入点移到 data3 区域之外，比标准高斯过程更适合数据。将来进一步测试这些功能将会很有趣。分类的扩展也是探索的自然途径。

伪集大小和/或高维输入空间，因为我们正在优化的空间变得不切实际。然而，我们目前只尝试使用“现成的”共轭梯度最小化器或 L-BFGS，并且在这方面肯定可以进行改进。例如，我们可以尝试迭代优化变量子集（分块）或随机梯度上升，或者我们可以通过随机选取一些点并优化其他点来进行混合。总的来说，尽管我们认为我们的方法在需要非常稀疏（因此可以快速预测）和准确的解决方案时最有用。处理大 D 的另一种方法是学习输入空间的低维投影。这在 [14] 之前已经被高斯过程考虑过，并且可以很容易地应用于我们的模型。

总之，我们提出了一种用于稀疏高斯过程回归的新方法，与其他方法相比，它显示出显着的性能提升，尤其是在搜索极其稀疏的解决方案时。我们已经表明，移动不受限于真实数据点的伪输入点的灵活性会带来更好的解决方案，甚至可以对一些非平稳效应进行建模。最后，我们证明了超参数可以与伪输入点联合学习并取得合理的成功。

参考文献

  • [1] A. J. Smola and P. Bartlett. Sparse greedy Gaussian process regression. In Advances in Neural Information Processing Systems 13. MIT Press, 2000.
  • [2] C. K. I. Williams and M. Seeger. Using the Nystr ̈ om method to speed up kernel machines. In Advances in Neural Information Processing Systems 13. MIT Press, 2000.
  • [3] V. Tresp. A Bayesian committee machine. Neural Computation, 12:2719–2741, 2000.
  • [4] L. Csat ́ o. Sparse online Gaussian processes. Neural Computation, 14:641–668, 2002.
  • [5] L. Csat ́ o. Gaussian Processes — Iterative Sparse Approximations. PhD thesis, Aston University, UK, 2002.
  • [6] N. D. Lawrence, M. Seeger, and R. Herbrich. Fast sparse Gaussian process methods: the informative vector machine. In Advances in Neural Information Processing Systems 15. MIT Press, 2002.
  • [7] M. Seeger, C. K. I. Williams, and N. D. Lawrence. Fast forward selection to speed up sparse Gaussian process regression. In C. M. Bishop and B. J. Frey, editors, Proceedings of the Ninth International Workshop on Artificial Intelligence and Statistics, 2003.
  • [8] M. Seeger. Bayesian Gaussian Process Models: PAC-Bayesian Generalisation Error Bounds and Sparse Approximations. PhD thesis, University of Edinburgh, 2003.
  • [9] J. Qui ̃ nonero Candela. Learning with Uncertainty — Gaussian Processes and Relevance Vector Machines. PhD thesis, Technical University of Denmark, 2004.
  • [10] D. J. C. MacKay. Introduction to Gaussian processes. In C. M. Bishop, editor, Neural Networks and Machine Learning, NATO ASI Series, pages 133–166. Kluwer Academic Press, 1998.
  • [11] C. K. I. Williams and C. E. Rasmussen. Gaussian processes for regression. In Advances in Neural Information Processing Systems 8. MIT Press, 1996.
  • [12] C. E. Rasmussen. Evaluation of Gaussian Processes and Other Methods for Non-Linear Regression. PhD thesis, University of Toronto, 1996.
  • [13] M. N. Gibbs. Bayesian Gaussian Processes for Regression and Classification. PhD thesis, Cambridge University, 1997.
  • [14] F. Vivarelli and C. K. I. Williams. Discovering hidden features with Gaussian processes regression. In Advances in Neural Information Processing Systems 11. MIT Press, 1998.