用于模式发现和外推的高斯过程核
【摘 要】 高斯过程是函数的丰富分布,它提供了贝叶斯非参数方法来进行平滑和插值。我们介绍了可与高斯过程一起使用以发现模式并启用外推的简单封闭形式核。这些核是通过使用高斯混合对谱密度(核的傅里叶变换)建模而得出的。所提出的核支持广泛类别的平稳协方差,但高斯过程推断仍然简单且具有解析性。我们通过发现模式并对合成示例以及大气 趋势和航空公司乘客数据进行远程外推来证明所提出的核。我们还表明,可以在我们的框架内重建几个流行的标准协方差。
【原 文】 Wilson, A.G. and Adams, R.P. (2013) ‘Gaussian Process Kernels for Pattern Discovery and Extrapolation’. arXiv. Available at: http://arxiv.org/abs/1302.4245 (Accessed: 21 March 2023).
1 简介
机器学习从根本上讲是关于模式发现的。第一个机器学习模型,例如感知器 (Rosenblatt, 1962 [19]),是基于一个简单的神经元模型 (McCulloch & Pitts, 1943 [14])。 Rumelhart 等 (1986 [20]) 的论文激发了人们的希望,即可以使用神经网络等模型开发智能代理,这些模型可以自动发现数据中的隐含表示。事实上,机器学习的目的不仅是为人类配备分析数据的工具,还旨在使学习和决策过程完全自动化。
机器学习社区内对高斯过程 (GP) 的研究是由神经网络研究发展而来的,由 Neal (1996 [16]) 发起,他观察到随着隐藏单元的数量接近无穷大,贝叶斯神经网络变成了高斯过程。 Neal (1996) 推测“在这种情况下可能有更简单的推断方法”。
这些简单的推断技术成为后续机器学习高斯过程模型的基石 (Rasmussen & Williams, 2006 [18])。这些模型直接在函数而不是参数上构建先验。假设高斯噪声,可以根据给定的数据分析地推断出这些函数的后验分布。高斯过程模型在非线性回归和分类中变得流行,并且通常具有令人印象深刻的实证性能(Rasmussen,1996 [17])。
高斯过程下函数的性质,例如平滑度、周期性等,由正定协方差核控制,该核是确定随机函数域中点对之间相似性的算子。核的选择会深刻影响高斯过程在给定任务上的性能,就像神经网络的架构、激活函数、学习率等选择一样会影响其性能。
高斯过程有时用作表达统计工具,其中模式发现由人类执行,然后硬编码到参数核中。但是,通常默认使用平方指数(高斯)核。在任何一种情况下,高斯过程都用作具有平稳(尽管是无限)基函数集的平滑插值器。这种简单的平滑设备并不是神经网络的现实替代品,神经网络被设想为可以通过自适应基函数发现数据中隐含特征的智能代理 (MacKay, 1998 [12])。
然而,贝叶斯非参数可以帮助构建能够推断和做出决策的自动化智能系统。有人提出,人类的归纳推断能力(用非常少的例子进行概念概括)可以源自先验结合贝叶斯推断(Yuille & Kersten,2006 年 [30];Tenenbaum 等,2011 年 [25];Steyvers 等,2006 年 [24])。贝叶斯非参数模型,尤其是高斯过程,是一种编码先验知识的表达方式,也反映了现实世界无限复杂的信念 (Neal, 1996 [16])。
使用更具表现力的核,可以使用高斯过程来学习数据中的隐含表示。已经有学者在贝叶斯神经网络结构中结合高斯过程开发了具有表达力的核(Salakhutdinov & Hinton, 2008 [22]; Wilson 等, 2012 [28]; Damianou & Lawrence, 2012 [6])。但这些方法虽然很有前途,但通常
-
- 旨在为特定类型的结构建模(例如,不同任务之间依赖于输入的相关性);
-
- 使用具有简单内插核的组件高斯过程;
-
- 间接归纳出不具有封闭形式且难以解释的复杂核;
-
- 需要复杂的近似推断技术,这些技术比简单的解析核所需的要求更高。
复杂的核通常是通过组合一些标准核函数来实现的(Archambeau & Bach,2011 年 [2];Durrande 等,2011 年 [7];Gonen & Alpaydın,2011 年[8];Rasmussen & Williams,2006 年 [18])。这些组分通常受到严格限制,并且是为专门应用手工制作的。如果没有这些限制,核的复杂组合会导致过度拟合和难以管理的超参数推断。此外,虽然某些组合(例如加法)具有可解释的效果,但许多其他操作会以难以识别的方式改变函数的分布。因此,很难为核组成构建有效的归纳偏好,从而在没有人为干预的情况下自动发现适当的统计结构。
如果不做任何假设,很难从单次抽取中说明随机过程的协方差函数,这一事实加剧了这种困难。如果我们允许输入空间中任意两点之间的协方差来自任何正定函数且概率相等,那么基本上不会从单一实现中获得任何信息。最常见的假设是对平稳核的限制,这意味着协方差对于输入空间中的平移具有不变性。
在本文中,我们探索了超越简单解析形式组合的灵活核类别,同时保持了平稳性的有用归纳偏好。我们提出了新的核,可用于自动发现模式并推断远远超出可用数据的范围。此类核包含许多平稳核,但具有简单的封闭形式,可导致直接的解析推断。这些核的简单性是它们最强大的品质之一。在许多情况下,这些核可以用作流行的平方指数核的替代品,在性能和表现力方面具有优势。通过学习数据中的特征,我们不仅可以提高预测性能,还可以更深入地了解手头问题的结构——温室气体、航空旅行、心脏生理学、大脑活动等。
论文结构:
- 在
第 2 节中简要回顾高斯过程后, - 在
第 3 节中通过混合高斯分布的谱密度建模来推导出新核。 - 在
第 4 节中将实验重点放在阐明所提出的核与 Rasmussen & Williams (2006) 中流行的替代品之间的根本区别。特别是,我们展示了所提出的核如何自动发现模式并在 Rasmussen & Williams (2006) 的 数据集、具有强负协方差的合成数据集、困难的合成 模式和航空公司乘客数据上进行推断。我们还使用我们的框架重构了几个流行的标准核。
2 高斯过程
略。
3 用于模式发现的核
在本节中,我们介绍了一类可以发现模式、推断和建模负协方差的核。此类包含大量平稳核。粗略地说,核测量数据点之间的相似性。与等 式(3) 中一样,高斯过程的协方差核决定了相关的随机函数将如何随输入(预测变量) 变化。平稳核是 的函数,即它对于输入的平移是不变的。
使用 Bochner 定理(Bochner,1959 [3];Stein,1999 [23]),任何平稳核(在概率测度下,核也称协方差函数)都可以表示为积分:
【定理 3.1 (Bochner)】 上的复值函数 是 上弱平稳均方连续复值随机过程的协方差函数,当且仅当它可以表示为:
其中 是正有限测度。
如果 具有密度 ,则 称为 的谱密度或功率谱, 和 是傅里叶对偶 (Chatfield, 1989 [4]):
换句话说,谱密度完全决定了平稳核的性质。将 式(5) 的平方指数核代入 式(8) ,可得其谱密度为 。因此,SE 核和平方指数(SE)核的混合只是所有可能的平稳核集合的一个非常小的角落,因为它们仅对应于以原点为中心的高斯谱密度。
然而,通过使用具有非零均值的混合高斯分布,可以实现更宽范围的谱密度。事实上,高斯混合在所有分布函数的集合中是密集的 (Kostantinos, 2000 [11])。因此,此集合的对偶在平稳协方差中也是密集的。也就是说,只要在谱表示中有足够的混合成分,我们就可以将任何平稳协方差核近似到任意精度。这一观察激发了我们的方法,即通过谱密度(可视为尺度-位置的高斯混合)对高斯过程的协方差函数建模。
我们先考虑一个简单的谱密度:
注意到该谱密度是对称的(Rasmussen & Williams, 2006 [18])。将 代入 式(7) , 我们发现:
如果 是 上 个高斯分布的混合,其中第 个分量具有平均向量 和协方差矩阵 , 并且 为 维向量 的第 个分量,则
即使当谱密度是任意高斯混合时,式(7) 中的积分也是易于处理的,这使我们能够推导出式(11)和式(12)中的精确封闭形式表达式,并用高斯过程进行解析推断。此外,这类核具有表现力(能包容许多平稳核),同时仍然具有简单的形式。
上述核易于解释,并为 Rasmussen & Williams (2006 [18]) 中的核提供了直接替换。权重 指定每个混合组分的相对贡献。均值倒数 是组分周期,标准差倒数 是长度尺度,确定组分随输入 变化的速度。式(12) 中的核也可以通过其相关的谱密度来解释。
在 第 4 节 中,我们使用学得的谱密度来解释数据中发现的模式数量以及这些模式如何泛化。后文中我们将 式 (12) 中的核称为 谱混合 (SM) 核。
4 实验
我们展示了 式(12) 中的谱混合核可用于发现模式、推断和建模负协方差。我们将谱混合核与流行的核进行对比,例如 Rasmussen & Williams (2006 [18]) 和 Abrahamsen (1997 [1]),这些流行核通常只提供平滑的插值。尽管谱混合核通常比流行的替代方法有更高预测似然,但我们仍将专注于清晰地可视化学习到的核和谱密度、检查模式和预测以及发现数据中的结构。我们的目标是阐明谱混合核与所替代方法之间的根本区别。
在所有实验中,都假定高斯噪声,因此可以以封闭形式执行对未知函数的边缘化。核超参数使用非线性共轭梯度进行训练,以优化给定超参数 的数据 的边缘似然 ,如第 2 节所述,假设高斯过程均值为零。一种 “自动相关性确定(ARD)”(MacKay 等,1994 年 [13];Tipping,2004 年 [26])发生在训练期间,通过边缘似然的复杂性惩罚(Rasmussen 和 Williams,2006 年 [18]),最大限度地减少建议模型中无关成分的影响)。对数边缘似然的复杂性惩罚是一个对数行列式,可以写成协方差矩阵的特征值之和。无关的权重缩小到零,因为它们会增加该协方差矩阵的特征值,但不会显著改善模型拟合。此外,式 (12) 中谱混合核中的指数项,对边缘似然有退火的效果,可以减少频率参数的多峰性,使得更容易天然地优化边缘似然而不会收敛到局部最优。对于完全贝叶斯处理,也可以使用马尔可夫链蒙特卡洛 (Murray & Adams, 2010 [15]) 对谱密度进行积分,而不是使用点估计。但我们想强调的是,谱混合核可以像其他流行核一样成功使用,无需额外的推断工作。
我们与流行的平方指数核 (SE)、Matern 核 (MA)、有理二次核 (RQ) 和周期核 (PE) 进行比较。在每次比较中,我们都试图公平对待这些替代核:根据已经在数据中看到的特征,将超参数初始化为具有高边缘似然且非常拟合数据集的值。相对来说,我们随机初始化谱混合核的参数。所有参与测试的核的训练运行时间都在几分钟的数量级。在这些示例中,与多核学习 (MKL) (Gonen & Alpaydın, 2011 [8]) 进行比较的附加值有限。因为多核学习通常并不用于模式发现,并且经常使用平方指数核的混合。 平方指数核的混合对应于高斯谱密度的尺度混合,并且在 “由多峰非高斯谱密度描述的” 测试数据上表现不佳。
4.1 外推大气二氧化碳
Keeling 和 Whorf(2004 年)记录了夏威夷莫纳罗亚天文台的月平均大气 浓度。数据如 图(1) 所示。前 200 个月用于训练(蓝色),其余 301 个月(≈ 25 年)用于测试(绿色)。
该数据集曾在 Rasmussen & Williams (2006) 中使用过,并经常在高斯过程教程中使用,以展示高斯过程如何成为灵活的统计工具:人类可以查看数据、识别模式,然后将这些模式硬编码到协方差核中. Rasmussen & Williams (2006) 通过查看 图(1a) 中的蓝色和绿色曲线,确定了长期上升趋势、季节性变化以及可能远离周期性衰减的季节性变化、中期不规则性和噪声,并对固定协方差核进行硬编码以代表这些特征中的每一个。
然而,在高斯过程建模的这种观点中,所有有趣的模式发现都是由人类用户完成的,并且高斯过程被简单地用作平滑设备,具有在先验中结合人类推理的灵活性。我们的论点是,这种模式识别也可以通过算法来执行。 为了在不先验地将它们编码到高斯过程中的情况下发现这些模式,我们使用方程式中的频谱混合核。 (12),Q = 10。结果如 图(1a) 所示。
在训练区域,使用每个核的预测本质上是等价的,并且与训练数据完全重叠。然而,与其他核不同的是,SM 核(黑色)能够发现训练数据中的模式并在很长的范围内准确地进行推断。 95% 的高预测密度 (HPD) 区域包含测量期间的真实 测量值。
我们可以在 图(1b) 中的学习对数谱密度中看到谱混合核发现的结构。在 Q = 10 个组件中,只使用了七个——这是训练期间自动确定相关性的一个例子。 图(1b) 是频谱密度混叠的一个很好的例子。频率接近 1.08 的尖峰对应于 12 个月的周期,与 读数的显著年度变化有关。由于 1.08 大于数据的采样率,1/月,它将混叠回 0.08,并且 1/0.08 = 12 个月。由于峰值宽度很小,该模型确信此特征(每年的周期性)应该可以推断出很长一段时间。还有一个频率为 1 的大峰,等于数据的采样率。该峰值对应于均值函数的混叠,也可能与噪声混叠有关。在这些示例中,别名不会影响预测,但会影响结果的可解释性。很容易停止混叠,例如,通过将学习频率限制为小于奈奎斯特频率(数据采样率的 1/2)。出于教学原因——并且因为它不会影响这些示例中的性能——我们在这里没有使用此类限制。最后,我们看到其他峰值对应于 6 个月、4 个月、3 个月和 1 个月的时间段。每个峰的宽度反映了模型对数据中相应特征的不确定性。在红色部分,我们显示了学习的平方指数(SE)核的频谱密度,它错过了许多使用谱混合核识别为重要的频率。
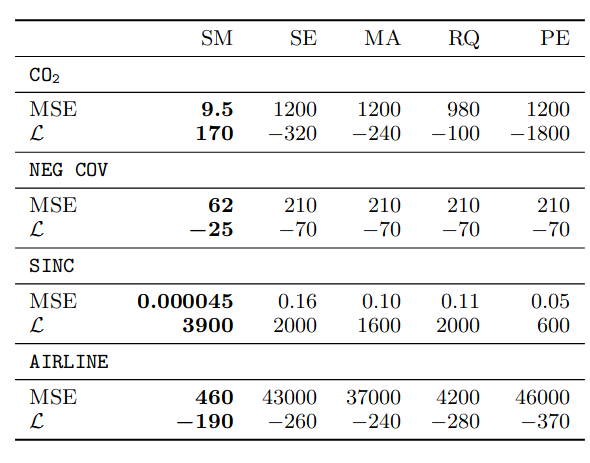
所有平方指数(SE)核都具有以零为中心的高斯谱密度。由于以原点为中心的高斯混合对许多密度函数的近似值很差,因此平方指数(SE)核的组合具有有限的表达能力。事实上, 图(1b) 中的谱混合核学习到的谱密度是高度非高斯分布的。使用 SM、SE、MA、RQ 和 PE 核的测试预测性能在表 1 中的 标题下给出。

图 1. Mauna Loa 浓度。 a) 预测二氧化碳。训练数据为蓝色,测试数据为绿色。使用谱混合核进行的平均预测为黑色,灰色阴影为平均值的 2 个标准偏差(预测质量的 95%)。使用 Matern (MA)、平方指数 (SE)、有理二次函数 (RQ) 和周期核 (PE) 的预测分别以青色、红色虚线、品红色和橙色表示。 b) 学习到的谱混合和平方指数核的对数谱密度分别为黑色和红色。

图 2. 恢复流行的相关函数(归一化核),其中 τ = x − x’。数据背后的真实相关函数为绿色,SM、SE 和经验相关函数分别为黑色虚线、红色和洋红色。数据由 a) Mate rn 核和 b)有理二次(RQ)和周期核的总和生成。
4.2 恢复流行核
SM 类核包含许多固定核,因为高斯混合可用于构建范围广泛的光谱密度。即使混合成分数量很少,例如 ,SM 核也可以接近恢复 Rasmussen & Williams (2006) 中列出的流行固定核。
作为示例,我们首先从具有自由度 的 Mat 核的一维高斯过程中采样 个点:
其中 且 。与具有平方指数核的高斯过程函数相比,使用此 Matern 核的高斯过程的样本函数远不如高斯过程函数平滑(只能一次微分)。
我们尝试通过训练 的谱混合核来重建数据底层的核。训练后,仅使用 个组件。使用经过训练的谱混合核,数据的对数边缘似然(已集成高斯过程)为 ,而生成数据的 Matern 核的对数边缘似然为 。在 式(5) 中训练平方指数(SE)核给出 的对数边缘似然。
图(2a) 显示了学习的谱混合相关函数4,与生成的 Matern 相关函数、经验自相关函数和学习的平方指数相关函数的比较。尽管在地质统计学中经常用于指导高斯过程核(和参数)的选择(Cressie,1993),但经验自相关函数往往不可靠,尤其是在数据量小(例如,)和高滞后(对于 )。在 图(2a) 中,经验自相关函数是不稳定的,并且与 的 Matern 核不相似。此外,平方指数核无法捕获 Mat 核的重尾,无论其长度尺度如何。即使谱混合核是无限可微的,它也可以非常接近有限可微的过程,因为高斯混合可以非常接近这些过程的谱密度,即使只有少量的分量,如 图(2a) 所示。
接下来,我们在 Rasmussen & Williams (2006) 中重建有理二次核 (RQ) 和周期核 (PE) 的混合:
式(14) 中的有理二次核被导出为具有不同长度尺度的平方指数核的尺度混合。 式(15) 中的标准周期核是通过 式(5) 中的平方指数核映射二维变量 得到的。 式(14) 和 式(15) 中有理二次(RQ)和 PE 核的推导在 Rasmussen & Williams (2006) 中。 Abrahamsen (1997) 也讨论了有理二次核和物质核。我们从核为 、、、、 的高斯过程中采样 个点。
我们使用 的谱混合核重建采样过程的核函数,结果如 图(2b) 所示。有理二次(RQ)核的重尾由两个具有大周期(基本上是非周期性)的分量以及一个短长度尺度和一个大长度尺度的分量建模。第三个分量的长度尺度相对较短,周期为 。 个样本点中没有足够的信息来证明使用超过 个分量是合理的,因此谱混合核中的第四个分量没有效果,通过边缘可能性的复杂性惩罚。经验自相关函数在某种程度上捕捉了数据的周期性,但明显低估了相关性。平方指数核学习长尺度:由于平方指数(SE)核与真正的生成核高度错误指定,因此数据被解释为噪声。

图 3. 负协方差。 a) 具有负协方差的离散时间自回归 (AR) 序列的观察结果。 b)谱混合学习核以黑色显示,而 AR 系列的真实核以绿色显示,。 c) 学习到的谱混合核的谱密度为黑色。
4.3 负协方差
标准机器学习高斯过程参考 Rasmussen & Williams (2006) 中的所有平稳协方差函数在任何地方都是正的,包括周期核 。虽然正协方差通常适用于插值,但捕获负协方差对于推断模式至关重要:例如,线性趋势具有长程负协方差。我们通过从简单的 AR(1) 离散时间高斯过程中采样 个点来测试谱混合核学习负协方差的能力:
其核为:
式 (16) 中的过程如 图(3a) 所示。这个过程遵循振荡模式,每 个单位系统地切换状态,但不是周期性的并且具有长范围协方差:如果我们只查看每个第二个数据点,则结果过程将变化得相当缓慢和平稳。
我们在 图(3b) 中看到,学习到的谱混合协方差函数准确地重构了真实的协方差函数。 图(3c) 中的频谱密度显示频率为 或周期为 时的尖峰。此特征表示过程在每 个单位时从正向负振荡的趋势。在这种情况下 ,但在训练中自动确定相关性后,只使用了 个组分。使用谱混合核,我们预测提前 个单位,并与表 1 (NEG COV) 中的其他核进行比较。
4.4 发现 Sinc 模式
sinc 函数定义为 。我们创建了一个组合三个 sinc 函数的模式:
这是一个复杂的振荡模式。仅给定 图(4a) 中所示的点,我们希望完成 的模式。与 4.1 节中的 示例不同,人类甚至可能很难从训练数据中推断出缺失的模式。专注于此图、识别特征并填写缺失部分是一个有趣的练习。
请注意,关于原点 、 和 处的峰值以及面向原点的峰值的每一侧存在相消干涉是完全对称的。因此,我们可能期望在 处有一个峰值,并且在 周围有一个对称模式。
如 图(4b) 所示, 的谱混合核从蓝色的 个训练点几乎完美地重建了 区域中的模式。此外,使用谱混合核, 的后验预测质量完全包含 中的真实模式。使用 Matern、SE、RQ 和周期性核的高斯过程能够在 个单位的训练数据内进行合理预测,但完全错过了 中的模式。
图(4c) 显示了学习的谱混合相关函数(归一化核)。对于 ,存在一个局部模式,大致代表单个 sinc 函数的行为。对于 ,有一个重复模式代表一个新的 sinc 函数,每 个单位一个人类可能做出的外推。对于以 为中心的 sinc 函数,我们可能期望每 个单位有更多的 sinc 模式。学到的 Matern 相关函数在 图(4c) 中以红色显示,无法发现数据中的复杂模式,它只是将高相关性分配给附近的点。
图(4d) 显示了谱混合核的(高度非高斯)谱密度,峰值位于 、、、、、、。在这种情况下,仅使用 个组件中的 个。 处的峰值表示周期为 :每 个单位重复一个 sinc 函数。该峰的方差很小,这意味着该方法将在长距离外推该结构。相比之下,平方指数谱密度仅具有以原点为中心的宽峰。表 1 (SINC) 给出了恢复缺失的 个测试点(绿色)的预测性能。

图 4. 发现 sinc 模式。 a) 训练数据以蓝色显示。目标是填充缺失区域 。 b) 训练数据为蓝色,测试数据为绿色。使用谱混合核的预测分布的平均值以黑色虚线显示。使用平方指数、Matern、有理二次核和周期核的预测分布的均值呈红色、青色、品红色和橙色。 c) 学习到的谱混合相关函数(归一化核)以黑色显示,学习到的 Matern 相关函数以红色显示,其中 。 d)谱混合和平方指数(SE)核的对数谱密度分别为黑色和红色。
4.5 航空公司乘客数据
图(5a) 显示了从 1949 年到 1961 年每月记录的航空公司乘客数量(Hyndman,2005 年[9])。仅基于前 96 个月的测量值(蓝色),我们希望预测未来 48 个月(4 年)的航空公司乘客数量;相应的 48 个测试测量值显示为绿色。
这些数据中有几个明显的特征:短期季节性变化、长期上升趋势以及没有白噪声伪影。许多流行的核被迫做出以下两种选择之一:1) 对短期变化建模并忽略长期趋势,以外推为代价。 2) 对长期趋势建模并将较短的变化视为噪声,以插值为代价。
如 图(5a) 所示,与更平滑的平方指数(SE)或有理二次(RQ)核相比,Matern 核更倾向于对短期趋势进行建模,从而导致合理的插值(预测与训练区域中的训练数据几乎相同的值),但外推效果不佳 –快速移动到先验均值,没有学到任何结构来概括数据。平方指数(SE)核插值有些明智,但似乎低估了波峰和波谷的大小,并将数据中的重复模式视为噪声。使用平方指数(SE)核的外推很差。
如 图(5a) 所示,与更平滑的平方指数(SE)或有理二次(RQ)核相比,Matern 核更倾向于对短期趋势进行建模,从而导致合理的插值(预测与训练区域中的训练数据几乎相同的值),但外推效果不佳 –快速移动到先验均值,没有学到任何结构来概括数据。平方指数(SE)核插值有些明智,但似乎低估了波峰和波谷的大小,并将数据中的重复模式视为噪声。使用平方指数(SE)核的外推很差。有理二次(RQ)核是平方指数(SE)核的尺度混合,更能够管理数据中的不同长度尺度,并且比平方指数(SE)核更好地概括长期趋势,但插值较差。
相比之下,SM 核插值很好(与训练区域的数据重叠),并且能够推断出远远超出数据的复杂模式,在数据结束后的几年内捕获真实的航空公司乘客数量,在一个包含 95 的小范围内预测概率质量的百分比。
在为谱混合核指定的 个初始组件中,有 个在训练后使用。 图(5b) 中学习到的频谱密度显示了一个大而尖锐的低频峰值(大约为 )。这个峰值对应于上升趋势,它概括得远远超出数据(小方差峰值),是平滑的(低频率),并且对于描述数据很重要(大的相对权重)。下一个最大峰值对应于 12 个月的年度趋势,这再次概括,但没有达到平滑上升趋势的程度,因为该峰值的方差大于原点附近的峰值。 (3 个月的周期)处的较高频率峰值对应于新季节的开始,这可以解释季节性假期对空中交通的影响。
对这些特征及其属性(频率、方差等)进行更详细的研究可以分离出影响航空公司乘客数量的不太明显的特征。表 1 (AIRLINE) 显示了预测 48 个月的航空公司乘客数量的预测性能

图 5. 预测航空公司乘客数量。 a) 训练和测试数据分别为蓝色和绿色。使用谱混合核的预测分布的均值以黑色显示,均值的 2 个标准差(预测概率质量的 )以灰色阴影显示。使用谱混合核的预测分布的均值以黑色显示。使用平方指数、Matern、有理二次核和周期核的预测分布的均值分别为红色、青色、品红色和橙色。在训练区域中,没有显示谱混合和 Matern 核,因为它们的预测基本上与训练数据重叠。 b)谱混合和平方指数核的对数谱密度分别为黑色和红色。
表 1. 我们比较了所提出的光谱混合 (SM) 核与平方指数 (SE)、矩阵 (MA)、有理二次 (RQ) 和周期 (PE) 核的测试性能。谱混合核始终具有最低的均方误差 (MSE) 和最高的对数似然 (L)。
5 讨论
我们推导出了富有表现力的封闭形式核,并且我们已经证明,当这些核与高斯过程一起使用时,能够发现数据中的模式并在很长变程内进行推断。这些核的简单性是它们最强大的特性之一:它们可以用作流行核(例如平方指数核)的直接替代品,在表现力和性能方面具有主要优势,同时保留简单的训练和推断过程。
高斯过程已证明自己是强大的平滑插值器。我们相信模式发现和外推是贝叶斯非参数方法的一个令人兴奋的新方向,它可以捕获数据中的丰富变化。在这里,我们展示了如何自然地使用贝叶斯非参数模型从少量示例中概括出一种模式。
我们才刚刚开始探索使用这种模式发现方法可以做什么。在未来的工作中,可以使用最近开发的用于高斯过程超参数的高效马尔可夫链蒙特卡罗来积分谱密度(Murray & Adams,2010 [15])。此外,最近的 Toeplitz 方法 (Saatchi, 2011 [undefined]) 也可以应用于谱混合核,以显著加快推断和预测速度。
参考文献
- [1] Abrahamsen, P. A review of Gaussian random fields and correlation functions. Norweigan Computing Center Technical report, 1997.
- [2] Archambeau, C. and Bach, F. Multiple Gaussian process models. arXiv preprint arXiv:1110.5238, 2011.
- [3] Bochner, Salomon. Lectures on Fourier Integrals.(AM42), volume 42. Princeton University Press, 1959.
- [4] Chatfield, C. Time Series Analysis: An Introduction. London: Chapman and Hall, 1989.
- [5] Cressie, N.A.C. Statistics for Spatial Data (Wiley Series in Probability and Statistics). WileyInterscience, 1993.
- [6] Damianou, A.C. and Lawrence, N.D. Deep Gaussian processes. arXiv preprint arXiv:1211.0358, 2012.
- [7] Durrande, N., Ginsbourger, D., and Roustant, O. Additive kernels for Gaussian process modeling. arXiv preprint arXiv:1103.4023, 2011.
- [8] Gonen, M. and Alpaydın, E. Multiple kernel learning algorithms. Journal of Machine Learning Research, 12:2211–2268, 2011.
- [9] Hyndman, R.J. Time series data library. 2005.
- [10] Keeling, C. D. and Whorf, T. P. Atmospheric CO2 records from sites in the SIO air sampling network. Trends: A Compendium of Data on Global Change. Carbon Dioxide Information Analysis Center, 2004.
- [11] Kostantinos, N. Gaussian mixtures and their applications to signal processing. Advanced Signal Processing Handbook: Theory and Implementation for Radar, Sonar, and Medical Imaging Real Time Systems, 2000.
- [12] MacKay, David J.C. Introduction to Gaussian processes. In Christopher M. Bishop, editor (ed.), Neural Networks and Machine Learning, chapter 11, pp. 133–165. Springer-Verlag, 1998.
- [13] MacKay, D.J.C. et al. Bayesian nonlinear modeling for the prediction competition. Ashrae Transactions, 100(2):1053–1062, 1994.
- [14] McCulloch, W.S. and Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bulletin of mathematical biology, 5(4):115–133, 1943.
- [15] Murray, Iain and Adams, Ryan P. Slice sampling covariance hyperparameters in latent Gaussian models. In Advances in Neural Information Processing Systems 23, 2010.
- [16] Neal, R.M. Bayesian Learning for Neural Networks. Springer Verlag, 1996.
- [17] Rasmussen, Carl Edward. Evaluation of Gaussian Processes and Other Methods for Non-linear Regression. PhD thesis, University of Toronto, 1996.
- [18] Rasmussen, Carl Edward and Williams, Christopher K.I. Gaussian processes for Machine Learning. The MIT Press, 2006.
- [19] Rosenblatt, F. Principles of Neurodynamics. Spartan Book, 1962.
- [20] Rumelhart, D.E., Hinton, G.E., and Williams, R.J. Learning representations by back-propagating errors. Nature, 323(6088):533–536, 1986.
- [21] Saatchi, Yunus. Scalable Inference for Structured Gaussian Process Models. PhD thesis, University of Cambridge, 2011.
- [22] Salakhutdinov, R. and Hinton, G. Using deep belief nets to learn covariance kernels for Gaussian processes. Advances in Neural Information Processing Systems, 20:1249–1256, 2008.
- [23] Stein, M.L. Interpolation of Spatial Data: Some Theory for Kriging. Springer Verlag, 1999.
- [24] Steyvers, M., Griffiths, T.L., and Dennis, S. Probabilistic inference in human semantic memory. Trends in Cognitive Sciences, 10(7):327–334, 2006.
- [25] Tenenbaum, J.B., Kemp, C., Griffiths, T.L., and Goodman, N.D. How to grow a mind: Statistics, structure, and abstraction. Science, 331(6022): 1279–1285, 2011.
- [26] Tipping, M. Bayesian inference: An introduction to principles and practice in machine learning. Advanced Lectures on Machine Learning, pp. 41–62, 2004.
- [27] Wilson, A.G. and Adams, R.P. Gaussian process kernels for pattern discovery and extrapolation supplementary material and code. 2013.
- [28] Wilson, Andrew G., Knowles, David A., and Ghahramani, Zoubin. Gaussian process regression networks. In Proceedings of the 29th International Conference on Machine Learning (ICML), 2012.
- [29] Wilson, Andrew Gordon, Knowles, David A, and Ghahramani, Zoubin. Gaussian process regression networks. arXiv preprint arXiv:1110.4411, 2011.
- [30] Yuille, A. and Kersten, D. Vision as Bayesian inference: analysis by synthesis? Trends in Cognitive Sciences, 10(7):301–308, 2006.





