无监督之聚类与降维任务--近邻嵌入方法(从LLE到t-SNE)
无监督学习Neighbor Embedding近邻嵌入–从LLE 到 T-SNE
2019-09-28
参考资料:李宏毅机器学习(2016);
Neighbor Embedding近邻嵌入不同于PCA,实际上是一种非线性的降维方法,本文对三种常用的近邻嵌入算法做简单的介绍。
概念:流形学习(Manifold Learning)
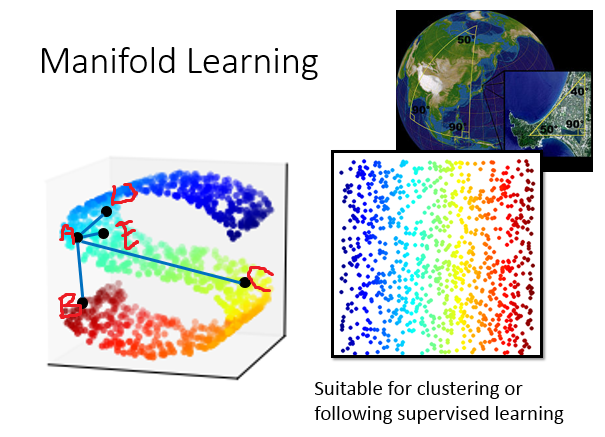
流形学习的目的抽象的来说就是寻找高维空间的低维规律,即样本点的分布其实可能是在低维的一个空间里,只是被扭曲被塞到高维空间里面。最常用的举例就是地球,地球的表面就是一个manifold(一个二维的平面,被塞到一个三维的空间里面)。在manifold里面只有很近距离的点,(欧式距离)Euclidean distance才会成立,如果距离很远的时候,欧式距离不一定成立。如在图中,a点计算离d,e两点的欧式距离都很近,这符合我们的直觉,但是同样根据欧式距离,a点距离b点比距离c点更近,但事实上如果我们把“S”形的数据点分布摊平展开,可能直觉上a点距离b点比a点距离点更加远。
所以流形计算要做的事情是把类似于图中“S”型的高维分布在低维度空间进行展开。展开的好处就是:把这个塞到高维空间里的manifold摊平以后,我们就可以在这个manifold上面用Euclidean distance来计算样本之间的距离,这会对接下来你要做supervised learning都是有帮助。
下面依次介绍几中近邻嵌入的降维方法。
Locally Linear Emedding(LLE)局部线性嵌入
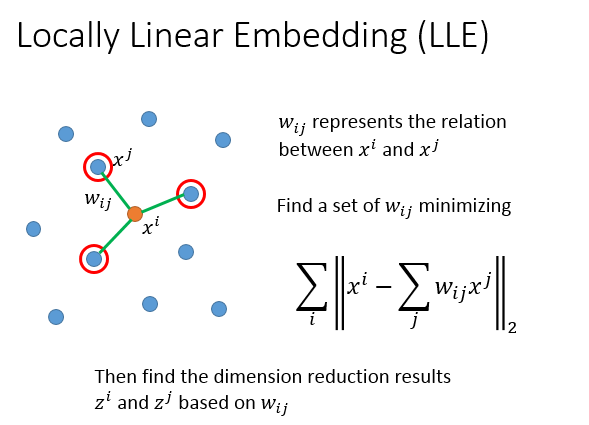
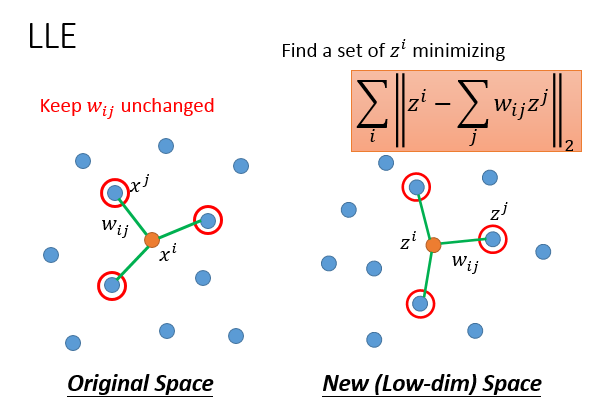
对于样本空间的任意一个样本点,x^ix**i,存在k个neighbor叫做x^jx**j(“局部”),满足假设条件每一个x^ix**i 都可以用它的neighborx^jx**j乘以关系权重w_{ij}wij以后组合而成(“线性”),w_{ij}wij可以通过优化算法,求解最小化以下公式求得,也就是对所有x^ix**i减掉w_{ij}wij乘以x^jx**j求和的L2-Norm是越接近越好。
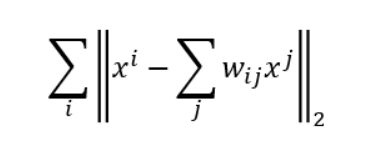
最后一步也就是降维,基于以上计算求得的w_{ij}wij,在w_{ij}wij不变的前提的,通过优化算法,把原来的x^ix**i,x^jx**j统统转成维度更低的z^iz**i,z^jz**j。
拉普拉斯特征映射(Laplaciain Eigenmaps)
概念
- Smoothness Assumption
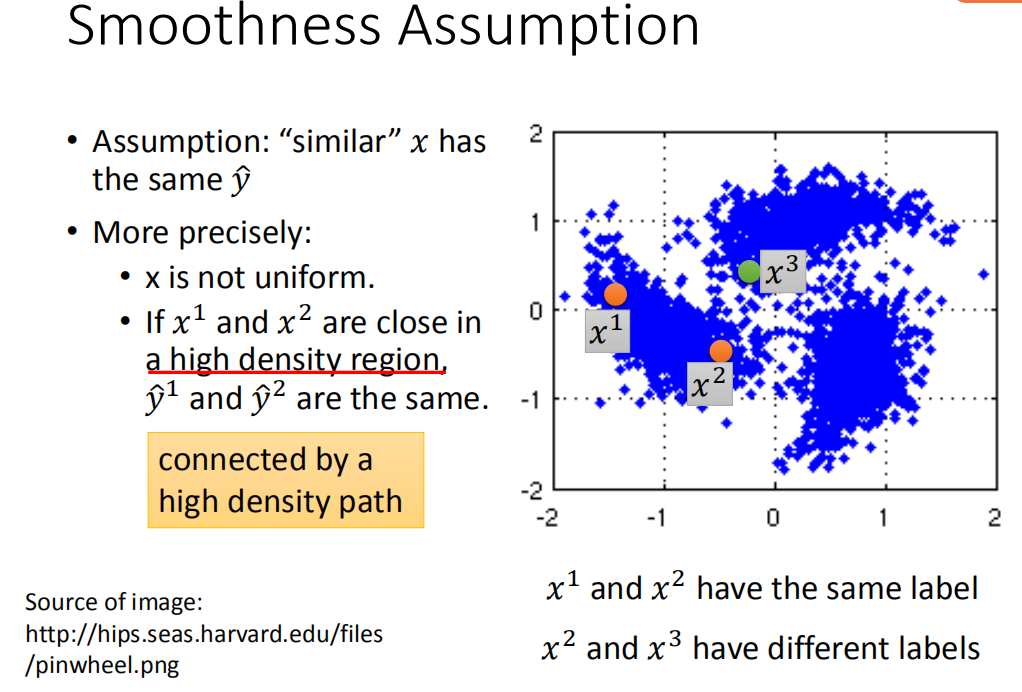
Smoothness Assumption的大概内容介绍如下图,简单的说就是如果x的分布是不平均的,它在某些地方是很集中,某些地方又很分散。如果x_1x1,x_2x2在高密度区域(high density region)距离很接近的话,他们的标签y^1y1,y^2,yy2,y才会是是很像的。(反面例子是x_2x2和x_3x3) - 拉普拉斯矩阵(graph Laplacian)
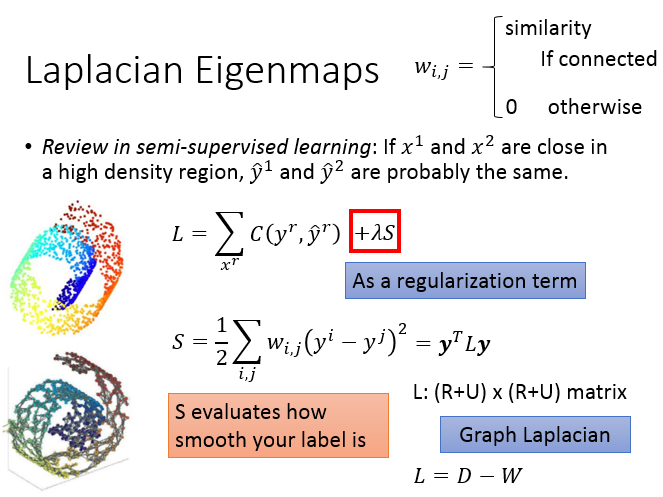
拉普拉斯矩阵(graph Laplacian)),也称为基尔霍夫矩阵, 是表示图的一种矩阵。给定一个有n个顶点的图G=(V,E) ,其拉普拉斯矩阵被定义为:L=D-W,其中D为图的度矩阵(各个顶点的度构成的对角矩阵),W为图的邻接矩阵(表示各个顶点相互连接关系的矩阵,取值为0,1)。
拉普拉斯特征映射是用局部的角度去构建数据之间的关系。具体来讲,拉普拉斯特征映射是一种基于图的降维算法,它希望相互间有关系的点(在图中相连的点)在降维后的空间中尽可能的靠近,从而在降维后仍能保持原有的数据结构,即同样尽可能的靠近(Smoothness Assumption)。
拉普拉斯特征映射的目标函数,相当于有监督学习的unlabel data项,也就是正则项。S这一项等于y^iy**i跟y^jy**j 之间的距离 乘以w_{i,j}w**i,j,w_{i,j}w**i,j意思是如果两个顶点它们在图上是相连的,w_{i,j}w**i,j是它们的相似程度;在图上没有相连就是0。如果x^ix**i跟x^jx**j接近的话,那w_{i,j}w**i,j 就是一个很大的值。根据上面拉普拉斯矩阵的概念,这个S还可以写成S=y^TLyS=yTL**y(L是graph laplacian,L=D-W)
同时,我们还需要施加一个限制条件,Y^TDY=IYTD**Y=I来保证问题有解,防止映射后的样本点被压缩到一个维度比m还小的空间中去(假设映射后的z向量的维度为m),比如下图的思考,在minimize S的时候,如果选择z^i=z^j=0,S=0z**i=z**j=0,S=0,优化过程会直接直接终止,这并不是我们想要的结果。

T-分布随机领域(t-SNE)

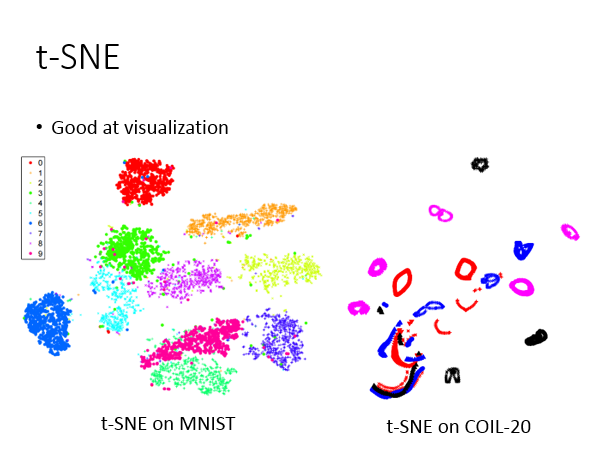
前述算法中,求解优化思路都是假设映射前后的相邻点都要尽可能接近,而不是不相似的点尽可能分开,这样就会导致一个降维中经常出现的问题,即拥挤问题(Crowding Problem)。如上图,LLE在MNIST上会遇到这样的情形:它确实会把同一个class聚集在一起,但它没有防止不同class的点不要叠成一团。

t-SNE的降维其实和上述算法仍然类似,把原来的样本点映射成低维向量z。在原来的空样本间上面,我们会计算所有样本对的相似度(同样的计算过程应用在低维向量z的样本空间中)。上图中P和Q的计算实际上是在做了一个normlization,通过scale转化,值会介于0-1之间。
那怎么衡量两个空间分布之间的相似度呢?就是KL距离。所以我们要做的事情就是找一组z,它可以做到,x^ix**i的样本分布跟z^iz**i样本分布的KL距离越小越好,然后汇总相加所有的样本点,使得上图中的L越小越好。
t-SNE的计算过程,会涉及到计算所有点的similarity,所以它的运算有点大。在样本量比较多的时候,t-SNE比较麻烦。第一个常见的做法是:你会先做降维,比如说:你原来的维度很大,你不会直接从很高的维度直接做t-SNE,因为你这样计算similarity时间会很长,你通常会先用PCA做将降维,降到50维,再用t-SNE降到2维,这个是比较常见的做法。
如果给t-SNE一个训练数据中没有新的样本点,没办法做到直接降维。t-SNE只能够你先给它一大群x,帮你把每个x的z先找出来,但你找完这些z以后,你再给它一个新的x,你要重新跑一遍这一整套演算法,所以就很麻烦。通常的应用场景是,有一大堆的高维度x的样本点,你想要知道它在二维空间的分布是什么样子,用t-SNE进行可视化,往往会有不错的效果。
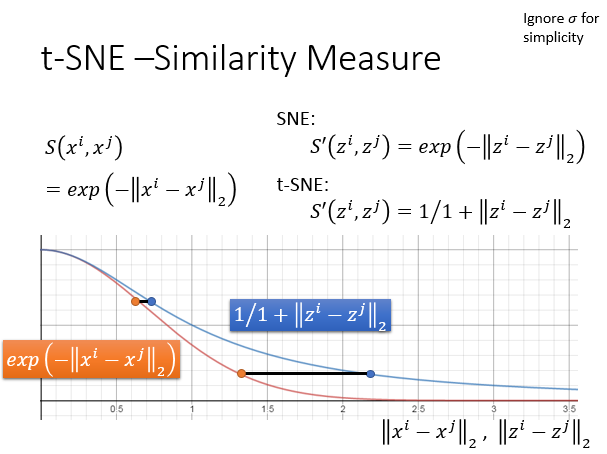
t-SNE算法的核心在于相似度计算上的创新,在原来的样本点空间上面,计算相似度是计算x^ix**i,x^jx**j之间的欧式距离,取一个负号,再取exponent,这种方法比较好,因为它可以确保说只有非常相近的点才有值,只要距离一拉开,similarity就会变得很小。 在t-SNE之前,有一个方法叫做SNE:对于降维以后向量z,它选择测量方式跟原来的样本是一样的。t-SNE神妙的地方在:降维以后的空间中,它选择的测量方式跟原来的样本空间是不一样的,它选择是t distribution变换的其中一种(S^{'}(z^i,z^j)=\frac{1}{1+||z^i-z^j||_2}(S′(z**i,z**j)=1+∣∣z**i−z**j∣∣21,做完变换过后,原本样本空间中距离相差较大的样本点,在低维度空间中,会被拉得更大。从下图使用t-SNE算法做的降维可视化中就可以看出。