常见概率分布
机器学习和深度学习中常用的概率统计知识
In Bayesian influence, probability distributions are heavily used to make intractable problems solvable. After discussing the normal distribution, we will cover other basic distributions and more advanced ones including Beta distribution, Dirichlet distribution, Poisson Distribution, and Gamma distribution. We will also discuss topics including the Conjugate prior, Exponential family of distribution, and Method of Moments.
1 离散型分布
伯努利分布

The Bernoulli distribution is a discrete distribution for a single binary random variable X ∈ {0, 1} with probability 1-θ and θ respectively. For example, when flipping a coin, the chance of head is θ.

The expected value and the variance for the Bernoulli distribution are:

二项分布
The binomial distribution is the aggregated result of independent Bernoulli trials. For example, we flip a coin N times and model the chance to have x heads.
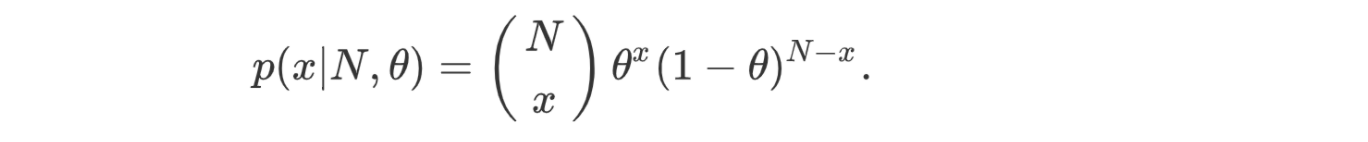

The expected value and the variance for the binomial distribution are:

类别分布
A Bernoulli distribution has two possible outcomes. In a categorical distribution, we have K possible outcomes with probability p₁, p₂, p₃, … and pk accordingly. All these probabilities add up to one.

多项分布
The multinomial distribution is a generalization of the binomial distributions. Instead of two outcomes, it has k possible outcomes. If binomial distribution is corresponding to the Bernoulli distribution, multinomial distribution is corresponding to categorical distribution.

Suppose these outcomes are associated with probabilities θ₁, θ₂, … and θk respectively. We collect a sample of size N and xᵢ represents the count for the outcome i. The joint probability is

The expected value and the variance for the multinomial distribution are:

2 连续型分布
贝塔分布
For a Bernoulli distribution or a binomial distribution, how can we model the value for θ? For example, if a new virus is discovered, can we use a probability distribution to model the infection probability θ?
The beta distribution is a distribution over a continuous random variable on a finite interval of values. It is often used to model the probability for some binary event like θ. The model has two positive parameters α and β that affect the shape of the distribution.

When we have no knowledge about the new virus, we can set α = β = 1 for a uniform distribution, i.e. any possible probability values for θ ∈ [0, 1] are equally likely. This is our prior.

α = β = 1 for uniform distribution
Then we can apply Bayes inference with the likelihood modeled by a binomial distribution. The posterior will be a beta distribution also with updates on α and β. This becomes the new infection rate distribution given the observed data and acts as the new prior when a new sample is observed.

Mathematical, the beta distribution is defined as:

The beta function B normalized the R.H.S. to a probability distribution.
The definition seems complicated but when it is used in Bayesian inference, the calculation becomes very simple. Let’s say CDC reports x new infections out of N people. Applying the Bayes’ Theorem, the posterior will be:

i.e. we simply add the new positives to α and the new negatives (N-x) to β.
The expected value and variance for the beta distribution are

狄利克雷分布
In the previous Bayesian inference example, the likelihood is modeled by the binomial distribution. We partner it with the beta distribution (prior) to calculate the posterior easily. For a likelihood with the multinomial distribution, the corresponding distribution is the Dirichlet distribution.

Dirichlet distribution is defined as:

This random process has K outcomes and the corresponding Dirichlet distribution will be parameterized by a K-component α.
Similar to the beta distribution, its similarity with the corresponding likelihood makes the posterior computation easy.

The expected value and the variance for the Dirichlet distribution are:

泊松分布
Poisson distribution models the probability for a given number of events occurring in a fixed interval of time. It models a Poisson process in which events occur independently and continuously at a constant average rate.

As shown, a binomial distribution can be simplified to the Poisson distribution if the event is relatively rare.

A Poisson process is assumed to be memoryless — the past does not influence any future predictions. The average wait time for the next event is the same regardless of whether the last event happened 1 minute or 5 hours ago.
The expected value and the variance for the Poisson distribution are:

指数分布
The exponential distribution is the probability distribution for the waiting time before the next event occurs in a Poisson process. As shown in the right diagram below, for λ = 0.1 (rate parameter), the chance of waiting for more than 15 is 0.22.

Mathematically, it is defined as:

The expected value and the variance for the exponential distribution are:

狄拉克分布
The Dirac delta distribution (δ distribution) can be considered as a function that has a narrow peak at x = 0. Specifically, δ(x) has the value zero everywhere except at x = 0, and the area (integral) under the peak is 1.

This function is a helpful approximation for a tall narrow spike function (an impulse) or some deterministic value in a probability distribution. It helps us to transform some models into mathematical equations.
伽马分布
The exponential distribution and the chi-squared distribution are special cases for the gamma distribution. The gamma distribution can be considered as the sum of k independent random variables with exponential distribution.

Intuitively, it is the distribution of the wait time for the _k_th events to occur.

Here is the mathematical definition for the gamma distribution.

Depending on the context, the gamma distribution can be parameterized in two different ways.

α (a.k.a. k) parameterizes the shape of the gamma distribution and β parameterizes the scale. As suggested by the Central Theorem, as k increases, the gamma distribution resembles the normal distribution.

As we change β, the shape remains the same but the scale of the x and y-axis change.

The expectation and the variance of the Gamma distribution are:

3 汇总
Here is a recap of some of the probability distributions discussed.

4 共轭先验
As discussed before, if we pair the distribution for the likelihood and the prior smartly, we can turn the Bayesian inference to be tractable.
In Bayesian inference, a prior is a conjugate prior if the corresponding posterior belongs to the same class of distribution of the prior.

For example, the beta distribution is a conjugate prior to the binomial distribution (likelihood). The calculated posterior with the Bayes’ Theorem is a beta distribution also. Here are more examples of conjugate priors.

5 充分统计量
By definition, when a distribution is written in the form of

T(x) is called sufficient statistics.
Here is an example applied to the Poisson distribution.

T(x) sums over _x_ⱼ.
The significance of sufficient statistics is that no other statistic calculated from x₁, x₂, x₃, … will provide any additional information to estimate the distribution parameter θ. If we know T(x), we have sufficient information to estimate θ. No other information is needed. We don’t need to keep x₁, x₂, x₃, … around to build the model. For example, given a Poisson distribution modeled by θ (a.k.a. λ), we can estimate θ by dividing T(x) with n.

6 指数族分布
Normal, Bernoulli, gamma, beta, Dirichlet, exponential, Poisson distribution, and many other distributions belong to a family of distribution called the exponential family. It has the form of

Here are the exponential family forms, represented by h(x), η, T(x), and A, for the binomial and Poisson distribution.

Modified from source
We can convert parameter θ and the natural parameter η from each other. For example, the Bernoulli parameter θ can be calculated from the corresponding natural parameter η using the logistic function.

Here is another example in writing the normal distribution in the form of an exponential family.

What is the advantage of this abstract generalization?
The exponential family provides a general mathematical framework in solving problems for its family of distributions. For example, computing the expected value for the Poisson distribution can be hard.

Instead, all the expected values for the exponential family can be calculated fairly easily for A. As shown on the left below, A’(η) equals the expected value for T(x). Since T(x) = x and λ = exp(η) and A(λ) = λ = exp(η) in the Poisson distribution, we differentiate A(η) to find 𝔼[x]. This equals λ.

This family of distribution has nice properties in Bayesian analysis also. If the likelihood belongs to an exponential family, there exists a conjugate prior that is often an exponential family. If we have an exponential family written as

the conjugate prior parameterized by γ will have the form

The conjugate prior, modeled by γ, will have one additional degree of freedom. For example, the Bernoulli distribution has one degree of freedom modeled by θ. The corresponding beta distribution will have two degrees of freedom modeled by α and β.
Consider the Bernoulli distribution below in the form of the exponential family,

We can define (or guess)

We get

i.e. beta distribution is a conjugate prior to the Bernoulli distribution.
7 最大熵原则
There are possibly infinite models that can fit the prior data (prior knowledge) exactly. The principle of maximum entropy asserts that the probability distribution that best represents a system is the one with the largest entropy. In information theory, the entropy of a random variable measures the “surprise” inherent to the possible outcomes. Under this principle, we avoid applying unnecessary and additional constraints on what is possible, as constraints decrease the entropy of the system.
Many distributions can satisfy the constraints imposed by sufficient statistics. But the one that we may choose is the one with the highest entropy. It can be proven that the exponential family has the maximum-entropy distribution consistent with the given constraints on sufficient statistics.
8 阶矩
A moment describes the shape of a function quantitatively. If the function f is a probability distribution, the zero moment is the total probability (=1), the first moment is the mean. For the 2nd and higher moments, the central moments provide better information about the distribution’s shape. The second central moment is the variance, the third standardized moment is the skewness, and the fourth moment is the kurtosis.
为了定量地描述概率分布的形状,科学家提出了 矩( Moment ) 的概念。矩是一个标量,不同阶的矩大小通常反映了概率分布形状的某一种特性。
如果函数 是随机变量 的概率分布,则:
零阶矩为总概率一阶矩为均值 (Mean),反映了分布的中心位置,定义为 。
在一阶矩基础上,通常采用中心矩的方式来定义其他矩,以便更好地提供分布形状的信息。
一阶中心距显然为二阶中心矩为方差 (Variance),反映了分布的离散度(或反之,聚集程度),定义为
在二阶中心矩基础上,可以对更高阶的矩做归一化处理,得到高阶的标准化矩:
三阶标准化距为偏度 (Skewness),反映了分布的对称程度,定义为 。偏度 时,为对称分布;偏度 时为右偏分布;偏度 时为左偏分布。四阶标准化距为峰度 (Kurtosis),反映了分布中峰值的尖度,定义为
在单变量矩以及中心矩基础上,可以定义两个随机变量 和 之间的 阶混合中心距 。
常用的混合中心矩为(1+1)阶混合中心距,即协方差

The _k_th moment, or the _k_th raw moment, of function f is defined as

This moment is called the moment about zero. But if we subtract x with the mean first, it will be called a central moment.

The _k_th moment equals the _k_th-order derivative of A(η).

9 矩的使用
现在考虑一种场景,根据矩的定义,当概率密度函数 比较简单时(如常见的高斯等分布),有些能够得到矩的解析解。但现实大部分场景中,随机变量的分布是复杂的,通常无法得到解析解,只能通过样本来获得近似的数值解。那么如何通过样本来估计概率分布(模型)的参数呢?或者说,如何用样本分布 对总体分布 建模呢?
有了对矩的认识,我们就可以从样本数据中计算矩,以使两者的充分统计量的期望能够匹配。

Consider a simple zero-centered distribution model f parameterized by θ with T(X)=x.

The first and second theoretical moment is:

Modified from source
The second-order sample moment is:

By letting the sample moment equal to the theoretical moment, we get an estimation of σ (sampled σ) as.

But the integration is not easy in general. But we can use the derivatives of A to compute the moment and solve the distribution parameter. For example, in the gamma distribution, its parameters α and β can be estimated from the sample mean and variance.






