似然与概率的区别
【摘要】“概率” 和 “似然” 这两个术语,在各种文献中使用非常混乱,大多数人可能会觉得它们就是一回事,很难发现/理解它们之间的区别。本文旨在理清 “概率” 和 “似然” 之间的区别,以便更好地理解贝叶斯方法。
“概率” 和 “似然” 之间的区别!
最重要的区别:概率依附于可能的结果;而似然依附于假设。
可能的结果是相互排斥且穷举的。假设我们要求受试者预测 次掷硬币的每一次结果,则只有 个可能的结果( 到 个可能正确的预测),而实际结果将始终是可能的结果中的一个且只有一个。因此,附加到可能结果的概率总和必须为 。
假设与结果不同,既不相互排斥,也不穷举。假设我们测试的对象正确地预测了 个结果中的 个。我也许会假设受试者只是在猜测,但你也许会假设受试者会以略高于机会率的方式正确预测结果。这些假设虽然不同,但它们之间并不相互排斥。因此,你允许你的假设中包括我的假设。在技术术语中表达为:我的假设嵌套在你的假设中。当然,其他人也许会假设测试对象具有超出常人的预测能力,而观察到的结果低估了该测试对象下一次预测正确的概率。还有些人可以完全假设其他事情。人们能够接受的假设是没有限制的,因此无法穷举。
被附加到似然上的假设集合会受到我们想像能力的限制。不过在实践中,我们很少能确信已经想象到了所有可能的假设,我们真正关心的是:估计出实验结果 “对不同假设的相对可能性” 的影响程度。我们通常不会考虑完整的假设集合,因为被附加在似然上的假设本身并没有任何意义;只有相对可能性(即两个似然之间的比率)才有意义。
当人们在通用的编程语言中使用概率分布函数时,概率和似然之间的区别就变得很明显了。在上例中,我们想要的函数是二项分布函数,在常见的编程语言中通常有三个输入参数:成功次数、尝试次数和成功概率。
当使用该函数来计算概率时,假设后两个参数( 尝试次数 和 成功概率)已给定,我们通过遍历第一个参数(即调整可能的 成功次数),找到与 成功次数 相关的概率(图 1 的顶部)。无论给定参数值如何,此概率总和为 。
在计算似然函数时,假设 成功次数(在示例中为 )和 尝试次数()已给定,我们尝试不同 成功概率 值(即现在改变第三个参数,不同的 成功概率 代表了不同假设),来判断哪种假设更符合实际数据,最终获得一个二项似然函数(图 1 的底部)。这是一个反向运行的函数,因此有时将似然称为反向概率。
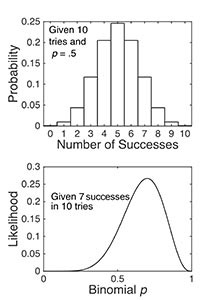
图 1. 二项概率分布函数,在 时尝试 次(上图),二项似然函数,在 次尝试中获得 次成功(下图)。两个图都是使用二项分布函数计算的。在上面的图中,我改变了可能的结果;在下部,我改变了参数 p 的值。概率分布函数是离散的,因为只有 个可能的实验结果(因此是条形图)。相比之下,似然函数是连续的,因为概率参数 p 可以取 到 之间的任何无限值。上图中的概率总和为 ,而下图中连续似然函数的积分远远小于 ;也就是说,似然总和不等于 ,因为假设并没有得到穷举。
二项似然函数传达的信息非常直观:鉴于我们在 次尝试中观察到了 次成功,我们从中得出的二项式分布的概率参数(来自该主题的成功预测的分布)不太可能是 ;它更有可能是 ,但 的值绝非不可能。 时的可能性(即 )与 时的可能性(即 )的比率仅为 。换句话说,鉴于这些实验结果( 次尝试 次成功),受试者长期成功率为 的假设仅是受试者长期成功率为 的假设的两倍多一点。
总之,似然函数是贝叶斯基础。要理解似然,您必须清楚概率和似然之间的区别:
概率依附于结果;似然依附于假设。在数据分析中,“假设” 通常会是某个分布的均值参数的一个可能值或一组可能值,如上例所示。
概率所依附的结果是互斥且穷举的;似然所依附的假设通常两者都不是;而且某个假设的范围可能包括另一个假设中的点。
为了在给定实验结果的情况下确定两个假设中的哪一个更有可能,我们应当考虑它们似然的比值,即相对似然比,也被称为 “贝叶斯因子”。
