🔥 深度克里金法（DeepKriging）

【摘 要】 在空间统计中，利用空间依赖性来预测未观测位置的空间过程值是一个共同的目标。克里金法使用协方差函数（或变异函数）提供了最佳线性无偏预测器，并且通常与高斯过程相关。但当考虑非高斯数据或分类数据的非线性预测问题时，克里金预测不再是最优的，而且其方差往往过于乐观。尽管深度神经网络 (DNN) 广泛用于分类和预测任务，但对具有空间依赖性的数据尚缺乏深入研究。在本文工作中，我们提出了一种用于空间预测的新型 DNN 结构，通过在 DNN 之前添加一个具有基函数的空间坐标嵌入层来捕获空间依赖性。理论和模拟研究结果表明：所提出的 DeepKriging 方法与高斯情况下的克里金法有直接联系。由于该方法提供的是非线性预测，因此相较于克里金法而言，新方法对于非高斯和非平稳数据会有更多优势，也具有更小的近似误差。DeepKriging 不需要对协方差矩阵进行运算，因此可扩展到大型数据集。当具有足够多隐神经元时，它能够根据模型容量提供最佳预测。我们进一步探讨了在不假设任何数据分布的情况下，基于密度预测来量化预测不确定性的可能性。最后，我们将该方法应用于预测整个美国大陆的 PM2.5 浓度。

【原 文】 Chen, W. et al. (2022) ‘DeepKriging: Spatially Dependent Deep Neural Networks for Spatial Prediction’. arXiv. Available at: http://arxiv.org/abs/2007.11972 (Accessed: 15 November 2022).

1 简介

空间预测是空间和时空统计的核心。它旨在通过考虑感兴趣区域的空间依赖性来预测未观测位置的空间过程值。空间预测的传统应用是在地质和环境科学领域（Cressie，2015 ^[11]），目前已经扩展到了生物科学、计算机视觉、经济学和公共卫生等其他领域（Anselin，2001 ^[3]；Austin，2002 ^[4]； Waller 和 Gotway，2004 年 ^[53]；Franchi 等，2018 年 ^[21]）。

空间预测方法主要基于最佳线性无偏预测 (BLUP)，也称为克里金法（Matheron，1963 年 ^[37]）。克里金预测是观测数据的加权平均，其中权重由随机过程的空间协方差函数（或变异函数）确定。在高斯分布假设下，克里金法还能够提供完整的预测分布（即预测均值和方差）。克里金法需要估计空间协方差函数，并且通常会作出二阶或本征平稳假设。

但是，真实世界中的物理过程往往是非高斯和非平稳的。例如：

• 非高斯分布：风速和细颗粒物 (PM2.5) 暴露物的数据呈正值右偏，有时呈重尾状（Hennessey Jr，1977 年 ^[26]；Adgate 等，2002 年 ^[1]）
• 空间变方差：空间协方差通常随时间和空间发生变化，例如，城市与农村地区（Sampson 等，2013 年^[49]）。
• 非高斯过程和非平稳性：尽管克里金法对于某些参数化的非高斯过程（Xu 和 Genton，2017 年 ^[56]；Rimstad 和 Omre，2014 年 ^[48]）和某些非平稳的协方差结构（Fuentes，2002 年 ^[23]；Paciorek 和 Schervish，2004 年 ^[43]；Li 和 Sun, 2019 ^[36]）可以得出最佳线性预测，但用于更普适空间过程的克里金法仍然是一个悬而未决的问题。
• 可扩展性：克里金法的一个缺点是其对于大型空间数据集的计算量太大，因为它涉及计算 $N \times N$ 协方差矩阵的求逆，其中 $N$ 是观测位置的数量（Heaton 等，2019 ^[25]），并且基于典型的 Cholesky 分解方法，计算需要 $\mathcal{O}(N^3)$ 时间和 $\mathcal{O}(N^2)$ 内存复杂度。

最近，深度学习或深度神经网络 (DNN) 已成为广泛应用的强大预测工具，特别是在计算机视觉和自然语言处理方面（LeCun 等，2015 年 ^[33]）。 DNN 对于具有复杂特征（例如非线性和非平稳性）的预测是有效的，并且它们在使用 GPU 分析海量数据集时计算效率高（Najafabadi 等，2015 年 ^[39]）。因此，有望将 DNN 应用于空间预测。然而，经典的 DNN 无法适当地结合空间依赖性。使用神经网络进行空间预测的应用通常仅将空间坐标作为特征（Cracknell 和 Reading，2014 ^[9]），这可能还不够。最近，据称卷积神经网络 (CNNs, Krizhevsky 等 2012 ^[32]) 通过相关滤波器成功捕获了图像处理中的空间和时间依赖性。然而，该框架是为具有大特征空间的应用而设计的，并且通常需要大量训练标签作为基本事实，这不适用于许多空间预测问题，其中只有原位和稀疏观测可用。

为了解决上述问题，我们开发了一种有效的空间预测深度神经网络：

• 在空间预测任务中，建立了 DNN 和克里金法之间的直接联系；
• 通过一组基函数对空间依赖性进行建模；
• 不需要矩阵运算，对大数据集而言具有可扩展性；
• 提供对协变量或观测值的非线性预测；
• 具有高斯过程表示，带来比单纯用坐标作为特征更灵活的空间协方差结构；
• 适用于不同的数据场景，例如非高斯或非平稳数据；
• 在不假设任何数据分布的情况下，通过预测密度函数隐式地测量不确定性。

我们将该方法称为 “深度克里金（DeepKriging）”，目的是使用深度神经网络来实现最佳空间预测，类似于 Kriging (Cressie, 1990 ^[10]) 的原始应用。我们还进行了模拟研究，并将方法应用于美国大陆的 PM2.5 浓度数据，以显示 DeepKriging 与克里金法和其他朴素 DNN 方法相比的性能。

我们论文的其余部分组织如下。

• 第 2 节 介绍了我们的 DeepKriging 方法的构造。
• 第 3 节 提供了其理论性质。
• 第 4 节 介绍了一些模拟研究，以展示 DeepKriging 的性能。
• 第 5 节 应用 DeepKriging 预测美国的 PM2.5 浓度。
• 第 6 节 总结了主要结果并提出了未来工作的方向。

2. 方法

2.1 空间预测中的深度学习

假设 $\mathbf{z} = \{z(\mathbf{s}_1),\ldots , z(\mathbf{s}_N )\}^T$ 是真实空间过程 $\{Y(\mathbf{s}) : \mathbf{s} \in \mathcal{D}\}$, $\mathcal{D} \subset \mathbb{R}^d$ 在 $N$ 个空间位置处观测得到的测量值。空间预测的目标是在未观测位置 $\mathbf{s}_0$ 处，利用已观测数据 $\mathbf{z}$ 找到真实过程的最佳预测 $\hat{Y}^{opt}(\mathbf{s}_0)$。在决策论中，$\hat{Y}^{opt}(\mathbf{s}_0)$ 应当是期望损失最小或风险函数最小的那个结果 (DeGroot, 2005 ^[14])：

$$\begin{align*} \hat{Y}^{opt}(\mathbf{s}_0) &= \arg \min_{\hat{Y}} \mathbb{E}\{L(\hat{Y}(\mathbf{s}_0), Y(\mathbf{s}_0))\} \\ &= \arg \min_{\hat{Y}} R(\hat{Y}(\mathbf{s}_0), Y(\mathbf{s}_0)) \tag{2.1} \end{align*}$$

其中 $L(·,·)$ 是损失函数，$R(·,·)$ 是风险函数。

在均方误差 (MSE) 损失情况下，最优预测器是 $Y$ 在 $\mathbf{s_0}$ 处的条件均值： $\hat{Y}^{opt}(\mathbf{s}_0) = \mathbb{E}\{Y(\mathbf{s}_0) | \mathbf{z}\}$。此预测器具有多个良好性质，具有在正则假设下的无偏性和渐近正态性（Lehmann 和 Casella，2006 ^[35]）。特别是：

• 如果 $Y(\mathbf{s}_0)$ 和 $\mathbf{z}$ 服从联合高斯分布（即高斯过程），则条件均值 $\mathbb{E}\{Y(\mathbf{s}_0) | \mathbf{z}\}$ 是观测值 $\mathbf{z}$ 的线性组合；
• 即使 $Y(\mathbf{s}_0)$ 和 $\mathbf{z}$ 不服从联合高斯分布，通过高斯假设获得的条件均值也仍然是最佳线性无偏预测 (BLUP)，即克里金法。

不过，如前所述，Kriging 预测器对于非高斯数据并非最优，而且对于大数据缺乏可扩展性。

在本文工作中，我们使用深度学习方法，通过神经网络的输出来近似 式（2.1） 中的最优预测器 $\hat{Y}^{opt}(\mathbf{s}_0)$。最佳神经网络预测器由能够使损失函数或风险最小的函数 $f^{opt}_{NN} (\mathbf{s}_0) = \arg \min_{f_{NN}} R \{f_{NN}(\mathbf{s}_0), Y(\mathbf{s}_0)\}$ 给出，其中 $f_{NN}(·) \in \mathcal{F}$ 是在函数空间 $\mathcal{F}$ 中能够由神经网络族表示的任意函数，而 $f^{opt}_{NN} (·)$ 则是 $\mathcal{F}$ 中能够最小化特定风险 $R(·,·)$ 的最佳函数。

该神经网络的输入是相关协变量 $\mathbf{x}(\mathbf{s}_0)$ 和/或 $\mathbf{s}_0$ 处的某些特征。通常，我们将神经网络函数写成具有未知参数 $\boldsymbol{\theta}$ 的参数化形式： $f_{NN}(\mathbf{s};\boldsymbol{\theta})$，其中 $\boldsymbol{\theta}$ 包括神经网络中的权重和偏差。请注意，最佳神经网络预测器 $f^{opt}_{NN}(\mathbf{s}_0)$ 实际上是无法实现的，因为并不存在 $Y(\mathbf{s}_0)$ 的真实值。所以，在实际工作中，都是通过最小化训练集 $\mathbf{z}$ 上的经验损失函数来得到参数估计 $\hat{\boldsymbol{\theta}}$，然后将其用于新输入点并实现近似预测 $\hat{Y}_{NN}(\mathbf{s}) = f_{NN}(\mathbf{s}; \hat{\boldsymbol{\theta}})$（Goodfellow 等，2016 ^[24]）。也就是说，最终预测为 $f_{NN}(\mathbf{s}_0; \hat{\boldsymbol{\theta}})$，其中：

$$\hat{\boldsymbol{\theta}} = \arg \min_{\boldsymbol{\theta}} \frac{1}{N} \sum^{N}_{n=1} L\{f_{NN}(\mathbf{s}_n; \boldsymbol{\theta}), z(\mathbf{s}_n)\} \tag{2.2}$$

将上述经典神经网络框架直接应用于空间预测至少存在两个方面问题：

• 空间依赖性问题：经典的深度神经网络并不考虑空间依赖性问题（本文通过空间嵌入来解决）；
• 样本稀疏性问题：空间预测通常将某一次观测数据视为空间过程的一次实验（即一个样本点，而不是很多个样本点，尽管观测的位置可能很多），因此尽管观测数据很多，但实际上存在样本稀疏性问题。这不同于常见的、具有大规模样本的神经网络应用。

具体来说，假设空间过程 $Y (\mathbf{s})$ 由 $Y(\mathbf{s}) = \mathbf{x}(\mathbf{s})^T \boldsymbol{\beta} + ν(\mathbf{s})$ 建模，其中 $\mathbf{x}(\mathbf{s}) \in \mathbb{R}^P$ 是 $P$ 个已知协变量的向量过程， $\boldsymbol{\beta}$ 是系数向量，$ν(\mathbf{s})$ 是空间相关的零均值随机过程，具有 协方差函数： $\operatorname{Cov}(ν(\mathbf{s}), ν(\mathbf{s}^{\prime})) = C(\mathbf{s},\mathbf{s}^{\prime})$ （注：协方差函数不一定是平稳的）。在传统神经网络中，一般假设 $Y(\mathbf{s})$ 以特征 $\mathbf{x}(\mathbf{s})$ 为条件，并且样本点之间独立同分布；但此假设在空间预测中并不成立，因为尽管特征（或协变量） $\mathbf{x}(\mathbf{s})$ 能够对 $Y(\mathbf{s})$ 中的均值结构作出贡献，而 $ν(\mathbf{s})$ 仍然是一个具有空间相关性的空间过程，也就是说，除了 $\mathbf{x}(\mathbf{s})$ 之外，仍然需要对空间依赖性进行建模。

为了将空间信息纳入考虑，最自然的方法是向输入的特征集合中添加坐标信息（例如，经度和纬度），将 $ν(\mathbf{s})$ 作为 $\mathbf{s}$ 的一个函数来学习（Cracknell 和 Reading，2014 年 ^[9]）。这样的话，调整后的神经网络输入变为了 $\mathbf{x}^{adj}(\mathbf{s}) = (\mathbf{x}(\mathbf{s})^T , \mathbf{s})^T$ 。但这对扩大输入的特征空间并没有太大帮助，因为通常空间坐标的维度 $d \leq 3$，而我们希望特征空间能够足够大。此外，此时神经网络可能效率并不高，因为如果真实函数离线性很远，则可能需要付出巨大的努力才能使神经网络实现很好的逼近。例如，在高斯假设和 MSE 损失下的最优预测器是 Kriging 预测器，它在特征 $\mathbf{x}(\mathbf{s})$ 上是线性的，但基于坐标 $\mathbf{s}$ 的协方差函数显然是非线性的。

深入研究 Kriging 预测的形式可能会给我们一些关于将空间依赖性纳入神经网络的提示。

假设 $\mathbf{z}$ 是从广义加性模型观测到的：$Z(\mathbf{s}) = Y (\mathbf{s}) + \varepsilon(\mathbf{s})$，其中 $Y(\mathbf{s}) = \mathbf{x}(\mathbf{s})^T \boldsymbol{\beta} + ν(\mathbf{s})$ 如上定义，并且 $\varepsilon(\mathbf{s})$ 是一个白噪声过程，称为块金效应，具有零均值和方差 $\sigma^2(\mathbf{s})$，由测量误差和精细尺度可变性引起。则传统 （泛）克里金预测为：

$$\hat{Y}_{UK}(\mathbf{s}_0) = \mathbf{x}(\mathbf{s}_0)^T \hat{\boldsymbol{\beta}} + \mathbf{c}(\mathbf{s}_0)^T \boldsymbol{\Sigma}^{-1}(\mathbf{z} − \mathbf{X} \hat{\boldsymbol{\beta}}) \tag{2.3}$$

其中已观测的协变量矩阵为 $\mathbf{X} = (\mathbf{x}(\mathbf{s}_1),\ldots ,\mathbf{x}(\mathbf{s}_N ))^T$，是一个 $N \times P$ 矩阵；预测位置与已观测位置之间的协方差向量为 $\mathbf{c}(\mathbf{s}_0) = \operatorname{Cov}(\mathbf{Z}, \mathbf{Z}(\mathbf{s}_0))$, 已观测数据的协方差矩阵为 $\boldsymbol{\Sigma} = \operatorname{Cov}(\mathbf{Z}, \mathbf{Z}^T)$，而均值结构的参数向量估计值为 $\hat{\boldsymbol{\beta}} = (\mathbf{X}^T \boldsymbol{\Sigma}^{-1} \mathbf{X})^{-1}\mathbf{X}^T \boldsymbol{\Sigma}^{-1} \mathbf{z}$。

在该方法中，空间相关性以协方差向量 $\mathbf{c}(\mathbf{s}_0)$ 的线性函数形式引入 $\hat{Y}_{UK}(\mathbf{s}_0)$ （ 式 2.3 右侧第二项），不过该线性函数的系数 $\boldsymbol{\Sigma}^{-1}(\mathbf{z} −\mathbf{X} \hat{\boldsymbol{\beta}})$ 未知，需要进行估计。

这种预测形式提醒我们：或许可以在神经网络的输入特征中，引入一组 $\mathbf{s}$ 的非线性函数作为嵌入，用来在神经网络中表征空间过程 $ν(\mathbf{s})$。这可以根据 Karhunen–Loeve ( KL ) 定理（Adler，2010 年 ^[2]）来实现，该定理认为 $ν(\mathbf{s})$ 可以分解为一组基函数的线性加权形式，即 $ν(\mathbf{s}) = \sum^{\infty}_{k=1} w_k \phi _k(\mathbf{s})$。其中 $\{w_k\}^{\infty}_{k=1}$ 是一组两两不相关的随机变量，$\phi_k(\mathbf{s})$ 是 $ν(\mathbf{s})$ 所在域内两两正交的基函数，并且可以是非线性的。也就是说，空间过程 $ν(\mathbf{s})$ 可以由 $\mathbf{s}$ 处的非线性基函数进行线性量化。

注解：

（1）此处 $w_k$ 之间两两不相关的设定过强。

（2）采用基函数方式表征空间过程的方法久已有之。Cressie 等（2008 ^[12]）提出的固定秩克里金法（ FRK ）、Nychka 等（2015 ^[42]）提出的格元克里金法（LatticeKriging）、Lindgren 等（2011）提出的高斯马尔可夫随机场方法，也都基于基函数展开形式。

（3）此处强调了采用正交基，但这不是强制的，例如 Cressie 等提出的固定秩方法中没有此硬性规定。

（4）在很多空间应用中，习惯于在按照某种规则剖分的区域网格上构建基函数的线性组合，对于域内任意位置，可以利用剖分网格中的每一个结点定义一个基函数。如，以规则网格方式在平面定义域内划出 $10 \times 10$ 的区域网格，则产生 $11 \times 11$ 个结点，则域内任意一点处，都可以根据到这 121 个点的距离得到一个基函数。这样的话，可以将原本 $n \times n$ 的协方差矩阵，通过 KL 分解，转变成 $121 \times 121$ 的矩阵。

在实际工作中，$ν(\mathbf{s})$ 的典型预测通常是 KL 展开的截断形式，根据给定正交基函数 $\phi_k(\mathbf{s})$ 的性质，我们可以找到某个整数 $K$，使得 $ν(\mathbf{s})$ 能够被近似为 $K$ 个基函数的有限加权和，即 $\hat{\nu}(\mathbf{s}) = \sum^{K}_{k=1} w_k \phi_k(\mathbf{s})$。根据 KL 定理，基函数的数量 $K$ 比其具体函数形式重要（我们在补充材料的 第 S4.1 节中进行的额外模拟也可以支持这一点）。基函数的选择是多样的，例如平滑样条基函数 (Wahba, 1990 ^[52])、小波基函数 (Vidakovic, 2009 ^[51]) 和径向基函数 (Friedman 等, 2001 ^[22])。通过添加一个具有足够大 $K$ 值的嵌入层，神经网络输入的宽度可以大大增加，从而使网络包含比单独使用坐标更多的空间信息。 Cheng 等 (2016 ^[7]) 在推荐系统中使用了类似想法。

注：

（1）可以被视为一种数据增强方法，或者人工特征方法。

（2）在空间变系数模型中，Fan 等（2022）、Wang 等（2022）曾提出样条方法，Fuglstad 等（2014）曾提出随机偏微分方程方法，或许可以与本文方法结合？

2.2 DeepKriging：具有空间依赖的神经网络

本节使用一个简单的 DNN 来说明 DeepKriging 框架。我们的模型也有潜力用于其他深度学习框架，例如卷积神经网络 (CNN) 和循环神经网络。

（1）采用基函数生成位置嵌入

首先，我们需要选择 $K$ 值和基函数来近似空间过程 $ν(\mathbf{s})$。我们采用了 Nychka 等 (2015 ^[42]) 的想法。他开发了一种用于大型数据集空间预测的多分辨率模型，每个分辨率级别的径向基函数都使用紧支撑的 Wendland 相关函数构建， “结” 则排列在矩形网格上。特别地，在一定分辨率水平下，令 $\{\mathbf{u}_j\}, j = 1,\ldots, m$ 是 “结” 构成的矩形网格（或径向基函数术语中的 node），设 $θ$ 为尺度参数。基函数由 $\phi^{*}_j(\mathbf{s}) = \phi (\| \mathbf{s} − \mathbf{u}_j\|/θ)$ 给出，其中

$$\phi (d) = \begin{cases} (1 − d)^6(35 d^2 + 18d + 3)/3, &d \in [0, 1]\\ 0, &\text{otherwise} \end{cases}$$

也就是说，在神经网络的嵌入层使用到了局部坐标到每个 “结” 的距离，这意味着空间模式在局部具有位置不变性。因此，DeepKriging 能够对空间非平稳性进行建模；正如将在 第 3.3 节 中展示的那样，无限宽 DeepKriging 网络的归纳协方差函数通常是非平稳的。

根据 Nychka 等 (2015 ^[42])，比例参数 $θ$ 设置为相关 “结” 间距的 $2.5$ 倍。更精细级别的网格按照 $2$ 倍因子依次增加间距，同时基函数按比例缩放以具有恒定的重叠。具体来说，在第 $h$ 级中， “结” 的数量为 $K_h = (9 \times 2^{h−1} + 1)^d$，其中 $d$ 是空间维度。对于海量数据集，为了得到 $K ≥ N$ ，我们需要 $H = 1 + \lceil \log_2( \sqrt[d]{N}/10) \rceil$ 个级别。例如，对于 $4$ 级的模型，在一维空间中我们需要 $K = 10 + 19 + 37 + 73 = 139$ 个基函数；而在二维空间中则需要 $K = 102 + 192 + 372 + 732 = 7159$ 个基函数。该方案很好地近似了标准协方差函数，并且还具有拟合更复杂形状的灵活性。

其他研究工作也采用了多分辨率逼近的方法，请参阅 Katzfuss (2017 ^[30]) 及其中的参考文献。

（2）位置嵌入作为神经网络输入

对于任何坐标 $\mathbf{s}$，我们计算 $K$ 个基函数以获得嵌入向量 $\phi (\mathbf{s}) = (\phi_1(\mathbf{s}),\ldots , \phi_K(\mathbf{s}))^T$ 。建议基函数采用基于 KL 展开的正交基。然后，令 $\mathbf{x}_{\phi}(\mathbf{s}) = (\mathbf{x}(\mathbf{s})^T , \boldsymbol{\phi}(\mathbf{s})^T )^T$ 为长度 $P + K$ 的神经网络输入，并将 $L$ 层 DNN 定义为:

$$\begin{align*} &\mathbf{u}_1(\mathbf{s}) = \mathbf{W}_1 \mathbf{x}_{\phi} (\mathbf{s}) + \mathbf{b}_1, \qquad \mathbf{a}_1(\mathbf{s}) = \psi_1 (\mathbf{u}_1(\mathbf{s})); \\ &\mathbf{u}_2(\mathbf{s}) = \mathbf{W}_2 \mathbf{a}_1(\mathbf{s}) + \mathbf{b}_2, \qquad \mathbf{a}_2(\mathbf{s}) = \psi_2(\mathbf{u}_2(\mathbf{s}));\\ &\ldots \\ &\mathbf{u}_L(\mathbf{s}) = \mathbf{W}_L \mathbf{a}_{L−1}(\mathbf{s}) + \mathbf{b}_L, \qquad f_{DK}(\mathbf{s}) = \psi_L(\mathbf{u}_L(\mathbf{s})) \end{align*} \tag{2.4}$$

对于具有 $N_l$ 个神经元的第 $l$ 层，$\mathbf{W}_l$ 是 $N_l \times N_{l−1}$ 的权重矩阵，$\mathbf{b}_l$ 是长度为 $N_l$ 的偏置向量，$\mathbf{a}_l$ 是长度为 $N_l$ 的神经元向量，$\psi_l(·)$ 是激活函数。

该神经网络的最终输出是 $f_{DK}(\mathbf{s})$，它是权重和偏差的函数。令 $\boldsymbol{\theta}$ 是未知权重和偏差的向量，并且 $\hat{\boldsymbol{\theta}}$ 是基于训练样本通过 式（2.2） 进行的参数估计值。则在未观测位置 $\mathbf{s}_0$ 处的最终 DeepKriging 预测被定义为：$\hat{Y}_{DK}(\mathbf{s}_0) = f_{DK}(\mathbf{s}_0;\hat{\boldsymbol{\theta}})$。

DeepKriging 方法的一大优势是可以调整神经元的数量、激活函数和损失函数，以适应不同的数据类型和模型解释。例如：

• 为了预测回归问题中的连续变量，可以选择 $N_L = 1$，$\psi_L(·)$ 为恒等函数，损失函数作为 MSE。图 1 提供了连续数据二维预测中 DeepKriging 结构的可视化。
• 为了在分类问题中预测类别变量，可以选择 $N_L$ 为类别数量，$\psi_L(·)$ 为 softmax 函数，损失函数为交叉熵损失。

对于隐藏层中的激活函数，我们默认选择整流线性单元（ReLU），这允许我们在 KL 展开中保持线性关系，但添加一些去活的神经元以便选择最佳数量的基函数。 DeepKriging 结构还允许协变量效应随空间变化。

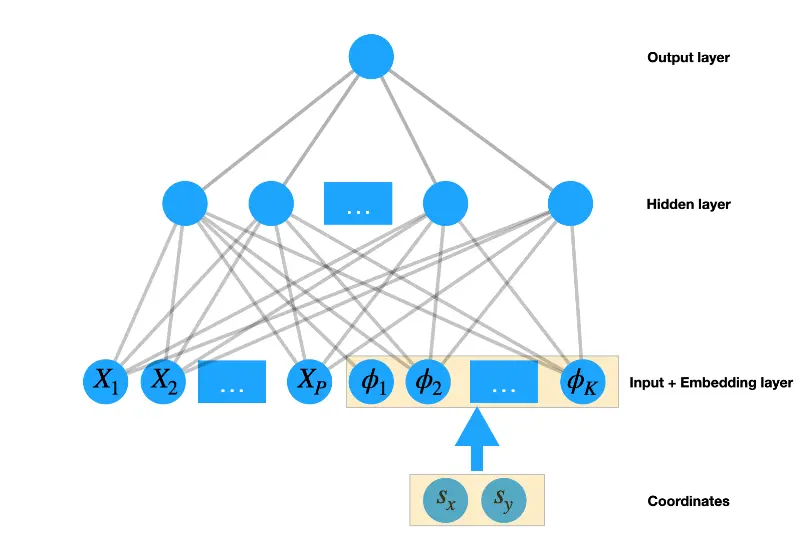
图 1：基于三层 DNN 的二维空间预测中 DeepKriging 结构的可视化

DeepKriging 神经网络结构的正则化方法包括：添加 dropout 层以减轻过拟合、添加批量归一化层以将协变量和基函数正则化到相同的尺度、移除基矩阵中可能存在的全零列等。DeepKriging 网络结构的详细设置信息在补充材料的 S2 节 中。DeepKriging 方法的时间复杂度约为 $\mathcal{O}(N_{neuron})$，其中 $N_{neuron}$ 是网络中神经元的数量。计算成本取决于神经网络的宽度和深度，计算是高度并行化的，可以通过 CPU 和 GPU 大大加速。

3 DeepKriging 的理论性质

使用深度学习的 DeepKriging 提供了一种新颖的空间预测框架。它与经典克里金方法存在以下几个方面的不同：

• （1）克里金预测是观测值的线性组合；DeepKriging 预测则通过经过训练的权重和偏差与观测数据相关联，并且是非线性的（请参阅第 S3.1 节）。
• （2）DeepKriging 不假设具有特定协方差函数的高斯过程，而是通过基函数对空间依赖性进行建模。
• （3）与 Kriging 在新位置处通过随机过程 $Y(\mathbf{s})$ 实现预测不同，DeepKriging 使用确定性连续函数来近似空间过程值。

在本节中，我们提供了 DeepKriging 的重要理论特性，包括：

• （1）DeepKriging 和 Kriging 之间的潜在联系；
• （2）与克里金法相比，深度克里金法在预测误差方面的准确性；
• （3）在 DeepKriging 框架中如何测量空间依赖性。

3.1 DeepKriging 和 Kriging 及其扩展方法的联系

DeepKriging 与 Kriging 的相关变体密切相关，大致可分为 多分辨率过程 (Nychka 等, 2015 ^[42]; Kleiber and Nychka, 2015 ^[31]; Katzfuss, 2017 ^[30]) 和 高斯预测过程 (Banerjee 等, 2008 ^[6], 2010 ^[5])，这些变体都导致空间预测被视为某些嵌入特征 $\mathbf{x}_\phi (\mathbf{s}_0)$ 的线性函数，因此可以通过 DeepKriging 进行近似。

一个例子是 Cressie 和 Johannesson (2008 ^[12]) 提出的固定秩克里金法 (FRK)，他们使用协方差矩阵的低秩近似来加速泛克里金法的计算。与 DeepKriging 类似，它们用 $K$ 个基函数表示来空间过程 $ν(\mathbf{s})$，即 $ν(\mathbf{s}) = \boldsymbol{\phi} (\mathbf{s})^T \boldsymbol{\eta}$，其中 $\boldsymbol{\eta}$ 是 $K$ 维高斯随机向量，其协方差矩阵为 $\operatorname{Cov}(\boldsymbol{\eta}) = \boldsymbol{\Sigma}_K$。在此基础上，他们还假设真实空间过程和观测为：

$$Y(\mathbf{s}) = \mathbf{x}(\mathbf{s})^T \boldsymbol{\beta} + ν(\mathbf{s}) = \mathbf{x}(\mathbf{s})^T \boldsymbol{\beta} + \boldsymbol{\phi} (\mathbf{s})^T \boldsymbol{\eta}$$

$$Z(\mathbf{s}) = Y(\mathbf{s}) + \varepsilon(\mathbf{s})$$

式中 $\varepsilon(\mathbf{s})$ 是方差为 $\sigma^2_\varepsilon (\mathbf{s})$ 的白噪声。因此，观测 $Z(\mathbf{s})$ 的协方差矩阵可以被简化为计算效率更高的形式： $\boldsymbol{\Sigma = \Phi \Sigma_K \Phi^T} + \mathbf{V}$，其中 $\boldsymbol{\Phi} = \{\phi ( \mathbf{s}_1),\ldots , \phi (\mathbf{s}_N )\}^T$ 是一个 $N \times K$ 的基矩阵，$\mathbf{V} = \operatorname{diag}\{\sigma^2_\varepsilon(\mathbf{s}_1),\ldots , \sigma^2_\varepsilon(\mathbf{s}_N )\}$ 是一个 $N \times N$ 的对角矩阵。

在空间预测方面，固定秩预测是 $\mathbf{z}$ 的线性函数，由下式给出：

$$\hat{Y}_{FRK}(\mathbf{s}_0) = \mathbf{x}(\mathbf{s}_0)^T\hat{\boldsymbol{\beta}} + \phi (\mathbf{s}_0)^T \boldsymbol{\Sigma}_K \Phi^T \boldsymbol{\Sigma}^{-1}( \mathbf{z} −\mathbf{X} \hat{\boldsymbol{\beta}}) \tag{3.5}$$

其中 $\mathbf{X} = (\mathbf{x}(\mathbf{s}_1), \ldots , \mathbf{x}(\mathbf{s}_N))^T$ 是 $N \times P$ 的协变量观测矩阵, $\hat{\boldsymbol{\beta}} = (\mathbf{X}^T \boldsymbol{\Sigma}^{-1} \mathbf{X})^{-1} \mathbf{X}^T \boldsymbol{\Sigma}^{-1} \mathbf{z}，\boldsymbol{\Sigma}^{-1}$ 是模型参数的估计值，由于采用了固定秩的简化形式，其中的矩阵求逆运算效率大大提升，仅涉及对 $K \times K$ 的固定秩正定矩阵 $\boldsymbol{\Sigma}_K$ 和 $N \times N$ 对角矩阵 $\mathbf{V}$ 的求逆。 可以将 式（3.5） 改写为 $\hat{Y}_{FRK}(\mathbf{s}_0) = \mathbf{x}(\mathbf{s}_0)^T \hat{\boldsymbol{\beta}} + \phi (\mathbf{s}_0)^T \hat{\boldsymbol{\alpha}}$ 的形式，其中 $\hat{\boldsymbol{\alpha}}= \boldsymbol{\Sigma_K \Phi^T \Sigma^{-1}} (\mathbf{z} −\mathbf{X} \hat{\boldsymbol{\beta}})$，这意味着 FRK 预测 $\hat{Y}_{FRK} (\mathbf{s}_0)$ 关于$\mathbf{x}(\mathbf{s}_0)$ 和基函数 $\phi (\mathbf{s}_0)$ 是线性的。如果将 DeepKriging 中所有激活函数均设置为线性，则 FRK 预测是 DeepKriging 的一个特例。

FRK 通常选择远小于 $N$ 的 $K$ 值，以加快大型数据集的计算速度。由于协方差 $\boldsymbol{\Phi \Sigma_K \Phi^T}$ 的阶数最多为 $K$，因此固定秩的这种低阶近似可能无法捕获到空间过程中的高频变化或小尺度空间依赖性 (Stein, 2014 ^[50])。相比之下，DeepKriging 中的 $K$ 需要足够大 ($K > N$ ) ，只有这样才能更好地近似空间随机效应 $ν(\mathbf{s})$，以便在预测中捕获更多空间信息。

如果在 FRK 中设置 $K = N$，则 式（2.3） 中的（泛）克里金预测也是 $\mathbf{x}_\phi (\mathbf{s}_0) = (\mathbf{x}(\mathbf{s}_0)^T , \boldsymbol{\phi}(\mathbf{s}_0)^T )^T$ 的线性函数。补充材料中的 S1.1 节 提供了详细证明。该结果意味着：具有任何协方差函数的克里金预测均可以由新的嵌入特征 $\mathbf{x}_{\phi} (\mathbf{s}_0)$ 线性表示。从此意义上来说，DeepKriging 在预测中允许 $\mathbf{x}_{\phi} (\mathbf{s}_0)$ 的非线性函数，这是对 Kriging 方法的一种泛化。

3.2 决策论中的 DeepKriging

DeepKriging 预测遵循 Fan 等（2019 ^[19]）所述的近似估计分解。

令 $\mathcal{F}$ 为特定 DNN 模型可表达的函数空间，并且 $\hat{Y}_N(\mathbf{s}_0)$ 是基于 $N$ 个已观测位置的最终模型预测结果。真实值 $Y(\mathbf{s}_0)$ 和预测值 $\hat{Y}_N(\mathbf{s}_0)$ 之间总风险的以下分解，暗示了三个错误来源：

$$R \{Y(\mathbf{s}_0),\hat{Y}_N(\mathbf{s}_0)\} = \underbrace{R \{Y (\mathbf{s}_0),\hat{Y}^{opt}_F(\mathbf{s}_0)\}}_{\text{approximation error}} + \underbrace{R\{\hat{Y}^{opt}_F(\mathbf{s}_0),\hat{Y}^{opt}_N(\mathbf{s}_0)\}}_{\text{estimation error}} + \underbrace{R \{\hat{Y}^{opt}_N (\mathbf{s}_0),\hat{Y}_N (\mathbf{s}_0)\}}_{\text{optimization error}}$$

其中：

• 近似误差 与模型容量有关，被定义为真实过程 $Y(\mathbf{s}_0)$ 和最佳预测 $\hat{Y}^{opt}_{\mathcal{F}}(\mathbf{s}_0) = \arg \min_{\hat{Y}(\mathbf{s}_0) \in \mathcal{F}} R(\hat{Y}(\mathbf{s}_0), Y(\mathbf{s}_0))$ 之间的风险，该风险是函数空间 $\mathcal{F}$ 中的一个函数。

• 估计误差 定义为 $\hat{Y}^{opt}_N(\mathbf{s}_0)$ 和 $\hat{Y}^{opt}_{\mathcal{F}}(\mathbf{s}_0)$ 之间的风险，其中 $\hat{Y}^{opt}_N(\mathbf{s}_0) =\hat{Y}_N(\mathbf{s}_0; \boldsymbol{\hat{\theta}})$，$\hat{\boldsymbol{\theta}} = \arg \min_{\boldsymbol{\theta}} \frac{1}{N} \sum^{N}_{n=1} L\{\hat{Y}_N(\mathbf{s}_n; \boldsymbol{\theta}),z(\mathbf{s}_n)\}$；这类误差受 $\mathcal{F}$ 复杂度的影响，与模型泛化能力有关。

• 优化误差 是 $\hat{Y}^{opt}_N(\mathbf{s}_0)$ 和 $\hat{Y}_N(\mathbf{s}_0)$ 之间的经验风险。

式（2.3） 中克里金预测的函数类 $\mathcal{F}_{UK}$，可以看作是 $\mathbf{x}(\mathbf{s}_0)$ 和 $\mathbf{z}$ 的线性函数空间，形式为 $\mathbf{x}(\mathbf{s}_0)^T \boldsymbol{\beta} + \mathbf{z}^T \boldsymbol{\gamma}$，而 DeepKriging 的函数类 $\mathcal{F}_{DK}$，是由 式（2.4） 中描述的 DNN 生成的函数空间。 万能近似定理（Csaji (2001 ^[13]) 的定理 2.3.1）称，特征 $\mathbf{x}_{\phi}(\mathbf{s})$ 的每个连续函数（表示为 $\mathbb{C}(\mathbf{x}_{\phi})$），都可以用一个包含有限数量隐神经元和任意激活函数的单隐层神经网络来近似。这表明具有单个隐藏层和有限损失函数的最优 DeepKriging 预测在 $\mathbb{C}(\mathbf{x}_{\phi})$ 中具有最大的模型容量，即 $\hat{Y}^{opt}_{\mathcal{F}_{DK}}(\mathbf{s}_0) = \hat{Y}^{opt}_{\mathbb{C}(\mathbf{x}_{\phi})}(\mathbf{s}_0)$。此结果适用于任何类型的数据（即连续或离散）和任何类型的任务（即回归或分类）。

因此，在最小化近似误差方面，最优 DeepKriging 预测比 Kriging 预测具有更强的能力，即 $\mathbb{E}\{L(\hat{Y}^{opt}_{\mathcal{F}_{DK}}(\mathbf{s}_0), Y(\mathbf{s}_0))\} \leq \mathbb{E}\{L(\hat{Y}^{opt}_{\mathcal{F}_{UK}} (\mathbf{s}_0), Y(\mathbf{s}_0))\}$。补充材料中的 S1.2 节 提供了详细证明。同样，最优 DeepKriging 预测也比 FRK 预测具有更大的模型容量。FRK 可以被看作是有限数量神经元和线性激活函数的单隐层 DeepKriging。通过允许大量的基函数、多层、更灵活的激活函数和宽网络，DeepKriging 产生的非线性预测可以恰当地捕捉空间过程中的空间依赖性。

3.3 作为高斯过程的 DeepKriging

Neal (1994 ^[40]) 表明： 神经网络参数（即权重和偏差）具有独立同分布先验的单层全连接神经网络，在无限宽（即无限数量的隐神经元）极限下，等效于高斯过程（GP）。后来，Lee 等 (2018 ^[34]) 得出了无限宽深度网络和高斯过程之间的精确等价性。因此，与高斯过程的类似对应关系也适用于 DeepKriging 网络。

（1）单隐层情况

我们从包含 $N_1$ 个神经元的单隐层回归型 DeepKriging 模型开始。该模型的输入特征为 $\mathbf{x}_{\phi} (\mathbf{s}) = (\mathbf{x}(\mathbf{s})^T , \phi (\mathbf{s})^T)^T \in \mathbb{R}^{P+K}$，输出为 $\hat{Y}_{DK}(\mathbf{s}) = \mathbf{b}_1 + \sum^{N_l}_{j=1} w^1_j a^1_j(\mathbf{s})$，其中 $a^1_j(\mathbf{s}) = \psi_1 (b^0_j + \sum^{P+K}_{i=1} w^0_{ji} \mathbf{x}^{(i)}_\phi (\mathbf{s}))$ 为第 $j$ 个隐单元的输出，$\mathbf{x}^{(i)}_\phi (\mathbf{s})$ 是 $\mathbf{x}_{\phi}$ 的第 $i$ 个分量。权重 $(w^1_j, w^{0}_{ji})$ 和偏差 $(b_1, b^0_j)$ 是独立且随机采样的，其均值为零，方差分别为 $\sigma^2_w/N_1$ 和 $\sigma^2_b$ 。因此，激活后的 $a^1_j$ 和 $a^{1}_{j^\prime}$ 对于 $j \neq j^{\prime}$ 是相互独立的。此外，由于 $\hat{Y}_{DK}(\mathbf{s})$ 是独立同分布项的和，根据中心极限定理，在无限宽度 $N_1 \rightarrow \infty$ 的极限下，$\hat{Y}_{DK}(\mathbf{s})$ 将服从高斯分布。同样，根据多维中心极限定理，$\{\hat{Y}_{DK}(\mathbf{s}_1), \hat{Y}_{DK}(\mathbf{s}_2), \ldots , \hat{Y}_{DK}(\mathbf{s}_n)\}$ 的任何有限集合，都将具有联合多元高斯分布，这正是高斯过程的定义。因此，我们得出结论：如果 $N_1$ 足够大，则 $Y_{DK}$ 是具有零均值和如下协方差函数的高斯过程：

$$C^1(\mathbf{s}, \mathbf{s}^{\prime}) = E\{ \hat{Y}_{DK}(\mathbf{s}) \hat{Y}_{DK}(\mathbf{s}^{\prime})\} = \sigma^2_b + \sigma^2_w E\{a^1_j(\mathbf{s})a^1_j (\mathbf{s}^{\prime})\} = \sigma^2_b + \sigma^2_w C(\mathbf{s}, \mathbf{s}^{\prime})$$

其中 $C(\mathbf{s}, \mathbf{s}^{\prime})$ 是通过对 $w^0$, $b^0$ 的分布进行积分获得的，如 Neal (1994 ^[40]) 中所述。

（2）多隐层情况

对于更深层的 DeepKriging，可以根据 Lee 等 (2018 ^[34]) 的方法以递归方式获得归纳协方差函数:

$$C^l(\mathbf{s},\mathbf{s}^{\prime}) = \sigma^2_b + \sigma^2_w F_\psi (C^{l−1}(\mathbf{s,s^{\prime}}), C^{l−1}(\mathbf{s, s}), C^{l-1}(\mathbf{s^{\prime}, s^{\prime}})) \tag{3.6}$$

其中 $F_{\psi} (·)$ 是一个确定性函数，仅取决于激活函数 $\psi$ 。

可以执行一系列迭代计算以获得描述网络最终输出 $\hat{Y}_{DK}(\mathbf{s})$ 的高斯过程协方差 $C^L$。对于基本情况，$C^0(\mathbf{s,s^{\prime}}) = \sigma^2_b + \sigma^2_w \{\mathbf{x_{\phi} (s)^T x_{\phi} (s^{\prime}})/(P + K)\}$。上述结果需要假设每一层都有无限多的隐藏神经元。然而，当权重和偏差的先验分布是高斯分布时，就不需要这个条件了。

对于某些激活函数，可以解析地计算 式（3.6） 。其中最简单的情况发生在激活函数是恒等函数 $\psi_l(x) = x$ 且不存在协变量效应时，此时 $\hat{Y}_{DK}(\mathbf{s})$ 是基函数 $\phi(\mathbf{s})$ 的线性函数，即 $\hat{Y}_{DK}(\mathbf{s}) = b + \mathbf{w}^T \boldsymbol{\phi}(\mathbf{s})$，其中 $b$ 和 $\mathbf{w}$ 分别是偏置和权重。在这种情况下，由 $C^L(\mathbf{s, s^{\prime}}) = \sigma^2_b +\sigma^2_w \boldsymbol{\phi} (\mathbf{s})^T \boldsymbol{\phi} (\mathbf{s}^{\prime})$ 给出 $\hat{Y}_{DK}$ 的归纳协方差函数，这是空间协方差函数的基本近似。

在 ReLU 非线性的情况下，式（3.6） 具有众所周知的反余弦核的闭合形式（Cho 和 Saul，2009 ^[8]）： $C^l(\mathbf{s}, \mathbf{s}^{\prime}) = \sigma^2_b + \frac{\sigma^2_w}{2 \pi} \sqrt{C^{l−1}(\mathbf{s}, \mathbf{s})C^{l−1}(\mathbf{s}^{\prime}, \mathbf{s}^{\prime})} \{ \sin (θ^{l−1}_{\mathbf{s},\mathbf{s}^{\prime}} ) + (\pi − θ^{l−1}_{\mathbf{s},\mathbf{s}^{\prime}}) \cos (θ^{l−1}_{\mathbf{s},\mathbf{s}^{\prime}}) \}$，其中 $θ^l_{\mathbf{s},\mathbf{s}^{\prime}} = \cos^{−1}(C^l(\mathbf{s}, \mathbf{s}^{\prime})/\sqrt{C^l(\mathbf{s}, \mathbf{s})C^l(\mathbf{s}^{\prime}, \mathbf{s}^{\prime})})$。也就是说，当协方差函数的解析形式不存在时，可以使用数值计算方法，如 Lee 等 (2018 ^[34]) 所述。

考虑具有单隐层且没有协变量效应的回归型 DeepKriging 模型。可以证明，对于无限多个隐藏神经元，任意两个邻近位置的输出 $\hat{Y}_{DK}(\mathbf{s})$ 的协方差函数具有以下形式

$$C(\mathbf{s},\mathbf{s}^{\prime}) = v(\mathbf{s}) + v(\mathbf{s}^{\prime}) − c \|\boldsymbol{\phi} (\mathbf{s}) − \boldsymbol{\phi} (\mathbf{s}^{\prime})\|^2 \tag{3.7}$$

其中 $\boldsymbol{\phi} (\mathbf{s})$ 是位置 $\mathbf{s}$ 处的基向量，$v(\mathbf{s}) > 0$ 与 $\mathbf{s} = \mathbf{s}^{\prime}$ 时的方差相关，$c$ 是缩放参数。证明在补充材料的 S1.3 节 中提供。作为一种特殊情况，如果在特征中仅使用坐标，则 $\| \boldsymbol{\phi} (\mathbf{s}) − \boldsymbol{\phi} (\mathbf{s}^{\prime})\|^2 = \|\mathbf{s} − \mathbf{s}^{\prime}\|^2$, $v(\mathbf{s}) = v(\mathbf{s}^{\prime}) = v$，因此 $C(\mathbf{s},\mathbf{s}^{\prime}) = v − c \|\mathbf{s} − \mathbf{s}^{\prime}\|^2$，其中包含的信息少于 式（3.7） 中的信息。因此，DeepKriging 中的嵌入层带来了比简单使用坐标更灵活的空间协方差结构。

此外，我们可以展示 DeepKriging 归纳协方差函数如何逼近空间统计中常见的平稳协方差函数。令基函数为 $\phi_l(\mathbf{s}) = k(\mathbf{u}, \mathbf{u}_l)$，基于某个核函数 $k(·,·)$ 和 “结” $\mathbf{u}_l, l = 1,\ldots , K$。如果 $\mathbf{u}_l$ 形成覆盖空间域的细网格 “结” ，则

$$\|\boldsymbol{\phi} (\mathbf{s}) − \boldsymbol{\phi} (\mathbf{s}^{\prime})\|^2 = \sum^{K}_{l=1} \{k(\mathbf{s}, \mathbf{u}_l) − k(\mathbf{s}^{\prime}, \mathbf{u}_l)\}^2 \approx \int \{k(\mathbf{s}, \mathbf{u}) − k(\mathbf{s}^{\prime}, \mathbf{u})\}^2 d \mathbf{u} = \int k(\mathbf{s, u})^2 + k(\mathbf{s}^{\prime}, \mathbf{u})^2 − 2k(\mathbf{s, u})k(\mathbf{s}^{\prime}, \mathbf{u})d \mathbf{u}$$

请注意，最后一项是协方差函数的核卷积逼近。 Higdon (2002 ^[27]) 表明，通过选择合适的核函数，我们可以基于核卷积逼近任何平稳的协方差函数。此外，DeepKriging 的归纳协方差函数也具有良好的物理解释。例如，DeepKriging 可以产生 Matern 协方差函数，该函数也常用于 Kriging，因为它与拉普拉斯类型的随机偏微分方程 (SPDE) 有关 (Whittle, 1954 ^[54])。此外，DeepKriging 可以根据 Neal (1996 ^[41]) 中提供的 DNN 示例导出近似分数布朗运动的高斯过程。

4.模拟研究

4.1 一维高斯过程的 DeepKriging

4.2 二维非平稳数据上的 DeepKriging

5 应用

5.1 预测 PM2.5 浓度的挑战

PM2.5，即小于2.5μm的细颗粒物，是一种有害的空气污染物。其不良反应与呼吸系统疾病(Peng 等, 2009 ^[44])、心肌梗死(Peters 等, 2001 ^[45])等多种疾病有关；参见世界卫生组织的评论（2013 年）。因此，获取 PM2.5 暴露物的高分辨率地图以评估其影响至关重要。监测网络的测量值是给定时间和地点 PM2.5 浓度的最佳表征。然而，来自监测地点的数据通常分布稀疏，因此它们在空间和时间上与健康结果不一致。同时，众所周知，PM2.5 浓度与温度和相对湿度等气象条件相关（Jacob 和 Winner，2009 ^[29]），气象数据或数据产品通常易于访问，具有良好的空间覆盖和分辨率。因此，利用监测网络数据和其他气象数据插值 PM2.5 浓度一直是一个很有前途的研究领域（Di 等，2016 年 ^[15]），其中空间预测起着核心作用。

PM2.5 浓度的建模和预测具有挑战性。首先，PM2.5浓度数据明显是非高斯分布的，经典的克里金法在这里不适用。其次，PM2.5 监测站数据不规则、稀疏，但很多插值方法需要点阵数据。第三，更重要但更具挑战性的是了解高污染的风险并预测污染水平，如低、中、高；从统计学上讲，这两个问题分别与估计超过阈值的概率和分类问题有关。分位数回归和卷积神经网络已被用来克服上述一些问题（Reich 等，2011 年 ^[47]；Porter 等，2015 年 ^[46]；Di 等，2016 年 ^[15]）。然而，处理所有上述任务的统一方法尚未得到充分开发。

5.2 数据和预处理

为了解决上述问题，我们将 DeepKriging 方法应用于基于气象变量的 PM2.5 浓度空间预测。气象数据来自 NCEP 北美区域 NARR 产品。NARR 是一个代表大气状态的网格数据集，结合了从过去到现在的数值天气预报模型的观测和输出。根据观测，NARR 数据通常用来表示大气的 “真实状态”，因此我们将 NARR 数据作为协变量的 “观测数据”。本研究总共使用了六个气象变量：1) $2m$ 分辨率的气温，2) $2m$ 分辨率的相对湿度，3) 累计总降水量，4) 表面压力，5) 风的 $u$ 分量，以及 6) $10 m$ 分辨率的风 $v$ 分量。 NARR 产品的协变量是 2019 年 6 月 5 日的网格数据，空间分辨率约为 $32 \times 32$ km，覆盖美国大陆，总共包含 $7, 706$ 个网格单元。由于气象变量的单位不同，我们在实施模型之前使用 “最小-最大归一化” 来重新缩放数据。 PM2.5 浓度日均数据来自 $841$ 个监测站。由于来自 NARR 的坐标和来自站点的坐标不相同，并且一些站点彼此距离太近，我们保持 NARR 的空间分辨率并对同一网格单元中附近监测站的 PM2.5 测量值进行平均。匹配后保留 $604$ 个网格单元用于模型训练，每个位置的 PM2.5 浓度值如 图 2(a) 所示。我们的目标是预测其他 $7, 706 − 604 = 7, 102$ 个位置的任何 $\mathbf{s}_0$ 处的 PM2.5 浓度，这些位置缺乏 PM2.5 浓度数据，但协变量取可以由 NARR 数据提供。

5.3 模型拟合及结果

我们的目标是预测未观测到的网格单元的 PM2.5 浓度值，其中提供了六个气象变量。我们使用 $10$ 折交叉验证来验证 DeepKriging 的性能。出于比较目的，我们还显示了克里金法和具有六个协变量和坐标的基线 DNN 的结果。我们计算 MSE 和 MAE 作为验证标准，如 表 1 的前两行所示，这意味着 DeepKriging 优于基线 DNN 和 Kriging。

为了评估 PM2.5 高污染的风险，我们可以使用 DeepKriging 进行空间数据分类。具体而言，我们将 PM2.5 浓度阈值设为 $12.0$ 微克/立方米，这是 EPA 国家环境空气质量标准 (NAAQS) 日均值 “良好” 和 “中等” 水平之间的阈值（EPA，2012）。基于分类数据，我们可以通过假设 PM2.5 浓度的实际值未知，使用 DeepKriging 实现二值分类。与 Kriging 直接比较是不可行的，因为 Kriging 不适合二值分类。相反，我们使用克里金法预测连续的 PM2.5 浓度，然后通过将它们设为 $12.0$ 微克/立方米的阈值来对预测进行分类。然后，我们使用 10 折交叉验证来显示分类精度，如 表 1 最后一行所示。我们可以看到，在分类精度方面，DeepKriging 明显优于 Kriging 和基线 DNN。

基于模型拟合，我们可以进一步预测基于 NARR 数据的未观测位置的 PM2.5 浓度值、污染等级和高污染等级超过阈值 $12$ 微克/立方米的风险。图 2(a) 显示了来自 AQS 数据库的原始 PM2.5 站点数据。图 2(b) 显示了 DeepKriging 预测的 PM2.5 浓度的平滑图。我们还提供分布预测（详细信息和算法包含在补充材料的第 S5 节中）以获得定义为 $\mathbb{P}\{PM2.5 > 12 μg/m^3\}$ 的预测风险，如 图 2(c) 所示。该地图表明美国东部大片地区存在高 PM2.5 污染风险。我们进一步将结果与 图 2(d) 中的 Kriging 预测进行了比较，这意味着 DeepKriging 比 Kriging 提供了更多的局部特征/模式。

图 2：(a) 从监测站收集的 PM2.5 浓度（$μg/m^3$）； (b) 使用 DeepKriging 预测的 PM2.5 浓度； © 基于 DeepKriging 的分布预测作出的高污染风险区分布 $\mathbb{P}\{PM_2.5 > 12 μg/m^3\}$。 (d) 使用克里金法预测的 PM2.5 浓度。

表 1: 基于 10 折交叉验证的模型性能。预测的 MSE 和 MAE，以及预测 PM2.5 浓度高于 $12.0 μg/m^3$ 的分类准确度 (ACC) 用作验证标准。表中提供了 10 组验证误差或准确度的平均值和标准偏差 (SD)。

6 讨论

在本文工作中，我们提出了一种使用深度神经网络的新空间预测模型，该模型通过一组基函数结合了空间依赖性。我们的方法不假设协方差函数或数据分布的参数形式，并且通常与非平稳性、非线性关系和非高斯数据兼容。可以使用补充材料第 S5 节中详述的分布预测方法，基于我们的 DeepKriging 框架提供不确定性量化。

经典克里金法将它们的预测视为观测值的线性组合，这阻碍了它们与多个机器学习框架的交互。自 1981 年以来，Matheron (1981) 就已知克里金法和径向基函数插值之间等价性的一些证据。然而，在没有现代机器学习工具的情况下，仅研究了线性组合和有限数量的径向基函数，这被视为对克里金法不太有利的选择 (Dubrule, 1983 ^[16], 1984 ^[17])。本文工作为具有大量基函数的空间预测中的深度学习提供了新的视角。我们已经证明，在我们的模拟和实际应用中，所提出的方法在理论上和数值上的许多方面都优于克里金法。例如，DeepKriging 对于大型数据集更具可扩展性，并且比 Kriging 适合更多的数据类型。 DeepKriging 还具有具有灵活空间协方差结构的高斯过程表示，它可以通过评估相应的高斯过程来对回归任务进行贝叶斯推断。更重要的是，所提出的 DeepKriging 框架连接了基于回归的预测和空间预测，因此可以应用许多其他机器学习算法。

在一般应用中，可能没有观测到新位置 $\mathbf{s}_0$ 处的协变量。解决这个问题的一种有前途的方法是为观测的一个子集找到缺失协变量的真实值，然后训练机器学习算法来预测其余协变量的值（参见，例如，Imai 和 Khanna（ 2016 ^[28])).然而，Fong 和 Tyler (2021 ^[20]) 表明，在不考虑预测误差的情况下插入这些预测会使回归分析出现偏差、不一致和过度自信。他们描述了避免这些不一致的程序。这种方法结合了新的样本拆分方案和广义矩量法 (GMM) 估计器，以生成高效且一致的估计器。总体而言，解决缺少协变量的问题并非易事：插入机器学习预测等直觉策略会导致偏差和不一致，而实现更复杂的方法（如 Fong 和 Tyler (2021 ^[20]) 中的方法）需要额外的假设（例如，排除限制条件）并增加计算负担。如果目标是同时预测响应和协变量，则可以开发 DeepKriging 的多变量版本。这些留作我们以后的工作。

补充材料

补充材料包含主要手稿中引用的详细信息，包括引理和定理的证明（第 S1 节）、DeepKriging 网络结构的设置（第 S2 节）、模拟研究的详细信息（第 S3 节）、其他模拟研究（ S4 节），分布预测和不确定性量化（S5 节），以及可重复研究的源代码和数据（S6 节）。

S3 模拟研究的详细信息

图 S1：从 GP 生成的一个模拟数据集的预测结果。蓝点是模拟数据（观测）。实线是来自仅具有截距的 DNN（蓝线）、具有截距和坐标的 DNN（橙色线）、DeepKriging（红线）、具有真实指数协方差函数的 Kriging（灰线）和具有估计的 Kriging 的预测曲线矩阵协方差函数（黑线）。

表 S1：来自高斯过程的五个预测的 100 个数据集中的训练集和测试集的均方根误差 (RMSE) 和平均绝对百分比误差 (MAPE) 的均值和标准差 (SD)。 Kriging I 和 II 分别是具有真实指数协方差函数的 Kriging 预测和具有估计的 Matern 协方差函数的 Kriging 预测。 DeepKriging 预测基于 MSE 损失。 DNN I 和 DNN II 分别是仅具有截距和具有截距和坐标的 DNN 预测。

图 S2：(a) 从 $Y (s) = \sin{30(\bar{s} − 0.9)4} \cos{2(\bar{s} − 0.9)} + (\bar{s} − 0.9)/2$ 生成的模拟数据的可视化，其中 $s = (s_x, s_y)^T \in [0, 1]^2$ 和 $\bar{s} = (s_x + s_y)/2$。 (b) 基于来自 DeepKriging（蓝色）、基线 DNN（绿色）和 Kriging（黄色）的 10 倍交叉验证的 10 个 RMSE 的箱线图。

S4 其他模拟研究

表 S2：基于 10 折交叉验证的训练集和测试集的模型性能。数据由 $Y (s) = \sin{30(\bar{s}− 0.9)4} \cos{2(\bar{s} − 0.9)} + (\bar{s} − 0.9)/2$ 生成，其中 $s = (s_x, s_y)^T \in [0, 1]^2$ 和 $\bar{s}= (s_x +s_y)/2$。计算 RMSE 和 MAPE，并给出 10 组验证误差的均值和标准差 (SD)。 DeepKriging 预测基于 MSE 损失。基线 DNN 仅包含特征中的坐标 s。克里金预测使用估计的指数协方差函数。

图 S3：从 GP 生成的一个模拟数据集的预测结果。蓝点是模拟数据（观测）。实线是仅具有截距的 DNN（蓝线）、具有截距和坐标的 DNN（橙色线）、具有 Wenland 核基函数的 DeepKriging（红线）、具有高斯核基函数的 DeepKriging（绿线）、Kriging 的预测曲线分别具有真实指数协方差函数（灰线）和 Kriging 与估计的 Mat ´ern 协方差函数（黑线）。

表 S3：来自高斯过程的六个预测的 100 个数据集中的训练集和测试集的均方根误差 (RMSE) 和平均绝对百分比误差 (MAPE) 的均值和标准差 (SD)。 Kriging I 和 II 分别是具有真实指数协方差函数的 Kriging 预测和具有估计的 Matern 协方差函数的 Kriging 预测。 DeepKriging I 和 II 分别是基于 MSE 损失的 Wenland 核和 Gaussian 核的 DeepKriging 预测。 DNN I 和 DNN II 分别是仅具有截距和具有截距和坐标的 DNN 预测。

图 S4：(a) 从 $Y (s) = \sin{30(\bar{s} − 0.9)4} \cos{2(\bar{s} − 0.9)} + (\bar{s} − 0.9)/2$ 生成的模拟数据的可视化，其中 $s = (s_x, s_y)^T \in [0, 1]^2$ 和 $\bar{s} = (s_x + s_y)/2$。 (b) 基于 DeepKriging 与 Wendland 核（蓝色）、DeepKriging 与高斯核（绿色）、基线 DNN（黄色）和 Kriging（灰色）的 10 折交叉验证的 10 个 RMSE 的箱线图。

表 S4：基于 10 折交叉验证的训练集和测试集的模型性能。数据由 $Y (s) = \sin{30(\bar{s}− 0.9)4} \cos{2(\bar{s} − 0.9)} + (\bar{s} − 0.9)/2$ 生成，其中 $s = (s_x, s_y)^T \in [0, 1]^2$ 和 $\bar{s}= (s_x +s_y)/2$。计算 RMSE 和 MAPE，并给出 10 组验证误差的均值和标准差 (SD)。 DeepKriging I 和 II 分别是基于 MSE 损失的 Wenland 核和高斯核的 DeepKriging 预测。基线 DNN 仅包含特征中的坐标 s。克里金预测使用估计的指数协方差函数。

图 S5：（a）模拟数据和预测的可视化。观测值（蓝点）$z(s)$ 由信号（绿线）$Y(s) \mathbb{1}_{\{Y (s)>0\}} + \varepsilon (s)$ 生成，其中 $Y (s) = 10 \cos(20s)$ ，具有标准的高斯噪声。 Kriging（紫线）和 DeepKriging（红线）的预测几乎相同。 (b) 来自 Kriging（红线）和 DeepKriging（蓝线）预测的 $z(50)$ 对 $\hat{Y}(51)$ 的关系和敏感性。$x$ 轴显示模型训练中 $z(50)$ 的 50 个不同值如果不使用 $z(51)$，则 $y$ 轴显示 $Y(51)$ 的 50 个预测值。

图 S6：不同样本大小 N 的 DeepKriging 和 Kriging 的计算时间（以秒为单位）（$\log_{10}$ 刻度）。绿线是克里金法的计算时间。蓝线和绿线分别是基于 Tesla P100 GPU 和 2.5 GHz Intel Core i7 CPU 的 DeepKriging 的计算时间。

S5. DeepKriging 的分布预测和不确定性量化

理想的空间预测不仅提供点预测，还提供分布信息，例如分位数或密度函数，以量化不确定性、风险和极值（Diggle 等，2007）。传统的 DNN 无法提供预测空间位置的不确定性信息。最近，已经提出了几种方法来通过预测整个概率分布来克服这个问题。

Gal 和 Ghahramani (2016 ^[63]) 以及 Posch 等 (2019 ^[70]) 将贝叶斯推断方法应用于神经网络，通过后验分布预测不确定性。但是，这些方法不能直接应用于空间数据。一些研究试图将深度学习和高斯过程结合起来，这可能应用于空间预测（Damianou 和 Lawrence，2013 年 ^[60]；Lee 等，2018 年 ^[34]；Kumar 等，2018 年 ^[67]；Zammit-Mangion 等，2019 年 ^[71]；Blomqvist 等, 2019 ^[59])。这些方法通常称为深度高斯过程，通过贝叶斯学习在高斯过程框架中表征深度学习（Neal，1996 ^[41]）。基于无限宽的 DeepKriging 和高斯过程之间的对应关系，如正文第 3.3 节所示，我们可以潜在地计算归纳高斯过程的协方差函数，然后使用得到的高斯过程对宽 DeepKriging 网络执行贝叶斯推断。然而，在实践中训练无限宽的 DNN 是不可行的，Lee 等 (2018 ^[34]) 发现，随着有限宽度训练的网络变得更宽且更类似于高斯过程，测试性能会提高，因此高斯过程预测通常优于有限宽度网络。相关的计算负担是大型数据集中应用的另一个问题。

上面提到的贝叶斯方法需要配置超参数的先验分布。Li 等 (2019 ^[69]) 提出了一种完全无分布的密度估计方法，称为深度分布回归 (DDR)，其中使用具有离散 bin 的直方图来近似密度，并使用神经网络通过多类分类来估计离散化密度。虽然该方法是为回归问题设计的，但我们可以将这个想法扩展到我们的 DeepKriging 框架以进行预测分布估计。思路很简单，方法也很容易实现。我们称该方法为深度分布空间预测 (DDSP)，如下图所示。

S5.1 深度分布空间回归

我们通过 $Y(\mathbf{s}_0)|\mathbf{z}, \mathbf{x}_\phi (\mathbf{s}_0)$ 在未观测位置 $\mathbf{s}_0$ 处的条件分布来量化 DeepKriging 预测的不确定性。我们将概率密度函数 (PDF) 表示为 $f_{UQ}(y|x)$，其支持区间为 $[l, u]$，其中 $l$ 和 $u$ 分别为下限和上限。该区间可以由 $M$ 个切点划分为 $M + 1$ 个 bin，$T_m = [c_{m−1}, c_m)$，使得 $c_0 < c_1 < \ldots < c_M < c_{M+1}$，其中 $c_0 = l$ 和 $c_{M+1} = u$。令 $|T_m|$ 表示第 $m$ 个 bin 的长度，$p_m(\mathbf{s}_0) = \mathbb{P}\{Y(\mathbf{s}_0) \in T_m | \mathbf{z}, \mathbf{x}_\phi(\mathbf{s}_0)\}$ 是 $Y (\mathbf{s}_0)$ 落入第 $m$ 个 bin 的条件概率。然后 $f_{UQ}(y|x)$ 由 $M + 1$ 个常数函数 $p_m(\mathbf{s}_0)/|T_m|, m = 1, \ldots , M + 1$。密度预测指定为：

$$\hat{f}_{UQ}(y|x) = \sum^{M +1}_{m=1} \frac{\hat{p}_m(\mathbf{s}_0) }{|T_m|} \mathbb{1}\{ y \in T_m\} \tag{S5.2}$$

式 (S5.2) 中的关键步骤是使用分类模型估计 bin 概率 $\{\hat{p}_1(\mathbf{s}_0),\ldots ,\hat{p}_{M+1}(\mathbf{s}_0)\}$，从而可以应用神经网络。Li 等 (2019 ^[69]) 提出了不同的损失函数和 bin 划分方法。最自然的方法是使用固定 bin 的多分类。在输出层，应用 softmax 函数来确保 $\{\hat{p}_1(\mathbf{s}_0), \ldots,\hat{p}_{M+1}(\mathbf{s}_0)\}$ 构成有效概率向量。这种情况的损失函数是负多项式对数似然函数，相当于多类交叉熵损失：$\sum^{N}_{n=1} \sum^{M+1}_{m=1} \mathbb{1} \{z(\mathbf{s}_n) \in T_m \} \log \{p_m(\mathbf{s}_n)\}$。

然而，在实践中，采用固定多分类对连续密度函数进行估计对 bins 的选择很敏感。因此，对于 DeepKriging 中的深度分布空间回归，我们使用具有联合二元交叉熵损失函数 (JBCE) 和集成方法来改进选择。 JBCE 函数指定为

$$\text{JBCE} = \sum^{N}_{n=1} \sum^{M}_{m=1} [ \mathbb{1} \{z(\mathbf{s}_n) ≤ c_m \} \log \{F(c_m; \mathbf{s}_n)\} + \mathbb{1} \{z(\mathbf{s}_n) > c_m\} \log \{1 − F(c_m; \mathbf{s}_n)\}] \tag{S5.3}$$

其中 $F(c_m; \mathbf{s}_n) = \sum^{m}_{i=1} p_i(\mathbf{s}_n)$ 和 $c_m, m = 1, \ldots, M$ 是 $M$ 个切点。

深度分布空间预测可能会提供不平滑的密度。因此，可以应用集成方法通过拟合 $I$ 个独立分类并计算分类器的平均值来进一步调整。算法 1 提供了利用随机划分的集合获得 DeepKriging 密度预测的过程：

请注意，虽然密度回归提供了没有任何分布假设的不确定性量化，但它可能会从神经网络中带来新的不确定性。因此，如果用标准差量化，高斯过程表示可能是一种更好的不确定性方法，尽管计算负担会增加。

此外，如果我们应用集成方法，则密度预测需要进一步的计算，其中集成中的每个步骤都将使用新的随机切点选择单独实施分类。然而，集成在密度预测中的主要目标是获得平滑的密度。如果研究目标是在没有密度曲线的情况下使用分位数来获得不确定性，那么并不总是需要系综。我们需要在密度预测中指定的另一个超参数是 bin 大小 $M + 1$。通常，大 $M$ 将提供更复杂的密度模式，而小 $M$ 将提供更稳定的估计。在实践中，我们可以遵循 Freedman–Diaconis 规则（Freedman 和 Diaconis，1981 ^[62]）作为直方图近似中的稳健估计，使得 $M = \lfloor \{\max(\mathbf{z}) − \min(\mathbf{z})\}\frac{\sqrt[3]{N}}{2 \times IQR(\mathbf{z})} \rfloor$ ，其中 $IQR(\mathbf{z})$ 是观测值的四分位距。

S5.2 不确定性量化：模拟研究

模拟数据由一维高斯混合模型生成：

$$z(s) = \{ \sin(5s) + 0.7 + τ_1(s)\} π(s) + \{2 \sin(8s) + τ_2(s))\} (1 − π(s))$$

其中 $τ_1(s) \stackrel{i.i.d.} \sim \mathcal{N}(0, 0.22)$，$τ_2(s) \stackrel{i.i.d.} \sim \mathcal{N}(0, 0.32)$，$π(s) \stackrel{i.i.d.} \sim Bernoulli(0.5)$ 和 $τ_2(s)$。$τ_2(s)$ 和 $π(s)$ 相互独立。从 $[0, 1]$ 中的 $2, 500$ 个规则间隔位置抽取观测值，其中 $2, 000$ 个是训练样本，$500$ 个是测试样本。

图 S7 显示了训练样本和测试样本的预测结果。 DeepKriging 对于不确定性量化的优势是显而易见的。当 $s$ 大于 $0.8$ 时，该过程是异方差的，方差明显较大。 DeepKriging 很好地捕获了异方差性，但被 Kriging 遗漏了。而且，Kriging 的预测带对于大 $s$ 太窄，对于小 $s$ 大两倍。

对测试样本的数值评估进一步用于基于均方根误差 (RMSE) 和平均分位数损失 (AQTL) 的比较。 AQTL 定义为 $\text{AQTL} = \sum^{99}_{t=1} \sum^{N}_{n=1}(\{\mathbf{z}(s_n)−\hat{Q}(t/100)\} [t/100− \mathbb{1} \{\mathbf{z}(s_n) \leq \hat{Q}(t/100) \}])$，其中 $\hat{Q}(t/100)$ 是估计的第 $t$ 个百分位数。

图 S7：高斯混合模型的预测结果。蓝点是从高斯混合模型模拟的观测结果。实线分别是真实过程（黄色）和 DeepKriging（红色）和 Kriging（蓝色）的预测。虚线分别代表 DeepKriging（红色）和 Kriging（蓝色）的 95% 预测带。

结果表明，Kriging 的 RMSE ($0.490$) 与 DeepKriging ($0.485$) 相当。但是，就分位数损失而言，Kriging 的 AQTL（$60.47$）远大于 DeepKriging 的 AQTL（$0.12$），这进一步暗示 Kriging 仅在均方误差方面是一个很好的估计，它反映了均值和方差，但不能反映分位数等其他重要性质。

S6.源代码和数据

• 源代码可在以下 Github 存储库中找到：https://github.com/aleksada/DeepKriging 。

• 这些方法是在 Keras 中实现的，Keras 是 Python 和 R 的库。本文工作的大部分代码都是用 Python 编写的。我们还提供了一些在 R 中使用 Keras 的 DeepKriging 的简单示例。

• 应用中使用的来自 AQS 的 PM2.5 站数据可以在 https://aqs.epa.gov/aqsweb/airdata/download_files.html 中找到。

• 应用中使用的来自NARR 的气象数据可以在 https://psl.noaa.gov/data/gridded/data.narr.html 中找到。

参考文献

• [1] Adgate, J. L., Ramachandran, G., Pratt, G., Waller, L., and Sexton, K. (2002). Spatial and temporal variability in outdoor, indoor, and personal PM2.5 exposure. Atmospheric Environment, 36(20):3255–3265.
• [2] Adler, R. J. (2010). The Geometry of Random Fields. SIAM.
• [3] Anselin, L. (2001). Spatial econometrics. A Companion to Theoretical Econometrics, 310330.
• [4] Austin, M. (2002). Spatial prediction of species distribution: an interface between ecological theory and statistical modeling. Ecological Modeling, 157(2-3):101–118
• [5] Banerjee, S., Finley, A. O., Waldmann, P., and Ericsson, T. (2010). Hierarchical spatial process models for multiple traits in large genetic trials. Journal of the American Statistical Association, 105(490):506–521.
• [6] Banerjee, S., Gelfand, A. E., Finley, A. O., and Sang, H. (2008). Gaussian predictive process models for large spatial data sets. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 70(4):825–848.
• [7] Cheng, H.-T., Koc, L., Harmsen, J., Shaked, T., Chandra, T., Aradhye, H., Anderson, G., Corrado, G., Chai, W., Ispir, M., et al. (2016). Wide & deep learning for recommender systems. In Proceedings of the 1st workshop on deep learning for recommender systems, pages 7–10.
• [8] Cho, Y. and Saul, L. K. (2009). Kernel methods for deep learning. In Advances in neural information processing systems, pages 342–350.
• [9] Cracknell, M. J. and Reading, A. M. (2014). Geological mapping using remote sensing data: A comparison of five machine learning algorithms, their response to variations in the spatial distribution of training data and the use of explicit spatial information. Computers & Geosciences, 63:22–33.
• [10] Cressie, N. (1990). The origins of kriging. Mathematical Geology, 22(3):239–252.
• [11] Cressie, N. (2015). Statistics for Spatial Data. John Wiley & Sons.
• [12] Cressie, N. and Johannesson, G. (2008). Fixed rank kriging for very large spatial data sets. Journal of the Royal Statistical Society: Series B, 70(1):209–226
• [13] Csaji, B. C. (2001). Approximation with artificial neural networks. Faculty of Sciences, Etvs Lornd University, Hungary, 24:48.
• [14] DeGroot, M. H. (2005). Optimal Statistical Decisions, volume 82. John Wiley & Sons.
• [15] Di, Q., Kloog, I., Koutrakis, P., Lyapustin, A., Wang, Y., and Schwartz, J. (2016). Assessing PM2.5 exposures with high spatiotemporal resolution across the continental United States. Environmental Science & Technology, 50(9):4712–4721.
• [16] Dubrule, O. (1983). Two methods with different objectives: splines and kriging. Journal of the International Association for Mathematical Geology, 15(2):245–257.
• [17] Dubrule, O. (1984). Comparing splines and kriging. Computers & Geosciences, 10(2-3):327–338.
• [18] EPA, U. (2012). National ambient air quality standards (NAAQS). https://www.epa.gov/ criteria-air-pollutants/naaqs-table. Date accessed: [Dec 15, 2019].
• [19] Fan, J., Ma, C., and Zhong, Y. (2019). A selective overview of deep learning. arXiv preprint arXiv:1904.05526.
• [20] Fong, C. and Tyler, M. (2021). Machine learning predictions as regression covariates. Political Analysis, 29(4):467–484.
• [21] Franchi, G., Yao, A., and Kolb, A. (2018). Supervised deep kriging for single-image superresolution. In German Conference on Pattern Recognition, pages 638–649. Springer.
• [22] Friedman, J., Hastie, T., and Tibshirani, R. (2001). The Elements of Statistical Learning. Springer
• [23] Fuentes, M. (2002). Spectral methods for nonstationary spatial processes. Biometrika, 89(1):197–210.
• [24] Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep Learning. MIT Press.
• [25] Heaton, M. J., Datta, A., Finley, A. O., Furrer, R., Guinness, J., Guhaniyogi, R., Gerber, F., Gramacy, R. B., Hammerling, D., Katzfuss, M., et al. (2019). A case study competition among methods for analyzing large spatial data. Journal of Agricultural, Biological and Environmental Statistics, 24(3):398–425.
• [26] Hennessey Jr, J. P. (1977). Some aspects of wind power statistics. Journal of Applied Meteorology, 16(2):119–128.
• [27] Higdon, D. (2002). Space and space-time modeling using process convolutions. In Quantitative methods for current environmental issues, pages 37–56. Springer.
• [28] Imai, K. and Khanna, K. (2016). Improving ecological inference by predicting individual ethnicity from voter registration records. Political Analysis, 24(2):263–272.
• [29] Jacob, D. J. and Winner, D. A. (2009). Effect of climate change on air quality. Atmospheric Environment, 43(1):51–63.
• [30] Katzfuss, M. (2017). A multi-resolution approximation for massive spatial datasets. Journal of the American Statistical Association, 112(517):201–214.
• [31] Kleiber, W. and Nychka, D. W. (2015). Equivalent kriging. Spatial Statistics, 12:31–49.
• [32] Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). ImageNet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems, pages 1097–1105.
• [33] LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learning. Nature, 521(7553):436–444.
• [34] Lee, J., Sohl-Dickstein, J., Pennington, J., Novak, R., Schoenholz, S., and Bahri, Y. (2018). Deep neural networks as Gaussian processes. International Conference on Learning Representations.
• [35] Lehmann, E. L. and Casella, G. (2006). Theory of point estimation. Springer Science & Business Media.
• [36] Li, Y. and Sun, Y. (2019). Efficient estimation of non-stationary spatial covariance functions with application to high-resolution climate model emulation. Statistica Sinica, 29(3):12091231.
• [37] Matheron, G. (1963). Principles of geostatistics. Economic Geology, 58(8):1246–1266.
• [38] Matheron, G. (1981). Splines and kriging: their formal equivalence. Down-to-Earth-Statistics: Solutions Looking for Geological Problems, pages 77–95.
• [39] Najafabadi, M. M., Villanustre, F., Khoshgoftaar, T. M., Seliya, N., Wald, R., and Muharemagic, E. (2015). Deep learning applications and challenges in big data analytics. Journal of Big Data, 2(1):1.
• [40] Neal, R. M. (1994). Priors for infinite networks. Technical Report.
• [41] Neal, R. M. (1996). Bayesian Learning for Neural Networks, volume 118. Springer Science Business Media.
• [42] Nychka, D., Bandyopadhyay, S., Hammerling, D., Lindgren, F., and Sain, S. (2015). A multiresolution Gaussian process model for the analysis of large spatial datasets. Journal of Computational and Graphical Statistics, 24(2):579–599.
• [43] Paciorek, C. J. and Schervish, M. J. (2004). Nonstationary covariance functions for Gaussian process regression. In Advances in Neural Information Processing Systems, pages 273–280.
• [44] Peng, R. D., Bell, M. L., Geyh, A. S., McDermott, A., Zeger, S. L., Samet, J. M., and Dominici, F. (2009). Emergency admissions for cardiovascular and respiratory diseases and the chemical composition of fine particle air pollution. Environmental Health Perspectives, 117(6):957–963.
• [45] Peters, A., Dockery, D. W., Muller, J. E., and Mittleman, M. A. (2001). Increased particulate air pollution and the triggering of myocardial infarction. Circulation, 103(23):2810–2815.
• [46] Porter, W. C., Heald, C. L., Cooley, D., and Russell, B. (2015). Investigating the observed sensitivities of air-quality extremes to meteorological drivers via quantile regression. Atmospheric Chemistry and Physics, 15(18):10349–10366.
• [47] Reich, B. J., Fuentes, M., and Dunson, D. B. (2011). Bayesian spatial quantile regression. Journal of the American Statistical Association, 106(493):6–20.
• [48] Rimstad, K. and Omre, H. (2014). Skew-Gaussian random fields. Spatial Statistics, 10:43–62.
• [49] Sampson, P. D., Richards, M., Szpiro, A. A., Bergen, S., Sheppard, L., Larson, T. V., and Kaufman, J. D. (2013). A regionalized national universal Kriging model using partial least squares regression for estimating annual PM2.5 concentrations in epidemiology. Atmospheric Environment, 75:383–392.
• [50] Stein, M. L. (2014). Limitations on low rank approximations for covariance matrices of spatial data. Spatial Statistics, 8:1–19.
• [51] Vidakovic, B. (2009). Statistical Modeling by Wavelets, volume 503. John Wiley & Sons.
• [52] Wahba, G. (1990). Spline Models for Observational Data, volume 59. SIAM.
• [53] Waller, L. A. and Gotway, C. A. (2004). Applied Spatial Statistics for Public Health Data, volume 368. John Wiley & Sons.
• [54] Whittle, P. (1954). On stationary processes in the plane. Biometrika, pages 434–449.
• [55] World Health Organization (2013). Health effects of particulate matter. Policy implications for countries in eastern Europe, Caucasus and central Asia, 1(1):2–10.
• [56] Xu, G. and Genton, M. G. (2017). Tukey g-and-h random fields. Journal of the American Statistical Association, 112(519):1236–1249.
• [57] Ba, S., Joseph, V. R., et al. (2012). Composite gaussian process models for emulating expensive functions. The Annals of Applied Statistics, 6(4):1838–1860.
• [58] Banerjee, K. S. (1973). Generalized inverse of matrices and its applications. Technometrics, 15(1):197–197.
• [59] Blomqvist, K., Kaski, S., and Heinonen, M. (2019). Deep convolutional gaussian processes. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases, pages 582–597. Springer
• [60] Damianou, A. and Lawrence, N. (2013). Deep gaussian processes. In Artificial Intelligence and Statistics, pages 207–215.
• [61] Diggle, P. J., Thomson, M. C., Christensen, O., Rowlingson, B., Obsomer, V., Gardon, J., Wanji, S., Takougang, I., Enyong, P., Kamgno, J., et al. (2007). Spatial modelling and the prediction of loa loa risk: decision making under uncertainty. Annals of Tropical Medicine & Parasitology, 101(6):499–509.
• [62] Freedman, D. and Diaconis, P. (1981). On the histogram as a density estimator: L2 theory. Zeitschrift f ̈ ur Wahrscheinlichkeitstheorie und verwandte Gebiete, 57(4):453–476.
• [63] Gal, Y. and Ghahramani, Z. (2016). Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In International Conference on Machine Learning, pages 1050–1059.
• [64] GPy (since 2012). GPy: A Gaussian process framework in python. http: //github.com/SheffieldML/GPy.
• [65] Ketkar, N. et al. (2017). Deep Learning with Python. Springer.
• [66] Kingma, D. P. and Ba, J. (2014). Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980.
• [67] Kumar, V., Singh, V., Srijith, P., and Damianou, A. (2018). Deep gaussian processes with convolutional kernels. arXiv preprint arXiv:1806.01655.
• [68] Lee, J., Bahri, Y., Novak, R., Schoenholz, S. S., Pennington, J., and Sohl Dickstein, J. (2017). Deep neural networks as gaussian processes. arXiv preprint arXiv:1711.00165.
• [69] Li, R., Bondell, H. D., and Reich, B. J. (2019). Deep distribution regression. arXiv preprint arXiv:1903.06023.
• [70] Posch, K., Steinbrener, J., and Pilz, J. (2019). Variational inference to measure model uncertainty in deep neural networks. arXiv preprint arXiv:1902.10189.
• [71] Zammit-Mangion, A., Ng, T. L. J., Vu, Q., and Filippone, M. (2019). Deep compositional spatial models. arXiv preprint arXiv:1906.02840.