🔥 神经过程(NP)

【摘 要】 神经网络 (NN) 是一种参数化函数，可以通过梯度下降进行调优，以高精度逼近有标签数据集。另一方面，高斯过程 (GP) 是一种概率模型，它定义了函数的分布，并利用概率推断规则根据数据进行更新。高斯过程具有概率性、数据效率和灵活性，但也是计算密集型的，因此适用范围受到了限制。在本文中，我们介绍了一类神经网络隐变量模型，我们称之为神经过程 (Neural Processes，NP)，它结合了两种方法的优点。与高斯过程一样，神经过程用于定义函数的分布，能够快速适应新观测，并且在预测时能够同步估计其不确定性。与神经网络一样，神经过程在训练和评估期间的计算效率很高，但同时能够学习根据数据调整先验。我们展示了神经过程在一系列学习任务中的表现，包括回归和优化，并与文献中的相关模型进行了比较和对比。

【原 文】 Garnelo, Marta, Jonathan Schwarz, Dan Rosenbaum, Fabio Viola, Danilo J. Rezende, S. M. Ali Eslami, and Yee Whye Teh. “Neural Processes.” arXiv, July 4, 2018. http://arxiv.org/abs/1807.01622.

1 简介

函数逼近是机器学习中众多问题的核心，深度神经网络是过去十年实现此目的最流行的方法。在高层次上，神经网络构成了一个黑盒函数逼近器，它从大量训练数据学习参数化的单一函数。因此，其大部分工作负载都落在训练阶段，而评估和测试阶段则主要是快速的前向传递。尽管对于许多实际应用来说，神经网络的高测试时间性能非常有价值，但其输出无法在训练后动态更新却也是一个显著事实（注：其实就是想说输出缺少不确定性），这在某些场景下并不可取。元学习正是解决此局限性的一个受欢迎的研究领域（Sutskever 等，2014 年^[38]；Wang 等，2016 年 ^[42]；Vinyals 等，2016 年^[41]；Finn 等，2017 年^[12]）。 作为一种替代方法，我们还可以对随机过程进行推断以执行函数回归。此类方法最常见的例子是高斯过程 (GP)，这是一种与神经网络之间具有互补性的模型：高斯过程没有昂贵的训练阶段，并且能够根据某些（可能含噪声的）观测对真实函数进行推断（注：其推断本质上只是简单地计算协方差），这使其在测试（或预测）阶段非常灵活。此外，在未被观测到的位置处，高斯过程能够表示无限多个不同的函数，从而在给定一些观测时，能够捕获其预测的不确定性。不过，高斯过程的计算成本很高：在其原始计算公式中，其计算成本是数据点数量的三次方规模，即便当前最先进的近似方法也仍然需要二次方规模 (Quinonero-Candela & Rasmussen, 2005)。此外，高斯过程的核通常在功能形式上有一些约束条件，需要另外一套优化程序来为给定任务识别出最优核和超参数。 因此，人们越来越有兴趣将神经网络与随机过程结合起来，作为解决两者某些缺点的解决方案（Huang 等，2015 年；Wilson 等，2016 年）。 在本文工作中，我们将介绍一种基于神经网络的、能够学习随机过程近似的新方法，我们称之为 **神经过程 (Neural Processes, NPs)**。神经过程展示了高斯过程的一些基本特性，即对函数的分布进行建模，能够根据观测来估计预测的不确定性，并将一些工作负载从训练阶段转移到测试阶段，从而实现模型灵活性。至关重要的是，神经过程以计算高效的方式生成预测。给定 $n$ 个已观测的背景点和 $m$ 个目标点的情况下（注：在高斯过程文献中通常分别被称为训练点和测试点），使用训练过的神经过程做推断，本质上只需要在深度神经网络中做前向传递即可，其运行时间的规模比例为 $\mathcal{O}(n+m)$， 而不是经典高斯过程的 $\mathcal{O}((n+m)^3)$。此外，神经过程能够直接从数据中学习 **隐式核**，从而克服许多功能设计上的限制。 我们的主要贡献是： - （1） 引入了神经过程，这是一类结合了神经网络和随机过程优点的新模型。 - （2） 将神经过程与元学习、深度隐变量模型和高斯过程中的相关工作进行比较。鉴于神经过程与其中许多领域相关，它们构成了许多相关主题之间进行比较的桥梁。 - （3） 将神经过程应用于一系列任务，包括一维回归、真实场景图像补全、贝叶斯优化和背景赌博机，展示了神经过程的优势和能力。 ## 2 神经过程模型 ### 2.1 用神经网络近似随机过程 通过有限维的边缘分布来定义随机过程是一种标准方法。具体来说，我们将过程视为一个随机函数 $F : \mathcal{X} \rightarrow \mathcal{Y}$，并且对于任意有限序列 $x_{1:n} = (x_1,\ldots,x_n)$ 且 $x_i \in \mathcal{X}$，我们定义函数值 $Y_{1:n} := (F(x_1), \ldots , F(x_n))$ 上的边缘联合分布。例如，在高斯过程情况下，联合分布是由均值和协方差函数参数化的一个多元高斯分布。 如果给定一个联合分布 $ρ_{x_{1:n}}$，定义一个能够使 $ρ_{x_{1:n}}$ 是其边缘分布的随机过程 $F$（即 $ρ_{x_{1:n}}$ 是 $F$ 的边缘分布 $(F(x_1),\ldots, F(x_n))$ ），存在两个必要条件： **可交换性** 和 **一致性**。根据 Kolmogorov 扩展定理 (Øksendal, 2003) ，这两者是定义一个随机过程的充分条件。 **【可交换性】** ：此条件要求联合分布对于 $x_{1:n}$ 中的元素具有排列不变性，或者说元素的前后顺序不会改变联合分布。更准确地说，对于有限的 $n$，如果 $π$ 是 $\{1, \ldots , n\}$ 的一个排列, 那么联合分布 $ρ_{x_{1:n}}(y_{1:n})$ 应当满足: $$ \begin{align*} ρ_{x_{1:n}}(y_{1:n}) &:= ρ_{x_1,\ldots ,x_n}(y_1,\ldots, y_n)\\ &=ρ_{x_{π(1)},\ldots ,x_{π(n)}} (y_{π(1)},\ldots , y_{π(n)}) =: ρ_{π(x_{1:n})} (π(y_{1:n})) \end{align*} \tag{1} $$ 其中 $π(x_{1:n}) := (x_{π(1)},\ldots,x_{π(n)})$ 和 $π(y_{1:n}) := (y_{π(1)},\ldots,y_{π(n)})$ 。 **【一致性】** ：此条件也被称为边缘化性质。如果我们边缘化掉了序列的一部分，则新序列上定义的边缘分布与原序列上定义的边缘分布应当保持一致。更准确地说，如果 $1 \leq m \leq n$，则： $$ ρ_{x_{1:m}} (y_{1:m}) = \int ρ_{x_{1:n}} (y_{1:n}) d y_{m+1:n} \tag{2} $$ **【示例】** 考虑三个不同的序列 $x_{1:n}$、$π(x_{1:n})$ 和 $x_{1:m}$ ，其对应的联合分布分别为 $ρ_{x_{1:n}}$ 、$ρ_{π(x_{1:n})}$ 和 $ρ_{x_{1:m}}$。为了使这三个联合分布都是随机过程 $F$ 给出的边缘分布，则它们必须满足上面的 `式 1` 和 `式 2`。 **【高斯过程的解析形式】** 给定随机过程的某个特定实例 $f$，联合分布被定义为： $$ ρ_{x_{1:n}} (y_{1:n}) = \int p(f) p(y_{1:n} \mid f, x_{1:n}) df \tag{3} $$ 这里 $p$ 表示随机量上的抽象概率分布。 与理想的高斯过程 $Y_i = F(x_i)$ 不同，我们通常会在模型中添加一些观测噪声，即令 $Y_i \sim \mathcal{N}(F(x_i),σ^2)$ 并将 $p$ 定义为（因为是高斯过程，所以是高斯的）： $$ p(y_{1:n} \mid f, x_{1:n}) = \prod^{n}_{i=1} \mathcal{N}(y_i|f(x_i), σ^2) \tag{4} $$ 将其代入`式 3`，则可以得到随机过程的如下解析表达形式： $$ ρ_{x_{1:n}} (y_{1:n}) = \int p(f) \prod^{n}_{i=1} \mathcal{N}(y_i \mid f(x_i), σ^2) df \tag{5} $$ 换句话说，联合分布集 $\{ ρ_{x_{1:n}} \}$ 的可交换性和一致性意味着：存在一个能够使得观测 $Y_{1:n}$ 成为其上的独立同条件分布的随机过程 $F$。这基本上对应于 **de Finetti 定理** 的条件分布版本（注：该定理锚定了大部分贝叶斯非参数方法，参见 De Finetti, 1937 ^[8]）。 **【神经过程近似方法】** 为了使用神经过程表示随机过程，我们将用神经网络对其进行近似。假设 $F$ 可以由高维随机向量 $z$ 参数化，并记为 $F(x) = g(x,z)$，其中 $g$ 是某些固定、可学习的函数（即 $F$ 的随机性依赖于对 $z$ 的指定）。 根从 `式 (5)` 可以推导出来一个生成式模型（`图 1a`）： $$ p(z, y_{1:n} \mid x_{1:n}) = p(z) \prod^{n}_{i=1} \mathcal{N}(y_i|g(x_i, z), σ^2) \tag{6} $$ 其中，根据变分自动编码器的思想，我们假设 $p(z)$ 是多元标准正态分布，而 $g(x_i, z)$ 是一个捕捉模型复杂性的神经网络。  > **图 1: 神经过程模型**。 (a) 神经过程的概率图模型。 $x$ 和 $y$ 是对应于 $y = f(x)$ 的数据。 $C$ 和 $T$ 分别是背景点和目标点的数量，$z$ 是全局隐变量。灰色圈表示变量是已观测变量。 (b) 神经过程的计算实现图。圆圈中的变量对应于 (a) 中图模型的变量，方框中的变量对应于 _神经过程_ 的中间表示，无边框的粗体字母对应于以下计算模块：$h$ - 编码器，$a$ - 聚合器和 $g$ - 解码器。在我们的实现中，$h$ 和 $g$ 对应于神经网络，$a$ 对应于均值函数。图中的实线描述了生成过程，虚线描述了推断过程。 **【可交换性的学习】** 想要学习一个随机函数的分布，而不是学习一个确定的函数，有必要使用多个数据集来训练系统，其中每个数据集都是 $x_{1:n}$ 和 $y_{1:n}$ 的一种序列形式，这样我们就可以从数据集的可变性中学习随机函数的可变性（参见`第 2.2 节`）。 由于解码器 $g$ 是非线性的，我们可以使用摊销变分推断来学习它。令 $q(z|x_{1:n}, y_{1:n})$ 为隐变量 $z$ 的变分后验（即真实后验的变分近似），并且能够被另一个对 $x_{1:n}$ 和 $y_{1:n}$ 的排列具有不变性的神经网络参数化。则证据下界 (ELBO) 可以由下式给出： $$ \log p(y_{1:n}|x_{1:n}) \geq \mathbb{E}_{q(z | x_{1:n} ,y_{1:n})} \left [ \sum^{n}_{i=1} \log p(y_i|z, x_i) + \log \frac{p(z)}{q(z | x_{1:n}, y_{1:n})} \right] \tag{7} $$ 在另一个更能反映测试所需的改进目标函数中，我们将整个数据集拆分成背景集 $x_{1:m}, y_{1:m}$ 和目标集 $x_{m+1:n},y_{m+1:n}$，并对给定背景集时的目标进行条件建模： $$ \log p(y_{m+1:n}|x_{1:n}, y_{1:m}) \geq \mathbb{E}_{q(z|x_{1:n},y_{1:n})} \left [\sum^{n}_{i=m+1} \log p(y_i|z, x_i) + \log \frac{p(z|x_{1:m}, y_{1:m})}{q(z|x_{1:n}, y_{1:n})} \right ] \tag{8} $$ 请注意，上式中的先验条件分布 $p(z|x_{1:m}, y_{1:m})$ 是 intractable 的，我们采用变分后验 $q(z|x_{1:m}, y_{1:m})$ 来近似它: $$ \log p(y_{m+1:n} | x_{1:n}, y_{1:m}) \geq \mathbb{E}_{q(z|x_{1:n} ,y_{1:n})} \left[\sum^{n}_{i=m+1} \log p(y_i | z, x_i) + \log \frac{q(z|x_{1:m}, y_{1:m})}{q(z|x_{1:n}, y_{1:n})} \right ] \tag{9} $$ ### 2.2 函数的分布 神经过程的一个关键动机是能够表示随机函数的分布而不是仅得到一个函数。为了训练这样的模型，我们需要一个反映此任务的训练过程。 更具体地说，为了训练神经过程，我们需要从基础分布 $\mathcal{D}$ 中采样并构造一个由很多函数 $f : X \rightarrow Y$ 支撑的数据集。作为一个说明性示例，考虑一个由若干函数 $f_d(x) \sim \mathcal{GP}$ 构成的数据集，并且这些函数是同一高斯过程（即具有固定核）的样本。对于每个函数 $f_d(x)$，数据集中均包含多个相应的 $(x, y)_i$ 元组，其中 $y_i = f_d(x_i)$。出于训练目的，我们将这些点划分为 $n$ 个背景点构成的背景集 $C = \{(x, y)_i\}^{n}_{i=1}$ 和 $n + m$ 个目标点构成的目标集 $T = \{(x, y)_i \}^{n+m}_{i=1}$，注意：目标集由 $C$ 中的所有点以及 $m$ 个无标签点一起组成。在测试期间，模型由某些背景集 $C$ 表征，并且要预测出目标位置 $x_T$ 处的目标值 $y_T =f(x_T)$。 为了准确预测整个数据集，模型需要在训练阶段学习一个能够覆盖所有已观测函数的分布，并且在测试阶段仍然能够将这些背景点纳入考虑。 ### 2.3 全局隐变量 如 `第 2.1 节` 所述，神经过程中包含一个用于捕获随机过程 $F$ 的全局隐变量 $z$。该隐变量特别令人感兴趣，因为它捕获了全局的不确定性，使我们能够在全局层面一次获得一个函数样本 $f_d$；而不是在局部的层面一次获得一个对应于输入 $x_i$ 的输出 $y_i$（注：独立于剩余 $y_T$ ）。

可以理解为每个 $z$ 的样本，对应于随机函数的一次实现。

此外，由于通过唯一的 $z$ 传递了所有背景集信息，因此我们可以在贝叶斯框架中来形式化该模型： - **先验**： 当没有背景集 $C$ 时，隐分布 $p(z)$ 对应于模型在训练期间学得的特定数据先验。 - **后验**： 当我们添加观测时，由模型编码的隐分布相当于在给定背景集时在函数上的后验 $p(z|C)$。 最重要的是，如 `式 9` 所示，我们并不使用无信息先验 $p(z)$，而是使用以背景集为条件的先验。因此，此先验相当于底层函数的低信息后验。这个公式清楚地表明，当包含其他背景点时，给定某个背景子集时的后验可以用作先验。通过使用此设置并使用不同大小的背景集进行训练，学得的模型将在背景点数量和位置方面具有更大灵活性。 ### 2.4 神经过程模型的实现 在神经过程的实现中，考虑了两个额外的需求：对于背景点排列的不变性和计算效率。最终模型可以被归纳为三个核心组件（见`图 1b`）： **【编码器】**：从输入空间到表示空间的编码器 $h$，该编码器接受成对的 $(x, y)_i$ 背景点，并为每一个配对生成相应的表示 $r_i = h((x, y)_i)$。编码器 $h$ 由一个神经网络进行参数化建模。 **【聚合器】**：汇总输入编码的聚合器 $a$ 。我们对获得一个具有排序不变性的全局表示 $r$ 感兴趣，它应当能够被用于（参数化的）隐分布 $z \sim \mathcal{N}(μ(r), I_σ(r))$。在实际工作中，我们选择均值函数 $r = a(r_i) = \frac{1}{n} \sum^{n}_{i=1} r_i$ 作为聚合器。至关重要的是，聚合器将运行时间减少到 $\mathcal{O}(n + m)$，其中 $n$ 和 $m$ 分别是背景点数量和目标点数量。 **【条件解码器】**：条件解码器 $g$ 的输入是全局隐变量 $z$ 的一个样本和目标输入 $x_T$，输出 $f(x_T) = y_T$ 的相应预测结果 $\hat{y}_T$。 ## 3 相关工作  > 图 2: 相关模型 (a-c) 和神经过程 (d) 的图模型。灰色阴影表示观测变量。 C 代表背景变量，T 代表目标变量，即给定 C 待预测的变量。 ### 3.1 条件神经过程 **（1）与条件神经过程的关系** 神经过程是条件神经过程 (CNP) 的泛化（ Garnelo 等，2018 ^[15] ）。条件神经过程共享神经过程背后的大部分想法，但缺少允许全局采样的隐变量（参见 `图 2c` 的模型图）。因此，条件神经过程无法为相同的背景点数据生成不同的函数样本，也就是说缺少不确定性建模能力。

条件神经过程与神经过程之间的关系

值得一提的是，最初的条件神经过程确实包括了除确定性连接之外的隐变量实验。但鉴于与预测确定性联系，全局隐变量的作用尚不清楚。相比之下，神经过程构成了对确定性条件神经过程的更明确的泛化，与其他隐变量模型和近似贝叶斯方法具有更强的相似性。这些相似之处使我们能够将本模型与广泛的相关研究领域进行比较。

**（2）与生成查询网络的关系** 神经过程和条件神经过程一起都可以被视为是 **生成查询网络 (GQN)** 的泛化，GQN 采用了类似训练过程来预测 3D 场景中给定背景观测的新视点（Eslami 等，2018 ^[11]）。 Consistent GQN 是 GQN 的扩展，专注于生成一致性样本，因此与神经过程也密切相关 (Kumar 等, 2018 ^[21])。 ### 3.2 高斯过程 **（1）概况** 神经网络算法适合直接从大量数据中学习单一函数；而高斯过程可以表示函数族的分布，并且该函数族会受到两点之间（某种假设形式的）协方差函数约束。在两者之间的广大范围内，存在大量可以将 _贝叶斯非参数思想_ 与 _神经网络_ 相结合的最新研究成果。例如： - Calandra 等,（2016 ^[6]）; Huang 等, （2015 ^[18]) 的方法接近于纯粹的高斯过程，但使用神经网络对输入数据进行了预处理。 - 深度高斯过程（DGP）与神经网络在概念上有相似之处，因为两者均通过堆叠高斯过程以获得深度模型（Damianou & Lawrence，2013 ^[7]）。 - 与神经网络更相似的方法包括：使用高斯过程对权重进行采样的神经网络（Wilson 等，2011 年 ^[44]）或每个单元代表不同核的神经网络（Sun 等，2018 年 ^[37]）。 **（2）与匹配网络和深度核学习的关系** 在此范围内，有两个模型与神经过程密切相关： - 一是 **匹配网络(MN)**, Vinyals 等 (2016 ^[41]) ; - 二是 **深度核学习(DKL)**, Wilson 等 (2016 ^[45])。 与神经过程一样，两者都使用神经网络从数据中提取表示。与上述两者将特征表示传递给显式的距离核不同，神经过程隐式地学习 “核” 。其中： - _匹配网络_ 使用显式核来测量背景点和目标点之间的相似性，以进行 few-shot 分类； - _深度核学习_ 的显式核则用于参数化高斯过程。 显式核使 _匹配网络_ 和 _深度核学习_ 的计算复杂度分别为 $\mathcal{O}(n^2)$ 和 $\mathcal{O}(n^3)$，而本文的神经过程则为 $\mathcal{O}(n + m)$。 为了克服这种自身的计算复杂性问题： - _深度核学习_ ： 将标准高斯过程替换为 KISS-GP (Wilson & Nickisch, 2015 ^[43]) ，从而给出了近似核。 - _匹配网络_ ： 引入原型网络 (Snell 等, 2017 ^[35]) 作为更轻量级的版本，可以实现 $\mathcal{O}(n + m)$。 **（3）与变分隐过程的关系** 最后，Ma 等也引入了变分隐过程，而且与神经过程的大部分想法类似，但采用了高斯过程形式实现（Ma 等，2018 ^[26]）。与之相比，神经过程可以被解释为其隐随机过程的神经网络实现。

作者原文： 在从神经网络到高斯过程的这个范围内， 神经过程比上面提到的大多数模型更接近神经网络这一端。由于放弃了对核的明确定义，神经过程失去了高斯过程的一些数学保证，但有助于数据驱动的 “先验” 和计算效率。

### 3.3 元学习 - 在当代元学习词汇中，神经过程和高斯过程可以看作是 **“小样本函数估计”** 的方法。在本节中，我们将与可用于同一目的的相关模型进行比较。一个突出的例子是匹配网络 (Vinyals 等, 2016)，但是有大量类似的分类模型文献 (Koch 等, 2015; Santoro 等, 2016)，强化学习 (Wang 等, 2016 年）、参数更新（Finn 等，2017 年；2018 年）、自然语言处理（Bowman 等，2015 年）和程序归纳（Devlin 等，2017 年）。 - 相关的是生成式元学习方法，它对数据密度进行少样本估计（van den Oord 等，2016 年；Reed 等，2017 年；Bornschein 等，2017 年；Rezende 等，2016 年）。

作者原文： 元学习模型与神经过程具有相同基本思想： 将工作量从训练阶段转移到了测试阶段。正是因为如此，神经过程也可以被解释为一种用于少样本函数回归的元学习算法，不过，正如 Garnelo 等 (2018 ^[15]) 所示，神经过程还可以应用于回归之外的学习任务。

### 3.4 贝叶斯方法 **（1）与分层贝叶斯的关系** 元学习方法与其他研究领域（如高斯过程和贝叶斯方法）之间的联系并不总是很明显。有趣的是，Grant (2018 ^[16]) 等的工作给出了 “模型不可知元学习 (MAML）” ^[12] 和 “分层贝叶斯推断” 之间的关系。在本文工作中，MAML 的元学习性质被定义为任务特定变量的结果，并且这些变量在给定更高级别变量的情况下是条件独立的。这种分层描述可以重写为概率推断问题，并且由此产生的边缘似然 $p(y|C)$ 与原始 MAML 目标相匹配。 与此类似的，神经过程和分层贝叶斯方法之间的相似之处同样简单明晰。给定 `图 2d` 中的图模型，我们可以将条件边缘似然写成层次推断问题： $$ \log p(y_t|C, x_t) = \log \int p(y_t | z, x_t)p(z | C)dz \tag{10} $$ **（2）与贝叶斯神经网络的关系** 将贝叶斯方法和神经网络连接在一起的另一个领域是贝叶斯神经网络（Gal & Ghahramani，2016 年 ^[14]；Blundell 等，2015 年 ^[3]；Louizos 等，2017 年 ^[24]；Louizos 和 Welling，2017 年 ^[24]）。这些模型学习神经网络权重的概率分布，并使用权重的后验来估计给定 $y_C$ 时的 $y_T$ 值。在这种场景中，神经过程可以被认为是贝叶斯深度学习的一种摊销版本（注：摊销通常意味着 “某些模型参数是神经网络输入的函数”）。 ### 3.5 条件隐变量模型 条件隐变量模型（`图 2a`）学习条件分布 $p(y_T |y_C, z)$，其中 $z$ 是一个隐变量，可以对其进行采样以生成不同的预测。训练此类有向图模型非常棘手。与变分自动编码器（VAEs）一样 ^[30][19]，条件变分自动编码器（CVAE）使用对数似然的变分下界来逼近目标函数 ^[36]： $$ \log p(y_t|y_c) \geq \mathbb{E}_{q(z_T |y_c,y_t)} \left[ \log p(y_t|z_T, y_c) + \log \frac{p(z_T |y_c)}{ q(z_T |y_c, y_t)} \right] \tag{11} $$ 我们将 CVAE 的隐变量 $z_T$ 称为局部隐变量，以区别于稍后出现在模型中的全局隐变量。之所以称之为局部隐变量，是因为其针对每一个输出预测 $y_{T,i}$ 都会重新采样。而全局隐变量则仅采样一次，就可用于所有的输出预测 $y_t$ 。在 CVAE 中，通过在先验 $p(z_T |y_c)$ 和解码器 $p(y|z_T , y_c)$ 中添加依赖性来建模背景点条件，因此它们可以被视为背景点的某个确定性函数。 CVAE 已通过多种方式得到扩展，例如通过增加注意力机制（Rezende 等，2016 年 ^[31]）。另一个相关扩展是生成匹配网络 (GMNs）^[2]，其中条件输入以类似于匹配网络模型的方式进行预处理。 与这种场景非常相关更复杂 CVAE 版本是 **神经统计学家 (NS）**^[10]。与神经过程类似，神经统计学家包含一个全局隐变量 $z$，用于捕获全局不确定性（见`图 2b`）。 一个关键的区别是： **神经过程表示函数的分布，而神经统计学家表示集合的分布**。 由于神经统计学家不包含每个 $y$ 值对应的 $x$ 值，因此它不像高斯过程和神经过程那样捕获成对关系，而是捕获 $y$ 值的一般性分布。神经统计学家不是通过查询具有不同 $x$ 值的模型来生成不同的 $y$ 值，而是通过额外地局部隐变量（ $z_T$ ）采样来生成不同的 $y$ 值。 神经统计学家的 ELBO 反映了模型的层次性质：对局部隐变量和全局隐变量具有不同的期望。如果我们为了与神经过程进行更直接的比较而忽略局部隐变量，则其 ELBO 变为： $$ \log p(y_t, y_c) \geq \mathbb{E}_{q(z|y_c,y_t)} \left[ \log p(y_t|z) + \log \frac{p(z)}{q(z|y_c, y_t)} \right] \tag{12} $$ 值得注意的是，神经统计学家的先验 $p(z)$ 不以背景点为条件。另一方面，神经过程的先验是有条件的（`式 9`），这使训练目标更接近模型在测试时的使用方式。 ELBO 的另一个变体出现在变分同源编码器 (Hewitt 等, 2018 ^[17]) 中，该模型与神经统计学家非常相似，但使用单独的数据点子集进行背景和预测。 如 `图 2` 所示，神经过程和条件隐变量模型之间的主要区别在于： **缺少允许对隐分布进行目标采样的 $x$ 变量**。这一变化尽管看起来很小，但却极大地改变了应用范围。例如，有针对性的采样允许生成和完成任务（例如图像完成任务）或添加一些下游任务（例如使用神经过程进行强化学习）。 值得一提的是，所有条件隐变量模型也被应用于小样本分类问题，其中数据空间通常由输入元组 $(x, y)$ 组成，而不仅仅是单个输出 $y$。这些模型能够通过将分类框架化为不同类别对数似然之间的比较，或通过查看不同后验概率之间的 KL 散度来实现，克服了使用数据元组的需要。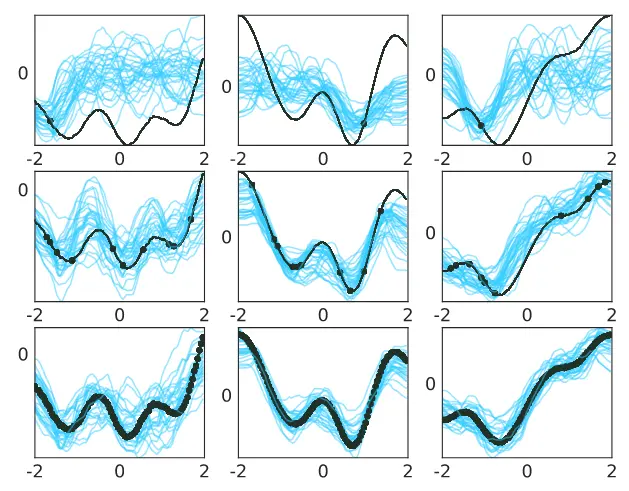 ## 4 结果  > 图 3. 一维函数回归。这些图显示了以越来越多的上下文点（每行分别为 1、10 和 100）为条件的曲线样本。真正的底层曲线显示为黑色，上下文点显示为黑色圆圈。每列对应一个不同的示例。只有一次观察，采样曲线之间远离该上下文点的方差很高。随着上下文点数量的增加，采样曲线越来越像地面真值曲线，并且整体方差减小。  > 图 4. MNIST 和 CelebA 上的逐像素回归 左图可视化了如何将逐像素图像补全构建为二维回归任务，其中 f（像素坐标）= 像素亮度。图表右侧的数字显示了 MNIST 和 CelebA 的图像补全结果。顶部的图像对应于提供给模型的上下文点。为了更清晰，未观察到的像素在 MNIST 图像中标为蓝色，在 CelebA 中标为白色。给定上下文点，每一行对应于不同的样本。随着上下文点数量的增加，预测像素会更接近底层像素，并且样本间的方差会减小。  > 图 5. 对一维目标函数使用神经过程进行 Thompson 采样。这些图显示了五次迭代的优化过程。每个预测函数（蓝色）是通过对以越来越多的上下文点（黑色圆圈）为条件的潜在变量进行采样来绘制的。底层真值函数被描绘为黑色虚线。红色三角形表示下一个评估点，对应于采样的NP曲线的最小值。以下迭代中的红色圆圈对应于此评估点，其基础真值作为 NP 的新上下文点。  > 表 1. 使用汤普森抽样的贝叶斯优化。达到高斯过程生成的一维函数的全局最小值所需的平均优化步骤数。这些值通过使用随机搜索所采取的步骤数进行归一化。具有正确内核的高斯过程的性能构成了性能的上限。  > 表 2. 增加 $δ$ 值时 wheel bandit 问题的结果。显示的是超过 $100$ 次试验的累积和简单后悔（最终政策质量的一种衡量标准）的平均误差和标准误差。结果相对于统一代理的性能做了归一化。  > 图 6. 具有不同 $δ$ 值的 wheel bandit 问题。 ## 5 讨论 本文介绍了神经过程，这是一个将随机过程和神经网络优点相结合的模型族。神经过程能够学习对 “函数的分布” 的表示，并在测试阶段根据某些背景点做出灵活预测。神经过程的优点在于： **不需要手工指定核，而是直接从数据中学习隐式度量**。 我们将神经过程应用于一系列回归任务以展示其灵活性。本文的目的是介绍神经过程并将其与其他研究进行比较。因此，此处呈现的任务比较多样化，但维度都相对比较低。我们期待未来的工作能够将神经过程扩展到更高维度，这可能有助于突出神经过程的两个优势： “较低计算复杂度” 和 “数据驱动的表示”。 ## 参考文献

• [1] Agrawal, S. and Goyal, N. Analysis of thompson sampling for the multi-armed bandit problem. In Conference on Learning Theory, pp. 39–1, 2012.
• [2] Bartunov, S. and Vetrov, D. P. Fast adaptation in generative models with generative matching networks. arXiv preprint arXiv:1612.02192, 2016.
• [3] Blundell, C., Cornebise, J., Kavukcuoglu, K., and Wierstra, D. Weight uncertainty in neural networks. arXiv preprint arXiv:1505.05424, 2015.
• [4] Bornschein, J., Mnih, A., Zoran, D., and J. Rezende, D. Variational memory addressing in generative models. In Advances in Neural Information Processing Systems, pp. 3923–3932, 2017.
• [5] Bowman, S. R., Vilnis, L., Vinyals, O., Dai, A. M., Jozefowicz, R., and Bengio, S. Generating sentences from a continuous space. arXiv preprint arXiv:1511.06349, 2015.
• [6] Calandra, R., Peters, J., Rasmussen, C. E., and Deisenroth, M. P. Manifold gaussian processes for regression. In Neural Networks (IJCNN), 2016 International Joint Conference on, pp. 3338–3345. IEEE, 2016.
• [7] Damianou, A. and Lawrence, N. Deep gaussian processes. In Artificial Intelligence and Statistics, pp. 207–215, 2013.
• [8] De Finetti, B. La pr ́ evision: ses lois logiques, ses sources subjectives. In Annales de l’institut Henri Poincar ́ e, volume 7, pp. 1–68, 1937.
• [9] Devlin, J., Bunel, R. R., Singh, R., Hausknecht, M., and Kohli, P. Neural program meta-induction. In Advances in Neural Information Processing Systems, pp. 2077–2085, 2017.
• [10] Edwards, H. and Storkey, A. Towards a neural statistician. arXiv preprint arXiv:1606.02185, 2016.
• [11] Eslami, S. A., Rezende, D. J., Besse, F., Viola, F., Morcos, A. S., Garnelo, M., Ruderman, A., Rusu, A. A., Danihelka, I., Gregor, K., et al. Neural scene representation and rendering. Science, 360(6394):1204–1210, 2018.
• [12] Finn, C., Abbeel, P., and Levine, S. Model-agnostic metalearning for fast adaptation of deep networks. arXiv preprint arXiv:1703.03400, 2017.
• [13] Finn, C., Xu, K., and Levine, S. Probabilistic modelagnostic meta-learning. arXiv preprint arXiv:1806.02817, 2018.
• [14] Gal, Y. and Ghahramani, Z. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In international conference on machine learning, pp. 1050–1059, 2016.
• [15] Garnelo, M., Rosenbaum, D., Maddison, C., Ramalho, T., Saxton, D., Shanahan, M., Teh, Y. W., Rezende, D. J., and Eslami, A. Conditional neural processes. In International Conference on Machine Learning, 2018.
• [16] Grant, E., Finn, C., Levine, S., Darrell, T., and Griffiths, T. Recasting gradient-based meta-learning as hierarchical bayes. arXiv preprint arXiv:1801.08930, 2018.
• [17] Hewitt, L., Gane, A., Jaakkola, T., and Tenenbaum, J. B. The variational homoencoder: Learning to infer high-capacity generative models from few examples. 2018.
• [18] Huang, W.-b., Zhao, D., Sun, F., Liu, H., and Chang, E. Y. Scalable gaussian process regression using deep neural networks. In IJCAI, pp. 3576–3582, 2015.
• [19] Kingma, D. P. and Welling, M. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114, 2013.
• [20] Koch, G., Zemel, R., and Salakhutdinov, R. Siamese neural networks for one-shot image recognition. In ICML Deep Learning Workshop, volume 2, 2015.
• [21] Kumar, A., Eslami, S. M. A., Rezende, D. J., Garnelo, M., Viola, F., Lockhart, E., and Shanahan, M. Consistent generative query networks. In CoRR, 2018.
• [22] LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. Gradientbased learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.
• [23] Liu, Z., Luo, P., Wang, X., and Tang, X. Deep learning face attributes in the wild. In Proceedings of International Conference on Computer Vision (ICCV), December 2015.
• [24] Louizos, C. and Welling, M. Multiplicative normalizing flows for variational bayesian neural networks. arXiv preprint arXiv:1703.01961, 2017.
• [25] Louizos, C., Ullrich, K., and Welling, M. Bayesian compression for deep learning. In Advances in Neural Information Processing Systems, pp. 3290–3300, 2017.
• [26] Ma, C., Li, Y., and Hern ́ andez-Lobato, J. M. Variational implicit processes. arXiv preprint arXiv:1806.02390, 2018.
• [27] Øksendal, B. Stochastic differential equations. In Stochastic differential equations, pp. 11. Springer, 2003.
• [28] Qui ̃ nonero-Candela, J. and Rasmussen, C. E. A unifying view of sparse approximate gaussian process regression. Journal of Machine Learning Research, 6(Dec):19391959, 2005.
• [29] Reed, S., Chen, Y., Paine, T., Oord, A. v. d., Eslami, S., J. Rezende, D., Vinyals, O., and de Freitas, N. Few-shot autoregressive density estimation: Towards learning to learn distributions. 2017.
• [30] Rezende, D. J., Mohamed, S., and Wierstra, D. Stochastic backpropagation and approximate inference in deep generative models. arXiv preprint arXiv:1401.4082, 2014.
• [31] Rezende, D. J., Mohamed, S., Danihelka, I., Gregor, K., and Wierstra, D. One-shot generalization in deep generative models. arXiv preprint arXiv:1603.05106, 2016.
• [32] Riquelme, C., Tucker, G., and Snoek, J. Deep bayesian bandits showdown: An empirical comparison of bayesian deep networks for thompson sampling. arXiv preprint arXiv:1802.09127, 2018.
• [33] Santoro, A., Bartunov, S., Botvinick, M., Wierstra, D., and Lillicrap, T. One-shot learning with memory-augmented neural networks. arXiv preprint arXiv:1605.06065, 2016.
• [34] Shahriari, B., Swersky, K., Wang, Z., Adams, R. P., and De Freitas, N. Taking the human out of the loop: A review of bayesian optimization. Proceedings of the IEEE, 104 (1):148–175, 2016.
• [35] Snell, J., Swersky, K., and Zemel, R. Prototypical networks for few-shot learning. In Advances in Neural Information Processing Systems, pp. 4080–4090, 2017.
• [36] Sohn, K., Lee, H., and Yan, X. Learning structured output representation using deep conditional generative models. In Advances in Neural Information Processing Systems, pp. 3483–3491, 2015.
• [37] Sun, S., Zhang, G., Wang, C., Zeng, W., Li, J., and Grosse, R. Differentiable compositional kernel learning for gaussian processes. arXiv preprint arXiv:1806.04326, 2018.
• [38] Sutskever, I., Vinyals, O., and Le, Q. V. Sequence to sequence learning with neural networks. In Advances in neural information processing systems, pp. 3104–3112, 2014.
• [39] Thompson, W. R. On the likelihood that one unknown probability exceeds another in view of the evidence of two samples. Biometrika, 25(3/4):285–294, 1933.
• [40] van den Oord, A., Kalchbrenner, N., Espeholt, L., Vinyals, O., Graves, A., et al. Conditional image generation with pixelcnn decoders. In Advances in Neural Information Processing Systems, pp. 4790–4798, 2016.
• [41] Vinyals, O., Blundell, C., Lillicrap, T., Wierstra, D., et al. Matching networks for one shot learning. In Advances in Neural Information Processing Systems, pp. 3630–3638, 2016.
• [42] Wang, J. X., Kurth-Nelson, Z., Tirumala, D., Soyer, H., Leibo, J. Z., Munos, R., Blundell, C., Kumaran, D., and Botvinick, M. Learning to reinforcement learn. arXiv preprint arXiv:1611.05763, 2016.
• [43] Wilson, A. and Nickisch, H. Kernel interpolation for scalable structured gaussian processes (kiss-gp). In International Conference on Machine Learning, pp. 1775–1784, 2015.
• [44] Wilson, A. G., Knowles, D. A., and Ghahramani, Z. Gaussian process regression networks. arXiv preprint arXiv:1110.4411, 2011.
• [45] Wilson, A. G., Hu, Z., Salakhutdinov, R., and Xing, E. P. Deep kernel learning. In Artificial Intelligence and Statistics, pp. 370–378, 2016.