NLP预训练模型【5】 -- Transformer

NLP预训练模型【5】 – $Transformer$

1. 什么是 $Transformer$

《 $Attention$ Is All You Need》是一篇Google提出的将 $Attention$ 思想发挥到极致的论文。这篇论文中提出一个全新的模型，叫 $Transformer$ ，抛弃了以往深度学习任务里面使用到的CNN和RNN。目前大热的BERT就是基于 $Transformer$ 构建的，这个模型广泛应用于NLP领域，例如机器翻译，问答系统，文本摘要和语音识别等等方向。

2. $Transformer$ 结构

2.1 总体结构

$Transformer$ 的结构和 $Attention$ 模型一样， $Transformer$ 模型中也采用了 $Encoer- Decoder$ 架构。但其结构相比于 $Attention$ 更加复杂，论文中 $Encoder$ 层由6个 $Encoder$ 堆叠在一起， $Decoder$ 层也一样。

不了解 $Attention$ 模型的，可以回顾之前的文章。

每一个 $Encoder$ 和 $Decoder$ 的内部结构如下图：

• $Encoder$ ，包含两层，一个 $self-Attention$ 层和一个前馈神经网络， $self-Attention$ 能帮助当前节点不仅只关注当前词，还能获取到上下文的语义。
• $Decoder$ 也包含 $Encoder$ 提到的两层网络，但是在这两层中间还有一层 $Attention$ 层，帮助当前节点获取到当前需要关注的重点内容。

2.2 $Encoder$ 层结构

首先，模型需要对输入的数据进行一个 $Embedding$ 操作，也可以理解为类似 $word2vec$ 的操作， $Embedding$ 结束之后，输入到 $Encoder$ 层， $self-Attention$ 处理完数据后把数据送给前馈神经网络，前馈神经网络的计算可以并行，得到的输出会输入到下一个 $Encoder$ 。

2.2.1 Positional Encoding

$Transformer$ 模型中缺少一种解释输入序列中单词顺序的方法，它跟序列模型还不不一样。为了处理这个问题， $Transformer$ 给 $Encoder$ 层和 $Decoder$ 层的输入添加了一个额外的向量 $Positional \quad Encoding$ ，维度和 $Embedding$ 的维度一样，这个向量采用了一种很独特的方法来让模型学习到这个值，这个向量能决定当前词的位置，或者说在一个句子中不同的词之间的距离。这个位置向量的具体计算方法有很多种，论文中的计算方法如下：

$$\begin{equation} \begin{aligned} P E(p o s, 2 i)&=\sin \left(\frac{p o s}{10000^{\frac{1}{d_{m o d e l}}}}\right) \\\\ P E(p o s, 2 i+1)&=\cos \left(\frac{\text { pos }}{10000^{\frac{1 i}{d_{m o d e l}}}}\right) \end{aligned} \end{equation}$$

其中 $pos$ 是指当前词在句子中的位置，$i$ 是指向量中每个值的 $index$ ，可以看出，在偶数位置，使用正弦编码，在奇数位置，使用余弦编码。

最后把这个 $Positional Encoding$ 与 $Embedding$ 的值相加，作为输入送到下一层。

2.2.2 $Self- Attention$

接下来我们详细看一下 $self- Attention$ ，其思想和 $Attention$ 类似，但是 $self-Attention$ 是 $Transformer$ 用来将其他相关单词的“理解”转换成我们正在处理的单词的一种思路，我们看个例子：

The animal didn’t cross the street because it was too tired

这里的 it 到底代表的是 animal 还是 street 呢，对于我们来说能很简单的判断出来，但是对于机器来说，是很难判断的，$self-Attention$ 就能够让机器把 it 和 animal 联系起来，接下来我们看下详细的处理过程。

首先，$self-Attention$ 会计算出三个新的向量，在论文中，向量的维度是512维，我们把这三个向量分别称为 $Query$ 、 $Key$ 、 $Value$ ，这三个向量是用 $Embedding$ 向量与一个矩阵相乘得到的结果，这个矩阵是随机初始化的，维度为（64，512）注意第二个维度需要和 $Embedding$ 的维度一样，其值在 BP的过程中会一直进行更新，得到的这三个向量的维度是64。

然后，计算 $self-Attention$ 的分数值，该分数值决定了当我们在某个位置 $Encode$ 一个词时，对输入句子的其他部分的关注程度。这个分数值的计算方法是 $Query$ 与 $Key$ 做点乘，以下图为例，首先我们需要针对 Thinking 这个词，计算出其他词对于该词的一个分数值，首先是针对于自己本身即 $q_1·k_1$，然后是针对于第二个词即 $q_1·k_2$ 。

接下来，把点乘的结果除以一个常数，这里我们除以 8 ，这个值一般是采用上文提到的矩阵的第一个维度的开方即 64 的开方 8 ，当然也可以选择其他的值，然后把得到的结果做一个 $softmax$ 的计算。得到的结果即是每个词对于当前位置的词的相关性大小，当然，当前位置的词相关性肯定会会很大。

下一步就是把 $Value$ 和 $softmax$ 得到的值进行相乘，并相加，得到的结果即是 $self-attention$ 在当前节点的值。

在实际的应用场景，为了提高计算速度，我们采用的是矩阵的方式，直接计算出 $Query$ , $Key$ , $Value$ 的矩阵，然后把 $Embedding$ 的值与三个矩阵直接相乘，把得到的新矩阵Q与K相乘，乘以一个常数，做 $softmax$ 操作，最后乘上V矩阵。

这种通过 $Query$ 和 $Key$ 的相似性程度来确定 $Value$ 的权重分布的方法被称为 scaled dot-product Attention 。

2.2.3 Multi-Headed $Attention$

这篇论文更牛逼的地方是给 $self-Attention$ 加入了另外一个机制，被称为 $Multi-Header \quad Attention$ ，该机制理解起来很简单，就是说不仅仅只初始化一组 $Q、K、V$ 的矩阵，而是初始化多组， $Tranformer$ 是使用了 8 组，所以最后得到的结果是 8 个矩阵。

2.2.4 Layer normalization

在 $Transformer$ 中，每一个子层（$self-attention$ ，$Feed \quad Forward \quad Neural \quad Network$ ）之后都会接一个残差模块，并且有一个 $Layer \quad Normalization$ 。

$Normalization$有很多种，但是它们都有一个共同的目的，那就是把输入转化成均值为 0 方差为 1 的数据。我们在把数据送入激活函数之前进行 $normalization$（归一化），因为我们不希望输入数据落在激活函数的饱和区。

Batch Normalization

BN 的主要思想就是：在每一层的每一批数据上进行归一化。我们可能会对输入数据进行归一化，但是经过该网络层的作用后，我们的数据已经不再是归一化的了。随着这种情况的发展，数据的偏差越来越大，我的反向传播需要考虑到这些大的偏差，这就迫使我们只能使用较小的学习率来防止梯度消失或者梯度爆炸。BN 的具体做法就是对每一小批数据，在批这个方向上做归一化。

Layer normalization

它也是归一化数据的一种方式，不过** LN 是在每一个样本上计算均值和方差**，而不是 BN 那种在批方向计算均值和方差！公式如下：

$$L N\left(x_{i}\right)=\alpha * \frac{x_{i}-\mu_{L}}{\sqrt{\sigma_{L}^{2}+\varepsilon}}+\beta$$

2.2.5 Feed Forward Neural Network

这给我们留下了一个小的挑战，前馈神经网络没法输入 8 个矩阵呀，这该怎么办呢？所以我们需要一种方式，把 8 个矩阵降为 1 个，首先，我们把 8 个矩阵连在一起，这样会得到一个大的矩阵，再随机初始化一个矩阵和这个组合好的矩阵相乘，最后得到一个最终的矩阵。

2.3 $Decoder$ 层结构

根据上面的总体结构图可以看出， $Decoder$ 部分其实和 $Encoder$ 部分大同小异，刚开始也是先添加一个位置向量 $Positional \quad Encoding$ ，方法和2.2.1节一样，接下来接的是 $Masked \quad Mutil-head \quad Attention$ ，这里的 $mask$ 也是 $Transformer$ 一个很关键的技术，下面我们会进行一一介绍。

其余的层结构与 $Encoder$ 一样，请参考 $Encoder$ 层结构。

2.3.1 Masked Mutil-head Attention

mask表示掩码，它对某些值进行掩盖，使其在参数更新时不产生效果。 $Transformer$ 模型里面涉及两种 $mask$ ，分别是 $padding \quad mask$ 和 $sequence \quad mask$ 。其中， $padding \quad mask$ 在所有的 $scaled dot-product Attention$ 里面都需要用到，而 $sequence \quad mask$ 只有在 $Decoder$ 的 $self-Attention$ 里面用到。

（1） $padding \quad mask$

什么是 $padding \quad mask$ 呢？因为每个批次输入序列长度是不一样的也就是说，我们要对输入序列进行对齐。具体来说，就是给在较短的序列后面填充0。但是如果输入的序列太长，则是截取左边的内容，把多余的直接舍弃。因为这些填充的位置，其实是没什么意义的，所以我们的 $Attention$ 机制不应该把注意力放在这些位置上，所以我们需要进行一些处理。

具体的做法是，把这些位置的值加上一个非常大的负数(负无穷)，这样的话，经过 $softmax$ ，这些位置的概率就会接近0！

而我们的 $padding \quad mask$ 实际上是一个张量，每个值都是一个Boolean，值为false的地方就是我们要进行处理的地方。

（2） $sequence \quad mask$

文章前面也提到， $softmax$ 是为了使得 $Decoder$ 不能看见未来的信息。也就是对于一个序列，在time_step为t的时刻，我们的解码输出应该只能依赖于t时刻之前的输出，而不能依赖t之后的输出。因此我们需要想一个办法，把t之后的信息给隐藏起来。

那么具体怎么做呢？也很简单：产生一个上三角矩阵，上三角的值全为0。把这个矩阵作用在每一个序列上，就可以达到我们的目的。

• 对于 $Decoder$ 的 $self-Attention$ ，里面使用到的 $ scaled dot-product Attention$ ，同时需要 $padding \quad mask$ 和 $sequence \quad mask$ 作为 $attn-mask$ ，具体实现就是两个 $mask$ 相加作为 $attn-mask$ 。
• 其他情况，$attn-mask$一律等于 $padding \quad mask$ 。

2.3.2 Output层

当 $Decoder$ 层全部执行完毕后，怎么把得到的向量映射为我们需要的词呢，很简单，只需要在结尾再添加一个全连接层和 $softmax$ 层，假如我们的词典是1w个词，那最终 $softmax$ 会输入1w个词的概率，概率值最大的对应的词就是我们最终的结果。

2.4 动态流程图

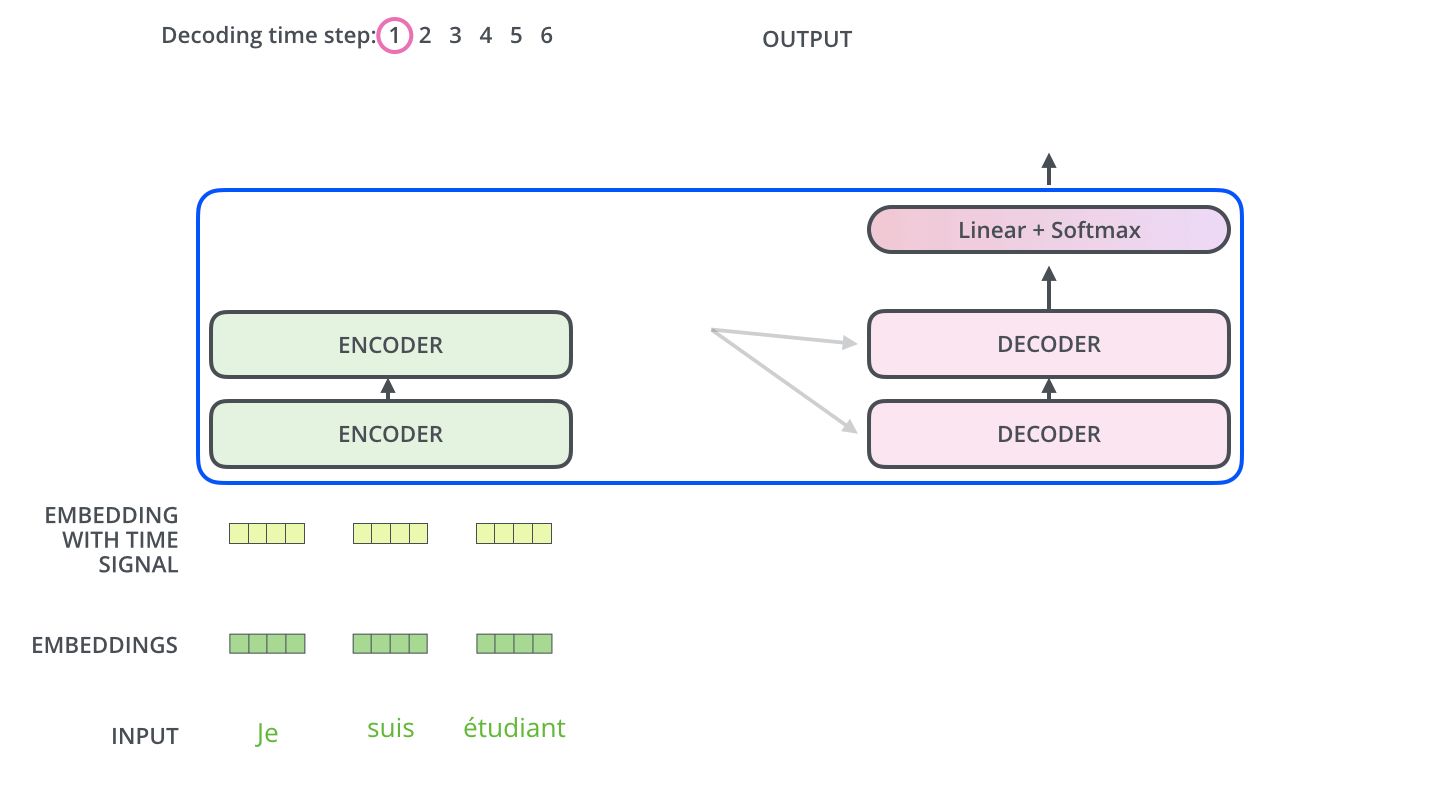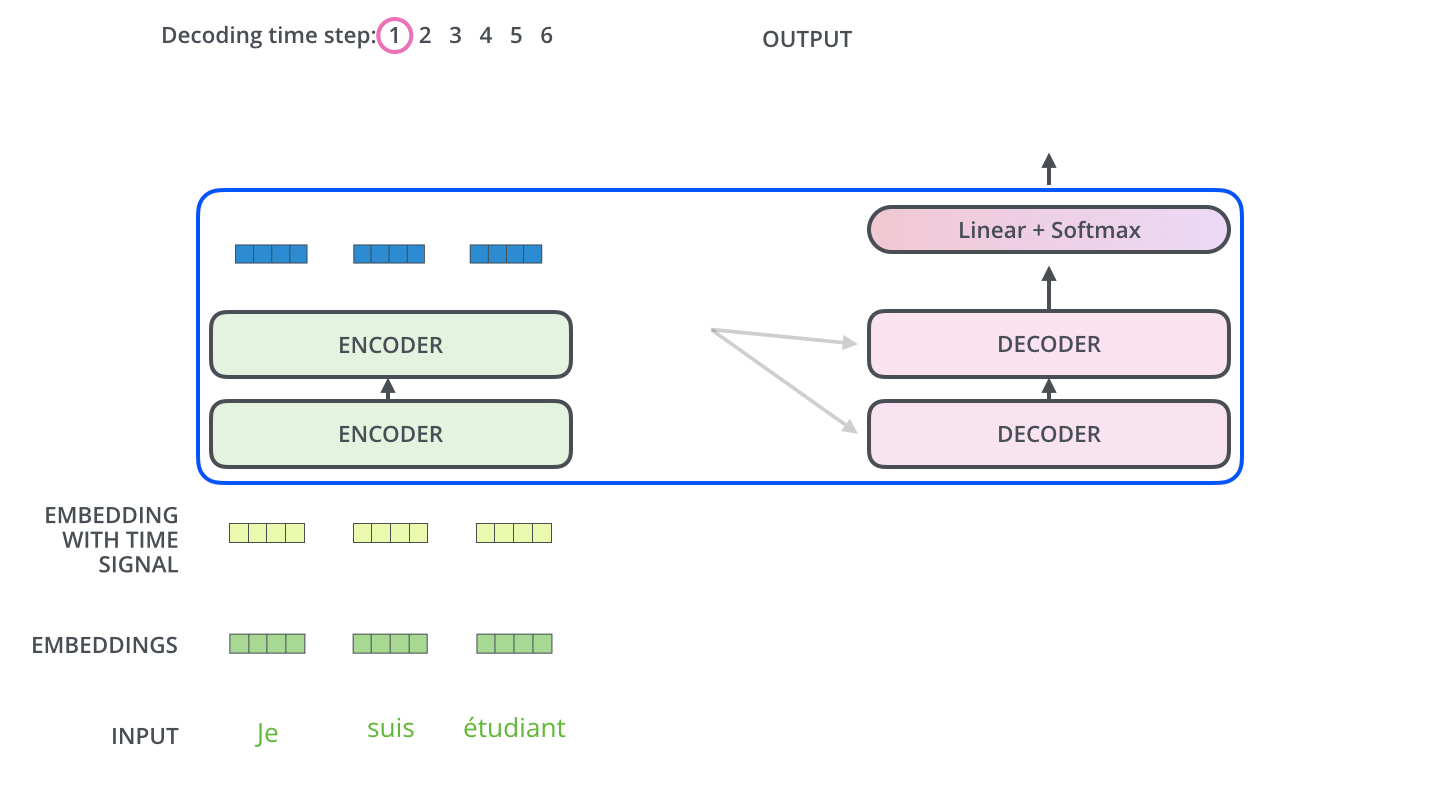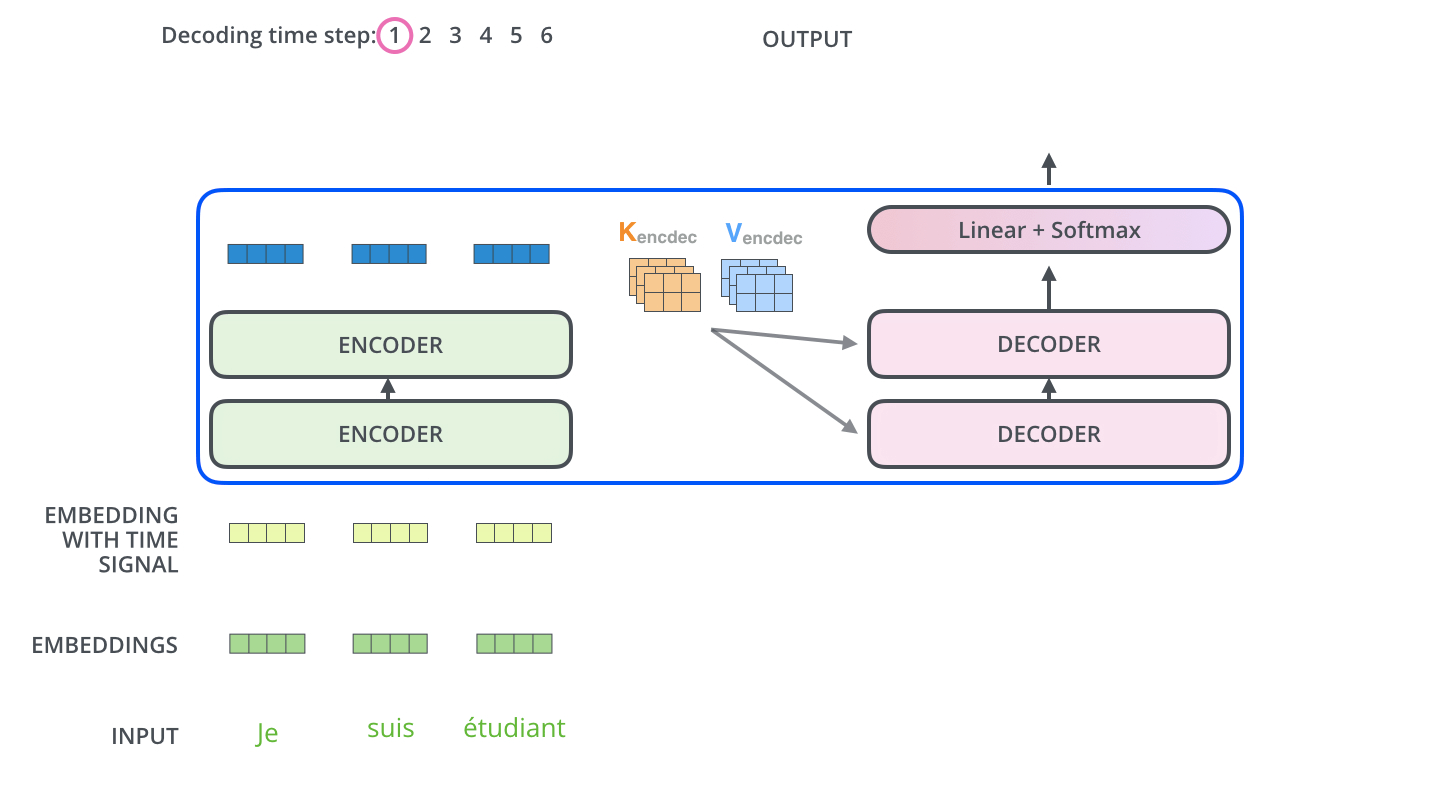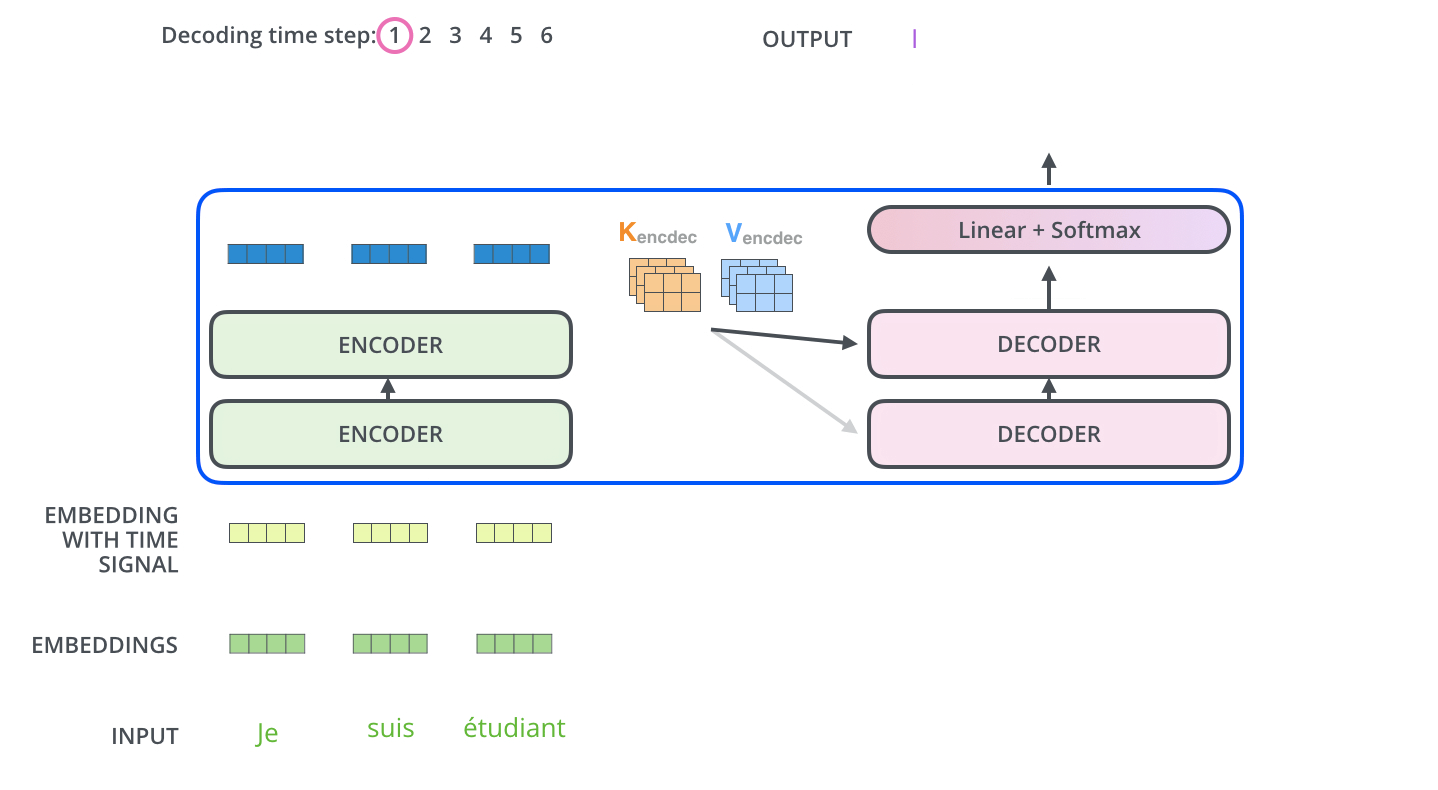
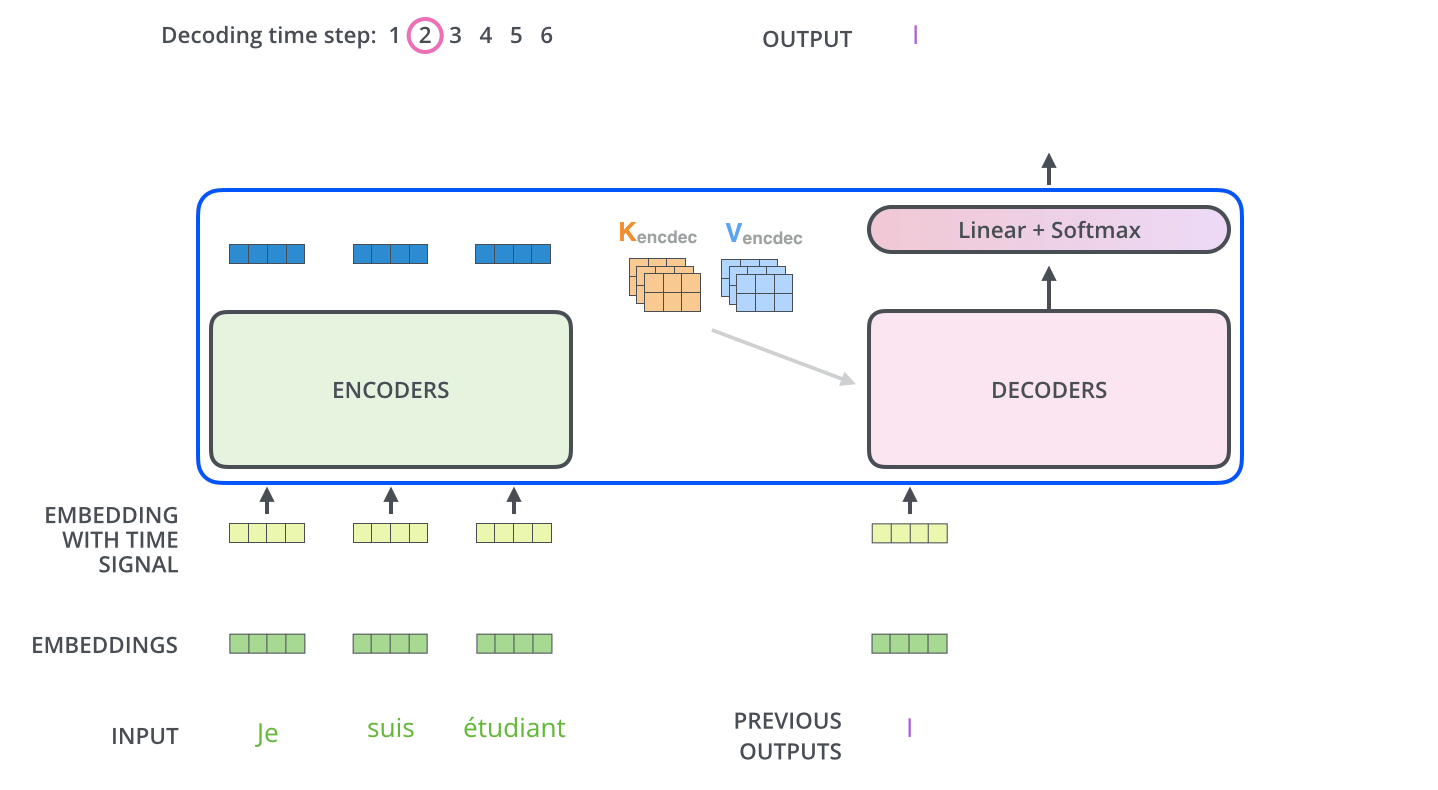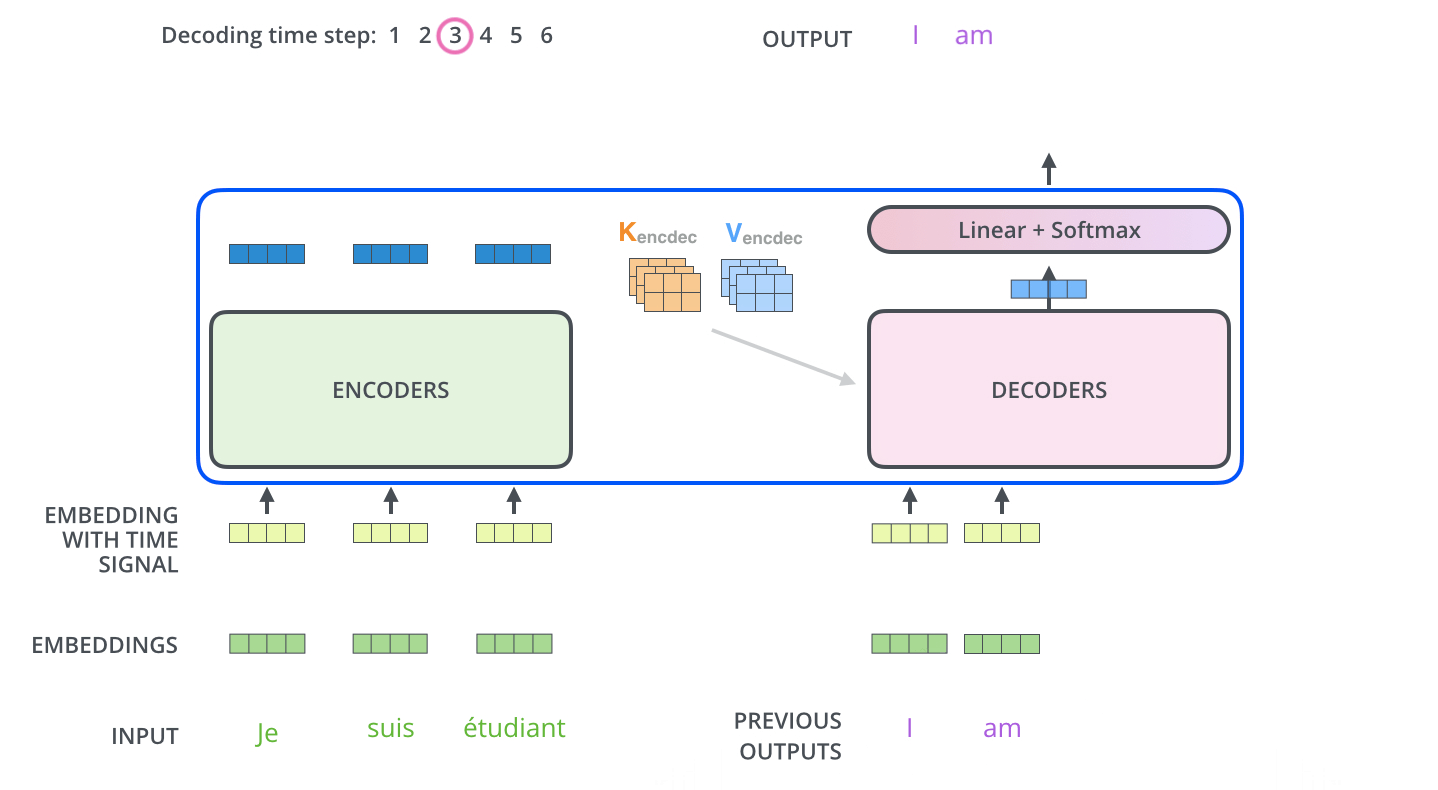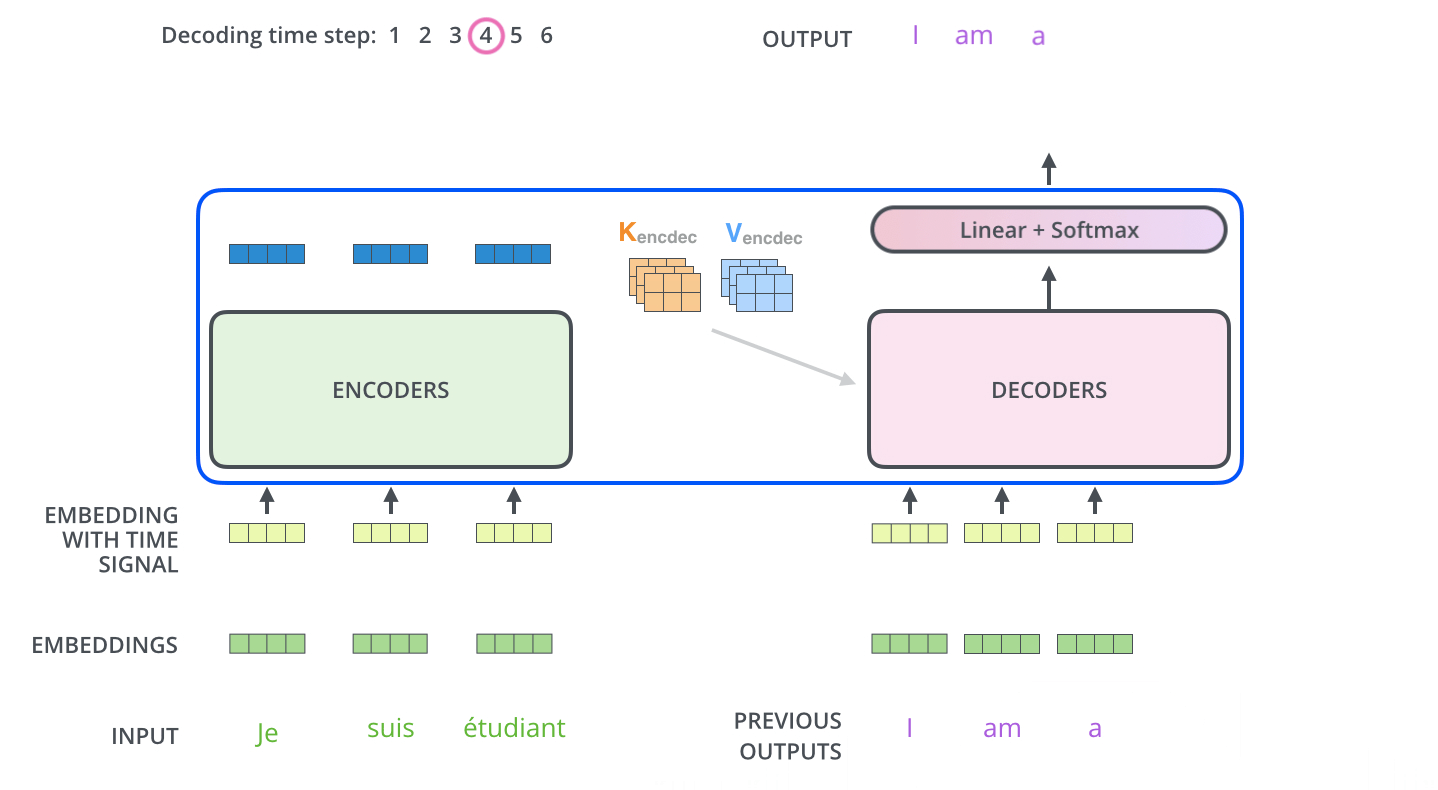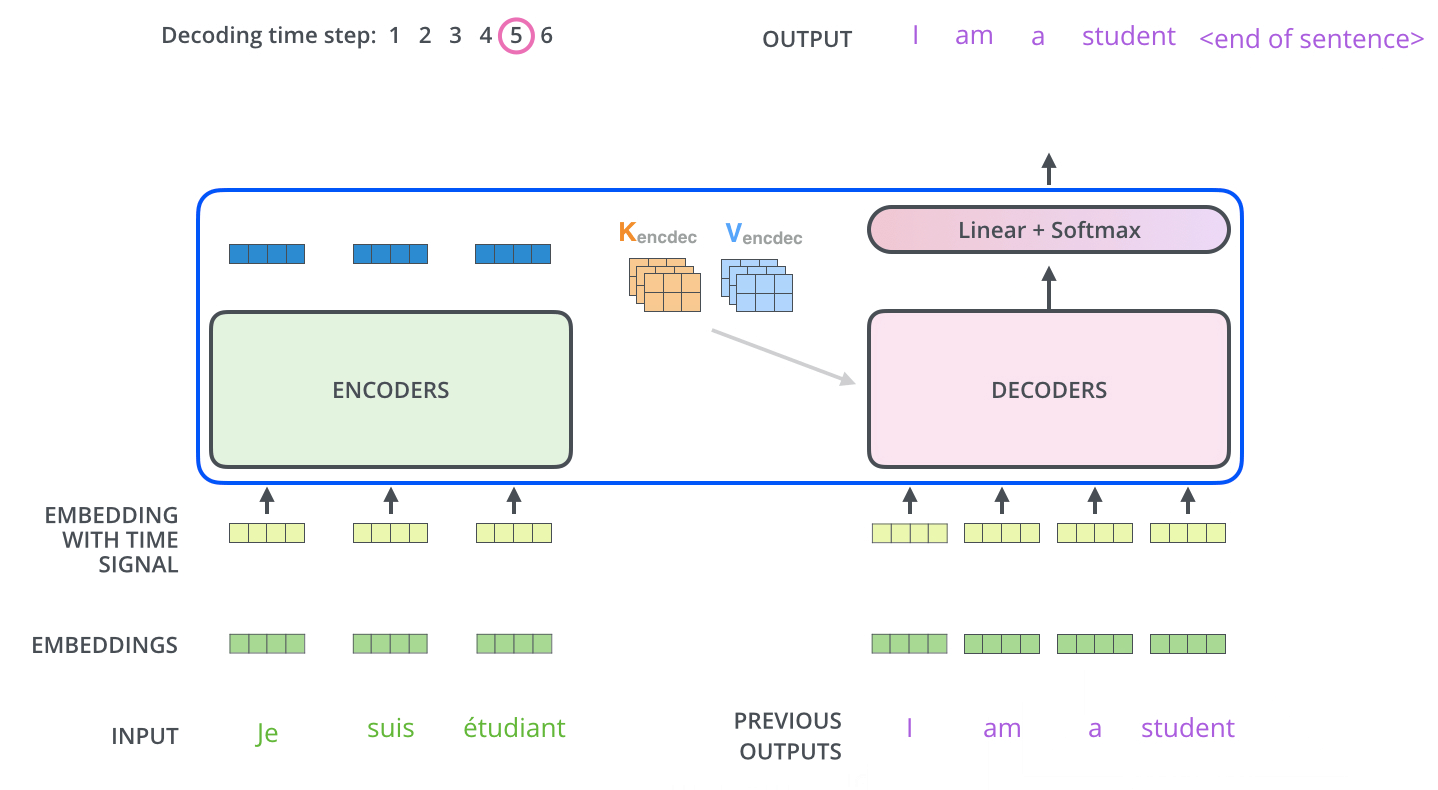
编码器通过处理输入序列开启工作。顶端编码器的输出之后会变转化为一个包含向量 $K$（键向量）和$V$（值向量）的注意力向量集 ，这是并行化操作。这些向量将被每个解码器用于自身的“编码-解码注意力层”，而这些层可以帮助解码器关注输入序列哪些位置合适：

在完成编码阶段后，则开始解码阶段。解码阶段的每个步骤都会输出一个输出序列（在这个例子里，是英语翻译的句子）的元素。

接下来的步骤重复了这个过程，直到到达一个特殊的终止符号，它表示 $Transformer$ 的解码器已经完成了它的输出。每个步骤的输出在下一个时间步被提供给底端解码器，并且就像编码器之前做的那样，这些解码器会输出它们的解码结果 。

3. $Transformer$ 为什么需要多头注意力？

原论文中说到进行 $Multi-head \quad Attention$ 的原因是将模型分为多个头，形成多个子空间，可以让模型去关注不同方面的信息，最后再将各个方面的信息综合起来。其实直观上也可以想到，如果自己设计这样的一个模型，必然也不会只做一次 $Attention$ ，多次 $Attention$ 综合的结果至少能够起到增强模型的作用，也可以类比CNN中同时使用多个卷积核的作用，直观上讲，多头的注意力有助于网络捕捉到更丰富的特征/信息。

4. $Transformer$ 相比于 $RNN/LSTM$ 有何优势？

（1）$RNN$ 系列的模型，并行计算能力很差。 $RNN$ 并行计算的问题就出在这里，因为 $T$ 时刻的计算依赖 $T-1$ 时刻的隐层计算结果，而 $T-1$ 时刻的计算依赖 $T-2$ 时刻的隐层计算结果，如此下去就形成了所谓的序列依赖关系。

（2） $Transformer$ 的特征抽取能力比 $RNN$ 系列的模型要好。

具体实验对比可以参考：放弃幻想，全面拥抱Transformer ：自然语言处理三大特征抽取器（CNN/RNN/TF）比较

但是值得注意的是，并不是说 $Transformer$ 就能够完全替代 $RNN$ 系列的模型了，任何模型都有其适用范围，同样的，$RNN$ 系列模型在很多任务上还是首选，熟悉各种模型的内部原理，知其然且知其所以然，才能遇到新任务时，快速分析这时候该用什么样的模型，该怎么做好。

5. 为什么 $Transformer$ 可以代替 $seq2seq$ ？

$seq2seq$ 缺点：这里用代替这个词略显不妥当， $seq2seq$ 虽已老，但始终还是有其用武之地， $seq2seq$ 最大的问题在于将 $Encoder$ 端的所有信息压缩到一个固定长度的向量中，并将其作为 $Decoder$ 端首个隐藏状态的输入，来预测 $Decoder$ 端第一个单词（token）的隐藏状态。在输入序列比较长的时候，这样做显然会损失 $Encoder$ 端的很多信息，而且这样一股脑的把该固定向量送入 $Decoder$ 端， $Decoder$ 端不能够关注到其想要关注的信息。

$Transformer$ 优点： $Transformer$ 不但对 $seq2seq$ 模型这两点缺点有了实质性的改进（多头交互式 $Attention$ 模块），而且还引入了 $self-Attention$ 模块，让源序列和目标序列首先“自关联”起来，这样的话，源序列和目标序列自身的 $Embedding$ 表示所蕴含的信息更加丰富，而且后续的 $FFN$ 层也增强了模型的表达能力，并且 $Transformer$ 并行计算的能力是远远超过 $seq2seq$ 系列的模型，因此我认为这是 $Transformer$ 优于 $seq2seq$ 模型的地方。

6. 代码实现

地址：https://github.com/Kyubyong/Transformer

代码解读： Transformer 解析与tensorflow代码解读

7. 参考文献

• Transformer 模型详解
• 图解 Transformer （完整版）
• 关于Transformer 的若干问题整理记录

---

作者：@mantchs

GitHub：https://github.com/NLP-LOVE/ML-NLP