0️⃣ 概率图模型简介
〖摘要〗概率图模型是机器学习的一个分支,它研究如何使用概率分布来描述世界并对其做出有用的预测。
〖原文〗Stanford’s CS228
〖参考〗
1 简介
概率图模型是机器学习的一个分支,它研究如何使用概率分布来描述世界并对其做出有用的预测。
学习概率建模的原因有很多。
- 一方面,这是一个引人入胜的科学领域,有一个美丽的理论,它以惊人的方式连接了两个非常不同的数学分支:概率论和图论。概率建模也与哲学有着有趣的联系,尤其是因果关系问题。
- 同时,概率建模在机器学习和许多实际应用中得到广泛应用。这些技术可用于解决医学、语言处理、视觉和许多其他领域的问题。
这种优雅的理论与应用相结合,使概率图模型成为现代人工智能和计算机科学中最引人入胜的话题之一。2011 年图灵奖(被认为是计算机科学”“诺贝尔奖”)最近被授予 Judea Pearl 以表彰其在概率图建模领域的创立。
2 概念
但是,究竟什么是概率建模?
当试图用数学解决现实世界的问题时,以方程的形式定义世界的数学模型是很常见的。 也许最简单的模型是以下形式的线性方程
其中 是我们想要预测的结果变量, 是影响结果的已知(给定)变量。例如, 可能是房子的价格, 是影响这个价格的一系列因素,例如位置、卧室数量、房子的年龄等。我们假设 是这个输入的线性函数(由 参数化)。
通常,我们试图建模的现实世界非常复杂。特别是,它往往涉及大量的不确定性(例如,如果新的地铁站在一定距离内开放,房子的价格有一定的上涨机会)。因此,通过以概率分布的形式对世界建模来处理这种不确定性是非常自然的。关于为什么应该使用概率论而不是其他的,请参阅 Dutch Book Argument 了解概率。
给定这样一个模型,我们可以提出诸如“房价在未来五年内上涨的概率是多少?”或“假设房子售价 100,000 美元,它有三间卧室的概率是多少?”之类的问题。建模的概率方面非常重要,因为:
- 通常,我们无法完美地预测未来。我们常常对世界没有足够的了解,而且世界本身往往是随机的。
- 我们需要评估我们预测的可信度;通常,预测单个值是不够的,我们需要系统输出其对世界上正在发生的事情的信念。
在本课程中,我们将研究推断不确定性的原则方法,并使用概率论和图论的思想来为这项任务推导出有效的机器学习算法。我们将找到许多有趣问题的答案,例如:
- 计算复杂性和概率模型的丰富性之间的权衡是什么?
- 在给定固定数据集和计算预算的情况下,推断未来事实的最佳模型是什么?
- 如何以一种原则性的方式将先验知识与观测到的证据结合起来进行预测?
- 我们如何严格分析是否是的原因,反之亦然?
此外,我们还将看到许多如何将概率技术应用于各种问题的示例,例如疾病预测、图像理解、语言分析等。
3 主要难点
为了初步了解摆在我们面前的挑战,请考虑概率建模的一个简单应用:垃圾邮件分类。
假设我们有一个模型 \pt(y, x_1, \dotsc, x_n) 在垃圾邮件和非垃圾邮件中出现的单词。每个二进制变量 对电子邮件中是否存在第 个英文单词进行编码;二进制变量 指示电子邮件是否为垃圾邮件。为了对一封新邮件进行分类,我们可以查看 $ P(y=1 \mid x_1, \dotsc, x_n) $ 的概率。
我们刚刚定义的函数 \pt 的“大小”是多少?我们的模型为每个输入组合 定义了一个以 为单位的概率;指定所有这些概率将需要我们写下惊人的 不同的值,每个赋值给我们的 二进制变量。由于 是英语词汇的大小,从计算(我们如何存储这个大列表?)和统计(我们如何有效地从有限的数据估计参数?)点,这显然是不切实际的。观点。更一般地说,我们的示例说明了本课程将处理的主要挑战之一:概率本质上是指数大小的对象;我们可以操纵它们的唯一方法是对它们的结构进行简化假设。
我们将在本课程中做出的主要简化假设是变量之间的条件独立。例如,假设给定 ,英语单词都是条件独立的。换句话说,鉴于一条消息是垃圾邮件,看到两个单词的概率是独立的。这显然过于简单化了,因为“药丸”和“购买”这两个词的概率明显相关;然而,对于大多数单词(例如,“企鹅”和“松饼”)来说,概率确实是独立的,我们的假设不会显著降低模型的准确性。
我们将这种特定的独立性选择称为朴素贝叶斯假设。给定这个假设,我们可以将模型概率写成因子的乘积
每个因子 可以用少量参数(准确地说是 2 个自由度的 4 个参数)完全描述。整个分布由 参数参数化,我们可以从数据中轻松估计并做出预测。
4 技术途径
我们的独立性假设可以方便地以图的形式表示。朴素贝叶斯垃圾邮件分类模型的图表示。我们可以将有向图解释为表明数据是如何生成的:首先,随机选择垃圾邮件/非垃圾邮件标签;然后独立随机抽取 个可能的英语单词的子集。
这种表示具有易于理解的直接优势。它可以解释为告诉我们一个故事:首先随机选择该电子邮件是否为垃圾邮件(以 表示),然后一次一个地抽取单词,从而生成一封电子邮件。相反,如果我们有关于如何生成数据集的故事,我们可以自然地将其表示为具有相关概率分布的图。
更重要的是,我们希望向模型提交各种查询(例如,鉴于我看到“药丸”这个词,垃圾邮件的概率是多少?);回答这些问题将需要使用图论概念最自然地定义的专门算法。我们还将使用图论来分析学习算法的速度并量化不同学习任务的计算复杂度(例如,NP-hardness)。
我们想要了解的要点是,概率分布和图之间存在密切联系,我们将在整个课程中利用这些联系来定义、学习和使用概率模型,这就是概率图模型。
4.1 什么是图模型(Graphical Model, GM)?
图模型用于表示高维空间中的多元分布,图中的结构可以表示变量之间的依赖关系,进而能够有效简化分布的表示。

4.2 什么是概率图模型(Probabilistic Graphical Model,PGM)?
如果图模型中的每个节点 都是条件独立的,则该图模型被称为概率图模型(Probabilistic Graphical Model,PGM)。在概率图模型中,多元变量的联合分布可以被因子化为简单项的乘积,例如: 如果上图是一个概率图的话,则其表示的多元联合概率分布可以因子化为:
4.3 概率图的优势
(1)优势 1: 能够结合领域知识和因果(逻辑)结构
分布的表示成本从 减少了 倍。图模型天然支持数据集成,
(2)优势 2:支持异构部件的模块化组合,即数据融合
(3)优势 3:贝叶斯哲学的天然支持者
概率图模型 = 多元统计 + 结构
图模型 = 多元对象函数 + 结构
4.4 概率图到底是什么?
非正式的简介:概率图模型是一种无需付出指数级成本,即可 『编写/指定/组合/设计』 指数级概率分布的聪明方法。与此同时,它为联合概率分布赋予了结构化的语义。
更正式的描述:概率图模型指一组随机变量上的分布族,该分布族与连接这些随机变量的图所编码的概率独立性命题之间相互兼容。
4.5 概率图的类型
(1)有向图模型:有向边给出因果关系(贝叶斯网络)

图结构: 有向无环图。
- 含义:一个节点有条件地独立于其马尔可夫毯之外的网络中的每个其他节点
- 局部条件分布 (CPD) 和 DAG 完全确定联合分布。
- 提供因果关系,并促进生成过程
(2)无向图模型:无向边仅给出变量之间的相关性(马尔可夫随机场)

图结构:无向图
- 含义:一个节点在给定其有向邻居的情况下,有条件地独立于网络中的所有其他节点
- 局部应急函数(势)和图中的团完全确定了联合分布。
- 给出变量之间的相关性,但没有明确的方式来生成样本
4.6 概率图的结构规范
- 概率图中的分离性质表示了相关变量之间的独立性
- 为了使概率图有效,需要保证:从概率图中得出的所有条件独立性,都应当与该图所表示的概率分布保持一致。
- 等价定理
- 对于图 ,令 表示满足 的所有分布族,令 表示根据 分解得出的所有分布族,应当有 。
4.7 常见概率图模型
(1)传统的概率图模型

(2)更高级的概率图模型



4.8 为何选用概率图?
-
概率论提供了将各部分结合起来的粘合剂,确保系统作为一个整体是一致的,并提供了将模型与数据接口的方法。
-
图模型的图论支持既提供了一个直观的、吸引人的界面,人类可以通过该界面对高度交互的变量集进行建模,也提供了一种数据结构,可以自然地用于设计高效的通用算法。
-
在统计学、系统工程、信息论、模式识别和统计力学等领域研究的许多经典多元概率系统都是广义图模型形式主义的特例。
-
图模型框架提供了一种将所有这些系统视为某种基本形式主义实例的方法。
5 主要任务
我们对概率图模型的讨论将分为三个主要部分:表示(如何指定模型)、推断(如何从模型获得答案)和学习(如何使模型适应现实世界的数据)。这三个主题也将密切相关:为了获得有效的推断和学习算法,模型需要被充分表示;此外,学习模型需要将推断作为子程序。因此,最好始终牢记这三个任务,而不是孤立地关注它们。
5.1 表示
任务 1:我们如何捕捉(模拟)世界中的不确定性?如何体现我们的领域知识/假设/约束?
此类问题的本质是获得关于 多变量的联合概率分布 的表示,即 。
这并非一个简单问题:我们已经看到一个简单的垃圾邮件分类模型。对于 个可能的词通常需要我们指定 个参数。我们将通过构建易处理的模型来解决这个困难。这些方法将大量使用到图论;概率将由图结构来描述,其属性(例如,连通性、树宽)将揭示模型的一些概率和算法特性(例如:独立性、学习复杂性等)。
5.2 推断
任务 2:依据我们的概率模型和(或)给定的数据,如何能够得到世界中关于问题的答案?
此类问题通常简化为查询某些感兴趣事件的边缘概率或条件概率,例如: P(X_i \mi \mathcal{D})。再具体一点,我们通常会对向系统提出两种类型的问题感兴趣:
( 1 )边缘推断 (Marginal Inference):在我们将其他所有内容相加后,模型中指定变量的概率是多少?一个典型示例是查询随机选择的房屋中,拥有三间以上卧室的概率。
( 2 )最大后验推断 (MAP):寻求最可能的变量赋值。例如,我们可以尝试确定最可能的垃圾邮件,以便解决问题
通常查询将涉及证据(如上面的 MAP 示例),在这种情况下,我们将固定某些变量的赋值。
事实证明,推断是一项非常具有挑战性的任务。对于许多感兴趣的概率,回答这些问题中的任何一个都是 NP 难的。特别是: 推断是否易于处理将取决于描述该概率的图结构!
需要提醒的是:当面临非常棘手的问题时,我们还能够通过近似推断方法来获得有价值的结果。有趣的是,这部分课程中描述的算法将在很大程度上基于 20 世纪中叶统计物理学领域所做的工作。
5.3 学习
任务 3:如何将模型拟合到数据集?或者说,什么样的模型对于我们的数据(如大量标记的垃圾邮件样本)是 “正确的”? 例如:
通过分析数据,我们可以推断出一些有用的模式(例如,哪些词在垃圾邮件中出现的频率更高),然后可以使用这些模式来预测未来。不过,学习和推断也能够以某种更微妙的方式内在地联系在一起,后面我们将会看到:推断将成为学习算法中一个反复被调用的关键子程序。
此外,学习问题与计算学习理论领域(处理有限数据的泛化和过拟合等问题)、贝叶斯统计领域(告诉我们如何以有原则的方式将先验知识和观测到的证据结合在一起)有着重要的联系。
6 实际应用
概率图模型在现实世界中有许多应用。在此,我们简单概述以下应用,并且仅仅给出了众多用途中的几个例子。
6.1 图像
考虑图像上的分布 ,其中 是表示为像素向量的图像,它将高概率分配给看起来逼真的图像,而将低概率分配给其他所有图像。给定这样的模型,我们可以解决如下有趣的问题。
(1)图像生成
Radford 等人 训练了一个概率模型 $ p(\mathbf{x}) $,该模型将高概率分配给看起来像卧室的图像。为此,他们在卧室图像数据集上训练了模型,其样本如下所示:
训练数据

现在有了这个卧室的概率模型,我们可以通过从这个分布中采样来 生成 新的卧室图像。具体来说,新的采样图像 是直接从我们的模型 创建的,现在可以生成类似于训练数据集的数据。
此外,生成模型强大的原因之一在于:其参数比训练它们的数据量少得多(因此,模型必须有效地提取训练数据的精华,以便能够生成新的样本)。可以看到,我们特定的卧室概率模型在捕获数据精华方面做得很好,因此能够生成高度逼真的图像,其中一些示例如下所示:
生成的数据

同样,我们也可以学习人脸模型。

与卧室图像一样,这些面孔完全是合成的,图像中中的并不是真人。
相同方法可以用于其他对象。

请注意,图像并不完美,可能需要细化;但是,采样生成的图像与人们可能期望的非常相似。
(2)图像填充
使用相同的面部模型 ,我们还可以 “填充” 图像的其余部分。例如,给定 和某个现有图像的补丁,我们可以从 中采样,并以不同的可能方式生成补全图像:

请注意能够捕获不确定性的概率模型具有非常重要的作用:他们有多种可能的方法来补全图像!
(3)图像去噪
同样,给定一张被噪声破坏的图像(例如一张旧照片),我们可以尝试根据图像的概率模型来恢复它。具体来说,我们想要得到一个能够对后验分布 进行良好建模的概率图模型,有了它之后,我们就可以通过采样或精确推断,从观测到的含噪声图像中预测出原始图像。

6.2 自然语言
了解概率分布还可以帮助我们对自然语言进行建模。在这种情况下,我们想要在单词或字符 的序列上构建概率分布 ,将高概率分配给正确的(英语)句子。我们可以从各种来源(例如 Wikipedia 文章)中了解此分布。
(1)生成
假设我们已经从 Wikipedia 文章中构建了单词序列的概率分布。那么我们就可以从这个分布中进行采样,以生成类似 Wikipedia 的新文章,如下所示。源自: The Unreasonable Effectiveness of Recurrent Neural Networks 。

(2)翻译
假设我们收集了一组用英文和中文转录的段落训练集。我们可以建立一个概率模型 ,以对应的中文句子 为条件生成一个英文句子 ;这是 机器翻译 的一个实例。

6.3 音频
我们还可以将概率图模型用于音频应用程序。假设我们在音频信号上构建一个概率分布 ,它将高概率分配给听起来像人类语音的信号。
(1)上采样或超分辨率
给定音频信号的低分辨率版本,我们可以尝试提高其分辨率。可以将这个问题表述为:给定语音的概率分布 ,它 “知道” 典型的人类语音听起来像什么,并且输入了音频信号的一些观测值,我们的目标是计算中间时间点的信号值。在下图中,给定观测到的音频信号(蓝色)和音频概率模型,我们的目的是通过预测中间信号(白色)来重建原始信号(虚线)的更高保真版本。

我们可以通过对 进行采样或执行推断来解决此问题,其中 是我们想要预测的中间信号,而 是观测到的低分辨率音频信号。
(2)语音合成
正如在图像处理中所做的那样,我们还可以对模型进行采样并生成或合成语音信号(文本 → 音频) 。
(3)语音识别
给定语音信号和语言(文本形式)的(联合)模型,我们可以尝试从音频信号中推断出语言(文本),实现音频的语音识别。

6.4 科学
(1)纠错码
在非理论的世界中,概率模型常用于对通信通道(例如以太网或 Wifi)进行建模。即,如果通过频道发送消息,则由于噪音,您可能会在另一端得到不同的东西。纠错码以及基于概率图模型的技术常被用于检测和纠正通信错误。

(2)计算生物学
概率图模型也广泛用于计算生物学。例如,给定一个 DNA 序列随时间演变的模型,就可以从一组给定物种的 DNA 序列中重建系统发育树。

(3)生态
概率图模型用于研究随空间和时间演变的现象,捕捉空间和时间依赖性。例如,它们可用于研究鸟类迁徙。

(4)经济学
概率图模型可用于模拟兴趣量(如基于资产或支出的财富测量值)的空间分布。
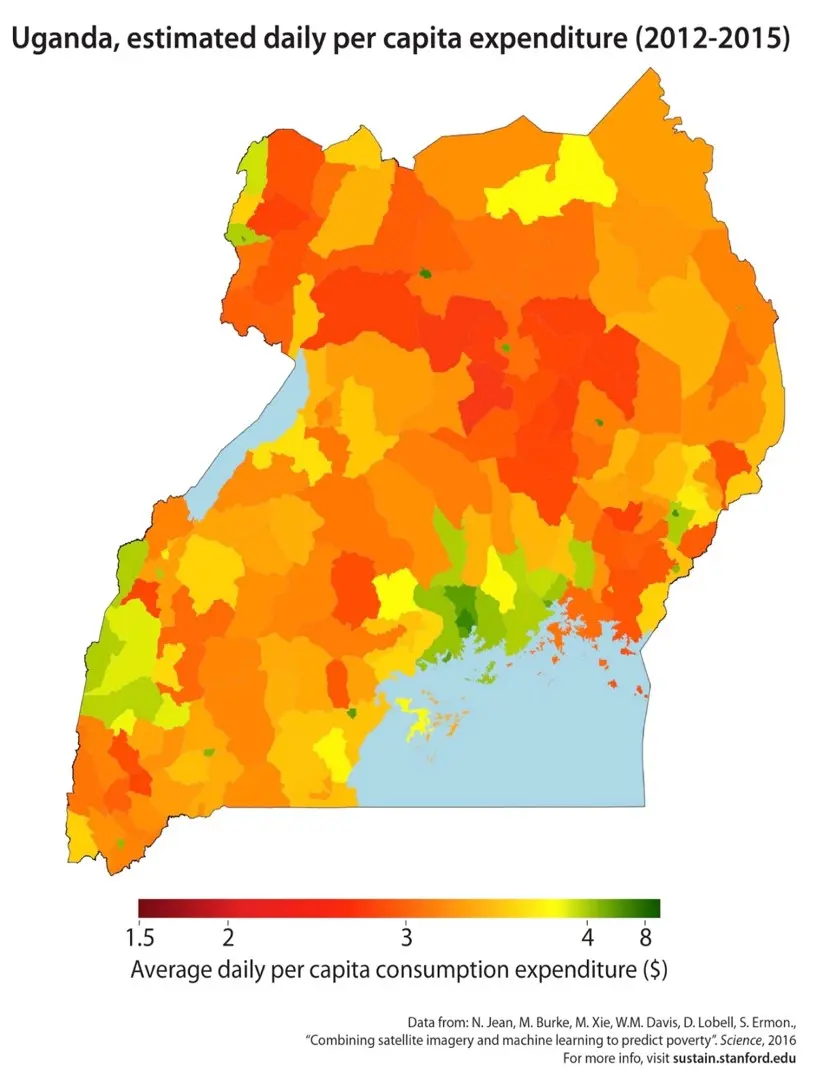
此处的生态和经济学应用都是所谓的时空模型,它们依赖于跨时间和跨空间收集的数据。
6.5 健康与医药
(1)医学诊断
概率图模型可以帮助医生诊断疾病和预测不良后果。例如,1998 年犹他州盐湖城的 LDS 医院开发了一个用于诊断肺炎的贝叶斯网络模型。他们的模型能够以高敏感性(0.95)和特异性(0.965)区分肺炎患者和其他疾病患者,并在临床上使用了很多年。他们的网络模型概述如下:

你可以 在这里 阅读更多关于他们模型开发的信息。






