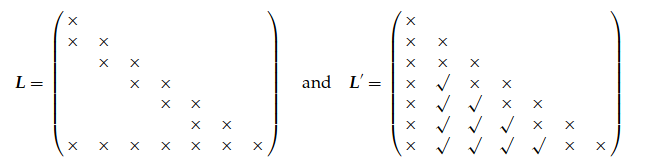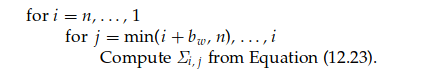马尔可夫随机场

【摘 要】在空间统计学中，面元数据的空间统计建模通常是采用马尔可夫随机场实施的。本文针对单随机变量（随机过程）情况，介绍了其定义、性质、推断方法、分布的计算等内容，尤其突出了高斯马尔可夫随机场（GMRF）。内容摘自 Gelfand 的 《空间统计手册》第十二章。

【原 文】 Gelfand, A.E. et al. (2010)， Handbook of spatial statistics (chapter 12). CRC press.

空间随机变量的有限集合的统计建模，通常通过马尔可夫随机场 (MRF) 完成。 MRF 是通过一组条件分布来指定的，其中每一个条件对应于某个分量在给定其他分量时的条件分布。这使人们能够每次只专注于单个随机变量，并导致了基于模拟的简单 MRF 计算程序，特别是利用马尔可夫链蒙特卡罗 (MCMC) 进行贝叶斯推断。

本章的主要目的是全面介绍高斯马尔可夫随机场（ GMRF ）的情况，重点是通用性质和高效计算方法。示例和应用将会出现在 第 13 章 和 第 14 章。我们将在本章最后讨论联合分布不是高斯的一般情况，特别是著名的 Hammersley-Clifford 定理。

涉及本章的主要参考文献：

• Rue 和 Held (2005) 的专著对 GMRF 给出了现代和一般性的参考；
• 对于更一般的马尔可夫随机场，大家可以参考 Guyon (1995) 和 Lauritzen (1996) 的方法背景和 Li (2001) 的图像空间应用分析；当然，J. Besag (1974, 1975) 的开创性论文仍然值得一读。

12.1 符号

• $\mathbf{x} = (x_1,\ldots ,x_n)^{\top}$ 表示 $n$ 维向量，$x_i$ 表示第 $i$ 个元素
• $\mathbf{x}_A = \{ x_i : i \in A\}$，$\mathbf{x}_{-A} =\{x_i : i \notin A\}$，$\mathbf{x}_{i : j} = (x_i ,\ldots ,x_j )^{\top},\quad j \geq i$
• 用 $\pi(\cdot)$ 和 $\pi(\cdot | \cdot)$ 表示其参数的（概率）密度，例如 $\pi(\mathbf{x})$ 和 $\pi(x_i |\mathbf{x}_{-i})$
• 高斯分布用 $\mathcal{N}(\boldsymbol{\mu,\Sigma})$ 表示，随机变（向）量 $\mathbf{x}$ 的密度为 $\mathcal{N}(\mathbf{x};\boldsymbol{\mu,\Sigma})$，其中 $\boldsymbol{\mu}$ 是期望值， $\boldsymbol{\Sigma}$ 是协方差矩阵
• 缩写 SPD 表示 对称正定矩阵
• 矩阵 $|\mathbf{A}|$ 的带宽是在所有 $i$ , $j$ 上 $A_{i,j} \neq 0$ 的 $\max |i − j|$ 。

12.2 高斯马尔可夫随机场（ GMRF ）

12.2.1 定义

我们将首先一般性地讨论 GMRF，然后稍后讨论其条件分布的定义。 GMRF 是一个高斯分布的随机向量 $\mathbf{x}$，但其服从一些条件独立性质。具体来说，对于某些 $i \neq j$，有：

$$x_i \perp x_j | \mathbf{x}_{-(i,j)} \tag{12.1}$$

上式意味着：如果以 $\mathbf{x}_{-(i,j)}$ 为条件，则 $x_i$ 和 $x_j$ 是独立的。

这种条件独立性可以使用（无向）有标签图 $\mathcal{G} = (\mathcal{V}, \mathcal{E})$ 来表示，其中 $\mathcal{V} =\{1,\ldots ,n\}$ 是结点集合，$\mathcal{E} =\left \{\{i, j\} : i, j \in \mathcal{V} \right \}$ 是边集合。对于所有 $i, j \in \mathcal{V}$，如果 式（12.1） 成立，则边 $\{i, j\}$ 不包含在 $\mathcal{E}$ 中，反之则包含。

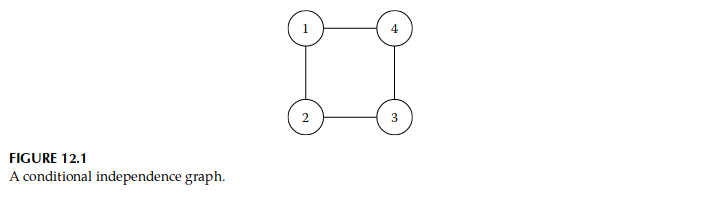
图 12.1 显示了这样一个图，其中 $n = 4$ 且 $\mathcal{E} = \left \{\{1, 2\}, \{2, 3\}, \{3, 4\}, \{4, 1\} \right \}$。从这个图中我们推断出 $x_2 \perp x_4|\mathbf{x}_{1,3}$ 和 $x_1 \perp x_3|\mathbf{x}_{2,3}$。现在的中心目标是利用图 $\mathcal{G}$ 来定义包含特定条件独立性质的 GMRF $\mathbf{x}$。事实表明，使用 $\mathbf{x}$ 的精度矩阵 $\mathbf{\mathbf{Q}} = \boldsymbol{\Sigma}^{-1}$ 来做到这一点非常简单。

【定理 12.1】

设 $\mathbf{x}$ 是具有对称正定 (SPD) 精度矩阵 $\mathbf{Q}$ 的高斯分布，则对于 $i \neq j$

$$x_i \perp x_j | \mathbf{x}_{-(i,j)} \Leftrightarrow \mathbf{Q}_{i,j} = 0$$

因此，任何具有 $\mathbf{Q}_{2,4} = \mathbf{Q}_{4,2} = \mathbf{Q}_{1,3} = \mathbf{Q}_{3,1} = 0$ 的 SPD 精度矩阵 $\mathbf{Q}$ 都具有如 图 12.1 所示的条件独立性质。我们通常称 $\mathbf{x}$ 是关于 $\mathcal{G}$ 的一个 GMRF。GMRF 的正式如下：

【定义 12.1 (GMRF)】

随机向量 $\mathbf{x} = (x_1,\ldots ,x_n)^{\top} \in \mathbb{R}^n$ 被称为关于有标签图 $\mathcal{G} = (\mathcal{V}, \mathcal{E})$ 的一个均值为 $\boldsymbol{\mu}$、 SPD 精度矩阵为 $\mathbf{Q}$ 的高斯马尔可夫随机场（ GMRF )，当且仅当其具有如下密度形式

$$\pi(\mathbf{x}) = (2\pi)^{−n/2} |\mathbf{Q}|^{1/2} \exp \left(-\frac{1}{2} (\mathbf{x} − \boldsymbol{\mu})^{\top} \mathbf{Q}(\mathbf{x} − \boldsymbol{\mu}) \right ) \tag{12.2}$$

其中对于所有 $i \neq j$，有 $\mathbf{Q}_{i,j} \neq 0 \Leftrightarrow \{ i , j\} \in \mathcal{E}$ 。

当精度矩阵 $\mathbf{Q}$ 奇异时，仍然能够为 GMRF 提供上述联合密度的显式形式，只是该联合密度不正确。这样的指定不能用于数据模型，但当其能够产生正确后验时，可以作为先验使用。这种示例包括 第 13 章 和 第 14 章 中将讨论的本征自回归。

下面是一个（正确的）GMRF 示例。

【示例 12.1】

令 $\{x_t\}$ 为平稳的一阶自回归过程，即对于 $t = 2,\ldots ,n$，有 $x_t|x_{t-1} = \phi x_{t-1} + \epsilon_t$，其中 $|\phi| < 1$ 且 $\epsilon_t$ 是一个具有零均值、单位方差的独立高斯分布量。如果进一步假设 $x_1$ 是均值为零、方差为 $1/(1−\phi^2)$ 的高斯分布（这是该过程的平稳分布）。那么 $\mathbf{x}$ 是关于 $\mathcal{G}$ 的一个 GMRF ，其中 $\mathcal{E} =\left \{\{1, 2\}, \{2, 3\},\ldots , \{n − 1,n\} \right \}$。其精度矩阵中有如下非零元素： （1）当 $|i − j |=1$ 时， $\mathbf{Q}_{i,j} = −\phi$； （2） $\mathbf{Q}_{1,1} = \mathbf{Q}_{n,n} = 1$ ； （3）当 $i = 2,\ldots ,n− 1$ 时，对角元素 $\mathbf{Q}_{ii} = 1 + \phi^2$。

这个例子很好地说明了为什么 GMRF 非常有用：

• 首先，对于滞后为 $k$ 的随机变量，其自相关为 $\phi^{|k|}$，也就是说，其 $\mathbf{x}$ 的协方差矩阵是密集的（即处处非零）。
• 其次，精度矩阵足够稀疏，在 $\mathbf{Q}$ 中的 $n^2$ 个元素中，只有 $n + 2(n − 1) = 3n − 2$ 个非零元素。

需要注意的是：稀疏精度矩阵使得用于模拟自回归过程的快速 $\mathcal{O}(n)$ 算法成为可能。

12.3 基本性质

12.3.1 条件性质

虽然 GMRF 可以看作是一般的多元高斯随机变量，但某些性质会被简化，某些特征会更容易计算。最直观的一点就是：由于精度矩阵的稀疏性，使得条件分布更容易计算了。为了看到这一点，我们先将结点集 $\mathcal{V}$ 分割为两个非空的集合： $\mathbf{A}$ 和 $B = −A$，则根据高斯分布性质，有 $\mathbf{x}$、$\boldsymbol{\mu}$ 和 $\mathbf{Q}$ 的如下划分:

$$\mathbf{x}= \binom{ \mathbf{x}_A}{ \mathbf{x}_B}, \boldsymbol{\mu} = \binom{\boldsymbol{\mu}_A}{\boldsymbol{\mu}_B} , \mathbf{Q} = \begin{pmatrix} \mathbf{Q}_{AA} & \mathbf{Q}_{AB}\\ \mathbf{Q}_{BA} & \mathbf{Q}_{BB} \end{pmatrix}$$

此外，我们还需要具有子图的概念。子图 $\mathcal{G}^A$ 指限制在结点子集 $A$ 内的一个图：去掉 $\mathcal{G} $ 中所有不属于 $A$ 的结点和所有至少有一个结点不属于 $A$ 的边后生成的新图。

有了上述概念，下面的定理成立。

【定理 12.2】

令 $\mathbf{x}$ 为关于 $\mathcal{G}$ 的 GMRF，其均值为 $\boldsymbol{\mu}$ 和 SPD 精度矩阵为 $\mathbf{Q}$。令 $A \subset \mathcal{V}$，另外令 $B = \mathcal{V} \setminus A$ 且 $A，B \neq \emptyset$。则条件分布 $\mathbf{x}_A|\mathbf{x}_B$ 是一个关于子图 $\mathcal{G}^A$ 的 GMRF，且其均值为 $\boldsymbol{\mu}_{A|B}$ 、 SPD 精度矩阵为 $\mathbf{Q}_{A|B}$，其中

$$\boldsymbol{\mu}_{A|B} = \boldsymbol{\mu}_A − \mathbf{Q}^{-1}_{AA} \mathbf{Q}_{AB} (\mathbf{x}_B − \boldsymbol{\mu}_B) \quad \text{和} \quad \mathbf{Q}_{A|B} = \mathbf{Q}_{AA}$$

【备注 12.1】 请注意，此结果只是采用了高斯条件分布的另一种视角。事实上，我们通常也会使用协方差矩阵 $\boldsymbol{\Sigma}$ 的分块形式来表示

$$\boldsymbol{\Sigma} = \begin{pmatrix} \boldsymbol{\Sigma}_{AA} & \boldsymbol{\Sigma}_{AB}\\ \boldsymbol{\Sigma}_{BA} & \boldsymbol{\Sigma}_{BB} \end{pmatrix}$$

根据上述表示，条件分布的协方差矩阵为 $\operatorname{Cov}(\mathbf{x}_A|\mathbf{x}_B) = \boldsymbol{\Sigma}_{AA} − \boldsymbol{\Sigma}_{AB} \boldsymbol{\Sigma}^{-1}_{BB} \boldsymbol{\Sigma}_{BA}$，其与 $\mathbf{Q}^{-1}_{AA}$ 本质上是相同。与此类似，条件分布的均值也可以表示为分块协方差矩阵的形式。

精度矩阵表示方法 “引人注目” 的特征是：

• 条件精度矩阵 $\mathbf{Q}_{A|B}$ 竟然是 $\mathbf{Q}$ 的一个子矩阵。因此，条件精度矩阵也是显式可用的，只需删除掉 $\mathbf{Q}$ 中属于 $B$ 的行和列即可。换句话说，$\mathbf{Q}$ 的稀疏性会继承给 $\mathbf{Q}_{A|B}$。
• 条件均值 $\boldsymbol{\mu}_{A|B}$ 涉及逆 $\mathbf{Q}^{-1}_{AA}$，但可以被写成 $\boldsymbol{\mu}_{A|B} = \boldsymbol{\mu}_A − \mathbf{b}$ 的形式，其中 $\mathbf{b}$ 可以被视为稀疏线性方程组 $\mathbf{Q}_{AA} \mathbf{b} = \mathbf{Q}_{AB} (\mathbf{x}_B − \boldsymbol{\mu}_B)$ 的解。请注意，只有 $A$ 中的结点与 $B$ 中的结点存在边时，$\mathbf{Q}_{AB}$ 中的相应元素才非零，因此通常只有少数项会进入该矩阵向量乘积。
• 单结点的条件预测形式非常简单。在只有一个结点的特殊情况 $A =\{i\}$ 下，表达式可以简化为：

$$\mu_{i|−i} = \mu_i − \sum\limits_{j: j \sim i} \frac{ \mathbf{Q}_{i,j}}{\mathbf{Q}_{ii}} (x_j − \mu_j ) \quad \text{且} \quad \mathbf{Q}_{i|−i} = \mathbf{Q}_{ii} \tag{12.3}$$

上式中，符号 $j : j \sim i$ 表示与结点 $i$ 相邻的所有结点 $j$ 的集合，即满足 $\{i, j\} \in \mathcal{E}$。所以 $x_i$ 的条件精度为 $\mathbf{Q}_{ii}$，$x_i$ 的条件均值为其邻居结点值 $x_j$ 按照权重 $−\mathbf{Q}_{i,j}/\mathbf{Q}_{ii}$ 实施的线性加权平均。

【例 12.2】

重新回顾 例 12.1。此时根据 式（12.3），我们可以得到 $x_i |\mathbf{x}_{-i}$ 的均值和精度矩阵分别为：

$$\mu_{i|-i} = \frac{\phi}{1 + \phi^2} (x_{i−1} + x_{i+1}) \quad \text{和} \quad \mathbf{Q}_{i|-i} = 1 + \phi^2, 1 < i < n$$

12.3.2 马尔可夫性质

一个 GMRF 的图 $\mathcal{G}$ 是通过查看哪些 $x_i$ 和 $x_j$ 之间存在条件独立来定义的，这种结点合结点之间的条件独立性，被称为 成对马尔可夫性质（pairwise Markov property）。

但初此之外，我们还可以从图 $\mathcal{G}$ 导出更一般的马尔可夫性质。

路径（path）：从结点 $i_1$ 到结点 $i_m$ 的路径是一个由 $\mathcal{V}$ 中不同结点组成的结点序列（ $i_1,i_2,\ldots ,i_m$ ），其中任意相邻结点之间均存在边，即对于任意 $j = 1,\ldots ,m−1$，都有 $(i_j,i_{j+1}) \in \mathcal{E}$ 。

分隔（separate)： 对于某个结点子集 $C \subset \mathcal{V}$，如果从结点 $i \notin C$ 和结点 $j \notin C$ 的所有 路径 中都包含至少一个来自 $C$ 的结点，则我们称结点 $i$ 与结点 $j$ 被 $C$ 分隔。更进一步的，对于两个不相交的集合 $A \subset \mathcal{V} \setminus C$ 和 $B \subset \mathcal{V} \setminus C$ ，如果所有结点 $i \in A$ 和 $j \in B$ 均被 $C$ 分隔，则我们称 $A$ 和 $B$ 被 $C$ 分隔。换句话说，不经过 $C$，我们无法在图上从 $A$ 的某处开始到 $B$ 的某处结束。

基于上述概念，可以定义如下 ：

全局马尔可夫性质：对于互不相交的集合 $A$、$B$ 和 $C$，如果 $A$ 和 $B$ 被 $C$ 分隔，且 $A$ 和 $B$ 非空，则有

$$\mathbf{x}_A \perp \mathbf{x}_B | \mathbf{x}_C \tag{12.4}$$

【定理 12.3】 如果 $\mathbf{x}$ 是关于 $\mathcal{G}$ 的 GMRF，则 $\mathbf{x}$ 满足全局马尔可夫性质。

注意： $A \cup B \cup C$ 可以是 $\mathcal{V}$ 的子集；因此，该结果也提供了有关边缘 $\mathbf{x}_{A\cup B\cup C}$ 的条件独立性质的信息。

【例 12.3】

继续回顾 例 12.1。利用 成对条件独立性，我们知道 $x_1 \perp x_n | \mathbf{x}_{-{1,n}}$，但依据 全局马尔可夫性质，我们也可以知道：对于所有 $1 < j < n$，都有 $x_1 \perp x_n|x_j$。

12.4 条件指定

依据 J. Besag (1974, 1975) 的开创性工作，通常会通过 完全条件分布 $\{\pi(x_i |\mathbf{x}_{-i})\}$ 来隐式指定一个 GMRF，并且我们可以根据需要从 完全条件分布 中推导出相应 联合分布 的均值和精度矩阵。但 完全条件分布 不能完全随意指定，因为还要确保其对应的联合分布是正确的（ 我们将在 第 12.8 节 中讨论此问题）。

一种条件指定方法是将 完全条件分布 $\{\pi(x_i |\mathbf{x}_{-i} )\}$ 定义为高斯分布，其矩满足

$$\mathbb{E}(x_i |\mathbf{x}_{-i} ) = \mu_i + \sum_{j \neq i} \beta_{i,j} (x_j − \mu_j) \quad \text{和} \quad \operatorname{ Precision}(x_i | \mathbf{x}_{-i}) = \kappa_i > 0 \tag{12.5}$$

这种方法的合理性在于：指定完全条件分布比指定联合分布更容易。

比较 式（12.5） 和 式（12.2） ，如果我们选择 $\boldsymbol{\mu}$ 为均值，$Q_{ii} = \kappa_i$ , $\beta_{i,j} = −\mathbf{Q}_{i,j}/\mathbf{Q}_{ii}$，则可以得到相同的 完全条件分布；请参阅下面的正式证明。

不过，由于 $\mathbf{Q}$ 是对称矩阵，我们必须要求对于所有 $i \neq j$

$$\kappa_i \beta_{i,j} = \kappa_j \beta_{j,i} \tag{12.6}$$

特别是，如果 $\beta_{i, j}$ 不为零，则 $\beta_{j,i}$ 不能为零。图 $\mathcal{G}$ 中的边定义为 $\left \{\{i, j\} : \beta_{i,j} \neq 0 \right \}$。

除了 式（12.6） 的对称约束之外，还有一个联合分布要求是 $\mathbf{Q}$ 必须是 SPD。不幸的是，这是一个联合分布的性质，我们很难进行局部验证。避免此问题的一种便捷方法是选择对角占优的参数化形式以确保 $\mathbf{Q}$ 为 SPD，即对于所有 $i$ 有 $Q_{i,i} > \sum\limits_{j} |Q_{i, j}|$ 。这意味着

$$\sum\limits_{j} |\beta _{i,j} | <1 , \forall i$$

但这种假设可能具有局限性（Rue 和 Held，2005 年，第 2.7 节和第 5.1 节）。

尽管我们能够识别具有相同完全条件分布的高斯，但我们仍然需要知道联合分布的唯一性。 Brook 引理（Brook，1964）回答了这个问题。

【引理 12.1（Brook 引理）】

令 $\pi(\mathbf{x})$ 为 $\mathbf{x} \in \mathbb{R}^n$ 的密度并定义 $\Omega =\{\mathbf{x} \in \mathbb{R}^n: \pi(\mathbf{x}) > 0 \}$。令 $\mathbf{x}, \mathbf{x'} \in \Omega$ ，则

$$\begin{align*} \frac{\pi(\mathbf{x})}{\pi(\mathbf{x'})} &= \prod^{n}_{i=1} \frac{ \pi(x_i |x_1,\ldots,x_{i−1},x'_{i+1},\ldots ,x'_n)}{\pi(x'_i |x_1,\ldots ,x_{i−1},x'_{i+1},\ldots ,x'_n)} \tag{12.7}\\ &= \prod^{n}_{i=1} \frac{ \pi(x_i |x'_1,\ldots ,x'_{i−1},x_{i+1},\ldots ,x_n)}{\pi(x'_i |x'_1,\ldots ,x'_{i−1},x_{i+1},\ldots ,x_n)} \tag{12.8} \end{align*}$$

唯一性论证遵循固定 $\mathbf{x}'$，然后 $\pi(\mathbf{x})$ 与 式（12.7） 右侧的完全条件分布成正比。比例常数是利用 $\pi(\mathbf{x})$ 对一进行积分得到的。结果是我们可以从完全条件分布中推导出联合密度，我们将在下面说明。为简单起见，固定 $\boldsymbol{\mu} = 0$ 和 $\mathbf{x'} = 0$。使用 式（12.5） 中的完全条件分布，然后 式（12.7） 简化为

$$\log \frac{ \pi(\mathbf{x})}{\pi(\mathbf{0})} = − \frac{1}{2} \sum^n_{i=1} \kappa_i x^2_i − \sum^n_{i=2} \sum\limits^{i-1}_{j=1} \kappa_i \beta_{ij} x_i x_j \tag{12.9}$$

并且 式（12.8） 简化为

$$\log \frac{ \pi(\mathbf{x})}{\pi(\mathbf{0})} = −\frac{1}{2} \sum^n_{i=1} \kappa_i x^2_i − \sum\limits^{n-1}_{i=1} \sum\limits^{n}_{j=i+1} \kappa_i \beta_{ij} x_i x_j \tag{12.10}$$

由于 式（12.9） 和 式（12.6） 必须相同，因此 对于 $i \neq j$ 有 $\kappa_i \beta_{ij} = \kappa_j \beta_{ji}$ 。 $\mathbf{x}$ 的密度可以表示为

$$\log \pi(\mathbf{x}) = \quad \text{const} − \frac{1}{2} \sum^n_{i=1} \kappa_i x^2_i - \frac{1}{2} \sum\limits_{i \neq j} \kappa_i \beta_{ij} x_i x_j$$

因此，如果 $\mathbf{Q}$ 是 SPD，则 $\mathbf{x}$ 是零均值 GMRF

我们现在将在一个简单的例子中说明条件指定的实际使用。

【例 12.4】

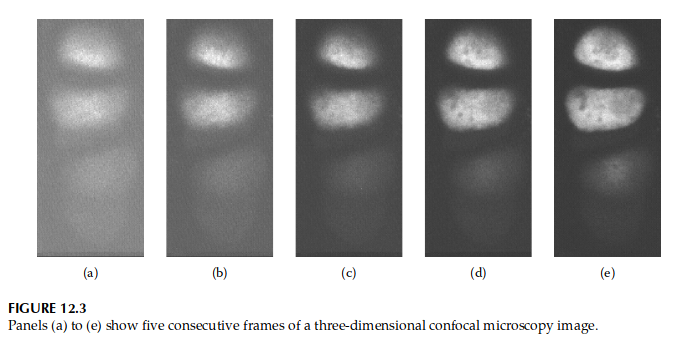
图 12.2(a) 中的图像是 $256 × 256$ 伽马相机图像，旨在反映癌性骨骼的预期结构。图像圆形部分中的每个像素 $\mathcal{I}$ 代表伽马辐射计数，其中黑色像素代表（基本上）零计数，白色像素代表最大计数。图像噪声很大，本例中的任务是（尝试）去除噪声。噪声过程可以通过泊松分布非常准确地描述，因此对于每个像素 $i$，记录的计数 $y_i$ 与真实信号 $\eta_i$ 相关，其中 $y_i \sim \operatorname{ Poisson}(\eta_i)$ 。为简单起见，我们将使用以下近似值

$$\sqrt{y_i} | \eta_i \sim \mathcal{N} \left (\sqrt{ \eta_i} , \frac{1}{4} \right ) ,i \in \mathcal{I}$$

平方根变换后的图像如 图 12.2(b) 所示。采用贝叶斯方法，我们需要为（平方根变换的）图像 $\mathbf{x} = (x_1,\ldots ,x_n)^{\top}$ 指定先验分布，其中 $x_i = \sqrt{ \eta_i}$ 。 （我们需要 $\eta_i$ 比零（稍微）大一些才能使这个近似值足够）。虽然这通常是一个令人生畏的问题，但对于此类噪声去除任务，通常指定先验就足以说明真实图像的局部行为。由于图像本身是局部平滑的，我们可以通过 式（12.5） 的完全条件分布指定先验。使用完全条件分布，我们只需要回答这样的问题： 如果不知道像素 $i$ 中的真实信号，那么所有其他信号怎么办？我们对 $x_i$ 的信念是什么？ 一种选择是将 $\beta_{i,j}$ 设置为零，除非 $j$ 是 $i$ 的四个最近邻居之一；比方说 $N_4(i)$。由于对方向没有特别偏好，我们可能会为每个 $i$ 设置，

$$\beta_{i,j} = \frac{\delta}{4}, \quad j \in N_4(i)$$

其中 $\delta$ 被认为是固定值。此外，我们将 $\kappa_i$ 视为对所有 $i$ 都共同（且未知），并将 $\delta$ 限制为 $|\delta| < 1$ 以便（先验）精度矩阵对角占优势。 （我们在这里忽略了边界像素可能少于四个邻居的校正问题）。我们进一步采用 $\boldsymbol{\mu} = \mathbf{0}$ 和 $\kappa$ 的共轭先验 $\Gamma(a, b)$（密度正比于 $\kappa^{a-1} \exp(−b\kappa))$，则 $(x, \kappa)$ 的后验为：

$$\begin{align*} \pi(\mathbf{x}, \kappa | \mathbf{y}) &\propto \pi( \mathbf{x} | \kappa) \pi(\kappa) \prod\limits_{i \in \mathcal{I}} \pi( y_i | x_i ) \\ & \propto \kappa^{a-1} \exp(−b_{\kappa}) | \mathbf{Q}_{prior}(\kappa) |^{1/2} \exp \left( − \frac{1}{2} \mathbf{x}^{\top} \mathbf{Q}_{post}(\kappa) \mathbf{x} + \mathbf{b}^{\top} \mathbf{x} \right) \tag{12.11} \end{align*}$$

这里，对于 $i \in \mathcal{I}$，$b_i = 4\sqrt{ y_i}$，否则为零，$\mathbf{Q}_{post}(\kappa) = \mathbf{Q}_{prior}(\kappa) + \mathbf{D}$ 其中 $\mathbf{D}$ 是对角矩阵，当 $i \in \mathcal{I}$ 时，$D_{i,i} = 4$ ，否则为零，并且

$$\mathbf{Q}_{prior}(\kappa)_{i, j} = \kappa \begin{cases} 1, & i=j\\ \delta/4, &j \in N_4(i)\\ 0, & \text{otherwise} \end{cases}$$

以 $\kappa$ 和观测值为条件，则 $\mathbf{x}$ 是具有精度矩阵 $\mathbf{Q}_{post}$ 的 GMRF，其中平均 $\boldsymbol{\mu}_{post}$ 由以下的解给出

$$\mathbf{Q}_{post} \boldsymbol{\mu}_{post} = \mathbf{b} \tag{12.12}$$

12.5 GMRF 的 MCMC 推断

GMRF 的一个吸引人的特性是可以很好地与 MCMC 方法结合起来进行贝叶斯推断（参见 Gilks、Richardson 和 Spiegelhalter，1996 年；Robert 和 Casella，1999 年关于 MCMC 的一般背景）。 GMRF 中使用的完全条件分解（即相应的条件指定）与 MCMC 算法之间的良好对应关系，是 GMRF 被广泛使用的主要原因之一。

事实证明，GMRF 与稀疏矩阵的数值方法之间存在很好的联系，这导致了 GMRF 的精确算法；我们将在 第 12.7 节 讨论此问题。

为了描述方便，设 $\pi(\boldsymbol{\theta})$ 为我们感兴趣的后验，而任务是计算如下后验边缘分布（或其摘要信息，如均值 $\mathcal{E}(\theta_1)$ 和方差 $\operatorname{Var}(\theta_1)$ 等）：

$$\pi(\theta_1),\ldots , \pi(\theta_n)$$

对于 例 12.4，相应的 $\boldsymbol{\theta} = (\mathbf{x}, \kappa)$，而我们的任务是计算所有 $i \in \mathcal{I}$ 的 $\mathbb{E}(x_i |\mathbf{y})$，并将其用作对 $\sqrt{ \eta_i}$ 的估计。我们可以根据 $\operatorname{Var}(x_i |\mathbf{y})$ 或后验边缘分布 $\pi(x_i |\mathbf{y})$ 的分位数来量化估计的不确定性。

12.5.1 MCMC背后的基本思想

MCMC 的基本思想很简单。我们将简要介绍两个基本思想，马尔可夫链和蒙特卡罗，它们共同构成了马尔可夫链蒙特卡罗。用于（也称为贝叶斯）推断的蒙特卡罗方法主要是关于蒙特卡罗积分，它用经验方法代替积分；对于一些合适的函数 $f (·)$，我们有

$$\mathbb{E}( f (\boldsymbol{\theta})) = \int f (\boldsymbol{\theta})\pi(\boldsymbol{\theta}) d\boldsymbol{\theta} \approx \frac{1}{N} \sum^{N}_{i=1} f (\boldsymbol{\theta}^{(i)}) \tag{12.13}$$

其中：

$$\boldsymbol{\theta}^{(1)}, \boldsymbol{\theta}^{(2)},\ldots , \boldsymbol{\theta}^{(N)}$$

是来自 $\pi(\boldsymbol{\theta})$ 的 $N$ 个样本。通过将积分解释为期望值，我们可以将其近似为来自 $\pi(\boldsymbol{\theta})$ 的 $N$ 个样本的经验平均值。如果样本是独立的，那么我们也可以控制误差，因为

$$\frac{1}{\sqrt{N}} \sum^{N}_{i=1} f(\boldsymbol{\theta}^{(i)}) \approx \mathcal{N}(\mathbb{E}( f(\boldsymbol{\theta})), \operatorname{Var}( f (\boldsymbol{\theta})))$$

在相当一般的假设下。我们的估计可以尽可能精确，选择足够大的 $N$。请注意，误差的表现类似于 $\mathcal{O}(1/\sqrt{N})$，因此精度增加一位需要 $100 × N$ 个样本。

即使对于低维，从分布 $\pi(\boldsymbol{\theta})$ 生成样本也可能很困难，但在一维情况下更难。除了维度之外的主要障碍是 $\pi(\boldsymbol{\theta})$ 中经常缺失的归一化常数；我们通常只知道密度的非归一化版本，要对其进行归一化就像计算 $\mathbb{E}( f (\boldsymbol{\theta}))$ 一样困难。

第二个主要思想是绕过直接从 $\pi(\boldsymbol{\theta})$ 生成样本的问题，但是隐式地从 $\pi(\boldsymbol{\theta})$ 生成样本。这是通过构造一个以 $\pi(\boldsymbol{\theta})$ 为均衡分布的马尔可夫链来完成的，我们可以模拟这个马尔可夫链来获得一个样本。事实证明，这可以在不知道 $\pi(\boldsymbol{\theta})$ 的归一化常数的情况下完成。原则上，我们可以通过长时间模拟马尔可夫链，从 $\pi(\boldsymbol{\theta})$ 生成一个样本，直到它收敛，这时马尔可夫链的状态就是一个样本。

我们现在将介绍 Gibbs 采样器，它是两种最流行的 MCMC 算法之一。我们将推迟到 第 12.9 节 讨论第二个算法，即 Metropolis-Hastings 算法。吉布斯采样器由 Geman 和 Geman (1984) 引入主流 IEEE 文献，由 Gelfand 和 Smith (1990) 引入统计。后来，很明显，一般思想（及其含义）已经围绕 Hastings（1970 年）展开；参见（Robert and Casella，1999，第 7 章）的历史记录。

12.5.2 吉布斯采样器

最直观的 MCMC 算法称为 Gibbs 采样器。吉布斯采样器通过从完全条件分布中重复采样来模拟马尔可夫链。马尔可夫链中的状态向量 $\boldsymbol{\theta}$ 在以下 Gibbs 采样算法中会在每个实例中被覆盖

该算法定义了一个具有平衡分布 $\pi(\boldsymbol{\theta})$ 的马尔可夫链；直观地，如果 $\boldsymbol{\theta}$ 是来自 $\pi(\boldsymbol{\theta})$ 的样本，并且我们用来自 $\pi(\theta_i |\boldsymbol{\theta}_{-i})$ 的样本更新它的第 $i$ 个分量 $\theta_i$，那么 $\boldsymbol{\theta}$ 仍然根据 $\pi(\boldsymbol{\theta})$ 分布。此外，该算法将在时间 $t = 1、2、\ldots$ 时输出一个新状态 $\boldsymbol{\theta}$。将这些样本表示为 $\boldsymbol{\theta}^{(1)}, \boldsymbol{\theta}^{(2)},\ldots$。

在相当一般的条件下，$\boldsymbol{\theta}^{(k)}$ 的分布将收敛，因为 $k \rightarrow \infty$ 到平衡分布 $\pi(\boldsymbol{\theta})$。对于一些大的 $k$，比如 $k_0$，我们可以认为 $\boldsymbol{\theta}^{(k_0)}$ 是来自 $\pi(\boldsymbol{\theta})$ 的样本。但是，如果 $\boldsymbol{\theta}^{(k_0)}$ 具有正确的分布，那么下一个状态 \boldsymbol{\theta}(k_0+1) 也将如此；但是，他们将依赖。 式（12.13） 中的蒙特卡洛估计将修改为

$$\mathbb{E}( f (\boldsymbol{\theta})) = \frac{1}{N − k_0 + 1} \sum^{N}_{i=k_0} f (\boldsymbol{\theta}^{(i)})。 `式（12.14）`$$

请注意，$\{\boldsymbol{\theta}^{(i)}\}$ 其中 $i = k_0,\ldots$ 现在通常是相关的。 式（12.14） 的方差估计必须考虑这种依赖性。我们已经从马尔可夫链中释放了前 $k_0 − 1$ 个状态，这被称为老化。要（尝试）确定 $k_0$ 的值，主要思想是查看 $\theta_i$ 的轨迹，例如；抽取 $\{\boldsymbol{\theta}^{(k)}_i \}$ 对 $k = 1, 2,\ldots$ ，并尝试确定 $k_0$ ，其中围绕平均值的波动似乎相当稳定（在分布意义上），（参见 Robert，1998；Robert和 Casella，1999 年，了解详情）。选择太大的 $k_0$ 不会使估计产生偏差，但选择太小的 $k_0$ 则会。

【例 12.5】

我们现在将说明如何使用 Gibbs 采样器从 GMRF 生成样本。如果我们通过完全条件分布 式（12.5） 指定 GMRF，我们将立即拥有 Gibbs 采样器。该算法如下：

GMRF 的 Gibbs 采样器的吸引力在于简单性和速度。它很简单，因为我们不需要计算 $\mathbf{x}$ 的联合分布来从 $\pi(\mathbf{x})$ 生成样本。只要完全条件分布定义了有效的联合分布，吉布斯采样器就会收敛到正确的分布。通常每个测点 $i$ 的邻居数不依赖于 $n$。在这种情况下，运行 Gibbs 采样器进行一次迭代（更新 $\mathbf{x}$ 的所有 $n$ 个元素）的计算成本是 $\mathcal{O}(n)$ 次操作，这在顺序意义上是最优的。

【例 12.6】

让我们回到 例 12.4，它比 例 12.5 复杂一些，原因有二。首先，我们需要处理未知精度 $\kappa$。其次，对于固定的 $\kappa$，GMRF 仅隐式已知，因为均值作为 式（12.12） 的解给出。事实证明，我们不需要求解 式（12.12） 即可构建 Gibbs 采样器。

在此示例中，$\boldsymbol{\theta} = (\kappa, \mathbf{x})$，我们需要从后验 式（12.11） 计算所有完全条件分布。使用 $\mathbf{Q}_{post}(\kappa) = \kappa \mathbf{Q}_{prior}(1) + D$，$\kappa$ 的完全条件分布是

$$\kappa | \mathbf{x, y} \sim \Gamma ( n/2 + a, b + \frac{1}{2} \mathbf{x}^{\top} \mathbf{Q}_{prior}(1) \mathbf{x} )$$

$x_i$ 的完全条件分布是使用

$$\begin{align*} \pi(x_i | \mathbf{x}_{-i} , \kappa, \mathbf{y}) &\propto \pi(\mathbf{x}, \kappa | \mathbf{y})\\ &\propto \exp \left ( − \frac{1}{2} x^2_i \mathbf{Q}_{post,i,i} (\kappa) − x_i \sum\limits_{ j \in N_4(i)} \mathbf{Q}_{prior,i , j} (\kappa)x_j + b_i x_i \right ) \\ &= \exp \left (- \frac{1}{2}c_i x^2_i + d_i x_i \right) \end{align*}$$

其中 $c_i$ 取决于 $\kappa$，而 $d_i$ 取决于 $\kappa$ 和 $\{x_j\}$ 对于 $j \in N_4(i)$。那么 $x_i$ 的完全条件分布是 $\mathcal{N}(d_i /c_i , 1/c_i )$。然后吉布斯采样算法变为

$\mathbf{x}$ 的后验平均值显示在 图 12.2(c) 中，使用 $a = 1$，$b = 0.01$ 和 $\beta = 1/4$。令人惊讶的是，我们可以使用这个简单的算法从 $(\kappa, \mathbf{x})$ 的后验生成样本。另请注意，以观察 $\mathbf{y}$ 为条件不会改变 $x_i$ 的邻域，它仍然是 $N_4(i)$。结果是 Gibbs 采样器的计算成本与没有数据时相同，即每次迭代的 $\mathcal{O}(n)$。这包括更新 $\kappa$ 的成本，它主要由计算 $\mathbf{x}^{\top} \mathbf{Q}_{prior}(1) \mathbf{x}$（也是 $\mathcal{O}(n)$ ）的成本决定。

12.6 多变量 GMRF

为了修正想法，我们将考虑 示例 12.4 的一般化，其中观察现在是图像序列。该序列可以是电影，其中序列中的每一帧都按时间索引，也可以是将三维对象记录为一组二维图像的高度。其他示例包括一个国家每个行政区域疾病计数空间模型的时间版本。图 12.3 显示了共聚焦显微镜拍摄的三个连续的三维细胞帧。第一帧有很多噪音，但信号在图像堆栈中越往上越强。我们考虑与示例 12.4 相同的问题；我们想在存在噪声的情况下估计真实信号。五帧代表相同的三维对象，但在不同的高度。

当我们指定完全条件分布时，我们可以使用这些信息。然后指定完全条件分布 式（12.5） 的多变量版本更容易也更自然，我们现在将对其进行描述。设 $x_i$ 表示像素 $i$ 处的所有 $p = 5$ 个观测值

$$x_i = (x_{i,1},x_{i,2},x_{i,3},x_{i,4},x_{i,5})^{\top}$$

这里，$x_{i,2}$ 是第 2 帧中位置 $i$ 处的像素，依此类推。条件指定 式（12.5） 自然延伸至

$$\mathbb{E}(\mathbf{x}_i | \mathbf{x}_{-i} ) = \boldsymbol{\mu}_i − \sum\limits_{j: j \sim i} \beta_{i,j}(\mathbf{x}_j − \boldsymbol{\mu}_j) \quad \text{and} \quad Precision(\mathbf{x}_i | \mathbf{x}_{-i} ) = \boldsymbol{ \kappa}_i > 0 \tag{12.15}$$

对于某些 $p × p$ 矩阵 $\{\beta_{i,j}\}$ 和 $\{\kappa_i\}$（另见 Mardia，1988）。在这个中，我们现在可以指定我们对 $x_{i,3}$ 的了解可能受益于了解 $x_{i,2}$ 和 $x_{i,4}$。这些像素位于相同的 $x_i$ 向量中，尽管它们代表前一帧和下一帧的第 $i$ 个像素。此外，我们可以在同一帧内具有来自邻居的依赖性，例如 $\{x_{j,3},j\in N_4(i)\}$。简而言之，我们可以指定 $\mathbf{x}_i$ 如何依赖于 $\{\mathbf{x}_j \}，j \neq i$，并考虑作为（小 $p$-）向量的邻居。

此示例中的条件指定激发了多元 GMRF 的引入，我们将其表示为 MGMRF$_p$。它的定义是 式（12.1） 的直接扩展。设 $\mathbf{x} = (\mathbf{x}^{\top}_1 ,\ldots , \mathbf{x}^{\top}_n )^{\top}$ 服从高斯分布，其中每个 $\mathbf{x}_i$ 是一个 $p$ 向量。类似地，令 $\boldsymbol{\mu} = (\boldsymbol{\mu} ^{\top}_1 ,\ldots , \boldsymbol{\mu}^{\top})^{\top}$ 表示均值，并且 $\tilde{\mathbf{Q}} = (\tilde{\mathbf{Q}}_{i,j})$ 具有 $p × p$ 个元素 $\tilde{\mathbf{Q}}_{i,j}$ 的精度矩阵。

【定义 12.2 (MGMRF$_p$)】

随机向量 $\mathbf{x} = (\mathbf{x}^{\top}_1 ,\ldots , \mathbf{x}^{\top}_n )^{\top}$ 其中 $\text{dim}(x_i ) = p$，称为关于 $\mathcal{G} = (\mathcal{V} = \{1,\ldots,n\}, \mathcal{E})$ 的 MGMRF$_p$ ，其均值为 $\boldsymbol{\mu}$ ，SPD 精度矩阵为 $\tilde{\mathbf{Q}}$，当且仅当其密度具有以下形式

$$\begin{align*} \pi(\mathbf{x}) &= (\frac{1}{2 \pi})^{np/2} |\tilde{\mathbf{Q}}|^{1/2} \exp \left (\frac{1}{2} (\boldsymbol{x} − \boldsymbol{\mu} )^{\top} \tilde{\mathbf{Q}}(\mathbf{x} − \boldsymbol{\mu} ) \right ) \\ &= (\frac{1}{2\pi})^{np/2} |\tilde{\mathbf{Q}}|^{1/2} \exp \left (− \frac{1}{2} \sum\limits_{ij} (\mathbf{x}_i − \boldsymbol{\mu}_i )^{\top} \tilde{\mathbf{Q}}_{i,j} (\mathbf{x}_j − \boldsymbol{\mu}_j \right)\\ \tilde{\mathbf{Q}}_{i,j} \neq 0 &\Leftrightarrow \{ i, j\} \in \mathcal{E} \quad \text{for all} \quad i \neq j \end{align*}$$

重要的是要注意大小为 $n$ 的 MGMRF$_p$ 只是另一个维度为 $np$ 的 GMRF；因此我们之前的所有结果和即将推出的 GMRF 稀疏矩阵算法也适用于 MGMRF$_p$。然而，一些结果使用块更容易解释，例如

$$\mathbf{x}_i \perp \mathbf{x}_j | \mathbf{x}_{−\{i, j\}} \Leftrightarrow \tilde{\mathbf{Q}}_{i,j} = \mathbf{0}$$

并且

$$\mathbb{E}(\mathbf{x}_i | \mathbf{x}_{-i} ) = \boldsymbol{\mu}_i − \tilde{ \mathbf{Q}}^{-1}_{ i,i} \sum\limits_{ j: j \sim i} \tilde{ \mathbf{Q}}_{i,j}(\mathbf{x}_j − \boldsymbol{\mu}_j) \quad \text{和} \quad Precision(\mathbf{x}_i | \mathbf{x}_{-i}) = \tilde{\mathbf{Q}}_{ii} \tag{12.16}$$

从 式（12.16） ，我们可以通过选择条件指定 式（12.15） 获得一致性要求

$$\mathbf{Q}_{i,j} = \begin{cases} \boldsymbol{ \kappa_i \beta}_{i,j} & i \neq j\\ \boldsymbol{ \kappa}_i & i \neq j \end{cases}$$

因为 $\tilde{ \mathbf{Q}}_{i,j} = \tilde{ \mathbf{Q}}^{\top}_{j,i}$，那么对于 $i \neq j$，我们有 $\boldsymbol{ \kappa_i \beta}_{i,j} = \boldsymbol{ \beta}^{\top}_{j,i} \boldsymbol{ \kappa}_j$ 的要求，此外对于所有 $i$，$\boldsymbol{ \kappa}_i > 0$。最后，还有一个 “全局” 的要求，就是 $\tilde{\mathbf{Q}}$ 必须是 SPD，相当于 $(\mathbf{I} + ( \boldsymbol{ \beta}_{i,j}) )$ 是 SPD。

12.7 GMRF 的精确推断算法

GMRF 与稀疏矩阵的高效数值算法之间也有着良好联系，并产生了 GMRF 的精确算法。本节将讨论这种联系，并首先从各种精确算法开始，然后讨论如何有效地从 GMRF 中采样。这其中包括无条件采样、有条件采样、线性硬约束采样、线性软约束采样、特定 GMRF 对数密度的计算、GMRF 边缘方差的计算等任务。

尽管所有这些任务在形式上都是 “矩阵代数”，但我们需要确保在所有步骤中都利用了稀疏精度矩阵 $\mathbf{Q}$，以便这些任务可以充分利用成熟的稀疏矩阵高效数值算法。我们可以通过考虑 GMRF 的条件独立性来推导出稀疏矩阵的所有算法，这些算法的核心是精度矩阵 $\mathbf{Q}$ 的 Cholesky 分解 $\mathbf{Q} = \mathbf{LL}^{\top}$ （ $\mathbf{L}$ 为下三角矩阵）。我们会暂时推迟计算 $\mathbf{L}$ 的细节讨论，并简单地假设此分解已经可用。

我们将始终假设 $\mathbf{x}$ 是关于 $\mathcal{G}$ 的一个 GMRF，且其均值为 $\boldsymbol{\mu}$，SPD 精度矩阵为 $\mathbf{Q}$。

12.7.1 为什么精确算法很重要？

在存在精确有效算法时，通常会选择精确方法，即使它需要比简单迭代算法更复杂的算法。即使对于统计建模，计算可行性也很重要，因为如果不能足够有效地进行推断，那么统计模型就没有多大用处。

使用精度矩阵的 Cholesky 分解可以精确完成 GMRF 的采样，这在算法上比简单 Gibbs 采样器复杂得多。不过，精确算法是精确和自动的，而 Gibbs 采样算法是近似的，并且在大多数情况下，Gibbs 采样需要人工干预来判断样本的正确性和收敛性。事实证明，在空间场景中，我们能够以 $\mathcal{O}(n^{3/2})$ 次运算为代价精确实施 GMRF 采样。这对应于 $\mathcal{O}(\sqrt{n})$ 次迭代的单一测点 Gibbs 采样。精确算法可以进一步产生独立样本，生成每个样本的代价是 $\mathcal{O}(n \log n)$。

让我们再次回到 例 12.4 。现在稍微修改此示例以证明 Gibbs 采样算法并不总是那么简单。之前的举例中，我们假设参数 $\delta$ 是固定的。现在假设 $\delta$ 也同样需要推断。在这种情况下，需要对 Gibbs 采样算法进行修改，必须如下分布中对 $\delta$ 采样:

$$\pi(\delta | \mathbf{x}, \kappa, \mathbf{y}) \propto \pi(\delta) |\mathbf{Q}_{prior}(\kappa, \delta)|^{1/2} \exp ( - \frac{1}{2} \mathbf{x}^{\top} \mathbf{Q}_{prior}(\kappa, \delta) \mathbf{x}) \tag{12.17}$$

其中 $\pi(\delta)$ 是先验分布。其要点是先验精度矩阵同时依赖于 $\kappa$ 和 $\delta$ ，并且需要我们计算 $\mathbf{Q}_{prior}(\kappa,\delta)$ 的行列式。这个量在解析上不易处理。通常，我们不得不计算 $\mathbf{Q}_{prior}(\kappa, \delta)$ 的行列式，而如果在 Gibbs 采样算法中这样做，则必须做很多次。

当任务是推断 GMRF 的未知参数时，也有类似的结论。

精确算法也可用于改进（单点） Gibbs 采样算法。此想法是一次只更新 $\boldsymbol{\theta}$ 的一个子集而不是一个组分，例如从 $\pi(\boldsymbol{\theta}_{a} |\boldsymbol{\theta}_{-a} )$ 中更新 $\boldsymbol{\theta}_{a}$。这里，$\boldsymbol{\theta}_{a}$ 可以是模型的 GMRF 部分。再次回到 例 12.4 ，我们可以将 Gibbs 采样算法改进为在两个块中更新 $(\kappa, \mathbf{x})$ 的算法：

$$\kappa \sim \pi(\kappa|\mathbf{x, y}) \quad \text{and} \quad \mathbf{x} \sim \pi(\mathbf{x}|\kappa, \mathbf{y})$$

这是可能的，因为 $\pi(\mathbf{x}|\kappa, \mathbf{y})$ 是 GMRF。

在许多情况下（包括 GMRF），因为精确（直至数值积分）或近似解的存在，是可以避免使用 MCMC 的；有关详细信息、应用和扩展，请参见 Rue、Martino 和 Chopin (2009)。这种方法的好处在于没有蒙特卡洛误差，并且提高了计算速度。再次回到 例 12.4，对于任意 $\mathbf{x}$，有

$$\pi(\kappa | \mathbf{y}) \propto \frac{\pi(\mathbf{x}, \kappa|\mathbf{y})}{\pi(\mathbf{x}|\kappa, \mathbf{y})}$$

要计算右侧（对于给定的 $\kappa$），我们需要使用精确算法求解 式 (12.12) 。在得到 $\kappa$ 的后验密度后，我们可以使用它来计算任意 $x_i$ 的后验密度:

$$\pi(x_i | \mathbf{y}) = \int \pi(\kappa | \mathbf{y}) \pi(x_i | \kappa,\mathbf{y}) d \kappa,$$

上式可以用有限求和来近似。在这个例子中，$x_i |\kappa, \mathbf{y}$ 是高斯的，所以 $\pi(x_i |\mathbf{y})$ 可以用高斯分布的有限混合来近似。

这里的额外任务是计算 $x_i$ 的边缘方差。将这个例子扩展到未知的 $\delta$，我们有：

$$\pi(\kappa, \delta | \mathbf{y}) \propto \pi(\mathbf{x}, \kappa, \delta|\mathbf{y}) \pi(\mathbf{x} |\kappa, \delta,\mathbf{y}) \tag{12.18}$$

和

$$\pi(x_i | \mathbf{y}) = \int\int \pi(\kappa, \delta | \mathbf{y}) \pi(x_i | \kappa, \delta,\mathbf{y}) d \kappa d \delta$$

我们还需要计算 $\mathbf{Q}_{prior}(\kappa, \delta)$ 的行列式。同样，$\pi(x_i |\mathbf{y})$ 可以通过高斯分布的有限混合来近似，而 $\pi(\kappa|\mathbf{y})$ 和 $\pi(\delta,\mathbf{y})$ 必须使用数值积分从 式 (12.18) 计算得出。

12.7.2 一些基本的线性代数

令 $\mathbf{A}$ 为 SPD，则存在唯一的 (Cholesky) 分解 $\mathbf{A} = \mathbf{LL}^{\top}$ ，其中 $\mathbf{L}$ 是下三角，称为 Cholesky 三角矩阵。

Cholesky 分解是求解 $\mathbf{Ay = b}$ 的起点（即计算 $\mathbf{A^{-1}b}$ ），其求解过程大致包括两步：

• 首先求解 $\mathbf{Lv = b}$，得到 $\mathbf{v=L^{-1}b}$
• 然后求解 $\mathbf{L^{\top} y = v}$，得到 $\mathbf{y=L^{-\top}v}$。

在具体算法实现上，第一个线性方程 $\mathbf{Lv = b}$ 直接使用正向代入法求解：

$$v_i = \frac{1}{\mathbf{L}_{i,i}}\left (b_i − \sum^{i-1}_{j=1} L_{i,j} v_j \right ) ,i= 1,\ldots ,n,$$

而对于第二个线性方程 $\mathbf{L^{\top} y = v}$，则使用向后替换法求解

$$y_i = \frac{1}{\mathbf{L}_{i,i}} \left (v_i − \sum^{n}_{j=i+1} \mathbf{L}_{j,i}y_j \right ) ,i= n, \ldots , 1$$

当 $\mathbf{b}$ 被替换为矩阵 $\boldsymbol{\Upsilon}$ 时，目标变成了计算 $\mathbf{A^{-1}\boldsymbol{\Upsilon}}$，其中 $\mathbf{\boldsymbol{\Upsilon}}$ 是一个 $n × k$ 矩阵。此时，只需要利用上述算法为 $\mathbf{\boldsymbol{\Upsilon}}_j$ 中的每一列计算 $\mathbf{A^{-1}\boldsymbol{\Upsilon}_j}$ 即可。在此过程中，$\mathbf{A}$ 只需分解一次。

显然，当 $\mathbf{\boldsymbol{\Upsilon}} = \mathbf{I}$（且 $k = n$）或 $\mathbf{b=1}$ 时，上述算法变成了对矩阵 $\mathbf{A}$ 求逆。在 R（R 开发核心团队，2007）中，用于矩阵求逆的命令 solve(A) 正是采用了此方法。

12.7.3 GMRF 的采样

（1）采样方法

可以使用以下步骤从 GMRF 进行采样： 采样 $\mathbf{z} \sim \mathcal{N}(\mathbf{0, I})$，即 $n$ 个标准高斯变量，求解 $\mathbf{L^{\top} v = z}$，并计算 $\mathbf{x} = \boldsymbol{\mu} + \mathbf{v}$。样本 $\mathbf{x}$ 具有正确的分布，因为 $\mathbb{E}(\mathbf{v}) = \mathbf{0}$, 并且 $\operatorname{Cov}(\mathbf{v}) = \mathbf{L}^{-\top} \mathbf{I} \mathbf{L}^{-1} = (\mathbf{LL}^{\top})^{-1} = \mathbf{Q}^{-1}$。

（2）计算对数密度

样本 $\mathbf{x}$ 的对数密度（对数似然）为：

$$\log \pi(\mathbf{x}) =−\frac{n}{2} \log 2\pi + \frac{1}{2} \log |\mathbf{Q}| − \frac{1}{2} \underbrace{(\mathbf{x}-\boldsymbol{\mu})^{\top} \mathbf{Q} (\mathbf{x}-\boldsymbol{\mu})}_{q}$$

其主要计算步骤如下：

• 计算 $q$：如果使用上述算法对 $\mathbf{x}$ 进行采样，则上式中的 $q = \mathbf{z^{\top}z}$，否则，我们计算 $\boldsymbol{w} = \mathbf{x} − \boldsymbol{\mu}$，$\boldsymbol{u} = \mathbf{Q} \boldsymbol{w}$，然后 $q = \boldsymbol{w^{\top}u}$。请注意，$\boldsymbol{u} = \mathbf{Q} \boldsymbol{w}$ 是一个稀疏的矩阵向量乘积，可以高效计算：

$$u_i = \mathbf{Q}_{i,i} w_i + \sum\limits_{ j: j \sim i} \mathbf{Q}_{i,j} w_j$$

由于 $i$ 不是 $i$ 的邻居，因此显式添加了对角线项。

• 计算 $\mathbf{Q}$ 的行列式： 可以从 Cholesky 分解中得到 $|\mathbf{Q}| = |\mathbf{LL}^{\top}| = |L|^2$。由于 $\mathbf{L}$ 是下三角矩阵，因此可以通过对角元素计算：

$$\frac{1}{2} \log |\mathbf{Q}| = \sum\limits_{i} \log L_{i,i}$$

（3）条件分布的采样

如 定理 12.2 中所述，对以 $\mathbf{x}_B$ 为条件的 $\mathbf{x}_A$ 的条件分布进行采样，可以采用类似方法。对 $\mathbf{Q}_{AA}$ 进行 Cholesky 分解，然后为 $\mu_{A|B}$ 求解线性方程组：

$$\mathbf{Q}_{AA}(\mu_{A|B} − \mu_{A}) = − \mathbf{Q}_{AB} (\mathbf{x}_B − \mu_{B})$$

依然可以使用正向和反向替换方法。右侧的（稀疏）矩阵向量乘积使用 $\mathbf{Q}_{AB}$ 中的非零元素计算即可，其余步骤皆与通用算法相同。

12.7.4 在线性约束条件下实施 GMRF 采样

（1）采样方法

在实际应用中，我们经常希望在线性约束下从 GMRF 中采样，

$$\mathbf{Ax = e}$$

对于秩为 $k$ 的 $k × n$ 矩阵 $\mathbf{A}$。常见的情况是 $k \ll n$。一种蛮力方法是直接计算条件（高斯）密度 $\pi(\mathbf{x |Ax = e})$，但这将使精度矩阵（通常）不再稀疏。例如，如果没有约束 $x_i \perp x_j | \mathbf{x}_{−\{i, j\}}$ ，则 sum-to-zero 约束 $\sum x_i = 0$ 会使 $x_i$ 和 $x_j$ 负相关。为了不损失计算效率，我们必须对无约束样本 $\mathbf{x}$ 进行精细地修正，以获得有约束样本 $\mathbf{x}^c$ 以解决此问题：

$$\mathbf{x}^c = \mathbf{x} − \mathbf{Q}^{-1}\mathbf{A}^{\top} (A\mathbf{Q}^{-1}\mathbf{A}^{\top} )^{-1}(\mathbf{Ax-e}) \tag{12.19}$$

直接计算表明 $\mathbf{x}^c$ 具有正确的均值和协方差。仔细观察 式 (12.19) 可以清楚地看到所有的矩阵项都很容易计算：

• $\mathbf{Q}^{-1}\mathbf{A}^{\top}$ 仅求解类型为 $\mathbf{Q} \mathbf{v}_j = (\mathbf{A}^{\top})_j$ 的 $k$ 个线性方程，其中 $j = 1,\ldots ,k$；
• $\mathbf{A}\mathbf{Q}^{-1}\mathbf{A}^{\top}$ 是一个 $k × k$ 矩阵，其 Cholesky 分解计算速度很快，因为 $k$ 在典型应用中很小。

请注意，具有约束 $k$ 的额外成本是 $\mathcal{O}(nk^2)$，因此，当$k$ 较小时可以忽略不计。

（2）计算对数密度

计算受约束的对数密度可能需要更多关注，因为 $\mathbf{x|Ax}$ 是奇异的，其秩为 $n − k$。但可以使用以下公式：

$$\pi(\mathbf{x |Ax}) = \frac{\pi(\mathbf{Ax|x}) \pi(\mathbf{x})}{\pi(\mathbf{Ax})}$$

现在请注意，右侧的所有项都很容易计算：

• $\pi(\mathbf{x})$ 是具有均值 $\boldsymbol{\mu}$ 和精度矩阵 $\mathbf{Q}$ 的 GMRF
• $\pi(\mathbf{Ax})$ 是（$k$ 维）高斯分布，具有均值 $\mathbf{A}\boldsymbol{\mu}$ 和协方差 $\mathbf{A}\mathbf{Q}^{-1}\mathbf{A}^{\top}$
• $\pi(\mathbf{Ax|x})$ 为 $0$ （当配置 $\mathbf{x}$ 与 $\mathbf{Ax}$ 的值不一致时）或等于 $|\mathbf{A}\mathbf{A}^{\top}|^{-1/2}$。

【例 12.7】

令 $\mathbf{x}$ 为 $n$ 个独立的零均值高斯随机变量，方差为 $\{\sigma^2_i \}$。可以从无约束的样本 $\mathbf{x}$ 生成一个 sum-to-zero 的有约束样本 $\mathbf{x}^*$：

$$x^*_i = x_i − c\sigma^2_i ，\quad \text{其中} \quad c = \sum x_j / \sum \sigma^2_j \quad \text{,} \quad i= 1,\ldots ,n$$

上面的构造可以泛化至以 软约束 为条件，即以 $k$ 个观测 $\mathbf{y} = ( y_1,\ldots ,y_k)^{\top}$ 为条件，其中

$$\mathbf{y | x} \sim \mathcal{N}(\mathbf{Ax},\mathcal{\boldsymbol{\Upsilon}})$$

这里，$\mathbf{A}$ 是一个 $k × n$ 矩阵，秩为 $k$ 并且 $\mathbf{\boldsymbol{\Upsilon}} > 0$。条件密度 $\mathbf{x|y}$ 具有精度矩阵 $\mathbf{Q} + \mathbf{A}^{\top} \mathbf{\boldsymbol{\Upsilon}}^{-1} \mathbf{A}$，它通常是一个密集矩阵。我们可以使用与方程 式 (12.19) 中相同的方法，现在将其概括为

$$\mathbf{x}^c = \mathbf{x} − \mathbf{Q}^{-1}\mathbf{A}^{\top} (\mathbf{AQ}^{-1}\mathbf{A}^{\top} + \boldsymbol{\Upsilon} )^{-1}(\mathbf{Ax} − \boldsymbol{\epsilon} ) \tag{12.21}$$

其中 $\boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{y},\boldsymbol{\Upsilon})$。

（3）条件分布的采样

类似地，如果 $\mathbf{x}$ 是来自 $\pi(\mathbf{x})$ 的样本，则 式 (12.21) 计算的 $\mathbf{x}^c$ 可以被视为条件分布 $\pi(\mathbf{x} |\mathbf{y})$。为了计算条件密度，我们使用与 式 (12.20) 中相同的方法，有

$$\pi(\mathbf{x} |\mathbf{y}) = \frac{ \pi(\mathbf{y|x}) \pi(\mathbf{x}) }{\pi(\mathbf{y})}$$

此处，$\pi(\mathbf{x})$ 是 GMRF 的密度，$\pi(\mathbf{y|x})$ 是均值为 $\mathbf{Ax}$ 、协方差矩阵为 $\boldsymbol{\Upsilon}$ 的 $k$ 维高斯分布，而 $\pi(\mathbf{y})$ 是均值为 $\mathbf{A} \boldsymbol{\mu}$ 、协方差矩阵为 $\mathbf{A} \mathbf{Q}^{-1}\mathbf{A}^{\top} + \boldsymbol{\Upsilon}$ 的 $k$ 维高斯分布。

12.7.5 Cholesky 分解的优化

上述所有精确模拟算法都基于 Cholesky 三角矩阵 $\mathbf{L}$，它是通过将 $\mathbf{Q}$ 分解为 $\mathbf{LL}^{\top}$ 得到的。下面更详细地讨论这种因式分解，说明为何稀疏矩阵能够实现更快的因式分解，并且讨论通过对索引进行重新排序，如何能够加快计算速度。

12.7.6 Cholesky 三角矩阵的解释

$\mathbf{Q}$ 的 Cholesky 分解是明确可用的；这只是按正确顺序进行计算的问题。根据定义，我们有

$$Q_{i,j} = \sum^{j}_{k=1} L_{i,k} L_{j,k} \quad \text{,} \quad i \geq j$$

其中 $\mathbf{L}$ 是下三角矩阵，意味着对于所有 $k > i$，有 $L_{i,k} = 0$。例如，假设 $n = 2$，则 $Q_{1,1} = L^2_{1,1}$, $Q_{2,1} = L_{2,1} L_{1,1}$，并且 $Q_{2,2} = L_{2,1} L_{2,1} + L^2_{2,2}$。可以很快看出，我们能够按此特定顺序计算 $L_{1,1}$、$L_{2,1}$ 和 $L_{2,2}$。

这 $n > 2$ 也适用，我们可以为 $i = 1,\ldots ,n$（按此顺序）计算 $L_{i,1}$，然后为 $i = 2,\ldots ,n$ 计算 $L_{i,2}$，依此类推。由于这种简单的显式结构，可以快速计算 Cholesky 分解，并且标准线性代数库中提供了有效的实现（Anderson、Bai、Bischof、Demmel 等，1995 年）。然而，计算复杂度为 $\mathcal{O}(n^3)$。

利用精度矩阵或 Cholesky 三角矩阵中的特定结构可以加速 Cholesky 分解。对于 GMRF，$\mathbf{Q}$ 中的稀疏性会带来 $\mathbf{L}$ 中的稀疏性。这意味着，如果已知 $L_{j,i} = 0$，那么就不需要计算它了。如果 $\mathbf{L}$ 的主体为零，那么我们可以节省大量计算。

为了理解此问题，我们需要理解 $\mathbf{L}$ 在统计解释方面的真正含义。零均值 GMRF 的模拟算法，需要求解 $\mathbf{L}^{\top} \mathbf{x} = \mathbf{z}$，其中 $\mathbf{z} \sim \mathcal{N}(\mathbf{0, I})$ ，给出以下结果。

【定理 12.4】

设 $\mathbf{x}$ 是关于有标签图 $\mathcal{G}$ 的 GMRF，其均值为 $\boldsymbol{\mu}$ 、SPD 精度矩阵为 $\mathbf{Q}$。令 $\mathbf{L}$ 为 $\mathbf{Q}$ 的 Cholesky 三角矩阵。那么对于 $i \in \mathcal{V}$ 有：

$$\mathbb{E}(x_i | \mathbf{x}_{(i+1):n}) = \mu_i − \frac{1}{L_{i,i}} \sum^{n}_{j=i+1} L_{j,i}(x_j − \mu_j )$$

和

$$Precision (x_i | \mathbf{x}_{(i+1):n} ) = L^2_{i,i}$$

也就是说，$L$ 中的元素可以被解释为对 $x_i$ 以所有 $x_j$ 为条件（ $j > i$）的均值和精度的贡献。这与 $\mathbf{Q}$ 的元素类似，精度矩阵也具有类似的解释，不过精度矩阵中会以所有其他 $x_j$ 为条件。此解释的一个简单推论是：对于所有 $i$ 有 $\mathbf{Q}_{i,i} \geq L^2_{i,i}$。

如果我们将 式 (12.2) 与 定理 12.4 合并，将得到以下结果。

【定理 12.5】

设 $\mathbf{x}$ 为有标签图 $\mathcal{G}$ 的 GMRF，具有均值 $\boldsymbol{\mu}$ 和 SPD 精度矩阵 $\mathbf{Q}$。令 $\mathbf{L}$ 为 $\mathbf{Q}$ 的 Cholesky 三角矩阵，并将 $i$ 的除 $j$ 之外的未来结点集合定义为 ( $1 \leq i < j \leq n$ )：

$$F (i, j) =\{i + 1, \ldots ,j− 1,j+ 1, \ldots ,n\}$$

那么

$$x_i \perp x_j | \mathbf{x}_{F (i, j)} \Leftrightarrow L_{ j,i} = 0$$

所以，如果我们考虑 $\mathbf{x}_{i:n}$ 的边缘分布，那么 $L_{j,i} = 0$ 等价于 $x_i$ 和 $x_j$ 条件独立。这是一个有用的结果，因为它表明：如果能够利用边缘的有序序列 $\{\mathbf{x}_{i:n}\}$ 中存在的条件独立性来确定 $\mathbf{L}$ 中的零元素，那么边缘 $\{x_{i:n}\}$ 会更容易通过 Cholesky 三角矩阵来计算。不过，我们可以使用一个放宽了的准则：$x_i \perp x_j | \mathbf{x}_{F(i,j)}$，也就是 定理 12.3 中的全局马尔可夫性质。

【推论 12.1】

如果 $F (i, j)$ 分隔了结点 $i < j \in \mathcal{G}$，则 $L_{j,i} = 0$。

这是一个主要的结果。如果我们可以仅仅通过图结构来验证 $i < j$ 是否被 $F (i, j)$ 分隔，而不用考虑 $\mathbf{Q}$ 中元素的数值，则无论 $\mathbf{Q}$ 中的数值如何，我们都可以得到 $L_{j,i} = 0$ 。如果 $i < j$ 没有被 $F (i, j)$ 分隔，则 $L_{j,i}$ 通常不为零（尽管可以为零）。由于邻居 $i \sim j$ 之间不会被任何集合分隔，因此对于邻居来说 $L_{j,i}$ 通常是非零的。

【例 12.8】

考虑一个带有 图 12.1 中的图的 GMRF。然后我们知道 $L_{1,1}$、$L_{2,2}$、$L_{3,3}$、$L_{4,4}$ 是非零的，而 $L_{2,1}$、$L_{3,2}$、$L_{4,3}$ 和 $L_{4,1}$ 通常是非零的。剩下的两个元素是 $L_{3,1}$ 和 $L_{4,2}$，我们使用 推论 12.1 检查它们；结点 1 和 3 由 $F(1, 3) =\{2, 4\}$ 分隔，所以 $L_{3,1}$ 必须为零，而 $F (4, 2) =\{3\}$ 由于结点 1 而不会分隔 2 和 4，因此 $L_{4,2}$ 通常是非零的。

12.7.7 带状矩阵的 Cholesky 分解

尽管 例 12.8 中 Cholesky 三角矩阵中只有一个元素是必然为零的，但自回归模型通常会为我们带来大量的零元素。

设 $\mathbf{x}$ 为 $p$ 阶自回归过程 AR($p$)，即有：

$$x_{t} | x_{t-1}, \ldots ,x_1 \sim \mathcal{N}(\phi_1 x_{t-1} + \ldots +\phi_p x_{t−p}, \sigma^2),t= 1, \ldots ,n$$

为简单起见，我们设置 $\mathbf{x}_0 = \mathbf{x}_{−1} = \ldots = \mathbf{x}_{−p+1} = 0$。

AR($p$) 过程的精度矩阵是一个带宽为 $b_w = p$ 的带状矩阵。使用 推论 12.1，可以得出对于所有 $j − i > p, \quad j > i$，有 $L_{j,i} = 0$，因此 $\mathbf{L}$ 也是一个具有相同带宽的带状矩阵。

【定理 12.6】

如果 $\mathbf{Q}$ 是带宽为 $b_w$ 的 SPD 带状矩阵，则其 Cholesky 三角矩阵 $\mathbf{L}$ 是具有相同带宽的下三角带状矩阵。

在这个例子中，$\mathbf{L}$ 中的 $\mathcal{O}(n^2)$ 个项中，只有 $\mathcal{O}(n(b_w + 1))$ 个项是非零的，这是一种显著地减少。一个直接结果是可以简化计算 Cholesky 分解的算法；三个循环中的两个只需要在带宽内进行即可，复杂度从 $\mathcal{O}(n^3)$ 降低到 $\mathcal{O}(nb_w^2)$。这给出了固定带宽对应的计算代价，仅与 $n$ 成线性关系。

12.7.8 重新排序技术：带状矩阵

带状矩阵的计算效率优势自然会引发这样一个问题：是否可以将此方法用于 “非带状” 但稀疏的矩阵？ 一种合理的方法是：如果图中的索引是任意排列的，那么或许我们可以通过索引的重新排列获得更小的带宽，用其完成计算后，再将结果逆排列至原始索引顺序。

在形式上，可以令 $\mathbf{P}$ 表示 $n!$ 个 $n × n$ 置换矩阵之一；$\mathbf{P}$ 的每一行和每一列都有一个且只有一个非零项，即 $1$。置换矩阵的转置是其逆置换，也就是 $\mathbf{P^{\top} P} = \mathbf{I}$。以 $\mathbf{Q} \boldsymbol{\mu} = \mathbf{b}$ 为例，利用上述思路，我们可以在方程两边都乘以 $\mathbf{P}$ 后做求解：

$$\underbrace{(\mathbf{P\mathbf{Q}P^{\top}})}_{\widetilde{\mathbf{Q}}} \underbrace{\mathbf{P} \boldsymbol{\mu}}_{\widetilde{\boldsymbol{\mu}}} = \underbrace{\mathbf{Pb}}_{\widetilde{\mathbf{b}}}$$

原问题被转换为求解 $\widetilde{ \mathbf{Q}} \widetilde{\mu} = \widetilde{\mathbf{b}}$ 的问题，对其解应用逆置换即可得到原始解：$\boldsymbol{\mu} = \mathbf{P}^{\top} \widetilde{\boldsymbol{\mu} }$ 。

下一个问题是如何置换稀疏矩阵以获得小带宽。这个问题有点技术性，但在计算机科学领域有大量文献（Duff、Erisman 和 Reid，1989 年；George 和 Liu，1981 年）和算法。因此，任何运行速度快并给出合理结果的算法都可以采纳。

图 12.4 显示了一个示例，其中 图 12.4a 显示了从空间应用中找到的精度矩阵（Rue 和 Held，2005 年，第 4.2.2 节），图 12.4b 是使用 Gibbs–Poole–Stockmeyer 重排序算法得到的结果 (Lewis, 1982)，图 12.4c 是重排序精度矩阵的 Cholesky 三角矩阵。其中重新排序后的带宽为 $38$。

12.7.9 重新排序技术：一般稀疏矩阵

虽然带状矩阵方法为某些图提供了非常有效的算法，但我们经常会遇到需要更通用方法的情况。一个典型例子是图中存在一些 “全局结点”，即某些结点与所有其他结点都相邻。在统计应用中，这种情况经常发生，如下例所示。

【例 12.9】

设 $\boldsymbol{\mu} \sim \mathcal{N}(0, 1)$ 和 $\{z_t\}$ 是长度为 $T$ 且均值为 $\mu$ 的 AR( $1$ ) 过程；那么 $\mathbf{x} = (\mathbf{z}^{\top} , \mu)^{\top}$ 是关于 $\mathcal{G}$ 的 GMRF，其中结点 $\mu$ 是所有其他结点的邻居。带宽为 $n − 1$，其中 $n = T + 1$，对于所有 $n!$ 重新排序。

带状矩阵方法在这个例子中并不成功，但我们可以通过使用一般（和复杂的）因式分解方案来推导有效的因式分解。一般方案仅计算 $\mathbf{L}$ 中的非零项，这需要大大增加复杂性。接下来的问题是重新排序以最小化 $\mathbf{L}$ 中未知为零的项数。将 M(G) 定义为使用 推论 12.1 找到的 $\mathbf{L}$ 中的非零项数。

然后通常使用填充数来比较任何重新排序的效率

$$\operatorname{fill-ins}(\mathcal{G}) = M(\mathcal{G}) − (|\mathcal{V}|+|\mathcal{E}|/2)$$

由于 $L_{i,i} > 0$ 对于所有 $i$，并且 4L_{j,i}4 对于 $i \sim j$ 和 $j > i$ 通常是非零的，因此 $\operatorname{fill-ins}(\mathcal{G}) \geq 0$。

$p$ 阶自回归过程是最优的，因为精度矩阵是带宽为 $p$ 的带状矩阵（并且带内密集），并且使用恒等排序，填充的数量为零（见 定理 12.6 ）。对于其他 GMRF，填充数（在大多数情况下）是非零的，并且可以比较不同的重新排序方案以找到合理的重新排序。请注意，无需找到最佳重新排序，但任何合理的重新排序就足够了。

让我们重新考虑 例 12.9 ，我们比较了两个重新排序，其中全局结点 $\boldsymbol{\mu}$ 分别排在第一位和最后一位； $\mathbf{x} = (\mathbf{z}^{\top} , \mu)^{\top}$ 和 $\mathbf{x}' = (\mu, \mathbf{z}^{\top})^{\top}$ 。精度矩阵分别是

此处，$×$ 表示非零值。使用 推论 12.1，我们获得 Cholesky 三角矩阵的（一般）非零结构

其中 $√$ 表示填充。将全局结点 $\mu$ 放在最后不会给出任何填充，而将其放在最前面会给出最大数量的填充。这种洞察力可用于推导称为嵌套剖面的重新排序方案，如下所示。

• 选择一组（小的）结点，移除这些结点会将图分成两个大小几乎相等的不连通子图
• 在对两个子图中的所有结点进行排序后对所选结点进行排序
• 将此过程递归地应用于每个子图中的结点

形式上，这可以描述如下：

【引理 12.2】

令 $\mathbf{x}$ 为关于 $\mathcal{G}$ 的 GMRF，其 SPD 精度矩阵为 $\mathbf{Q}$，并将 $\mathbf{x}$ 划分为 $(\mathbf{x}^{\top} \mathbf{A}, \mathbf{x}^{\top} \mathbf{B}, \mathbf{x}^{\top} \mathbf{C} )^{\top}$ 。将 $\mathbf{Q}$ 的 Cholesky 三角矩阵划分为

$$\mathbf{L}= \begin{pmatrix} \mathbf{L}_{AA} & &\\ \mathbf{L}_{BA} & \mathbf{L}_{BB}& \\ \mathbf{L}_{CA} & \mathbf{L}_{CB}& \mathbf{L}_{CC} \end{pmatrix}$$

如果 $C$ 在 $\mathcal{G}$ 中分隔了 $A$ 和 $B$，则有 $\mathbf{L}_{BA} = \mathbf{0}$

递归方法通过类似地划分 $A$ 和 $B$ 来进行，依此类推。事实证明，嵌套剖面重新排序为从离散化晶格或立方体中找到的 GMRF 提供了最佳重新排序（在顺序意义上）：考虑一个具有 $n$ 个站点的规则方形晶格，其中每个结点都与最近的四个结点相邻。嵌套剖面重新排序将使用 $C$ 作为中间列，$A$ 和 $B$ 作为左右部分。然后递归地重复这个过程。事实证明，重新排序的精度矩阵的因式分解成本将为 $\mathcal{O}(n^{3/2})$，这比使用带宽方法快 $\sqrt{n}$ 倍。填充数将（仅）为 $\mathcal{O}(n \log n)$。可以证明，应用任何重新排序的精度矩阵因式分解大于或等于 $\mathcal{O}(n^{3/2})$；因此在顺序意义上是最优的。对于具有 $n$ 个结点的 3D 网格，计算成本为 $\mathcal{O}(n^2)$，填充数为 $\mathcal{O}(n^{4/3})$。

在长图和细图的带重新排序和格状图的嵌套剖面重新排序之间，还有其他几种重新排序方案可以根据具体情况提供更好的重新排序。尝试哪一个取决于哪个实现可用；但是，任何合理的重新排序选择都足够了。请注意，可以（通过稀疏矩阵库）计算特定图的填充数，而无需进行实际的因式分解，因为它仅取决于图；因此，如果应该对同一个图执行多个因式分解，比较（一些）重新排序并选择填充次数最少的一个可能会有好处。

我们通过重新访问 图 12.4a 中显示的 $380 × 380$ 精度矩阵来结束本次讨论。带重新排序给出了 $11,112$ 个填充，嵌套剖面给出了 $2,460$，而 “最佳” 产生了 $2,182$ 个填充。最佳重新排序的精度矩阵和相应的 Cholesky 三角矩阵显示在 图 12.5 中。

12.7.10 批量边缘方差的精确计算

我们现在将转向一个更 “统计” 的问题；如何计算 GMRF 的所有（或几乎所有）边缘方差。这是一项不同于仅计算一个方差（比如 $x_i$ ）的任务，后者可以简单地通过求解 $\mathbf{Qv = 1_i}$ 来完成，其中 $\mathbf{1}_i$ 在位置 $i$ 处为 $1$，否则为零，然后是 $\operatorname{Var}(x_i ) = v_i$ 。尽管方差计算是统计学的核心，但在计算机科学中却不一定如此：我们不熟悉任何提供这种功能的稀疏矩阵库，尽管一般解决方案是已知的（Erisman 和 Tinney，1975 年；Takahashi，Fagan，和 Chen，1973）。我们将从统计的角度推导递归，从 $\mathbf{Q}$ 是没有额外线性约束的 SPD 的情况开始。有约束的情况将在后面讨论。

12.7.11 一般递归

出发点再次是 $\mathbf{L}^{\top} \mathbf{x = z}$ 的解提供了具有精度矩阵 $\mathbf{Q}$ 的样本 $\mathbf{x}$，这意味着

$$x_i = z_i /L_{i,i} − \frac{1}{L_{i,i}} \sum^{n}_{k=i+1} L_{k,i} x_k ,\qquad i = n, \ldots , 1$$

对于 $j \geq i$，两边都乘以 $x_j$。然后期望值读取

$$\Sigma_{i,j} = \delta_{i,j} / L^2_{i,i} − \frac{1}{L_{i,i}} \sum^{n}_{k=i+1} L_{k,i} \Sigma_{k, j}, \qquad j \geq i, i = n,\ldots , 1 \tag{12.22}$$

其中，如果 $i = j$，则 $\delta_{i,j}$ 为 $1$，否则为 $0$。 式 (12.22) 中的和只需要在所有非零 $L_{j,i}$ 上，或者至少是所有那些 $k$ 使得 $i$ 和 $k > i$ 不被 $F (i, k)$ 分隔；见 推论 12.1。为了简化符号，将此索引集定义为

$$\mathcal{I}(i) = \{k > i : i \quad \text{和} \quad k \quad \text{不被} \quad F (i, k) \quad \text{分隔} \quad \}$$

和他们的 “联合”，

$$\mathcal{I} =\left \{\{i, k\} : k > i, i \quad \text{和} \quad k \quad \text{不被} \quad F (i, k) \quad \text{分隔} \quad \right \}$$

对于 $k，i = 1，\ldots ，n$。注意 $\mathcal{I}$ 的元素是集合；因此如果 $\{i, j\}\in \mathcal{I}$，那么 $\{j, i\}$ 也是。 $\mathcal{I}$ 表示 $\mathbf{L}$ 中所有那些事先不知道为零的索引；因此，必须通过 Cholesky 分解来计算。使用此符号，方程 式 (12.22) 变为

$$\Sigma_{i,j} = \delta_{i,j} / L^2_{i,i} − \frac{1}{L_{i,i}} \sum\limits_{ k \in \mathcal{I} (i)} L_{k,i} \Sigma_{k, j},\qquad j \geq i, i = n,\ldots, 1 \tag{12.23}$$

更仔细地研究这些方程，结果表明，如果以正确的顺序应用 式 (12.23)，我们可以显式计算所有 $\Sigma_{i,j}$：

尽管这个直接过程计算了所有边缘方差 $\Sigma_{n,n},\ldots , \Sigma_{1,1}$，但很自然地会问是否有必要计算所有 $\Sigma_{i,j}$ 以获得边缘方差。令 $\mathcal{J}$ 为一组指数对 $\{i, j\}$，并假设我们可以仅对所有 ${i, j} \in \mathcal{J} $ 从 式 (12.23) 计算 $\Sigma_{i,j}$，并且仍然获得所有边缘方差。那么集合 $\mathcal{J} $ 必须满足两个要求：

【需求 1】 $\mathcal{J}$ 必须包含 $\{1, 1\},\ldots , \{n, n\}$

【要求 2】 在从 式 (12.23) 计算 $\Sigma_{i,j}$ 时，我们需要已经计算出我们需要的所有那些 $\Sigma_{k,j}$，即，

$$\{i, j\}\in \mathcal{J} \quad \text{且} \quad k \in \mathcal{I}(i) \Rightarrow \{ k, j\} \in \mathcal{J} \tag{12.24}$$

相当令人惊讶的结果是 $\mathcal{J = I}$ 满足这些要求；结果仅取决于 $\mathcal{G}$ 而不是 $\mathbf{Q}$ 中的数值。该结果意味着我们可以按如下方式计算所有边缘方差：

对于 $i = n,\ldots , 1$ 用于减少 $\mathcal{I}(i)$ 中的 $j$ 从 式 (12.23) 计算 $\Sigma_{i,j}$，

其中 $j$ 循环以降序访问 $\mathcal{I}(i)$ 中的所有条目。证明是直接的。需求 1 平凡为真，需求 2 通过验证方程 式 (12.24) 得到验证： $\{i, j\}\in \mathcal{J} , j \geq i$，表示必须存在从 $i$ 到 $j$ 的路径，其中所有结点都小于 $i$，而 $k \in \mathcal{I}(i)$ 表示必须存在一条从 $i$ 到 $k$ 的路径，其中所有结点都小于 $i$。如果 $k \leq j$，则必须存在一条从 $k$ 到 $i$ 到 $j$ 的路径，其中所有索引都小于 $k$，因为 $k > i$，否则，如果 $k > j$，则必须存在从 $k$ 到 $i$ 再到 $j$ 的路径，其中所有索引都小于 $j$，因为 $j \geq i$。

解决这些递归的计算成本比分解精度矩阵要小。考虑使用嵌套剖面重新排序的 2D 方格重新排序，然后 $|\mathcal{I}|=\mathcal{O}(n \log n)$，并且每个 $\Sigma_{i,j}$ 将涉及大约 $\mathcal{O}(\log n)$ 项，给出 $\mathcal{O}(n(\log n)^2)$ 的总成本。类似地，对于具有嵌套剖面重新排序的 3D 盒格，成本将为 $\mathcal{O}(n^{5/3})$。

12.7.12 带状矩阵的递归

当 $\mathbf{Q}$ 是带宽为 $b_w$ 的带状矩阵时，简化可能是最明显的，我们之前已经证明 $\mathcal{I}(i) =\{i + 1,\ldots , \min(n, i + b_w)\}$；参见 定理 12.6 。在这种情况下，$需求 2$ 读取（对于内部结点和 $j \geq i$），

$$0 \leq j − i \leq b_w \quad \text{和} \quad 0 < k − i \leq b_w \Rightarrow − b_w \leq k − j \leq b_w$$

这是千真万确的。然后算法变成

请注意，此算法在形式上等同于用于平滑的卡尔曼递归。自回归模型的计算成本为 $\mathcal{O}(n)$。

12.7.13 校正线性约束

使用额外的线性约束，受约束的精度矩阵将不那么稀疏，因此我们需要一种方法来校正额外线性约束的边缘方差。这类似于方程 式 (12.19) 。设 $\widetilde{\Sigma}$ 是具有附加 $k$ 个线性约束 $\mathbf{Ax = e}$ 的协方差矩阵，而 $\Sigma$ 是没有约束的协方差矩阵。两个协方差矩阵的关系如下：

$$\tilde{\boldsymbol{\Sigma}} = \boldsymbol{\Sigma} − \mathbf{Q}^{-1}\mathbf{A}^{\top} (A\mathbf{Q}^{-1}\mathbf{A}^{\top} )^{-1} A\mathbf{Q}^{-1} \tag{12.25}$$

令 $\mathbf{W}$ 为 $\mathbf{QW} = \mathbf{A}^{\top}$ 的 $n×k$ 矩阵解，$\mathbf{V}$ 为 $\mathbf{AW}$ 的 $k×k$ Cholesky 三角矩阵，$\boldsymbol{\Upsilon}$ 为 $\mathbf{V}\boldsymbol{\Upsilon} = \mathbf{W}^{\top}$ 的 $k×n$ 矩阵解，则 式(12.25) 的第 $i$、$j$ 个元素可写为

$$\tilde{\Sigma}_{i,j} = \Sigma_{i,j} − \sum^{k}_{t=1} \Upsilon_{t,i} \Upsilon_{t, j} \tag{12.26}$$

我们通过求解方程 式 (12.23) 计算的所有 $\boldsymbol{\Sigma}$ 项现在都可以使用方程 式 (12.26) 进行校正。此校正的计算成本主要是计算 $\boldsymbol{\Upsilon}$，其成本为 $\mathcal{O}(nk^2)$。同样，在没有太多约束的情况下，这种校正不需要任何额外的计算负担。

12.7.14 一些实际问题

虽然可以使用稀疏矩阵的数值方法来进行 GMRF 计算，但它并非没有实际麻烦。

• 首先，相当多的库有免费的二进制版本但封闭源代码，这会造成复杂性。由于只有少数库具有解决 $\mathbf{L}^{\top} \mathbf{x = z}$ 的程序，并且（据我们所知）没有一个库支持计算边缘方差，因此需要访问内部存储格式以实现此类功能。但除非使用开源代码，否则并不总是记录内部存储格式。在撰写本文时，我们建议使用开源库之一：TAUCS（Toledo、Chen 和 Rotkin，2002 年）或 CHOLMOD（Chen、Dav_is、Hager 和 Rajamanickam，2006 年），它是用 C 语言编写的；有关比较和概述，请参阅 Gould、Scott 和 Hu (2007)。

• 由于开源，提供求解 $\mathbf{L}^{\top} \mathbf{x = z}$ 的例程相对容易。但是，如果在递归 式 (12.23) 中使用计算的 $L$，则必须小心；例如，TAUCS 库删除了结果为零的项 $\mathbf{L}_j$，但我们需要所有未知为零的项。简单的解决方法是在库中禁用此功能，或者使用 Rue 和 Martino (2007), Sec. 2.3 中的修复程序。 GMRFLib 库（Rue 和 Held，2005 年，App.B）确实提供了本章基于 TAUCS 库讨论的所有算法的实现。

12.8 马尔可夫随机场

我们现在将离开高斯案例并更一般地讨论马尔可夫随机场 (MRF)。我们将首先研究每个 $x_i$ 是 $K$ 种不同 “颜色” 或状态之一的情况；即，$x_i \in \mathcal{S}_i =\{0, 1,\ldots ,K− 1\}$，且 $\mathbf{x} \in \mathcal{S} = \mathcal{S}_1 × \mathcal{S}_2 ×\dots×\mathcal{ S}_n$。 $K = 2$ 的情况特别重要，对应于二值 MRF。然后可以将主要结果 定理 12.7 推广到非有限 $\mathcal{S}$。本节中的介绍受到 J. Besag 一些未发表的讲义的启发；参见 Besag 1974； Geman and Geman, 1984;Guyon , 1995; Lauritzen, 1996;李, 2001; Winkler, 1995 提供更多理论和应用，Hurn、Husby 和 Rue (2003) 提供图像分析教程。

12.8.1 背景

回想一下联合分布 $\pi(\mathbf{x})$ 的完全条件分布的概念，即 $n$ 个条件分布 $\pi(x_i |\mathbf{x}_{-i} )$。从完全条件分布，我们可以定义邻居的概念

【定义 12.3（邻居）】

如果 $x_j$ 对 $x_i$ 的完全条件分布有贡献，则测点 $j \neq i$ 被称为 $i$ 的邻居。

用 $∂i$ 表示测点 $i$ 的所有邻居构成的集合，则对于所有 $i$，有：

$$\pi(x_i | \mathbf{x}_{-i} ) = \pi(x_i | \mathbf{x}_{∂i})$$

在空间环境中，很容易将其可视化，例如，将 $∂i$ 视为在某种意义上（空间上）靠近测点 $i$ 的那些测点。

当我们想要使用自下而上的方法通过 $n$ 个完全条件分布和一组邻居 $∂i$ 指定 $\mathbf{x}$ 的联合密度时，问题就开始了。如果我们知道联合分布，则完全条件分布为

$$\pi(x_i | \mathbf{x}_{-i} ) \propto \pi(\mathbf{x})$$

但是，如果我们只知道完全条件分布，我们如何导出联合分布呢？令 $\mathbf{x}^{*}$ 表示 $\pi(\mathbf{x}^{*}) > 0$ 的任何参考状态，然后 Brook 引理（引理 12.1）给出 $n = 2$（仅为简单起见）

$$\pi(x_1,x_2) = \pi(\mathbf{x}^{*}_1 ,\mathbf{x}^{*}_2) \frac{\pi(x_1|x_2)}{ \pi(\mathbf{x}^{*}_1 |x_2)} \cdot \frac{\pi ( x_2 |\mathbf{x}^{*}_1)}{ \pi(\mathbf{x}^{*}_2 |\mathbf{x}^{*}_1 )} \tag{12.27}$$

前提是分母中没有零，这意味着（通常）

$$\pi(\mathbf{x}) > 0, ∀ \mathbf{x} \in S$$

我们将这种条件称为积极性条件，它在下文中被证明是必不可少的。如果我们对所有 $\mathbf{x} \in S$ 保持 $\mathbf{x}^{*}$ 固定为 $0$ 来计算 式（12.27） ，那么我们就知道 $h(\mathbf{x})$ 其中 $\pi(\mathbf{x}) \propto h(\mathbf{x})$。缺失的常量是从 $\sum_{\mathbf{x} \in S} \pi(\mathbf{x}) = 1$ 中找到的。结论是完全条件分布决定了联合分布。

这个论点有一个小问题，即完全条件分布是（或可以）从联合分布中导出的隐含假设。然而，如果我们指定完全条件分布的候选者，那么我们必须确保我们获得相同的联合分布，而不管导致 式（12.27） 的排序选择如何，例如，

$$\pi(x_1,x_2) = \pi(\mathbf{x}^{*}_1 ,\mathbf{x}^{*}_2) \frac{\pi(x_2|x_1)}{\pi (x_1 |\mathbf{x}^{*}_2)} \frac{ \pi(\mathbf{x}^{*}_2 |x_1)}{ \pi(\mathbf{x}^{*}_1 |\mathbf{x}^{*}_2)}$$

当然，这两个指定必须一致。对于 $n > 2$，这样的排序有很多，而且都必须一致。这意味着我们不能任意选择完全条件分布，但它们必须满足一些约束以确保它们定义有效的联合分布。在我们陈述定义联合分布在完全条件分布的邻居指定下必须采用什么形式的主要结果之前，我们需要一些新的定义。

12.8.2 哈默斯利-克利福德（ Hammersley–Clifford ）定理

让 $\mathcal{G} = (\mathcal{V}, \mathcal{E})$ 表示通过对每个测点的邻居指定来定义的图； $\mathcal{V} =\{1,\ldots ,n\}$ 如果 $j \in ∂i$ 和 $i \notin ∂j$，则绘制一条从 $j$ 到 $i$ 的有向边。如果 $i$ 和 $j$ 互为邻居，则绘制一条无向边。 （事实上 ，如果 $i$ 是 $j$ 的邻居，那么 $j$ 也必须是 $i$ 的邻居）。

【定义 12.4（马尔可夫随机场）】 如果 $\pi(\mathbf{x}), \mathbf{x} \in \mathcal{S}$ 的完全条件分布符合给定图 $\mathcal{G}$，则该分布被称为一个关于图 $\mathcal{G}$ 的马尔可夫随机场。

对于主要结果，我们还需要 “团” 的概念。

【定义 12.5（团）】

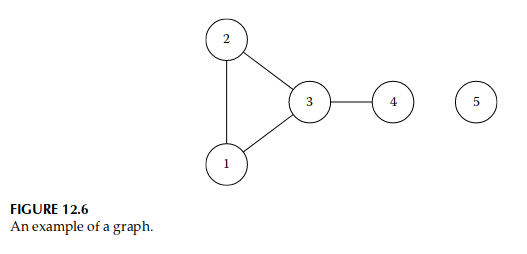
任何单一测点或内部不同测点之间相互都是邻居的一组测点，被称为 “团” 。

【示例 12.10】 图 12.6 中图中的 “团” 为： $\{1\}$ 、 $\{2\}$ 、 $\{3\}$ 、 $\{4\}$ 、 $\{5\}$ 、 $\{1, 2\}$ 、 $\{1, 3\}$ 、 $\{2, 3\}$ 、 $\{ 1, 2, 3\}$ , $\{3, 4\}$ 。

主要结论是 Hammersley–Clifford 定理（参见 Clifford，1990 ），它说明联合分布必须采用什么形式才能符合给定的图 $\mathcal{G}$ 。

【定理 12.7 (Hammersley–Clifford)】

令 $\pi(\mathbf{x}) > 0, \mathbf{x} \in \mathcal{S}$ 是一个关于具有团 $\mathcal{C}$ 的图 $\mathcal{G}$ 的马尔可夫随机场，则 ：

$$\pi(\mathbf{x}) \propto \prod\limits_{ C \in \mathcal{C}} \Psi_C (\mathbf{x}_C) \tag{12.28}$$

其中函数 $\Psi_C$ 可以任意选择，但须满足 $0 < \Psi_C (\mathbf{x}_C ) < \infty$。

这个结果有一个有趣的历史；参见 Besag (1974) 和 Clifford (1990) 的章节。这个结论的一个重要结果是：对于给定的图，完全条件分布应该要么通过 $\Psi$ 函数隐式指定，要么对于某些 $\Psi$ 函数可以被从 式（12.28） 导出的所选完全条件分布验证。

【示例 12.11】

图 12.6 对应的一般分布形式是：

$$\pi(x_1,x_2,x_3,x_4,x_5) \propto \Psi_{1,2,3}(x_1,x_2,x_3) \Psi_{3,4}(x_3,x_4) \Psi_5(x_5)$$

我们现在将陈述 Hammersley-Clifford 定理的一些推论：

【推论 12.2】 图 $\mathcal{G}$ 必须是无向的，所以如果 $i \in ∂j$ ，则必然 $j \in ∂i$ 。

【推论 12.3】 式（12.28） 的MRF 也满足全局马尔可夫性质 式（12.4） 。

【推论 12.4】 如果定义 $Q(\mathbf{x}) = \log(\pi(\mathbf{x})/\pi(\mathbf{0}))$ ，则存在唯一表示，

$$Q(\mathbf{x}) = \sum\limits_{i} x_i G_i(x_i ) + \sum\limits_{i<j} x_i x_j G_{i, j} (x_i ,x_j ) + \sum\limits_{i< j<k} x_i x_j x_k G_{i, j,k}(x_i ,x_j ,x_k ) + \ldots \\j+ x_1 x_2 \ldots x_n G_{1,2,\ldots ,n}(x_1,x_2,\ldots ,x_n) \tag{12.29}$$

其中 $G_{i, j,\ldots,s}(x_i ,x_j ,\ldots ,x_s) \equiv 0$ 除非测点 $i, j,\ldots , s$ 形成一个团，并且其中 $G$ 函数是任意但有限的。

【推论 12.5】 Hammersley–Clifford 定理可以扩展到多元 MRF，其中每个 $\mathbf{x}_i$ 是 $p$ 维随机向量，更进一步，可以扩展到受 $\pi(\mathbf{x})$ 可积性约束的无限域 $S$ 。

式（12.28） 的联合分布也可以写成

$$\pi(\mathbf{x}) = \frac{1}{Z} \exp \left( − \sum\limits_{ C \in \mathcal{C}} V_C (\mathbf{x}_C) \right)$$

其中 $V_C (·) =−\log \Psi_C (·)$ 并且 $Z$ 是归一化常数。这种形式在统计物理学中称为吉布斯分布， $V_C(·)$ -函数称为势函数；参见如，Geman and Geman (1984)。

12.8.3 二值 MRF

我们现在将更详细地讨论 $K = 2$ 的情况，我们有一个二值 MRF。设 $∂i$ 是规则正方形格子上离测点 $i$ 最近的四个测点。然后从 式（12.29） 。对于某些 $\alpha_i$ 和 $\alpha_{i,j}$，我们有

$$Q(\mathbf{x}) = \sum\limits_{i} \alpha_i x_i + \sum\limits_{i<j} \alpha_{i, j} x_i x_j$$

这是给定图的分布可以采用的通用形式。对于 $\beta_{i,j} = \beta_{j,i} = \alpha_{i, j}, i < j$ 我们可以将 $\mathbf{x}$ 的分布写为

$$\pi(\mathbf{x}) = \frac{1}{Z} \exp \left( \sum\limits_{i} \alpha_i x_i + \sum\limits_{ i \sim j} \beta_{ij}x_i x_j\right)$$

参数 $\{\alpha_i \}$ 控制水平，而参数 $\{\beta_{i,j}$ } 控制交互。当我们查看完全条件分布时，解释可能会更透明

$$\pi(x_i | \mathbf{x}_{-i} ) = \frac{ \exp \left( x_i (\alpha_i + \sum\limits_{ j\in ∂i} \beta_{i,j} x_j) \right)}{ 1 + \exp \left( \alpha_i + \sum\limits_{ j\in ∂i} \beta_{i,j} x_j \right)}$$

$x_i$ 的完全条件分布类似于与其邻居的逻辑回归，被称为自动逻辑模型（Besag，1974）

式（12.31） 的一个有趣的特例是

$$\pi(\mathbf{x} | \beta) = \frac{1}{Z_{\beta}} \exp \left ( \beta \sum\limits_{ i \sim j} 1 [x_i = x_j ] \right) \tag{12.32}$$

其中 $1[·]$ 是指示函数， $\beta$ 是常用交互参数。该模型是著名的铁磁性 Ising 模型，可追溯到 1925 年的 Ernst Ising。为了以后使用，我们写成 $|\beta$ 并注意归一化常数也取决于 $\beta$ 。通过将 式（12.32） 重写为

$$\pi(\mathbf{x} | \beta) = \frac{1}{Z_{\beta}} \exp (\beta \times \text{相等邻居的数量} )$$

因此，实现将有利于邻居平等，但对于邻居应该处于哪个状态 $0$ 或 $1$ 是不变的。这也可以通过研究完全条件分布来看出，

$$\pi(x_i = 1 | \beta, \mathbf{x}_{∂i} ) = \frac{\exp(\beta_{n1})}{\exp(\beta_{ n0 }) + \exp(\beta_{n1})'}$$

其中 $n_0$ 是 $x_i$ 的为零的邻居数， $n_1$ 类似。很明显，这个模型有利于 $x_i$ 等于其邻居中的主导状态。在两个或多个维度上，它可以显示出相变；存在一个临界值 $\beta^*$ （等于 $\log(1 + \sqrt{2} ) = 0.88 \ldots$ 在第二维中），其中 $\beta > \beta^*$ 。然后分布是严重的双峰分布，即使晶格的大小趋于无穷大。此外， $x_i$ 和 $x_j$ ，即使相距任意远，也将呈正相关。

12.9 面向 MRF 的 MCMC

12.9.1 固定 $\beta$ 时的 MCMC

我们现在将讨论如何从固定 $\beta$ 的 $\pi(\mathbf{x})$ 生成样本，重点关注二值情况和 Ising 模型 式（12.30） 。 第 12.5.2 节 中的 Gibbs 采样器也适用于离散 MRF。

同样，要更新 $x_i$ ，我们只需要考虑邻居 $\mathbf{x}_{∂i}$ ，在本例中是四个最近的邻居。

直觉上，在 $\beta$ 高且一种颜色占主导地位的情况下，吉布斯采样器将倾向于提出与已有颜色相同的颜色。请注意，伊辛模型是对称的，因此配置 $\mathbf{x}$ 和 $\mathbf{1 − x}$ 具有相同的概率。如果我们建议始终更改测点 $i$ 的颜色（Frigessi、Hwang、 Sheu 和 di Stefano，1993 年）。如果我们这样做，那么我们需要更正这个提议以维持均衡分布。由此产生的 MCMC 算法称为 Metropolis–Hastings 算法。

我们应该接受提议的新状态 $p_i$ 的概率也只取决于邻居 $\mathbf{x}_{∂i}$ 。请注意，如果 $R_i \geq 1$ ，则始终接受新提议的状态。

图 12.7 显示了来自 $64 × 64$ 环形网格的样本，使用 Metropolis–Hastings 算法，其中 $\beta = 0.6、0.88\ldots$ 和 $1.0$ 。在 $\beta^*$ 以下，样本更分散，而在 $\beta^*$ 以上，样本更集中在一种颜色上。

12.9.2 随机 $\beta$ 时的 MCMC

我们在 例 12.4 中的 MCMC 算法中遇到了复杂情况，当时交互参数 $\delta$ 是随机的，因为归一化常数取决于 $\delta$ ；参见 式（12.17） 。在离散 MRF 的情况下，由于同样的原因， $\beta$ 的推断变得很麻烦。事实上，情况更糟，因为除了小格子之外，我们无法精确计算归一化常数。

回想一下 $Z(\beta)$ 定义为

$$Z(\beta) = \sum\limits_{\mathbf{x}} \exp(\beta S(\mathbf{x})) \tag{12.33}$$

其中 $S(\mathbf{x})$ 是充分统计量 $\sum\limits_{ i \sim j} 1[x_i = x_j]$ 。一种可能性是查看 $Z(\beta)$ 关于 $\beta$ 的导数是否比 $Z(\beta)$ 本身更容易估计。

$$\begin{align*} \frac{dZ(\beta)}{d\beta} &= \sum\limits_{\mathbf{x}} S(\mathbf{x}) \exp(\beta S(\mathbf{x})) \\ &= Z(\beta) \sum\limits_{\mathbf{x}} (S(\mathbf{x})) \exp(\beta S(\mathbf{x})) /Z(\beta)\\ &= Z(\beta )\mathbb{E}_{\mathbf{x}|\beta} S(\mathbf{x}) \end{align*}$$

通过解微分方程，我们得到

$$\log (Z(\beta')/Z(\beta)) = \int^{\beta'}_{\beta} \mathbb{E} _{\mathbf{x}| \tilde{ \beta}} S(\mathbf{x}) d \tilde{\beta} \tag{12.34}$$

正如我们所见，这一技巧已将问题的难度降低到可以使用以下过程解决的问题（有关应用，请参阅 Hurn、Husby 和 Rue，2003 年）。

1. 使用基于一系列 MCMC 算法的输出的后验均值估计，估计一系列不同 $\beta$ 值的 $\mathbb{E}_{\mathbf{x}|\beta} S(\mathbf{x})$ 。这些值将取决于图像大小，因此需要针对每个新问题重新计算。

2.构造平滑样条 $f(\beta)$ 来平滑 $\mathbb{E}_{\mathbf{x}|\beta} S(\mathbf{x})$ 的估计值。

3. 使用 $f(\beta)$ 的数值或解析积分来计算 式（12.34） 的估计，

$$\log ( \widehat{ Z(\beta')}/Z(\beta)) = \int^{ \beta'}_{ \beta} f(\tilde{\beta}) d \tilde{\beta}$$

式（12.34） 背后的思想在物理学文献中通常称为热力学积分，请参阅 Gelman 和 Meng (1998) 从统计角度进行很好的介绍。 Geyer 和 Thompson (1992) 也有类似的想法。伪似然法（Besag，J.E.，1974）是一种早期但仍然流行的方法，用于推断离散值 MRF（Frank 和 Strauss，1986；Strauss 和 Ikeda，1990），参见 Robins、Snijders、Wang、Handcock 等阿尔。 (2007) 更新概览。