Transformer 神经过程：通过序列建模进行不确定性感知元学习

【摘 要】 神经过程 (NPs) 是一类流行的元学习方法。与高斯过程 (GP) 类似，神经过程定义函数的分布并可以估计其预测中的不确定性。然而，与 GP 不同，神经过程及其变体存在欠拟合问题，并且通常具有难以处理的似然，这限制了它们在顺序决策中的应用。我们提出了 Transformer Neural Processes (TNPs)，这是神经过程家族的新成员，它将不确定性感知元学习转化为序列建模问题。我们通过基于自回归似然的目标来学习 TNP，并使用一种新颖的基于 transformer 的架构对其进行实例化。模型架构尊重问题结构固有的归纳偏差，例如对观测到的数据点的不变性和对未观测到的点的等变性。我们进一步研究了 transformer 神经过程框架内的旋钮，这些旋钮在解码分布的表现力与额外计算之间进行了权衡。根据经验，我们表明 transformer 神经过程在各种基准问题上实现了最先进的性能，在元回归、图像补全、上下文多臂老虎机和贝叶斯优化方面优于所有以前的神经过程变体。

【原 文】 Nguyen, T. and Grover, A. (2023) ‘Transformer Neural Processes: Uncertainty-Aware Meta Learning Via Sequence Modeling’. arXiv. Available at: http://arxiv.org/abs/2207.04179 (Accessed: 9 May 2023).

1. 简介

元学习 (Schmidhuber, 1987; Vanschoren, 2018) 的目标是学习仅需少量有标签样本即可快速拟合未知任务的模型。由于任何新任务的有标签数据量都是有限的，因此理想情况下，我们要求模型既具有高精度又能量化其预测中的不确定性。这在顺序决策中尤为重要，例如贝叶斯优化（Mockus 等，1978 年；Schonlau 等，1998 年；Shahriari 等，2015 年；Hakhamaneshi 等，2021 年）和多臂老虎机 (Cesa-Bianchi & Lugosi, 2006; Riquelme 等，2018)，其中量化的不确定性可以指导数据收集。我们将这种范式称为不确定性感知元学习，这是本文的主要焦点。

神经过程 (NPs)（Garnelo 等，2018a；b）是针对此类问题的一类丰富的模型。神经过程提供了一种灵活的方法来对函数分布进行建模，并通过元学习框架进行训练，该框架可以在测试时快速拟合新函数。更具体地说，神经过程的结构类似于数据集上的变分自动编码器 (VAE) (Kingma & Welling, 2013)，其中我们使用隐变量模型来估计给定一组无标签（背景）点的条件分布有标签（目标）点。通过对编码隐变量中函数不确定性的摊销推断，神经过程可以在测试时快速拟合新任务。

然而，神经过程及其变体有两个主要缺点。

• 首先，由于隐变量的存在，许多神经过程变体通常具有难以处理的边缘似然，而是针对对数似然的替代变分下界进行优化。使用隐变量的标准理由是它们可以表示函数不确定性并在某些情况下提高预测性能（Le 等，2018）。然而，优化对数似然的变分下界不一定会产生有意义的潜在表示，并且可能需要对目标进行重大调整（Chen 等，2016 年；Alemi 等，2018 年）
• 其次，据观测，神经过程往往不适合数据分布。注意力神经过程 (ANP)（Kim 等，2019 年）通过将注意力机制纳入神经过程编码器-解码器架构来部分解决这个问题。虽然 ANP 提供了显著改进的拟合，但这些模型往往会做出过于自信的预测，并且在顺序决策问题上表现不佳。

我们提出了 Transformer Neural Processes (TNPs)，这是一种从序列建模角度派生的不确定性感知元学习的新框架。transformer 神经过程的学习目标是以背景点（在训练和测试期间观测到）为条件，自回归最大化目标点（仅在训练期间观测到）的条件对数似然。这消除了对隐变量和任何变分近似的需要，同时允许预测分布的表达参数化。我们通过具有因果掩码的基于 transformer 的架构实例化 TNP，类似于 GPT-x 模型（Radford 等，2018 年；2019 年；Brown 等，2020 年）。此类模型已导致各种领域和模式的最先进性能（Brown 等，2020 年；Lu 等，2021 年；Chen 等，2021 年）。然而，传统 transformers 不能直接用于参数化神经过程，因为它们缺乏对条件有标签的不变性，并且与目标点的顺序不等变。我们提出了适当的修改来满足这些需求，方法是删除位置嵌入，对背景和目标点使用新颖的填充和掩蔽方案，并考虑对设计等变的对称预测分布的蒙特卡罗近似。

最后，我们还提出了 transformer 神经过程的两种变体，它们可以权衡自回归因子分解的表现力与计算易处理性和精确等方差。这些变体考虑了对输出分布协方差矩阵的对角和 Cholesky 近似。根据经验，我们根据先前工作中提出的各种基准问题评估 TNP，包括元回归、图像补全、上下文老虎机和贝叶斯优化 (BO)。元回归和图像补全评估 transformer 神经过程生成的预测质量，上下文老虎机和贝叶斯优化衡量 transformer 神经过程在顺序决策任务中的表现。在所有这些问题上，我们观察到 transformer 神经过程的表现大大优于神经过程的几个注意力变体（Kim 等，2019；Lee 等，2020）和非注意力的变体（Garnelo 等，2018a；2018b）。

2. 背景

2.1 不确定性感知元学习

在元学习中，我们假设函数分布未知，比如 $\mathcal{F}$ 。在训练期间，我们从 $\mathcal{F}$ 中采样固定数量的函数，并从每个函数 $f : \mathcal{ X \rightarrow Y}$ 中观测一组有限的评估 $\{x_i, y_i\}^{N}_{i=1}$ 。在测试时，我们通过一组未见过的函数来评估模型的泛化能力，假设它们来自与 $\mathcal{F}$ 相同或相似的分布。对于每个测试函数，我们提供一小组有标签的训练点 $D_{train}$ ，并测试模型在测试集 $D_{test}$ 上做出预测的能力。

我们在这项工作中的重点是不确定性感知元学习。也就是说，假设模型在整个测试集 $D_{test}$ 上输出一个联合预测分布。例如，如果我们假设预测分布是具有对角协方差的多变量高斯分布，我们会为每个输入 $x_j \in D_{test}$ 输出均值 $\mu_j$ 和标准差 $\sigma_j$ 。此处， $\sigma_j$ 量化了模型预测中的不确定性。

2.2 神经过程

神经过程 (NP) 是一种随机过程，它描述了在给定训练集有标签点（背景）的情况下一组无标签点（目标）的预测分布（Garnelo 等，2018a;2018b）。此外，神经过程包含一个隐变量 $z$ 来表示函数不确定性。形式上，神经过程模型的似然给出如下：

$$p(y_{m+1:N} |x_{m+1:N} , C) = \int_z p(y_{m+1:N} |x_{m+1:N}, z)p(z|C)dz \tag{1}$$

其中 $C = \{x_i, y_i\}^{m}_{i=1}$ 和 $T = \{x_i, y_i\}^{N}_{i=m+1}$ 分别是背景和目标对的集合。我们注意到也存在没有隐变量的神经过程变体；我们建议读者参阅第 5 节进行详细审查。由于似然难以处理，神经过程最大化对数似然的证据下限 ( $\mathrm{ELBO}$ )：

$$\log p(y_{m+1:N} |x_{m+1:N} , C) \geq \mathbb{E}_{q(z|C,T)}[\log p(y_{m+1:N} |x_{m+1:N} , z)] − \mathrm{KL}(q( z|C, T)||p(z|C)) \tag{2}$$

等效地，我们可以将神经过程视为以背景对和目标输入为条件的目标标签上的变分自编码器（Kingma & Welling，2013）。编码器 $q(z|C, T)$ 是一个置换不变函数，它将背景对映射到 $z$ 上的分布。在实践中， $q$ 包含一个将每对 $(x_i, y_i)$ 映射到其表示的 MLP，一个组合这些表示的聚合器，以及另一个输出 $z$ 的均值和方差的 MLP。解码器 $p(y_{m+1:N} |x_{m+1:N} , z) = \|\prod\limits^{N}_{i=m+1} p(y_i|x_i, z)$ 在给定推断 $z$ 的情况下独立预测每个目标的标签。

2.3 Transformer

Transformer 是由 Vaswani 等 (2017) 提出的用于建模序列数据的有效架构。 Transformer 由一个编码器和一个解码器组成，它们都由一堆具有残差连接的自注意力层组成。自注意力层接收与 $n$ 个输入有标签相关联的 $n$ 个嵌入 $\{ e^{in}_{i} \}^{n}_{i=1}$ ，并输出 $n$ 个对应的嵌入 $\{e^{out}_{i} \}^{n}_{i=1}$ 。每个嵌入向量 $e^{in}_{i}$ 首先通过线性变换映射到键 $k_i$ 、查询 $q_i$ 和值 $v_i$ 。输出嵌入 $e^{out}_{i}$ 是所有输入值的加权线性组合，其中权重由其查询 $q_i$ 和其他键 $k_j$ 之间的归一化点积给出：

$$e^{out}_{i}= \sum^{n}_{j=1} \frac{\exp(\langle q_i, k_j \rangle)}{ \sum\limits^{n}_{j'=1}\exp(\langle q_i, k_j' \rangle) } \cdot v_j \tag{3}$$

在第一个自注意力层之前，每个输入有标签都通过一个位置编码器，它将顺序信息合并到输入序列中。这种灵活的架构允许 transformer 处理任意长度的输入序列，并提供一种简单而有效的方式来对输入有标签之间的关系进行建模。这种架构是近期许多语言和视觉突破的关键（Radford 等，2019 年；Dosovitskiy 等，2020 年；Chen 等，2020 年；Brown 等，2020 年）。在本文中，我们研究了如何将 transformer 应用于不确定性感知元学习问题。

3. Transformer 神经过程

我们建议通过序列建模的视角来解决不确定性感知元学习。为此，我们将模型在训练期间观测到的每组评估 $\{x_i, y_i\}^{N}_{i=1}$ 视为 $N$ 个数据点的有序序列。由于我们观测来自多个此类函数的评估，因此我们将每个训练序列的随机子集分离为背景对集 $(x_{1:m}, y_{1:m})$ 作为序列模型的少样本条件。此后，我们对剩余 $(N − m)$ 个目标点的预测似然进行自回归建模，并最大化以下目标：

$$\begin{align*} \mathcal{L}(\theta) &= \mathbb{E}_{x_{1:N},y_{1:N},m} [\log p_{\theta}(y_{m+1:N} | x_{1:N} , y_{1:m})] \tag{4}\\ &= \mathbb{E}_{x_{1:N} ,y_{1:N} ,m} \left[\sum^{N}_{i=m+1} \log p_{\theta}(y_i | x_{1:i}, y_{1:i-1}) \right] \tag{5} \end{align*}$$

上述目标中的每个条件都是单变量高斯分布。在实践中，我们优化了式（5） 中目标的蒙特卡罗近似，我们考虑一批训练函数及其随机抽样的评估。我们统一采样一个索引 m，该索引确定每组评估的背景和目标点。接下来，我们列出架构的需求

【性质 3.1】上下文不变性

如果对于置换函数 $\pi$ 和 $m \in [1, N − 1]$ 的任意选择，有 $p_{\theta}(y_{m+1:N} | x_{m+1:N} , x_{1:m}, y_{1:m}) = p_{\theta}( y_{m+1:N} | x_{m+1:N} , x_{\pi(1):\pi(m)}, y_{\pi(1):\pi(m)})$，则称模型 $p_{\theta}$ 是上下文不变的。

【性质 3.2】目标等方差性

果对于置换函数 $\pi$ 和 $m \in [1, N − 1]$ 的任意选择， $p_{\theta}(y_{m+1:N} | x_{m+1:N} , x_{1:m}, y_{1:m}) = p_{\theta}( y_{\pi(m+1):\pi(N)} | x_{\pi(m+1):\pi(N)}, x_{1:m}, y_{1:m})$ ，则称模型 $p_{\theta}$ 是目标等变的。

上下文不变性要求对于任何基础函数 $f$ ，如果我们置换背景点，目标点的预测不应改变。目标等方差性要求每当置换目标输入 $\{x_i\}^{N}_{i=m+1}$ 时，预测都会相应地置换。我们实例化 式（5）中的目标。 具有如 图 1 所示的 transformer 架构。GPT（Radford 等，2018）等标准 transformer 采用临时掩码来强制执行 式 (5) 所需的自回归结构。 然而，自回归 transformer 的这种天然应用无法满足性质 3.1 和性质 3.2 中的需求。由于该模型将 $x_i$ 和 $y_i$ 视为两个单独的token ，因此我们需要为它们添加一个位置嵌入向量，以便模型将它们关联为一对 $(x_i, y_i)$ 。不幸的是，这种位置编码使模型的输出取决于目标点的排列。此外，自回归 transformer 也违反了目标等变性，因为点的排序会影响它们的嵌入，因此，不同的排序会导致非等变预测。接下来，我们介绍了 Transformer Neural Processes (TNPs)，这是一系列基于 Transformer 的神经过程，可以缓解上述挑战。

3.1 自回归 Transformer 神经过程

我们对 transformer 神经过程的首次尝试建立在 式（5） 中的自回归因式分解之上。传统 transformer 由于使用了位置编码而违反了性质 3.1。然而，这些编码对于建立 $x_i$ 和 $y_i$ 之间的关联也很有用。为了应对这一挑战，我们首先将 $x_i$ 和 $y_i$ 连接起来形成一个 token，这允许我们删除位置编码并将它们视为一对。虽然该方案适用于背景点 $(x_i, y_i)^{m}_{i=1}$ ，但我们不能天真地将它应用于任何依赖于先前对 $(x_j, y_j)^{i-1}_{j=1}$ 及其输入 $x_i$ 的目标点 $y_{i>m}$。为了尊重这些点的自回归结构，我们引入了由 $x_{i>m}$ 填充的辅助有标签（在我们的例子中为 $0$ ）并将它们附加到我们的原始序列。我们的填充序列包含 $N$ 个实数对 $(x_i, y_i)^{N}_{i=1}$ 和 $N − m$ 个填充对 $(x_i, 0)^{N}_{i=m+1}$ :

$$\tau = \{(x_1, y1),\ldots , (x_N , yN ), (x_{m+1}, 0),\ldots , (x_N , 0)\} \tag{6}$$

为了保持 式（5） 中的自回归排序，我们在注意力层设计了一种掩蔽机制，使得：

• (1) 背景点 $(x_i, y_i)^{m}_{i=1}$ 只关注它们自己；
• (2) 目标点 (x_i, y_i) for (i > m) attends to all context points and previous target points (x_j, y_j)i j=m+1;
• (3) $(i > m)$ 的填充目标点 $(x_i, 0)$ 关注所有背景点和先前的目标点 $(x_j, y_j)^{i−1}_{j=m+1}$ 。我们将此模型称为自回归 transformer 神经过程 (TNP-A)。

图 1 说明了模型， 图 2 显示了 $N = 5$ 和 $m = 2$ 的样本掩码。由于上述掩码方案，它满足性质 3.1。为了满足性质 3.2，我们遵循对称论证。在这里，我们注意到，通过对整个组的函数评估进行平均，可以使任何函数与一个组等变（Murphy 等，2018 年）。形式上，让我们将我们的联合兴趣分布表示为 $\tilde{p}_{\theta}(y_{m+1:N} | x_{1:N} , y_{1:m})$ 。我们根据基本自回归模型 $p_{\theta}$ 将 $\tilde{p}_{\theta}$ 定义为：

$$p_{\theta}(y_{m+1:N} |x_{1:N} , y_{1:m}) = \mathbb{E}_{\pi}[p_{\theta}(y_{\pi(m+1):\pi(N)} | x_{\pi( m+1):\pi(N)}, x_{1:m}, y_{1:m})] \tag{7}$$

由于排列组难以枚举，我们改为考虑随机采样排列的蒙特卡罗平均值来近似 $\tilde{p} _{\theta}$。即使使用蒙特卡洛意味着我们仅在极限情况下满足性质 3.2，但我们可以在训练和评估期间轻松地计算预测分布。接下来，我们介绍了完全满足性质 3.2 的 transformer 神经过程替代解码器，同时牺牲了计算易处理性的表达能力。

3.2 对角 transformer 神经过程

我们可以通过假设在给定背景点和目标输入 $x_{m+1:N}$ 时，$y_{m+1:N}$ 条件独立来简化 式 (5) 中的目标。换句话说，我们考虑因式分解：

$$p_{\theta}(y_{m+1:N} |x_{1:N} , y_{1:m}) = \prod\limits^{N}_{i=m+1} p_{\theta}(y_i|x_i, x_{1:m}, y_{1:m}) \tag{8}$$

由于目标点是独立的，我们从 式 (6) 中的输入序列中删除 $\{(x_i, y_i)^{N}_{i=m+1}\}$ 并且只提供由背景点和填充的目标点组成的序列 $\{(x_i, 0)^{N}_{i=m+1}\}$ 。这种解码分布可以看作是具有对角协方差矩阵的多元正态分布，因此，我们将其称为对角变换神经过程 (TNP-D)。与 TNP-A 不同，我们不需要对排列进行平均来满足性质 3.2。然而，对于许多场景，目标点之间的独立性假设对于准确建模底层函数来说可能非常强。

3.3 非对角 transformer 神经过程

最后，我们介绍了非对角 transformer 神经过程 (Non-Diagonal Transformer Neural Processes, TNP-ND)，这是 transformer 神经过程的第三个变体，它在 TNP-D 的易处理性和 TNP-A 的表现力之间取得平衡，同时满足性质 3.1 和性质 3.2。我们将解码分布参数化为具有非对角协方差矩阵的多元正态分布：

p_{\theta}(y_{m+1:N} | x_{1:N} , y_{1:m}) = \mathcal{N}(y_{m+1:N} | \mu_{\theta}(x_{1:N} , y_{1:m}), \\sum\limits_{\theta}(x_{1:N}, y_{1:m})) \tag{9}

与 TNP-D 类似，我们从输入序列中删除 $\{(x_i, y_i)^{N}_{i=m+1}\}$ ，因为目标点是联合预测的。由于计算完整的协方差矩阵可能很昂贵，我们考虑两种近似来参数化 $\Sigma$：

• (1) Cholesky 分解： $\Sigma = LL^{\top}$ ，其中 $L$ 是具有正对角线值的下三角矩阵；
• (2) 低秩近似： $\Sigma = \exp(D) + \mathbf{AA}^{\top}$ ，其中 $D$ 是对角矩阵， $A$ 是低秩矩阵。对于本文的主要实验，由于其计算方便，我们使用 Cholesky 分解。低秩近似的结果在 附录 A.1 中。

对于维数为 $n$ 的分布，我们需要一个输出 $\frac{n(n+1)}{2}$ 个值的神经网络来表示下三角矩阵 $L$ 。实际上，分布的维数取决于目标点的数量，目标点的数量在培训和评估。这意味着我们不能简单地使用神经网络直接输出 L。我们而是按如下方式对解码器进行参数化。首先，最后一个掩码自注意力层的输出向量 $z_{m+1:N}$ 被馈送到 MLP，该 MLP 产生平均值 $\mu_{m+1:N}$ 。然后，我们将 $z_{m+1:N}$ 传递给另一个头部，该头部由额外的自注意力层堆栈和输出 $N − m$ 个向量 $h_{m+1:N}$ 的最终投影层（MLP）组成。每个向量 $h_i \in \mathbb{R}^{p}$ 都被投影到维度 $p$ 。然后计算下三角矩阵 $L$ 为：

$$L = \mathrm{lower}(HH^{\top}), \, H \in \mathbb{R}^{n \times p} \tag{10}$$

其中 $H$ 是 $\{h_i\}^{N}_{i=m+1}$ 的逐行堆栈， $\mathrm{ lower}(L)$ 移除 $L$ 的上三角部分， $n = N −m$ 是目标点的数量。虽然这种特殊的参数化并不能普遍表示所有可能的下三角矩阵，但它提供了两个主要好处。

• 首先，它允许我们用任意数量的目标点参数化多元正态分布。
• 其次，如果我们直接输出 $L$ 的分量，与 $\mathcal{O}(n^2)$ 相比，此参数化的空间复杂度仅为 $\mathcal{O}(n)$ 。

4. 实验

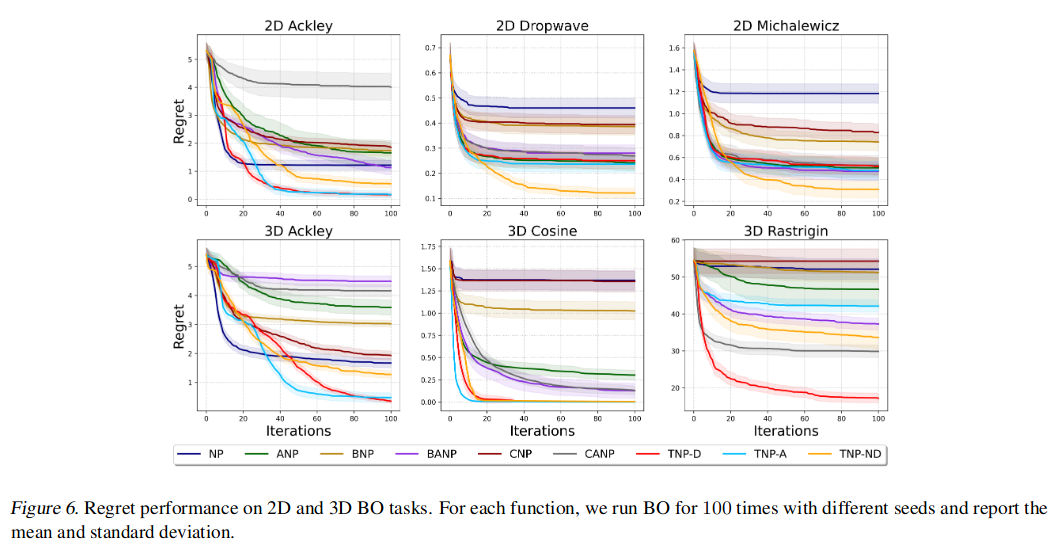
我们在多项任务上评估了 Transformer Neural Processes (TNPs)：回归、图像补全、贝叶斯优化和上下文老虎机。这组实验已被广泛用于在先前的工作中对基于神经过程的模型进行基准测试（Garnelo 等，2018b；Kim 等，2019；Lee 等，2020）。我们将 transformer 神经过程与神经过程家族的其他成员进行比较，即条件神经过程 (CNP) (Garnelo 等，2018a)、神经过程 (NP) (Garnelo 等，2018b) 和引导神经过程 (BNP) (Lee 等，2020)，以及他们的细心版本 (Kim 等，2019)，分别是 CANP、ANP 和 BANP。我们已经开源了用于重现我们实验的代码库。基线的实现借鉴了 BNP 的官方实现。

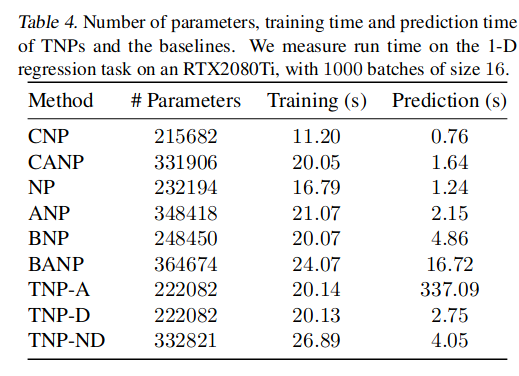
4.5 transformer 神经过程的内存和时间复杂度

Transformer 在语言（Brown 等，2020）和视觉（Dosovitskiy 等，2020）方面的主要成功很大程度上归功于能够扩展到数十亿个参数，从而取得前所未有的成果。类似地，可以声称 transformer 神经过程的优越性能仅仅是因为具有比基线更多的参数。因此，我们比较了 transformer 神经过程的参数计数、训练和预测时间以及 表 4 中的基线。所有模型都具有可比性，但 TNP-A 除外，正如预期的那样，由于自回归性质会导致更长的预测时间。这表明缩放并不是我们所需要的全部， transformer 架构本身也很重要。

5. 相关工作

（1）神经过程

条件神经过程 (CNP)（Garnelo 等，2018a）是神经过程家族的第一个成员。 CNP 将背景点编码为确定性潜在向量 z，因此没有函数不确定性的概念。神经过程 (NP)（Garnelo 等，2018b）被提议通过以隐变量的形式引入随机性来解决这些缺点。乐等。 (2018) 在训练神经过程时对不同的目标和超参数选择进行了仔细的实证检查。从那时起，已经提出了许多扩展，通过建立平移等方差（Gordon 等，2019），结合对解决欠拟合的关注（Kim 等，2019），使用自举来克服高斯假设对隐变量的局限性变量 (Lee 等，2020)，以及建模预测相关性 (Bruinsma 等，2021)。此外，许多工作还将神经过程扩展到更广泛的问题，包括对一系列随机过程进行建模（Singh 等，2019 年）和对随机物理场进行建模（Holderrieth 等，2021 年）。马修等。 (2021) 最近提出了一个对比学习框架，该框架取代了神经过程中的重建目标，以学习更好的表示。在徐等。 (2020)，作者提出了一种基于 CANP 的元学习器，在大规模图像分类上取得了良好的效果。格罗弗等。为通过各种神经过程建模的不确定性提供一系列细粒度诊断。最后，Galashov 等。 (2019) 实证研究了神经过程作为元学习者在各种顺序决策问题中的有效性。

（2）Transformer

Transformer 架构由 Vaswani 等引入。 (2017) 用于自然语言的灵活建模。近年来，transformers 在语言（Devlin 等，2018; Radford 等，2018; 2019; Brown 等，2020）和视觉（Dosovitskiy 等，2020; Radford 等，2021）方面取得了突破；陈等，2020 年）。

最近的工作（Lee 等，2019 年；Kossen 等，2021 年）除了对同一数据点的组件之间的交互进行建模外，还应用 transformer 对不同数据点之间的关系进行建模。 Set Transformers (Lee 等，2019) 与 transformer 神经过程密切相关，旨在解决集合输入问题，例如找到集合中的最大数量或计算唯一字符。 Set Transformers 采用 transformer 架构来模拟同一集合的项目之间的交互，并删除位置编码以实现排列不变性。然而，我们在这项工作中的重点是不确定性感知元学习。对于此类任务，TNP 包含重要的架构设计选择，例如输入表示和屏蔽机制。transformer 神经过程对输入 x’s 之间的相互作用以及 x 和 y 之间的关系进行建模以准确推断潜在函数至关重要。陈等。 (2021) 提出了一种基于自回归 transformer 的离线强化学习模型，Zheng 等将其扩展到在线设置。 (2022)。除了代理设置的差异外，这项工作还考虑了单个任务的轨迹，这与我们对元学习的关注不同。同时，M uller 等。开发了先验数据拟合网络 (PFN)，一种与 transformer 神经过程非常相似的方法。 PFN 可以在单个前向传播中对新任务进行预测，并满足两个所需的性质 3.1 和 3.2。然而，PFN 将元学习视为贝叶斯推理问题，其中模型学习在给定输入和训练数据的情况下近似估计地面实况的后验分布。因此，训练数据对应于 transformer 神经过程中的背景点，而输入和基本事实对应于目标点。 PFN 侧重于贝叶斯推理方面，而我们对不确定性感知任务更感兴趣，从而导致不同的实验设置。此外，PFN 仅预测边缘分布，这相当于 TNP-D。

6. 讨论

神经过程为直接从数据中学习灵活的随机过程提供了一种很有前途的方法。然而，尚不清楚其设计的哪些方面对于不确定性感知元学习的下游应用至关重要，例如回归和顺序决策。流行的说法，例如使用隐变量来表示函数不确定性和多样化采样，具有混合的经验证据（Garnelo 等，2018b）并且编码器和解码器之间的确定性路径对于良好的性能很重要（Le 等， 2018）。此外，变分自动编码器（包括神经过程）的标准证据下限可以完全忽略具有强大解码器的潜在代码（Chen 等，2016 年；Alemi 等，2018 年）。

在这方面，我们提出了 Transformer Neural Processes (TNPs)，这是一种通过序列建模进行不确定性感知元学习的替代框架。transformer 神经过程优化自回归建模目标并受益于 transformer 主干的使用（Vaswani 等，2017 年；Radford 等，2018 年）。虽然注意力机制之前也已用于参数化神经过程（Kim 等，2019 年），但我们表明替换整个架构堆栈可以显著提高各种基准测试任务的性能。我们还表明，这些经验收益不能仅仅归因于使用像 TNP-A 中那样更具表现力的解码分布，还可以通过易处理和等变（但表现力相对较低）的参数化（例如 TNP-D）在很大程度上获得和 TNP-ND。

未来，我们热衷于进一步利用 transformer 神经过程架构的优点，以扩展到超出当前基准的高维问题。我们也有兴趣在未来的工作中彻底分离函数和点不确定性（如在 GP 中），可能通过随机 transformer 的最新进展（Lin 等，2020 年）。

参考文献

• [1] Alemi, A., Poole, B., Fischer, I., Dillon, J., Saurous, R. A., and Murphy, K. Fixing a broken elbo. In International Conference on Machine Learning, pp. 159–168. PMLR, 2018.
• [2] Balandat, M., Karrer, B., Jiang, D., Daulton, S., Letham, B., Wilson, A. G., and Bakshy, E. Botorch: A framework for efficient monte-carlo bayesian optimization. Advances in neural information processing systems, 33, 2020.
• [3] Brown, T. B., Mann, B., Ryder, N., Subbiah, M., Kaplan, J., Dhariwal, P., Neelakantan, A., Shyam, P., Sastry, G., Askell, A., et al. Language models are few-shot learners. arXiv preprint arXiv:2005.14165, 2020.
• [4] Bruinsma, W. P., Requeima, J., Foong, A. Y., Gordon, J., and Turner, R. E. The gaussian neural process. arXiv preprint arXiv:2101.03606, 2021.
• [5] Cesa-Bianchi, N. and Lugosi, G. Prediction, learning, and games. Cambridge university press, 2006.
• [6] Chan, S. C., Santoro, A., Lampinen, A. K., Wang, J. X., Singh, A., Richemond, P. H., McClelland, J., DeepMind, S., and Hill, F. Data distributional properties drive emergent in-context learning in transformers. CoRR, 2022.
• [7] Chen, L., Lu, K., Rajeswaran, A., Lee, K., Grover, A., Laskin, M., Abbeel, P., Srinivas, A., and Mordatch, I. Decision transformer: Reinforcement learning via sequence modeling. arXiv preprint arXiv:2106.01345, 2021.
• [8] Chen, M., Radford, A., Child, R., Wu, J., Jun, H., Luan, D., and Sutskever, I. Generative pretraining from pixels. In International Conference on Machine Learning, pp. 1691–1703. PMLR, 2020.
• [9] Chen, X., Kingma, D. P., Salimans, T., Duan, Y., Dhariwal, P., Schulman, J., Sutskever, I., and Abbeel, P. Variational lossy autoencoder. arXiv preprint arXiv:1611.02731, 2016.
• [10] Chung, Y., Char, I., Guo, H., Schneider, J., and Neiswanger, W. Uncertainty toolbox: an open-source library for assessing, visualizing, and improving uncertainty quantification. arXiv preprint arXiv:2109.10254, 2021.
• [11] Cohen, G., Afshar, S., Tapson, J., and Van Schaik, A. Emnist: Extending mnist to handwritten letters. In 2017 International Joint Conference on Neural Networks (IJCNN), pp. 2921–2926. IEEE, 2017.
• [12] Devlin, J., Chang, M.-W., Lee, K., and Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805, 2018.
• [13] Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn, D., Zhai, X., Unterthiner, T., Dehghani, M., Minderer, M., Heigold, G., Gelly, S., et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv preprint arXiv:2010.11929, 2020.
• [14] Foong, A. Y., Bruinsma, W. P., Gordon, J., Dubois, Y., Requeima, J., and Turner, R. E. Meta-learning stationary stochastic process prediction with convolutional neural processes. arXiv preprint arXiv:2007.01332, 2020.
• [15] Frazier, P. I. A tutorial on bayesian optimization. arXiv preprint arXiv:1807.02811, 2018.
• [16] Galashov, A., Schwarz, J., Kim, H., Garnelo, M., Saxton, D., Kohli, P., Eslami, S., and Teh, Y. W. Meta-learning surrogate models for sequential decision making. arXiv preprint arXiv:1903.11907, 2019.
• [17] Gardner, J. R., Pleiss, G., Bindel, D., Weinberger, K. Q., and Wilson, A. G. Gpytorch: Blackbox matrix-matrix gaussian process inference with gpu acceleration. arXiv preprint arXiv:1809.11165, 2018.
• [18] Garnelo, M., Rosenbaum, D., Maddison, C., Ramalho, T., Saxton, D., Shanahan, M., Teh, Y. W., Rezende, D., and Eslami, S. A. Conditional neural processes. In International Conference on Machine Learning, pp. 1704–1713. PMLR, 2018a.
• [19] Garnelo, M., Schwarz, J., Rosenbaum, D., Viola, F., Rezende, D. J., Eslami, S., and Teh, Y. W. Neural processes. arXiv preprint arXiv:1807.01622, 2018b.
• [20] Gordon, J., Bruinsma, W. P., Foong, A. Y., Requeima, J., Dubois, Y., and Turner, R. E. Convolutional conditional neural processes. arXiv preprint arXiv:1910.13556, 2019.
• [21] Grover, A., Tran, D., Shu, R., Poole, B., and Murphy, K. Probing uncertainty estimates of neural processes. Hakhamaneshi, K., Abbeel, P., Stojanovic, V., and Grover, A. Jumbo: Scalable multi-task bayesian optimization using offline data. arXiv preprint arXiv:2106.00942, 2021.
• [22] Holderrieth, P., Hutchinson, M. J., and Teh, Y. W. Equivariant learning of stochastic fields: Gaussian processes and steerable conditional neural processes. In International Conference on Machine Learning, pp. 4297–4307. PMLR, 2021.
• [23] Kim, H., Mnih, A., Schwarz, J., Garnelo, M., Eslami, A., Rosenbaum, D., Vinyals, O., and Teh, Y. W. Attentive neural processes. arXiv preprint arXiv:1901.05761, 2019.
• [24] Kim, J. Benchmark functions for bayesian optimization. https://github.com/jungtaekkim/ bayeso-benchmarks, 2020.
• [25] Kim, J. and Choi, S. BayesO: A Bayesian optimization framework in Python. https://bayeso.org, 2017.
• [26] Kingma, D. P. and Welling, M. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114, 2013.
• [27] Kossen, J., Band, N., Lyle, C., Gomez, A. N., Rainforth, T., and Gal, Y. Self-attention between datapoints: Going beyond individual input-output pairs in deep learning. arXiv preprint arXiv:2106.02584, 2021.
• [28] Le, T. A., Kim, H., Garnelo, M., Rosenbaum, D., Schwarz, J., and Teh, Y. W. Empirical evaluation of neural process objectives. In NeurIPS workshop on Bayesian Deep Learning, 2018.
• [29] Lee, J., Lee, Y., Kim, J., Kosiorek, A., Choi, S., and Teh, Y. W. Set transformer: A framework for attentionbased permutation-invariant neural networks. In International Conference on Machine Learning, pp. 3744–3753. PMLR, 2019.
• [30] Lee, J., Lee, Y., Kim, J., Yang, E., Hwang, S. J., and Teh, Y. W. Bootstrapping neural processes. arXiv preprint arXiv:2008.02956, 2020.
• [31] Lin, Z., Winata, G. I., Xu, P., Liu, Z., and Fung, P. Variational transformers for diverse response generation. arXiv preprint arXiv:2003.12738, 2020.
• [32] Liu, Z., Luo, P., Wang, X., and Tang, X. Large-scale celebfaces attributes (celeba) dataset. Retrieved August, 15 (2018):11, 2018.
• [33] Lu, K., Grover, A., Abbeel, P., and Mordatch, I. Pretrained transformers as universal computation engines. arXiv preprint arXiv:2103.05247, 2021.
• [34] Mathieu, E., Foster, A., and Teh, Y. W. On contrastive representations of stochastic processes. arXiv preprint arXiv:2106.10052, 2021.
• [35] Mockus, J., Tiesis, V., and Zilinskas, A. The application of bayesian methods for seeking the extremum. Towards global optimization, 2(117-129):2, 1978.
• [36] Muller, S., Hollmann, N., Arango, S. P., Grabocka, J., and Hutter, F. Transformers can do bayesian inference. In International Conference on Learning Representations. Murphy, R. L., Srinivasan, B., Rao, V., and Ribeiro, B. Janossy pooling: Learning deep permutationinvariant functions for variable-size inputs. arXiv preprint arXiv:1811.01900, 2018.
• [37] Radford, A., Narasimhan, K., Salimans, T., and Sutskever, I. Improving language understanding with unsupervised learning. 2018.
• [38] Radford, A., Wu, J., Child, R., Luan, D., Amodei, D., Sutskever, I., et al. Language models are unsupervised multitask learners. OpenAI blog, 1(8):9, 2019.
• [39] Radford, A., Kim, J. W., Hallacy, C., Ramesh, A., Goh, G., Agarwal, S., Sastry, G., Askell, A., Mishkin, P., Clark, J., et al. Learning transferable visual models from natural language supervision. arXiv preprint arXiv:2103.00020, 2021.
• [40] Riquelme, C., Tucker, G., and Snoek, J. Deep bayesian bandits showdown: An empirical comparison of bayesian deep networks for thompson sampling. arXiv preprint arXiv:1802.09127, 2018.
• [41] Schmidhuber, J. Evolutionary principles in self-referential learning, or on learning how to learn: the meta-meta... hook. PhD thesis, Technische Universit ̈ at M ̈ unchen, 1987.
• [42] Schonlau, M., Welch, W. J., and Jones, D. R. Global versus local search in constrained optimization of computer models. Lecture Notes-Monograph Series, pp. 11–25, 1998.
• [43] Shahriari, B., Swersky, K., Wang, Z., Adams, R. P., and De Freitas, N. Taking the human out of the loop: A review of bayesian optimization. Proceedings of the IEEE, 104 (1):148–175, 2015.
• [44] Singh, G., Yoon, J., Son, Y., and Ahn, S. Sequential neural processes. arXiv preprint arXiv:1906.10264, 2019.
• [45] Vanschoren, J. Meta-learning: A survey. arXiv preprint arXiv:1810.03548, 2018.
• [46] Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I. Attention is all you need. In Advances in neural information processing systems, pp. 5998–6008, 2017.
• [47] Xu, J., Ton, J.-F., Kim, H., Kosiorek, A., and Teh, Y. W. Metafun: Meta-learning with iterative functional updates. In International Conference on Machine Learning, pp. 10617–10627. PMLR, 2020.
• [48] Zheng, Q., Zhang, A., and Grover, A. Online decision transformer. In ICML, 2022.