〖摘要〗设计一个高效的迭代式模拟采样算法可能很困难，但对其进行推断并且监控其收敛性相对容易。本文首先给出了我们推荐的推断策略（遵循 Gelman et al., 2003 的第 11.10 节），并解释了推荐原因；然后用我们最近研究的一个关于 “民意调查数据分层模型拟合” 的案例进行说明。

〖原文〗 Inference from Simulations and Monitoring Convergence, Handbook of Markov Chain Monte Carlo， 2011

1 背景

现实世界的数据分析通常需要在仅给出对某些相关可观测量的序列观测的情况下估计未知量。在贝叶斯框架中，人们通常掌握模型的一些先验知识：不可观测兴趣量的先验分布和似然函数（将可观测量与不可观测量关联）。不可观测值的后验分布可以使用贝叶斯定理计算，这允许人们对未观测到的量进行推断。

在某些情况下，按顺序处理观测结果是很自然的。这些案例是本文重点，例如，不断有新数据实时输入的雷达跟踪或金融估算工具等在线应用，尝试更新之前形成的后验分布，肯定比从头开始重新计算更容易。

如果上述观测数据可以由线性高斯状态空间模型建模，则可以导出精确的解析表达式来计算后验分布的演化序列，而这种递归方法就是众所周知的 卡尔曼滤波。如果将数据建模为部分可观测的有限状态空间马尔可夫链，则还可以获得隐变量的解析解，即 隐马尔可夫模型（HMM）滤波。这两个过滤器是最常见和最著名的，此外还有一些动态系统使用其他有限维滤波（Vidoni 1999，West 和 Harrison 1997）

上述过滤器的问题在于： 它们依赖于高斯、线性等假设来确保数学上的易处理性。真实数据是非常复杂的，通常涉及非高斯性、高维性和非线性等情况，得到易处理的解析解几乎不可能，并且这是一个贯穿大多数科学学科的重要问题。在不同的兴趣领域中，此类问题以许多不同名称出现，如： 贝叶斯滤波、 最优（非线性）滤波、 随机过滤、 在线推断和学习等。

已经提出了许多近似方案来解决该问题，例如 扩展卡尔曼滤波器、高斯和近似 和 基于网格的滤波 。前两种方法未能考虑到目标过程的所有显著统计特征，往往导致很差的结果。基于确定性数值积分方法的网格滤波可以产生准确的结果，但难以实现，而且计算成本太高，在高维中无法实际使用。

序贯蒙特卡罗 (SMC) 方法是一组基于模拟的方法，它提供了一种方便且有吸引力的方法来计算后验分布。与基于网格的方法不同，序贯蒙特卡罗方法非常灵活、易于实施、可并行化并且适用于非常普遍的设置。廉价而强大的计算能力的出现，连同应用统计学、工程学和概率论的一些最新发展，促进了该领域的许多进展。

在过去的二十几年里，关于序贯蒙特卡罗方法及其应用的科学论文层出不穷，通常以 粒子滤波、自举滤波、聚合、蒙特卡洛滤波、交互粒子近似 等名称出现在不同的研究领域。

2 问题陈述

为了简单起见，在此将范围限制在非线性、非高斯的马尔可夫状态空间模型，尽管序贯蒙特卡罗也可以应用于更一般的设置。

Fig01

令符号 $z_{0:t} \equiv {z_0,\ldots ,z_t}$ 和符号 $x_{0:t} \equiv {x_1,\ldots ,x_t}$。则：

（1）令 ${z_t}^\infty_{t=0}$ 是一个马尔可夫过程，其中 $z_t \in \mathcal{Z}$ 表示不可观测的状态序列，其初始分布为 $p(z_0)$、状态转移概率为 $p(z_t|z_{t-1})$。因为作出了马尔科夫性假设，所以每个隐变量只与前一个时刻的隐变量有关，而与其他历史状态无关，即 $p(z_{t} | z_{0:t-1}) = p(z_{t} |z_{t-1})$。

（2）令 ${x_t}^\infty_{t=1}$ 表示具有 $x_t \in \mathcal{X}$ 的观测序列。假设给定 $z_t$ 时，观测 $x_t$ 条件独立，即边缘分布 $p(x_{t} | z_{0:t}) = p(x_{t} |z_{t})$。

也就是说，该模型由以下分布形式化定义（或者观测数据由以下过程生成）：

$$
\begin{align*}
&p(z_0)\
&p(z_t|z_{t-1}) \text{ for } t \geq 1\
&p(x_t|z_t) \text{ for } t \geq 1
\end{align*} \tag{1}
$$

如果令 $p(z|x)$ 表示已经观测到 $x$ 后，隐变量 $z$ 的后验概率，则问题可以被陈述为： **在观测到数据序列 ${x}{t=1}^{T}$ 后, 隐变量序列 ${z}{t=0}^{T}$ 的后验概率 $p(z_0,z_1,\ldots,z_T | x_1,x_2,\ldots,x_T)$；尤其是在某些场景中，我们更关心边缘分布 $p(z_T)| x_1,x_2,\ldots,x_T)$**。

也就是说，我们的目标是递归地估计出后验联合分布 $p(z_{0:t} | x_{1:t})$ 或其关联特征（如后验边缘分布 $p(z_t|x_{1:t})$，也被称为滤波分布），此外，我们还期望基于后验概率分布计算某些函数 $f_t$的期望值：

$$
I(f_t) \equiv \mathbb{E}{z{0:t} | x_{1:t}} [f_t(z_{0:t})] \triangleq \int f_t(z_{0:t}) p(z_{0:t} | x_{1:t}) d z_{0:t} \tag{2}
$$

其中函数 $f_t: \mathcal{Z}^{t+1} \rightarrow \mathbb{R}^{n_{f_t}}$ 关于后验分布 $p(z_{0:t} | x_{1:t})$ 可积分。典型的函数包括：条件均值函数 $f_t(z_{0:t}) = z_{0:t}$；条件方差函数 $f_t(z_{0:t}) = z_t z_t^T - \mathbb{E}{p(z_t|x{1:t})}[z_t] \mathbb{E}^T_{p(z_t| x_{1:t})}[z_t]$。

3 递归解法

根据贝叶斯定理，在任意时间 $t$ 时，隐变量的后验联合分布为：

$$
p(z_{0:t} | x_{1:t}) = \frac{p(x_{1:t} | z_{0:t}) p(z_{0:t}) }{\int p(x_{1:t} | z_{0:t}) p(z_{0:t}) d z_{0:t}} \tag{3}
$$

我们很自然地可以获得该后验联合概率分布的递归形式，即用 $p(z_{0:t}|x_{1:t})$ 来表示 $p(z_{0:t+1} | x_{1:t+1})$：

$$
\begin{align*}
p(z_{0:t+1} | x_{1:t+1}) &= \frac{p(z_{0:t+1},x_{1:t+1}) }{p(x_{1:t+1})}\
&=\frac{p(z_{t+1},x_{t+1}| z_{0:t},x_{0:t}) p(z_{0:t},x_{1:t})}{p(x_{t+1}|x_{1:t})p(x_{1:t})}\
&= p(z_{0:t}|x_{1:t}) \frac{p(x_{t+1} | z_{t+1})p(z_{t+1}|z_t )}{p(x_{t+1}|x_{1:t})}
\end{align*} \tag{4}
$$

其中最后一个等式使用条件密度的定义、条件独立假设和马尔可夫假设。分母中的表达式相对于 $z_{0:t+1}$ 是常数。

后验边缘分布 $p(z_t | x_{1:t})$ 也满足以下递归:

$$
\begin{align*}
&\text{预测：} p(z_t | x_{l:t-1}) = \int p(z_t | z_{t-1}) p(z_{t-1} | x_{1:t-1}) d z_{t-1} \tag{5}\
&\text{更新：} p(z_t | x_{1:t}) = \frac{p(x_t|z_t)p(z_t|x_{1:t-1})}{\int p(x_t|z_t)p(z_t|x_{1:t-1})d z_t} \tag{6}
\end{align*}
$$
上述表达式和递归看似简单，但通常很难计算，尤其是其中的归一化常数 $p(x_{1:t})$、边缘后验 $p(z{0:t}| x_{1:t})$、 $p(z_{t} | x_{t})$ 和 $I(f_t)$，因为它们需要计算复杂的高维积分。

这就是为什么从 20 世纪 60 年代中期开始，大量论文和书籍致力于获得这些分布的近似值，包括扩展卡尔曼滤波器（Anderson 和 Moore 1979，Jazwinski 1970） 、高斯和滤波器（Sorenson 和 Alspach 1971）和基于网格的方法（Bucy 和 Senne 1971）。在 20 世纪 80 年代后期，计算能力的大幅提升使得用于贝叶斯滤波的数值积分方法的快速发展成为可能（Kitagawa 1987）

2 重要性采样(Importance Sampling)

这部分详细资料参见 《直接采样、拒绝采样与重要性采样》。其中拒绝采样在算法中通过对提议的样本接受或拒绝，得到最终满足要求的样本；而重要性采样则接受所有的样本，但给每个样本赋予不同的权重。

重要性采样实现的核心能力是： 将原本无法基于样本（模拟）实施的均值计算问题，转换成了能够基于样本实施计算的问题。当某个分布 $p(z)$ 非常复杂无法直接采样时， 式（2） 的计算就无法基于样本（模拟）实现。此时可以借助一个容易采样的分布 $q(z)$ 来生成样本（例如：形态最接近真实分布的一个高斯分布），然后根据两个分布之比赋予该样本相应权重，从而间接实现对复杂分布的采样。相对于拒绝采样而言，重要性采样的优点在于将 “接受-拒绝” 判决改成了重要性权重。

也就是说，当后验概率分布非常复杂并难以采样时，式（2） 的均值可以进一步改写成如下重要性采样的形式：

$$
E[f(z)]=\int f(z) p z d z=\int f(z) \frac{p(z)}{q(z)}q(z)dz=\frac{1}{N} \sum_{i=1}^{N} f\left(z^{i}\right) \frac{p\left(z^{i}\right)}{q\left(z^{i}\right)} \tag{7}
$$

其中：

  • 引入了一个可参数化的简单分布 $q(z)$, 最重要的是可以很容易从 $q(z)$ 中进行采样，这样的 $q(z)$ 被称为提议分布；
  • $p(z)$ 为真实分布，而 $\frac{p\left(z^{i}\right)}{q\left(z^{i}\right)}$ 被称为从 $q(z)$ 中抽取的第 $i$ 个样本的权重；
  • 将关于真实分布 $p(z)$ 求期望的问题，转化成了关于提议分布 $q(z)$ 求期望的问题，由于 $q(z)$ 容易采样，所以使期望可实现基于模拟的计算。

现在回归第一节的滤波问题设置，其关键在于：
-（1）求后验联合概率分布 $f\left(z_{0:t} | x_{1 :t}\right)$ 或后验边缘概率分布 $f\left(z_{t} | x_{1 :t}\right)$ ；
-（2）基于后验联合概率分布 $f\left(z_{t} | x_{1 :t}\right)$ 计算某些函数的后验均值 $I(f_t)$。当后验概率分布 $f\left(z_{t} | x_{1 :t}\right)$ 较为复杂无法采样时，我们可以采用重要性采样方法来获得近似的后验均值。

假设对于时刻 $t$，我们令 $w_{t}^{i}=\frac{p\left(z_{t}^{i} | x_{1 : t}\right)}{q\left(z_{t}^{i} | x_{1 : t}\right)}$，此时根据重要性采样原理，如果从提议分布 $q(z_{t}^{i} | x_{1 : t})$ 中抽取 $N$ 个样本来实现 $t$ 时刻后验均值的基于样本的计算。也就是说，我们需要计算：
$$
\begin{array}{l}
t=1 : w_{1}^{i}, {i=1,2, \ldots, N } \
t=2 : w_{2}^{i}, {i=1,2, \ldots, N}\
\ldots \
t = T: w_{T}^{(i)}, {i=1,2, \ldots, N }
\end{array}
$$

上式中每个时刻需要 $N$ 个样本（其中每一个都被称为 粒子 Partile），而每个样本的权重 $w_{t}^{i}$ 都需要计算后验概率 $p\left(z_{t}^{i} | x_{1 : t}\right)$，$p$ 很难求，因此如果能够像 式（4） 一样找到一个递推公式，将可以大大减少计算量。

下面的顺序重要性采样（ Sequential Importance Sampling, SIS），就是针对该问题而开发的。

3 顺序重要性采样（SIS）

顺序重要性采样的目的很明确，那就是找到一个 $w_{t-1}^{i} \rightarrow w_{t}^{i}$ 的递推关系。

为了避免积分运算，我们先不考虑后验边缘分布 $p\left(z_{t} | x_{1: t}\right)$ 的计算问题，而是先考虑后验联合分布 $p\left(z_{1 : t} | x_{1 : t}\right)$ 。因为在 $t$ 时刻已经知道了前面各时刻的状态后验值，所以权重正比于联合分布之比，即 $w_{t}^{i} \propto \frac{p(z_{1: t} | x_{1 :t})}{q(z_{1: t} | x_{1 :t})}$ ，其中：

$$
\begin{align*}
p(z_{1:t} | x_{1:t}) &= \frac{p\left(z_{1 : t}, x_{1: t}\right)}{\underbrace{p\left(x_{1 : t}\right)}{C}}\
&=\frac{1}{C} p\left(z{1 : t}, x_{1: t}\right)\
&=\frac{1}{C} p\left(x_{t} | z_{1 :t}, x_{1: t-1}\right) p\left(z_{1: t}, x_{1: t-1}\right) \
&=\frac{1}{C} p\left(x_{t} | z_{t}\right) p\left(z_{t} | z_{t-1}, x_{1: t-1}\right) p\left(z_{1 :t-1}, x_{1 :t-1}\right)\
&=\frac{1}{C} p\left(x_{t} | z_{t}\right) p\left(z_{t} | z_{t-1}\right) p\left(z_{1 :t-1} | x_{1: t-1}\right) \underbrace{p\left(x_{1: t-1}\right)}{D} \
&=\frac{D}{C} p\left(x{t} | z_{t}\right) p\left(z_{t} | z_{t-1}\right) p\left(z_{1: t-1} | x_{1: t-1}\right)
\end{align*} \tag{8}
$$

在 式(8) 中：

  • 因为在时刻 $t$ 时，之前的观测都已知，所以 $p(x_{1:t})=C$ 和 $p(x_{1:t-1})=D$ 都是常数；
  • 基于先前l独立性假设，有 $p(x_{t} | z_{1:t}, x_{1:t-1})=p(x_{t} | z_{t}), \quad p(z_{t} | z_{1:t-1}, x_{1:t-1})=p(z_{t} | z_{t-1})$

我们假定有：

$$
q\left(z_{1 : t} | x_{1 : t}\right)=q\left(z_{t} | z_{1 : t-1}, x_{1:t}\right) q\left(z_{1:t-1} | x_{1:t-1}\right) \tag{9}
$$

则可以得到如下有关权重的递归公式：

$$
w_{t}^{i} \propto \frac{p\left(z_{1 :t} | x_{1 :t}\right)}{q\left(z_{1 :t} | x_{1 :t}\right)}
\propto \frac{p\left(x_{t} | z_{t}\right) p\left(z_{t} | z_{t-1}\right) p\left(z_{1 :t-1} | x_{1: t-1}\right)}{q\left(z_{t} | z_{1 : t-1}, x_{1 : t}\right) q\left(z_{1: t-1} | x_{1: t-1}\right)}
=\frac{p\left(x_{t} | z_{t}\right) p\left(z_{t} | z_{t-1}\right)}{q\left(z_{t} | z_{1 : t-1}, x_{1 : t}\right)} w_{t-1}^{i} \tag{10}
$$

也就是说，当 $t=1$ 时，我们需要计算得到 $N$ 个权重值，当 $t \geq 2$ 时，我们就可以通过 式（10） 的递推式计算权重。

式(10) 还能够进一步简化为：

$$
w_{t}^{i} \propto \frac{p\left(x_{t} | z_{t}\right) p\left(z_{t} | z_{t-1}\right)}{\underbrace{q\left(z_{t} | z_{1 :t-1}, x_{1 :t}\right)}{q\left(z{t} | z_{t-1}, x_{1 :t}\right)}} w_{t-1}^{i}=\frac{p\left(x_{t} | z_{t}\right) p\left(z_{t} | z_{t-1}\right)}{q\left(z_{t} | z_{t-1}, x_{1: t}\right)} w_{t-1}^{i} \tag{11}
$$

对于此算法流程，可以用下面的流程表示：

fig02

上图中的算法流程其实会产生 权值退化 问题，即算法运行一定的时间之后， $w_{t}^{i}$ 会变得运来越不平均，其中某个权重会非常大，而其余权重趋近于零。例如，假设有 $100$ 个粒子，其中 $99$ 个粒子的权重都是 $0.001$，但是有一个粒子非常接近于 $1$。此时，我们需要通过重采样来解决这个问题。

4 重采样策略

重采样的核心思想其实是一个优胜劣汰的过程，也就是： 根据权重大小来增加或丢弃粒子数量。

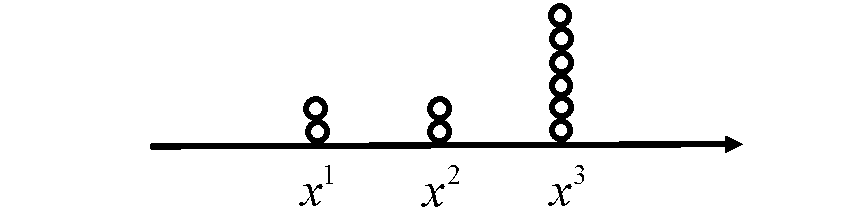
Fig03

例如，上图是 $3$ 个样本的初始权重情况，如果对其进行重采样，可以为权重低的样本少生成几个粒子，而权重高的样本多生成几个粒子，则可以得到如下图所示的结果：

fig03

重采样之后，粒子数量可能有所增加，但不会出现权重退化问题。换句话说，我们用粒子数量部分表达了原先的权重。

fig04

在算法实现上，可以采用基于 CDF 的直接采样方法（见上图），即从一个均匀分布 $u \sim \mathcal{U}(0,1)$ 中抽取随机数：

  • 当随机数为 $0.0-0.2$ 时，取样本 $x^{1}$ ；
  • 当随机数为 $0.2-0.4$ 时，取样本 $x^{2}$ ；
  • 当随机数为 $0.4-1.0$ 时，取样本 $x^{3}$ ；

5 基础粒子滤波

基础粒子滤波的主要思想就是：顺序重要性采样 + 重采样策略。但当采用重采样策略时，如果维度过高，则需要的粒子数目会呈指数级往上增加。为了解决这个问题，可以借用重要性采样的思路，即用更合适的提议分布 $q(z)$ 来制造权重。

重采样之后，所有的粒子权重都一样，这在上一节已经说明。 对于选择合适的提议分布，令 $q(z)$ 为状态转移矩阵，即 $q\left(z_{t} | z_{1:t-1}, x_{1:t}\right) = p\left(z_{t} | z_{t-1}\right)$，这时权重为：

$$
w_{i}^{j}=\frac{p\left(x_{i} | z_{t}^{i}\right) p\left(z_{t}^{i} | z_{t-1}^{i}\right)}{q\left(z_{t}^{i} | z_{t-1}^{i}, x_{1 :t}\right)} w_{t-1}^{i}=\frac{p\left(x_{t} | z_{t}^{i}\right) p\left(z_{t}^{i} | z_{t-1}^{i}\right)}{p\left(z_{t}^{i} | z_{t-1}^{i}\right)} w_{t-1}^{i}=p\left(x_{t} | z_{t}^{i}\right) w_{t-1}^{i} \tag{12}
$$

粒子从哪里来？

$$
z_{t}^{i} \sim p\left(z_{t}^{i} | z_{t-1}^{i}\right) \tag{13}
$$

权重如何确定？

$$
w_{t}^{i}=p\left(x_{t} | z_{t}^{i}\right) w_{t-1}^{i} \tag{14}
$$

上面整个系统就是 SIR Filter（采样重要性重采样滤波器），其实本质上，它是 顺序重要新采样（SIS） + 重采样（Resampling） + $q(z)$ ，这里的 $q(z)$ 取为 $p\left(z_{t} | z_{t-1}\right)$ 。

6 物理意义

将 $q(z)$ 选择为 $p\left(z_{t} | z_{t-1}\right)$ 有什么物理意义吗？

其直观感受是一个 生成和测试 的过程：

  • 首先，从 $z_{t-1}$ 按照 $z_{t} \sim p\left(z_{t} | z_{t-1}\right)$ 生成一个 $z_{t}$ ；
  • 然后基于观测数据，按照公式 $w_{t}^{i}=p\left(x_{t} | z_{t}^{i}\right) w_{t-1}^{i}$ 得到权重，这个公式的解释就是我观测得到的概率越大， $w_{t}^{i}$ 的权重就越高，也就越准确。

7 粒子滤波器预测的代码示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
%% SIR 粒子滤波的应用，算法流程参见博客 http://blog.csdn.net/heyijia0327/article/details/40899819
clear all
close all
clc
%% initialize the variables
x = 0.1; % initial actual 状态
x_N = 1; % 系统过程噪声的协方差  （由于是一维的，这里就是方差）
x_R = 1; % 测量的协方差
T = 75;  % 共进行 75 次
N = 100; % 粒子数，越大效果越好，计算量也越大

%initilize our initial, prior particle distribution as a gaussian around
%the true initial value

V = 2; %初始分布的方差
x_P = []; % 粒子
% 用一个高斯分布随机的产生初始的粒子
for i = 1:N
    x_P(i) = x + sqrt(V) * randn;
end

z_out = [x^2 / 20 + sqrt(x_R) * randn];  %实际测量值
x_out = [x];  % the actual output vector for measurement values.
x_est = [x];  % time by time output of the particle filters estimate
x_est_out = [x_est]; % the vector of particle filter estimates.

for t = 1:T
    x = 0.5*x + 25*x/(1 + x^2) + 8*cos(1.2*(t-1)) +  sqrt(x_N)*randn;
    z = x^2/20 + sqrt(x_R)*randn;
    for i = 1:N
        %从先验 p(x(k)|x(k-1))中采样
        x_P_update(i) = 0.5*x_P(i) + 25*x_P(i)/(1 + x_P(i)^2) + 8*cos(1.2*(t-1)) + sqrt(x_N)*randn;
        %计算采样粒子的值，为后面根据似然去计算权重做铺垫
        z_update(i) = x_P_update(i)^2/20;
        %对每个粒子计算其权重，这里假设量测噪声是高斯分布。所以 w = p(y|x)对应下面的计算公式
        P_w(i) = (1/sqrt(2*pi*x_R)) * exp(-(z - z_update(i))^2/(2*x_R));
    end
    % 归一化。
    P_w = P_w./sum(P_w);

    %% Resampling 这里没有用博客里之前说的 histc 函数，不过目的和效果是一样的
    for i = 1 : N
        x_P(i) = x_P_update(find(rand <= cumsum(P_w),1));   % 粒子权重大的将多得到后代
    end                                                     % find( ,1) 返回第一个符合前面条件的数的下标

    %状态估计，重采样以后，每个粒子的权重都变成了 1/N
    x_est = mean(x_P);

    % Save data in arrays for later plotting
    x_out = [x_out x];
    z_out = [z_out z];
    x_est_out = [x_est_out x_est];

end

t = 0:T;
figure(1);
clf
plot(t, x_out, '--b', t, x_est_out, '-*r','linewidth',2);
set(gca,'FontSize',12); set(gcf,'Color','White');
xlabel('time step'); ylabel('flight position');
legend('True flight position', 'Particle filter estimate');

代码运行后的图形为：

Fig05

9 粒子滤波与卡尔曼滤波的不同

卡尔曼滤波建立在随机过程的高斯假设基础之上，即状态噪音的概率密度函数（状态 probability density）和观测模型（observation model）是高斯分布。卡尔曼的数学基础是高斯模型的可计算性：两个高斯模型的运算，将得到一个新的高斯模型，并且新高斯模型的参数（均值和方差）可完全由原来两个高斯模型的参数计算得到。应用在具用马尔可夫性假设的时间序列中，就可以给出似然和后验分布的封闭表达形式，实现高效地迭代运算。同时，卡尔曼滤波是线性的，$t$ 时刻的状态可以由 $t-1$ 时刻的状态经过一个矩阵（状态转移概率矩阵）乘法得到。

在高斯和线性两个假设之下，我们既可以得到状态的取值（由线性假设得到），又可以得到状态取值的概率密度（由高斯假设得到），这时就可以通过迭代实现对系统每一时刻状态的预测；然后结合观测值，对预测结果进行纠正（更新），从而实现一个完整的递归预测系统。也就是说，卡尔曼滤波器就是一个信息融合器，把不准确的预测结果和不准确的测量结果融合在一起，得到一个估计结果。

以上过程可由线性随机微分方程（Linear Stochastic Difference equation）来描述：

$$
X(t) = F X(t-1) + B U(t) + W(t)
$$

再加上系统的测量值：

$$
Z(t)=H X(t)+V(t)
$$

上面两个式子中，$X(k)$ 是 $k$ 时刻的系统状态，$U(k)$ 是 $k$ 时刻对系统的控制量。$F$ 是状态转移模型和 $B$ 是控制模型的系统参数，对于状态向量维度高于一的系统，他们为矩阵。$Z(k)$ 是 $k$ 时刻的测量值，$H$ 是测量系统的参数，对于多测量系统，$H$ 为矩阵。$W(k)$ 和 $V(k)$ 分别表示真实过程和测量中的噪声，被假设成高斯白噪声，方差分别是为 $Q$ 和 $R$。

卡尔曼滤波中的高斯和线性假设有时并不能满足实际情况，因为高斯模型是单峰的。比如当一个运动目标被遮挡后，我们不知道它将在遮挡物的后面做什么运动，是继续前进，或是停下，还是转向或后退。这种情况下，卡尔曼滤波只能给出一个位置的预测，至多加大这个预测的不确定性（即增大协方差矩阵或方差）。这种情况下，预测位置的不确定噪音事实上已不是高斯模型，它将具有多个峰值。而这种噪音通常无法解析表达。

粒子滤波就是针对该应用场景产生的。

粒子滤波是一种蒙特卡洛方法，简言之就是用样本点来表达概率密度函数。样本点密集的地方，概率密度就大。在时间序列中，就对是序贯蒙特卡洛。所以粒子滤波在机器视觉中的应用，也被称为条件密度传播，它和 Bootstrap Filter 一样，同属于序贯蒙特卡洛范畴。

具体实施上，粒子滤波对状态的更新不再采用卡尔曼滤波中的高斯模型更新，而是基于采样方法，所使用的样本被形象地称为粒子。简单说，就是对 $t-1$ 时刻的所有粒子，根据其概率重新采样，高概率粒子将得到高采样率，而低概率粒子对应低采样率。这样，高概率粒子可能被多次采样，而低概率粒子可能就被放弃了。如此得到 $t$ 时刻的粒子。然后，将 $t$ 时刻每一个粒子所对应的测量值结合起来，为 $t$ 时刻的粒子重新赋以新概率，以用于 $t+1$ 时刻新粒子的生成。

所以卡尔曼滤波和粒子滤波的相同点是：两者均为递推序列，并且都分为三个步骤：预测，测量和更新（或校正）。

但两者在步骤的实现上不同：

  • 在预测阶段，卡尔曼滤波利用高斯模型进行预测，而粒子滤波用基于样本模拟的方法对上一步的粒子做重采样。
  • 在测量阶段，卡尔曼滤波将得到唯一的测量，而粒子滤波将为每一个粒子得到一份测量。
  • 在更新阶段，卡尔曼滤波将由状态计算得到的观测值和实际观测值比较结合，得到更新后的系统参数。而粒子滤波通过比较每个粒子所对应的观测值和模型预测值之间的差别，更新每个粒子的概率。

由此可知，卡尔曼滤波和粒子滤波之间最大的不同就在于：对状态概率密度函数的表达方式上。卡尔曼滤波采用高斯模型，而粒子滤波利用蒙特卡洛样本来近似。

参考文献

  1. 白板推导粒子滤波器

  2. Heyijia 写的粒子滤波器（经过其他人合并）