可扩展结构化高斯过程的核插值 (KISS-GP)

【摘 要】引入了一种新的结构化核插值 (SKI) 框架，它泛化并统一了可扩展高斯过程 (GP) 的归纳点方法。 SKI 方法通过核插值生成核近似值以进行快速计算。 SKI 框架阐明了归纳点方法的质量与归纳（也称为插值）点数量、插值策略和协方差核之间的关系。 SKI 还允许通过选择不同的核插值策略来创建新的可扩展核。使用 SKI 框架，通过局部的三次核插值，我们引入了 KISS-GP，该方法：1) 比归纳点替代方案更具可扩展性；2) 自然地使 Kronecker 和 Toeplitz 代数，并在可扩展性方面获得实质性收益，且无需任何网格数据支撑；3)可用于快速和富有表现力的核学习。 KISS-GP 花费 $\mathcal{O}(n)$ 的时间和存储复杂度来进行高斯过程推断。

【原 文】 Wilson, A. and Nickisch, H. (2015) ‘Kernel interpolation for scalable structured gaussian processes (KISS-GP)’, in F. Bach and D. Blei (eds) Proceedings of the 32nd international conference on machine learning. Lille, France: PMLR (Proceedings of machine learning research), pp. 1775–1784. Available at: https://proceedings.mlr.press/v37/wilson15.html.

【难 度】 ⭐⭐⭐⭐⭐

1 引言

高斯过程 (GP) 正是我们想要应用于大数据的模型类型：灵活的函数逼近器，能够使用大型数据集中的信息通过可解释和表达的协方差核来学习复杂的结构。然而，它们的 $\mathcal{O}(n^3)$ 计算复杂度和 $\mathcal{O}(n^2)$ 存储复杂度要求将高斯过程限制为除最小数据集以外的所有数据集，最多包含几千个训练点。迄今为止，他们令人印象深刻的实证成功只是对可能发生的事情的一瞥，只要我们能够克服这些计算限制（Rasmussen，1996 年 ^[15]）。 **（1）稀疏方法** 归纳点方法（Snelson & Ghahramani, 2006 ^[22]; Hensman 等，2013 ^[4]; Quinonero Candela & Rasmussen, 2005 ^[11]; Silverman, 1985 ^[21]）已被引入以将高斯过程扩展到更大的数据量。对于 $m$ 个归纳点和 $n$ 个训练数据点，这些方法需要 $\mathcal{O}(m^2n + m^3)$ 计算复杂度和 $\mathcal{O}(mn + m^2)$ 存储复杂度。归纳法因其通用的 “开箱即用” 适用性而广受欢迎，不需要数据中的任何特殊结构。不过，这些方法的局限性在于：只有归纳输入的数量 $m \ll n$ 时，效率才能得到体现，但这可能会导致预测性能下降，并且无法执行可表达的核学习（Wilson 等，2014 年 ^[28]）。 **（2）结构利用方法** 与归纳点方法相比，结构利用方法具有正交的优势，例如 Kronecker (Saatchi, 2011 ^[18]) 或 Toeplitz (Cunningham 等，2008 ^[3]) 方法。这些方法利用协方差核中的现有结构进行高度准确和可扩展的推断，并可用于大型数据集上的灵活核学习（Wilson 等，2014 年 ^[28]）。然而，Kronecker 方法要求输入（预测变量）位于多维网格（笛卡尔积网格）上，这使得它们不适用于大多数数据集。尽管 Wilson 等 (2014) 扩展出了只需要部分网格结构的 Kronecker 方法，但这些扩展并不适用于任意位置的输入。同样，Luo & Duraiswami (2013 ^[9]) 中基于 Kronecker 的方法通常不适用于任意位置的输入，并且涉及代价高昂的 rank-1 更新。 Toeplitz 方法同样具有局限性，它要求数据位于规则间隔的一维网格上。 **（3）本文贡献** 根据上述分析，很容易想到将上述两者结合的方法，即在网格上放置归纳点，然后利用 Kronecker 或 Toeplitz 结构进一步提高可扩展性。不过，这种朴素的方法仅有助于减少归纳点方法中的 $m^3$ 的复杂性项，而不是更关键的 $m^2n$ 项，此项来自于训练输入和归纳输入之间的交叉协方差矩阵。 在本文中，我们介绍了一种用于归纳点方法的新框架，称为结构化核插值 (SKI)。该框架提高了快速核方法的可扩展性和准确性，并自然地结合了归纳点和结构利用方法的优点。尤其是： - 我们展示了当前的归纳点方法如何在真正的底层核上执行全局高斯过程插值，以创建用于可扩展计算的近似核，作为更通用的结构化核插值方法系列的一部分。 - SKI 框架有助于理解归纳点方法的准确性和效率如何受归纳点数量 $m$、核选择和插值方法选择的影响。此外，通过为 SKI 选择不同的插值策略，我们可以创建新的归纳点方法。 - 我们引入了一种新的归纳点方法 KISS-GP，它使用局部三次和反距离加权插值策略来创建归纳点和训练点之间的交叉协方差矩阵的稀疏近似。这种方法自然可以与 Kronecker 和 Toeplitz 代数相结合，以允许 $m \gg n$ 个归纳点，并进一步提高可扩展性。当利用 Toeplitz 结构时，KISS-GP 需要 $\mathcal{O}(n + m \log m)$ 计算复杂度和 $\mathcal{O}(n + m)$ 存储复杂度。当利用 Kronecker 结构时，对于 $P > 1$ 维输入，KISS-GP 需要 $\mathcal{O}(n + P m^{1+1/P})$ 计算复杂度和 $\mathcal{O}(n + P m^{2/P})$ 存储复杂度。 - KISS-GP 可以看作解除了 Toeplitz 和 Kronecker 方法中的网格限制，因此可以使用任意位置的输入。 - 我们展示了 KISS-GP 有效使用大量归纳点使能了可表达的核学习，并且比 FITC（Snelson 和 Ghahramani，2006 年 ^[22]）等流行方法的准确性和效率高出几个数量级。 - 我们已将代码实施为 GPML 工具箱的扩展（Rasmussen & Nickisch，2010 ^[17]）。有关更新和演示，请参阅 http://www.cs.cmu.edu/~andrewgw/pattern - 总的来说，SKI 框架的简单性和通用性使得设计新的可扩展高斯过程变得容易。 本文结构： - 在 `第 2 节` 介绍高斯过程的背景（第 2.1 节）、归纳点方法（第 2.2 节）和结构利用方法（第 2.3 节）。 - 在 `第 3 节` 介绍结构化核插值 (SKI) 框架和 KISS-GP 方法。 - 在 `第 4 节` 对核矩阵重建、核学习和自然声音建模进行实验。 - 在 `第 5 节` 总结。 ## 2 背景 ### 2.1 高斯过程 我们简要回顾了高斯过程 (Rasmussen & Williams, 2006 ^[14])，以及推断和学习的相关计算要求。在整个过程中，我们假设有一个包含 $n$ 个输入（预测变量）向量$X = \{\mathbf{x}_1, \ldots ,\mathbf{x}_n \}$ 的数据集 $\mathcal{D}$ , 每个输入的维度均为 $D$, 对应的目标是 $\mathbf{y} = (y(\mathbf{x}_1), \ldots , y(\mathbf{x}_n))^{\top}$ 的 $n \times 1$ 向量。 高斯过程 (GP) 是随机变量的集合，其中任何有限数量的随机变量都服从联合高斯分布。使用高斯过程，我们可以定义函数 $f(\mathbf{x}) \sim \mathcal{GP}(μ, k)$ 的分布，这意味着函数值 $\mathbf{f}$ 的任何集合都具有联合高斯分布： $$ \mathbf{f} = f(X) = [f (\mathbf{x}_1)，\ldots , f(\mathbf{x}_n)]^{\top} \sim \mathcal{N}(\boldsymbol{μ}, K) \tag{1} $$ $n \times 1$ 均值向量 $\boldsymbol{\mu}_i = μ(\mathbf{x}_i)$ 和 $n \times n$ 协方差矩阵 $K_{ij} = k(\mathbf{x}_i, \mathbf{x}_j)$，由用户指定的均值函数 $μ(\mathbf{x}) = \mathbb{E}[f(\mathbf{x})]$ 和协方差定义高斯过程的核 $k(\mathbf{x,x'}) = \operatorname{cov}(f(\mathbf{x}), f(\mathbf{x'}))$。高斯过程的平滑性和泛化特性由协方差核及其超参数 $θ$ 编码。例如，流行的 RBF 协方差函数具有长度尺度超参数 $\ell$，其形式为 $$ k_{RBF}(\mathbf{x,x'}) = \exp(−0.5 \| \mathbf{x − x'}\|^2/\ell^2) \tag{2} $$ 如果目标 $y(\mathbf{x})$ 由具有加性高斯噪声的高斯过程建模，例如 $y(\mathbf{x})|f(\mathbf{x}) \sim \mathcal{N}(y(\mathbf{x}); f(\mathbf{x}), σ^2)$，则 $n_*$ 处的预测分布测试点 $X_*$ 由 $$ \begin{align*} &\mathbf{f}_*|X_*,X, \mathbf{y}, θ, σ^2 \sim \mathcal{N}(\bar{\mathbf{x}}_*, \operatorname{cov}(\mathbf{f}_*)) \\ &\bar{\mathbf{f}}_*= \boldsymbol{μ}_{X_*} + K_{X_*,X} [K_{X,X} + \sigma^2 I]^{-1} \mathbf{y} \\ &\operatorname{cov}(\mathbf{f}_*) = K_{X_*,X_*} − K_{X_*,X} [K_{X,X} + \sigma^2 I]^{-1}K_{X,X_*} \end{align*} \tag{3} $$ 例如，$K_{X_*,X}$ 表示在 $X_*$ 和 $X$ 处评估的高斯过程之间的 $n_* \times n$ 协方差矩阵。$\boldsymbol{\mu}_{X_*}$ 是 $n_* \times 1$ 均值向量，$K_{X_*,X}$ 是评估的 $n \times n$ 协方差矩阵在训练输入 $X$ 处。所有协方差矩阵都隐含地依赖于核超参数 $θ$。 我们可以通过分析将高斯过程 $f(\mathbf{x})$ 边缘化以获得数据的边缘似然，仅以协方差超参数 $θ$ 为条件： $$ \log p(\mathbf{y}| \boldsymbol{\theta}) \propto −[ \overbrace{\mathbf{y}^{\top} (K_θ + \sigma^2 I )^{−1} \mathbf{y}}^{\text{model fit}} + \overbrace{\log |K_θ + \sigma^2 I|}^{\text{complexity penalty}}] \tag{4} $$ `式 (4)` 分离成模型拟合项和复杂性惩罚项 (Rasmussen & Ghahramani, 2001 ^[16])，并且可以优化以学习核超参数 $θ$，或用于通过 MCMC 整合出 $θ$ (Rasmussen, 1996 ^[15])。 使用高斯过程的计算瓶颈是求解线性系统 $(K + \sigma^2 I)^{-1}\mathbf{y}$（用于核学习和预测）和 $\log |K + \sigma^2 I|$ （用于核学习）。为此，标准程序是计算 $K$ 的 Cholesky 分解，需要 $\mathcal{O}(n^3)$ 操作和 $\mathcal{O}(n^2)$ 存储复杂度。之后，单个测试点 $\mathbf{x}_*$ 的预测均值和方差分别花费 $\mathcal{O}(n)$ 和 $\mathcal{O}(n^2)$。 ### 2.2 归纳点法 许多流行的扩展高斯过程推断的方法都属于归纳点方法家族 (Quinonero Candela & Rasmussen, 2005 ^[11])。这些方法都可以被视为用近似 $\tilde{k}(\mathbf{x,z})$ 代替精确核 $k(\mathbf{x,z})$ 以进行快速计算。 例如，回归子集方法 (SoR) (Silverman, 1985 ^[21]) 和完全独立训练条件 (FITC)方法 (Snelson & Ghahramani, 2006 ^[22]) 分别使用如下近似核函数（采用一组 $m$ 个归纳点 $U = [\mathbf{u}_i]_{i=1 \ldots m}$ ）： $$ \tilde{k}_{SoR}(\mathbf{x,z}) = K_{\mathbf{x},U} K^{-1}_{U,U} K_{U,\mathbf{z}} \tag{5} $$ $$ \tilde{k}_{FITC}(\mathbf{x,z}) =\tilde{k}_{SoR} + \delta_{\mathbf{xz}} ( k(\mathbf{x,z}) −\tilde{k}_{SoR} ) \tag{6} $$ 其中，$K_{\mathbf{x},U}$ 、$K^{-1}_{U,U}$ 和 $K_{U,\mathbf{z}}$ 是从精确核 $k(\mathbf{x,z})$ 生成的 $1 \times n$、$m \times m$ 和 $n \times 1$ 协方差矩阵。 SoR 方法产生阶数最多为 $m$ 的 $n \times n$ 协方差矩阵 $K_{SoR}$，对应于一个退化（有限基）高斯过程，而 FITC 方法由于其在对角线上的校正而产生一个满秩的协方差矩阵 $K_{FITC}$。因此，FITC 是一个更可靠的近似，在实践中更受欢迎。 请注意：精确的用户核 $k(\mathbf{x,z})$ 通常被 $θ$ 参数化，因此归纳点方法中的核学习过程，会采用 SoR 或 FITC 的边缘似然关于超参数 $θ$ 的最优化方法。 上述近似核在高斯过程推断和学习中产生 $\mathcal{O}(m^2n+m^3)$ 的计算复杂度和 $\mathcal{O}(mn + m^2)$ 存储复杂度 (Quinonero Candela & Rasmussen, 2005 ^[11])，在高斯过程均值预测和方差预测时，对于每个测试用例分别产生 $\mathcal{O}(m)$ 和 $\mathcal{O}(m^2)$ 的计算复杂度。 此类方法为了达到真实的效率提升，必须选择 $m \ll n$，但这会导致预测性能的严重恶化，并且无法执行可表达的核学习（Wilson 等，2014 年 ^[28]）。 ### 2.3 利用结构的快速推断 Kronecker 和 Toeplitz 方法利用高斯过程协方差矩阵 $K$ 的结构来提升推断和学习阶段的可扩展性。Saatchi (2011 ^[18]) 的 `第 5 章` 提供了对 Kronecker 方法的完整介绍。 Wilson (2014 ^[26]) 的第 2 章更详细地讨论了 Toeplitz 方法。 #### 2.3.1 Kronecker 方法 **（1）基本原理** 如果我们在笛卡尔的网格上有多维输入 $\mathbf{x} \in \mathcal{X}_1 \times \ldots \times \mathcal{X}_P$ ，以及跨网格维度的乘积核 $k(\mathbf{x}_i, \mathbf{x}_j) = \prod^{P}_{p=1} k(\mathbf{x}^{(p)}_i,\mathbf{x}^{(p)}_j)$，那么 $m \times m$ 的协方差矩阵 $K$ 可以被表示为 Kronecker 积的形式： $K = K_1 \otimes \ldots \otimes K_P$ （网格点的数量 $m = \prod^{P}_{i=1} n_p$，是每个网格维度点数 $n_p$ 的乘积 ）。如果满足上述条件，则我们可以分别计算各维度上 $K_1,\ldots,K_P$ 的特征分解，而后通过 Kronecker 积高效地计算协方差矩阵 $K = QVQ^{\top}$ 的特征分解。人们也可以类似地利用 Kronecker 结构来获得快速矩阵-向量积（Wilson 等，2014 年 ^[28]）。 通过 Kronecker 快速矩阵特征分解和矩阵-向量积，我们能够有效地计算推断和预测所需的 $(K + \sigma^2 I)^{-1}\mathbf{y}$ 和 $\log |K +\sigma^2 I|$。具体来说，如果协方差矩阵 $K$ 具有特征分解为 $QV Q^{\top}$，则有： - **矩阵向量积**：$(K + \sigma^2 I)^{-1}\mathbf{y} = (QV Q^{\top} + \sigma^2 I)^{-1} \mathbf{y} = Q(V + \sigma^2 I)^{−1} Q^{\top} \mathbf{y}$ - **行列式**： $\log |K + \sigma^2 I| = \sum_i \log(V_{ii} + σ^2)$。 由于矩阵 $V$ 是特征值构成的对角矩阵，因此上述计算较容易实现。$Q$ 是特征向量构成的正交矩阵，也可分解为 Kronecker 积，能够实现快速的矩阵-向量积。 总体而言，此方法的推断和学习成本为 $\mathcal{O}(P m^{1+ \frac{1}{P}} )$ 的计算复杂度和 $\mathcal{O}(P m^{\frac{2}{P}})$ 的存储复杂度（Saatchi，2011 ^[18]；Wilson 等，2014 ^[28]）。 **（2）$(K + \sigma^2 I)^{-1}\mathbf{y}$ 的计算** 核学习和高斯过程预测都需要计算 $(K + \sigma^2 I)^{-1}\mathbf{y}$，而 Kronecker 协方差矩阵显然具有更好的计算效率。 但在具体使用时，虽然构造乘积核较为容易，并且很多流行核（例如 RBF 核）都已经具有乘积结构，但需要多维输入网格可能是一个过于严格的要求。因此，Wilson 等 (2014 ^[28]) 将 Kronecker 方法扩展到仅有部分网格结构的数据集，例如，具有随机缺失像素的图像。他们使用虚拟观测来完成部分网格，并且使用对角的噪声协方差矩阵 $A$ 来消除虚拟观测的影响： $$ K^{(n)}+\sigma^2 I \rightarrow K^{(m)} + A $$ 其中： - $K^{(n)}$ 是原始数据集（ $n$ 个数据点）形成的 $n \times n$ 协方差矩阵； - $K^{(m)}$ 是虚拟输入形成的协方差矩阵。 虽然我们无法高效地对 $K^{(m)} + A$ 进行特征分解，但由于 $K^{(m)}$ 是 Kronecker 矩阵并且 $A$ 是对角矩阵，所以我们可以高效地计算矩阵-向量积 $(K^{(m)} + A) \mathbf{y}^{(m)}$。因此，我们可以将 $(K^{(m)} + A)^{-1}\mathbf{y}^{(m)} = (K^{(n)} + \sigma^2 I)^{-1}\mathbf{y}^{(n)}$ 计算至机器精度，并且进一步地结合仅涉及矩阵-向量积的迭代方法（例如线性共轭梯度）执行高效推断。 **（3） $|K + \sigma^2 I|$ 的计算** 为了计算用于核学习的边缘似然，我们还必须计算对数行列式 $\log |K^{(n)}+\sigma^2 I|$，其中 $K^{(n)}$ 是由具有 $n$ 个数据点的原始数据集形成的 $n \times n$ 协方差矩阵。 Wilson 等 (2014 ^[28]) 提出，使用 $K^{(m)}$ 的 $n$ 个最大特征值 $\lambda_i$ 来近似 $K^{(n)}$ 的特征值 $\lambda^{(n)}_i$。其中，$K^{(m)}$ 为完整网格形成的 Kronecker 协方差矩阵，能够进行高效的特征分解。 特别是， $$ \log |K^{(n)} + \sigma^2 I| = \sum^{n}_{i=1} \log(\lambda^{(n)}_i + σ^2) \approx \sum^{n}_{i=1} \log( \frac{n}{m} \lambda_i + σ^2) $$ Baker (1977 ^[1]) 的 `定理 3.4` 证明：只要训练输入是完整网格，这种特征值近似就是渐近一致的（例如，收敛于大 $n$ 的极限）。 Williams & Shawe-Taylor (2003 ^[24]) 还表明，可以使用 PCA 方法来近似真实特征值。 值得注意的是：在边缘似然中，只有对数行列式项（见 `式（4）` 的复杂性惩罚项）会被近似。Wilson 等 (2014 ^[28]) 表明，在实际工作中，这种近似对于快速和富有表现力的核学习非常有效。 然而，Wilson 等 (2014 ^[28]) 的扩展仅在输入空间具有部分网格结构时才有效，不适用于通用设置。 #### 2.3.2 Toeplitz 方法 Toeplitz 和 Kronecker 方法是互补的。 当输入 $\mathbf{x}$ 在规则间隔的一维网格上时，如果协方差矩阵 $K$ 是从平稳协方差核 $k(\mathbf{x,x'}) = k(\mathbf{x − x'})$ 生成的，则 $K$ 是一个 Toeplitz 协方差矩阵。Toeplitz 矩阵的性质是：沿着对角方向保持不变，即$K_{i,j} = K_{i+1,j+1} = k(\mathbf{x}_i − \mathbf{x}_j)$ 。

摘自 Wilson 的博士论文：

可以将上述 $N × N$ 的Toeplitz 矩阵 $K$，嵌入到 $2(N + 1) × 2(N + 1)$ 的循环矩阵 $C$ 中（每一列都从下一列移动一个位置）：

请注意：$C$ 中的所有信息都包含在其第一列 $c$ 中，并且该元素 $C_{t,j} = c_{(j−t) mod N}$。

可以将 Toeplitz 矩阵嵌入到循环矩阵中，以使用快速傅立叶变换执行矩阵-向量积（例如，Wilson，2014 ^[26]）。 对于 $m$ 个网格数据点，可以使用线性共轭梯度在 $\mathcal{O}(m \log m)$ 的计算复杂度和 $\mathcal{O}(m)$ 的空间复杂度中得到 $(K + \sigma^2 I)^{-1}\mathbf{y}$ 的解。在 Turner (2010 ^[23]) 和 Cunningham 等 (2008 ^[3]) 中，包含应用于高斯过程的 Toeplitz 方法示例。 ## 3 结构化核插值 我们希望降低高斯过程相关的 $\mathcal{O}(n^3)$ 计算复杂度和 $\mathcal{O}(n^2)$ 存储复杂度，同时保留模型的灵活性和通用性。 `第 2.2 节` 的归纳点方法很受欢迎，因为它们可以 “开箱即用” ，不需要数据含有特殊结构。然而，由于归纳点数量较少，此类方法的预测准确性会大幅下降，并且无法执行可表达的核学习（Wilson 等，2014 年 ^[28]），而这往往在大型数据集上是最有价值的。 `第 2.3 节` 的结构利用方法也是引人注目的，因为它们能够在可扩展性方面提供了令人难以置信的收益，同时保证预测准确性基本上没有损失。但是结构利用方法对输入网格的要求，使得其难以应用于大多数问题。 查看 `式(5)` 和 `式(6)`，其实在 SoR 或 FITC 方法中，可以尝试将归纳点 $U$ 的位置放置在一个网格上，然后利用 Kronecker 或 Toeplitz 代数有效地求解涉及 $K^{−1}_{U,U}$ 的线性系统 。这种朴素的方法可以降低与 $K^{-1}_{U,U}$ 相关的 $\mathcal{O}(m^3)$ 计算复杂度，以及与 $K_{X,U}$ 相关的 $\mathcal{O}(m^2n)$ 计算复杂度。 **（1）SKI 基本原理** 我们观察到，可以通过在 $m × m$ 协方差矩阵 $K_{U,U}$ 基础上，通过插值来近似在训练输入和归纳输入 $X$ 和 $U$ 处计算的交叉-协方差矩阵 $K_{X,U}$ （ 大小为 $n × m$ ）。例如，如果对于输入点 $\mathbf{x}_i$ 和归纳点 $\mathbf{u}_j$，为了计算其交叉协方差 $k(\mathbf{x}_i, \mathbf{u}_j)$，我们可以： - 先找到与 $\mathbf{x}_i$ 最接近的两个归纳点 $\mathbf{u}_a$ 和 $\mathbf{u}_b$ ： $\mathbf{u}_a \leq \mathbf{x}_i \leq \mathbf{u}_b$（为便于理解，先假设 $D = 1$ ，并且 Toeplitz 协方差矩阵 $K_{U,U}$ 来自于规则网格 $U$ ）。 - 然后计算 $\tilde{k}(\mathbf{x}_i, \mathbf{u}_j) = w_i k(\mathbf{u}_a, \mathbf{u}_j) + (1 − w_i) k(\mathbf{u}_b, \mathbf{u}_j)$，其中线性插值权重 $w_i$ 和 $(1 − w_i)$ 表示与 $\mathbf{x}_i$ 的相对距离指向 $\mathbf{u}_a$ 和 $\mathbf{u}_b$。更通用的，我们形式化为： $$ K_{X,U} \approx W K_{U,U} \tag{7} $$ 其中 $W$ 是一个 $n \times m$ 的插值权重矩阵，它可以非常稀疏。对于局部线性插值，$W$ 每行仅包含 $c = 2$ 个非零元素（ 即插值权重）， 其总和为 $1$。为了更准确，我们可以在等距网格上使用局部三次插值 (Keys, 1981 ^[5])，在这种情况下 $W$ 每行有 $c = 4$ 个非零元素。对于更为通用的、没有规则间距的网格 $U$，我们可以使用反距离加权方法（Shepard，1968 ^[20]），其中 $W$ 的每行有 $c = 2$ 个非零权重。 如果将 `式 (7)` 的结果以 $\tilde{K}_{XU}$ 代入 $K_{X,X}$ 的 SoR 近似，则有本文提出的插值协方差形式： $$ K_{X_*,X} \stackrel{SoR} \approx K_{X,U} K^{-1}_{U,U} K_{U,X} \stackrel{Eq. (7)} \approx W K_{U,U} K^{-1}_{U,U} K_{U,U} W^{\top} = W K_{U,U} W^{\top} = K_{SKI} \tag{8} $$ 我们将这种用于近似高斯过程核函数的通用方法命名为 **构化核插值 (structured kernel interpolation，SKI)**。 尽管 `式（8）` 使用了 SoR 近似作为示例，但 SKI 方法基本上可以应用于任何归纳点方法，例如 FITC。 **（2）SKI 的矩阵向量积计算** 基于 SKI 近似，我们可以计算快速矩阵-向量积 $K_{SKI} \mathbf{y}$，各种近似下的复杂度分析如下： - 如果不利用 $K_{U,U}$ 中的 Toeplitz 或 Kronecker 结构，则对于稀疏 $W$，与 $K_{SKI}$ 的矩阵-向量积需要 $\mathcal{O}(n + m^2)$ 计算复杂度和 $\mathcal{O}(n + m^2)$ 存储复杂度。 - 如果利用 Kronecker 结构，我们只需要 $\mathcal{O}(P m^{1+1/P})$ 计算复杂度和 $\mathcal{O}(n + P m^{2/P})$ 存储复杂度。 - 如果利用 Toeplitz 结构，我们需要 $\mathcal{O}(n + m \log m)$ 计算复杂度和 $\mathcal{O}(n + m)$ 存储复杂度。 **（3）结合线性共轭梯度的推断** **$K^{-1}_{SKI} \mathbf{y}$ 的计算**： 可以通过线性共轭梯度来进一步对 $K^{-1}_{SKI} \mathbf{y}$ 进行推断，该过程只需要计算上述矩阵-向量积，并且只需要 $j \ll n$ 次少量迭代即可收敛到机器精度范围。 **$\log |K_{SKI}|$ 的计算**：要计算（边缘似然所需的）行列式 $\log |K_{SKI}|$，对于核学习中使用的边缘似然评估，可以遵循 Wilson 等 (2014) 的近似值。如`第 2.3.1 节`所述，其中 $K_{U,U}$ 扮演 $K^{(m)}$ 的角色，并且不需要虚拟观测。或者，我们可以在标准的特征值求解器中使用 $K_{SKI}$ 来精确地计算对数行列式。我们还可以生成最大和最小特征值的近似。这种方法在 Wilson 等(2014 ^[28])中原来是无法做到的（因为不能使用 $K^{(n)}$ 进行快速矩阵-向量积计算）。并且总体来说，学习的计算复杂度并不比推断（预测）高。 即使我们不在 $K_{U,U}$ 中利用潜在的 Kronecker 或 Toeplitz 结构，SKI 中的推断和学习也会比传统归纳点方法效率更高。无论如果，与固定的数据输入 $X$ 不同，我们可以自由选择归纳点 $U$ 的位置，因此可以轻松地在 $K_{U,U}$ 中创建（例如 Toeplitz 或 Kronecker）结构，而这在 $K_{X,X}$ 中可能是不存在的。在 SKI 中，我们可以唯一地利用这种结构来显著提高效率，并使用前所未有数量的归纳点，同时提升 $X$ 上的任何网格要求。 虽然这里我们在 `式 (8)` 中使用了 SoR 近似。 我们可以简单地应用 FITC 对角线校正（`第 2.2 节`），或与其他方法结合使用。然而，在 SKI 框架内，FITC 的对角线校正没有那么大的价值：因为当使用 $m > n$ 时，$K_{SKI}$ 可以很容易地变为满秩并且仍然拥有计算优势。重要的是，在传统归纳近似方法中，永远不会设置 $m > n$，因为这会比精确高斯过程推断的效率更低。 **（4）SKI 作为统一框架** 最后，我们可以将过去所有归纳方法理解为结构化核插值 (SKI) 框架的一部分。无噪声、零均值高斯过程($σ = 0, μ(\mathbf{x}) \equiv 0$) 的预测均值 $\bar{f}_*$ 可以从两个方面来解释其线性预测关系： - 一方面，可以被视为观测值 $\mathbf{y}$ 的线性加权和，其权重为 $\mathbf{w}_X (\mathbf{x}_*) = K^{-1}_{X,X} K_{X,\mathbf{x}_*}$； - 另一方面，可以被视为 $\boldsymbol{α} = K^{-1}_{X,X} \mathbf{y}$ 的线性加权和，其权重为训练-测试交叉协方差 $K_{X,\mathbf{x}_*}$: $$ \bar{f}_* = \mathbf{y}^{\top} \mathbf{w}_X (\mathbf{x}_*) = \boldsymbol{\alpha}^{\top} K_{X,\mathbf{x}_*} \tag{9} $$ 如果我们要对核本身执行无噪声零均值高斯过程回归，则此时有数据集 $\mathcal{D} = (\mathbf{u}_i, k(\mathbf{u}_i, \mathbf{x}))^{m}_{i=1}$，我们就恢复 `式 (5)` 的 SoR 核 $\tilde{k}_{SoR}(\mathbf{x,z})$ 作为高斯过程在测试点 $\mathbf{x}_* = \mathbf{z}$ 的预测均值。 这一发现为归纳点方法提供了一个新的统一视角： **所有传统的归纳点方法，如 SoR 和 FITC，都可以被视为在真实核上执行了零均值高斯过程插值**。事实上，我们可以写插值点而不是归纳点。在所有常规情况下，$n \times m$ 插值权重矩阵 $W$ 将具有所有非零项，这会产生巨大的计算开销。此外，与传统方法相对应的零均值全局高斯过程核插值除了会降低计算效率外，还会损害准确性：低估大多数核给出的通常简单、平滑、严格正指数形式的协方差。 SKI 对归纳点方法的解释提供了一种创建新归纳点方法的机制。通过用局部反距离加权或三次插值代替全局高斯过程核插值（ SKI 框架的一部分），我们可以使 $W$ 变得非常稀疏。我们在补充材料的 `图 1` 中说明了局部和全局核插值之间的差异。除了 $W$ 中的稀疏性之外，这种插值视角天然使我们能够利用核中的（例如，Toeplitz 或 Kronecker）结构来进一步提高可扩展性，而不要求输入 $X$ 必须位于网格上。 这种将归纳点方法作为核插值的统一视角，也阐明了这些方法何时表现最佳。在所有这些方法中，关键假设是底层真实核 $k$ 的平滑度。我们可以预期插值方法在流行核上运行良好（例如 RBF 核），它是一个简单的指数函数。更具表现力的核，例如谱混合核 (Wilson & Adams, 2013)，由于其准周期性，将需要更多的归纳（插值）点才能获得良好近似。 我们的观点是：从全局高斯过程核插值到局部立方核插值的潜在精度损失，可以通过大大增加归纳点数量来弥补。此外，我们相信流行核函数的结构化有利于局部插值与全局插值，从而产生强近似并大大提高可扩展性。 当 SKI 与 **高斯过程**、 **稀疏（例如三次）插值** 和 **Kronecker 或 Toeplitz 代数** 相结合时，我们将其命名为 **KISS-GP**。 ## 4 实验 我们评估 SKI 的核矩阵近似（第 4.1 节）、核学习（第 4.2 节）和自然声音建模（第 4.3 节）。 我们特别与 FITC (Snelson & Ghahramani, 2006) 进行比较，因为 1) FITC 是最流行的归纳点方法，2) FITC 已被证明具有优越的预测性能和与其他归纳方法相似的效率，并且通常被推荐 (Naish Guzman & Holden, 2007 ^[10]; Quinonero Candela 等，2007 ^[12])，以及 3) FITC 广为人知，因此 FITC 比较有助于阐明 SKI 的基本特性，这是我们的主要目标。然而，我们还提供了与 SoR 和 SSGPR（Lazaro-Gredilla 等，2010 年 ^[6]）的比较，后者是一种最新的可扩展高斯过程方法，基于具有 $\mathcal{O}(m^2n)$ 计算复杂度和 $\mathcal{O}(m^2)$ 存储复杂度的随机投影 $m$ 个基函数和 $n$ 个训练点（另见 Rahimi & Recht，2007；Le 等，2013；Lu 等，2014；Yang 等，2015）。 此外，我们专注于 SKI 允许 Kronecker 和 Toeplitz 方法松弛到任意位置输入的能力。由于 Toeplitz 方法仅限于一维输入，而 Kronecker 方法只能用于低维（例如，$D < 5$）输入空间（Saatchi，2011），我们考虑低维问题。 所有实验均在配备 Intel i5 2.3 GHz 处理器和 4 GB RAM 的 2011 MacBook Pro 上进行。 ### 4.1 协方差矩阵重建 准确的推断和学习依赖于高斯过程协方差矩阵 K，它用于形成高斯过程的预测分布和边缘似然。我们在`式 (8)`中评估 SKI 对 $K$ 的近似值。作为归纳点数 $m$、归纳点位置和稀疏插值策略的函数。 我们从 RBF 核生成一个 $1000 \times 1000$ 的协方差矩阵 $K$，该核在从 $\mathcal{N}(0, 25)$ 随机采样的（排序的）输入 $X$ 处进行评估，如 `图 1(a)` 所示。请注意，输入没有网格结构。 SKI 使用局部三次插值和仅 $40$ 个插值点生成的近似 $K$，如 `图 1(b)` 所示，与原始 $K$ 几乎没有区别。`图 1(c)` 说明了 $|K − K_{SKI}，m=40|$，绝对值 `图 1(a)` 和 `图 1(b)` 中的矩阵之间的差异。近似值通常是准确的，在 $K$ 的对角线和外边缘附近精度最高。 在 `图 1(d)` 中，我们展示了重建误差如何随着归纳点和插值策略的变化而变化。使用规则网格的局部三次和线性插值分别以蓝色和紫色显示。对于小的 $m$，三次插值明显更准确。在黑色中，我们还展示了在数据输入 $X$ 上使用 k-means 来选择归纳点位置的准确性。在这种情况下，我们使用局部反距离加权插值，一种适用于不规则网格的线性插值。这种 kmeans 策略通过选择最接近原始输入的归纳点改进了规则网格上的标准线性插值。然而，当我们允许更多的插值点时，使用 k-means 的价值会降低，因为这些插值点的精确位置然后变得不那么重要，只要我们对输入域有一般覆盖。实际上，除了小的 $m$ 之外，规则网格上的三次插值通常优于使用 k-means 的反距离加权。毫不奇怪，与 SoR 近似对应的具有全局高斯过程核插值的 SKI（以红色显示）比非常小的 $m \ll n$ 的其他插值策略准确得多。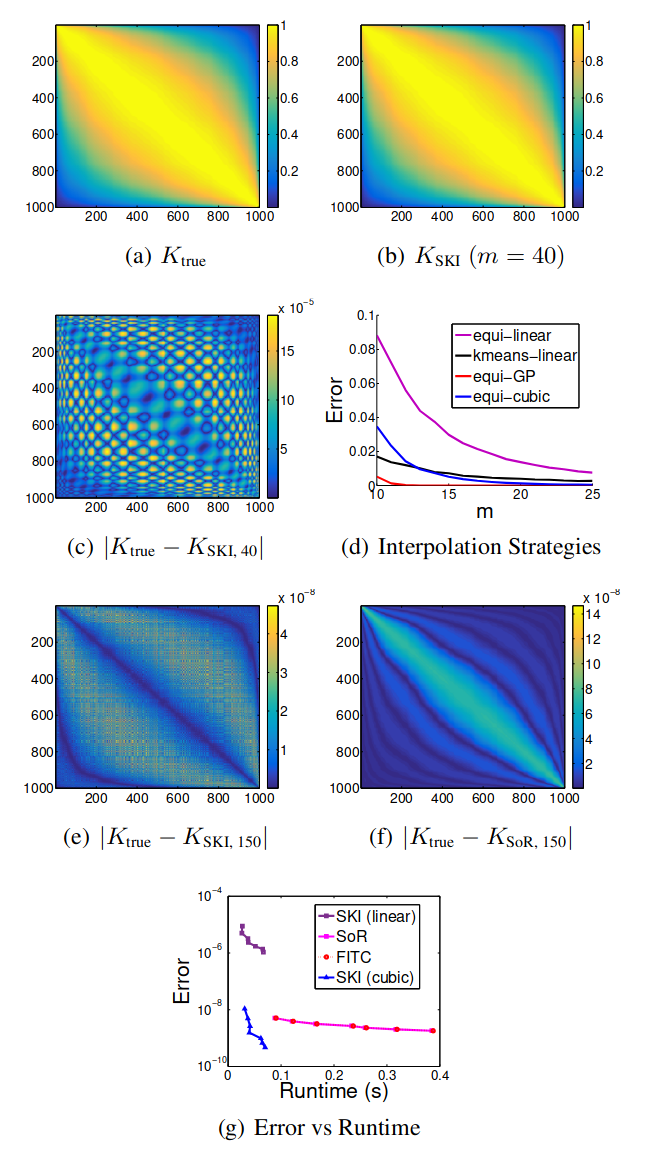  > 图 1. 重建协方差矩阵。 a) 真正的 $1000 × 1000$ RBF 协方差矩阵 $K$。 b) 使用局部三次插值和 $m = 40$ 个插值点的 $K_{SKI}$ 重建。 c) SKI 绝对重建误差，对于 $m = 40$。d) 重建 $K$ 的每个元素的平均绝对误差（(c) 中元素的平均值）作为 $m$ 的函数，使用具有线性、三次和 GP 插值的规则网格（分别为紫色、蓝色和红色），以及通过 $k$ 均值形成的不规则网格，具有反距离加权插值（黑色）。 e)-f) SKI（立方）和 SoR 绝对重构误差，$m = 150$。g) 平均绝对（对数刻度）误差与运行时间，$m \in [500, 2000]$。 然而，全局高斯过程核插值的效率远低于局部三次核插值，并且这些精度差异随着 $m$ 的增加而迅速缩小。事实上，在 `图 1(e)` 和 `图 1(f)` 中，我们看到对于 $m = 150$，两个重建误差同样很小，但质量不同。 SoR 重建中的误差集中在对角线附近，而三次插值的 SKI 中的误差从未达到 SoR 中的顶部误差，并且比对角线附近的 SoR 更准确，但也更分散；因此结合这些方法可以提高准确性。 然而，归根结底，重要的问题不是对于给定的 $m$ 哪个近似值最准确，而是对于给定的运行时间哪个近似值最准确（Chalupka 等，2013 年）。在 `图 1(g)` 中，我们将 SoR、FITC 和 SKI 的精度和运行时间与局部线性和局部三次插值进行比较，$m \in [500, 2000]$，$m = 150$ 个单位增量。 $m$ 足够大，SoR 和 FITC 之间的准确性差异可以忽略不计。一般来说，从具有全局高斯过程插值（例如 SoR 或 FITC）的 SKI 到具有局部三次插值（KISS-GP）的 SKI 的差异比 SoR 和 FITC 之间的差异要深刻得多。此外，从局部线性插值到局部三次插值在不显著影响运行时间的情况下极大地提高了精度。我们还看到，随着 $m$ 的增加，具有局部插值的 SKI 会迅速提高精度，对于给定的 $m$，局部三次插值的精度实际上超过了 SoR 和 FITC。最重要的是，对于任何给定的运行时间，具有三次插值的 SKI 比替代方案更准确。 在这个实验中，我们正在测试构建近似协方差矩阵的错误和运行时间，但我们还没有使用该协方差矩阵进行推断，这通常要昂贵得多，而 SKI 的帮助最大。此外，我们还没有使用 Kronecker 或 Toeplitz 结构来加速 SKI。 ### 4.2 核学习 我们现在测试 SKI 使用高斯过程从数据中学习核的能力。事实上，SKI 旨在将高斯过程扩展到大型数据集——而大型数据集为表达核学习提供了机会。 流行的归纳点方法，如 FITC，提高了高斯过程的可扩展性。然而，Wilson 等 (2014) 表明这些方法通常不能用于表达核学习，并且最适合简单的平滑核。换句话说，可扩展的高斯过程方法经常错过结构学习，这是首先考虑大型数据集的最大动机之一。出现这种限制是因为流行的归纳方法要求归纳点的数量为 $m \ll n$，以实现计算的易处理性，这剥夺了我们学习复杂核的必要信息。 SKI 不会遇到这个问题，因为我们可以自由选择大 $m$；事实上，$m$ 可以大于 $n$，同时与标准高斯过程相比保持显著的效率提升。 为了测试 SKI 和 FITC 的核学习，我们从使用已知地面实况核的高斯过程中采样数据，然后尝试从数据中学习这个核。特别是，我们从高斯过程中采样 $n = 10, 000$ 个数据点 $\mathbf{y}$，并在从 $\mathcal{N}(0, 4I)$ 提取的输入 $x \in \mathbb{R}^2$ 处查询复杂的乘积核 $k_{true} = k_1k_2$（输入没有网格结构）。产品中的每个组件核都在单独的输入维度上运行，如 `图 2` 中的绿色所示。顺便说一下，$n = 10^4$ 点大约是我们可以从具有非平凡协方差矩阵的多元高斯分布中采样的上限。即使来自具有这么多数据点的高斯过程的单个样本以及这个复杂的核也是计算密集型的，在这种情况下需要 $1030$ 秒。另一方面， SKI 可以使人们能够从极高维 ($n > 10^{10}$) 非平凡多元高斯分布中有效地采样，这通常很有用 为了学习数据背后的核，我们使用非线性共轭梯度优化高斯过程 $p(\mathbf{y}|θ)$ 相对于谱混合核的超参数 $θ$ 的 SKI 和 FITC 边缘似然。详细而言，SKI 和 FITC 核近似于由 $θ$ 参数化的用户指定（例如，谱混合）核。为了执行核学习，我们希望从数据中学习 $θ$。谱混合核 (Wilson & Adams, 2013) 构成了所有平稳协方差核的基础，并且非常适合核学习。对于 SKI，我们使用三次插值和 $100 \times 100$ 归纳点网格，在每个输入维度上等距分布。也就是说，我们有与训练数据点一样多的归纳点 $m = 10, 000$。我们对每种方法使用相同的 $θ$ 初始化。 结果如 `图 2(a)` 和 `图 2(b)` 所示。真正的核为绿色，SKI 重建为蓝色，FITC 重建为红色。 SKI 提供了很强的近似值，而 FITC 无法接近重建真正的核。在此多维示例中，SKI 利用 Kronecker 结构提高效率，运行时间为 $2400$ 秒（$0.67$ 小时），使用 $m = 10, 000$ 个归纳点。另一方面，FITC 的运行时间为 $2.6 \times 10^4$ 秒（$7.2$ 小时），只有 $m = 100$ 个归纳点。使用 FITC 的更多归纳点打破了计算的易处理性。 尽管训练点的位置是随机采样的，但在 SKI 中，我们在归纳点 $U$ 上利用协方差矩阵 $K_{U,U}$ 中的 Kronecker 结构，将使用 $10, 000$ 个归纳点的成本降低到小于使用 $100$ 个归纳点与 FITC。 FITC 和其他归纳点方法不能有效地利用 Kronecker 结构，因为非稀疏交叉协方差矩阵 $K_{X,U}$ 和 $K_{U,X}$ 限制缩放到最佳 $\mathcal{O}(m^2n)$，如`第 3 节`所述。  > 图 2. 核学习。两个核的乘积（以绿色显示）用于从 GP 中采样 $10, 000$ 个数据点。根据这些数据，我们使用 SKI（立方）和 FITC 进行核学习，结果分别以蓝色和红色显示。所有核都是 $τ = x − x'$ 的函数，并按 $k(0)$ 缩放。 ### 4.3 自然声音建模 GP 已成功应用于自然声音建模，以实现自动语音识别，并更深入地了解大脑中的听觉处理 (Turner, 2010)。我们使用 SKI 对 `图 3(a)` 中的自然声音时间序列进行建模，这是 Turner (2010) 在不同背景下考虑的。我们在数据的一个子集上训练了一个完整的高斯过程，学习了 RBF 核的超参数，用于 FITC 和 SKI。然后，我们使用这些方法中的每一种来重建信号中大的连续缺失区域。由于大量任意定位的缺失区域，该时间序列不具有网格结构，因此不能应用直接 Toeplitz 方法。总共有 $59$ 个，$306$ 个训练点和 $691$ 个测试点。我们将所有归纳点放置在规则网格上，并利用 SKI 中的 Toeplitz 结构实现可扩展性。 `图 3(b)` 显示了经验运行时间（在对数尺度上）作为两种方法中归纳点 $m$ 的函数，$图 3(c)$ 显示了每种方法在测试点上的标准化平均绝对误差 (SMAE) 作为运行时间的函数（对数尺度)。 对于 $m \in [2500, 5000]$，SKI 的运行时间基本上不受 $m$ 增加的影响，并且比 FITC 快数百倍，FITC 的运行时间随着 $m$ 的增加而显著增加。此外，`图 3(c)` 证实了我们的直觉，对于给定的运行时间，从 FITC 中的高斯过程核插值到 SKI 的 KISS-GP 变体中更简单的立方核插值的精度损失可以通过以下方式恢复通过更多的归纳点实现准确性的提高。 SKI 的错误率不到 FITC 运行成本的 $1\%$，而错误率不到一半。 SKI 通常能够推断出函数中的正确曲率，而 FITC 无法为任何给定的运行时间使用尽可能多的归纳点，因此倾向于过度平滑数据。我们还测试了 SSGPR (Lazaro-Gredilla 等，2010)，这是一种最新的可扩展高斯过程建模方法。对于 $m \in [250, 1250]$ 的范围，SSGPR 具有 $SMAE \in [1.12, 1.23]$ 和运行时间 $\in [310, 8400]$ 秒。总的来说，SKI 在最短的运行时间提供了最好的信号重建。  > 图 3. 自然声音建模。我们从 $n = 59、306$ 次观察中重建自然声音的连续缺失区域。 a) 观察到的数据。 b) SKI 和 FITC（对数刻度）的运行时间作为诱导点数 $m$ 的函数。 c) 测试 SMAE 错误作为（对数刻度）运行时间的函数。 ## 5 讨论 我们引入了一个新的结构化核插值 (SKI) 框架，它概括和统一了可扩展高斯过程推断的归纳点方法。特别是，我们展示了标准归纳点方法如何对应于通过全局高斯过程核插值形成的核近似。通过更改为局部三次核插值，我们引入了 KISS-GP，这是一种高度可扩展的归纳点方法，它自然地与 Kronecker 和 Toeplitz 代数相结合，以获得可扩展性的额外收益。事实上，我们可以将 KISS-GP 视为将 Kronecker 和 Toeplitz 方法中严格的网格假设放宽到任意位置的输入。我们展示了 KISS-GP 有效处理大量归纳点的能力，使表达核学习和预测准确性得到提高，除了改进的运行时间外，还超过了流行的替代方案。特别是，对于任何给定的运行时间，KISS-GP 比替代方案准确几个数量级。总体而言，简单性和通用性是 SKI 框架的主要优势。 我们才刚刚开始探索使用这个新框架可以做什么。结构化核插值为大量新的研究方向打开了大门。例如，可以通过改变插值策略来创建全新的可扩展高斯过程模型。这些模型可能具有截然不同的特性和应用。我们可以使用结构化核插值给出的视角来更好地理解任何归纳点方法的属性——例如，哪些核最适合给定的方法，以及需要多少归纳点才能获得良好的性能。我们还可以将 SKI 生成的新模型与最近基于随机变分推断的高斯过程的正交优势结合起来。此外，将 SKI 协方差矩阵分解为 Toeplitz 矩阵的 Kronecker 积为统一可扩展的 Kronecker 和 Toeplitz 方法提供了动力。我们希望 SKI 将激发许多新模型和统一观点，并加深对可扩展高斯过程方法的理解。 ## 参考文献

• [1] Baker, Christopher TH. The numerical treatment of integral equations. Clarendon Press, 1977.
• [2] Chalupka, Krzysztof, Williams, Christopher KI, and Murray, Iain. A framework for evaluating approximation methods for Gaussian process regression. The Journal of Machine Learning Research, 14(1):333–350, 2013.
• [3] Cunningham, John P, Shenoy, Krishna V, and Sahani, Maneesh. Fast Gaussian process methods for point process intensity estimation. In International Conference on Machine Learning, 2008.
• [4] Hensman, J, Fusi, N, and Lawrence, N.D. Gaussian processes for big data. In Uncertainty in Artificial Intelligence (UAI). AUAI Press, 2013.
• [5] Keys, Robert G. Cubic convolution interpolation for digital image processing. IEEE Transactions on Acoustics, Speech and Signal Processing, 29(6):1153–1160, 1981.
• [6] Lazaro-Gredilla, M., Quinonero Candela, J., Rasmussen, C.E., and Figueiras-Vidal, A.R. Sparse spectrum Gaussian process regression. The Journal of Machine Learning Research, 11:1865–1881, 2010.
• [7] Le, Q., Sarlos, T., and Smola, A. Fastfood-computing Hilbert space expansions in loglinear time. In Proceedings of the 30th International Conference on Machine Learning, pp. 244–252, 2013.
• [8] Lu, Z., May, M., Liu, K., Garakani, A.B., D., Guo, Bellet, A., Fan, L., Collins, M., Kingsbury, B., Picheny, M., and Sha, F. How to scale up kernel methods to be as good as deep neural nets. Technical Report 1411.4000, arXiv, November 2014.
• [9] Luo, Yuancheng and Duraiswami, Ramani. Fast nearGRID Gaussian process regression. In Proceedings of the Sixteenth International Conference on Artificial Intelligence and Statistics, pp. 424–432, 2013.
• [10] Naish-Guzman, A and Holden, S. The generalized fitc approximation. In Advances in Neural Information Processing Systems, pp. 1057–1064, 2007.
• [11] Quinonero Candela, Joaquin and Rasmussen, Carl Edward. A unifying view of sparse approximate Gaussian process regression. Journal of Machine Learning Research (JMLR), 6:1939–1959, 2005.
• [12] Quinonero Candela, Joaquin, Rasmussen, Carl Edward, and Williams, Christopher KI. Approximation methods for gaussian process regression. Large-scale kernel machines, pp. 203–223, 2007.
• [13] Rahimi, A and Recht, B. Random features for large-scale kernel machines. In Neural Information Processing Systems, 2007.
• [14] Rasmussen, C. E. and Williams, C. K. I. Gaussian processes for Machine Learning. The MIT Press, 2006.
• [15] Rasmussen, Carl Edward. Evaluation of Gaussian Processes and Other Methods for Non-linear Regression. PhD thesis, University of Toronto, 1996.
• [16] Rasmussen, Carl Edward and Ghahramani, Zoubin. Occam’s razor. In Neural Information Processing Systems (NIPS), 2001.
• [17] Rasmussen, Carl Edward and Nickisch, Hannes. Gaussian processes for machine learning (GPML) toolbox. Journal of Machine Learning Research (JMLR), 11:30113015, Nov 2010.
• [18] Saatchi, Yunus. Scalable Inference for Structured Gaussian Process Models. PhD thesis, University of Cambridge, 2011.
• [19] Seeger, Matthias. Bayesian Gaussian process models: PAC-Bayesian generalisation error bounds and sparse approximations. PhD thesis, University of Edinburgh, 2005.
• [20] Shepard, Donald. A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 1968 ACM National Conference, pp. 517–524, 1968.
• [21] Silverman, Bernhard W. Some aspects of the spline smoothing approach to non-parametric regression curve fitting. Journal of the Royal Statistical SocietyB, 47(1): 1–52, 1985.
• [22] Snelson, Edward and Ghahramani, Zoubin. Sparse Gaussian processes using pseudo-inputs. In Advances in neural information processing systems (NIPS), volume 18. MIT Press, 2006.
• [23] Turner, Richard E. Statistical Models for Natural Sounds. PhD thesis, University College London, 2010.
• [24] Williams, CKI and Shawe-Taylor, J. The stability of kernel principal components analysis and its relation to the process eigenspectrum. Advances in neural information processing systems, 15:383, 2003.
• [25] Wilson, Andrew Gordon. A process over all stationary kernels. Technical report, University of Cambridge, 2012.
• [26] Wilson, Andrew Gordon. Covariance kernels for fast automatic pattern discovery and extrapolation with Gaussian processes. PhD thesis, University of Cambridge, 2014.
• [27] Wilson, Andrew Gordon and Adams, Ryan Prescott. Gaussian process kernels for pattern discovery and extrapolation. International Conference on Machine Learning (ICML), 2013.
• [28] Wilson, Andrew Gordon, Gilboa, Elad, Nehorai, Arye, and Cunningham, John P. Fast kernel learning for multidimensional pattern extrapolation. In Advances in Neural Information Processing Systems, 2014.
• [29] Yang, Zichao, Smola, Alexander J, Song, Le, and Wilson, Andrew Gordon. A la carte - learning fast kernels. Artificial Intelligence and Statistics, 2015.