稀疏高斯过程归纳点的变分学习（Titsias2009 ）

【摘 要】 使用归纳变量的稀疏高斯过程方法需要选择归纳输入和核超参数。我们引入了一种用于稀疏近似的变分公式，它通过最大化真实对数边缘似然的下限来联合推断归纳输入和核超参数。该公式的关键属性是归纳输入被定义为变分参数，这些变分参数是通过最小化变分分布与隐函数值的精确后验分布之间的 Kullback-Leibler 散度来选择的。我们将这种技术应用于回归，并将其与文献中的其他方法进行比较。

【原 文】 Titsias, Michalis. “Variational Learning of Inducing Variables in Sparse Gaussian Processes.” In Proceedings of the Twelth International Conference on Artificial Intelligence and Statistics, edited by David van Dyk and Max Welling, 5:567–74. Proceedings of Machine Learning Research. Hilton Clearwater Beach Resort, Clearwater Beach, Florida USA: PMLR, 2009. https://proceedings.mlr.press/v5/titsias09a.html.

1 简介

高斯过程 (GP) 模型的应用对于大型数据集来说是棘手的，因为时间复杂度为 $\mathcal{O}(n^3)$，存储为 $\mathcal{O}(n^2)$，其中 $n$ 是训练示例的数量。为了克服这一限制，文献中提出了许多近似或稀疏方法（Williams 和 Seeger，2001 年 ^[12]；Smola 和 Bartlett，2001 年 ^[8]；Csato 和 Opper，2002 年^[1]；Lawrence 等，2002 年 ^[2]；Seeger 等，2003 年^[6]；Schwaighofer 和 Tresp，2003 年^[5]；Snelson 和 Ghahramani，2006 年 ^[10]；Quinonero-Candela 和 Rasmussen，2005 年^[3]）。这些方法基于一小组 $m$ 支撑或归纳变量构造近似，允许将时间复杂度从 $\mathcal{O}(n^3)$ 降低到 $\mathcal{O}(nm^2)$。它们的主要区别在于它们用于选择通常从训练或测试示例中选择的归纳输入的策略。 Snelson 和 Ghahramani (2006 ^[10]) 允许将归纳变量视为辅助伪输入，使用连续优化与核超参数一起推断。

近似边缘似然是稀疏高斯过程模型中模型选择的恰当目标函数。现有的最先进方法（Snelson 和 Ghahramani，2006 年 ^[10]；Seeger 等，2003 年 ^[6]）往往先修改高斯过程先验（Quinonero-Candela 和 Rasmussen，2005 年 ^[3]），然后计算修改后模型的边缘似然。此类方法将归纳输入转化为额外的核超参数。虽然可以增加拟合数据时的灵活性，但当我们关于所有未知超参数做优化时，也可能导致过拟合。此外，拟合一个修改后的模型本身，并不是特别严格，因为缺少精确模型与修改后的模型之间可以用来最小化的距离度量。

在本文中，我们介绍了一种 通过最大化精确边缘似然的下限来联合选择归纳输入和超参数 的变分方法。这种形式和以前方法之间的重要区别在于：归纳输入（注：归纳输入可以直观地理解为归纳点的位置））被定义为一种变分参数，并可以通过最小化 “变分高斯过程” 与 “真实后验高斯过程” 之间的 Kullback Leibler ( $\mathrm{KL}$) 散度进行选择。这使得：

• 能够避免过拟合（注：过多的归纳输入点相当于增加了模型参数的数量，容易产生过拟合；而本文提出的变分方法通过一个正则化项有效避免了此问题）；
• 通过最小化稀疏近似模型和精确模型之间的距离，实现对精确模型的严格近似。

归纳输入和超参数的选择要么通过对所有未知量应用 连续优化 获得，要么采用 变分 EM 算法 从训练输入中自动选择。在 EM 算法中，$E$ 步骤从训练数据中贪心地选择归纳输入，而 $M$ 步骤则用于更新超参数。与之前的贪心方法相反 (Seeger 等，2003 ^[6])，我们的方案只会单调地增加目标函数值（注：本文中指变分下界）。

我们将变分方法应用于含加性高斯噪声的回归任务，并将其性能与投影后过程的边缘似然方法（Seeger 等，2003 年；Csato 和 Opper，2002 年）和稀疏伪输入的边缘似然方法（Snelson 和 Ghahramani，2006 年）进行了比较。

我们的方法与（Csato 和 Opper，2002 年 ^[1]；Seeger，2003 年 ^[6]）中描述的变分稀疏高斯过程方法联系比较紧密，但我们的方法的主要区别在于：我们通过最大化变分下界来联合选择归纳输入和核超参数，而其他方法仅使用变分界来估计核超参数。

2 稀疏高斯过程回归

（1）高斯过程

高斯过程是一组随机变量 $\{ \mathbf{f(\mathbf{x})}| \mathbf{x} \in \mathcal{X} \}$，其中任何有限子集都服从多元高斯分布。要描述一个高斯过程，我们只需要指定均值函数 $m(\mathbf{x})$ 和协方差函数 $k(\mathbf{x,x'})$。协方差函数通常取决于一组超参数 $\boldsymbol{\theta}$。高斯过程可以作为实值函数 $f(\mathbf{x})$ 的先验。根据贝叶斯原理，该先验可以与数据结合，并给出函数的后验。

假设我们有一个训练数据集 $\{(\mathbf{x}_i, y_i)\}^{n}_{i=1}$，其中包含未被观测到的底层隐函数的 $n$ 个含噪声实现，因此每个标量 $y_i$ 是通过在输入 $\mathbf{x}_i$ 处向真实函数 $f(\mathbf{x})$ 添加高斯含噪声来获得的，即 $y_i = f_i + \epsilon_i$，其中 $\epsilon_i \sim \mathcal{N}(0, \sigma^2)$ 和 $f_i = \mathbf{f} (\mathbf{x}_i)$。令 $X$ 表示所有训练输入，$\mathbf{y}$ 表示所有输出，$\mathbf{f}$ 表示相应的训练隐函数值。联合概率模型是 $p(\mathbf{y, f}) = p( \mathbf{y|f})p(\mathbf{f})$ 其中 $p(\mathbf{y|f})$ 是似然，$p(\mathbf{f})$ 是高斯过程先验。数据会推导出后验高斯过程，该分布由后验均值函数和后验协方差函数指定：

$$\begin{align*} m_{\mathbf{y}}(\mathbf{x}) = K_{\mathbf{x}n}(\sigma^2 I + K_{nn})^{-1} \mathbf{y} \\ k_{\mathbf{y}}(\mathbf{x,x'}) = k(\mathbf{x,x'}) − K_{\mathbf{x}n}(\sigma^2 I + K_{nn})^{-1} K_{n\mathbf{x'}} \end{align*} \tag{1}$$

这里：

• $K_{nn}$ 是训练输入上的 $n \times n$ 协方差矩阵；
• $K_{\mathbf{x}n}$ 是测试输入 $\mathbf{x}$ 和 $n$ 个训练输入处函数值之间的相关向量，并且有 $K_{n \mathbf{x}} = K^{\top}_{\mathbf{x} n}$。
• 任何与后验高斯过程相关的查询都可以通过 式（1） 的均值函数和协方差函数来解答。例如，测试数据集底层的隐真实过程值 $\mathbf{f}$ 上的高斯后验分布 $p(\mathbf{f|y})$ 可以根据 式 (1) 在输入 $X$ 处计算的；而在尚未观测的输入 $\mathbf{x}_*$ 处的含噪声预测输出 $y_* = f_* + \epsilon_*$，则可以由 $p(y_*| \mathbf{y}) = \mathcal{N}(y_*|m_{\mathbf{y}}(\mathbf{x}_*), k_{\mathbf{y}}(\mathbf{x}_*, \mathbf{x}_*) + \sigma^2)$ 计算。后验高斯过程由超参数 $(\boldsymbol{\theta}, \sigma^2)$ 的值指定，可以通过最大化下式中的对数边缘似然来估计：

$$\log p(\mathbf{y}) = \log [\mathcal{N}(\mathbf{y}| \mathbf{0}, \sigma^2 I + K_{nn})] \tag{2}$$

（2）伪输入高斯过程与投影高斯过程

尽管高斯过程方法很优雅，但它很难处理大型数据集，因为计算 $n \times n$ 矩阵的逆和行列式，其计算法度为 $\mathcal{O}(n^3)$。因此，我们会考虑使用稀疏方法来近似处理大型数据集。稀疏方法使用一小组 $m$ 个归纳点作为 支撑集 或 归纳变量集，因此计算只需要 $\mathcal{O}(nm^2)$ 的时间复杂度。稀疏高斯过程方法中的重要问题是：“归纳变量” 选择问题和 “超参数” 选择问题，关于这些问题的讨论，请参阅 Rasmussen and Williams （ 2006 ^[4] ）中的 第 8 章 和 Quinonero Candela and Rasmussen（ 2005 ^[3] ）。

假设我们使用 $m$ 个归纳变量来构造稀疏高斯过程。归纳变量是在某些输入 $X_m$ 处评估的隐函数值。 $X_m$ 可以是训练输入的某个子集（早期采用了这种做法），也可以是训练数据之外的辅助伪点 (Snelson and Ghahramani, 2006)。学习归纳点 $X_m$ 和超参数 $(\boldsymbol{\theta}, \sigma^2)$ 是获得稀疏高斯过程要解决的主要问题。通过对 式 (2) 中真实对数边缘似然进行近似，我们可以推断出这些量。

在边缘似然的选择方面，Snelson and Ghahramani （2006 ^[10]) 提出的稀疏伪输入高斯过程 (Sparse Pseudo-inputs GP, SPGP) 给出了当前 SOTA 的近似边缘似然； Seeger 等 (2003 ^[6]) 使用的目标函数为投影过后的过程近似 (Projected Process, PP)。两者的近似对数边缘似然都具有以下形式：

$$F = \log [\mathcal{N}(\mathbf{y}| \mathbf{0}, \sigma^2 I + Q_{nn})] \tag{3}$$

其中 $Q_{nn}$ 是真实协方差矩阵 $K_{nn}$ 的近似。

• 在投影过程中，$Q_{nn} = K_{nm}K^{-1}_{mm}K_{mn}$，即精确协方差被 Nystrom 近似代替。这里，$K_{mm}$ 是归纳输入上的 $m \times m$ 协方差矩阵，$K_{nm}$ 是训练点和归纳点之间的 $n \times m$ 互协方差矩阵，$K_{mn} = K^{\top}_{nm}$。
• 在稀疏伪输入高斯过程中，$Q_{nn} = \text{diag}[K_{nn} − K_{nm}K^{-1}_{mm}K_{mn}] + K_{nm} K^{-1}_{mm}K_{mn}$，即将 Nystrom 近似对角线上的元素修成了精确值。

（3）稀疏高斯过程推断及其存在问题

对比 式 (2) 同 式 (3) 可知，$F$ 是修改高斯过程先验后得到的。这意味着，归纳输入 $X_m$ 扮演了类似于核超参数的角色（类似于 $\boldsymbol{\theta}$），参与了对协方差矩阵 $Q_{nn}$ 的参数化 ^[10]。

但由于高斯过程先验发生了变化，边缘似然 $F$ 关于归纳输入 $X_m$ 的连续优化过程有可能无法可靠地逼近精确高斯过程。更进一步地，由于 $F$ 使用了大量额外超参数 $X_m$，模型过拟合的可能性也越来越大，尤其在对 $(X_m, \boldsymbol{\theta}, \sigma^2)$ 进行联合优化的时候。

在下一节中，我们提出了遵循另一种推断哲学的稀疏高斯过程回归： 我们没有修改精确高斯过程，而是最小化精确后验高斯过程和其变分近似之间的某种距离。在我们的新方法中，归纳输入 $X_m$ 被表述为变分参数，并通过最小化 $\mathrm{KL}$ 散度进行理论上地严格选择。

3 稀疏高斯过程的变分学习原理

3.1 变分公式的推导

（1）精确的预测分布

我们希望定义一种能够直接近似 式(1) 中后验高斯过程均值和协方差函数的方法。该后验高斯过程可以表述为预测分布的概念形式：

$$p(\mathbf{f^*|y}) = \int p(\mathbf{f^*|f})p( \mathbf{f |y})d \mathbf{f}$$

其中 $\mathbf{f^*}$ 表示测试点处的函数值集；$\mathbf{f}$ 表示训练点处的真实函数值集；$\mathbf{y}$ 表示训练点处的含噪声观测值集；$p(\mathbf{f^*|f})$ 表示 $\mathbf{f^*}$ 的条件分布。 上式也表明，预测分布是通过对真实高斯过程后验 $p(\mathbf{f|y}| )$ 的边缘化得到的。

假设我们希望通过 $m$ 个在伪输入 $X_m$ 处的辅助归纳变量 $\mathbf{f}_m$ 来近似上述贝叶斯积分（ 假设独立于训练输入 ），那么归纳变量 $\mathbf{f}_m$ 应该与真实过程变量 $\mathbf{f}$ 来自同一个高斯过程。通过使用增强的联合模型 $p(\mathbf{y|f})p(\mathbf{f^*}, \mathbf{f}_m, \mathbf{f})$，我们可以将 $p(\mathbf{f^*|y})$ 等效地写为（参见 ^[3]）：

$$p(\mathbf{f^*|y}) = \int p(\mathbf{f^*}|\mathbf{f}_m, \mathbf{f})p( \mathbf{f} |\mathbf{f}_m, \mathbf{y})p(\mathbf{f}_m| \mathbf{y})d \mathbf{f} d \mathbf{f}_m \tag{4}$$

（2） 预测分布的近似

如果假设 $\mathbf{f}_m$ 是 $\mathbf{f}$ 的充分统计量 ，在给定 $\mathbf{f}_m$ 时，测试函数值集 $\mathbf{f^*}$ 和训练函数值集 $\mathbf{f}$ 之间相互独立，即模型满足 $p(\mathbf{f^*}|\mathbf{f}_m, \mathbf{f}) = p(\mathbf{f^*}|\mathbf{f}_m)$。我们可以将上面的预测分布写成如下形式：

$$\begin{align*} q(\mathbf{f^*}) &= \int p(\mathbf{f^*}|\mathbf{f}_m)p(\mathbf{f}|\mathbf{f}_m)\phi (\mathbf{f}_m)d \mathbf{f} d \mathbf{f}_m \\ &= \int p(\mathbf{f^*}|\mathbf{f}_m)\phi (\mathbf{f}_m)d\mathbf{f}_m \\ &= \int q(\mathbf{f^*}, \mathbf{f}_m) d\mathbf{f}_m \tag{5} \end{align*}$$

其中 $q(\mathbf{f^*}) = p(\mathbf{f^*|y})$ 、$\phi (\mathbf{f}_m) = p(\mathbf{f}_m|\mathbf{y})$。此处，$p(\mathbf{f}|\mathbf{f}_m) = p(\mathbf{f} |\mathbf{f}_m, \mathbf{y})$ 成立，因为 $\mathbf{y}$ 是 $\mathbf{f}$ 的含噪声版本，且 假设在给定 $\mathbf{f}_m$ 时，$\mathbf{f^*}$ 独立于的 $\mathbf{f}$ 。

$p(\mathbf{f^*} | \mathbf{f}_m, \mathbf{y}) = \frac{\int p(\mathbf{y|f})p(\mathbf{f^*},\mathbf{f}_m,\mathbf{f})d \mathbf{f}}{\int p(\mathbf{y|f})p(\mathbf{f^*},\mathbf{f}_m,\mathbf{f})d \mathbf{f} d \mathbf{f^*}}$，由于假设 $p(\mathbf{f^*}| \mathbf{f}_m, \mathbf{f}) = p( \mathbf{f^*}|\mathbf{f}_m)$，所以$p(\mathbf{f}|\mathbf{f}_m) = p(\mathbf{f} |\mathbf{f}_m, \mathbf{y})$ 成立。

在实际工作中，很难找到满足充分统计量的归纳变量 $\mathbf{f}_m$。因此，我们只能期望 $q(\mathbf{f^*})$ 是 $p(\mathbf{f^*|y})$ 的近似。此时，如果假设 $\phi (\mathbf{f}_m)$ 是一个近似于 $p(\mathbf{f}_m|\mathbf{y})$ 的可参数化简单分布（例如，一个均值向量为 $\boldsymbol{\mu}$ 、协方差矩阵为 $A$ 的高斯分布），则问题可以得到极大简化。这个简单分布 $\phi (\mathbf{f}_m)$ 被称为 $p(\mathbf{f}_m|\mathbf{y})$ 的变分分布。

（3）近似的后验高斯过程

基于变分分布，可以根据 式 (5)写出近似后验高斯过程的均值和协方差函数（请对比 式（1））：

$$\begin{align*} m^q_{\mathbf{y}}(\mathbf{x}) &= K_{\mathbf{x} m}K^{-1}_{mm} \boldsymbol{μ} \\ k^q_{\mathbf{y}}(\mathbf{x,x'}) &= k(\mathbf{x,x'}) − K_{\mathbf{x} m}K^{-1}_{mm} K_{m \mathbf{x'}} + K_{\mathbf{x} m} BK_{m \mathbf{x'}} \tag{6} \end{align*}$$

式中 $B = K^{-1}_{mm} A K^{-1}_{mm}$。

上式定义了稀疏后验高斯过程的一般形式，其计算复杂度为 $\mathcal{O}(nm^2)$。

现在出现的问题是如何确定变分分布 $\phi$（即确定 $\boldsymbol{μ}$ 和 $A$）以及归纳输入 $X_m$。接下来，我们描述了一种允许联合估计这些量的变分方法，该方法将 $X_m$ 视为一种变分参数，并且能够通过最小化 $\mathrm{KL}$ 散度来严格选择。

3.2 变分下界

确定 $\phi$ 和归纳输入 $X_m$ 的原理性过程，是构造训练函数值集 $\mathbf{f}$ 上的变分分布 $q(\mathbf{f})$，然后最小化其与精确后验分布 $p(\mathbf{f|y})$ 之间的某种距离测度。同样，我们也可以最小化增强的真实后验 $p(\mathbf{f}, \mathbf{f}_m| \mathbf{y})$ 和增强的变分后验 $q(\mathbf{f}, \mathbf{f}_m)$ 之间的距离，其中根据式 (5)可以看出，$q(\mathbf{f}, \mathbf{f}_m) = p(\mathbf{f} |\mathbf{f}_m)\phi (\mathbf{f}_m)$。

增强的真实后验与增强的联合模型有关：

$$p(\mathbf{y}, \mathbf{f}, \mathbf{f}_m) = p(\mathbf{y|f})p( \mathbf{f} |\mathbf{f}_m)p(\mathbf{f}_m) \tag{7}$$

这等价于初始模型 $p(\mathbf{y},\mathbf{f} ) = p(\mathbf{f|y})p(\mathbf{f})$，因为从 式（7） 左右两侧中边缘化掉 $\mathbf{f}_m$，我们总是可以恢复后者。特别要注意到：条件先验 $p(\mathbf{f} |\mathbf{f}_m)$ 和边缘先验 $p(\mathbf{f}_m)$ 取决于归纳输入 $X_m$。不过，这种依赖性不会影响后验 $p(\mathbf{f|y})$ 或边缘似然 $p(\mathbf{y})$。因此，增强的表示具有一组 “自由” 的参数 $X_m$，可以将其视为不同于模型参数的一种 “变分参数”。

为了确定变分量 $(X_m, \phi)$，可以最小化变分分布与真实分布之间的 $\mathrm{KL}$ 散度：$\mathrm{KL}(q(\mathbf{f}, \mathbf{f}_m)||p(\mathbf{f}, \mathbf{f}_m| \mathbf{y}))$。根据变分原理，最小化 $\mathrm{KL}$ 散度等效于最大化证据下界（ $\mathrm{ELBO}$ ）：

$$F_V (X_m, \phi ) = \int p(\mathbf{f} |\mathbf{f}_m)\phi (\mathbf{f}_m) \log \frac{p(\mathbf{y|f} )p(\mathbf{f}_m)}{\phi (\mathbf{f}_m)} d \mathbf{f} d \mathbf{f}_m \tag{8}$$

其中对数中的项 $p(\mathbf{f} |\mathbf{f}_m)$ 消去了。我们可以通过优化选择变分分布 $\phi$，实现最大化的求解。最大化后的变分下界应当为：

$$F_V (X_m) = \log [\mathcal{N}( \mathbf{y}| \mathbf{0}, \sigma^2 I + Q_{nn})] − \frac{1}{2 \sigma^2} \text{Tr}(\widetilde{K} ) \tag{9}$$

其中 $Q_{nn} = K_{nm}K^{-1}_{mm}K_{mn}$ 和 $\widetilde{K} = \text{Cov}( \mathbf{f} |\mathbf{f}_m) = K_{nn} − K_{nm}K^{-1}_{mm}K_{mn}$。技术报告 (Titsias, 2009 ^[11]) 中给出了该界推导的详细信息。

上述目标函数的新颖之处在于:它包含一个正则化项：$−\frac{1}{2\sigma^2} \text{Tr}(\widetilde{K})$。这将 $F_V$ 与以前应用于稀疏高斯过程回归的 式（3） 描述的边缘似然区分开来。我们会简短地分析该迹项。

式 (9) 中量的计算复杂度为 $\mathcal{O}(nm^2)$，并且是真实对数边缘似然的下界（对于任意归纳输入 $X_m$）。我们可以通过优化 $X_m$ 及其数量来进一步最大化界。请注意，归纳输入决定了变分分布 $q(\mathbf{f} , \mathbf{f}_m) = p(\mathbf{f}|\mathbf{f}_m)\phi (\mathbf{f}_m)$ 的灵活性，因为通过调整 $X_m$，我们可以调整 $p(\mathbf{f}|\mathbf{f}_m)$ 和底层的最优分布 $\phi^*$。为了计算这个最优的 $\phi^*$，我们对 式 (8) 关于 $\phi (\mathbf{f}_m)$ 求微分，得到：

$$\phi^*(\mathbf{f}_m) = \mathcal{N}(\mathbf{f}_m | \boldsymbol{μ}, A) \tag{10}$$

其中 $\boldsymbol{\mu} = \sigma^{-2} K_{mm} \Sigma K_{mn} \mathbf{y}$ 、$A = K_{mm} \Sigma K_{mm}$ 、 $\Sigma = (K_{mm} + \sigma^{-2}K_{mn}K_{nm})^{-1}$。

这现在完全指定了变分高斯过程，我们可以使用 式 (6) 对未观测输入处的值进行预测。显然，预测分布正是之前在 (Csato and Opper, 2002; Seeger 等，2003) 中提出的投影过程所使用的分布。因此，就预测分布而言，上述方法等同于投影过程。

不过，就归纳输入和核超参数的选择而言，变分方法与投影过程和稀疏伪输入高斯过程有很大不同。这是因为 式 (9) 的界中出现了额外的正则化项，并且没有出现在投影过程（Seeger 等，2003 年）和 $\mathrm{SPGP}$（Snelson 和 Ghahramani，2006 年）中使用的近似对数边缘似然中。如 第 2 节 所述，对于后面的目标函数，$X_m$ 的作用是形成一组额外的核超参数。相反，对于下界，由于 $\mathrm{KL}$ 散度最小化，输入 $X_m$ 变为变分参数。

要查看界的函数形式，请注意 $F_V$ 是投影过程对数似然和正则化迹项 $− \frac{1}{2} \sigma^{-2} \text{Tr}(\widetilde{K})$ 的总和。因此，$F_V$ 试图最大化投影过程对数似然并同时最小化轨迹 $\text{Tr}(\widetilde{K})$。 $\text{Tr}(\widetilde{K})$ 表示条件先验 $p(\mathbf{f}|\mathbf{f}_m)$ 的总方差，它也对应于从归纳变量 $\mathbf{f}_m$ 预测训练隐值 $\mathbf{f}$ 的平方误差： $\int p(\mathbf{f}, \mathbf{f}_m)||K_{nm}K^{-1}_{mm}\mathbf{f}_m − \mathbf{f} ||^2 d \mathbf{f} d \mathbf{f}_m$。当 $\text{Tr}(\widetilde{K}) = 0$ 时，Nystrom 近似是精确的，即 $K_{nn} = K_{nm}K^{-1}_{mm}K_{mn}$，这意味着归纳变量成为充分的统计量，我们可以精确地再现完整的高斯过程预测。请注意，轨迹 $\text{Tr}(\widetilde{K})$ 本身已被用作从 (Smola and Scholkopf, 2000 ^[9] ) 中的训练数据中选择归纳点的标准，并且类似于 (Lawrence 等，2002 ^[2]）。

当我们最大化变分下界时，超参数 $(\sigma^2, \boldsymbol{\theta})$ 被正则化。很容易看出这是如何针对含噪声方差 $\sigma^2$ 实现的。在局部最大值处，$\sigma^2$ 满足：

$$\sigma^2 = \frac{1}{n} \int_{\mathbf{f}_m} \phi^*(\mathbf{f}_m) || \mathbf{y} − \boldsymbol{\alpha}||^2 d\mathbf{f}_m + \frac{1}{n} \text{Tr}(\widetilde{K}) \tag{11}$$

其中 $||f^*||$ 表示欧几里德范数，$\boldsymbol{\alpha} = \mathbb{E} [\mathbf{f}|\mathbf{f}_m] = K_{nm}K^{-1}_{mm}\mathbf{f}_m$。这种分解表明，获得的 $\sigma^2$ 将等于估计的“实际”含噪声加上“校正”项，即从归纳变量预测训练隐值的平均平方误差。

3.3 推断算法

到目前为止，我们假设归纳输入是通过基于梯度的优化来选择的。但这在高维输入空间中会非常困难，因为变量的数量会变得非常大。此外，核函数对于输入可能不可微。在此情况下，我们可以从训练输入中选择归纳输入并仍然使用变分法。这种离散优化方案的一个重要特性是：当我们贪心地选择归纳输入并调整超参数时，$F_V$ 会单调增加。下一节我们将讨论这种贪心选择法。

让 $m \subset \{1,\ldots, n\}$ 是用作归纳变量的数据子集的索引，与此相对地，不属于归纳集合的训练点则由 $n-m$ 索引，我们称之为剩余点，则 $\mathbf{f}_{n-m}$ 表示剩余的隐函数值。

此时变分法的应用类似于伪输入的情况。假设变分分布 $q(\mathbf{f}) = p(\mathbf{f}_{n-m}|\mathbf{f}_m)\phi (\mathbf{f}_m)$，我们可以使用一个与 式 (9) 中的界具有相同形式的变分界，唯一的区别是 $\widetilde{K} = \text{Cov}(\mathbf{f}_{n-m}|\mathbf{f}_m)$。

在训练数据中选择归纳变量需要禁止组合搜索。次优解是采用贪心选择方案，即从空归纳集 $m = ∅$ 和满剩余集 $n − m = \{1, \ldots ，n\}$ 开始进行迭代。在每次迭代中，根据最大化选择准则 $\Delta_j$，将一个训练点 $j \in J \subset n − m$ （ $J$ 是一个随机选择的工作集）添加到归纳集中。

重要的是将贪心选择过程与超参数 $(\sigma^2, \boldsymbol{\theta})$ 的自适应交织在一起。这可以被视为一种类似于 $EM$ 的算法；在 $E$ 步骤，我们将一个点添加到归纳集中；在 $M$ 步骤，我们更新超参数。为了获得可靠的收敛，近似边缘似然必须在每个 $E$ 或 $M$ 步单调增加。投影过程和稀疏伪输入高斯过程中的对数似然不满足此要求，因为它们也会随着归纳集中点数的增加而减少。相反，本文的 $F_V$ 界保证了单调增加，因为现在的类 $EM$ 算法是变分 $EM$。为了澄清这一点，我们陈述以下命题：

【命题 1】 令 $(X_m, \mathbf{f}_m)$ 为当前的归纳点集，$m$ 为相应索引集。添加到归纳集中的任何点 $i \in n − m$ 将永远不会减少下界。

证明：

在加入新点 $(f_i, \mathbf{x}_i)$ 之前，变分分布为 $p(\mathbf{f}_{n-m}|\mathbf{f}_m)\phi^*(\mathbf{f}_m) = p(f_{n−(m \cup i)}|f_i, \mathbf{f}_m) p(f_i| \mathbf{f}_m) \phi^* (\mathbf{f}_m)$。当我们添加新点时，项 $p(f_i|\mathbf{f}_m) \phi^*(\mathbf{f}_m)$ 将替换为最佳 $\phi^*(f_i, \mathbf{f}_m)$ 分布。这可以增加下限或使其保持不变。在 (Titsias, 2009) 中给出了更详细的证明。

上述命题的结果是：贪心选择过程只会单调增加变分下限，这适用于任何可能的准则 $\Delta$。一个明显的选择是使用 $F_V$ 作为准则，它可以在 $\mathcal{O}(nm)$ 时间内对工作集 $J$ 中的任何候选点进行计算。此选择过程最大限度地减少了散度 $\mathrm{KL}(q(\mathbf{f}) || p(\mathbf{f|y}))$。

4 比较

在本节中，我们比较了玩具问题中的变分界 $F_V$ 、投影过程的对数似然和稀疏伪输入高斯过程的对数似然。所有这些函数关于 $(X_m, \sigma^2, \boldsymbol{\theta})$ 都是连续的，并且可以使用基于梯度的优化方法实现最大化。

我们的工作示例是 Snelson 和 Ghahramani (2006 ^[10]) 中考虑的一维数据集，它包含 $200$ 个训练点；参见 图 1。我们使用 $\sigma^2 \mathbf{f} \exp(− \frac{1}{2 \ell^2} || x_i − x_j||^2)$ 平方指数核训练了一个稀疏高斯过程模型。由于数据集较小并且完整高斯过程模型可处理，因此我们可以将稀疏近似与精确高斯过程预测进行比较。图 1 第一行中的图显示了 $15$ 个归纳输入时三种方法的预测分布。左图显示了最大化 $F_V$ 获得的平均预测（显示为蓝色实线，含两倍标准差曲线），完整高斯过程模型的预测使用红色虚线显示。中图显示了投影过程找到的相应解，右图显示了稀疏伪输入高斯过程找到的解。通过变分方法获得的预测几乎完全再现了完整高斯过程预测。变分下限的最终值为 $-55.5708$，而最大真实对数边缘似然的值为 $-55.5647$。此外，$F_V$ 找到的超参数与通过最大化真实对数边缘似然找到的超参数也相匹配。相反，使用投影过程对数似然训练的稀疏模型给出的近似较差。稀疏伪输入高斯过程方法给出了比投影过程更令人满意的答案，尽管也不如变分方法。

为了考虑更具挑战性的问题，我们减少了原始 $200$ 个训练示例的数量，仅保留了其中 $20$ 个，然后使用完全相同的设置重复上面的实验。图 1 的第二行显示了三种方法的预测分布。变分方法的预测与完整高斯过程预测相同，超参数与完整高斯过程训练获得的超参数相匹配。投影过程 对数似然会导致训练数据显著过拟合，因为均值曲线对训练点进行插值并且误差条非常嘈杂。稀疏伪输入高斯过程提供的解在均值预测和误差方面都与完整高斯过程预测有很大不同。请注意，$\mathrm{SPGP}$ 发现的错误条的宽度在不同输入区域变化很大。这种非平稳性是通过将 $\sigma^2$ 设置为非常接近于零并通过异方差对角矩阵 $\text{diag}[K_{nn} − K_{nm}K^{-1}_{mm}K_{mn}]$ 对实际噪声建模来实现的。这个对角矩阵（其元素之和是轨迹 $\text{Tr}(\widetilde{K})$ ）很大的事实，表明完整高斯过程模型并没有被很好地近似。

当我们优化 $(X_m, \sigma^2, \boldsymbol{\theta})$ 时，投影过程 和稀疏伪输入高斯过程没能恢复完整高斯过程模型的原因并非局部最大值。为了阐明这一点，我们通过将投影过程和稀疏伪输入高斯过程对数似然初始化为最佳归纳输入和超参数值来重复实验，其中后者是通过完整高斯过程训练获得的。其预测类似于 图 1。一种确保在我们增加归纳输入数量时恢复完整高斯过程模型的方法，是从训练输入中选择它们。但这将连续优化问题变成了离散优化问题，而且投影过程和稀疏伪输入高斯过程面临非平滑收敛的问题。

关于 $F_V$，从 第 3 节 可以清楚地看出，通过最大化 $X_m$，我们在 $\mathrm{KL}(q(\mathbf{f}, \mathbf{f}_m)|p( \mathbf{f}, \mathbf{f}_m| \mathbf{y}))$ 意义上接近于完整高斯过程模型。$F_V$ 有效地正则化了超参数 $(\sigma^2, \boldsymbol{\theta})$，从而避免了过拟合。这是通过正则化的迹项 $− \frac{1}{2} \sigma^{-2}\text{Tr}(\widetilde{K})$ 实现的。当 $\text{Tr}(\widetilde{K})$ 很大时，因为没有足够多的归纳变量，这一项有利于提供更平滑函数的核参数。此外，当 $\text{Tr}(\widetilde{K})$ 很大时，式(11) 中的分解意味着 $\sigma^2$ 也必须增加。这些性质对于避免过拟合很有用，也意味着 $F_V$ 获得的预测将比完整高斯过程模型的预测更平滑。相比之下，投影过程 和稀疏伪输入高斯过程对数似然可以找到比完整高斯过程预测更灵活的解，这表明它们容易过拟合。

图 1：第一行对应 $200$ 个训练点，第二行对应 $20$ 个训练点。第一列显示通过在 $15$ 个伪输入和超参数上最大化 $F_V$ 获得的预测（蓝色实线）。完整的高斯过程预测以红色虚线显示。伪输入的初始位置在顶部显示为十字，而最终位置在底部以十字显示。第二列显示了投影过程发现的预测分布，第三列类似地显示了稀疏伪输入高斯过程的预测分布。

5 实验

在本节中，我们比较了四个真实数据集中的变分下界 ($\mathrm{VAR}$)、投影后过程 (投影过程) 和稀疏伪输入高斯过程(稀疏伪输入高斯过程) 的近似对数似然。我们选择数据子集 ($\mathrm{SD}$) 方法作为基线。对于所有稀疏高斯过程方法，我们共同最大化替代目标函数关于超参数 $(\boldsymbol{\theta}, \sigma^2)$ 和归纳输入 $X_m$ 使用共轭梯度算法。$X_m$ 被初始化为随机选择的训练输入子集。在每次运行中，所有方法都被初始化为相同的归纳输入和超参数。我们使用的性能指标是标准化均方误差 (SMSE)，由 $\frac{1}{T} \frac{||\mathbf{y}_* − \mathbf{f}_* ||^2 }{\text{var}(y_*)}$ 给出，以及在 (Rasmussen， 2006 年 ^[4]）中定义的标准化负对数概率密度 (SNLP) 。两个误差度量的值越小意味着性能越好。在所有实验中，使用具有不同长度尺度的平方指数核。

首先，我们考虑波士顿住房数据集，它由 $455$ 个训练示例和 $51$ 个测试示例组成。

由于数据集很小，完整的高斯过程训练很容易处理。在第一个实验中，我们将参数 $(\boldsymbol{\theta}, \sigma^2)$ 固定为通过训练完整高斯过程模型获得的值。因此，我们可以仅根据如何选择归纳输入来研究这些方法的差异。我们通过计算真实测试后验 $p(\mathbf{f}_*|\mathbf{y})$ 和每个近似测试后验之间的矩匹配散度 $\mathrm{KL}(p(\mathbf{f}_*|\mathbf{y})||q(\mathbf{f}_*))$ 来严格比较这些方法。对于稀疏伪输入高斯过程方法，近似测试后验分布是通过使用精确测试条件 $p(\mathbf{f}_*|\mathbf{f}_m)$ 计算的。

图 2(a) 显示了随着归纳点数量的增加时的 $\mathrm{KL}$ 散度。通过重复实验 $10$ 次获得均值和一个标准误差条。请注意，只有 $\mathrm{VAR}$ 方法能够匹配完整的高斯过程模型；对于大约 $200$ 个点，我们与完整高斯过程的预测非常匹配。有趣的是，当归纳输入被初始化为所有训练输入时，尽管超参数保持固定为完整高斯过程模型的值，$X_m = X$、投影过程 和稀疏伪输入高斯过程仍然给出了与完整高斯过程模型不同的解。发生这种情况的原因是它们不是真实对数边缘似然的下限，如 图 2(c) 所示，它们成为上限。为了表明 $\mathrm{VAR}$ 实现的归纳输入的有效选择并非巧合，我们将其与输入保持固定为其初始随机选择的训练输入的情况进行比较。图 2(b) 显示了 $\mathrm{VAR}$、随机选择 +投影过程($\mathrm{RSPP}$) 和 $\mathrm{SD}$ 方法的 $\mathrm{KL}$ 散度的演变。

请注意，$\mathrm{VAR}$ 和 $\mathrm{RSPP}$ 之间的唯一区别是 $\mathrm{VAR}$ 优化了归纳输入初始值的下限，而 $\mathrm{RSPP}$ 只是保持它们固定。显然 $\mathrm{RSPP}$ 显着改善了 $\mathrm{SD}$ 预测，而 $\mathrm{VAR}$ 显着改善了 $\mathrm{RSPP}$

在第二个实验中，我们联合学习归纳变量和超参数，并根据 SMSE 和 SNLP 误差比较这些方法。结果显示在 图 2 的第二行中。请注意，投影过程 和稀疏伪输入高斯过程方法获得的对数似然值（ 图 2(f)）比真正的对数边缘似然值高得多。但错误度量清楚地表明投影过程对数似然显着过拟合。稀疏伪输入高斯过程给出了比完整高斯过程模型更好的 SMSE 误差，但其相对于 SNLP 误差来说存在过拟合。变分法仍然能够匹配完整高斯过程模型。

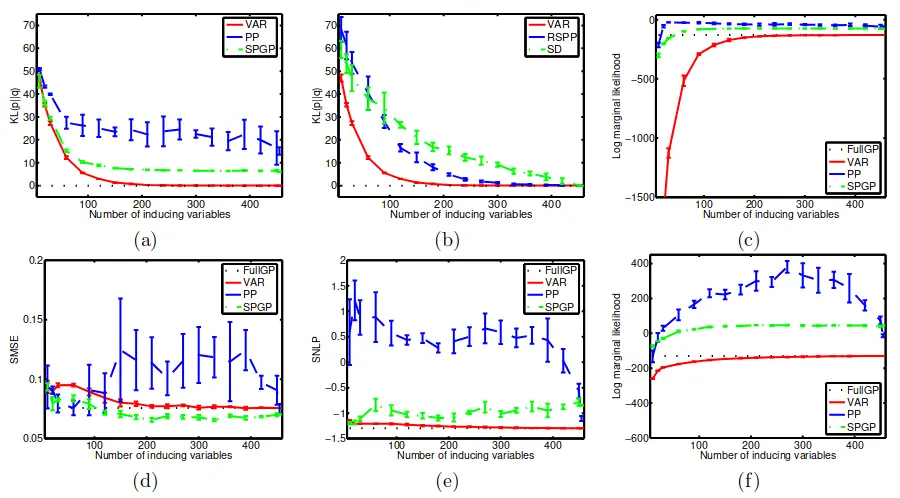
图 2：(a) 显示 $\mathrm{KL}$ 散度随着 $\mathrm{VAR}$、投影过程 和稀疏伪输入高斯过程方法的归纳变量数量增加。 (b) 显示 $\mathrm{VAR}$、$\mathrm{RSPP}$ 和 $\mathrm{SD}$ 方法的差异。 ( c ) 显示了近似对数边缘似然；使用水平虚线显示真实对数边缘似然值。 (d) 和 (e) 显示 SMSE 和 SNLP 误差（通过联合学习超参数和归纳输入获得）与归纳变量的数量。 (f) 显示了相应的对数边缘似然。

我们现在考虑三个大型数据集：kin40k 数据集、sarcos 和以前广泛使用的鲍鱼数据集。请注意，鲍鱼数据集足够小，因此我们能够训练完整的高斯过程模型。输入被归一化为在训练集上具有零均值和单位方差，并且输出被居中以在训练集上具有零均值。对于 kin40k 和 sarcos 数据集，SD 方法是在 2000 个训练点的子集中获得的。我们在 16 到 1024 之间改变归纳变量的大小（以 2 的幂为单位）。对于 sarcos 数据集，没有进行 1024 的实验，因为它的成本高得不切实际。通过引入输入和超参数，所有目标函数都被联合最大化。实验重复 5 次。图 3 显示了结果。

从图 3 中的图表，我们可以得出以下结论。正如 SNLP 错误清楚表明的那样，PP 对数似然非常容易过度拟合。但是，请注意，在 kin40k 和 sarcos 数据集中，PP 给出了最好的性能 w.r.t。到 SMSE 错误。这可能是因为 PP 能够在实际观测含噪声较低时对训练示例进行插值，从而导致良好的 SMSE 误差。稀疏伪输入高斯过程通常在 SMSE 错误方面表现最差，而在 SNLP 错误方面几乎总是表现最好。在鲍鱼数据集中，SPGP 的 SNLP 误差明显优于完整高斯过程模型。由于 SNLP 误差取决于预测方差，我们认为稀疏伪输入高斯过程的良好性能是由于其异方差能力。例如，在 kin40k 数据集中，SPGP 使 \sigma^2 几乎为零，因此似然中的实际含噪声由异方差协方差 \text{diag}[K_{nn} − K_{nm}K^{-1}{mm}K{mn}] 建模。后一项很大的事实可能表明完整的高斯过程模型没有得到很好的近似。最后，变分法具有良好的性能。 $\mathrm{VAR}$ 从未有过最差的表现，也没有表现出过度拟合。第 4 节中的例子，波士顿住房和鲍鱼数据集表明，$\mathrm{VAR}$ 方法比其他方法更接近于完整的高斯过程模型

图 3：第一列显示 kin40k 数据集相对于归纳点数量的 SMSE（顶部）和 SNLP（底部）错误。第二列显示了 sarcos 数据集的相应图，类似地，第三列显示了鲍鱼数据集的结果。

6 结论

我们提出了一种用于稀疏高斯过程回归的变分框架，它可以通过最小化真实后验高斯过程和近似后验高斯过程之间的 $\mathrm{KL}$ 散度来可靠地学习归纳输入和超参数。这种方法可以普遍适用。目前我们将这种技术应用于分类。未来一个有趣的话题是将此方法应用于假设多个隐函数的高斯过程模型。

参考文献

• [1] Csato, L. and Opper, M. (2002). Sparse online Gaussian processes. Neural Computation, 14:641–668.
• [2] Lawrence, N. D., Seeger, M., and Herbrich, R. (2002). Fast sparse Gaussian process methods: the informative vector machine. In Neural Information Processing Systems, 13. MIT Press.
• [3] Quinonero-Candela, J. and Rasmussen, C. E. (2005). A unifying view of sparse approximate Gaussian process regression. Journal of Machine Learning Research, 6:19391959.
• [4] Rasmussen, C. E. and Williams, C. K. I. (2006). Gaussian Processes for Machine Learning. MIT Press.
• [5] Schwaighofer, A. and Tresp, V. (2003). Transductive and inductive methods for approximate Gaussian process regression. In Neural Information Processing Systems 15. MIT Press.
• [6] Seeger, M. (2003). Bayesian Gaussian Process Models: PAC-Bayesian Generalisation Error Bounds and Sparse Approximations. PhD thesis, University of Edinburgh.
• [7] Seeger, M., Williams, C. K. I., and Lawrence, N. D. (2003). Fast forward selection to speed up sparse Gaussian process regression. In Ninth International Workshop on Artificial Intelligence. MIT Press.
• [8] Smola, A. J. and Bartlett, P. (2001). Sparse greedy Gaussian process regression. In Neural Information Processing Systems, 13. MIT Press.
• [9] Smola, A. J. and Sch ̈olkopf, B. (2000). Sparse greedy matrix approximations for machine learning. In International Conference on Machine Learning.
• [10] Snelson, E. and Ghahramani, Z. (2006). Sparse Gaussian process using pseudo-inputs. In Neural Information Processing Systems, 13. MIT Press.
• [11] Titsias, M. K. (2009). Variational Model Selection for Sparse Gaussian Process Regression. Technical report, School of Computer Science, University of Manchester.
• [12] Williams, C. K. I. and Seeger, M. (2001). Using the Nystr ̈om method to speed up kernel machines. In Neural Information Processing Systems 13. MIT Press.