最大似然法与受限最大似然法的比较
【摘 要】 当混合效应模型中既包含固定效应又包含随机效应时,参数估计是否应该采用最大似然法呢? 如果不使用最大似然法,那应当使用什么方法呢?本文介绍了在此应用场景中最大似然法存在的问题,即低估随机效应(方差)分量并导致固定效应的一类错误膨胀,并简单介绍了响应的处置方法:受限最大似然法和 KR 校正法。作者参考了 McNeish Daniel 的一篇文章,用人类能看懂的非数学语言介绍了 MLE、REML、KR 三者的核心以及背后的统计思想。
【原 文】 Carnap, 最大似然估计和限制性极大似然估计
【参 考】Daniel McNeish (2017): Small Sample Methods for Multilevel Modeling: A Colloquial Elucidation of REML and the Kenward-Roger Correction, Multivariate Behavioral Research, DOI: 10.1080/00273171.2017.1344538
1 最大似然估计
当混合效应模型中同时包含固定效应和随机效应(如:含方差成分的线性模型、均值函数不为常数的空间随机过程等)时,采用最大似然估计方法进行参数估计,通常不存在封闭形式解,因此大多采用迭代式的 EM 或 IGLS 方法方法交替地估计固定效应参数和随机效应参数。当估计随机效应参数时需要有个参考点,那就是某个参数(如均值)确定的固定效应;而当估计固定效应参数时,也需要认为随机效应参数为已知的确定值。依次迭代,直到参数估计值变化小于指定阈值为止。下图是上述最大似然估计的过程:

图 2. ML(顶部)和 REML(底部)之间迭代过程的比较。 ML 使用同步估计并在固定效应和方差分量之间交替,直到满足收敛。 REML 迭代估计方差分量直到收敛,然后估计固定效应作为 GLS 的最后一步
然而首先估计固定效应,这就意味着在估计随机效应(方差)时把固定效应视为已知并且固定,此时会出现两个问题:第一固定效应的变异没有考虑,第二估计固定效应时消耗的自由度没有考虑(这点没太理解)。大样本时,这两个问题都不是问题,小样本时这两个问题对估计随机效应(方差)有比较大的影响。
作者举了个很好的例子方便读者理解:均值的总体随机效应(方差)计算时采用“各个 X 值减去总体均值的平方和”作分子,分母用 N;样本随机效应(方差)计算时采用“各个 X 值减去样本均值的平方和”作分子,分母用 N-1(因为均值是估计出来的,所以此时需要惩罚);而 ML 估计就类似于总体随机效应(方差)的估计,但是实际中却用了样本均值,分子却用了 N,没有用 N-1。大样本时估计值相差无几,小样本时相差很大。这会导致估计出来的随机效应(方差)偏小,导致固定效应的标准误偏小,从而导致一类错误膨胀。
2 受限最大似然估计
REML 类似于“N-1”版本的 MLE,把随机效应(方差)进行了校正。REML 把估计固定效应和随机效应(方差)的过程分开,在小样本时可以更准确的估计随机效应(方差),由此得到更准确的固定效应的标准误,从而控制一类错误膨胀。REML 的第一步是忽略层次结构,先通过 OLS 得到残差(technically, when implemented in software, this step is conducted with an error contrast of the outcome variable and the projection matrix rather than actually fitting a single-level model with OLS and saving the residuals)。OLS 残差和原始结果具有同样的条件随机效应(方差)(基于 X 变量)。用 OLS 残差估计随机效应(方差)时固定效应被限制为 0(如下图),所以 REML 估计随机效应(方差)成分时无需考虑考虑固定效应。第二步是估计固定效应。采用 GLS 通过 matrix multiplication 的方法估计固定效应,即把 REML 估计出的随机效应(方差)成分放入 GLS 估计方程中去估计固定效应(见下图)。

图 .结果与预测变量(上图)之间以及 OLS 残差与预测变量(下图)之间关系的比较。然后保存来自 OLS 拟合 (ei) 的残差。根据定义,OLS 残差 (ei) 独立于预测变量。这意味着 e 和 Hours Studie 之间的相关性必然为 0。然后使用 ML 和 OLS 残差作为结果而不是原始结果变量来拟合 MLM。这可能看起来很奇怪,但这是有道理的。 OLS 残差作为原始数据的线性变换,现在独立于预测变量(本例中的研究小时数)但具有相同的随机效应(方差)量(以预测变量为条件)。这在图 1 中使用假设的模拟数据集对此示例进行了演示。顶部面板显示了HoursStudied 上的原始数学分数结果和底部面板显示了 OLS 残差和 HoursStudyed 的关系。当使用 OLS 残差时,不再需要估计固定效应,因为它们根据定义(通过 OLS 的属性)已知为零,如图 1 底部面板中的水平线所示(即,根据定义,OLS 残差的平均值为 0,并且根据定义,e 和学习时间之间的相关性也为 0)。这实质上具有旋转数学分数和学习时间的关系的效果,因此截距和斜率的固定效应必然等于 0。也就是说,如果图 1 围绕旋转顺时针60° ,顶部面板中的点基本上映射到底部面板中的点
下图是 REML 的估计过程:


REML(GLS)估计出的固定效应和 ML 估计出的固定效应几乎相等,区别在于随机效应(方差)成分 REML 估计的更准确。
3 固定效应的随机效应(方差)/标准误
上面讲完了 REML 和 MLE 的对比,那么固定效应和随机效应(方差)成分的估计算是大功告成。但是在小样本情况下,固定效应的随机效应(方差)成分(可以理解为标准误)估计是不准确的,无论是 MLE 还是 REML。更进一步说,在计算固定效应的 p-value 时,需要用到的 fisher information 和中心极限定理(asympotics)在小样本下会失效,导致随机效应(方差)估计偏低,从而导致一类错误膨胀。有学者指出用 Bayesian 方法可以解决这个问题(贝叶斯方法不依赖于 asympotics),但是 Kackar-Harville 以及后来的 Kendward-roger 通过校正随机效应(方差)的方式在频率学派内部得到解决。
4 Kackar-Harville correction
Kackar-Harville 发现了如下公式,固定效应的随机效应(方差)等于固定效应样本估计值的 REML 随机效应(方差)估计值加上小样本偏差。
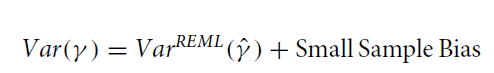
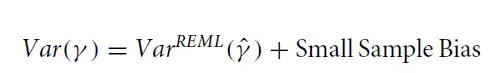
所以接下来从 KH 到 KR 的一系列研究都是针对如何估计 small sample bias 的。KH 发现,Small sample bias(SSB)的估计需要用到随机效应(方差)成分的总体值(而非样本估计值);接着他们采用了 Taylor series expansion 方法用随机效应(方差)和协随机效应(方差)成分的样本估计值去渐进估计了 SSB;之后 Prasad-Rao, Harville-Jeske 在 KH 的基础上,进一步扩展和发展了该方法。所以这个校正有时也被称为 Prasad-Rao-Jeske-kackar-Harville correction。
5 Kendward-Roger correction
KR 进一步发现“固定效应样本估计值的 REML 随机效应(方差)估计值”在小样本下也有问题,也就是 REML 在估计固定效应时直接用估计出的随机效应(方差)放入 GLS 估计方程去估计固定效应,此时并没有考虑随机效应(方差)成分本身的变异,而是直接把其视为已知并且固定(known and fixed)。KR 进一步用泰勒公式展开去估计“固定效应样本估计值的 REML 随机效应(方差)估计值”,此时考虑了在估计固定效应时的随机效应(方差)成分是估计值并且不是已知的这个事实。小样本情况下,采用 t 检验而非 Z 检验(多元情况对应的是卡方检验而非 F 检验)。KR 的第一步相当于是针对“t=固定效应/残差”中的残差给出了准确的估计,这还不够;接下来第二部是计算准确的自由度。在混合效应模型中,自由度的计算公式往往不存在,此时难以估计出准确的自由度。KR 采用了矩估计匹配方法(method of moments matching procedure, a scaled version of the Satterthwaite procedure),此时的估计更加准确,有时候甚至会出现分数形式的自由度。对于协随机效应(方差)矩阵中包含非线性情况时,KR 进一步改进了方法,提出了 KR2 来解决该问题。
6 总结
小样本情况下用混合效应模型时,采用贝叶斯或者频率方法都可以。重点不是选择贝叶斯还是频率框架,而是频率或者贝叶斯框架中具体采用什么方法;借用 McNeish 的原话:We want researchers to be aware that small sample methods exist in either framework and that small samples can be addressed with either frequentist or Bayesian methods—the choice of modeling framework to employ is less important than the choices made within the selected framework—and that there are associated risks in either framework. 如果选择贝叶斯应该重点考虑如何选择恰当的先验,如果选择频率学派需要考虑选择什么样的估计方法,比如 REML+KR。但是,样本多小才算小,这是个问题 w?





