最大似然法、EM 、变分推断的关系

【摘 要】 最大似然方法、期望最大化、变分推断三种方法，都可以用于对模型参数进行推断，但三者之间在应用场景上存在着显著区别，但也存在一定的关系。在知乎上看到一篇博文，内容貌似合理，但有更多概念是错误的，感觉有必要系统地梳理一下。

【参 考】 Reid, N. (2010) ‘Likelihood inference: Likelihood inference’, Wiley Interdisciplinary Reviews: Computational Statistics, 2(5), pp. 517–525. Available at: https://doi.org/10.1002/wics.110.

【原 文】 https://zhuanlan.zhihu.com/p/378988804

1 建模场景设置

当建模的场景中存在混合效应时，通常会分别对 固定效应 和 随机效应 进行建模。例如，在空间统计场景中，通常将观测建模为如下形式：

$$\mathbf{Y}(\mathbf{s}) = \mathbf{X}(\mathbf{s}) \boldsymbol{\beta} + \eta_{\boldsymbol{\phi}}(\mathbf{s}) + \epsilon(\mathbf{s})$$

其中：

• $\mathbf{X}(\mathbf{s}) \boldsymbol{\beta}$ 代表固定效应，可以是线性和非线性的（此处简化为线性的），$\boldsymbol{\beta}$ 为其参数；
• $\eta_{\boldsymbol{\phi}}(\mathbf{s})$ 代表随机效应，通常用均值为 $0$ 的空间随机场来建模（可以是高斯的或非高斯的，此处假定为高斯的），其（超）参数为 $\boldsymbol{\phi}$；
• $\epsilon(\mathbf{s})$ 被认为是一个独立同分布的白噪声，即 $\epsilon(\mathbf{s})=\epsilon \sim \mathcal{N}(0,\sigma^2_{\epsilon})$，其参数为 $\sigma^2_{\epsilon}$

此类模型在现实中是最常见的，需要根据样本对参数向量 $\boldsymbol{\theta} = (\boldsymbol{\beta},\boldsymbol{\phi},\sigma^2_{\epsilon})$ 进行推断（），该如何做呢？

2 基础推断方法

根据贝叶斯定理：

$$postoir = \frac{likelihood \times proir}{evidence}$$

$$p(\boldsymbol{\theta} | \mathcal{D}; \mathcal{M}) = \frac{p(\mathcal{D} | \boldsymbol{\theta};\mathcal{M} )p(\boldsymbol{\theta};\mathcal{M} )}{p(\mathcal{D}; \mathcal{M})}$$

其中：

• $\mathcal{M}$ 指代模型的结构形式，$\boldsymbol{\theta}$ 为该模型形式中的参数，$\mathcal{D}$ 为观测数据
• $p(\boldsymbol{\theta} ; \mathcal{M})$ 为模型参数的 先验分布（简称先验），代表了人们对参数的先验知识
• $p(\mathcal{D} |\boldsymbol{\theta}; \mathcal{M})$ 为 似然函数（简称似然），代表了在特定 $\boldsymbol{\theta}$ 值时模型成立的可能性，注意不是概率分布
• $p(\mathcal{D}; \mathcal{M})$ 为归一化常数（通常被称为 证据或边缘似然），只是为了使后验是一个合理的概率，没有其他特殊解释
• $p(\boldsymbol{\theta} | \mathcal{D}; \mathcal{M})$ 为模型参数的 后验分布（简称后验）

我们的目标是根据已知数据 $\mathcal{D}$ 和假设（已知）的模型形式 $\mathcal{M}$，来估计（推断）模型参数 $\boldsymbol{\theta}$ 的值或分布，进而为未观测的变量做预测。

常用三种推断方法：

• 最大似然法 ：仅考虑能够使 “ 似然 ” （即 $p(\mathcal{D} |\boldsymbol{\theta} ; \mathcal{M})$ ）最大化的 $\hat{\boldsymbol{\theta}}$ 作为参数的点估计。此类推断方法不考虑模型参数的完整先验和后验分布；其推断结果是一个确切的值。
• 最大后验法 ：考虑能够使分子项 “先验 $\times$ 似然” （即 $p(\mathcal{D} | \boldsymbol{\theta};\mathcal{M})p(\boldsymbol{\theta};\mathcal{M})$ ）最大化的 $\hat{\boldsymbol{\theta}}$ 作为参数的点估计。此类推断方法仅考虑模型参数的完整先验分布和后验分布中的最大值，其推断结果是一个确切的值。
• 贝叶斯方法 ：将所有可能的参数值及其概率都列出，既考虑了模型参数的完整先验分布，又考虑了模型参数的完整后验分布，其推断结果是模型参数的一个概率分布。

在实际工作中，最大似然法和贝叶斯方法使用比较广泛。可以很容易看出：

• 最大似然法 ： 计算快捷，但丢失了不确定性度量；
• 贝叶斯方法 ： 由于要处理涉及一个区间的概率分布，而非单一的点，所以计算量巨大，并导致其应用受限，但能够保留不确定信息。

注： 似然函数通常基于对感兴趣变量的建模假设和选择，但通常这些假设必须是可参数化的，因为这是参数估计的基础：

• 最常见的选择是简单分布，例如：
  • 假设感兴趣的连续型变量 $y$ 服从高斯分布；
  • 假设感兴趣的计数型变量 $count$ 服从泊松分布；
  • 假设类别型变量 $class$ 服从类别分布等。
• 通过组合形成对感兴趣变量的建模假设，例如：
  • 假设感兴趣的连续性变量 $y$ 服从高斯混合分布；
• 通过变换形成对感兴趣变量的建模假设，例如：
  • 广义线性回归模型
• 更复杂的情况出现在感兴趣变量无法作出概率分布建模的情况，这通常被称为 无似然方法（Free-Likelyhood Method） 或 近似贝叶斯计算（ABC） 参见 《近似贝叶斯计算简明教程》

3 基于似然的推断

将 第 1 节 的场景和 第 2 节 的方法结合，我们重点关注 最大似然估计方法 和 贝叶斯估计方法。本节没有直接以 最大似然估计方法 为标题，是因为最大似然估计方法只是基于似然的推断方法中的一类，难以涵盖更广泛的知识体系。即便在最大似然估计方法范畴内，也多种改进版本（如剖面最大似然估计方法、受限最大似然估计方法）以及各种对似然函数的重新定义。

关于似然方法的基础资料见：

• 参见 普度大学机器人视觉实验室的 《最大似然、最大后验与贝叶斯方法的区别》
• 参见 Reid 等 2010 年的 《似然函数与基于似然的推断》
• 参见 Cousineau 等 2016 年 《似然概念的扫盲帖》

3.1 似然函数

假设感兴趣的随机变量 $Y$ 具有参数化的概率密度函数为 $f(y; \boldsymbol{\theta})$，粗体符号 $\boldsymbol{y}$ 表示由 $n$ 个分量 $y_1, ..., y_n, y_i \in \mathbb{R}$ 组成的观测向量， $\boldsymbol{\theta} \in \Theta$ 为模型参数（ 通常认为 $\Omega$ 是 $\mathbb{R}^d$ 或 $\mathbb{R}^d$ 的子集， $d$ 为模型参数的数量）。当观测 $\boldsymbol{y}$ 确定时，该模型的似然函数被视为模型参数 $\boldsymbol{\theta}$ 的函数：

$$\mathcal{L}(\boldsymbol{\theta}; \boldsymbol{y}) = c(y) f(y;\boldsymbol{\theta}) \propto f(y;\boldsymbol{\theta}) \tag{1}$$

读者可能会比较常见到没有 $c(y)$ 的似然函数，此处将其显式表达出来，主要为了让读者理解似然函数与模型概率密度函数之间的正比关系，同时也可以表明，似然函数值之间仅在相对比较时有意义。

出于计算稳定性考虑，通常不会直接使用似然函数，而是使用对数似然函数（有些文献中也称对数密度，但两者之间还是有一些区别的）：

$$\ell(\boldsymbol{\theta}; y) = a(y) + \log f (y; \boldsymbol{\theta}) \tag{2}$$

特别是当 $\boldsymbol{y}$ 的各分量相互独立时（即满足独立同分布假设），对数似然函数显然更有价值。

1️⃣ 例 1 : 独立同分布的高斯似然

若 $Y = (Y_1, \ldots, Y_n)$ 中的随机变量之间相互独立，且都服从均值为 $μ$，方差为 $\sigma^2$ 的高斯分布，则 $y_i$ 可以被视为抽取自 $Y_i$ 的样本，此时的对数似然可以分解为各样本的对数似然之和，根据高斯分布的密度函数，可得：

$$\ell(\boldsymbol{\theta}; \boldsymbol{y}) = \log \prod\limits^{n}_{i=1} p(y_i) = \sum\limits^{n}_{i=1} \log p(y_i) = − \frac{n}{2}\log \sigma^2 − \frac{1}{2\sigma^2} \sum (y_i − μ)^2$$

其中模型参数为 $\boldsymbol{\theta} = (μ, \sigma^2)$, 参数空间为 $\Theta = \mathbb{R} \times \mathbb{R}^+$,显然我们忽略了高斯密度函数中的常数项 $−(n/2) \log (2\pi)$。

2️⃣ 例 2 : 线性回归模型的高斯似然

上例可以推广到以条件分布建模为主的回归任务中。例如，我们可以假设 $Y_i$ 是协变量 $\mathbf{x}$ 的线性函数，并假设 $Y_i$ 之间独立但不同分布（均值不同，方差相同）。此时如果令 $Y_i$ 的均值为 $\mu_i$，则有 $\mu_i = x_i^T \beta$，进而可以得到一个标准的线性回归模型，其对数似然函数为：

$$\ell(\boldsymbol{\theta}; \boldsymbol{y,x}) =− \frac{n}{2} \log \sigma^2 − \frac{1}{2\sigma^2} \sum (y_i − x_i^T\beta)^2$$

此时，模型参数由协变量系数 $\boldsymbol{\beta}$ 和方差 $\sigma^2$ 组成： $\boldsymbol{\theta} = (\boldsymbol{\beta}, \sigma^2)$。

3.2 最大似然估计

可以看出，似然函数是在数据和模型假设已知情况下，关于模型参数的函数。顾名思义，最大似然估计就是找到使似然最大化的参数值。

3.2.1 最大似然估计

（1）分值函数（Score function）

为了实现最大似然估计，根据函数的极值定理，通常会选择使对数似然的一阶(偏)导数为 $0$ 时的解作为参数的估计：

$$\mathcal{s}(\boldsymbol{\theta} ) = \ell^\prime (\boldsymbol{\theta}) = \frac{\partial \ell(\boldsymbol{\theta};\boldsymbol{y})}{\partial \boldsymbol{\theta}}$$

这个一阶导数 $\mathcal{s}(\boldsymbol{\theta})$ 通常也被称为Fisher 分值函数（Fisher Score function）或简称分值函数（Score function）。

（2）Fisher 信息量

分值函数 $\mathcal{s}(\boldsymbol{\theta})$ 的二阶矩被称为 Fisher 信息量：

$$I(\boldsymbol{\theta})=E_{\boldsymbol{\theta}}\left[\mathcal{s}(\boldsymbol{\theta}) \right]^{2}$$

如果对数似然存在二阶导数（满足二次可微条件）

$$j(\hat{\theta}) = \frac{\mathrm{d}^{2}}{\mathrm{d} \boldsymbol{\theta} ^{2}} \int_{-\infty}^{+\infty} p(y ; \boldsymbol{\theta} ) \mathrm{d} y=\int_{-\infty}^{+\infty} \frac{\partial^{2} p(y ; \boldsymbol{\theta} )}{\partial \boldsymbol{\theta} ^{2}} \mathrm{d} y$$

则可以证明 Fisher 信息量是对数似然的负二阶导数关于所有样本的期望值：

$$I(\boldsymbol{\theta} )=E_{\boldsymbol{\theta} }\left[\frac{\partial}{\partial \boldsymbol{\theta} } \ln p(y ; \boldsymbol{\theta} )\right]^{2} \Leftrightarrow I(\boldsymbol{\theta} )=-E_{\boldsymbol{\theta}}\left[\frac{\partial^{2}}{\partial \boldsymbol{\theta}^{2}} \log p(y ; \boldsymbol{\theta})\right]$$

根据定义，Fisher 信息量 ${I(\boldsymbol{\theta} )}$ 是 $\boldsymbol{\theta}$ 的函数，衡量了参数值为 $\boldsymbol{\theta}$ 时的信息多少。在样本数量趋于无穷时，最大似然估计的方差会逼近 Fisher 信息量的倒数，这就是最大似然的高斯渐进性质。

分值函数与 Fisher 信息量的统计学意义

对于随机变量 $Y$ ，假设它的分布属于一个由参数 $\boldsymbol{\theta}$ 定义的函数族 $f(\mathbf{y};\boldsymbol{\theta})$。当不清楚满足 $Y \sim f(\mathbf{y};\hat{\boldsymbol{\theta}})$ 的 $\hat{\boldsymbol{\theta}}$ 应该是什么值时，我们通常希望描述某个特定指标（如对数似然的一阶导数）随 $\boldsymbol{\theta}$ 变化的情况。

假设分布具有一些正则性。想要研究的是 $Y$ 的对数似然关于 $\boldsymbol{\theta}$ 的一阶导数 $\frac{\partial}{\partial \boldsymbol{\theta}}\log f(x;\boldsymbol{\theta})$，则此指标被称为 Fisher score function $\mathcal{s}(\boldsymbol{\theta})$ ，它描述了对数似然随 $\boldsymbol{\theta}$ 的变化率。

我们第一个感兴趣的是 Fisher score 在 $\hat{\boldsymbol{\theta}}$ 处的 期望。Fisher score 的期望描述了平均意义上 $Y$ 的对数似然相对于 $\boldsymbol{\theta}$ 的变化率，显然在 $\hat{\boldsymbol{\theta}}$ 处 Fish score 的期望应当为 $0$ 。

我们第二个感兴趣的东西是 Fisher score 在 $\hat{\boldsymbol{\theta}}$ 周围的 方差。Fisher score 的方差描述了平均意义上 $Y$ 的对数似然在 $\boldsymbol{\theta}$ 周围的散布情况，对应于 Fisher 信息量 $\mathcal{I}(\boldsymbol{\theta})$。

在满足二次可微的条件下（例如二次可微），Fisher 信息量可以用对数似然的二阶导数来描述，也就是 $\mathcal{I}(\boldsymbol{\theta}) = - \mathbb{E}[\frac{\partial^2}{\partial \boldsymbol{\theta}^2} \log f(x;\theta)]$。二阶导数描述了对数似然图形在 $\boldsymbol{\theta}$ 处的 曲率（导数的变化率）。该值越大则在 $\boldsymbol{\theta}$ 处曲率的期望值越大，也就是对数似然图形在随机变量 $Y$ 的平均意义上越 “尖锐”。

对于 $n$ 个 独立同分布 的随机变量 $\mathbf{Y} = \{Y_1,Y_2,\dots,Y_n \}$ ，它们的整体 Fisher 信息量为 $\mathcal{I}(\boldsymbol{\theta} | Y_1,\dots,Y_n) = n \mathcal{I}(\boldsymbol{\theta} )$。也就是说，随着样本数量增加，Fisher 信息量呈递增趋势。当 $n$ 趋于无穷时， $\boldsymbol{\theta}$ 的极大似然估计会依分布收敛至 $\mathcal{N}(\hat{\theta},\mathcal{I}^{-1}(\hat\theta|Y_1\dots,Y_n))$，这就是 Fisher 信息量的 渐进正态性，也就是：在样本数量趋于无穷时，最大似然估计的方差会逼近 Fisher 信息量的倒数。

在某些模型中，人们仅对模型参数 $\boldsymbol{\theta}$ 中的部分分量直接感兴趣，而并不关心其他的分量，此时通常记为 $\boldsymbol{\theta}=(\psi, \lambda)$，其中 $\psi$ 是感兴趣参数。此时可以天然地将 Fisher 信息量进行分块表示：

$$I(\theta)=\left(\begin{array}{cc} I_{\psi \psi}(\theta) & I_{\psi \lambda}(\theta) \\ I_{\lambda \psi}(\theta) & I_{\lambda \lambda}(\theta) \end{array}\right) .$$

（3）渐进性质

在相当广泛的普遍性中，可以得出以下渐进收敛性质：

$$\begin{align*} \ell^{\prime}(\theta)^T\{j(\hat{\theta})\}^{-1} \ell^{\prime}(\theta) & \stackrel{\mathcal{L}}{\rightarrow} & \chi_d^2 \tag{5}\\ (\hat{\theta}-\theta)^T j(\hat{\theta})(\hat{\theta}-\theta) & \stackrel{\mathcal{L}}{\rightarrow} & \chi_d^2 \tag{6}\\ 2\{\ell(\hat{\theta})-\ell(\theta)\} & \stackrel{\mathcal{L}}{\rightarrow} & \chi_d^2 \tag{7} \end{align*}$$

其中取指样本数量 $n$ 趋近于 $\infty$；$\chi_d^2$ 为 $d$ 自由度上的卡方分布，$d$ 为模型参数 $\boldsymbol{\theta}$ 的维数。

获得此渐进结果的条件是：中心极限定理可被用于 Fisher 分值函数 $\ell^\prime (\boldsymbol{\theta; y})$，如果 $\boldsymbol{y}$ 的各分量之间相互独立，则分值函数可被分解为 $n$ 个似然分量之和。

最大似然估计 $\hat{\boldsymbol{\theta}}$ 需要（概率）收敛于真实值 $\boldsymbol{\theta}$，这对于某些模型来说通常很难成立；不过，在许多讨论中，它被简单地直接被假定为真。

3.2.2 剖面最大似然估计

如果令 $\hat{\lambda}_\psi$ 表示固定感兴趣参数 $\psi$ 时对其他参数 $\lambda$ 的有约束最大似然估计，则可以定义如下感兴趣参数 $\psi$ 的 剖面（profile）对数似然函数（或 concentrated 对数似然函数）：

$$\ell_{\mathrm{P}}(\psi) = \sup_\lambda \ell(\psi, \lambda; \boldsymbol{y}) = \ell \left(\psi, \hat{\lambda}_\psi ; \boldsymbol{y}\right) \tag{8}$$

根据 式（7）的极限性质，有如下渐进性质：

$$\begin{align*} \ell_{\mathrm{P}}^{\prime}(\psi)^T j^\psi \psi(\hat{\theta}) \ell_{\mathrm{P}}^{\prime}(\psi) & \stackrel{\mathcal{L}}{\rightarrow} & \chi_q^2, \tag{9}\\ (\hat{\psi}-\psi)^T\left\{j^{\psi \psi}(\hat{\theta})\right\}^{-1}(\hat{\psi}-\psi) & \stackrel{\mathcal{L}}{\rightarrow} & \chi_q^2, \tag{10}\\ 2\left\{\ell(\hat{\psi}, \hat{\lambda})-\ell\left(\psi, \hat{\lambda}_\psi\right)\right\} & \stackrel{\mathcal{L}}{\rightarrow} & \chi_q^2, \tag{11} \end{align*}$$

其中 $q$ 是参数组分 $\psi$ 的维数。

上述渐进性质产生模型参数的例如下一阶近似，并在实践中被广泛用于对 $\boldsymbol{\theta}$ 的推断：

$$\begin{align*} \hat{\theta} \sim \mathcal{N} \left\{\theta, j^{-1}(\hat{\theta})\right\}, \tag{12}\\ \hat{\psi} \dot{\sim}\left\{\psi, j^{\psi \psi}(\hat{\theta})\right\}, \tag{13} \\ \pm \sqrt{2}\left\{\ell(\hat{\psi}, \hat{\lambda})-\ell\left(\psi, \hat{\lambda}_\psi\right)\right\} \dot{\sim} \mathcal{N}(0,1), \tag{14} \end{align*}$$

大多数统计软件包都包含计算上述近似值的通用代码。其中第三个近似仅适用于 $q = 1$，符号通常取为 $\text{sign}(\hat{\psi} − \psi)$。

3.3 贝叶斯估计

基于似然函数的贝叶斯推断原则上也非常简单：将 $\boldsymbol{\theta}$ 的先验概率分布 （表示为 $\pi (\boldsymbol{\theta})$）与似然函数 $\mathcal{L}(\boldsymbol{\theta}; \boldsymbol{y})$ 结合，形成 $\boldsymbol{\theta}$ 的后验概率分布。

$$\pi(\boldsymbol{\theta} | y) = \frac{ \mathcal{L}(\boldsymbol{\theta}; y) \pi(\boldsymbol{\theta})}{ \int \mathcal{L}(\boldsymbol{\theta}; y)\pi(\boldsymbol{\theta})d\boldsymbol{\theta}} \tag{15}$$

对感兴趣的部分参数 $\psi(\boldsymbol{\theta})$ 的推断，则来自于 $\psi$ 的边缘后验密度：

$$\pi_m(\psi | \boldsymbol{y} ) = \int_{\psi(\boldsymbol{\theta})=\psi} \pi (\boldsymbol{\theta}|y)d\boldsymbol{\theta} \tag{16}$$

部分参数 $\psi$ 的点估计可能是此边缘后验的均值或众数。边缘后验的概率性陈述也很容易获得，例如，概率为 $(1 − α)$ 的后验区间由 $(\psi_L, \psi_U)$ 给出， $\psi_L$ 和 $\psi_U$ 的边界值可以利用边缘后验分布计算获得，只需满足如下条件：

$$\int^{\psi = \psi_U}_{\psi = \psi_L} \pi_m(\psi | y)d\psi$$

仅上述条件形成的区间并不唯一，通常推荐的一种选择是同时要求 区间具有最高的后验密度，相应的区间被称为最高后验密度区间（HPDI）。

事实上，式 (15) 和 式 (16) 所需的积分计算比较复杂，因此大多只能通过数值方法给出近似解。

• 当维度较低时，可以采用 拉普拉斯近似法 或 求积法则。
• 在高维情况下，可以采用 马尔可夫链蒙特卡罗 (MCMC) 方法，先从后验密度中采样，通过样本做计算。根据 MCMC 原理，需要构建一条以后验密度 $\pi (\boldsymbol{\theta} | \boldsymbol{\theta})$ 作为平稳分布的马尔可夫链，在运行马尔可夫链足够长时间后，产生的模拟均是来自平稳分布的样本。

在贝叶斯方法的大多数科学应用中，了解推断结果在某个固定参数 $\boldsymbol{\theta}_0$ 处的模型表现（即 $p(y|\boldsymbol{\theta}_0)$ 时的样本表现）是非常有意义的。这提供了一种研究手段，可以用于判断 $\psi$ 的边缘后验概率区间在采样模型下是否具有有效性。

在模型和先验给定的条件下，可以证明 $\boldsymbol{\theta} − \hat{\boldsymbol{\theta}}$ 的后验密度也是渐近高斯的，均值为 $0$，方差样本的 Fisher 信息矩阵的逆给出；这通常被描述为：先验 “被数据淹没”。

4 MLE 数值算法

在常规模型中，最大似然估计结果来自于分值函数等于 0 时的解：

$$\ell^\prime (\boldsymbol{\theta; y}) = 0$$

通常使用 Newton-Raphson、梯度下降 、EM 算法 等方法迭代求解方程。

（1）Newton-Raphson 算法

前面提到的 Fisher 评分方法使用了 Newton-Raphson，不过将 Newton-Raphson 中的二阶导数替换为其期望值。当方程存在多个根时，理论上可以通过找到所有根并选择似然最大的那个根作为最终的最大似然估计。

（2）梯度下降算法

在广义线性模型（GLM）中，模型通常具有足够的平滑度来确保分值函数具有唯一解，并可以通过迭代地 加权最小二乘拟合 来找到该解。这使得用对数似然函数代替平方误差后，许多线性回归技术可以扩展到非线性模型。

【示例 5】

假设响应 $Y_i$ 服从二项分布，样本量为 $n_i$，成功概率为 $p_i$，并且有 $k$ 个独立观测样本，则其对数似然函数为：

$$\ell(p) = \sum^k_{i=1} \{y_i \log (p_i) + (n_i − y_i) \log (1− p_i) \}$$

由于没有进一步的信息来链接观测结果，$p$ 的最大似然估计仅仅是观测到的比例向量 $(y_1/n_1, ..., y_k/n_k)$。当有许多协变量 $x_{i1}, \ldots, x_{iq}$ 可能与每个 $y_i$ 存在关联时，我们可以考虑如下关于 $p$ 的逻辑斯谛模型：

$$\log \frac{p_i}{1 − p_i} = x_i^T\beta,$$

这使得

$$\ell(β) = \sum^k_{i=1} y_i x_i^T \beta − n_i \log \{1 + \exp (x_i^T \beta)\}$$

分值函数为：

$$\sum(y_i/n_i) x_i^T = \sum p_i(β) x_i^T$$

其中 $p_i(β) = \exp (x_i^T \beta)/\{1 + \exp (x_i^T \beta)\}$。这可以被构建成加权最小二乘问题，权重取决于 $β$。初始猜测为 $β$ 提供了起始权重值，并且在每一步做最小二乘方程求解并更新权重，直到收敛。一种特殊情况是当 $n_i = 1$ 时的二值数据，这在实际工作中经常遇到，其诊断和拟合需要更加小心^[14]。

【示例 6】

在具有一个隐藏层的前馈神经网络中，该模型可以表示为非线性回归模型 ^[2]（第 10 章）：

$$\begin{align*} Y_i &\sim \text{Bin}(n_i, p_i)\\ \log \frac{p_i}{1-p_i} &= \beta_0 + Z_i^T \beta\\ Z_{im} &= \frac{\exp (x_i^T α_m) }{1 + \exp (x_i^T α_m)} \end{align*}$$

其中 $Z$ 是不可观测的。这与逻辑回归模型有一些相似之处，使用交叉熵损失来拟合该模型与最大似然估计相同。然而，对数似然函数本质上是过度参数化的，因此有多个局部最大值。标准算法不会尝试找到所有解，然后自动选择似然最大那个解。因此，Venables 和 Ripley ^[14] （第 9 章）推荐的方法是使用多个随机起点，从而拟合多个神经网络，并对预测结果进行平均。

（3）期望最大化算法

Dempster 等 ^[15] 的 EM 算法允许为缺失数据（或着含不可观测变量）的模型计算最大似然估计。该算法在估计缺失观测值和最大化完整数据的似然函数之间交互迭代。有关介绍，请参阅参考文献 ^[6]（第 5 章），有关更详细的讨论和进一步参考，请参阅参考文献 ^[16][17]。

期望最大化（EM） 算法从形式上看，与 第 3.2 节 中的剖面最大似然估计极为相似，似乎都是先给出部分参数的估计值，而后再通过最大似然法估计剩余参数的值。但两者之间事实上存在着截然不同的本质和意义。其中最大的不同在于建模场景和模型假设，EM 算法的 E 步骤给出的是隐变量的期望值，而非参数的估计值。也就是说，EM 算法将 E 步骤估计的变量视为一个感兴趣的隐变量，而非模型参数。隐变量与模型参数之间的最大区别在于：隐变量往往每个样本有一个估计值，因此也可以被称为局部估计量；而模型参数是全局性的，所有样本共享相同的估计值。

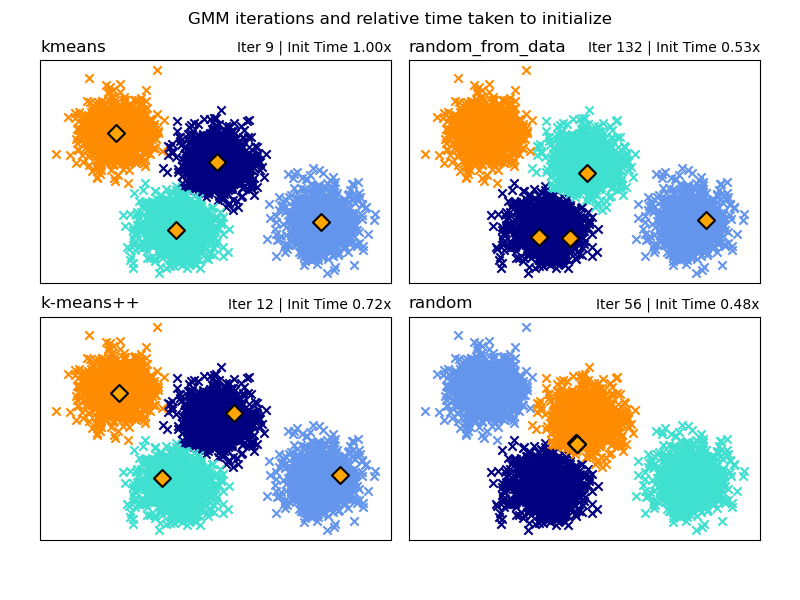
具体来说，在机器学习的很多现实应用中，人们经常会发现一些相关的特征，但其中只有部分可观测，其余特征不可观测（例如：可以听到来自多个音箱的声音，但无法观测到具体是哪个音箱参与了声音）。当所有特征都可观测时，我们通过建模并简单采用 第 3 节 中给出的推断方法，基本就能获得最优参数值；但当存在具有局部性质的隐变量时，问题会变得非常复杂。此时最常用的推断方法是期望最大化算法，该算法需要预设隐变量的参数化概率分布形式，并通过最大似然估计获取该概率分布参数的值。 一个常见的隐变量模型是高斯混合模型：

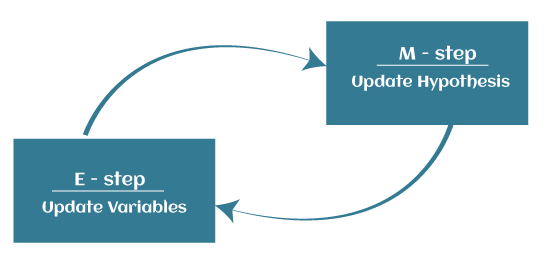
EM 算法作为一种迭代方法，它由两种模式组成。在第一种模式中，估计缺失变量或隐变量，因此被称为期望估计步骤（Expectation/estimation step）或 E 步。另一种模式用于优化模型参数，使其能够更清楚地解释数据，因此被称为最大化步骤（maximization-step ）或 M 步。

EM 算法的 4 个步骤：

• 第一步，初始化参数值 。系统提供了不完整的观测数据，并假设数据来自特定模型。
• 第二步：E-步 ，使用已观测数据来估计或猜测隐变量（或缺失数据）的值，也就是说，E-步主要用于更新隐变量。
• 第三步：M 步 ，使用从第二步获得的完整数据来更新模型参数值。也就是说，M-步主要用于更新模型假设。
• 第四步：检查隐变量值的收敛性 。如果收敛则停止算法，否则继续从 步骤 2 开始重复，直至收敛。

5 受限最大似然估计

重新审视 式 (9)、式(10) 和 式 (11) 中给出的剖面最大似然估计。直观上很明显，剖面对数似然过于聚集在其最大值点 $\hat{\psi}$ 附近，因为我们没有允许参数 $\lambda$ 可以有估计误差。也就是说，剖面似然 $\ell_P$ 在 $\hat{\psi}$ 处的曲率，很有可能代表了最大似然估计结果 $\hat{\psi}$ 的精度存在过于乐观的估计。

示例 3

如果模型是 $y_i = x_i^T \beta + \epsilon_i$，其中 $x_i$ 是一个 $q × 1$ 的已知协变量值的向量，$\epsilon_i$ 假设服从 $N(0, \psi)$ 分布，则 $\psi$ 的最大似然估计为：

$$\hat{\psi} = \frac{1}{n} \sum (y_i − x_i^T \hat{β})^2 \tag{18}$$

它往往太小，因为它不允许 $q$ 个未知参数（$β$ 的分量）已估计这一事实。在这个例子中，基于 $(β, \psi)$ 的似然函数因子分解，可以有一个简单的改进结果：

$$L_1 (β, \psi; \bar{y}) L_2 \left(\psi; \sum (y_i − x_i^T \hat{β})^2 \right) \tag{19}$$

因子 $L_2(\psi)$ 与残差的边缘密度 $\sum(y_i − x_i^T \hat{\beta})^2$ 成正比，并且仅基于此边缘似然推断 $\psi$，会导致对 $\psi$ 的无偏估计，例如最大边缘似然估计:

$$\hat{\psi}_m = \frac{1}{n − q} \sum (y_i − x_i^T \hat{\beta})^2 \tag{20}$$

基于残差边缘似然的估计通常称为受限最大似然 (REML) 估计，REML 方法在估计具有随机效应的线性模型中的方差分量时尤为重要。参考文献 ^[20] 中提供了长达一本书的讨论。

高阶近似理论已被用于推导对剖面似然或剖面对数似然函数的一般调整，其形式为：

$$\ell_A(\psi) = \ell_P(\psi) + \frac{1}{2} \log |J_{\lambda\lambda}(\psi, \hat{\lambda}_\psi)| + B(\psi) \tag{21}$$

其中 $J_{\lambda\lambda}$ 由观测到的 Fisher 信息量的划分定义，$B(\psi)$ 是进一步的调整函数，即 $\mathcal{O}_p(1)$。统计文献中已经提出了 $B(\psi)$ 的几个版本：主要目标是针对无用参数 $\lambda$ 估计中的错误调整剖面对数似然，主要是通过找到 (19) 因式分解的近似值。Fraser 讨论了具有非正态误差的线性回归模型中尺度参数的边缘似然 ^[21] 。Barndorff-Nielsen 提出了基于高阶近似的 $B(\psi)$ 的一般形式^[22] ，Fraser 提出了一个密切相关的版本，无需明确指定近似辅助统计即可计算 ^[23] 。

在 $\psi$ 与关于 Fisher 信息预期值的无用参数 $\lambda$ 正交的特殊情况下，即 $I_{\psi\lambda}(\boldsymbol{\theta}) = 0$，$\ell_A(\psi)$ 的简化形式是可用的：

$$\ell_{CR}(\psi) = \ell_P(\psi) − \frac{1}{2} \log |J_{\lambda\lambda}(\psi, \hat{\lambda}_\psi)| \tag{22}$$

该式由 Cox 和 Reid 引入 ^[24] 。 $\log |J_{\lambda\lambda}|$ 上符号的变化来自正交方程。在独立同分布抽样中，$\ell_P(\psi)$ 是 $\mathcal{O}_p(n)$，即 $n$ 个有界随机变量之和，而 $\log |J_{\lambda\lambda}|$ 是 $\mathcal{O}_p(1)$。 $\ell_{CR}$ 的一个缺点是它对 $\lambda$ 的一对一重参数化不是不变的，所有这些都与 $\psi$ 正交。相反 $\ell_A(\psi)$ 对从 $\boldsymbol{\theta}=(\psi,\lambda)$ 到 $\tilde{\boldsymbol{\theta}} =\{\psi, η(\psi, \lambda)\}$ 的变换具有不变性，该变换有时被称为兴趣相关变换。 DiCiccio 等 ^[25] 、Chang 和 Mukerjee ^[26] 讨论了基于 $\ell_A(·)$ 的各种版本的推断方法，即 $B(·)$ 的各种选择。

从参考文献 ^{[27][28][29][30]} 开始，已经在一系列论文中开发了一些基于似然量的高阶近似理论，并精化了近似值，例如 (12)、(13) 和 (14)。这些依次建立在 Daniels ^[31] 和 Edgeworth ^[8] 展开式的鞍点近似上。 该理论的简明描述可在包括参考文献 ^[8]、 ^[32] 和 ^[33] 在内的几本书中找到。Brazzale 等 ^[34] 介绍了高阶渐近的许多应用。

6 似然函数的常见变体

除了直接使用似然函数作为目标函数之外，还有大量根据不同目的提出的改进似然函数。其中常见的有：偏似然、近似似然（组合似然）、准似然、经验似然等。

6.1 偏似然

类似然函数扩展中最重要的一类，是删失生存数据的 偏似然（partial likelihoods ^[35] , ^[36]。

【示例 6】

假设我们对 $n$ 个个体中的每一个都有一个响应 $y_i$，其中 $y_i$ 对应于真实故障时间或删失故障时间，配套以标识未删失观测的指示变量。一个与 示例 4 的非齐次泊松过程密切相关的模型，是假设第 $i$ 个个体的故障率采用以下形式：

$$λ(t_i) = \exp (x_i^T \beta) λ_0(t_i) \tag{23}$$

其中 $x_i$ 是与个体相关的协变量向量，$λ_0(t)$ 是基线失败率，未指定。 $k$ 个观测到的故障时间排序为 $y(1) < ··· < y(k)$，我们用 $\mathcal{R}_i$ 表示在时间 $y_{(i)}$ 故障的个体的风险集，即观测到的 $y$ 值的所有个体（删失或未删失的），都大于 $y_{(i)}$。Cox ^[35] 建议 $β$ 的推断基于偏似然：

$$\prod^k_{i=1} \frac{\exp (x_{(i)}^T β)}{\sum_{j \in \mathcal{R}_i} \exp (x_j^T β)}$$

其中 $x_{(i)}$ 是观测时间为 $y_{(i)}$ 的个体的协变量向量。这忽略了记录故障时间之间信息的似然部分。它不是边缘似然或条件似然，除非在特殊情况下，但基于偏似然的推断具有基于全似然函数的推断的许多特性，包括一致性和渐近正态性，渐近协方差一致地由二阶导数估计偏似然函数的对数。这已经扩展到许多类型的随时间演变的过程，以及许多类型的未完全观测到的数据。

模型 (23) 是一个半参数模型，此类模型的一般似然理论可通过参考文献 ^[36] 和 ^[38] 获得。

6.2 近似似然与组合似然

许多其他类似然函数可以仅使用部分数据的密度来构造。 Besag ^[39] 提出了空间数据的伪似然函数（pseudo-likelihood function） 概念，伪似然由每个数据点的条件密度相乘得到，而每个数据点的条件密度则均以其直接邻居为条件。在 Lindsay 之后，这通常代表一大类被称为 组合似然（composite likelihoods） 的似然 ^[40] 。

【示例 8】

对相关的二值数据建模的一种方法，是从不可观测的隐变量建模开始，例如，

$$\begin{align*} z_{ir} &= x_{ir}^T β + w_{ir}^T b_i + \epsilon_{ir}\\ b_i &\sim N(0, \Sigma_b)\\ \epsilon_{ir} &\sim N(0, 1) \end{align*}$$

其中 $r = 1, ..., n_i$ 索引某个聚簇中的观测值，$i = 1, ..., n$ 索引不同的聚簇，即共有 $n$ 个聚簇，每个簇中有 $n_i$ 个观测值。$x_{ir}$ 和 $w_{ir}$ 是与第 $i$ 个簇中的第 $r$ 个个体相关的协变量。如果我们观测到 $y_{ir} = 1$ 时，有隐变量 $z_{ir} ≥ 0$，则 $\boldsymbol{y}$ 的联合似然可以写为：

$$\mathcal{L}(\boldsymbol{\theta; y}) = \prod^n_{i=1} \log \int^\infty_{-\infty} \prod^{n_i}_{r=1} p^{y_{ir}}_{ir} (1 − p_{ir})^{1−y_{ir}} \phi (b_i, \Sigma_b)d b_i$$

其中 $p_{ir} = \Phi(x_{ir}^T β + w_{ir}^T b_i)$，$\Phi(·)$ 是标准正态分布函数，$\phi(·;μ,\Sigma)$ 是均值向量为 $μ$、协方差矩阵为 $\Sigma$ 的正态密度函数。该似然中的积分非常难以计算，尤其是模型中包含的随机效应 $b_i$ 的维度超过两维或三维时。Renard 等 ^[41] 在这种情况下研究了另一种选择：每个簇内所有可能观测点对构成的联合似然，即成对似然（pairwise likelihoods），成对似然可以被视为组合似然的一个例子。 Renard 等 ^[41] 表明，相对于完全似然推断，基于成对似然的推断效率更高。有大量关于组合似然法计算效率的文献；参见参考文献 ^[42]

6.3 准似然

用基于似然的方法分析复杂数据，还有一种稍微有些不同的方法，那就是 Wedderburn 的准似然（quasi-likelihood） ^[43]。 这种方法首先为响应的均值和方差指定参数形式，例如：

$$\begin{align*} \mathbb{E}(y_i | x_i) &= μ(x_i^T \beta)\\ \mathbb{V}ar(y_i | x_i) &= \varphi V(\mu_i) \end{align*}$$

其中 $μ(·)$ 和 $V(·)$ 是已知函数，$\varphi$ 是方差函数的附加尺度参数。 $β$ 的推断基于估计方程：

$$\sum^n_{i=1} V(\mu_i)^{−1/2} \left(y_i − μ(x_i^T \beta) \right) = 0$$

如果该模型存在，上式将对应于具有二阶矩的广义线性模型的得分方程。

准似然推断理论由 McCullagh 提出 ^[44]，Liang 和 Zeger ^[45] 根据广义估计方程 (GEE) 的描述，将其扩展到纵向数据分析。Liang 和 Zeger 提议对 $V(·)$ 使用他们所谓的 “工作协方差” 函数，并表明即使工作协方差函数不正确，均值中参数的估计值也是一致的。在撰写本文时，GEE 方法与组合似然法之间的关系尚不清楚。

如果均值函数是用固定效应和随机效应建模的，如 示例 8 所示，那么这种准似然法也会涉及到积分计算。 Breslow 和 Clayton ^[46] 表明，对该积分的拉普拉斯近似产生了广义线性混合模型的带惩罚准似然版本。 Green ^[47] 对基于带惩罚似然函数的推断进行了一般性讨论，在这种情况下，控制第 $i$ 个观测值分布的参数可以表示为：

$$\boldsymbol{\theta}_i = x_i^T \beta + m(w_i)$$

$m(·)$ 是具有式 (3) 形式的 “平滑” 函数。Nelder 和 Lee 开发了一种不同的方差分量准似然估计方法；例如，参见参考文献 ^[48] 和 ^[49] 。

6.4 经验似然

Owen ^[50] 提出了一种被称为 经验似然（empirical likelihood） 的非参数似然。

在最简单的情况下，$y_1, \ldots, y_n$ 是关于密度 $f$ 的独立同分布观测数据，通常的非参数似然法将概率质量 $1/n$ 平均配置在每个观测值上。这并不是严格意义上的似然函数，因为密度不受 sigma-有限度量的控制。 Owen 表明，如果假设 $f$ 的所有可能密度都有一个共同参数，例如均值 $μ$，则最大化下式的经验最大似然估计是一致和渐进正态的，而且可以基于经验似然做类似于式 (7) 或 (14) 的似然比检验。

$$\prod^n_{i=1} p_i \text{,subject to } \sum p_i y_i = μ \text{ , and } \sum p_i = 1$$

经验似然允许在非参数设置中使用基于似然的参数。自 Owen 的原始论文以来，它已得到相当大的扩展和概括，例如，参见参考文献 ^[51] 。

在 Owen 的 ^[50] 经验似然法中，重点是推断少量或至少有限数量的参数，这些参数假定具有恰当的解释，而无需指定模型的参数形式。

非参数似然推断的另一个版本是使用参数为函数的 类似然参数（likelihood-like arguments）。例如，从一个此类密度的独立样本中，对对数凹密度的最大似然估计。这方面的理论要复杂得多：有关此类估计量一致性的最新结果，请参阅参考文献 ^[52] 及其中的参考文献。一些理论工作与半参数模型密切相关，例如 示例 7 的比例风险模型，参考文献 ^[53] （第 21 章）是一个很好的介绍。

7 结论

似然函数以及其派生的量是所有基于数学建模的统计推断方法的基础。基于似然函数派生出的各种量为未知参数估计、不确定性估计、假设检验、模型选择提供了方法。此外，为解决应用中出现的特定复杂模型，人们也发展出了大量似然的扩展，证明了似然和基于似然的思想在统计推断中的核心作用。

参考文献

• [1] Wood S. Generalized Additive Models: An Introduction with R.NewYork:Chapman&Hall/CRC;2006.
• [2] Hastie T, Tibshirani RJ, Friedman J. The Elements of Statistical Learning.2nded.NewYork:SpringerVerlag; 2009.
• [3] Fisher RA. Statistical Methods and Scientific Inference. Edinburgh: Oliver & Boyd; 1956.
• [4] Edwards AF. Likelihood (Expanded Edition).Baltimore: Johns Hopkins University Press; 1992.
• [5] Azzalini A. Statistical Inference.London:Chapman &Hall;1998.
• [6] Davison AC. Statistical Models.Cambridge:Cambridge University Press; 2003.
• [7] Cox DR, Hinkley DV. Theoretical Statistics.London: Chapman & Hall; 1974.
• [8] Barndorff-Nielsen OE, Cox DR. Inference and Asymptotics.London:Chapman&Hall;1994.
• [9] Casella G, Robert CP. Monte Carlo Statistical Methods. New York: Springer-Verlag; 1999.
• [10] Gilks WR, Richardson S, Spiegelhalter D. Markov Chain Monte Carlo in Practice.NewYork:Chapman &Hall/CRC;1996.
• [11] Berger JO. Statistical Decision Theory and Bayesian Analysis.NewYork:Springer-Verlag;1985.
• [12] Berger JO. The case for objective Bayes analysis. Bayesian Stat 2006, 1:385–402, doi:10.1214/06BA115.
• [13] Goldstein M. Subjective Bayesian analysis: principles and practice. Bayesian Stat 2006, 1:403–420, doi:10.1214/06-BA116.
• [14] Venables WN, Ripley BD. Modern Applied Statistics with S.NewYork:Springer-Verlag;2003.
• [15] Dempster A, Laird N, Rubin D. Maximum likelihood from incomplete data via the EM algorithm. JRStat Soc B 1977, 39:1–38.
• [16] Little RJA, Rubin DB. Statistical Analysis with Missing Data.2nded.NewYork:JohnWiley&Sons;2002.
• [17] McLachlan GJ, Krishnan T. The EM Algorithm and Extensions.NewYork:JohnWiley&Sons;2007.
• [18] Claeskens G, Hjort NL. Model Selection and Model Averaging.Cambridge:CambridgeUniversityPress; 2008.
• [19] Kass RE, Wasserman L. Formal rules for selecting prior distributions: a review andannotatedbibliography.J Am Stat Assoc 1996, 91:1343–1370.
• [20] Searle SR, Casella G, McCulloch CE. Variance Components.NewYork:JohnWiley&Sons;1992.
• [21] Fraser DAS. Inference and Linear Models.NewYork: McGraw-Hill; 1979.
• [22] Barndorff-Nielsen OE. On a formula for the distribution of the maximum likelihood estimator. Biometrika 1983, 70:343–365.
• [23] Fraser DAS. Likelihood for component parameters. Biometrika 2003, 90:327–339.
• [24] Cox DR, Reid N. Parameter orthogonality and approximate conditional inference (with discussion). JRStat Soc B 1987, 49:1–39.
• [25] Diciccio TJ, Martin MA, Stern SE, Young GA. Information bias and adjusted profile likelihoods. JRStat Soc B 1996, 58:189–203.
• [26] Chang H, Mukerjee R. Probability matching property of adjusted likelihoods. Stat Probab Lett 2006, 76:838 – 842.
• [27] Barndorff-Nielsen OE. Conditionality resolutions. Biometrika 1980, 67:293–310.
• [28] Cox DR. Local ancillarity. Biometrika 1980, 67:279 – 286.
• [29] Durbin J. Approximations for densities of sufficient statistics. Biometrika 1980, 67:311–333.
• [30] Hinkley DV. Likelihood as approximate pivotal. Biometrika 1980, 67:287–292.
• [31] Daniels HE. Saddlepoint approximations in statistics. Ann Math Stat 1954, 46:631–650.
• [32] Pace L, Salvan A. Principles of Statistical Inference: From a Neo-Fisherian Perspective.Singapore:World Scientific; 1997.
• [33] Severini TA. Likelihood Methods in Statistics.Oxford: Oxford University Press; 2001.
• [34] Brazzale AR, Davison AC, Reid N. Applied Asymptotics.Cambridge:CambridgeUniversityPress;2007.
• [35] Cox DR. Regression models and life tables (with discussion). JRStatSocB1972, 34:187–220.
• [36] Cox DR. Partial likelihood. Biometrika 1975, 62:269 – 276.
• [37] Murphy SA, van der Vaart AW. On profile likelihood (with discussion). JAmStatAssoc2000, 95:449–485.
• [38] Murphy SA, van der Vaart AW. Semiparametric likelihood ratio inference. Ann Stat 1997, 25:1471–1509.
• [39] Besag JE. Spatial interaction and the statistical analysis of lattice systems (with discussion). JRStatSocB1974, 34:192 – 236.
• [40] Lindsay BG. Composite likelihood methods. Contemp Math 1988, 80:220–239.
• [41] Renard D, Molenberghs G, Geys H. A pairwise likelihood approach to estimation in multilevel probit models. Comput Stat Data Anal 2004, 44:649–667.
• [42] Varin C. On composite marginal likelihoods. Adv Stat Anal 2008, 92:1–28.
• [43] Wedderburn RWM. Quasi-likelihood functions, generalized linear models, and the Gauss–Newton method. Biometrika 1974, 61:439–447.
• [44] McCullagh P. Quasi-likelihood functions. Ann Stat 1983, 11:59–67.
• [45] Liang K-Y, Zeger S. Longitudinal data analysis using generalized linear models. Biometrika 1986, 73:13–22.
• [46] Breslow N, Clayton D. Approximate inference in generalized linear mixed models. JAmStatAssoc1993, 88:9 – 25.
• [47] Green PJ. Penalized likelihood for general semiparametric regression models. Int Statist Rev 1987, 55:245 – 259.
• [48] Lee Y, Nelder JA. Hierarchical generalised linear models: a synthesis of generalised linear models, randomeffect models and structured dispersions. Biometrika 2001, 88:987–1006.
• [49] Nelder JA, Lee Y. Likelihood, quasi-likelihood and pseudolikelihood: some comparisons. JRStatSocB 1992, 54:273–284.
• [50] Owen AB. Empirical likelihood ratio confidence intervals for a single functional. Biometrika 1988, 75:237 – 249.
• [51] Hjort NL, McKeague IW, van Keilegom I. Extending the scope of empirical likelihood. Ann Stat 2009, 37:1079 – 1111.
• [52] Balabdaoui F, Rufibach K, Wellner JA. Limit distribution theory for maximum likelihood estimation of a log-concave density. Ann Stat 2009, 37:1299–1331.
• [53] van der Vaart AW. Asymptotic Statistics. Cambridge: Cambridge University Press; 1998.