2️⃣ 概率视角看变分自编码器

〖摘要〗 本文从神经网络和概率机器学习两个视角，介绍了 VAE 背后的数学原理。严格意义上来说，变分自编码器（ VAE）是一种面向连续型隐变量的黑盒变分推断方法。其建立在基于神经网络的函数逼近之上，并可用随机梯度下降进行训练。VAE 已在生成多种复杂数据方面显示出很好的前景，包括手写数字、人脸、门牌号、CIFAR 图像、场景物理模型、分割以及从静态图像预测未来。

〖原文〗 Jaan Altosaar；Understanding Variational Autoencoders (VAEs) from two perspectives: deep learning and graphical models.；2016

1 问题的提出

为什么深度学习研究人员和概率机器学习人员在讨论变分自编码器时会感到困惑？什么是变分自编码器？为什么围绕这个术语存在不合理的混淆？

这是因为存在概念和语言上的代沟！!!

神经网络科学和概率模型之间缺少共同的语言。本文的目标之一是弥合这一差距，并允许它们之间进行更多的协作和讨论，并提供一致的实现（Github 链接。

变分自编码器让我们可以设计复杂的数据生成模型，并将其拟合到大型数据集。变分自编码器可以生成虚构的名人面孔图像和高分辨率 数字艺术作品。变分自编码器还在 图像生成 和 强化学习 中产生了最先进的机器学习结果。

Kingma 等人 和 Rezende 等人 于 2013 年定义了变分自编码器 (VAE)。

下面让我们先使用神经网络来分析它们，然后在概率模型中使用变分推断。

2 神经网络的视角

在神经网络语言中，一个变分自编码器有编码器、解码器和损失函数构成。

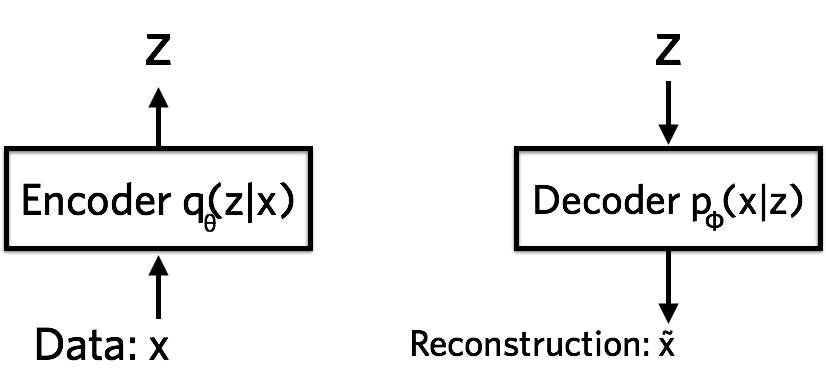
编码器（ Encoder ） 是一个神经网络。它输入一个数据点 $x$ ，输出一个隐藏表示 $z$，神经网络的权重和偏差为 $\theta$。具体来说，假设 $ x $ 是一张 $28 \times 28$ 像素的手写数字照片。编码器将 $784$ 维的数据 “编码” 到远远小于 $784$ 维的潜在（隐藏）表示空间 $z$ 中，并称其为 “瓶颈”。因为编码器必须学习如何将数据有效压缩到低维空间中。编码器用 $q_\theta (z \mid x)$ 来表示，这里我们注意到低维空间具有随机性：编码器将神经网络参数输出到 $q_\theta (z \mid x)$，而这是一个高斯概率密度。我们可以从该分布中采样以获得表示 $z$ 的含噪声值。

解码器（ Decoder ） 是另一个神经网络。它输入隐表示 $z$ ，输出数据概率分布的参数，神经网络的权重和偏差 $\phi$ 。解码器用 $p_\phi(x\mid z)$ 表示。以手写数字为例，假设照片是黑白的，每个像素表示为 $0$ 或 $1$，可以使用伯努利分布表示单个像素的概率分布。解码器将某个数字的隐表示 $z$ 作为输入，并输出 $784$ 个伯努利参数，图像中的每个像素对应一个。解码器将 $z$ 中的实值数字 “解码” 为 $784$ 个 $0$ 和 $1$ 之间的实值数字。来自原始 $784$ 维向量的信息无法完全传输，因为解码器只能访问信息的摘要（以远小于 $784$ 维向量的 $z$ 的形式）。损失了多少信息？我们使用量纲为 nats 的重建对数似然 $\log p_\phi (x\mid z)$ 来衡量。该度量告诉我们，解码器在给定隐表示 $z$ 的情况下，学习重建输入图像 $x$ 的效率如何。

损失函数（Loss Function） 是带有正则化的负对数似然。由于没有所有数据点共享的全局参数，我们可以将损失函数分解为只取决于单个数据点 $l_i$ 的项。对于 $N$ 个数据点，总损失为 $\sum_{i=1}^N l_i$ 。数据点 $x_i$ 的损失函数 $l_i$ 为：

注：在隐变量模型中，通常将隐变量区分为与所有数据点都有关的全局隐变量，和只与单个数据点有关的局部隐变量，进而有助于更为高效地推断。此处的变分自编码器可视为只有局部隐变量的特殊情况，在概率机器学习中，这种情况也被称为摊销变分推断（Amortized VI）。

$$l_i(\theta, \phi) = - \mathbb{E}_{z\sim q_\theta(z\mid x_i)}[\log p_\phi(x_i\mid z)] + \mathbb{KL}(q_\theta(z\mid x_i) \mid\mid p(z))$$

上式中第一项为重建损失（ 或第 $i$ 个数据点的负对数似然期望 ），该期望是关于隐表示 $z$ 的分布 $z \sim q_\theta(z\mid x_i)$ 的。该项鼓励解码器学习更好的重建数据。如果解码器的输出不能很好地重建数据，从统计学上来说解码器参数化了一个似然分布，但它不会在真实数据上放置太多的概率质量。例如，如果我们的目标是对黑白图像进行建模，并且模型在实际存在白点的地方存在黑点的可能性很高，那么这将产生一个糟糕的重建。糟糕的重建会在该损失函数中产生很大的成本。

式中第二项为正则化项（稍后将看到它是如何导出的）。这是编码器产生的隐表示分布 $q_\theta(z\mid x)$ 和 $ p(z) $ 之间的 KL 散度。散度衡量了使用 $q$ 表示 $p$ 时丢失了多少信息（以 nats 为量纲）。它是衡量 $q$ 到 $p$ 之间接近程度的一种方法。

在变分自编码器中，$p$ 被指定为均值为 $0$ 且方差为 $1$ 的标准正态分布，或形式化为 $p(z) = \text{Normal}(0,1)$ 。如果编码器输出的隐表示 $z$ 与标准正态分布的表示不同，则将在损失中受到惩罚。该正则化项的意思是 “保持每个数字的表示 $z$ 足够多样化” 。如果我们不包括正则化器，编码器可以学会作弊并在欧式空间的不同区域中为每个数据点提供一个表示。这很糟糕，因为两个相同数字的图像（ 比如不同人写的 2 ，$2_{Alice}$ 和 $2_{Bob}$ ）最终可能会得到非常不同的隐表示 $z_{Alice}, z_{Bob}$ 。我们希望 $z$ 的表示空间有意义，所以惩罚这种行为。这会起到将相似数字的表示保持在一起的效果（ 例如，数字 2 的隐表示 ${z_{Alice}, z_{Bob}, z_{Ali}}$ 保持足够接近 ）。

我们使用梯度下降法训练变分自编码器，以优化得到编码器和解码器的参数 $\theta$ 和 $\phi$ 。对于步长为 $\rho$ 的随机梯度下降，使用 $\theta \leftarrow \theta - \rho \frac{\partial l}{\partial \theta}$ 更新编码器参数，并对解码器做类似的更新。

3 概率模型的视角

现在从概率模型的角度考虑变分自编码器。请暂时忘记对深度学习和神经网络的了解。将以下概念与神经网络分开思考会清楚一些，我们最后会再回到神经网络。

在概率模型框架中，变分自编码器是一个包含数据 $x$ 和隐变量 $z$ 的特定概率模型。可以将该模型的联合概率分布写为 $p(x, z) = p(x \mid z) p(z)$。其生成过程可以写成如下：

对于每个数据点 $i$ :

• 从 $p(z)$ 中抽取一个隐变量值 $z_i \sim p(z)$
• 从 $p(x\mid z)$ 中抽取一个数据点 $x_i$

可以将该模型表示为如下概率图模型：

这是我们从概率模型视角讨论变分自编码器时考虑的核心对象。隐变量是从先验 $p(z)$ 中提取的，数据 $x$ 的似然 $p(x \mid z)$ 以隐变量 $z$ 为条件。上面的概率图模型实质上定义了数据和隐变量的联合概率分布：$p(x, z) = p(x\mid z)p(z) $。对于黑白二值数字像素而言，似然 $p(x \mid z)$ 为伯努利分布。

现在可以考虑在该模型中进行推断。目标是在给定观测数据的情况下，推断隐变量的可能值，或者是贝叶斯框架中所说的，计算后验 $p(z \mid x)$：

$$p(z \mid x) = \frac{p(x \mid z)p(z)}{p(x)}$$

分母项 $p(x)$ 为边缘似然（或称为证据），要计算它需要关于隐变量的先验做边缘化处理：$p(x) = \int p(x \mid z) p(z) dz$，而边缘化所做的积分需要指数时间来计算，无法接受。因此，通常不会直接求后验 $p(z \mid x)$ 的精确解，而是想办法追求其近似解。

变分推断采用由变分参数 $\lambda$ 索引的变分分布族 $q_\lambda(z \mid x)$ 来近似后验分布 $p(z \mid x)$ 。例如，如果 $q$ 是高斯分布，则变分参数是每个数据点对应隐变量的均值和方差 $\lambda_{x_i} = (\mu_{x_i}, \sigma^2_{x_i})$。

如何知道变分后验 $q(z \mid x)$ 接近真实后验 $p(z \mid x)$ 的程度？我们可以使用 KL 散度，它衡量使用 $q$ 近似 $p $ 时丢失的信息（以 nats 为单位）：

$$\mathbb{KL}(q_\lambda(z \mid x) \mid \mid p(z \mid x)) = \mathbf{E}_q[\log q_\lambda(z \mid x)]- \mathbf{E}_q[\log p(x, z)] + \log p(x)$$

我们的目标是找到最小化这种差异的变分参数 $\lambda$。因此最优近似后验是：

$$q_\lambda^* (z \mid x) = {\arg\min}_\lambda \mathbb{KL}(q_\lambda(z \mid x) \mid \mid p(z \mid x))$$

该式不能直接计算，因为其中的边缘似然 $p(x)$ 难以处理，需要另外一种元素来进行易处理的变分推断。考虑以下函数：

$$ELBO(\lambda) = \mathbf{E}_q[\log p(x, z)] - \mathbf{E}_q[\log q_\lambda(z \mid x)]$$

请注意，我们可以将其与 KL 散度 结合起来，并将边缘似然重写为：

$$\log p(x) = ELBO(\lambda) + \mathbb{KL}(q_\lambda(z \mid x) \mid \mid p(z \mid x))$$

根据 Jensen 不等式 ，KL 散度始终大于或等于 0。这意味着最小化 KL 散度等效于最大化证据下界 ELBO。证据下界允许我们采用另外一种方式进行近似后验推断，即不必计算和最小化 KL 散度，而是最大化等效的、在计算上用于处理的 ELBO。

在变分自编码器模型中，只有局部隐变量。因此，可以将 ELBO 分解为若干项的总和，其中每个项都取决于单个数据点，进而可以对变分参数 $\lambda$ 使用随机梯度下降（ 注意：虽然隐变量均为局部的，但变分参数却是在数据点之间共享的 - 详情参见 平均场变分推断）。

变分自编码器中单个数据点的 ELBO 为：

$$ELBO_i(\lambda) = \mathbb{E}{q_\lambda(z\mid x_i)}[\log p(x_i\mid z)] - \mathbb{\mathbb{KL}}(q_\lambda(z\mid x_i) \mid\mid p(z))$$

要看到这与我们之前对 ELBO 的定义等效，将对数联合分布扩展为先验和似然项，并对对数使用乘法法则。

让我们转换到神经网络语言：我们使用 推断网络（或编码器） 参数化近似后验 $q_\theta (z \mid x, \lambda)$，该推断网络输入数据 $x$ 并输出参数 $\lambda$ ；我们使用 生成网络（或解码器） 参数化似然 $p(x \mid z)$，该网络输入隐变量并输出数据分布 $p_\phi(x \mid z)$ 的参数。推断和生成网络分别有参数 $\theta$ 和 $\phi$ ，通常是神经网络的权重和偏差。我们使用随机梯度下降法来优化这些参数，以最大化 ELBO（ 没有全局隐变量，因此对数据进行小批量处理很方便 ）。我们可以进一步推导 ELBO 并将推断和生成网络参数做一区分：

$$ELBO_i(\theta, \phi) = \mathbb{E}{q_\theta(z\mid x_i)}[\log p_\phi(x_i\mid z)] - \mathbb{KL}(q_\theta(z\mid x_i) \mid\mid p(z))$$

此证据下界是从神经网络角度讨论的变分自动编码器损失函数的负值： $ELBO_i(\theta, \phi) = -l_i(\theta, \phi)$ ，不过这次是从概率模型和近似后验推断得出的。我们仍然可以将 KL 散度 项解释为正则化项，将 预期似然项 解释为重建损失。但概率模型方法清楚地说明了为什么存在这些术语：最小化近似后验 $q_\lambda(z \mid x)$ 和模型后验 $p(z \mid x)$ 之间的 KL 散度。

模型参数该如何处理呢？ 变分推理的核心就是相对于变分参数 $\lambda$ 最大化 ELBO ，以求得最优的 $\lambda$ 。我们可以根据模型参数 $\phi$（ 例如，参数化似然的生成神经网络的权重和偏差 ）最大化 ELBO。这种技术称为变分 EM（期望最大化），因为需要最大化数据相对于模型参数的对数似然的期望。

就是这样！我们遵循了变分推断的方法。我们已经定义了：

• 一个隐变量和数据的概率模型 $p$
• 一个为隐变量设置的变分族 $q$ ，用于近似后验

以后就是使用变分推断算法来学习变分参数了（ 即通过 ELBO上的梯度上升学习 $\lambda$ ）。我们使用模型参数的 变分 EM 算法（ 即通过 ELBO 上的梯度上升学习 $\phi$）。

4 可视化展示

现在我们已经准备好查看模型中的样本了。有两种选择来衡量进度：从先验采样或从后验采样。为了更好地了解如何解释学习到的隐空间，可以做隐变量 $q_\lambda(z \mid x)$ 的后验分布可视化。

在计算上，这意味着通过推断网络馈入图像 $x$ 以获得隐变量 $z$ 的正态变分分布参数；然后基于变分分布对隐变量 $z$ 进行采样。我们可以在训练期间绘制此图，以查看推断网络如何学习更好地近似隐变量的后验，并将不同类别数字的隐变量放置在隐空间的不同位置。请注意，在训练开始时，隐变量的分布接近于先验（ $0$ 附近的圆形区域）。

在训练期间可视化学习到的近似后验。随着训练的进行，数字类别在二维潜在空间中变得不同。

我们还可以可视化基于先验的预测分布，将隐变量的值固定在 $-3$ 和 $3$ 之间等距。然后可以从由生成网络参数化的似然中取样。这些 “虚幻” 图像展示了模型与隐空间的每个部分相关联的内容。

通过查看似然的样本来可视化基于先验的预测分布。 $x$ 和 $y$ 轴表示 $-3$ 和 $3$ 之间（二维）等距的隐变量值。

5 词汇表

我们需要以清晰简洁的方式决定用于讨论变分自编码器的语言。以下是令人困惑的术语表：

• 变分自编码器 Variational Autoencoder (VAE)
  • 在神经网络语言中，变分自编码器由编码器、解码器和损失函数组成。
  • 在概率模型术语中，变分自编码器是指隐变量的后验高斯近似推断，只是其中近似后验推断和模型似然生成由神经网络做了参数化（推断网络和生成网络）。
• 损失函数 Loss function:
  • 在神经网络语言中，我们关注损失函数。训练通常意味着最小化损失函数。
  • 在变分推断语境中，我们通常关注最大化证据下界 ELBO 。这导致在使用神经网络框架做ELBO 优化时，只能用 optimizer.minimize(-elbo) 作为优化器。
• 编码器 Encoder:
  • 在神经网络语言中，编码器是一个用于将数据的原始表征 $x$ 转换为新表征 $z$ 的神经网络。
  • 在概率模型术语中，推断网络参数化了隐变量 $z$ 的近似后验推断，其输出为变分分布 $q(z \mid x)$ 的参数。不过，现在也有人人为，贝叶斯推断过程就是生成 $x$ 的新表征 $z$ 的过程，只是 $z$ 不再是确切的固定值，而是一个具有概率分布的随机变量。
• 解码器 Decoder:
  • 在深度学习中，解码器是一个用于学习从表征 $z$ 重构（或恢复）数据原始表征 $x$ 的神经网络。
  • 在概率模型术语中，解码器是被生成网络参数化了的数据似然，其输出为似然函数 $p(x \mid z)$ 的参数。
• 局部隐变量 Local latent variables:
  • 在变分自编码器语境中，每个数据点 $x_i$ 都有对应的局部隐变量 $z_i$，没有全局隐变量。正是因为只有局部隐变量，我们才可以轻松地将 ELBO 分解为依赖于单个数据点 $x_i$ 的求和项 $\mathcal{L}_i$ ，进而使得随机梯度下降成为可能。
  • 在概率模型术语中，上述方法被称为摊销变分推断。
• 推断 Inference:
  • 在神经网络语境中，推断往往意味着给定新数据点 $x^*$ 后，预测其隐表征 $z^*$。
  • 在概率模型术语中，推断通常指给定观测数据后，找出其隐变量的值（或区间）.

注：关于变分推断的详细介绍，参见 XishanSnow’s 博客

6 PyTorch/TensorFlow 代码实现

这是用于生成本文中数字图像数据集的代码库：Github 链接

注：

（ 1 ）在变分自编码器的原文中，由于损失函数也具有不确定性，因此传统优化方法中的梯度计算转换成了对损失函数期望（或均值）的梯度计算。设计这种随机最优化问题的主要方法包括评分函数法和重参数化技巧，而变分自编码器采用的是后者。详情参见 XishanSnow’s 博客

（ 2 ）如果认真分析，本文为 MNIST 数据集设置的 伯努利似然 并不完全正确。 手写数字图像非常接近于二值图，但事实上确实连续的。这篇文章 采用 连续伯努利分布 修正了这个问题。

参考文献

[1] Many ideas and figures are from Shakir Mohamed’s excellent blog posts on the reparametrization trick and autoencoders.

[2] Durk Kingma created the great visual of the reparametrization trick.

[3] Great references for variational inference are this tutorial and David Blei’s course notes.

[4] Dustin Tran has a helpful blog post on variational autoencoders.

[5] David Duvenaud’s course syllabus on “Differentiable inference and generative models”.

Cite this work: