SPDE: 高斯场和高斯马尔可夫随机场之间的明确联系

【摘 要】 连续索引的高斯场 (GF) 是空间统计建模和地统计学中最重要的组成部分，通过协方差函数的定义给出了场性质的直观解释。在计算方面，高斯场受到大 $n$ 问题限制，因为密集矩阵的分解计算成本是维度的三次方（$\mathcal{O}(n^3)$）。尽管当前计算能力处于历史最高水平，但这一事实似乎仍然是许多应用中的瓶颈。与高斯场同样中要的，还有一类离散索引的高斯马尔可夫随机场 (GMRF)，其马尔可夫性质导致精度矩阵的稀疏性，从而使我们可以使用稀疏矩阵的数值算法。对于 $\mathbb{R}^2$ 中的场， GMRF 仅使用了一般算法所需时间的平方根（$\mathcal{O}(\sqrt{n^3})$）。 GMRF 由其完整条件分布分布定义，但在这种参数化形势下，其边缘分布性质并不明确。在本文中，我们展示了：对于 Matérn 类型的某些高斯场，（线性）随机偏微分方程的近似随机弱解，可以为 $\mathbb{R}^d$ 上的任何三角形剖分提供在高斯场和 GMRF 之间的显式链接，进而可以将该高斯场表示为基函数的形式。其好处是：我们既能使用高斯场进行建模，又能够利用 GMRF 进行高效计算。更重要的是，此方法可以推广到由随机偏微分方程生成的其他协方差函数，包括振荡协方差函数、非平稳高斯场、流形上的高斯场等。我们使用在球面上定义的非平稳模型分析了全球温度数据，进而说明了方法的有效性。

【原 文】 Lindgren, F., Rue, H. and Lindström, J. (2011) ‘An explicit link between Gaussian fields and Gaussian Markov random fields: the stochastic partial differential equation approach’, Journal of the Royal Statistical Society: Series B (Statistical Methodology), 73(4), pp. 423–498. Available at: https://doi.org/10.1111/j.1467-9868.2011.00777.x.

1 引言

（1）大 n 问题

高斯场 (Gaussian Fields, GFs) 在空间统计中起着主导作用，尤其是在传统地统计学领域（Cressie，1993 年 ^[22]；Stein，1999 年 ^[77]；Chiles 和 Delfiner，1999 年^[20]；Diggle 和 Ribeiro，2006 年^[29]），并在现代空间分层建模中构成了重要组成部分 (Banerjee et al., 2004 ^[6])。高斯场是少数合适的多变量模型之一，具有明确且可计算的归一化常数，并且具有良好的分析特性。在坐标为 $s \in \mathcal{D}$ 的域 $\mathcal{D} \in \mathbb{R}^d$ 中，如果所有有限集合 $\{x(\mathbf{s}_i)\}$ 都是联合高斯分布，则 $x(\mathbf{s})$ 是一个连续索引的高斯场。在大多数情况下，高斯场是使用均值函数 $\mu( \cdot )$ 和协方差函数 $C( \cdot , \cdot )$ 指定的，因此均值是 $\boldsymbol{\mu} = \left(\mu(\mathbf{s}_i) \right)$，协方差矩阵是 $\boldsymbol{\Sigma} = \left(C(\mathbf{s}_i, \mathbf{s}_j) \right)$。通常，协方差函数只是两个位置之间的相对位置的函数，在这种情况下，它被称为平稳的；如果协方差函数仅取决于位置之间的欧几里德距离，则它是各向同性的。由于常规协方差矩阵是正定的，因此协方差函数必须是正定函数。这种限制使得很难 “发明” 表示为封闭形式表达式的协方差函数。 Bochner 定理可以在这种情况下使用，因为它刻画了 $\mathbb{R}^d$ 中所有连续的正定函数。

尽管从分析和实践的角度来看高斯场都很方便，但计算问题一直是一个瓶颈。这是由于在使用过程中，需要计算 $n × n$（协方差）矩阵的 Cholesky 分解，其一般成本为 $\mathcal{O}(n^3)$ 。虽然今天的计算能力是历史最高的，但趋势似乎是维度 $n$ 总是在超越，似乎总是比给期望的计算时间高一点。贝叶斯分层模型的日益普及，使得这个问题变得更加严重，因为 “其中基于随机模拟的重复计算可能非常缓慢，甚至不可行”（Banerjee 等，2004 年，第 387 页）。这种情况被非正式地称为 “大 n 问题”。

（2）常见解决途径

有几种方法试图克服或避免 “大 n 问题” ：

• 似然的谱表示方法 ： (Whittle, 1954 ^[83]) 可以估计（功率）谱（使用离散傅里叶变换计算）并从中计算对数似然（Guyon, 1982 ^[44]; Dahlhaus 和 Kunsch, 1987 ^[26]; Fuentes, 2008 ^[36]），但这仅适用于（近）规则网格上直接观测到的平稳高斯场。
• 似然的条件近似方法 ：Vecchia (1988 ^[79]) 和 Stein 等 (2004 ^[78]) 基于排序表示的条件分布来构造似然，然后通过简化条件集来降低计算复杂度，类似想法也适用于计算条件期望 (Kriging)。
• 低秩方法 ：另一种方法是对简化的低秩高斯模型进行精确计算（Banerjee 等，2008 年^[7]；Cressie 和 Johannesson，2008 年 ^[24]；Eidsvik 等，2010 年^[32]）。
• 协方差锥化 ：Furrer 等 (2006 ^[37]) 将协方差锥化（一种稀疏化方法）应用于协方差矩阵的零输出部分以获得计算加速。然而，稀疏模式将取决于高斯场的变程，以及相关方法的潜力。
• Banerjee 等 (2004 ^[6]) 提出了一种 “Lattice 方法”，优于协方差锥化的想法。

（3）本文方法

在本文方法中，高斯场将被高斯马尔可夫随机场 (GMRF) 取代；参见 Rue 和 Held (2005 ^[69]) 的详细介绍和 Rue 等（2009 ^[70]）的综述。

GMRF $\mathbf{x}$ 是 离散索引的 高斯场，其中每个测点 $i，i = 1, \ldots, n$ 的完整条件分布 $\pi (x_i | \mathbf{x}_{-i})$ 仅依赖于一组邻居 $∂i$，一致性要求意味着如果 $i \in ∂j$ 那么 $j \in ∂i$。在 GMRF 的计算中，效益主要来自以下事实：精度矩阵 $\mathbf{Q}$（即高斯场中协方差矩阵的逆矩阵）可以直接直接建模，并且器中零值的模式与邻居直接相关； $Q_{ij} \neq 0 \leftrightarrow i \in ∂j \cup j$，参见 Rue and Held (2005 ^[69], Sec 2.2)。 因此，在 MCMC 算法中可以根据其简单的完整条件分布高效计算似然并更新后验（这一点恰恰是贝叶斯框架中的高斯场模型存在的问题），这在很大程度上解释了自 J. Besag 发表开创性论文 (Besag, 1974 ^[9], 1975 ^[9]) 以来， GMRF 流行的原因。

此外， GMRF 还允许使用快速直接数值算法（Rue，2001 ^[68]），因为矩阵 $\mathbf{Q}$ 的数值分解可以使用稀疏矩阵算法实现（George 和 Liu，1981 ^[38]；Duff 等，1989 ^[30]；Davis，2006 ^[28]），其在二维情况下的典型成本为 $\mathcal{O}(n^{3/2})$ ；有关详细算法请参见（Rue 和 Held，2005 ^[69]）。

GMRF 具有非常好的计算特性，这在贝叶斯推断中非常重要。将 GMRF 与嵌套集成拉普拉斯近似 (INLA)（Rue 等，2009 年 ^[70]）结合，可以在分层贝叶斯框架中，对隐高斯场模型进行快速准确的贝叶斯推断，进而进一步增强了此优势。

（4）关键问题

尽管 GMRF 具有非常好的计算特性，但当前基于 GMRF 的统计模型相对简单（主要应用于面元数据）。其主要原因包括：

首先， 缺少参数化 GMRF 精度矩阵的好方法 ，理想的参数化应当能够使精度矩阵根据两个测点之间的相关性实现预定义的某种行为，并能够有效控制边缘方差。根据矩阵原理而言，构造一个正定的精度矩阵可以相应地获得一个正定的协方差矩阵，因此，可以考虑将基于协方差矩阵的条件分布替换为基于稀疏精度矩阵的等价条件分布。为此，人们尝试采用一些简化的方法来构造精度矩阵，例如让 $Q_{ij}$ 与测点 $i$ 和 $j$ 之间的相互距离相关^{[14][4][82][65][42]}；但更详细的分析表明，这样的基本原理是次优的 ^[12][71]，并且可能会产生令人意外的结果 ^[81]。

其次，尚不清楚 GMRF 模型的适用类别到底有多大。这里的复杂问题在于全局正定性约束， 采用 GMRF 到底对完整条件分布的参数化带来何种影响似乎并不明确 。Rue 和 Tjelmeland (2002 ^[71]) 凭经验证明 GMRF 可以非常接近地统计学中大多数常用的协方差函数。从计算角度出发（例如克里金法），他们提议将其用作高斯场的计算替代品。不过他们的方法存在几个问题： 首先， GMRF 到高斯场的拟合被限制在一个规则网格（或环面）上； 其次，拟合本身必须为某些参数（如平滑度和变程）提前执行一些耗时的数值优化算法。 此外，尽管有了一些 “概念验证” 结果，但在方法论上并没有取得任何显著进展^[53][75][25]。

尽管存在上述问题，但该方法本身已经表明甚至对时空模型也很有用（Allcroft 和 Glasbey，2003 ^[3]）。

（5）基本思路

上述讨论揭示了一种解决 “大 n 问题” 的、看似不错的建模和计算策略：

( a ) 像传统方法一样，在一组位置 $\{\mathbf{s}_i\}$ 上使用高斯场进行建模，构建具有协方差矩阵 $\boldsymbol{\Sigma}$ 的高斯场；

( b ) 找到一个具有局部邻域结构的 GMRF，尽最大可能来 “表示” 该高斯场，即令该 GMRF 的 $Q^{-1}$ 尽量接近 $\boldsymbol{\Sigma}$。

( c ) 利用稀疏矩阵的数值方法，基于这种 GMRF 表示进行高斯场的相关计算。

不过，上述想法依赖于两个基本假设：

• 首先，该高斯场本身具备 GMRF 的可表示性，即能够被表示为具有局部邻域的 GMRF ，并保持对参数和结果的可解释性。

• 其次，无论采用任何位置集合，都必须能够从高斯场计算出这种 GMRF 表示，而且要达到比直接处理高斯场更大的总体效益。

（6）本文贡献

本文证明： 对于 $\mathbb{R}^d$ 中某些满足 Matérn 协方差函数的高斯场， GMRF 表示可以明确地满足上述要求，从而为解决 “大 N 问题” 提供了理论上的支撑。此结果具有对 Matérn 协方差函数的局限性，不过 Matérn 协方差函数涵盖了空间统计中最重要和最常用的大多数协方差模型，参见 Stein ，1999 ^[77], p.14 。

可以使用随机偏微分方程 (SPDE) 来明确构造高斯场的 GMRF 表示，不过该方程需要满足如下要求： 当该 SPDE 被高斯白噪声驱动时，其解是一个具有 Matérn 协方差的高斯场 。按照此方法构造的 GMRF 表示， 将是一个由分段线性基函数组成的表示 ，该表示中的高斯权重满足马尔可夫依赖性，且可以由问题域内的三角剖分来确定。

限制性条件：
（1）高斯场的协方差函数必须是 Matérn 的；
（2）该高斯场是某个随机偏微分方程的解；
（3）该高斯场的 GMRF 表示，是一个由若干基函数组成的线性分段函数，并且基函数的高斯权重值直接体现马尔可夫性，其邻接关系由问题域内的三角剖分确定。

对这个基本结果的扩展似乎打开了新的大门和机会，并为相当困难的建模问题提供了简单答案。例如，这种方法可以扩展到流形上的 Matérn 场、非平稳场、振荡协方差函数场等多种复杂场景。此外，我们将讨论本方法与 Sampson 和 Guttorp (1992) 的变形方法（主要针对非各向同性、非平稳协方差的模型）之间的联系，并探讨如何将新方法自然地扩展到不可分离的时空模型。

我们的一个重要观察是： 在此建模策略中，不必为协方差函数构造显式公式，而是通过随机偏微分方程（ SPDE ） 隐式定义。

本文其余部分安排如下：

• 在第 2 节中，我们讨论了 Matérn 协方差与特定随机偏微分方程之间的关系，并基于该关系给出了显式构建 GMRF 精度矩阵的两个重要结果。
• 在第 3 节中，将结果扩展到三角流形上的场、非平稳场、振荡协方差函数场和不可分离时空模型上的场。
• 在第 4 节中，通过对全球温度数据的非平稳分析对上述扩展进行了说明。
• 第 5 节 为讨论和总结。

文中最后是四个技术附录，包括：(A)显式表示结果； (B) 流形上随机场的理论；© 希尔伯特空间表示的细节；(D) 技术细节的证明。

2 预备知识

本节将介绍 Matérn 协方差模型，并讨论如何通过随机偏微分方程（ SPDE ）来表示它。我们将规则网格上给出利用 GMRF 表示 Matérn 场的明确结果，并进行非正式总结。

2.1 Matérn 协方差模型

令 $\|·\|$ 表示 $\mathbb{R}^d$ 中的欧氏距离。位置 $\mathbf{u,v} \in \mathbb{R}^d$ 之间的 Matérn 协方差函数定义为：

$$r(\mathbf{u,v}) = \frac{ \sigma^2 }{2^{ν−1} \Gamma(ν)}(\kappa \|\mathbf{v-u}\|)^{ν} K_ν (\kappa \|\mathbf{v-u}\|) \tag{1}$$

式中，$ν > 0$ 为平滑参数、$\kappa > 0$ 为尺度参数，两者也被成为协方差函数的正定（超）参数；$\sigma^2$ 为边缘方差（即自方差）。其中：

• 平滑参数 $ν$：$ν$ 既可以是整数也可以是非分数，其整数值决定了过程的均方可微性，这对于使用此类模型进行的预测很重要；$ν$ 通常是固定的。
• 尺度参数 $\kappa$：更自然的解释是变程参数 $ρ$，$ρ$ 表示当位置 $x(\mathbf{u})$ 和 $x(\mathbf{v})$ 处的随机变量之间几乎不再相关（即独立)时的欧氏距离阈值。$\kappa$ 和 $ρ$ 之间不存在简单的对应关系，为方便理解，我们将在整篇论文中使用根据经验得出的定义 $ρ = \sqrt{8ν}/\kappa$，对应于在距离 $ρ$ 处约 $0.1$ 的相关性（对于所有 $ν$ ）。
• $\Gamma(ν)$：是伽玛函数。
• $K_ν(\cdot)$：是第二类修正贝塞尔函数。

Matérn 协方差函数及其随机场的谱

（1）Matérn 协方差函数

当 Matérn 协方差仅与随机变量之间的欧式距离 $d=\|\mathbf{v-u}\|$ 相关时，也可以表示为：

$$r(d) = \frac{ \sigma^2 }{2^{ν−1} \Gamma(ν)}(\kappa d)^{ν} K_ν (\kappa d)$$

Rasmussen 等的 《Gaussian Processes for Machine Learning》 一书提到：

具有 Matérn 协方差的高斯过程在均方意义上 $\lceil ν \rceil − 1$ 阶可微。

（2）空间随机场的谱密度

具有 Matérn 协方差的空间随机场，其 $\mathbb{R}^n$ 域上的功率谱被定义（$n$ 维）傅里叶变换（参见 Wiener–Khinchin 定理）：

$$S(f) = \sigma^2 \frac{2^n \pi^{n/2}\Gamma(ν + n/2)(2ν)^{ν}}{\Gamma(ν) ρ^{2ν}} \left( \frac{2ν}{ρ^2} + 4 \pi^2 f^2\right)^{-(ν + n/2)}$$

（3）分数的简化

当平滑参数 $\nu = p + 1 / 2, p \in \mathbb{N}^{+}$ 时, Matérn 协方差可以被写为一个指数函数和一个 $p$ 阶多项式的乘积：

$$C_{p+1 / 2}(d)=\sigma^2 \exp \left(-\frac{\sqrt{2 p+1} d}{\rho}\right) \frac{p !}{(2 p) !} \sum_{i=0}^p \frac{(p+i) !}{i !(p-i) !}\left(\frac{2 \sqrt{2 p+1} d}{\rho}\right)^{p-i},$$

例如：

• 对于 $\nu=1 / 2(p=0): 有 C_{1 / 2}(d)=\sigma^2 \exp \left(-\frac{d}{\rho}\right)$,
• 对于 $\nu=3 / 2(p=1)$ : 有 $C_{3 / 2}(d)=\sigma^2\left(1+\frac{\sqrt{3} d}{\rho}\right) \exp \left(-\frac{\sqrt{3} d}{\rho}\right)$,
• 对于 $\nu=5 / 2(p=2): 有 C_{5 / 2}(d)=\sigma^2\left(1+\frac{\sqrt{5} d}{\rho}+\frac{5 d^2}{3 \rho^2}\right) \exp \left(-\frac{\sqrt{5} d}{\rho}\right)$.

（4）与平方指数核的关系

当 $\nu \rightarrow \infty$ 时, Matérn 协方差收敛到平方指数协方差函数（高斯）：

$$\lim _{\nu \rightarrow \infty} C_\nu(d)=\sigma^2 \exp \left(-\frac{d^2}{2 \rho^2}\right) .$$

（5）零处的泰勒展开与谱的矩

当 $d \rightarrow 0$ 时的表现，可以用如下泰勒展开表示 (需要参考，当 $\nu = 1$ 时，下式会导致除以零):

$$C_\nu(d)=\sigma^2\left(1+\frac{\nu}{2(1-\nu)}\left(\frac{d}{\rho}\right)^2+\frac{\nu^2}{8\left(2-3 \nu+\nu^2\right)}\left(\frac{d}{\rho}\right)^4+\mathcal{O}\left(d^5\right)\right) .$$

当定义满足时，可以从泰勒展开式得到以下谱的矩:

$$\begin{aligned} & \lambda_0=C_\nu(0)=\sigma^2, \\ & \lambda_2=-\left.\frac{\partial^2 C_\nu(d)}{\partial d^2}\right|_{d=0}=\frac{\sigma^2 \nu}{\rho^2(\nu-1)} . \end{aligned}$$

2.2 Matérn 场与随机偏微分方程

概念解释：
随机微分方程：在方程中包含随机项或随机系数的微分方程。
随机偏微分方程：在方程中包含随机项或随机系数的偏微分方程。
例如： 随机热方程可以被表示为 $\partial_t u=\Delta u + \xi$，其中 $\Delta$ 表示拉普拉斯算子，$\xi$ 为随机白噪声。

Matérn 协方差函数出现在许多科学领域（Guttorp 和 Gneiting，2006 ^[43]），本文主要利用的关系是： 线性分数随机偏微分方程的解是一个具有 Matérn 协方差的高斯场”：

$$(\kappa^2 − \Delta)^{α/2} x(\mathbf{u}) = \mathcal{W}(\mathbf{u}) \tag{2}$$

式中：

• $x(\mathbf{u})$ ： 表示随机场，其中 $\mathbf{u} \in \mathbb{R}^d$；
• $(\kappa^2 − \Delta )^{α/2}$ ：表示伪微分算子，我们将在 式 (4) 中对其进行定义。其中 $\Delta$ 代表拉普拉斯算子: $\Delta= \sum^{d}_{i=1} \frac{∂^{2} }{∂x_i^2}$； $α = ν + d/2$，$ν > 0$； $\kappa > 0$；
• $\mathcal{W}$ ：表示具有单位方差的空间高斯白噪声过程，是该随机偏微分方程中的唯一随机项，其方差为：$\sigma^2 = \frac{\Gamma(ν) }{\Gamma(ν + d/2)(4\pi )^{d/2} \kappa^{2ν}}$

在后文中，我们将 式 (2) 的解称为 Matérn 场。不过存在特殊情况：当 $\kappa \rightarrow 0$ 或 $ν \rightarrow 0$ 时，式(2) 的极限解存在，但并不具有 Matérn 协方差函数，即当 $\kappa = 0$ 或 $ν = 0$ 时方程仍有解，而且是可以明确定义的随机量（具体讨论见 附录C.3 ）。

式 (2) 隐含了一个边界条件假设，即：当 $α ≥ 2$ 时，该微分算子的零空间是非平凡的，例如包含函数 $\exp(\kappa\mathbf{e}^{T}\mathbf{u})$。

零空间（Null Space）： 一个算子 $A$ 的零空间是方程 $Av = 0$ 的所有解 $v$ 构成的集合，也被成为 $A$ 的核空间。

非平凡解（non-trivial solution）：假设 $Av=0$，此时如果 $A$ 可逆，则解 $v=0$，是平凡解，如果 $A$ 不可逆，则 $v$ 具有不等于 $0$ 的非平凡解。

因此，上文中 “微分算子的零空间是非平凡的”，指假设偏微分算子具有非零解。也就是说，假设 $\alpha \geq 2$ 时，方程的解为非零的 Matérn 场。注意， $\alpha \geq 2$ 意味着当 $d=1$ 时，$\nu \geq 1.5$，当 $d=2$ 时，$\nu \geq 1$。

需要强调的是： Matérn 场是该随机偏微分方程的唯一平稳解。 Whittle ^[83][84] 表明，平稳 Matern 场具有如下波数谱：

$$R(\mathbf{k}) = (2\pi )^{−d} (\kappa^2 + \|\mathbf{k}\|^2)^{−α} \tag{3}$$

根据 $\mathbb{R}^d$ 空间中的分数拉普拉斯算子的傅里叶变换定义，有：

$$\{ \mathcal{F} (\kappa^2 − \Delta)^{α/2} \phi \} (\mathbf{k}) = (\kappa^2 + \|k\|^2)^{α/2}(\mathcal{F}\phi)(\mathbf{k}) \tag{4}$$

其中 $\phi$ 是 $\mathbb{R}^d$ 上的函数，在上式右侧具有明确定义的傅里叶逆变换。

介绍比较粗旷，需要参考 附录 A 《流形、随机场和算子标识符》。

3 主要结论

本节包含我们的主要结果，但是形式松散且不精确。本文附录中的陈述是精确的，并给出了证明。在讨论中，我们将问题域限制在二维 $d = 2$，不过结果具有一般性。

3.2 主要结果一

我们将使用一些非正式的论据和 Besag (1981 ^[11]) 提出的一个分析结果，结果正确性的证明见附录。

令 $\mathbf{x}$ 是由 $ij$ 索引的二维规则网格（趋于无限）上的 GMRF ，则其完整条件分布可以简化为：

$$\begin{align*} \mathbb{E}(x_{ij} | \mathbf{x}_{-ij} ) &= \frac{1}{a} (x_{i-1,j} + x_{i+1,j} + x_{i,j-1} + x_{i,j+1})\\ \mathbb{Var}(x_{ij} \mid \mathbf{x}_{-ij} ) &= \frac{1}{a} \tag{5} \end{align*}$$

其中 $|a| > 4$。为了简化符号表示，我们将这个特定模型用图形化方式表示为:

图 0.0

该符号仅显示了与 “a” 所在位置相关的精度矩阵元素（参见 Rue and Held，2005 年 ^[69] 第 3.4.2 节图形符号解释）。由于精度矩阵具有对称性，所以该符号只显示了以 “a” 为中心元素时的右上象限，省略了左下象限。

Besag (1981 ^[11], 式 (14)) 给出了协方差函数近似为：

$$\mathbb{Cov}(x_{ij}, x_{i^{\prime} j^{\prime}}) \approx \frac{1}{2\pi } K_0\{l \cdot \sqrt{(a − 4)}\}, l \neq 0$$

其中 $l$ 是位置 $ij$ 和位置 $i^{\prime}j^{\prime}$ 之间的欧氏距离。上式是一个广义的协方差函数，是 式（1） 在参数 $\kappa^2 = a − 4$、 $\sigma^2 = a/(4\pi)$，极限 $ν \rightarrow 0$ 的情况下的结果（ 尽管 式 (1) 要求 $ν > 0$ ）。这意味着：当 $ν = 0$ 时，由 式 (5) 所定义的离散模型是单位距离规则网格上随机偏微分方程的近似解。

当 $α = 1, \kappa^2 = a − 4$ （因为默认 $d=2$，所以此处亦指 $ν = 0$）时，根据 式（3） 可知，式(2) 的解是一个具有如下谱的广义随机场：

$$R_1(\mathbf{k}) \propto (a − 4 + \|\mathbf{k}\|^2)^{-1}$$

这意味着: 随机偏微分方程就像一个 “平方转移函数等于 $R_1$ 的” 线性滤波器。如果我们用具有谱 $R_1$ 的高斯噪声替换 式(2) 右侧的噪声项，则解的谱 $R_2 = R^2_1$，依此类推。其结果是：当 $ν = 1$ 和 $ν = 2$ 时， Matérn 场的 GMRF 表示的系数，是 图0.0 中系数的卷积。

当 $ν = 1$ 时，有:

当 $ν = 2$ 时，有:

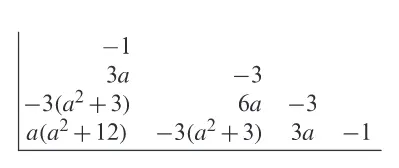
此时边缘方差为 $1/\{4\pi ν(a − 4)^ν\}$。

图 1 显示了当平滑参数为 $ν = 1$ 、变程分别为 $10$ 和 $100$ 时，上述近似的准确性。图中显示和比较了 Matérn 相关性（实线）和 GMRF 表示下整数滞后处的线性插值相关性。对于变程 $100$，两者几乎无法区分。对于变程 $10$ 和 $100$，两种相关性之间的均方根误差分别为 $0.01$ 和 $0.0003$（绘至两倍变程处）。边缘方差的误差在变程为 $10$ 时是 $4\%$，但在变程为 $100$ 时可忽略不计。

图 1. 变程为 10 (a) 和 100 (b) 时的 Matérn 相关性 (用实线表示)，以及 GMRF 表示的相关性 (用“ $\circ$ ” 表示)

我们的第一个结果证实了上述直觉。

【主要结果 I】 在二维单位距离规则（无限）网格上，当平滑参数 $ν = 1, 2, \ldots$ 时，式（2） GMRF 表示中的系数，可以通过对 图 0.0 做 $ν$ 次自身卷积得到。

该结果的简单扩展包括沿主轴的各向异性（如 附录 A 中所示）。在本文附录中导出了结果的严格表述，表明上述结果是随机偏微分方程和 GMRF 之间更广义链接的一个特例。

3.3 主要结果二

【主要结果 I】 很有用，但还不完全实用，因为在很多应用中，我们并不希望使用规则网格，并希望能够在细节不清晰的地方获得必要的、更为精细的分辨率。因此，我们通过将 $\mathbb{R}^2$ 细分为一组不相交的三角形剖分，将规则网格扩展成了不规则网格，其中任意两个三角形至多在公共边或角处相交。三角形的三个角被称为顶点。在大多数情况下，我们将初始顶点放置在观测位置处，并添加额外的顶点以满足三角形的整体软约束，例如最大允许边长和最小允许角度。

在工程中，这是使用有限元方法求解偏微分方程的标准问题（Ciarlet，1978 年^[21]；Brenner 和 Scott，2007 年^[17]；Quarteroni 和 Valli，2008 年^[66]），其解的质量取决于三角剖分的性质。通常，选择能够最大化最小内角的三角剖分，即所谓的 Delaunay 三角剖分，这有助于确保小三角形和大三角形之间的平滑过渡。此外，可以以尽量减少（满足大小和形状约束的）三角形总数为约束目标，试探式地添加额外的顶点。有关算法的详细信息参见例如 Edelsbrunner (2001 ^[31])； Hjelle 和 Dæhlen (2006 ^[52]) 。我们在 R-inla 包 (www.r-inla.org) 中的实现主要基于 Hjelle 和 Dæhlen (2006 ^[52])。

为了说明 $\mathbb{R}^2$ 的三角剖分过程，我们将使用 Henderson 等 (2002 ^[49]) 的示例。模拟英格兰西北部白血病生存数据的空间变化。 图 2(a) 显示了 1982 年至 1998 年间在英格兰西北部诊断出的 $1043$ 例成人急性髓性白血病病例的位置。在分析中，空间尺度已经归一化，使得研究区域的宽度等于 $1$。图 2(b) 显示感兴趣区域的三角测量，在数据位置周围采用了精细分辨率，在感兴趣区域外采用了粗分辨率。此外，我们将三角形顶点放置在所有的观测数据位置处。此示例中的顶点数为 $1749$，三角形数为 $3446$。

图 2. (a) 白血病存活观测的位置，(b) 由 $3446$ 个三角形构成的三角剖分， © 平稳相关函数 (用实线表示) 和相应的 GMRF 近似 (用 $\bullet$ 表示)，其中尺度 $ν = 1$， 近似变程为 $0.26$。

为了在三角剖分上构建 Matérn 场的 GMRF 表示，我们从 式（2） 的随机弱公式开始。

（1）测试函数集

首先定义内积

$$\langle f, g \rangle = \int f (\mathbf{u})g(\mathbf{u})d \mathbf{u} \tag{7}$$

其中积分是关于整个感兴趣区域的。

随机偏微分方程的随机弱解可以通过如下方式找到： 对于每个适当的有限测试函数集 $\{\phi_j(\mathbf{u}), j = 1, \ldots, m\}$，下式的内积成立。

$$\{ \langle \phi_j, (\kappa^2 − \Delta)^{α/2} x \rangle \} \stackrel{d} = \{ \langle \phi_j, \mathcal{W} \rangle \} \tag{8}$$

其中 “$\stackrel{d} =$” 表示一对一对等分布。

（2）有限元表示

下一步是构建随机偏微分方程解的有限元表示（Brenner 和 Scott，2007 年^[17]），对于选定的基函数 $\{\psi_k\}$，随机场的有限元表示为：

$$x(\mathbf{u}) = \sum^{n}_{k=1} \psi_k (\mathbf{u})w_k \tag{9}$$

其中 $n$ 为是角剖分中的顶点数，$\{w_k\}$ 为基函数的（高斯）权重。

我们选择使用在每个三角形中分段线性的函数 $\psi_k$，定义方法是在顶点 $k$ 处令 $\psi_k$ 为 $1$，在所有其他顶点处令 $\psi_k$ 为 $0$。对采用此基函数选择方法的 式(9)，可以解释为：权重决定了顶点处的场值，而三角形内部的场值由线性插值决定。连续索引解的完全分布由权重的联合分布决定。

待消化

通过找到 式(9) 中表示权重的分布，可以获得有限维的解。其方法是仅针对一组特定的测试函数，能够满足 式 (8)，其中 $m = n$。

（3）测试函数的构造

测试函数的选择与基函数相关，它决定了所得模型表示的近似性质：

• 对于 $α = 1$，我们选择 $\phi_k = (\kappa^2 − \Delta )^{1/2} \psi_k$，代表最小二乘解；
• 对于 $α = 2$，我们选择 $\phi_k = \psi_k$，代表 Galerkin 解。
• 对于 $α \geq 3$，我们在 式(2) 左侧设 $α = 2$，并用 $α − 2$ 生成的场替换 式（2） 右侧，同时设 $\phi_k = \psi_k$。本质上，这会生成一个终止于 $α = 1$ 或 $α = 2$ 的递归 Galerkin 公式，参见 附录 C 了解详情。

定义 $n × n$ 矩阵 $\mathbf{C}$、$\mathbf{G}$ 和 $\mathbf{K}$ 的元素如下：

$$\begin{align*} C_{ij} = \langle \psi_i, \psi_j \rangle \\ G_{ij} = \langle \nabla \psi_i, \nabla \psi_j \rangle \\ (\mathbf{K}_{\kappa^2})_{ij} = \kappa^2 C_{ij} + G_{ij} \end{align*}$$

使用 Neumann 边界条件（边界处的零法向导数），我们可以得到第二个主要结果（ 采用面向 $\mathbb{R}^1$ 和 $\mathbb{R}^2$ 的表示）。

【主要结果 II 】令 $\mathbf{Q}_{α,\kappa^2}$（ $α = 1, 2, \ldots$ ）代表 式(9) 中高斯权重 $\mathbf{w}$ 的精度矩阵，则该精度矩阵是 $\kappa^2$ 的一个函数，并且 式 (2) 解的有限维表示的精度为：

$$\left.\begin{array}{l} \mathbf{Q}_{1, \kappa^2}=\mathbf{K}_{\kappa^2}, \\ \mathbf{Q}_{2, \kappa^2}=\mathbf{K}_{\kappa^2} \mathbf{C}^{-1} \mathbf{K}_{\kappa^2}, \\ \mathbf{Q}_{\alpha, \kappa^2}=\mathbf{K}_{\kappa^2} \mathbf{C}^{-1} \mathbf{Q}_{\alpha-2, \kappa^2} \mathbf{C}^{-1} \mathbf{K}_{\kappa^2}, \quad \text { for } \alpha=3,4, \ldots \end{array}\right\} \tag{10}$$

关于这个结果的一些讨论：

(1) 矩阵 $\mathbf{C}$ 和 $\mathbf{G}$ 易于计算，因为其元素仅当基函数对之间共享同一个三角形（ $\mathbb{R}^1$ 中为同一线段 ）时才非 $0$，并且其值不依赖于 $\kappa^2$。 附录 A 中给出了明确公式。

(2) 矩阵 $\mathbf{C}^{-1}$ 是稠密的，这使得精度矩阵也很稠密。在 附录 C.5 中，我们证明 $\mathbf{C}$ 可以用对角矩阵 $\tilde{\mathbf{C}}$ 代替，其中 $\tilde{C}_{ii} = \langle \psi_i, 1 \rangle$ ，这能够使精度矩阵变稀疏，并获得 GMRF 模型。

(3) 上述讨论的结果是：我们有了一个从 “高斯场模型的参数” 到 “ GMRF 的精度矩阵元素” 之间的显式映射，其对于任何三角剖分的计算代价为 $\mathcal{O}(n)$。

(4) 当所有顶点都是规则网格上的点时，使用规则的三角剖分会将【主要结果 II 】 降至【主要结果 I 】。请注意，在 $\mathbb{R}^2$ 中，当 $α = 1$ 时相应 GMRF 的邻域为 $3 × 3$ , 当 $α = 2$ 时为 $5 × 5$，依此类推。增加随机场的平滑度 $\nu$ 会导致 GMRF 表示中出现更大的邻域。

(5) 就 Matérn 协方差函数中的平滑参数 $ν$ 而言，式（10） 的结果分别对应于 $\mathbb{R}^1$ 中的 $ν = 1/2, 3/2, 5/2, \ldots$ 和 $\mathbb{R}^2$ 中的 $ν = 0, 1, 2, \ldots$。

(6) 我们目前无法提供其他 $α$ 值时的结果；主要障碍是随机偏微分方程中的分数导数，它采用 式(4) 的傅立叶变换定义。 Rozanov（1982 ^[67]，第 3.1 章）对连续索引随机场的一个结果称： 当且仅当谱的倒数是多项式时，随机场具有马尔可夫性质。对于 式(2)，这对应于 $α = 1, 2, 3, \ldots$; 见 式（3）。该结果表明，当 $α$ 不是整数时，可能需要一种不同的方法来提供表示结果（例如对谱本身做近似）。给定 $0 ≤ α ≤ 2$ 时的近似值，可以通过递归方法将其用于 $α > 2$。

尽管该方法确实给出了三角区域上 Matérn 场的 GMRF 表示，但它仅仅是对随机弱解的近似，因为我们只使用了所有可能测试函数的一个子集。不过，对于给定的三角剖分来说，该表示是一种最佳近似（附录 C 中具有明确表示，其中还展示了对完整随机偏微分方程解的弱收敛）。使用有限元文献中的标准结果（Brenner 和 Scott，2007 年 ^[17]），也可以得出收敛率结果。

例如，当 $α = 2$ 时，

$$\sup _{f \in \mathcal{H}^1 ;\|f\|_{\mathcal{H}^1} \leqslant 1}\left\{E\left(\left\langle f, x_n-x\right\rangle_{\mathcal{H}^1}^2\right)\right\} \leqslant c h^2 \tag{11}$$

式中，$x_n$ 是随机偏微分方程解 $x$ 的 GMRF 表示，$h$ 是三角剖分中三角形内接最大圆的直径，$c$ 是某个常数。附录 B 的 定义 2 有希尔伯特空间标量积、范数、场值和梯度等的定义。如果最小网格角远离零，则上述结果在 $d ≥ 1$ 且 $h$ 与顶点之间的边长成正比时成立。

为了展示能够近似 Matérn 协方差到何种程度，图 2(c) 显示了 $ν = 1$ 、近似变程为 $0.26$ 时的经验相关函数（用点表示）和理论相关函数（使用 图 2(b) 中的三角剖分）。对比结果相当不错，一些点显示出了与真实相关性的差异，但可以被理解为用于减少边缘效应的、兴趣区之外的粗略三角剖分所引起。在实践中，在 GMRF 表示的准确性与顶点数量之间存在权衡。在 图 2(b) 中，我们选择在研究区域使用高分辨率，而在外部降低了分辨率。

使用 GMRF 代替给定平稳协方差模型的一个缺点是：因随机偏微分方程的边界条件所引起的边界效应。在 【主要结果 2】 中，我们使用了 Neumann 条件 扩大了边界附近的方差（详见 附录 A.4 ），但其他选择也是可能的（见 Rue 和 Held，2005 年^[69]，第 5 章）。

3.4 白血病示例

我们现在将回到 Henderson 等 (2002) ^[49] 第 2.3 节 的例子。模拟英格兰西北部白血病生存数据的空间变化。在（伪）Wilkinson-Rogers 表示法中（McCullagh 和 Nelder，1989 ^[62]，第 3.4 节）定义为：

$$\text{survival(time, censoring)} \sim \text{intercept + sex + age + wbc + tpi + spatial(location)}$$

使用 Weibull 似然 来估计生存时间，其中 “wbc” 是诊断时的白细胞计数，“tpi” 是 Townsend 剥夺指数（衡量相关地区经济剥夺程度的指标）， “spatial” 是取决于每次测量空间位置的空间分量。该模型中的超参数是：空间分量的边缘方差、变程、Weibull 分布中的形状参数。

Kneib 和 Fahrmeir (2007)^[59] 使用 Cox 比例风险模型重新分析了同一数据集，但出于计算原因，对空间分量使用了低秩近似。通过我们的 GMRF 表示，可以轻松地为空间分量使用 $1749 × 1749$ 的稀疏精度矩阵。

我们在 R-inla (www.r-inla.org) 中使用 集成嵌套拉普拉斯近似 运行了完整的贝叶斯分析（Rue 等，2009 年）^[70]。图 3 显示了空间分量的后验均值和标准差。在四核笔记本电脑上进行完整的贝叶斯分析大约需要 $16$ 秒，$2797 × 2797$（总）精度矩阵的分解平均需要大约 $0.016$ 秒。

图 3. (a) 后验平均值和 (b) 使用 GMRF 表示的生存空间效应的标准差

4. 几种扩展方法

在本节中，我们将讨论随机偏微分方程的五个扩展，以扩大 GMRF 构建结果的实用性。第一个扩展是考虑流形上偏微分方程的解，以便允许我们在球面等域上定义 Matérn 场；第二个扩展是空间变参数的随机偏微分方程，以便允许我们构建非平稳的、局部的各向同性高斯场；第三个扩展是 式(2) 的复数版本，这使得构建振荡型协方差场成为可能；第四个扩展将非平稳偏微分方程推广到更一般的非各向同性场；第五个扩展展示了随机偏微分方程在不可分离时空模型中的推广。

所有这些扩展仍然能够给出类似于 式(9) 和 式(10) 的显式 GMRF 表示，即使所有扩展都组合在一起也能实现。相当惊人的结果是，我们可以在球面上构建非平稳振荡高斯场的 GMRF 表示，并且不需要任何超出三角剖分几何特性的计算。在 第 5 节 我们将通过全球温度的非平稳模型来说明这些扩展的使用。

4.1 流形上的 Matérn 场

我们现在将离开 $\mathbb{R}^2$ 并考虑流形上的 Matérn 场。流形上的高斯场是一个经过充分研究的主题，在大脑映射中的偏移集有重要应用（Adler 和 Taylor，2007；Bansal 等，2007；Adler，2009）。我们的主要目标是在球面上构建 Matérn 场，这对于分析全球空间和时空模型非常重要。因此，为了简化当前的讨论，我们将把 Matérn 场的构造限制在三维中的单位半径球面 $\mathbb{S}^2$ 上，更为通用的情况请参见附录。

与 $\mathbb{R}^d$ 一样，球面上的模型也可以通过谱方法构建（Jones，1963）。在球面上定义协方差模型的一种更直接的方法是将二维空间 $\mathbb{S}^2$ 解释为嵌入 \mathb{R}^3 中的曲面。然后可以使用任何三维协方差函数来定义球面上的模型，只考虑函数对表面的限制。这具有使用弦距离来确定点之间的相关性的解释缺点。在原始协方差函数中使用大圆距离通常不起作用，因为对于可微分域，这不会产生有效的正定协方差函数（这遵循 Gneiting，1998，定理 2）。因此，$\mathbb{R}^d$ 中的 Matérn 协方差函数不能用于定义嵌入在 \mathb{R}^3 中的单位球面上的高斯场，其距离自然定义为相对于表面内的距离。但是，我们仍然可以使用它的起源，即 SPDE！为此，我们简单地将 SPDE 重新解释为定义在 $\mathbb{S}^2$ 而不是 $\mathbb{R}^d$ 上，解仍然是我们所说的 Matérn 场，只是直接针对给定的流形定义。驱动 SPDE 的高斯白噪声可以很容易地在 $\mathbb{S}^2$ 上定义为（零均值）随机高斯场 $W (·)$，其属性是 $W(A)$ 和 $W(B)$ 之间的协方差，对于$\mathbb{S}^2$ 的任何子集 $A$ 和 $B$ ，与 $A \cap B$ 上的表面积分成正比。任何规则的 2-流形 在局部表现得像 $\mathbb{R}^2$，这启发式地解释了为什么弱解的 GMRF 表示只需要将内积 (7) 的定义更改为 $\mathbb{S}^2$ 上的曲面积分。 附录 B - 附录 D 中的理论涵盖一般的流形设置。

为了说明球面上 Matérn 场的连续指数定义和马尔可夫表示，图 4 显示了全球 $7280$ 个气象测量站的位置，以及不规则三角测量。基于 $6370$ 公里的平均地球半径，三角测量被限制为具有最小角度 $21°$ 和对应于 $500$ 公里的最大边长。三角测量包括所有相距 $10$ 公里以上的测点，总共需要 $15182$ 个顶点和 $30360$ 个三角形。 $α = 2$ 的结果高斯场模型如图 5 所示，对于 $\kappa^2 = 16$，对应于单位半径地球上的近似相关变程 $0.7$。数值计算赤道上的一个点和所有其他点之间的协方差表明，在 图 5(a) 中，尽管三角剖分高度不规则，但与 SPDE 确定的理论协方差的偏差（通过球面傅里叶级数计算）是对于大于局部边缘长度（$≤ 0.08$）的距离几乎无法检测到，即使对于更短的距离也几乎无法检测到。模型的随机实现如 图 5（b）所示，重新采样到具有区域保留圆柱投影的经度/纬度网格。每个节点的马尔可夫邻居数量变程为 $10$ 到 $34$，平均为 $19$。由此产生的精度矩阵结构如图 6(a) 所示，节点的相应排序如图 6(b) 所示。通过将节点索引映射到灰度。排序使用马尔可夫图结构递归地将图划分为条件独立的集合（Karypis 和 Kumar，1999），这有助于使精度矩阵的 Cholesky 因子稀疏。

图 4. (a)、(b) 数据位置和 ©、(d) 第 4 节中分析的全球温度数据集的三角测量，叠加了海岸线图

图 5. (a) 协方差（ 实心圈 – GMRF 近似的数值结果；实线 – 理论协方差函数）和 (b) 来自单位球面上平稳 SPDE 模型 (2) 的随机样本，其中 $ν = 1$ 和 $\kappa^2 = 16$

图 6.（a）（重新排序的）$15182 \times 15182$ 精度矩阵的结构和（b）重新排序的可视化表示：每个三角剖分节点的索引已映射到灰度，显示重新排序算法的控制原则，递归将图划分为条件独立的集合

4.2 非平稳场

从传统角度来看，SPDE 框架中最令人惊讶的扩展是我们如何对非平稳性进行建模。许多应用确实需要相关函数的非平稳性，并且有大量关于此主题的文献（Sampson 和 Guttorp，1992 年；Higdon，1998 年；Hughes-Oliver 等，1998 年；Cressie 和 Huang，1999 年；Higdon 等 ，1999 年；Fuentes，2001 年；Gneiting，2002 年；Stein，2005 年；Paciorek 和 Schervish，2006 年；Jun 和 Stein，2008 年；Yue 和 Speckman，2010 年）。 SPDE 方法具有额外的巨大优势，即生成的（非平稳）高斯场是 GMRF，它允许快速计算并且可以在流形上做定义。

在（2）中定义的 SPDE 中，参数 $\kappa^2$ 和新方差在空间上是常数。一般来说，我们可以允许两个参数都依赖于坐标 $\mathbf{u}$，我们记为

$$\{\kappa^2(\mathbf{u}) − \Delta\}^{α/2} \{τ (\mathbf{u}) x(\mathbf{u})\} = \mathcal{W}(\mathbf{u}) \tag{12}$$

为简单起见，我们选择保持新方差不变，而是使用尺度参数 $τ(\mathbf{u})$ 缩放生成的过程 $x(\mathbf{u})$。当一个或两个参数不是常数时，就会实现非平稳性。特别感兴趣的是它们随 $\mathbf{u}$ 缓慢变化的情况，例如在像这样的低维表示中:

$$\log(\kappa^2(\mathbf{u})) = \sum_i β^{(\kappa^2)}_i B^{(\kappa^2)}_i (\mathbf{u})$$

和

$$\log \{ τ(\mathbf{u}) \}= sum_i β^{(τ)}_i B^{(τ)}_i (\mathbf{u})$$

其中基函数 $\{B^{(·)}_i (·)\}$ 在感兴趣的域上是平滑的。随着参数 $\kappa^2(\mathbf{u})$ 和 $τ(\mathbf{u})$ 的缓慢变化，将 (12) 作为 Matérn 场的局部解释保持不变，而实现的非平稳相关函数的实际形式是未知的。 “将所有局部 Matérn 域组合成一个一致的全局域” 的实际过程是由 SPDE 自动完成的。

式 (12) 的 GMRF 表示是使用与平稳情况相同的方法找到的，但有细微的变化。为方便起见，我们假设 $\kappa^2$ 和 $τ$ 在基函数 $\{\psi_k \}$ 的支持下都可以被认为是常数，因此

$$\langle \psi_i, \kappa^2\psi_j \rangle = \int \psi_i(\mathbf{u}) \psi_j(\mathbf{u}) \kappa^2(\mathbf{u}) d \mathbf{u} \approx C_{ij} \kappa^2(u_j^∗) \tag{13}$$

对于在 $\psi_i$ 和 $\psi_j$ 的支持下自然定义的 $u_j^∗$。结果是在不增加成本的情况下对 (10) 中的矩阵进行简单缩放，请参阅附录 A.3。如果我们将积分近似 (13) 从考虑 $\kappa^2(\mathbf{u})$ 局部常数改进为局部平面，计算预处理成本会增加，但对于精度矩阵 $Q_α$ 中的每个元素仍然是 $\mathcal{O}(1)$。

4.3 振荡协方差函数

另一个扩展是考虑基本方程 (2) 的复数版本。为简单起见，我们只考虑 $α = 2$ 的情况。将创新过程 $\mathcal{W}_1$ 和 $\mathcal{W}_2$ 作为两个独立的白噪声场， 和振荡参数 $θ$，复数版本变为:

$$\{\kappa^2 \exp(i\pi θ) − \Delta\} \{x_1(\mathbf{u}) + ix_2(\mathbf{u})\} = \mathcal{W}_1(\mathbf{u}) + i \mathcal{W}_2(\mathbf{u}), 0 ≤ θ < 1 \tag{14}$$

实部和虚部平稳解分量 $x_1$ 和 $x_2$ 是独立的，具有在 $\mathbb{R}^d$ 上的谱密度

$$R(\mathbf{k}) = (2\pi )^{−d} (\kappa^4 + 2 cos(\pi θ) \kappa^2 \| \mathbf{k} \|^2 + \| \mathbf{k} \|^4)$$

$\mathbb{R}$ 和 $\mathbb{R}^2$ 的相应协方差函数在 附录 A 中给出。对于一般流形，找不到封闭形式的表达式。在 图 7 中，我们通过比较 $\mathbb{R}^2$ 和单位球面 $\mathbb{S}^2$ 的振荡协方差来说明紧凑域获得的共振效应。结果场的精度矩阵是通过对常规情况的构造进行简单修改而获得的，即 附录 A 中给出的精确表达式。附录 C.4 中给出的细节，也揭示了多变量场的可能性，类似于 Gneiting 等（2010）。

对于 $θ = 0$，恢复了 $ν = 2 − d/2$ 的常规 Matérn 协方差，振荡随 $θ$ 增加。极限情况 $θ = 1$ 生成本征平稳随机场，在 $\mathbb{R}^d$ 上对任意方向的余弦函数的加法不变，波数为 $\kappa$。

图 7. 振荡 SPDE 模型的相关函数，对于 $θ = 0, 0.1,\ldots,1$，在 (a) $\mathbb{R}^2$ 和 (b) $\mathbb{S}^2$ 上，$\kappa^2 = 12$ 和 $ν = 1$

4.4 非各向同性模型和空间变形

在 第 4.2 节 中定义的非平稳模型 ，尽管具有全局非平稳相关性，但具有局部各向同性相关性。这可以通过扩大所考虑的 SPDE 的类别、允许非各向同性拉普拉斯算子以及包括方向导数项来放宽。这也提供了与 Sampson 和 Guttorp (1992) 引入的非平稳协方差变形方法的链接。

在变形方法中，域被变形到场平稳的空间中，导致原始域中的非平稳协方差模型。使用指向 SPDE 模型的链接，生成的模型可以解释为原始域中的非平稳 SPDE。

为了符号简单，假设变形在两个 d-流形 $\Omega \subseteq \mathbb{R}^d$ 到 $\tilde{\Omega} \subseteq \mathbb{R}^d$ 之间，其中 $\mathbf{u} = f (\tilde{\mathbf{u}})，\mathbf{u} \in \Omega， \tilde{u} \in \tilde{\Omega}$。限制在 $α = 2$ 的情况下，考虑变形空间 $\tilde{\Omega}$ 上的平稳 SPDE，

$$(\kappa^2 −\tilde{\nabla} \cdot \tilde{\nabla}) \tilde{x}(\tilde{\mathbf{u}}) =\tilde{\mathcal{W}}(\tilde{\mathbf{u}}) \tag{15}$$

生成平稳的 Matérn 场。变量在未变形空间 $\Omega$ 上的变化产生（Smith，1934）

$$\frac{1}{\operatorname{det}\{F(\mathbf{u})\}}\left[\kappa^2-\operatorname{det}\{F(\mathbf{u})\} \nabla \cdot \frac{F(\mathbf{u}) F(\mathbf{u})^{\mathrm{T}}}{\operatorname{det}\{F(\mathbf{u})\}} \nabla\right] x(\mathbf{u})=\frac{1}{\operatorname{det}\{F(\mathbf{u})\}^{1 / 2}} \mathcal{W}(\mathbf{u}) \tag{16}$$

其中 $F(\mathbf{u})$ 是变形函数 $f$ 的雅可比矩阵。这种非平稳 SPDE 精确地再现了具有 Matérn 协方差的变形方法（Sampson 和 Guttorp，1992）。可以使用与第 4.2 节中更简单的非平稳模型相同的原理来构造稀疏 GMRF 近似。

重要的一点是，最终 SPDE 的参数并不直接取决于变形函数本身，而仅取决于它的雅可比行列式。在没有显式构造变形函数的情况下对模型进行参数化的一个可能选项是通过矢量场控制由 $F (\mathbf{u})$ 给出的局部变形的主轴，该矢量场由协变量信息或作为矢量基函数的加权和给出。添加减去方向导数项进一步概括了模型。允许所有参数（包括白噪声的方差）在整个域中变化，会产生一个非常通用的非平稳模型，其中包括变形方法和第 4.2 节中的模型。模型类可以解释为黎曼流形中度量的变化，这是欧几里得空间中嵌入的域之间变形的自然推广。完整的分析超出了本文的变程，但技术附录涵盖了大部分必要的理论。

4.5 不可分的时空模型

可分离的时空协方差函数可以被表征为具有可以写成仅在空间或时间中的谱的乘积或和的谱。相反，不可分离模型可以在空间和时间依赖结构之间进行交互。虽然显式构造不可分离的非平稳协方差函数很困难，但使用局部指定的参数可以相对容易地获得不可分离的 SPDE 模型。可以说，可以应用于 GMRF 方法的最简单的不可分离 SPDE 是传输和扩散方程，

$$\left \{\frac{∂ }{∂t} + (\kappa^2 + \mathbf{m} \cdot ∇ − ∇ \cdot \mathbf{H} ∇ ) \right \} x(\mathbf{u}, t) = \mathcal{E}(\mathbf{u}, t) \tag{17}$$

其中 $\mathbf{m}$ 是传输方向向量，$\mathbf{H}$ 是正定扩散矩阵（对于一般流形严格来说是张量），$\mathcal{E}(\mathbf{u}, t)$ 是随机时空噪声场。很明显，即使这个固定公式也会产生不可分离的场，因为解的时空功率谱是

$$R_x(\mathbf{k}, ω) = R_{\mathcal{E}} (\mathbf{k}, ω) \{ (ω + \mathbf{m} \cdot \mathbf{k})^2 + (\kappa^2 + \mathbf{k} \cdot \mathbf{Hk})^2\}^{-1} \tag{18}$$

即使 $\mathbf{m} = 0$ 和 $\mathbf{H = I}$，它也是严格不可分的。驱动噪声是规范的重要组成部分，可能需要在模型中增加一层。为了确保解决方案的预期规律性，可以选择噪声过程在时间上是白色的但具有空间依赖性，例如 $(\kappa^2 − ∇ \cdot ∇ )^{α/2} \mathcal{E}(\mathbf{u}, t) = \mathcal{W}(\mathbf{u}, t)$ ，对于某些 $α ≥ 1$，其中 $\mathcal{W}(\mathbf{u}, t)$ 是时空白噪声。 GMRF 表示可以通过首先应用普通空间方法，然后使用例如欧拉方法离散化耦合时间 SDE 的结果系统来获得。允许所有参数随空间位置（可能随时间）变化会生成一大类不可分离的非平稳模型。 Heine (1955) 评估的平稳模型可以作为特例获得。

5 实例：全球温度重建

5.1 问题背景

在分析过去观测到的天气和气候时，通常使用全球历史气候学网络 (GHCN) 数据集（Peterson 和 Vose，1997）。在 2010 年 8 月 8 日，数据包含来自各大洲 $7280$ 个测点的气象观测数据，其中 $597373$ 行观测数据中的每一行，都包含特定测点和年份的月平均温度。数据跨越 1702 年到 2010 年期间，尽管每年只计算没有缺失值的测点，但年平均值能追溯到 1835 年。空间覆盖变程从 1880 年之前的不到 $400$ 个测点到 1970 年代的 $3700$ 个不等。对于每个测点，协变量信息（例如位置、海拔和土地使用）均可用。

GHCN 数据用于分析 GISS（Hansen 等，1999 年^[45]、2001 年 ^[46]）和 HadCRUT3（Brohan 等，2006 年 ^[18]）全球温度序列中的区域和全球温度，以及其他数据，例如基于海洋的海面温度测量。这些分析以不同的方式处理数据以减少测点特定影响的影响（一种称为均质化的过程），以及有关温度异常的信息（天气与当地气候的差异，后者定义为平均天气 30 年参考期）然后聚合到经纬度网格框。然后使用基于区域的权重将网格框异常合并为每年全球平均异常的估计值。分析伴随着对由此产生的估计不确定性的推导。

尽管在细节上有所不同，但网格化程序是基于算法的，即没有针对天气和气候的基础统计模型，仅针对观测本身。我们将在这里提出基于随机模型的方法来估计过去的区域和全球温度问题的基础，作为非平稳随机偏微分方程模型如何在实践中使用的示例。最终目标是重建整个时空年（甚至月）平均温度场，采用适当的不确定性措施，同时考虑模型参数的不确定性。

在接收卫星数据时，NASA 对其进行校准（“1 级”）并对其进行预处理，以产生空间和时间上不规则的 TCO 测量值（“2 级”）。随后处理 2 级数据以生成每日、空间规则的数据产品，并广泛发布给科学界（“3 级”）。 TCO 的 3 级数据产品使用 1° 纬度 x 1:25° 经度 (1°×1:25°) 像素（McPeters 等（1996），第 44 页）。 2 级 TCO 数据来自 NASA-Goddard 的臭氧处理团队分布式活动存档中心，并以伊利诺伊大学国家超级计算应用中心开发的分层数据格式存储。

5.2 模型概要

气候和观测模型由参数向量 $\boldsymbol{\theta} = \{\boldsymbol{\theta}_\mu, \boldsymbol{\theta}_\kappa, \boldsymbol{\theta}_τ , \boldsymbol{\theta}_s, \boldsymbol{\theta}_\varepsilon \}$ 控制，我们表示年温度场 $\mathbf{x} = \{\mathbf{x}_t\}$ 和年观测值 $\mathbf{y} = \{ \mathbf{y}_t\}$，其中 $t = 1970, \ldots, 1989$. 使用基函数矩阵 $\mathbf{B}_\mu$（所有 $49$ 次球谐函数，包括 $6$ 阶，参见 Wahba，1981 ^[80]），$\mathbf{B}_\kappa$ 和 $\mathbf{B}_τ$（sin（纬度）中的 2 阶 B 样条曲线，如 图 8 所示），期望场由 $\mathbf{\mu}_{x|\boldsymbol{\theta}} = \mathbf{B}_\mu \boldsymbol{\theta}_\mu$ 给出，局部空间相关性 $\kappa(\mathbf{u})$ 通过 $\log(\boldsymbol{\kappa}^2) = \mathbf{B}_\kappa \boldsymbol{\theta}_\kappa$ 定义，局部方差缩放 $τ(\mathbf{u})$ 通过 $\log(\boldsymbol{τ}) = \mathbf{B}_τ \boldsymbol{\theta}_τ$ 定义。选择气候场的先验分布为 SPDE $\Delta \mu(\mathbf{u}) = σ_\mu\mathcal{W}(\mathbf{u})$ 的近似解，其中 $σ_\mu \gg 0$，它为球谐函数提供自然的相对先验权重。

图 8. (a) 三个转换后的 2 阶 B 样条基函数，以及 (b) 标准偏差和 © 年度天气的近似相关范围的近似 $95\%$ 可信区间，作为纬度的函数

年温度场 $\mathbf{x}_t$ 根据气候有条件地定义为

$$(\mathbf{x}_t|\boldsymbol{\theta}) \sim \mathcal{N}(\boldsymbol{\mu}_{\mathbf{x} \mid \boldsymbol{\theta}}, \mathbf{Q}^{-1}_{\mathbf{x} \mid \boldsymbol{\theta}} )$$

其中 $\mathbf{Q}_{\mathbf{x} \mid \boldsymbol{\theta}}$ 是对应于模型 (12) 的 GMRF 精度，其参数由 $(\boldsymbol{\theta}_\kappa, \boldsymbol{\theta}_τ)$ 确定。引入观测矩阵 $\mathbf{A}_t$，从 $\mathbf{x}_t$ 中提取节点用于每次观测，观测到的年度天气被建模为

$$(\mathbf{y}_t \mid \mathbf{x}_t, \boldsymbol{\theta}) \sim \mathcal{N}(\mathbf{A}_t \mathbf{x}_t + \mathbf{S}_t \boldsymbol{\theta}_s, \mathbf{Q}^{-1}_{\mathbf{y}|\mathbf{x},\boldsymbol{\theta}} )$$

其中 $\mathbf{S}_t \boldsymbol{\theta}_s$ 是测点特定效应，$\mathbf{Q}_{\mathbf{y} \mid \mathbf{x},\boldsymbol{\theta}} = \mathbf{I} \exp(\theta_\varepsilon)$ 是观测精度。由于我们在这里仅将数据用于说明目的，因此我们将忽略除海拔之外的所有测点特定影响。我们还忽略了连续年份之间任何剩余的剩余依赖性，仅分析每年的边缘分布特性。

贝叶斯分析从 $(\boldsymbol{\theta} \mid y)$ 和 $(\mathbf{x \mid y})$ 的后验分布的属性中得出所有结论，因此关于天气 $\mathbf{x}_t$ 的所有不确定性都包含在模型参数 $\boldsymbol{\theta}$ 的分布中，反之亦然。最重要的步骤之一是如何确定给定观测和模型参数的天气条件分布

$$(\mathbf{x}_t|\mathbf{y}_t, \boldsymbol{\theta}) \sim \mathcal{N} \{ \mathbf{\mu}_{x \mid \boldsymbol{\theta}} + \mathbf{Q}^{-1}_{\mathbf{x \mid y},\boldsymbol{\theta}} \mathbf{A}_t^T \mathbf{Q}_{\mathbf{y|x},\boldsymbol{\theta}} ( \mathbf{y}_t − \mathbf{A}_t \mathbf{\mu}_{\mathbf{x}|\boldsymbol{\theta}} − \mathbf{S}_t \boldsymbol{\theta}_s) , Q^{-1}_{\mathbf{x} \mid \mathbf{y},\boldsymbol{\theta}} \}$$

其中 \mathbf{Q}_{\mathbf{x} \mid \mathbf{y},\boldsymbol{\theta}} = \mathbf{Q}_{\mathbf{x} \mi \boldsymbol{\theta}} + \mathbf{A}_t^T \mathbf{Q}_{\mathbf{y} \mid \mathbf{x},\boldsymbol{\theta}} \mathbf{A}_t 是条件精度，期望是 $\mathbf{x}_t$ 的 Kriging 估计量。由于由三角剖分确定的基函数的紧凑支持，每个观测值最多依赖于 $\mathbf{x}_t$ 中的三个相邻节点，这使得条件精度与场精度 $\mathbf{Q}_{\mathbf{x}|\boldsymbol{\theta}}$ 具有相同的稀疏结构。克里金估计的计算成本在观测数量上为 $\mathcal{O}(n)$ ，在基函数数量上约为 $\mathcal{O}(n^{3/2})$ 。如果使用具有非紧凑支持的基函数，例如傅里叶基，则后验精度将是完全密集的矩阵，无论先验精度的稀疏性如何，基函数数量的计算成本为 $\mathcal{O}(n^3)$ .这表明，在构建计算效率高的模型时，仅考虑先验模型的理论特性是不够的，还需要考虑整个计算序列。

5.3 结果

我们使用 R-inla 实现了该模型。由于 $(\mathbf{x} \mid \mathbf{y}, \boldsymbol{\theta})$ 是高斯分布的，因此结果只是关于协方差参数 $(\boldsymbol{\theta}_\kappa, \boldsymbol{\theta}_τ , \boldsymbol{\theta}_\varepsilon)$ 的数值积分的近似值。由于数据集较大，本次初步分析仅基于 1970 年至 1989 年期间的数据，年温度场、测量值和线性协变量参数的联合模型需要 $336960$ 个节点，每个模型有 $15182$ 个节点场，每年的观测次数大约在 $1300$ 到 $1900$ 之间，每年包括所有没有缺失月值的测点。在 12 核计算机上完成完整的贝叶斯分析大约需要一个小时，在并行数值积分阶段，内存使用峰值约为 $50$ GB。这是对 Das (2000) ^[27] 早期工作的显著改进，在 Das (2000) 中，部分估计了 第 4.4 节中基于变形的协方差模型中的参数。在超级电脑上运行了一个多星期。

测量标准偏差的 $95\%$ 可信区间（包括局部未建模效应）计算为 $(0.628, 0.650) °C$，后验期望为 $0.634 °C$。空间协方差参数更难单独解释，但我们在 图 8 中显示了由此产生的空间变化场标准偏差和相关变程，包括逐点 $95\%$ 可信区间。两条曲线都显示出对纬度的明显依赖性，与赤道相比，两极附近的方差和相关变程都更大。标准偏差变程在 $1.2$ 和 $2.6$ °C 之间，相关变程在 $1175$ 和 $2825$ 公里之间变化。方差存在不对称的北极/南极效应，但在可信区间内可以接受对称曲线。

评估仅 $20$ 年期间的估计气候和天气是困难的，因为 “气候” 通常被定义为 $30$ 年期间的平均值。此外，用于气候模型的球谐函数的阶数不够高，无法捕捉所有区域效应。为了缓解这些问题，我们将演示文稿建立在可以合理称为 1970 年至 1989 年期间的经验气候和天气异常的基础上，实际上使用期间平均值作为参考。因此，我们不是评估 $(\boldsymbol{\mu} \mid \mathbf{y})$ 和 $(\mathbf{x}_t − \boldsymbol{\mu} \mid \mathbf{y})$ 的分布，而是考虑 $(\bar={\mathbf{x}} \mid \mathbf{y})$ 和 $(\mathbf{x}_t − \bar{\mathbf{x}} \mid \mathbf{y})$，其中 $\bar{\mathbf{x}} = \sum^{1989}_{t=1970} \mathbf{x}_t/20$。在图 9(a) 和 (c) 中，显示了经验气候的后验期望 $\mathbb{E}(\bar{\mathbf{x}} \mid \mathbf{y})$ （包括估计的海拔影响），以及 1980 年温度异常的后验期望, $\mathbb{E}(\mathbf{x}_{1980} − \bar{\mathbf{x}} \mid \mathbf{y})$。相应的标准偏差如图 9（b） 和（d） 所示。正如预期的那样，两极附近的温度较低，赤道附近的温度较高，并且还可以看到温盐环流对阿拉斯加和北欧气候的一些相对变暖效应。区域地形有明显的影响，在喜马拉雅山、安第斯山脉和落基山脉等高海拔地区显示出寒冷的区域，正如每升高 $1$ 公里海拔的估计降温效果为 $5.2 °C$ 所表明的那样。从图 9（b）和（d）可以清楚地看出，包括基于海洋的测量对于区域海洋气候和天气的分析至关重要，特别是对于东南太平洋。

图 9. (a) 1970-1989 年气候经验和 (b) 1980 年经验平均距平分别具有 © 和 (d) 相应的后验标准差的后验均值：气候包括海拔的估计影响；使用区域保留圆柱投影

考虑到这一点，人们可能会认为分析周期和数据覆盖变程太小，无法检测全球趋势，尤其是因为我们先验使用的简单模型假设气候恒定。然而，目前的分析，包括所有参数不确定性的影响，仍然为所分析的 20 年期间的全球平均温度趋势得出每世纪 $95\%$ 的贝叶斯预测区间 $(0.87, 2.18) °C$（预期 $1.52 °C$）。每个全球平均温度异常的后验标准偏差计算为约 $0.09 °C$。将这些值与 GISS 系列中的相应估计值进行比较，该系列在此期间观测到的趋势为每世纪 $1.48 °C$，得出系列之间差异的标准偏差仅为 $0.04 °C$。因此，这里的结果与 GISS 结果相似，即使没有使用海洋数据。

估计趋势在分析中使用的时间平稳模型的随机样本中出现的概率小于 $2\%$。从纯粹的统计角度来看，这可能表明年度天气平均值中存在大量未建模的时间相关性，或者预期是非平稳的，即气候正在发生变化。

由于不可能仅使用统计方法在可用的实际气候和天气系统的单一实现上区分这两种情况，因此完整的分析应结合气候系统物理学的知识，以适当地平衡气候变化和短期-模型中天气的长期依赖性。

6 讨论

这项工作的主要结果是: 我们可以使用（某些）高斯场的随机偏微分方程的近似弱解，在该高斯场和 GMRF 之间建立显式联系。

虽然该结果并不普遍适用于所有协方差函数，但可适用的模型子类还是很多的，我们希望在未来找到更多的版本和扩展；参见例如 Bolin 和 Lindgren (2011) ^[16]。这种显式联系使高斯场更为实用，因为我们可以使用协方差函数建模和解释模型的同时，使用允许稀疏矩阵数值线性代数的 GMRF 表示进行计算。在大多数情况下，我们可以利用 INLA 方法进行近似贝叶斯推断（Rue et al., 2009）^[70]，这需要隐场是一个 GMRF。我们希望随机偏微分方程的这种链接，能够有助于建立起（连续索引的）高斯场（以及地统计学）与 GMRF （或条件自回归）之间的桥梁。

此外，随机偏微分方程参数定义的简单性提供了一种新的建模方法，该方法不依赖于构造正定协方差函数的理论。通过空间变化参数，随机偏微分方程方法允许以自然方式定义和构建非平稳模型，该模型能够提供良好的局部解释，并且在计算上非常高效。在流形上的扩展也很有用，以地球上的场作为主要示例。

尚未讨论的第三个问题是，随机偏微分方程方法可能有助于将外部协变量（例如风速）解释为相关随机偏微分方程中的适当的漂移项或类似项，然后该协变量将正确输入空间相关模型。这再次成为支持更多基于物理的空间建模的论据，但正如我们在本文中所展示的那样，这种方法还可以提供巨大的计算优势。

不利的一面是，该方法伴随着建立模型的实施和预处理成本，因为它涉及随机偏微分方程、三角剖分和 GMRF 表示，但我们坚信，当需要高效计算时，此类成本是不可避免的。

参考文献

• [1] Adler, R. J. (2009). The Geometry of Random Fields. In Applied Mathematics, Volume 62 of Classics in applied mathematics. Society for Industrial & Applied Mathematics.
• [2] Adler, R. J. and J. Taylor (2007). Random Fields and Geometry. Springer Monographs in Mathematics. Springer.
• [3] Allcroft, D. J. and C. A. Glasbey (2003). A latent Gaussian Markov random field model for spatiotemporal rainfall disaggregation. Journal of the Royal Statistical Society, Series C 52, 487–498.
• [4] Arjas, E. and D. Gasbarra (1996). Bayesian inference of survival probabilities, under stochastic ordering constraints. Journal of the American Statistical Association 91(435), 1101–1109.
• [5] Auslander, L. and R. E. MacKenzie (1977). Introduction to Differentiable Manifolds. New York: Dover Publications, Inc.
• [6] Banerjee, S., B. P. Carlin, and A. E. Gelfand (2004). Hierarchical Modeling and Analysis for Spatial Data, Volume 101 of Monographs on Statistics and Applied Probability. London: Chapman & Hall.
• [7] Banerjee, S., A. E. Gelfand, A. O. Finley, and H. Sang (2008). Gaussian predictive process models for large spatial datasets. Journal of the Royal Statistical Society, Series B 70(4), 825–848.
• [8] Bansal, R., L. H. Staib, D. Xu, H. Zhu, and B. S. Peterson (2007). Statistical analyses of brain surfaces using Gaussian random fields on 2-D manifolds. IEEE Transaction on Medical Imaging 26(1), 46–57.
• [9] Besag, J. (1974). Spatial interaction and the statistical analysis of lattice systems (with discussion). Journal of the Royal Statistical Society, Series B 36(2), 192–225.
• [10] Besag, J. (1975). Statistical analysis of non-lattice data. The Statistician 24(3), 179–195.
• [11] Besag, J. (1981). On a system of two-dimensional recurrence equations. Journal of the Royal Statistical Society, Series B 43(3), 302–309.
• [12] Besag, J. and C. Kooperberg (1995). On conditional and intrinsic autoregressions. Biometrika 82(4), 733–746.
• [13] Besag, J. and D. Mondal (2005). First-order intrinsic autoregressions and the de Wijs process. Biometrika 92(4), 909–920.
• [14] Besag, J., J. York, and A. Mollie (1991). Bayesian image restoration with two applications in spatial statistics (with discussion). Annals of the Institute of Statistical Mathematics 43(1), 1–59.
• [15] Bolin, D. and F. Lindgren (2009). Wavelet Markov models as efficient alternatives to tapering and convolution fields. Preprints in Mathematical Sciences, Lund University (2009:13), submitted.
• [16] Bolin, D. and F. Lindgren (2011). Spatial models generated by nested stochastic partial differential equations. Annals of Applied Statistics, to appear.
• [17] Brenner, S. C. and R. Scott (2007). The Mathematical Theory of Finite Element Methods (3rd ed.). Springer.
• [18] Brohan, P., J. Kennedy, I. Harris, S. Tett, and P. Jones (2006). Uncertainty estimates in regional and global observed temperature changes: a new dataset from 1850. Journal of Geophysical Research 111.
• [19] Chen, C. M. and V. Thom ́ ee (1985). The lumped mass finite element method for a parabolic problem. Journal of the Australian Mathematical Society, Series B 26, 329–354.
• [20] Chiles, J. P. and P. Delfiner (1999). Geostatistics: Modeling Spatial Uncertainty. Wiley Series in Probability and Statistics. Chichester: John Wiley & Sons, Ltd.
• [21] Ciarlet, P. G. (1978). The finite element method for elliptic problems. North-Holland Pub. Co.
• [22] Cressie, N. A. C. (1993). Statistics for spatial data. Wiley
• [23] Cressie, N. and Huang, H. C. (1999) Classes of nonseparable, spatio-temporal stationary covariance functions. J. Am. Statist. Ass., 94, 1330–1340.
• [24] Cressie, N. A. C. and G. Johannesson (2008). Fixed rank kriging for very large spatial data sets. Journal of the Royal Statistical Society, Series B 70(1), 209–226.
• [25] Cressie, N. and Verzelen, N. (2008) Conditional-mean least-squares fitting of Gaussian Markov random fields to Gaussian fields. Computnl Statist. Data Anal., 52, 2794–2807.
• [26] Dahlhaus, R. and H. R. Kunsch (1987). Edge effects and efficient parameter estimation for stationary random fields. Biometrika 74(4), 877–882.
• [27] Das, B. (2000) Global covariance modeling: a deformation approach to anisotropy. PhD Thesis. Department of Statistics, University of Washington, Seattle.
• [28] Davis, T. A. (2006) Direct Methods for Sparse Linear Systems. Philadelphia: Society for Industrial and Applied Mathematics.
• [29] Diggle, P. J. and Ribeiro, P. J. (2006) Model-based Geostatistics. New York: Springer.
• [30] Duff, I. S., Erisman, A. M. and Reid, J. K. (1989) Direct Methods for Sparse Matrices, 2nd edn. New York: Clarendon.
• [31] Edelsbrunner, H. (2001) Geometry and Topology for Mesh Generation. Cambridge: Cambridge University Press.
• [32] Eidsvik, J., Finley, A. O., Banerjee, S. and Rue, H. (2010) Approximate bayesian inference for large spatial datasets using predictive process models. Technical Report 9. Department of Mathematical Sciences, Norwegian University of Science and Technology, Trondheim.
• [33] Federer, H. (1951) Hausdorff measure and Lebesgue area. Proc. Natn. Acad. Sci. USA, 37, 90–94.
• [34] Federer, H. (1978) Colloquium lectures on geometric measure theory. Bull. Am. Math. Soc., 84, 291–338.
• [35] Fuentes, M. (2001) High frequency kriging for nonstationary environmental processes. Environmetrics, 12, 469–483.
• [36] Fuentes, M. (2008) Approximate likelihood for large irregular spaced spatial data. J. Am. Statist. Ass., 102, 321–331.
• [37] Furrer, R., Genton, M. G. and Nychka, D. (2006) Covariance tapering for interpolation of large spatial datasets. J. Computnl Graph. Statist., 15, 502–523.
• [38] George, A. and Liu, J. W. H. (1981) Computer Solution of Large Sparse Positive Definite Systems. Englewood Cliffs: Prentice Hall.
• [39] Gneiting, T. (1998) Simple tests for the validity of correlation function models on the circle. Statist. Probab. Lett., 39, 119–122.
• [40] Gneiting, T. (2002) Nonseparable, stationary covariance functions for space-time data. J. Am. Statist. Ass., 97, 590–600.
• [41] Gneiting, T., Kleiber, W. and Schlather, M. (2010) Matérn cross-covariance functions for multivariate random fields. J. Am. Statist. Ass., 105, 1167–1177.
• [42] Gschlößl, S. and Czado, C. (2007) Modelling count data with overdispersion and spatial effects. Statist. Pap., 49, 531–552.
• [43] Guttorp, P. and Gneiting, T. (2006) Studies in the history of probability and statistics XLIX: on the Matérn correlation family. Biometrika, 93, 989–995.
• [44] Guyon, X. (1982) Parameter estimation for a stationary process on a d-dimensional lattice. Biometrika, 69, 95–105.
• [45] Hansen, J., R. Ruedy, J. Glascoe, and M. Sato (1999). GISS analysis of surface temperature change. Journal of Geophysical Research 104, 30997–31022.
• [46] Hansen, J., R. Ruedy, M. Sato, M. Imhoff, W. Lawrence, D. Easterling, T. Peterson, and T. Karl (2001). A closer look at United States and global surface temperature change. Journal of Geophysical Research 106, 23947–23963.
• [47] Hartman, L. and O. Hossjer (2008). Fast kriging of large data sets with Gaussian Markov random fields. Computational Statistics & Data Analysis 52(5), 2331–2349.
• [48] Heine, V. (1955). Models for two-dimensional stationary stochastic processes. Biometrika 42(1), 170178.
• [49] Henderson, R., S. Shimakura, and D. Gorst (2002). Modeling spatial variation in leukemia survival data. Journal of the American Statistical Association 97(460), 965–972.
• [50] Higdon, D. (1998). A process-convolution approach to modelling temperatures in the North Atlantic Ocean. Environmental and Ecological Statistics 5(2), 173–190.
• [51] Higdon, D., J. Swall, and J. Kern (1999). Non-stationary spatial modeling. In J. M. Bernardo, J. O. Berger, A. P. Dawid, and A. F. M. Smith (Eds.), Bayesian Statistics, 6, pp. 761–768. New York: Oxford University Press.
• [52] Hjelle, Ø. and M. Dæhlen (2006). Triangulations and Applications. Springer.
• [53] Hrafnkelsson, B. and N. A. C. Cressie (2003). Hierarchical modeling of count data with application to nuclear fall-out. Environmental and Ecological Statistics 10, 179–200.
• [54] Hughes-Oliver, J. M., G. Gonzalez-Farias, J. C. Lu, and D. Chen (1998). Parametric nonstationary correlation models. Statistics and Probability Letters 40(15), 267–278.
• [55] Ilic, M., I. W. Turner, and V. Anh (2008). A numerical solution using an adaptively preconditioned Lanczos method for a class of linear systems related with the fractional Poisson equation. Journal of Applied Mathematics and Stochastic Analysis 2008(Article ID 104525).
• [56] Jones, R. H. (1963). Stochastic processes on a sphere. Annals of Mathematical Statistics 34(1), 213–218.
• [57] Jun, M. and M. L. Stein (2008). Nonstationary covariancs models for global data. The Annals of Applied Statistics 2(4), 1271–1289.
• [58] Karypis, G. and V. Kumar (1999). A fast and highly quality multilevel scheme for partitioning irregular graphs. SIAM Journal of Scientific Computing 20(1), 359–392.
• [59] Kneib, T. and L. Fahrmeir (2007). A mixed model approach for geoadditive hazard regression. Scandinavian Journal of Statistics 34(1), 207–228.
• [60] Krantz, S. G. and H. R. Parks (2008). Geometric Integration Theory. Birkhauser.
• [61] Lindgren, F. and H. Rue (2008). A note on the second order random walk model for irregular locations. Scandinavian Journal of Statistics 35(4), 691–700.
• [62] McCullagh, P. and J. A. Nelder (1989). Generalized Linear Models. London: Chapman and Hall.
• [63] Paciorek, C. and M. Schervish (2006). Spatial modelling using a new class of nonstationary covariance functions. Environmetrics 17, 483–506.
• [64] Peterson, T. and R. Vose (1997). An overview of the Global Historical Climatology Network temperature database. Bulletin of the American Meteorological Society 78(12), 2837–2849.
• [65] Pettitt, A. N., I. S. Weir, and A. G. Hart (2002). A conditional autoregressive Gaussian process for irregularly spaced multivariate data with application to modelling large sets of binary data. Statistics and Computing 12(4), 353–367.
• [66] Quarteroni, A. M. and A. Valli (2008). Numerical Approximation of Partial Differential Equations (2nd ed.). Springer.
• [67] Rozanov, A. (1982). Markov Random Fields. New York: Springer Verlag.
• [68] Rue, H. (2001). Fast sampling of Gaussian Markov random fields. Journal of the Royal Statistical Society, Series B 63(2), 325–338.
• [69] Rue, H. and L. Held (2005). Gaussian Markov Random Fields: Theory and Applications, Volume 104 of Monographs on Statistics and Applied Probability. London: Chapman & Hall.
• [70] Rue, H., S. Martino, and N. Chopin (2009). Approximate Bayesian inference for latent Gaussian models using integrated nested Laplace approximations (with discussion). Journal of the Royal Statistical Society, Series B 71(2), 319–392.
• [71] Rue, H. and H. Tjelmeland (2002). Fitting Gaussian Markov random fields to Gaussian fields. Scandinavian Journal of Statistics 29(1), 31–50.
• [72] Samko, S. G., A. A. Kilbas, and O. I. Maricev (1992). Fractional integrals and derivatives: theory and applications. Yverdon: Gordon and Breach Science Publishers.
• [73] Sampson, P. D. and P. Guttorp (1992). Nonparametric estimation of nonstationary spatial covariance structure. Journal of the American Statistical Association 87(417), 108–119.
• [74] Smith, T. (1934). Change of variables in Laplace’s and other second-order differential equations. Proceedings of the Physical Society 46(3), 344–349.
• [75] Song, H., M. Fuentes, and S. Gosh (2008). A compariative study of Gaussian geostatistical models and Gaussian Markov random field models. Journal of Multivariate Analysis 99, 1681–1697.
• [76] Stein, M. (2005). Space-time covariance functions. Journal of the American Statistical Association 100, 310–321.
• [77] Stein, M. L. (1999). Interpolation of Spatial Data: Some Theory for Kriging. New York: Springer-Verlag.
• [78] Stein, M. L., Z. Chi, and L. J. Welty (2004). Approximating likelihoods for large spatial data sets. Journal of the Royal Statistical Society, Series B 66(2), 275–296.
• [79] Vecchia, A. V. (1988). Estimation and model identification for continuous spatial processes. Journal of the Royal Statistical Society, Series B 50, 297–312.
• [80] Wahba, G. (1981). Spline interpolation and smoothing on the sphere. SIAM Journal of Scientific and Statistical Computing 2(1), 5–16.
• [81] Wall, M. M. (2004). A close look at the spatial structure implied by the CAR and SAR models. Journal of Statistical Planning and Inference 121(2), 311–324.
• [82] Weir, I. S. and A. N. Pettitt (2000). Binary probability maps using a hidden conditional autoregressive Gaussian process with an application to Finnish common toad data. Journal of the Royal Statistical Society, Series C 49(4), 473–484.
• [83] Whittle, P. (1954). On stationary processes in the plane. Biometrika 41(3/4), 434–449.
• [84] Whittle, P. (1963). Stochastic processes in several dimensions. Bull. Inst. Internat. Statist. 40, 974–994.
• [85] Yue, Y. and P. Speckman (2010). Nonstationary spatial Gaussian Markov random fields. Journal of Computational and Graphical Statistics 19(1), 96–116.