贝叶斯神经网络快速上手教程
【摘 要】 现代深度学习方法已经成为研究人员和工程师常用的强大工具,可以解决以前似乎不可能解决的问题。然而,深度学习是一种黑箱方法,与其预测相关的不确定性很难量化。而贝叶斯统计学提供了一种形式化方法来理解和量化与深度神经网络预测相关的不确定性。本文为正在使用机器学习(特别是深度学习)的研究人员和科学家,提供了一个相关文献和工具集的概述,以帮助大家设计、实现、训练、使用和评估贝叶斯神经网络。
【原 文】 Laurent Valentin Jospin, Wray Buntine, Farid Boussaid, Hamid Laga, and Mohammed Bennamoun. 2020.Hands-on Bayesian Neural Networks - a Tutorial for Deep Learning Users.ACM Comput. Surv.1, 1 ( July 2020),35 pages. arxiv.org/abs/2007.06823
【阅后感】 本文主要介绍其中贝叶斯神经网络方法,特别是其中深度贝叶斯神经网络方法。内容主要包括:传统贝叶斯神经网络推断方法、深度学习中的贝叶斯方法、不确定性估计的评价方法等内容。其中深层贝叶斯神经网络部分基本覆盖了 2020 年前比较重大的研究进展,如 MC Dropout、反向传播贝叶斯、Bayesian Teacher 等。 其他一些近年的新进展,如: 深度集成方法、单一确定性神经网络方法等,从技术特点上不算贝叶斯神经网络方法,因此本文没有涉及,有兴趣的读者可以参见 《深度神经网络中的不确定性调研报告》);另外,深度高斯过程也是一个值得讨论的话题,本文也并未涉及,感兴趣的读者可以参见 《贝叶斯神经网络技术浅析》 的 第 5 节 )。
1 概述
深度学习导致了机器学习的革命,为解决现实生活中复杂而具挑战性的问题提供了解决方案。然而,深度学习模型容易过拟合,这对其泛化能力产生了不利影响。此外,深度学习模型存在预测结果过于自信的问题。上述特点对于诸如自动驾驶汽车 [74]、医疗诊断 [38] 、交易和金融 [11] 等应用来说存在严重的问题,因为无声的失败会导致戏剧性的结果。因此,人们提出了许多方法来减轻风险,特别是通过随机神经网络(SNN)来估计模型预测结果的不确定性。贝叶斯范式为分析和训练随机神经网络提供了严格框架,并广泛地支持了学习算法的发展。
统计学中的贝叶斯范式通常与纯粹的频率主义范式相对立,其主要区别在于假设检验方面 [15]。
贝叶斯范式基于两个简单理念。第一,概率是对事件发生信念的衡量,而不仅是当样本数量趋于无穷大时对事件发生频率的某种约束。第二,先验信念会影响后验信念。而这些理念都被一个非常简单的逆概率公式(以及其在贝叶斯统计中的解释)概括,这就是贝叶斯定理:
在传统频率主义解释中, 和 可能被简单地认为是一组输出结果。但在贝叶斯解释中,明确认为 是模型假设(典型如深层神经网络中的一套权重),而 是数据集。 被称为似然, 被称为先验, 被称为边缘似然(或证据), 为后验。按照概率论的定义, 为 和 的联合概率。
这种解释可以理解为从数据中学习,这意味着贝叶斯范式不仅为深度学习模型中不确定性的量化提供了坚实的方法,它还为理解和解释经典深度学习中的正则化技术和学习策略提供了数学框架 [69] 。
在贝叶斯(深度)学习领域有丰富的文献,包括综述或概览 [50] [85] [89],但没有一篇文献以具体和详尽的方式探讨贝叶斯神经网络的一般理论。然而,贝叶斯机器学习的范畴远大于贝叶斯神经网络。这使得人们在缺乏贝叶斯方法和高级统计学知识的情况下,很难理解这些文献。这对于愿意了解贝叶斯神经网络的深度学习从业者来说,又增加了一层复杂性。同样,这也解释了为何该领域的理论贡献很多,而贝叶斯深度学习的实际应用却很少的原因。另一个主要原因可能来自于缺乏有效算法来解决贝叶斯方法和大数据之间的计算效率问题,或者人们缺乏对最近为解决这些挑战所做贡献的了解。
本文旨在填补这一空白。本文为那些已经熟悉深度学习方法,并对贝叶斯方法感兴趣的科学家和研究生提供。它涵盖了设计、实现、训练和评估贝叶斯神经网络所需的主要原理(图 1)。它还提供了关于贝叶斯神经网络相关文献的广泛概述,从 20 世纪末的早期开创性工作 [54] 到之前引用的任何综述中都未涉及的最新文献。
它还提供了有关贝叶斯神经网络相关文献的广泛概述,从追溯到 20 世纪末的早期开创性工作 [54] 到任何先前所提综述中都没有涉及的最新成果。本教程还将重点放在实践方面。人们已经开发了大量方法来构建贝叶斯神经网络,它们的内在方法有时存在很大不同,而对这些不同方法的良好理解是有效使用贝叶斯神经网络的先决条件。据我们所知,已有文献都没有提供对这些不同方法的系统回顾。

图 1. 本文所涉及主题的思维导图。大致可分为贝叶斯深度神经网络的概念、学习方法、评估方法、以及研究人员可用于实施的工具集。
本文在第 2 节首先定义了贝叶斯神经网络的概念。第 3 节提供了一些使用深度贝叶斯神经网络的动机以及为什么它有用。然后,第 4 节介绍了统计学中的一些重要概念,这些概念被用来构思和分析贝叶斯神经网络。第 5 节介绍了如何在贝叶斯深度学习中考虑先验知识,而先验是贝叶斯统计学的一个重要部分,此外,该节还讨论了贝叶斯神经网络的先验知识与传统神经网络正则化之间的关系。第 6 节解释了如何用贝叶斯设计工具来调整监督程度和定义学习策略。第 7 节探讨了一些用于贝叶斯推断的重要算法。第 8 节回顾了贝叶斯方法如何适应于深度学习,以减少计算复杂性或内存占用率。第 9 节介绍了评估贝叶斯神经网络性能的方法。第 10 节回顾了可用于贝叶斯深度学习的不同软件框架。最后,我们在第 11 节得出结论。
2 什么是贝叶斯神经网络?
贝叶斯神经网络在不同文献中的定义略有不同,但一个共识是:贝叶斯神经网络是一个使用贝叶斯推断训练的随机人工神经网络(图 2)。

图 2 从统计学角度对神经网络进行分类。可以划分为点估计神经网络和随机神经网络,点估计神经网络学习模型参数的单个实例,而随机神经网络则学习模型参数的概率分布。不含正则化的点估计模型隐含了均匀分布的先验假设,常采用最大似然估计法进行训练;含正则化的点估计模型则使用最大后验估计法进行训练。贝叶斯神经网络则是一种显式支持先验的随机神经网络。
(1)传统神经网络的问题
人工神经网络的目标是表示一个任意的函数 。传统的人工神经网络(如前馈网络、循环网络等)通常由一个输入层、若干个隐藏层和一个输出层连接在一起形成的。习惯上,把输入变量命名为 ,把输出变量命名为 。其中,在最简单的前馈网络中,每一层 都表示为前一层的线性转换,后接一个非线性运算 (又称激活函数)。
当然也存在更复杂的架构(例如,具有多个输入、输出和奇异激活函数的网络、循环架构网络等)。这意味着,一个给定的人工神经网络架构代表了一组与可能的模型参数 相对应的函数(模型参数 代表了神经网络的所有权重 和偏置 )。
深度学习是将参数 拟合到训练数据集 上的过程, 通常是一系列的输入 和对应的标签 。标准训练方法是使用反向传播算法对最小代价函数的点估计值 进行逼近( 图 3a )。代价函数通常被定义为训练数据集的对数似然,有时会有一个正则化项来惩罚过度的参数化。从统计学角度来看,不含正则化项时可以被视为最大似然估计(MLE),而当使用正则化项时,则是最大后验(MAP)估计( 图 2 )。
点估计方法相对容易实现,但往往缺乏可解释性,并且可能以不可预见和过度自信的方式泛化到样本外数据点 [27] [63]。点估计方法的上述性质使得人工神经网络自身无法回答不确定性问题,这在股票交易、自动驾驶或医疗应用等对预测结果要求非常严谨的应用领域中存在较大问题。
在点估计模型情况下,减轻这种风险的主要方法大致基于两种思路(以分类任务为例):一是调整 Softmax 函数输出的预测类别 logit 值 的阈值;二是对分布外的样本增加额外的分类模块 [28]。另一种用于分布外样本检测的方法是深度生成模型(Deep Generative Model),这是一种旨在对复杂数据分布进行编码的特殊神经网络(例如,生成性对抗性网络)[79]。尽管如此,人们对这些不同方法还是心存担忧的,因为它们要么过于简单,要么自身可能会存在过度自信的问题 [60]。这些方法在不确定性方面存在的缺陷,是引入随机神经网络的主要动机。

图 3. 点估计神经网络与随机神经网络。 (a) 图中的点估计神经网络仅学习一组最优权重; (b) 图是一个随机激活神经网络,该网络会学习一组最优权重和激活的概率分布; © 图是一个随机系数神经网络网络,该网络学习了神经网络中权重的概率分布。
(2)什么是随机神经网络?
随机神经网络是一种引入了随机成分的神经网络。它通过对神经网络权重或激活赋予随机性,来模拟多种可能的模型(由模型参数 定义) 及其概率分布 。从这个角度来看,随机神经网络可以被视为**集成学习(Ensemble Learning)**的一种特殊情况 [99],即随机神经网络训练的不是单个模型而是一组模型,并且会聚合这组模型的预测结果。
集成学习的主要动机来自以下观测:大量性能一般但独立的预测器输出,在聚合后可以产生比单个预测器更好的预测输出 [20]。此想法同样适用于随机神经网络,尽管没有证据能够证明随机神经网络是提高准确性的最佳方法,但经验主义表明其预测输出确实优于其对应的点估计结果。
不过,使用随机神经网络架构的主要目标是更好地了解与底层过程相关的不确定性,而这是通过比较不同 参数模型(通过对激活或者权重的随机采样获得)的预测结果来实现的。如果不同参数取值的模型输出基本一致,则不确定性较低;如果不一致,那么不确定性就很高。此过程可以总结如下:
其中 代表随机噪声,说明函数 只是一个近似。
(3)贝叶斯神经网络
使用贝叶斯推断 [54] 训练的任何随机神经网络,都可以被称为贝叶斯神经网络。
要设计贝叶斯神经网络,首先考虑三个方面的因素( 见 图 4a):
- 首先要选择深度神经网络架构,即函数模型 ;
- 然后要选择一个随机模型,其中包括对模型参数的先验信念(即先验分布) 和对模型预测能力的先验信念(即似然) ,模型参数集可以被认为代表了我们做出的假设 ;
- 具有指定的数据集 。
本文其余部分会将模型参数表示为 ,并使用 表示训练集,用 表示输入特征,用 表示输出标签,以便区分训练数据和输入/输出对 。应用贝叶斯定理,并强化模型参数和输入之间的区别,可以将贝叶斯后验写为:
计算上述后验分布并且采用传统方法从中采样,通常是一个棘手的问题,特别是其中边缘似然 的计算非常困难(式 4 中的分母项)。
为了解决该问题,前人设计了两种技术途径(图 4b):
第一种是马尔可夫链蒙特卡罗方法( MCMC )。该方法利用贝叶斯公式直接对后验进行采样,要求有良好的采样器,并且需要缓存抽取的样本 ,以完成后续推断或预测任务。
第二种是变分推断方法(VI)。该方法力图通过最优化方法,来学习一个能够近似真实后验的变分分布 。
这两种方法都绕过了边缘似然的计算,这也是为什么在讨论后验时,边缘似然仅被视为归一化常数的原因。上述两种方法将在第 7 节中介绍一般性原理,第 8 节会介绍其面向深度学习的改进方法。
在得到后验分布或者其变分近似后,对于给定的新输入 ,就可以计算模型的预测结果 的概率分布 [93],以准确量化模型的不确定性:
在实际计算时, 是利用式 3 进行间接采样而得到的,即首先对 采样,然后利用蒙特卡罗积分方法计算 。其中 抽取自变分分布 或来自 MCMC 的样本 ;蒙特卡罗估计方法可以计算一些统计量,对最终预测结果和不确定性做出汇总(图 4c)。
对于执行回归任务的贝叶斯神经网络来说,对预测结果做汇总的通常做法是执行模型平均 (Model Average)[17]:
该方法在集成学习中使用非常普遍,以至于有时也被直接称为集成,但读者一定要清楚它们之间是存在区别的。为量化不确定性,协方差矩阵可以计算如下:
对于执行分类任务的贝叶斯神经网络,上述模型平均方法会给出每个类别的相对概率,其也可以被视为对分类不确定性的度量:
在这种情况下,最有可能的类别将被视为最终预测结果(当所有类别的假阳性代价相等时)。
如果不同类别的假阳性代价不同,则应使用该代价来计算风险,并选择风险最小的预测。

图 4. 设计、训练和使用贝叶斯神经网络的基本工作流程。 (a) 图为设计阶段,包括人工神经网络架构和随机模型(包括先验、似然、可能的变分族等)的选择; (b) 图为训练阶段,通常被称为统计推断,包含
第 7 节中描述的通用方法和第 8 节中描述的面向深度学习的特定方法。© 图为预测阶段,由于统计推断的输出仅仅是模型参数的后验分布,因此需要将参数边缘化才能够得到预测结果的分布。
3 贝叶斯深度学习的动机
一些用户认为定义模型参数的先验 即便可能,也会很难。对于简单模型,定义先验通常是比较直观的,例如:可以明确地添加一个正则化项以支持低次多项式函数或平滑函数 [54]。但对深度学习中使用的多层模型来说,定义先验非常困难。
既然在定义先验时很难理解深度神经网络的行为,为什么还要使用贝叶斯方法呢?
人工神经网络所编码的函数关系隐含表示了条件概率 ,而贝叶斯公式是用来求逆条件概率的合适工具,即便人们事先没有关于 的信息也一样可以使用。有很强的理论方法可以作为贝叶斯公式的支撑 [76],但本节不打算深入探讨,而是将重点讨论使用贝叶斯深度神经网络的一些实际好处:
(1)贝叶斯方法提供了一种量化深度学习中不确定性的方法。
也有人观察到,对于分类问题而言,使用教师贝叶斯网络输出的类概率而不是独热 (one-hot) 标签,可以在保留原始贝叶斯神经网络的校准和不确定性的同时,帮助学生网络的学习 [57]。
使用贝叶斯神经网络可以区分 认知不确定性(epistemic uncertainty,也称模型不确定性) 和 偶然不确定性(aleatoric uncertainty,也称任意不确定性)。 认知不确定性是知识缺乏而导致的不确定性,用后验 来度量,此类不确定性会随着数据的增加而减少。 偶然不确定性是由于数据的偶然性(或部分)而导致的不确定性(如噪声),可以通过似然函数 来度量 [14] [44] 。这使得贝叶斯神经网络在学习时具有非常高的数据效率,因为它可以在不产生过拟合的情况下从小数据集开始学习。而在模型用于预测时,样本外数据只会产生认知不确定性。这也使贝叶斯神经网络成为主动学习(activate learning)任务非常感兴趣的工具 [19] [88],因为人们可以解释模型的预测结果,查看在相同输入、不同模型参数时,是否会导致不同预测结果。
(2)贝叶斯方法显式地提供了一种正则化手段。
机器学习 “没有免费的午餐定理” [94] 可以被解释为任何监督学习算法都包括隐含先验(虽然这种解释更多是哲学而非数学的),而贝叶斯方法则明确了先验。虽然并非不可能,但现在的黑盒工具确实在整合先验知识方面非常困难。而在贝叶斯深度学习中,先验被认为是一种软约束,类似于正则化。大多数用于点估计神经网络的正则化方法,基本都可以从贝叶斯角度理解为设置了某种先验(见第 5.3 节)。此外,当新数据点出现时,以前学到的后验可循环使用,这使贝叶斯神经网络成为在线学习的重要工具 [64]。
(3)贝叶斯范式有助于对学习方法的分析,并且能够建立不同学习方法之间的联系。
一些最初不被视为贝叶斯的方法可以被隐含地理解为近似贝叶斯方法,如正则化(见第 5.3 节)或集成概念(第 8.2.2 节)。这也解释了“为什么某些很好用的非贝叶斯算法,也仍然能给出贝叶斯理解?”。实践中大多数贝叶斯神经网络架构都依赖于近似或隐含的贝叶斯方法(见第 8 节),因为精确算法往往太昂贵了。贝叶斯范式还提供了一个系统框架来设计新的学习和正则化策略,即使模型是面向点估计的。
4 贝叶斯深度学习的随机模型
如前所述,在贝叶斯神经网络的设计阶段,我们需要选择一个深度网络架构(即函数模型),还要选择一个随机模型(即哪些变量被视为随机变量以及其先验分布)。本教程重点是随机模型的设计,不会涉及函数模型的设计,一来是因为几乎所有用于点估计的神经网络模型都可用于贝叶斯深度学习,二来是关于函数模型的文献已经非常丰富了 [71]。
本节将首先介绍一种用来表示随机变量及其条件依赖关系的工具:概率图模型(Probabilistic Graphical Models, PGM),特别是其中一种在贝叶斯统计中经常被使用到的概率图模型:贝叶斯信念网络(Bayesian belief networks)。然后再展示如何从概率图模型中实现贝叶斯神经网络的随机模型。
4.1 概率图模型
概率图模型是统计学家用于表示多个随机变量之间的相互依赖性,并用图形方式来分解其概率分布的一种工具。概率图涵盖了大量模型,而本教程中只讨论其中的贝叶斯信念网络(有时也称为信念网络或贝叶斯网络), 贝叶斯信念网络是用有向无环图表示的概率图模型。
有关概率图模型的详细回顾,请参阅 [9]。
虽然贝叶斯信念网络(随机模型)和贝叶斯神经网络(函数模型)都被表示为有向无环图,但两者的含义完全不同。贝叶斯神经网络模型表示一组函数关系,如式 2所示,而贝叶斯信念网络则表示模型中随机变量的联合分布和内部结构。在考虑贝叶斯神经网络时,贝叶斯信念网络通常代表了模型中先验分布和后验分布(当采用变分推断时,则为变分分布)的基础结构(见第 7.2 节)。

图 5 概率图模型中的常用符号。(a)可观测变量用浅灰色圆圈表示;(b)不可观测的变量用白色圆圈表示;(c)某些随机变量的确定性函数用虚线圆圈;(d)参数用矩形表示;(e)
plate表示为包围了部分图要素的矩形,代表该矩形框内子图的多个相互独立的实例构成的批次 B 。
在概率图模型中,节点代表随机变量,用不同符号的节点来区分所考虑的变量性质(图 5)。贝叶斯信念网络中仅允许有向链接,这意味着目标随机变量的概率分布是以源随机变量为条件来定义的(反过来不成立)。根据乘法法则,这种条件依赖性使得贝叶斯信念网络中所有变量 的联合概率分布,能够被分解为局部随机变量某些概率分布的组合。
在概率图中,随机变量 用节点来表示,不同样式的结点符号代表了不同性质的随机变量(图 5)。有向链接是贝叶斯信念网络中唯一被允许的链接形式,表示链接所指目标变量的概率分布是根据源变量定义的( 反向链接不成立,因为源变量的概率分布不是根据目标变量定义的)。这种方式允许我们利用链式法则计算概率图模型中所有随机变量 的联合概率分布:
为完成贝叶斯信念网络,必须定义所有的概率分布 。所用分布类型取决于上下文。一旦定义了 ,则贝叶斯信念网络描述了一个数据生成过程。有向无环图的约束条件,使得父变量总是在其子孙变量前被采样,而所有变量一起形成了联合概率分布 的一个样本。
模型通常基于同一分布中采样出的多个样本进行学习。为强调这一事实,引入了 plate (plate)符号(图 5e)。一个 plate 表示其所封装的子图中所有变量 会按照指定批次维度进行重复,这也意味着 plate 种所有节点在批次之间存在独立性。这种独立性质可被用来计算某个批次 的联合概率。
在概率图模型中,需要区分观测变量和非观测变量,前者用灰色圆圈表示(图 5a),作为数据来处理;后者用白色圆圈表示(图 5b),作为假设来处理。从概率图模型得出的联合概率来看,使用贝叶斯公式可以直接定义给定观测变量的隐变量后验。

图 6. 贝叶斯信念网络 (a) 对应于传统贝叶斯回归模型、系数作为随机变量的贝叶斯信念网络; (b) 模型中的激活 作为随机变量(作为确定性随机变量),此时需要考虑链式依赖关系。
4.2 定义随机模型
考虑图 6 中的两个模型,贝叶斯神经网络和相应的贝叶斯信念网络都被画出来了。将权重视为随机变量情况下的贝叶斯信念网络(图 6a)可以代表以下数据生成过程,假设神经网络是为了做回归。
模型中选择正态分布 完全是随意的,不过在实践中比较常见。
如果神经网络是为了做分类,那么该模型将有一个类别分布 来对预测进行采样,而不是正态分布。
可以利用训练集中数据点相互独立这一假设,即用图 6 中的“ plate ”符号表示,将训练集的概率写成:
图 6b 中所示的将激活视为随机变量的情况,数据生成过程可能变成:
贝叶斯公式的联合概率公式稍微复杂一些,因为必须考虑贝叶斯信念网络跨越多个潜在变量 的链式依赖关系:
定义 有时是可能的,而且通常是可取的。例如:图 6a 和图 6b 中所描述的贝叶斯信念网络可以被认为是等效的,例如,以下 的采样:
等价于如下对 的采样:
其中 表示克罗内克积。
图 6a 中描绘的贝叶斯回归架构在实践中更为常见。有时会使用图 6b 中的替代公式,因为它有助于在使用变分推断时压缩参数的数量 [92]。这为定义先验提供了不同的选择。
5 设置先验
为小型的、因果的概率模型,先验比较直观。但对于深层神经网络来说,情况不一样,设置一个好的先验往往是一项繁琐而且不直观的任务。主要问题是:对于像人工神经网络之类的、具有大量参数和复杂结构的模型,如何对给定参数进行归纳,并不十分明确 [98]。
本节将介绍与人工神经网络的 “统计不可辨识性” 有关的常见做法和相关问题。然后,在第 5.3 节,介绍贝叶斯深度学习中的先验如何与点估计方法的正则化相关。在那里会展示传统正则化方法如何帮助我们选择合适的先验,以及贝叶斯分析如何帮助传统方法设计新的目标函数。
5.1 良好的缺省先验
对于基本架构,如图 6a 中所示的带有人工神经网络的贝叶斯回归,标准程序是对网络系数采用均值为 、对角线协方差为 的正态先验:
正如在第 5.3 节中将证明的,在训练点估计网络时,该方法等同于权重为 的加权 正则化。概率编程语言 Stan [10] 提供了一些在知道所考虑参数预期规模的情况下,如何选择 的例子 [21]。但是,虽然该方法在实践中被普遍使用,但并没有理论上的依据表明其优于任何其他表示 [80]。正态分布因其数学特性和其对数的简单表示而受到青睐,因为大多数学习算法中都使用了概率分布的对数。
5.2 不可辨识问题及其解决
贝叶斯深度学习的主要问题之一是:深度神经网络可能是一个过度参数化的模型,即其中许多参数之间存在等价关系 [59]。这被称为统计学上的不可辨识问题,即推断不会产生唯一的结果。在训练贝叶斯神经网络时,这会导致很难采样和近似的复杂多峰后验。
有两种解决方案来处理该问题:一是调整函数模型的参数化形式;二是约束先验的支撑度以消除不可辨识性。
人工神经网络中最常见的两类非唯一性是:权重空间对称性和尺度对称性。两者都不是点估计神经网络的关注点,但对于贝叶斯神经网络来说则可能是。
(1)权重空间对称性
权重空间对称性意味着,我们可以改变其中一个隐藏层的权重 (暂时不考虑偏差 )中的两行和下一层权重矩阵 中的相应列,来建立一个至少有一个隐层的人工神经网络的等效参数化表示。这意味着,随着隐层和隐层中单元数量的增加,等价表征的数量也会以阶乘形式增长,这些表征大致对应于后验分布中的众数。一种缓解策略是强制每层的偏置向量按升序或降序排列。然而,其实际效果未知,在优化的早期阶段,权重空间对称性可能隐含着对参数空间探索的支撑。
(2)尺度对称性
尺度对称性是在使用具有 性质的非线因子时产生的不可辨识问题,典型的非线性因子包括 RELU 、 Leaky-RELU 这两个最受欢迎的激活函数。在这种情况下,给层 和 赋于权重 就严格等同于赋 。这可能会降低点估计神经网络的收敛速度,该问题在实践中可通过各种激活归一化技术来解决 [1]。对于贝叶斯神经网络来说,问题稍微复杂一些,因为尺度对称性会影响后验,使得它更难近似真实形态。一些作者提议使用 Givens 变换(有时也称 Givens 旋转)来约束隐层的范数 [70],以解决尺度对称问题。
在实践中,使用高斯先验已经减少了尺度对称问题,因为它有利于每个层上具有相同 Frobenius 范数 的权重。如第 5.4 节所述,激活归一化的软版本也可以通过使用一致性条件来实现。从计算复杂度角度来看,在受限空间中对网络参数进行采样的额外复杂性是不值得的。
5.3 正则化和先验之间的联系
点估计神经网络的常见学习过程是找到使损失函数最小的参数集 ,该参数集通过对训练集数据的学习得到。
通常损失为负对数似然函数,将其转换为最大似然表示可以重写为:
根据贝叶斯范式,这只是模型的前一半。现在如果有一个关于 的先验,而我们想从后验中找到最可能的点估计。那么原问题就变成了最大后验问题:
再次将其转换为对数似然表示,即为下式:
这个公式正是正则化在机器学习和许多其他领域的应用方式。其隐含着作为先验,我们有:
对于某些实践中使用的正则化,这可能并不是理想分布,但其想法具有一般性。另一个不太正式的说法是:正则化作为参数搜索空间的软约束,起到了先验对后验的相同作用。
5.4 满足一致性条件的先验
利用式 25 中的表述,在某些情况下可以使用函数模型的预期行为来扩展先验。为此,人们通常定义一个一致性条件 ,来评估在输入 和参数集 下,预测结果的相对对数似然。
例如: 可以被设置为有利于稀疏或规则的预测,鼓励预测与某些输入变量的单调性(例如:得流感的概率随年龄的增长而增加),或者在进行半监督学习时有利于低密度区域的决策边界(第 6 节)。
在实践中, 是未知的, 是从训练集的特征中近似估计出来的:
现在可以写一个与包含一致性条件的先验成正比的函数:
其中 是没有一致性条件的先验。
6 不同监督程度的贝叶斯对策
到目前为止,文中提出的贝叶斯神经网络架构主要集中在监督学习语境中使用。然而,在现实世界的应用中,获得真实标签的代价可能非常昂贵,因此应该采用新的学习策略 [72]。本节我们将介绍:如何使贝叶斯神经网络能够适应不同程度的监督,同时展示概率图模型 PGM(主要指贝叶斯信念网络)在设计或解释学习策略时的重要性。
特别是,在点估计神经网络足以满足应用的情况下,由图 8、图 9 和 图 10中的不同 PGM 得出的贝叶斯后验形式,可以被用于获得最大后验估计器的损失函数(第 5.3 节)。

图 7. 对应于 (a) 带噪声标签的学习和 (b) 半监督学习的贝叶斯信念网络。
6.1 半监督学习及其贝叶斯对策
6.1.1 半监督学习的贝叶斯表示
训练集的输入有时具有不确定性,例如,标签 被噪声破坏了 [61],或者一些数据点缺乏标签,即半监督学习的使用场景。
在含噪声标签的情况下,我们需要扩展 贝叶斯信念网络,为含噪声标签增加一个以 为条件的新随机变量 (图 7a)。由于噪声水平本身往往是未知的,所以添加一个变量 来描述噪声比较常见。
Frenay 和 Veleysen[16] 提出了在 PGM 中集成 的不同方法(图 8),他们区分了三种情况:完全随机噪声模型、随机噪声模型、非随机噪声模型。
- 在完全随机噪声模型中, 独立于任何其他随机变量,且噪声是同方差的。
- 在随机噪声模型中, 依赖于真实标签 ,但仍然独立于特征 ,且噪声是异方差的。
- 在非随机噪声模型中, 既依赖于真实标签 ,也依赖于特征 ,例如,图像中的噪声水平增加了图像被误标的机会,且噪声是异方差的。

图 8. 对应于 (a) 完全随机噪声 (NCAR)、(b) 随机噪声 (NAR) 和 © 非随机噪声 (NNAR) 模型的贝叶斯信念网络。
这些模型比 第 4 节 中介绍的纯粹的监督贝叶斯神经网络稍微复杂一些,但可以用类似方式来处理,即从 PGM 中推导出后验公式( 式 12)并使用推断算法。
我们在此仅介绍非随机噪声模型,这是最通用的一种模型。其后验成为:
在预测阶段,对于从后验中采样的每个元组 , 和 可以不被考虑。
6.1.2 半监督学习策略
在部分标记数据的情况下,也被称为半监督学习( 图 7b ),数据集 被分成有标签的 和无标签的 。理论上,这种 PGM 可以被认为等同于 图 6a 中描述的监督学习情况,只是在这种情况下,未观测到的数据 不会带来任何信息。
无标签数据的额外信息来自于也只能来自于先验。在传统机器学习中,最常见实施半监督学习的方法是使用某种数据驱动的正则化 [86],或者采用伪标签 [82],贝叶斯方法也不例外。
(1)数据驱动的正则化
数据驱动的正则化意味着对先验假设的修改(也就是调整随机模型),以便能够从无标签数据集 中提取有意义的信息。有两种常见的方法来处理这种情况:
方法一:模型参数的先验分布以无标签样本为条件,以便突出模型的某些性质,如:在低密度区域中的一个决策边界。也就是说,使用条件分布 而不是 作为先验。这意味着随机模型将被调整为:
其中 是一个如 公式 28 中定义的、具有一致性条件的先验。
方法二:假设数据集中的可观测和不可观测样本之间存在某种依赖关系。此类贝叶斯半监督学习依赖于 无向概率图模型 来建立先验 [96],或者至少不作训练样本点 之间的独立性假设 [48]。为了简单起见,我们在 图 7b 中通过去掉 周围的 plate 来表示( 解释:概率图中由若干随机变量构成的 plate ,表示相互独立的多个样本 )。这样,后验就能够以普通方式写出来了( 式 4 ),主要区别在于现在设定的 是为了在整个数据集中强制执行某种一致性。例如,可以通过假设两个靠近的点( 根据某种取决于输入空间的相似度概念 )有可能具有更相似的标签 ,而其中的不确定性水平会随着距离增加而增加。
上述两种方法有类似的效果,选择哪种方法取决于建立模型时倾向的数学形式。
(2)伪标签
半监督学习策略也可以被重新表述为有一个弱预测,能够给出一些伪标签 ,有时还具有一定的置信度。
许多用于半监督学习的算法使用一个初始版本的模型,用有标签样本来训练 [51],以产生伪标签 ;然后用这些标签来训练最终模型。这对贝叶斯神经网络来说存在一些问题,因为贝叶斯神经网络要考虑预测不确定性,而我们不可能减少与无标签数据相关的不确定性,至少在先验中并没有做额外假设。使用更简单的模型 [53] 来获得伪标签(即使在实践中不太现实)或许可以帮助缓解这个问题。
6.2 数据增强及其贝叶斯对策
数据增强是一种策略,可以在不需要实际收集新数据的情况下,大幅增加可用于深度模型训练的样本的多样性。数据增强依赖于在不改变标签的情况下,生成增强的数据集 。例如,在图像分类任务中,可以应用旋转、翻转、添加噪音等方式增加输入图像的数量和多样性,但不改变其类别标签。数据增强现在是图像处理 [82] 和自然语言处理 [3] 中最先进技术的前沿方法。
从贝叶斯角度来看,新增加的信息是由增强过程带来的,并非来自于额外的实际数据。 可以包含原始数据集的、无限可能的变体。在实践中, 通常不是事先在训练前生成的,而是在训练过程中不断采样产生的。在训练点估计神经网络时,此过程比较直接,但在应用贝叶斯方法时存在一些微妙变化。主要的问题是:我们关心的后验为 ( 表示有关数据增强的知识 ),而不是 。这意味着,从贝叶斯的角度来看,数据增强不应该( 或者至少不应该仅仅 )被视为新增的额外数据,而应当作为一种先验,被视为模型的某种隐性转换。此外,在传统统计学背景下( 指频率统计学派 ),数据增强的概念与缺失值建模问题有关 [84],而这是一个相关但不同的问题。
增加更多数据点或多次计算类似数据点,将使后验更加聚集在 MAP 点估计值周边,即假设一个具有指定似然 的模型计算了 次相同的数据,相当于将似然调整成为:
从贝叶斯角度来看,这是并非错误,因为它可以通过修改原始随机模型中的似然函数来实现。但当新增数据集的规模变得无限大时,会带来一个问题:“ 如何正确地解释认知不确定性 ?”
也有争论认为“ 数据增强是否应该在随机模型中实现?”,其想法是:如果一个人得到了数据 ,那么他也可能得到了数据 ,其中 中的每一个元素都被增强所替代。那么 就是数据 的一个不同角度。作为模型,增强分布 就表示使用增强模型 对观测到的数据进行增强处理后,产生 的概率。这个 是 附近的数据( 图 9 )。 可以被边缘化以简化随机模型:
通过设置:
我们可以将增强的贝叶斯后验定义为:
这是与邻近风险相对应的概率 [12] 。使用这种形式的增强似然,可以避免前述想当然的方法中可能出现的重复计数问题。
在实践中,这意味着可以用蒙特卡洛方法计算 公式(33)中的积分,因此,我们可以根据 采样生成增强 的一个样本集,并计算均值:
那么,在训练过程中使用的损失函数就变成了:
可以包含少至一个元素,只要它在每次优化迭代中被重新采样即可。这大大简化了 公式(36),特别是使用 指数族分布 建立随机模型的时候。
这种方法的一个扩展,是在半监督学习背景下,为鼓励增强下的预测一致性而在损失函数中增加训练成本 [82][95],其中无标签数据被用于构建一致性项的样本。请注意,这并不是给无标签样本添加标签,而只是增加了一个用来鼓励无标签数据和其增强具有一致性标签的数据项。

图 9. 对应于数据增强管道的贝叶斯信念网络( 通过对中间数据 采样 )。
6.3 元学习、迁移学习和自监督学习
广义元学习 [33],是指使用机器学习算法来协助其他机器学习模型的训练和优化。通过元学习获得的元知识可以区别于标准知识,因为它适用于一组相关的任务,而不是单一的任务。
迁移学习指的是在给定问题上获得的一些中间知识被重新用于解决一个不同的问题。在深度学习中,它主要用于领域适应,特别是当某感兴趣的领域中样本资源匮乏,而具有相似性的另外一个领域中标签数据可用且资源丰富的时候 [67]。另外,某些预训练模型 [73] 也是一种解决方案,适用于架构较大,以至于从头训练变得很不方便的场景。
自监督学习是一种由数据本身提供标签的学习策略 [36]。由于数据直接获得的标签与感兴趣的任务并不匹配,所以问题被当作元学习来处理,在感兴趣的任务之外还有一个代理任务。使用自监督结果现在被普遍认为是某些领域的必要步骤。例如,在自然语言处理中,大多数 SOTA 方法都使用这些预训练的模型 [73] 。
在对元学习的贝叶斯理解中,我们认为迁移学习和自监督学习都是元学习的特例。

图 10. (a) 对应于有监督层次贝叶斯的贝叶斯信念网络; (b) 结合自监督学习策略的贝叶斯信念网络。 是设计定义的神经网络的中间激活层, 表示共享参数, 是代理任务特有的参数, 为特定于主任务的参数, 为从数据中获得的标签, 为主任务的标签(其中一些可能未被观测到 [4])
(1)元学习
在贝叶斯统计中,元学习的一个常见方法是将问题重塑为层次贝叶斯 [25],其中每个任务的先验 都以一个新的全局变量 为条件( 图 10a )。 可以代表一些连续的元参数(本教程的重点)或关于贝叶斯神经网络结构的离散信息(学习可能的函数模型时)或 PGM 的底层子图(学习可能的随机模型时)。如果需要的话,可以增加多个层次来组织更复杂的任务,但我们将只介绍一个层次的情况。此时后验为:
在实践中,通常用经验贝叶斯法来处理该问题(第 7.4 节),并且只考虑全局变量的点估计值 ,理想情况下该点估计来自于边缘化 后获得的 MAP 估计,但也并非总是如此。
(2) 迁移学习
在迁移学习中,通常设置 , 是主任务的系数。然后,新的先验可以从 中获得,例如:
其中 是要传递的参数的选择函数, 是需要手动调整的参数。
未选择的参数按惯例被赋予 的平均值,但也可以使用其他方法来设计先验参数的这些部分。如果贝叶斯神经网络已经为主要任务进行了训练,那么 可以在以前的后验上进行估计,但仍然需要略微放大以考虑额外的不确定性。
(3)自监督学习
自监督学习可以分两步实现,首先学习代理任务,然后使用迁移学习。这可能被认为过于复杂,但如果代理任务具有较高计算复杂性( 例如,自然语言处理中的 BERT 模型 [73] ),则这样做可能是必须的。最近的文献表明,代理任务学习和最终任务学习的结合(图 10b),可以改善自监督学习获得的结果 [4]。此方法更接近于分层贝叶斯,允许一次性设置先验,同时保留了自监督学习的优点。
7 传统贝叶斯神经网络的推断算法
在使用贝叶斯神经网络实施预测等后续任务时,只需对后验进行采样并进行模型平均即可(见式 4 和 式 6 )。但一般情况下,后验采样并不容易。如果数据的条件概率 和模型概率 由我们通过模型和先验给出,那么边缘似然项 的积分就很难计算。对于复杂( Non-trivial )的模型,即便已经计算了边缘似然,也会因为高维度采样空间和均匀随机变量的复杂变换,而使后验很难采样。通常不会使用传统方法(如逆采样或拒绝采样)对贝叶斯神经网络的后验进行采样,而是设计和使用专用算法。其中最流行的:一是马尔科夫链蒙特卡洛(MCMC)方法,通过精确采样来近似后验分布的算法系列;二是变分推断(Variatial Inference, VI),通过最优化学习一个与后验比较近似的变分分布(图 4)。
7.1 MCMC 方法
马尔科夫链蒙特卡洛方法的思想是构建一条马尔科夫链,即由随机样本 构成的样本序列。该链中每个样本 被抽中的概率上只取决于前一个样本 ,因此链中的样本最终会按照一个期望的分布进行分布。MCMC 方法有以下几个特点:
- 预热:与标准的、简单的、低维的采样方法(如拒绝采样或逆采样)不同,大多数 MCMC 算法在底层马尔可夫链收敛到所需分布之前,需要一些初始的预热(
Burn-in)时间。 - 自相关:此外,相邻的 之间可能存在比较严重的自相关,使得采样效率大大降低,这意味着采样会生成一大批效率较低的样本 ,必须通过二次采样(重采样),才能获得真正有效的近似独立样本。
- 参数取舍问题:预热意味着序列开始时的部分初始样本必须被丢弃,而被丢弃的准确样本数量并不容易定义。
- 计算考虑:MCMC 方法在计算上存在一点有时比较棘手的问题,那就是样本集合 必须被缓存起来,否则无法继续后续预测等人物,而这有可能代价比较昂贵,特别是对于模型参数较多的深度学习模型。
尽管 MCMC 有其固有缺点,但仍然被认为是贝叶斯统计学中对后验分布进行精确采样的最佳可用和流行的解决方案之一 [2]。
然而,并非所有 MCMC 算法都与贝叶斯深度学习有关。例如,吉布斯采样 [22] 在传统统计学和无监督机器学习中非常流行,但很少用于贝叶斯神经网络。与贝叶斯神经网络最相关的一类 MCMC 方法是 Metropolis-Hastings 算法 [13]。该算法的特性是:不需要知道确切的概率分布 就能采样。也就是说,该算法只需要一个与该分布成比例的函数 就可以实施采样了,从而避免了边缘似然项的计算难题。
Metropolis-Hasting 算法的基本思想是以一个随机的初始猜测 开始,然后在该点 "周围 "抽取一个新的候选点。如果这个候选点比前一个候选点更有可能出现(依据被采样的分布判断),那么就接受它。如果它更不可能出现,那么以某个不确定的概率接受它,否则就拒绝它。简练地说就是:新候选点被抽中的概率更高时,直接接受新候选点;否则,按一定的随机概率接受新候选点。
更正式的描述见算法 1,该算法是用一个提议分布 构建的,它告诉我们如何 “围绕” 前一样本进行采样

算法 1 的接受概率可以被证明是产生所有可逆的 Makrov 链中接受度最高的。此外,如果选择 是对称的,即 ,则概率可以简化,接受率的公式为:
在此情况下,该算法被简单地称为 Metropolis 方法。 的常见选择有以前一样本为中心的正态分布 、或均匀分布 。
有时我们必须处理非对称的分布,例如为了适应模型的有界约束条件。此时必须考虑到完整 Metropolis-Hasting 算法 中引入的修正项。
提议分布的宽度范围必须加以小心。如果它太大,拒绝率会太高。如果它太小,样本就可能会存在过多自相关。目前还没有调整此参数的通用方法。不过,已经出现了一个能够减轻此影响并生成新样本 的巧妙策略,这就是Hamilton Monte-Carlo, HMC 方法。
Hamiltonian Monte-Carlo 算法 [62] 是 Metropolis-Hasting 算法的另一个例子,该算法为连续分布设计了一个抽取新提议 的巧妙方案,以确保尽可能少地拒绝样本,并且样本之间的相关性尽可能少。此外,该算法的预热时间也非常短。该算法产生新样本的过程基于汉密尔顿力学。首先,假设从实际位置 开始,我们以来自提议分布 的初始随机速度 移动。然后,定义系统的汉密尔顿力学为:
其中 被视为势能, 则被视为动能。我们让系统在给定的时间 内运动。相应的动力学系统被以下偏微分方程参数化:
其中,初始条件 并且 。这样做的好处是,我们仍然需要知道分布 ,但只需要知道一个比例系数。我们接受拟议的样本 ,其概率 计算为:
现在,由于哈密顿随着时间的推移而保存下来,所以 应该等于 ,而且新样本永远不会被拒绝。问题是,获得一个精确解往往也很难,所以必须依靠数字积分来代替。要做到这一点,需要使用一个对称的积分器。这是一个代表离散哈密顿系统 的积分器,与原来连续系统的 相比,只有轻微的变动。
这保留了 MCMC 算法中马尔科夫链的一个重要性质,即:如果所考虑的汉密尔顿路径在起点 处形成闭环,则数值积分器也会在 处闭环。请注意,大多数数值积分器不是辛积分器(包括流行的 Runge-Kutta 方案)。辛积分器的一个很好的选择是跃迁法,其时间步长为 。
有了这个辛积分器,我们在原哈密顿 和修正的哈密顿 之间有如下关系:
这意味着可以比较容易适应性地调整整合步长 ,来调整接受概率 。
现在问题变成选择提议分布 和积分时间 了。
- 提议分布 通常被选择为正态分布 ,其中 最明显的选择是 , 可以通过增加 来增加远离前一样本的新点的采样几率。
- 积分时间 的选择至关重要。如果它太短,相邻样本就有可能是自相关的。如果它太大,汉密尔顿路径就可能闭环,大量时间将被浪费在反复积分相同的东西上。
有人提出了对经典 HMC 算法的改进,能够实现自动调整积分时间,该算法被称为 No-U-Turn 采样器(简称 NUTS) [31],并且现代的大多数贝叶斯统计软件包都实现了此算法。
7.2 变分推断与随机变分推断
MCMC 算法是从精确后验中采样的得力工具。但其天生的特点,在面对深度学习中常见的大规模模型时,缺乏足够的可扩展性。尽管该问题可以得到在一定程度的缓解,但 MCMC 在贝叶斯深度学习领域中依然不太受欢迎。而变分推断 [6] 比 MCMC 算法的扩展性更好,因此更受欢迎。
变分推断是一种近似推断方法,其想法是存在一个由参数向量 描述(也可称索引)的分布族 ,通常被称为变分分布;变分推断通过优化算法,推断或学习参数 的值,使变分分布 尽可能地接近精确后验 。而信息论中,给出了度量两个分布之间接近程度的实用量化测度-- KL 散度。在变分推断场景中,KL 散度就是变分分布与真实后验分布之间近似度的度量,可以看出,它应该是参数 的函数。
计算 存在一个最大的难题就是要计算边缘似然 。不过有人推导出了一个不需要计算边缘似然的测度来代替 KL 散度,这就是证据下界(或 $ELBO$ ):
式中 只取决于先验,可视为常数。因此最小化 与最大化 等价。
目前几乎所有经典机器学习的大规模优化方法都适用于对 进行优化。在贝叶斯神经网络中,最流行的是随机变分推断( Stochastic Variational Inference, SVI) [32],其本质上是应用了变分推断的随机梯度下降(Stochastic Griedent Descent, SGD)。SVI 使得变分推断方法可以扩展到现代机器学习中遇到的大型数据集上,因为其每次迭代都可以在小批量上计算 。
请注意:
- 当用变分推断学习后验知识时,与普通反向传播相比,收敛速度会较慢。
- 在执行梯度步骤前,大多数 SGD 实现都会使用尽量少的样本量来计算损失函数(常常只用一个样本),这意味着作为损失函数的 在迭代过程中会相当嘈杂。
在传统机器学习和统计中, 大多由指数族分布构造而成,例如多元正态分布 [26]、Gamma 分布 和 Dirichlet 分布。另外,在对模型参数做出一些独立性假设(如平均场)后, 可以被戏剧性地简化为若干组分,从而导致期望最大化(EM)算法的扩展[23]。另外,为了考虑模型参数之间可能存在的相关性,也可以做一些近似建模,例如使用块对角线协方差矩阵 [75],或者低秩对角线协方差矩阵 [55]。
7.3 反向传播贝叶斯与概率反向传播
变分推断为贝叶斯推断提供了很好的数学工具,但它需要进一步适应深度学习。主要问题是:随机性限制了反向传播对网络内部节点发挥作用 [9]。不过已经提出了一些解决方多种方案来缓解此问题,比如:概率反向传播 [29] 或反向传播贝叶斯 [7]。这两种方法服务于相同目标,但反向传播贝叶斯可能对深度学习从业者来说更熟悉,因此重点关注它。反向传播贝叶斯是变分推断与重新参数化技巧 [42] 相结合的一种实现,可以确保反向传播能够照常工作。
其思想是使用随机变量 作为噪声的非变分来源。如此以来,原本对 ( 的采样,通过确定性变换 ,变成了对 的采样。即使在每次迭代中 的采样都在变化,但仍然可被视为相对于其他变量的一个常数,而其他所有的变换都是确定性、非随机的。因此,对于变分参数 而言,反向传播可以像传统神经网络一样照常工作。此时 的一般性公式转变为:
这项工作过于繁杂。取而代之,为了估计 的梯度,文献 [7] 建议使用 ,对于可微函数 ,有:
文献 [7] 提供相关证明。本文附录 A 中提供了另一个版本的证明,以更详细说明何时可以假设 ,其充分条件是 关于 可逆,且分布 和 不是退化的概率分布。
对于权重被视为随机变量,并且假设为 的情况(反向传播贝叶斯原始论文中考虑的场景),可以算法 2中描述的方法实现训练循环。

目标函数 对应于来自单样本的 估计值。这意味着梯度估计是嘈杂的。收敛图也将是嘈杂的,比经典反向传播的情况要杂乱得多(图 11)。为更好地估计收敛,可以对多轮的损失进行平均。
算法 2非常类似于点估计深度学习的经典训练循环。事实上,许多最近对深度学习的优化策略可直接用于反向传播贝叶斯,例如,使用 Adam 优化器 [41] 而不是随机梯度下降。自然梯度下降也被用作贝叶斯神经网络变分推断的优化工具 [65],因为如果在自然空间中参数化,则来自指数族的分布会导出一个非常简单的自然梯度公式 [39]。
注意: 自然梯度主要解决参数空间和数据空间之间的梯度表现差异性问题,其目的是使得损失在参数空间做到真正的最速下降。
还要注意的是,尽管该方法的原始算法主要针对具有随机权重的贝叶斯神经网络,但实际上其也可以直接用于具有随机激活的贝叶斯神经网络。在该情况下,激活 表示:假设 和权重 都是变分参数 的一个部分。

图 11. 反向传播贝叶斯算法的典型训练曲线。每个样本看起来都是随机的,但曲线仍然呈下降趋势。为方便比较,图中的 已做过归一化处理。
7.4 经验贝叶斯方法( 学习先验 )
尽管有悖于直觉,但在学习了后验之后再学习先验也是可能的。
在那些先验分布的部分参数可以通过已有知识设置的场景中,这样做非常有意义。它允许在得到后验之前,学习先验分布的剩余部分自由参数(注:此处指先验分布的参数,即超参数,并非指模型参数自身)。在标准贝叶斯统计学中,这被称为 经验贝叶斯。当待学习的的超参数数量远小于模型参数数量时,这通常是有效的近似。
给定一个参数化的先验分布 ,最大化数据似然是学习参数 的一个好方法。
一般来说,直接寻找 是一个难解的问题,但当使用变分推断时,可以利用 的一个特定性质 [26],即 是对数边缘似然 减去KL 散度 (见公式 46),进而得到:
这意味着最大化 (现在是 和 的函数) 相当于最大化观测数据的对数似然下界,当 是一个适合 的泛化分布族时,该下限会更紧致。第 7.3 节中介绍的反向传播贝叶斯算法只需稍作修改即可继续使用,见算法 3。

8 深度学习中的贝叶斯方法
检查后验 是否表现良好( 即网络对其预测既不过度自信也不缺乏自信)也很重要。执行此操作的标准方法是使用校准曲线(Calibration Curve),也被称为可靠性图 [37] [47]。
本节将介绍如何将贝叶斯方法应用于深度学习,从而产生新的、更有效的算法。
我们将加速训练(或预测)的方法分为两大类(图 12):推断算法和简化和压缩方法。推断算法可以根据其所依赖的随机性来源、是否 MCMC / 变分推断方法等因素,被进一步分类。深度学习中两个主要的随机性来源分别是:(1)神经网络的噪声层,以 Dropout 为代表;(2)随机梯度下降引起的噪声。

图 12 贝叶斯神经网络的简化算法可大致分为:(a)改进的推断算法;(b)简化和压缩策略。改进的推断算法可以进一步划分,首先看是
MCMC 算法还是变分推断方法,其次分析其所依赖的随机性来源,是由Dropout(或噪声层)产生的随机性,还是由随机梯度下降产生的随机性。
8.1 MC Dropout 方法
Dropout 最初是作为训练期间的正则化程序被提出来的 [83],用于对前一层施加乘法噪声。到目前为止,最常用的噪声类型是 Bernouilli 噪声,但有时也会使用其他类型的噪声(如:高斯噪声,此时该程序被称为高斯 Dropout [83]) 。
Dropout 也可以在评估阶段作为集成学习的一种形式使用,这提供了获得预测结果概率分布的能力 [18] [52]。这个被称为 MC-Dropout 的过程,可以被认为是一种变分推断方法,其为对每个权重矩阵定义的变分后验为:
其中 为随机激活或失活的系数; 为执行 Dropout 之前的权重矩阵; 为第 层的激活概率,可以通过学习得到或手动设置。
带 Dropout 的训练所使用的标准目标函数,与加性的 权重正则化器之间,存在这一定的等效性:
假设权重的先验采用正态分布,而变分后验为式 51 中的分布,则在使用类似于 第 5.3 节讨论后,用于变分推断的 已经被提出 [18]。
MC-Dropout 是一种非常方便的贝叶斯深度学习技术,因为它与传统方法相比几乎不需要额外的知识或建模努力。与其他变分推断方法相比,它通常会使训练阶段更快。
但是 MC-Dropout 可能缺乏一些表达能力,因此不能完全捕捉与模型预测相关的不确定性。与其他方法相比,它在贝叶斯在线学习或主动学习方面也缺乏一些灵活性。
MC-Dropout 的一个变种是 Variational Dropout,它试图在估值时应用高斯 Dropout [43]。Variational Dropout 被批评为非贝叶斯的 [34],因为作者选择的目标函数中,高斯 Dropout 是唯一的正则化形式。在这种情况下,先验分布(例如对数均匀分布)对应于一个退化的概率分布,进而导致一个退化的后验。必须强调的是,当使用 Dropout 作贝叶斯近似时,训练过程中必须考虑 Dropout 之上的先验正则化问题。
8.2 随机梯度下降方法
随机梯度下降(SGD)和类似算法是现代机器学习的核心。随机梯度下降的最初目标是在只有目标函数的含噪声梯度估计情况下,提供一种能够收敛到最优解的点估计算法,特别是当训练数据必须被分割成小批次时。在时间步 时的参数更新规则可以写为:
其中, 是在 时间步从数据集 中抽取的小批样本, 是 时间步的学习率, 是整个数据集的大小, 是小批次的大小。
SGD 或相关优化算法,如 Adam[41],可以被重新解释为将小批量的采样作为随机性来源的马尔科夫链算法 [56]。通常,需要调整算法的超参数以确保链能够收敛到 Dirac 分布,即最终的点估计指示分布。其中通过减小学习率 ,并确保 是常用策略。不过情况并不一定总是如此。如果学习率向某个常数降低,则马尔科夫链将收敛至一个平稳分布。如果为目标函数考虑了贝叶斯先验,那么该平稳分布可以被视为相应后验的近似。
8.2.1 基于 SGD 的 MCMC 算法。
(1) 朗之万动力学法
基于上述观察,人们基于 SGD 算法开发了一种特殊的 MCMC 方法,并称之为随机梯度郎之万动力学法(SGLD)[91]。将 SGD 与郎之万动力学 相结合的想法导致了一个略微修改的更新步骤:
有研究表明,如果 趋于 ,则这种方法能够使马尔科夫链对精确后验进行采样 [91]。但问题是,如果 趋近于 ,相邻样本就会变得越来越自相关。为处理此问题,作者建议在某个点上停止减少 ,从而使样本只能达到精确后验的近似值。与其他 MCMC 方法相比,如果应用场景中必须将数据集分割成小批,SGLD 还是提供了更好的理论保证,这使得该算法在贝叶斯深度学习中非常有用。
(2)热重启
为支持对后验的探索而非精确采样,SGD 也可以用一种稍微不同的方式,粗略地近似贝叶斯后验,同时在实践中容易实现。这个想法是使用热重启,即用大的学习率 和(可能的)新随机权重 重启梯度下降。
这种方法显然是对真正贝叶斯方法的一种粗略近似,但它具有多种优点,其中最重要的是避免了峰值坍塌问题 [49]。在贝叶斯神经网络情况下,真正的后验通常是一个复杂的多峰分布,因此网络可能存在多个并不等价的参数 能够拟合训练数据集。倾向于探索而非精确重建,可以帮助你更好地了解这些峰值。然后,由于从同一峰值采样的 更有可能使模型以相似的方式泛化,因此在处理不可观测数据时,使用热重启可以更好地估计模型的不确定性(即认知不确定性),即便该方法不是完美的贝叶斯方法。
(3)其他 MCMC 方法
还有一些文献中提出了利用上述想法的算法,例如 RECAST 法[78],该方法用热重启对 SGLD 方法进行了修改。
上述所有方法仍然存在 MCMC 方法的主要缺点,即内存占用大。因此,一些作者提出了更像传统变分推断的方法。
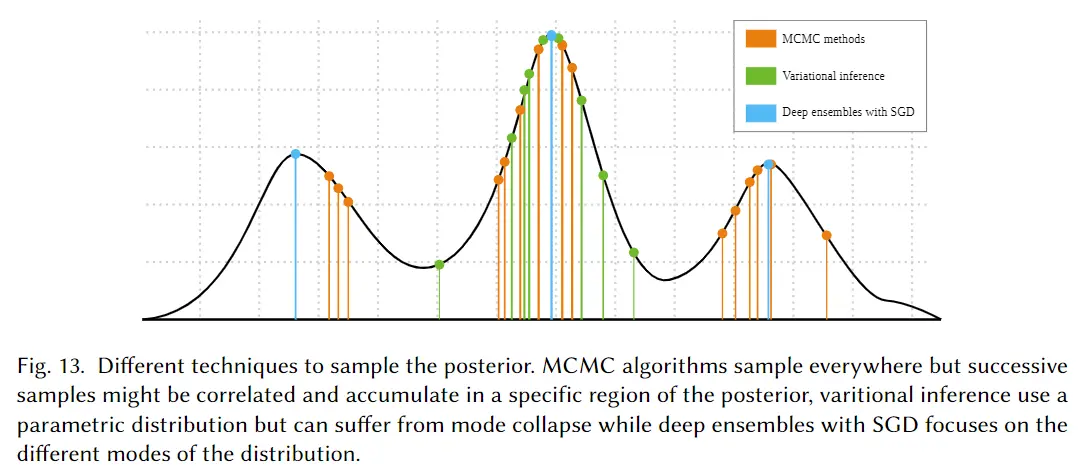
图 13. 对后验进行采样的不同技术。 MCMC 算法会随处采样,但相邻样本可能相关并在后验的特定区域内聚集,变分推断使用参数化的分布但很可能会遇到峰值坍塌的问题,而具有
SGD的深度集成方法则通常见注意力聚焦在分布的不同峰值处。
8.2.2 基于 SGD 的变分推断
与其从 SGD 中推导出 MCMC 算法,还不如用 SGD 来拟合一个变分分布。这种推断方法可以被认为属于变分推断,而此类方法大多是基于拉普拉斯近似的(注:也就是将后验分布简化为一个多元高斯分布)。
此类方法将最大后验估计作为均值、将损失的海森矩阵作为逆协方差矩阵,来拟合一个高斯形态的后验分布。损失的海森矩阵和曲率计算,对于现代大规模神经网络架构而言通常难以实现,所以提出了例如 KFAC[75] 的近似方法。KFAC 是一种可扩展方法,使用Kronecker 分解法来拟合一个具有块对角线协方差矩阵的高斯分布来近似后验。
另一种获得二阶导数(曲率与二阶导数有关)估计的方法是在多个 SGD 迭代中估计梯度的方差。SWAG 利用该思想拟合了一个具有低秩加对角协方差矩阵的高斯后验[55] 。还有一个名为 Vadam[40] 的类似方法,用于 Adam 算法。
上述方法存在的问题在于:如果它们能够捕捉到后验的某个峰值的精细形态,那么就无法再拟合其他的峰值区域了。
在实践中,校准曲线是一个函数 ,表示观测到的概率 (或称为经验频率)和预测得到的概率 之间的函数关系(图 15)。如果观测到的概率 小于预测得出的概率 ,则模型过度自信;否则,模型存在欠自信。一个经过良好校准的模型应该有 。此方法在实践中确实有用,它需要选择一组具有不同预测概率的事件 ,并使用测试集 测量每个事件的经验频率。
其中权重 是正常数,其和为 。
8.3 Last-n-Layer 混合贝叶斯神经网络
对于神经网络来说,成为真正贝叶斯方法的主要顾虑在于:深层神经网络的多层结构,使得 过多考虑前部层的不确定性 似乎显得过于冗余。因此,近年有些研究尝试了只使用位于网络末端的几个随机层 [8] [97]。
只训练少量几个随机层可以大大简化深层神经网络的学习过程。它消除了许多概念和训练问题,同时仍然能从贝叶斯角度给出有意义的结果。这种方法可以被解释为学习了一个传统神经网络的点估计变换,后接一个浅层的贝叶斯神经网络。
训练最后 层的贝叶斯神经网络起初似乎并不复杂,但事实上它与第 7.4 节所述的先验参数学习非常相似。非贝叶斯层的权重应当既被视为先验的参数,也被视为变分分布的参数。

图 14. 对应于
Last-n-layer 架构的贝叶斯信念网络和贝叶斯神经网络。
8.4 贝叶斯教师法
在实时性能要求很高的应用中,使用 MCMC 样本做估值仍然有问题,例如:自动驾驶汽车、内存有限的智能手机、嵌入式设备等,而且大量参数的 MCMC 样本存在严重的内存占用问题。
一些学者提出了一个解决方案,以加快使用贝叶斯神经网络的估值时间,该方案源自一个已经被用于贝叶斯建模的方法 – 贝叶斯教师法 [81]。该方法使用一个贝叶斯神经网络(被称为教师),来训练一个用于预测边缘概率 的非贝叶斯神经网络(被称为学生)[45]。
为此,需要最小化被 参数化的分布 与边缘分布 之间的 KL 散度,其中 是学生网络的系数:
这是很难做到的。Korattikara 等人 [45] 提出了一种蒙特卡洛近似方法:
这个量可以在训练数据集 上估计。这个方法的最大优点是:在训练中只需要特征 ,因为标签的概率 被贝叶斯神经网络定义了( 见第 4.2 节 )。如果不需要标签, 则 可以比原始数据集 (主要用用于训练教师贝叶斯神经网络)大很多,这样学生网络就更不可能出现意外的泛化缺陷了。
图 15. 欠自信 (a) 和过度自信 (b) 模型的校准曲线示例。
目前,对于希望压缩 MCMC 样本集的应用场景,贝叶斯教师法也是一个有希望的解决方案 [90]。此时,会采用一个基于 MCMC 样本训练的、用于生成系数样本 的生成式模型 ( 即 [90] 中的 GAN )来取代样本集 。该方法在某种程度上类似于变分推断,因为生成模型实际上表示了一个参数化的分布。不过,文中提出的算法可以用于训练比传统变分推断方法更复杂的模型。
9 评估贝叶斯神经网络的性能
贝叶斯神经网络的一大挑战是评估其性能,因为它们并不直接输出一个预测结果的点估计 ,而是输出一个条件概率分布 ,从该分布中可以抽取出一个 的最佳点估计 。
神经网络的预测性能(有时在统计学中被称为锐度)可以通过将估计值 视为实际预测结果来评估。此过程取决于神经网络要处理的数据类型,在实践中存在许多种评估指标,如:MSE 、 阶距离、交叉熵等。有关这些指标的解释不在本文范围内,详情请参考 [35]。
对于多类別分类器,校准曲线可以针对每一类独立地进行检查。这样问题就被简化为二元分类器。
现在,为指定的随机模型提供一个完整的校准曲线通常是好主意,因为它可以指出模型在哪里可能过于自信或不够自信。在一定程度上,它也允许重新校准模型 [47]。

AUC 值为 时,表明该模型平均且仅平均而言,具有良好的校准。
(1) 分类问题
对于二元分类器来说,测试事件集可以被选为所有数据点的集合,这些数据点被接受的预测概率在 对应的区间 内。或者对于小数据集来说,可以选择 或 。经验频率由以下公式给出:
与理想校准曲线(在函数希尔伯特空间中定义)之间的距离 ,也是一个很好的模型校准指标,不过在实践中较少使用:
(2)回归问题
回归问题稍微复杂一些,因为神经网络不会像分类器那样输出可信水平,而是输出所有可能值的分布。解决方案是使用具有已知概率分布的中间统计量。
假设对于一组数量足够大的、随机选择的输入 ,相应的 之间相互独立,则可以假设归一化的平方误差之和服从卡方律。
这允许将预测到的概率视为观测和真实值之间的方差归一化距离等于或低于实际距离的概率,归因于测试集合 中的所有数据点。形式上,预测到的概率计算如下:
其中 是自由度为 的卡方律累积分布。
观测到的概率可以被计算为:
当 时,模型是完全校准的。
除了曲线图之外,有必要提供一些汇总性的统计数字,以方便比较或解释。曲线下面积( AUC ) 即使这样一个标准指标,其形式为:
此外,学者们也提出了其他度量方法,如校准误差的期望及其变种 [63]。它们大多都是理想校准曲线距离的离散化变体。
这些度量方法对于总结校准很好用,但对于正确学习校准的模型并不适用。
统计学中用于优化校准的工具是评分规则 [24]。评分规则是一个函数 ,其中 是预测概率分布,类似贝叶斯神经网络给出的边缘概率, 是一个事件。给定目标分布 ,我们可以记为 。
一般情况下,评分规则是正值,进而保证优化目标为最大化 。评分规则的一个重要性质是:其最大值倾向于一个校准良好的模型,即:
理论上,要得到一个适当的校准后模型,只需确保训练损失与(严格)正确评分规则相对应即可。在实践中,这一点更为复杂,因为只有在大型数据集上才能准确估计分数的期望值。当训练好的模型出现在与原始训练集稍有偏差的数据中时,这可能会导致错误校准误差 [66]。这其实是贝叶斯模型真正的闪光点,因为它们在设计上遵循了正确评分规则,并且考虑了认知不确定性和偶然不确定性,使模型对这种变化即使不能做到免疫,也有足够弹性。
当然,经过训练的贝叶斯神经网络可能会是错误校准的。在这种情况下,可能需要考虑调整先验,原因可能是所做假设过于特殊而且不合理。另外,训练策略也可能需要重新考虑,特别是如果训练期间使用的变分分布不能正确逼近后验的时候。
title: 现代神经网络的校准
此时的打分规则被称为正确评分规则。如果我们同时有 $ ̄S(Q,Q) = ̄S(P,Q)⇒P=Q$ ,那么该评分规则被称为严格正确。
description: 现代神经网络的校准
- [BayesNN, 不确定性校准]
10 贝叶斯深度学习编程框架
在结束本教程之前,本节会简单介绍一些可用于贝叶斯深度学习的框架。
10.1 概率编程语言
概率编程语言(PPL)旨在描述概率分布,同时以类似概率图模型(PGM)的方式描述变量之间的关系,以加快推断速度。大多数概率编程语言包括许多不同的优化算法,例如: MCMC、变分推断和最大似然估计等,当然也有少部分仅关注特定的专门方法。
Stan [10] 和 PyMC3 [77] 是目前普遍使用的概率编程语言。Stan 采用 C++编写,使用一套自己的语言来定义概率模型。它为所有流行的科学软件提供了 API,包括 Python、R、Matlab、Julia 和一个命令行接口。PyMC3 是用 Python 编写的,基于 Theano 实现自动微分。
使用纯概率编程语言设计贝叶斯神经网络的问题在于:它们擅长于复杂的概率模型基础,但不是专门面向深度学习的。当然使用概率编程语言编写贝叶斯神经网络是可能的,但大部分工作需要从头开始,特别是深度学习的部分几乎要从头做起。
10.2 深度学习框架下的概率编程
概率编程语言和深度学习框架存在着或多或少相同的要求,其中最主要的要求是自动微分和大规模数据的优化程序。根据此思考,最近的进展主要集中在将概率编程语言整合到深度学习框架中。其中比较重要的成果是 Pyro[5],该框架构建在 PyTorch 之上。此外还有 Edward [87],其构建在 TensorFlow 之上,现在 Edward 已经被扩展并集成到了 Tensorflow 的 Tensorflow Probability (TFP)子模块中。
这些概率编程语言与各自的深度学习框架无缝集成,进而使其成为设计、训练和使用贝叶斯神经网络的理想工具。它们还可以很容易地重用为点估计神经网络设计的组件。
Pyro 的开发重点是变分推断。它基于函数式编程范式,再加上上下文管理器来轻松地修改随机函数。Pyro 包括一个封装类,可以将 PyTorch 的网络层转化为概率层,并允许用运行中( on-the-fly)样本来替换网络参数。
Edward 和 TFP 包括一些更高层次的结构,特别是可单独使用的概率层,以及一些建立概率网络的低层次结构。
在未做详细比较的情况下,我们建议你选择能够与自己熟悉的深度学习框架集成的概率变编程语言,而这两个框架都有类似潜力。Pyro 可能更适合动态概率图模型,因为 Pytorch 使用了动态计算图技术。如果你只是想在一个固定架构中使用贝叶斯层,那么 Edward 与 TFP 或许更适合你。
11 结论
本教程包括贝叶斯神经网络的设计、实现、训练、使用和评估。虽然其基本思想很简单,只是训练一个人工神经网络,并在其权重上附加一些概率分布,但其中隐含的挑战仍然难以解决,特别是设计高效的算法来训练或使用贝叶斯神经网络。这也解释了为何在实际应用中仍然很少使用贝叶斯神经网络。
但贝叶斯神经网络的潜在应用巨大,该范式提供了一个很有前途的技术途径,可以将深度学习应用于不允许出现失败泛化,而且必须发出警告的系统。
此外,传统深度学习算法和贝叶斯范式之间的联系比人们事先想象的要多,这意味着贝叶斯方法也可以帮助设计新的学习和正则化策略。
参考文献
- [1] Jimmy Lei Ba, Jamie Ryan Kiros, and Geoffrey E Hinton. Layer normalization.CoRR, arXiv:1607.06450, 2016. In NIPS 2016 Deep Learning Symposium.
- [2] Rémi Bardenet, Arnaud Doucet, and Chris Holmes. On Markov Chain Monte Carlo methods for tall data.J. Mach. Learn. Res., 18(1):1515–1557, January 2017. ISSN 1532–4435.
- [3] M Saiful Bari, Muhammad Tasnim Mohiuddin, and Shafiq Joty. MultiMix: A robust data augmentation strategy for cross-lingual nlp. InICML, 2020.
- [4] L. Beyer, X. Zhai, A. Oliver, and A. Kolesnikov. S4L: Self-supervised semi-supervised learning. In2019 IEEE/CVF International Conference on Computer Vision (ICCV), pages 1476–1485, 2019.
- [5] Eli Bingham, Jonathan P. Chen, Martin Jankowiak, Fritz Obermeyer, Neeraj Pradhan, Theofanis Karaletsos, Rohit Singh, Paul Szerlip, Paul Horsfall, and Noah D. Goodman. Pyro: Deep universal probabilistic programming.J. Mach. Learn. Res., 20(1):973âĂŞ978, January 2019. ISSN 1532-4435.
- [6] David M. Blei, Alp Kucukelbir, and Jon D. McAuliffe. Variational inference: A review for statisticians.Journal of the American Statistical Association, 112(518):859–877, 2017.
- [7] Charles Blundell, Julien Cornebise, Koray Kavukcuoglu, and Daan Wierstra. Weight uncertainty in neural network. In Proceedings of the 32nd International Conference on Machine Learning, volume 37 ofProceedings of Machine Learning Research, pages 1613–1622, 2015.
- [8] Nicolas Brosse, Carlos Riquelme, Alice Martin, Sylvain Gelly, and ÃĽric Moulines. On last-layer algorithms for classification: Decoupling representation from uncertainty estimation.CoRR, abs/2001.08049, 2020. URL http://arxiv. org/abs/2001.08049.
- [9] W. L. Buntine. Operations for learning with graphical models.Journal of Artificial Intelligence Research, 2:159–225, Dec 1994. ISSN 1076–9757.
- [10] Bob Carpenter, Andrew Gelman, Matthew D Hoffman, Daniel Lee, Ben Goodrich, Michael Betancourt, Marcus Brubaker, Jiqiang Guo, Peter Li, and Allen Riddell. Stan: A probabilistic programming language.Journal of statistical software, 76(1), 2017.
- [11] Rodolfo C. Cavalcante, Rodrigo C. Brasileiro, Victor L.F. Souza, Jarley P. Nobrega, and Adriano L.I. Oliveira. Computational intelligence and financial markets: A survey and future directions.Expert Systems with Applications, 55:194–211.
- [12] Olivier Chapelle, Jason Weston, Léon Bottou, and Vladimir Vapnik. Vicinal risk minimization. In T. K. Leen, T. G. Dietterich, and V. Tresp, editors,Advances in Neural Information Processing Systems 13, pages 416–422. MIT Press, 2001.
- [13] Siddhartha Chib and Edward Greenberg. Understanding the Metropolis-Hastings algorithm.The American Statistician, 49(4):327–335, 1995.
- [14] Stefan Depeweg, Jose-Miguel Hernandez-Lobato, Finale Doshi-Velez, and Steffen Udluft. Decomposition of uncertainty in Bayesian deep learning for efficient and risk-sensitive learning. InProceedings of the 35th International Conference on Machine Learning, volume 80 ofProceedings of Machine Learning Research, pages 1184–1193, 2018.
- [15] Alexander Etz, Quentin F. Gronau, Fabian Dablander, Peter A. Edelsbrunner, and Beth Baribault. How to become a Bayesian in eight easy steps: An annotated reading list.Psychonomic Bulletin & Review, 25:219–234, 2018.
- [16] B. Frenay and M. Verleysen. Classification in the presence of label noise: A survey.IEEE Transactions on Neural Networks and Learning Systems, 25(5):845–869, 2014.
- [17] Yarin Gal and Zoubin Ghahramani. Bayesian convolutional neural networks with Bernoulli approximate variational inference.CoRR, abs/1506.02158, 2015. URL http://arxiv.org/abs/1506.02158.
- [18] Yarin Gal and Zoubin Ghahramani. Dropout as a Bayesian approximation: Representing model uncertainty in deep learning. InProceedings of the 33rd International Conference on Machine Learning - Volume 48, ICMLâĂŹ16, page 1050âĂŞ1059, 2016.
- [19] Yarin Gal, Riashat Islam, and Zoubin Ghahramani. Deep Bayesian active learning with image data. InProceedings of the 34th International Conference on Machine Learning - Volume 70, ICMLâĂŹ17, page 1183âĂŞ1192, 2017.
- [20] Francis Galton. Vox Populi.Nature, 75(1949):450–451, Mar 1907. ISSN 1476–4687.
- [21] Andrew Gelman and other Stan developers. Prior choice recommendations, 2020. Retrieved from https://github.com/stan-dev/stan/wiki/Prior-Choice-Recommendations
- [22] Edward I. George, George Casella, and Edward I. George. Explaining the Gibbs sampler.The American Statistician, 1992.
- [23] Zoubin Ghahramani and Matthew J. Beal. Propagation algorithms for variational Bayesian learning. In T. K. Leen, T. G. Dietterich, and V. Tresp, editors,Advances in Neural Information Processing Systems 13, pages 507–513. MIT Press, 2001.
- [24] Tilmann Gneiting and Adrian E Raftery. Strictly proper scoring rules, prediction, and estimation.Journal of the American Statistical Association, 102(477):359–378, 2007.
- [25] Erin Grant, Chelsea Finn, Sergey Levine, Trevor Darrell, and Thomas L. Griffiths. Recasting gradient-based meta-learning as hierarchical Bayes. In6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, April 30 - May 3, 2018, Conference Track Proceedings, 2018.
- [26] Alex Graves. Practical variational inference for neural networks. In J. Shawe-Taylor, R. S. Zemel, P. L. Bartlett, F. Pereira, and K. Q. Weinberger, editors,Advances in Neural Information Processing Systems 24, pages 2348–2356. Curran Associates, Inc., 2011.
- [27] Chuan Guo, Geoff Pleiss, Yu Sun, and Kilian Q. Weinberger. On calibration of modern neural network. InProceedings of the 34th International Conference on Machine Learning - Volume 70, ICMLâĂŹ17, pages 1321–1330, 2017.
- [28] Dan Hendrycks and Kevin Gimpel. A baseline for detecting misclassified and out-of-distribution examples in neural networks. In5th International Conference on Learning Representations, ICLR 2017, Conference Track Proceedings, 2017.
- [29] José Miguel Hernández-Lobato and Ryan P. Adams. Probabilistic backpropagation for scalable learning of Bayesian neural networks. InProceedings of the 32nd International Conference on International Conference on Machine Learning - Volume 37, ICMLâĂŹ15, page 1861âĂŞ1869, 2015.
- [30] Geoffrey Hinton, Oriol Vinyals, and Jeff Dean. Distilling the knowledge in a neural network.arXiv preprint arXiv:1503.02531, 2015. In NIPS 2014 Deep Learning Workshop.
- [31] Matthew D Hoffman and Andrew Gelman. The No-U-Turn sampler: adaptively setting path lengths in Hamiltonian Monte Carlo.Journal of Machine Learning Research, 15(1):1593–1623, 2014.
- [32] Matthew D. Hoffman, David M. Blei, Chong Wang, and John Paisley. Stochastic variational inference.J. Mach. Learn. Res., 14(1):1303–1347, May 2013. ISSN 1532-4435.
- [33] Timothy Hospedales, Antreas Antoniou, Paul Micaelli, and Amos Storkey. Meta-learning in neural networks: A survey. CoRR, abs/2004.05439, 2020. URL http://arxiv.org/abs/2004.05439.
- [34] Jiri Hron, Alex Matthews, and Zoubin Ghahramani. Variational Bayesian dropout: pitfalls and fixes. InProceedings of the 35th International Conference on Machine Learning, volume 80 ofProceedings of Machine Learning Research, pages 2019–2028, 2018.
- [35] Katarzyna Janocha and Wojciech Marian Czarnecki. On loss functions for deep neural networks in classification. Schedae Informaticae, 1/2016, 2017. ISSN 2083-8476. doi: 10.4467/20838476si.16.004.6185. URL http://dx.doi.org/10.4467/20838476SI.16.004.6185.
- [36] L. Jing and Y. Tian. Self-supervised visual feature learning with deep neural networks: A survey.IEEE Transactions on Pattern Analysis and Machine Intelligence, pages 1–1, 2020.
- [37] Alex Kendall and Yarin Gal. What uncertainties do we need in Bayesian deep learning for computer vision? In Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPSâĂŹ17, page 5580âĂŞ5590, 2017. ISBN 9781510860964.
- [38] J. Ker, L. Wang, J. Rao, and T. Lim. Deep learning applications in medical image analysis.IEEE Access, 6:9375–9389, 2018.
- [39] M. E. Khan and D. Nielsen. Fast yet simple natural-gradient descent for variational inference in complex models. In 2018 International Symposium on Information Theory and Its Applications (ISITA), pages 31–35, 2018.
- [40] Mohammad Khan, Didrik Nielsen, Voot Tangkaratt, Wu Lin, Yarin Gal, and Akash Srivastava. Fast and scalable Bayesian deep learning by weight-perturbation in Adam. InProceedings of the 35th International Conference on Machine Learning, volume 80 ofProceedings of Machine Learning Research, pages 2611–2620, 2018.
- [41] Diederik Kingma and Jimmy Ba. Adam: A method for stochastic optimization.International Conference on Learning Representations, 12 2014.
- [42] Diederik P Kingma, Max Welling, et al. An introduction to variational autoencoders.Foundations and Trends®in Machine Learning, 12(4):307–392, 2019.
- [43] Durk P Kingma, Tim Salimans, and Max Welling. Variational dropout and the local reparameterization trick. In C. Cortes, N. D. Lawrence, D. D. Lee, M. Sugiyama, and R. Garnett, editors,Advances in Neural Information Processing Systems 28, pages 2575–2583. Curran Associates, Inc., 2015.
- [44] Armen Der Kiureghian and Ove Ditlevsen. Aleatory or epistemic? does it matter?Structural Safety, 31(2):105–112, 2009. ISSN 0167–4730. Risk Acceptance and Risk Communication.
- [45] Anoop Korattikara, Vivek Rathod, Kevin Murphy, and Max Welling. Bayesian dark knowledge. InProceedings of the 28th International Conference on Neural Information Processing Systems - Volume 2, NIPSâĂŹ15, page 3438âĂŞ3446, 2015.
- [46] Agustinus Kristiadi, Matthias Hein, and Philipp Hennig. Being Bayesian, even just a bit, fixes overconfidence in ReLU networks.CoRR, abs/2002.10118, 2020. URL http://arxiv.org/abs/2002.10118.
- [47] Volodymyr Kuleshov, Nathan Fenner, and Stefano Ermon. Accurate uncertainties for deep learning using calibrated regression. InProceedings of the 35th International Conference on Machine Learning, volume 80 ofProceedings of Machine Learning Research, pages 2796–2804, 2018.
- [48] R. Kunwar, U. Pal, and M. Blumenstein. Semi-supervised online Bayesian network learner for handwritten characters recognition. In2014 22nd International Conference on Pattern Recognition, pages 3104–3109, 2014.
- [49] Balaji Lakshminarayanan, Alexander Pritzel, and Charles Blundell. Simple and scalable predictive uncertainty estimation using deep ensembles. In I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett, editors,Advances in Neural Information Processing Systems 30, pages 6402–6413. Curran Associates, Inc., 2017.
- [50] Jouko Lampinen and Aki Vehtari. Bayesian approach for neural networksâĂŤreview and case studies.Neural Networks, 14(3):257 – 274, 2001. ISSN 0893-6080.
- [51] Dong-Hyun Lee. Pseudo-label: The simple and efficient semi-supervised learning method for deep neural networks. In Workshop on challenges in representation learning, ICML, volume 3, 2013.
- [52] Yingzhen Li and Yarin Gal. Dropout inference in Bayesian neural networks with lpha-divergences. InProceedings of the 34th International Conference on Machine Learning - Volume 70, ICMLâĂŹ17, pages 2052–2061, 2017.
- [53] Zhun Li, ByungSoo Ko, and Ho-Jin Choi. Naive semi-supervised deep learning using pseudo-label.Peer-to-Peer Networking and Applications, 12(5):1358–1368, 2019. ISSN 1936-6450.
- [54] David J. C. MacKay. A practical Bayesian framework for backpropagation networks.Neural Computation, 4(3):448–472, 1992.
- [55] Wesley J Maddox, Pavel Izmailov, Timur Garipov, Dmitry P Vetrov, and Andrew Gordon Wilson. A simple baseline for Bayesian uncertainty in deep learning. In H. Wallach, H. Larochelle, A. Beygelzimer, F. d'Alché-Buc, E. Fox, and R. Garnett, editors,Advances in Neural Information Processing Systems 32, pages 13153–13164. Curran Associates, Inc., 2019.
- [56] Stephan Mandt, Matthew D Hoffman, and David M Blei. Stochastic gradient descent as approximate Bayesian inference. The Journal of Machine Learning Research, 18(1):4873–4907, 2017.
- [57] Aditya Krishna Menon, Ankit Singh Rawat, Sashank J. Reddi, Seungyeon Kim, and Sanjiv Kumar. Why distillation helps: a statistical perspective.CoRR, abs/2005.10419, 2020. URL https://arxiv.org/abs/2005.10419.
- [58] John Mitros and Brian Mac Namee. On the validity of Bayesian neural networks for uncertainty estimation. InAICS,2019.
- [59] Kevin P. Murphy.Machine Learning: A Probabilistic Perspective. The MIT Press, 2012. ISBN 0262018020.
- [60] Eric Nalisnick, Akihiro Matsukawa, Yee Whye Teh, Dilan Gorur, and Balaji Lakshminarayanan. Do deep generative models know what they don’t know? InInternational Conference on Learning Representations, 2019.
- [61] Nagarajan Natarajan, Inderjit S Dhillon, Pradeep K Ravikumar, and Ambuj Tewari. Learning with noisy labels. In C. J. C. Burges, L. Bottou, M. Welling, Z. Ghahramani, and K. Q. Weinberger, editors,Advances in Neural Information Processing Systems 26, pages 1196–1204. Curran Associates, Inc., 2013.
- [62] Radford M Neal et al. MCMC using Hamiltonian dynamics.Handbook of Markov Chain Monte Carlo, 2(11):2, 2011.
- [63] Jeremy Nixon, Michael W. Dusenberry, Linchuan Zhang, Ghassen Jerfel, and Dustin Tran. Measuring calibration in deep learning. InThe IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, June 2019.
- [64] Manfred Opper and Ole Winther. A Bayesian approach to on-line learning.On-line learning in neural networks, pages 363–378, 1998.
- [65] Kazuki Osawa, Siddharth Swaroop, Mohammad Emtiyaz E Khan, Anirudh Jain, Runa Eschenhagen, Richard E Turner, and Rio Yokota. Practical deep learning with Bayesian principles. InAdvances in Neural Information Processing Systems 32, pages 4287–4299. Curran Associates, Inc., 2019.
- [66] Yaniv Ovadia, Emily Fertig, Jie Ren, Zachary Nado, D. Sculley, Sebastian Nowozin, Joshua Dillon, Balaji Lakshmi-narayanan, and Jasper Snoek. Can you trust your model's uncertainty? evaluating predictive uncertainty under dataset shift. In H. Wallach, H. Larochelle, A. Beygelzimer, F. d'Alché-Buc, E. Fox, and R. Garnett, editors,Advances in Neural Information Processing Systems 32, pages 13991–14002. Curran Associates, Inc., 2019.
- [67] S. J. Pan and Q. Yang. A survey on transfer learning.IEEE Transactions on Knowledge and Data Engineering, 22(10): 1345–1359, 2010.
- [68] Tim Pearce, Felix Leibfried, Alexandra Brintrup, Mohamed Zaki, and Andy Neely. Uncertainty in neural networks: Approximately Bayesian ensembling. InAISTATS 2020, 2020.
- [69] Nicholas G Polson, Vadim Sokolov, et al. Deep learning: a Bayesian perspective.Bayesian Analysis, 12(4):1275–1304, 2017.
- [70] Arya A Pourzanjani, Richard M Jiang, Brian Mitchell, Paul J Atzberger, and Linda R Petzold. Bayesian inference over the Stiefel manifold via the Givens representation.CoRR, abs/1710.09443, 2017. URL http://arxiv.org/abs/1710.09443.
- [71] Samira Pouyanfar, Saad Sadiq, Yilin Yan, Haiman Tian, Yudong Tao, Maria Presa Reyes, Mei-Ling Shyu, Shu-Ching Chen, and S. S. Iyengar. A survey on deep learning: Algorithms, techniques, and applications.
- [72] Guo-Jun Qi and Jiebo Luo. Small data challenges in big data era: A survey of recent progress on unsupervised and semi-supervised methods.CoRR, abs/1903.11260, 2019. URL http://arxiv.org/abs/1903.11260.
- [73] Xipeng Qiu, Tianxiang Sun, Yige Xu, Yunfan Shao, Ning Dai, and Xuanjing Huang. Pre-trained models for natural language processing: A survey.CoRR, abs/2003.08271, 2020.
- [74] Qing Rao and Jelena Frtunikj. Deep learning for self-driving cars: Chances and challenges. InProceedings of the 1st International Workshop on Software Engineering for AI in Autonomous Systems, SEFAIS âĂŹ18, pages 35–38, 2018.
- [75] Hippolyt Ritter, Aleksandar Botev, and David Barber. A scalable laplace approximation for neural networks. In International Conference on Learning Representations, 2018.
- [76] Christian Robert.The Bayesian choice: from decision-theoretic foundations to computational implementation. Springer Science & Business Media, 2007.
- [77] John Salvatier, Thomas V Wieckiâ, and Christopher Fonnesbeck. PyMC3: Python probabilistic programming framework. PeerJ Computer Science, 2:e55, 2016. https://doi.org/10.7717/peerj-cs.55.
- [78] Nabeel Seedat and Christopher Kanan. Towards calibrated and scalable uncertainty representations for neural networks. CoRR, abs/1911.00104, 2019. URL http://arxiv.org/abs/1911.00104.
- [79] Joan SerrÃă, David ÃĄlvarez, VicenÃğ GÃşmez, Olga Slizovskaia, JosÃľ F. NÃžÃśez, and Jordi Luque. Input complexity and out-of-distribution detection with likelihood-based generative models.CoRR, abs/1909.11480, 2020. URL http://arxiv.org/abs/1909.11480.
- [80] Daniele Silvestro and Tobias Andermann. Prior choice affects ability of Bayesian neural networks to identify unknowns. CoRR, abs/2005.04987, 2020. URL http://arxiv.org/abs/2005.04987.
- [81] Edward Snelson and Zoubin Ghahramani. Compact approximations to Bayesian predictive distributions. InProceedings of the 22nd International Conference on Machine Learning, ICML âĂŹ05, page 840âĂŞ847, 2005.
- [82] Kihyuk Sohn, David Berthelot, Chun-Liang Li, Zizhao Zhang, Nicholas Carlini, Ekin D. Cubuk, Alex Kurakin, Han Zhang, and Colin Raffel. FixMatch: Simplifying semi-supervised learning with consistency and confidence.CoRR, abs/2001.07685, 2020. URL https://arxiv.org/abs/2001.07685.
- [83] Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov. Dropout: A simple way to prevent neural networks from overfitting.Journal of Machine Learning Research, 15(56):1929–1958, 2014.
- [84] Martin A. Tanner and Wing Hung Wong. The calculation of posterior distributions by data augmentation.Journal of the American Statistical Association, 82(398):528–540, 1987.
- [85] D. M. Titterington. Bayesian methods for neural networks and related models.Statist. Sci., 19(1):128–139, 02 2004.
- [86] Adrian Corduneanu Tommi and Tommi Jaakkola. On information regularization. InIn Proceedings of the 19th UAI,2003.
- [87] Dustin Tran, Matthew D. Hoffman, Rif A. Saurous, Eugene Brevdo, Kevin Murphy, and David M. Blei. Deep probabilistic programming.CoRR, abs/1701.03757, 2017. URL http://arxiv.org/abs/1701.03757.
- [88] Toan Tran, Thanh-Toan Do, Ian Reid, and Gustavo Carneiro. Bayesian generative active deep learning.CoRR, abs/1904.11643, 2019. URL http://arxiv.org/abs/1904.11643.
- [89] Hao Wang and Dit-Yan Yeung. Towards Bayesian deep learning: A framework and some existing methods.IEEE Trans. on Knowl. and Data Eng., 28(12):3395–3408, December 2016. ISSN 1041–4347.
- [90] Kuan-Chieh Wang, Paul Vicol, James Lucas, Li Gu, Roger Grosse, and Richard Zemel. Adversarial distillation of Bayesian neural network posteriors. InProceedings of the 35th International Conference on Machine Learning, volume 80 of Proceedings of Machine Learning Research, pages 5190–5199, 2018.
- [91] Max Welling and Yee W Teh. Bayesian learning via stochastic gradient Langevin dynamics. InProceedings of the 28th international conference on machine learning, ICML âĂŹ11, pages 681–688, 2011.
- [92] Yeming Wen, Paul Vicol, Jimmy Ba, Dustin Tran, and Roger Grosse. Flipout: Efficient pseudo-independent weight perturbations on mini-batches. InInternational Conference on Learning Representations, 2018.
- [93] Andrew Gordon Wilson and Pavel Izmailov. Bayesian deep learning and a probabilistic perspective of generalization. CoRR, abs/2002.08791, 2020. URL http://arxiv.org/abs/2002.08791.
- [94] D. H. Wolpert. The lack of a priori distinctions between learning algorithms.Neural Computation, 8(7):1341–1390, 1996.
- [95] Qizhe Xie, Zihang Dai, Eduard H. Hovy, Minh-Thang Luong, and Quoc V. Le. Unsupervised data augmentation.CoRR, abs/1904.12848, 2019. URL http://arxiv.org/abs/1904.12848.
- [96] Shipeng Yu, Balaji Krishnapuram, Rómer Rosales, and R. Bharat Rao. Bayesian co-training.Journal of Machine Learning Research, 12(80):2649–2680, 2011.
- [97] Jiaming Zeng, Adam Lesnikowski, and Jose M. Alvarez. The relevance of Bayesian layer positioning to model uncertainty in deep Bayesian active learning.CoRR, abs/1811.12535, 2018. URL http://arxiv.org/abs/1811.12535.
- [98] Chiyuan Zhang, Samy Bengio, Moritz Hardt, Benjamin Recht, and Oriol Vinyals. Understanding deep learning requires rethinking generalization. In 5th International Conference on Learning Representations, ICLR, 2017.
- [99] Zhi-Hua Zhou.Ensemble Methods: Foundations and Algorithms. Chapman and Hall/CRC, 1st edition, 2012.






