高斯神经过程

【摘 要】 神经过程是一类丰富的元学习模型，可将数据集直接映射到预测性随机过程。我们对用于训练条件神经过程的标准最大似然目标进行了严格的分析。此外，我们向神经过程家族提出了一个新成员，称为高斯神经过程 (GNP)，它结合平移等方差性对预测相关性进行建模，能够提供通用的近似保证，并展示了很好的性能。

【原 文】 Bruinsma, W.P. 等 (2021) ‘The Gaussian Neural Process’. arXiv. Available at: http://arxiv.org/abs/2101.03606 (Accessed: 23 February 2023).

1 引言

神经过程 (Neural Processes, NPs; Garnelo 等，2018a ^[5],2018b ^[6]) 使用神经网络直接参数化并且学习 “从观测数据到随机过程的后验预测分布的映射” 。在本文工作中，我们为神经过程框架提供了两个贡献。

贡献 1: 对用于训练条件神经过程模型的标准最大似然 (ML) 目标进行严格分析。特别是，我们将目标与随机过程之间的 $\mathrm{KL}$ 散度联系起来 (d. G. Matthews 等，2016 ^[1])，我们称之为函数 $\mathrm{KL}$。对于基本事实 $\mathrm{P}$ 和近似过程 $\mathrm{Q}$，之前已经研究了最小化函数 $\mathrm{KL}$ 的学习过程（Sun 等，2018 ^[16]; Shi 等，2019 ^[15]; Ma 等，2018 ^[11]），但这些工作留下了关于目标的有限性和其最小化器的存在/唯一性问题未得到解答。在本文工作中，我们考虑目标 $\mathrm{KL(P, Q)}$。在定义明确且严格的设置中，我们证明了最大似然目标可以解释为该函数目标的良好松弛。

贡献 2: 解决了条件神经过程（Contional Nerual processes, CNPs；Garnelo 等，2018a ^[5]）无法模拟相关性并产生连贯样本的问题。几位作者建议通过引入隐变量来克服这一限制（Garnelo 等，2018b ^[6]；Kim 等，2019 年 ^[9]；Foong 等，2020 年 ^[4]）。不幸的是，这使得似然难以处理，使学习和计算复杂化。在 ConvCNP（Gordon 等，2020 年 ^[7]）的基础上，我们引入了高斯神经过程（Gaussian Neural Process， GNP），这是神经过程家族的一个新成员，它结合了平移等方差并直接使用高斯过程对预测分布进行建模（Rasmussen 和 Williams，2006 年^[13]）。高斯神经过程允许预测分布中的相关性，同时承认封闭形式的似然。此外，与 ConvCNP 一样，GNP 提供了通用近似保证，我们提供了经验证据证明：高斯神经过程可以根据似然和先验协方差函数恢复真实高斯过程的预测图。

2 高斯过程元学习的实用目标

本节中使用的符号和术语的详细描述可以在 附录 A 中找到。所有定理的陈述和证明推迟到 附录 B 到 附录 D。

【问题设置】：设 $f$ 是一个真实的随机过程。在元学习设置中，我们的目标是根据从 $f$ 中提取的一组观测数据集 $(D_i)^{N}_{i=1}$ 对 $f$ 进行多个预测。通过访问 $f$ ，这些预测由给定 $(D_i)^{N}_{i=1}$ 的 $f$ 的后验概率给出。我们可以将预测视为从观测数据集 $\mathcal{D}$ 到 $f$ 上的后验概率的映射。该映射称为后验预测映射 $\pi_f : \mathcal{D} \rightarrow \mathcal{P}$ (Foong 等，2020 ^[4])。我们的目标是学习一个 $\pi_f$ 的高斯近似 $\tilde{\pi} : \mathcal{D} \rightarrow \mathcal{P}_G$ (定义 C.4)，它用高斯过程近似 $f$ 上的后验。请注意，后验预测映射的高斯近似与学习先验 $f$ 的高斯近似明显不同，后验映射的高斯近似对 $\tilde{\pi}$ 的唯一要求是：对于所有 $D \in \mathcal{D}$，$\tilde{\pi}(D)$ 都是高斯过程；特别是，这些高斯过程并不受限于固定的先验，这意味着学习 $\tilde{\pi}$ 享有更大的灵活性。事实上，这种设置比最早提出的条件神经过程（Garnelo 等，2018a ^[5]）更灵活，因为条神经过程是一种不对相关性建模的 $\mathcal{D} \rightarrow \mathcal{P}_G$ 映射。

【函数目标】：我们直接用高斯过程 $μ$ 来近似 $\pi_f$，即对于每个 $D \in \mathcal{D}$，定义 $\tilde{\pi}$ 如下:

$$\tilde{\pi}(D) = \arg \min_{μ \in \mathcal{P}_G} \mathrm{KL}(\pi_f (D), μ) \tag{1}$$

在合理的正则条件下，如果存在一些能够使 $\mathrm{KL}(\pi_f (D), \mu_G) < \infty$ 的非退化高斯过程 $\mu_G \in \mathcal{P}_G$，则上述最小化存在并且是唯一的（Cor B.1），但是也有可能不存在这样的高斯过程 $\mu_G$。更进一步的，假设最小化的 $\tilde{\pi}(D)$ 存在且唯一（ 这意味着 式(1) 在 $\tilde{\pi}(D)$ 处必须是有限的），也可能不存在能够使 式 (1 ) 有限且围绕 $\tilde{\pi}(D)$ 的近似球；在这种情况下，最小化的 $\tilde{\pi}(D)$ 无法通过最小化 式 (1) 来近似。举一个例子，假设真实映射为 $\pi_f (D) = \mathcal{GP}(0, k)$，其协方差函数为 $k(t, t′) = \exp(− \frac{1}{2} (t − t′)^2)$，近似的高斯过程为 $μ_{\sigma^2} = \mathcal{GP}(0, \sigma^2 k)$，则对于所有的 $\sigma^2 \neq 1$，都会存在 $\mathrm{KL}(\pi_f (D), μ）{\sigma^2}) = \infty$ 的情况。因此，我们无法通过用一些合理的 $\sigma^2 > 0$ 初始化 $\mu_{\sigma^2}$ 并最小化 $\mathrm{KL}(\pi_f ( D), \mu_{\sigma^2})$, 因为除了 $\sigma^2$ 的真值外，其他情况的目标都是无限的。

【放松的目标】：为了解决可能缺少最小化的问题，我们采取务实的态度，仅仅近似如下的有限维分布 (f.d.d.s)：

$$\tilde{\pi}^{\mathbf{x}}(D) = \arg \min_{μ^{\mathbf{x}} \in \mathcal{P}^{|\mathbf{x}|}_G} \mathrm{KL}(P_{\mathbf{x}}\pi_f (D), μ^{\mathbf{x}}),\quad \text{ for all finite index sets } \mathbf{x} \tag{2}$$

其中，符号 $P_{\mathbf{x}}f = (f (x_1), \ldots , f(x_{|\mathbf{x}|}))$ （ $f \in \mathcal{Y}^{\mathcal{X}}$ ）表示 $f$ 在索引集 $\mathbf{x}$ 上的投影。在合理的正则条件下，假设对于所有有限索引集 $\mathbf{x}$，存在一个适当的 $|\mathbf{x}|$ 维高斯分布 $\mu^{\mathbf{x}}_G$，能够使 $\mathrm{KL}(P_{\mathbf{x}} \pi_f(D), \mu^{\mathbf{x}}_G) < \infty$，则其最小化存在并且唯一（ 【Prop B.1】 )。

这个条件比 式 (1) 的条件温和得多：如果 $P_{\mathbf{x}}\pi_f (D)$ 的微分熵是有限的，则对于任何适当的 $\mu^{\mathbf{x}}_G$ 都满足条件。至关重要的是，事实证明 式 (2) 产生了一个一致的 f.d.d.s 集合（命题 B.1），因此对于所有有限索引集 $\mathbf{x}$，能够唯一地定义了一个满足 $P_{\mathbf{x}} \tilde{\pi}(D) = \tilde{\pi}^{\mathbf{x}}(D)$ 的近似过程 $\tilde{\pi}(D)$ 。此外，如果 式(1) 的解存在，则它将等于 $\tilde{\pi}(D)$（Prop B.1 和 Cor B.1）。因此， 式(2) 定义了 式(1) 的松弛，可以在 式(1) 的解不存在的许多情况下使用。 式(1) 和 式(2) 的解如果存在，则可以由 矩匹配高斯过程 给出：也就是取 $\pi_f(D)$ 的均值函数和协方差函数得到的高斯过程，参见 Ma 等 (2018 ^[11])。

【近似目标】： 虽然 式（2） 解决了是否存在的问题，但仍然存在其他近似性问题： 式（1） 无法保证总是被最小化到近似最小化值（如果存在的话）。因此，我们定义了另一个目标，该目标始终有限，并且始终可以最小化到 式(2) 的近似解。此目标是通过在固定大小的索引集上平均 式 (2) 得到的：

$$\tilde{\pi}(D) = \arg \min_{μ\in\mathcal{P}_G} \mathbb{E}_{p(\mathbf{x})} [\mathrm{KL}(P_{\mathbf{x}} \pi_f(D), P_{\mathbf{x}}μ)] \tag{3}$$

其中 $p(\mathbf{x})$ 是 Borel 分布，完全支持固定大小为 $n \geq 2$ 的所有索引集。（有关 $\overline{ \mathcal{P}}_G$ 的定义，请参见 Def C.1。）这个目标定义明确（命题 D.1）。如果 (i) $\pi_f (D)$ 和 $μ$ 的均值和协方差函数存在并且由 $M > 0$ 统一界定，并且 (ii) 过程 $\pi_f (D)$ 和 $μ$ 是有噪声的（Def C.1），那么命题 D.3 表明目标是有限的，因此适合优化；命题 D.4 表明 式(2) 和 式(3) 的最小值相等。 式(3) 的一个有用特征是它对固定大小 $n \geq 2$ 的索引集进行平均，这与以前的目标不同，例如 Foong 等 (2020 ^[4])的 命题 1 ，该方法中需要对所有大小的索引集进行平均。

【实践目标】：我们进一步在适当选择的数据集中平均 式（3），这形成了一个能够捕获 $\tilde{\pi}$ 的总近似误差的̃单一目标：

$$\tilde{\pi} = \arg \min_{π \in \overline{\mathcal{M}}^{\text{f.d.d.}}_G} \mathbb{E}_{p(D)p(\mathbf{x})}[\mathrm{KL}(P_{\mathbf{x}} π_f(D), P_{\mathbf{x}} π(D))] \tag{4}$$

其中 $p(D)$ 是 Borel 分布，完全支持一组开放且有界的数据集 $\tilde{\mathcal{D}} \subset \mathcal{D}$ (Def C.5)。 （参见 Def C.6 了解 $\overline{\mathcal{M}}^{\text{f.d.d.}}_G$ 的定义）。此目标也有明确的定义（命题 D.2）。在类似于 式(3) 的条件下， 式(4) 是有限的，并且 式(2) 和 式(4) 的最小值相等（命题 D.5 和 命题 D.6）。因此，我们建议通过最小化 式(4) 来学习 $\tilde{\pi}$。

在实践中，我们优化了 式(4) 的蒙特卡罗近似。设 $(D_i)^{N}_{i=1} \subset \mathcal{D}$ 为数据集的集合，全部从 $f$ 采样并将 $D_i = (D^{(c)}_i, D^{(t)}_i)$ 拆分为上下文集 $D^{(c)}_i$ 和目标集 $D^{(t)} = (\mathbf{x}^{(t)}_i , \mathbf{y}^{(t)}_i)$（Vinyals 等，2016 年 ^[17]；Ravi 和 Larochelle，2017 年 ^[14]）。然后我们最大化

$$\tilde{\pi} \approx \arg \max_{π \in \overline{\mathcal{M}}^{\text{f.d.d.}}_G} \frac{1}{N} \sum^{N}_{i=1} \log \mathcal{N}(\mathbf{y}^{(t)}_i | \mathbf{m}_i, \mathbf{K}_i) \text{ with } P_{\mathbf{x}^{(t)}_i} \pi (D^{(c)}_i) = \mathcal{N}(\mathbf{m}_i, \mathbf{K}_i) \tag{5}$$

我们忽略不依赖于 $π$ 的不相关附加常数。该目标正是用于训练 条件神经过程 模型的标准最大似然目标（Garnelo 等，2018a ^[5]；Gordon 等，2020 ^[7]）。

最小化过程的分析很困难，并且取决于特定算法的细节。但我们可以说的是，一个最小化序列要么发散要么收敛到正确的极限；并且，在某些条件下，最小化序列总是有一个收敛的子序列（命题 D.7）。

3 高斯神经过程

定义了一个合适的目标后，为了在实践中学习近似 $\tilde{\pi}$，我们通常参数化 $\tilde{\pi}$。在本文中，我们范围限制在平稳的真实过程 $f$ 上。

【平移等变】 Foong 等（2020 ^[4]）表明，$f$ 的平稳性等同于 $f$ 的后验预测映射 $π_f$ 的平移等价性（TE）。 对于所有 $D \in \mathcal{D}, \top_{\tau} \pi_f (D) = \pi_f (D + τ )$ 对于所有 $τ \in \mathcal{X}$ 其中 $\top_{\tau}f = f( \cdot − τ )$ 是移位算子，$\top_{\tau} \pi_f (D)$ 是推入的测度 $\pi_f (D)$ 通过 $\top_{\tau}$ 和 $D + τ = (\mathbf{x, y}) + τ = ((x_1 + τ,\ldots , x_{|\mathbf{x}|} + τ ), \mathbf{y})$。如果 $\pi_f$ 是 $TE$，那么限制我们的近似 $\tilde{\pi}$ 也是 $TE$ 是合理的。已证明将平移等方差直接纳入模型可显着提高泛化能力、参数效率和预测性能（Gordon 等，2020 年 ^[7]；Foong 等，2020 年 ^[4]）。表示 $\tilde{\pi}(D) = \mathcal{GP}(m(D), k(D))$ 其中 $m : \mathcal{D} \rightarrow C(\mathcal{X , Y})$ 是我们近似 $\tilde{\pi}$ 和 $k : \mathcal{D} \rightarrow C^{\text{p.s.d.}}(\mathcal{X}^2,\mathcal{Y})$ 是 TE 核映射；有关更多详细信息，请参阅附录 E。

【均值和核的通用参数化】：对于均值映射 m，我们使用 ConvDeepSet 架构（在 ConvCNP 中使用，Gordon 等，2020），它可以近似从数据集到连续均值函数的任何平移等变映射（Thm 1 戈登等，2020 年）。不幸的是，正如我们在 附录 E.1 中解释的那样，ConvDeepSet 架构并不直接适用于核映射 k。在 附录 E 中，我们修改了 ConvDeepSet 架构，使其适合核。该架构具有类似于 ConvDeepSet (Thm E.1) 的通用近似保证，从而完成了 \tilde{\pi} 的通用近似参数化。直观上，该架构的工作原理如下。协方差函数是函数 X × X \rightarrow R，因此可以解释为图像（例如，假设 X = {1, . . . , n}）。 ConvCNP 通过将数据嵌入一维数组并将其传递给一维卷积来生成均值，而核的体系结构类似地将数据嵌入二维图像并传递给二维卷积。令 D^{©} 为上下文集，\mathbf{x}^{(t)}$ 为目标集的输入。然后生成目标点 \mathbf{x}^{(t)}$处的协方差矩阵 \mathbf{K}^{(t)}如下：

$$\text{ ➊ } \mathbf{H} = \text{enc}(D^{(c)}, \mathbf{Z}), \qquad \text{ ➋ } \mathbf{K} = \prod^{\text{p.s.d.}} \text{CNN}(\mathbf{H}), \qquad \text{ ➌ } \mathbf{K}^{(t)} = \text{dec}(\mathbf{K}, \mathbf{text}^{(t)}) : \tag{6}$$

➊ $\mathbf{H} = \text{enc}(D^{(c)}, \mathbf{Z})$ 将目标集 $D^{(c)}$ 映射到编码 $\mathbf{H} \in \mathbb{R}^{M×M×3}$ 在预先指定的网格 $\mathbf{Z} \in \mathbf{R}^{M×M}$ 对于一些 $M \in \mathbb{N}$（c.f. ConvCNP (Gordon 等，2020 ^[7])），包括数据通道 $\mathbf{H}_{::1}$（参见 ConvDeepSet 中的数据通道）、密度通道 $\mathbf{H}_{::2}$（参见 ConvDeepSet 中的密度通道）和源通道 $\mathbf{H}_{::3} = I$（不存在于 ConvDeepSet 中；参见 附录 E.2）；

➋ $\mathbf{K} = \prod^{\text{p.s.d.}} \text{CNN}(\mathbf{H})$ 通过 CNN 传递编码 $\mathbf{H}$，生成 $M × M$ 矩阵，并使用 $\prod^{\text{p.s.d}}$ 投影该矩阵。到最近的关于 Frobenius 范数的半正定 (PSD) 矩阵 (Higham, 1988 ^[8])；

➌ $\mathbf{K}^{(t)} = \text{dec}(\mathbf{K}, \mathbf{text}^{(t)})$ 最后将获得的 PSD 矩阵 $K$ 插值到目标输入 $\mathbf{x}^{(t)}$ 的所需协方差 $\mathbf{K}^{(t)}$。

$\text{enc}$ 和 $\text{dec}$ 的体系结构和精确定义在 附录 E.2 中有更详细的描述。在我们的实验中，与上面的描述和 附录 E.2 相反，我们将 2 替换为更简单的操作 $\mathbf{K} = \text{CNN}(\mathbf{H}) \text{CNN}(\mathbf{H})^{\top}$，这也保证了正半定性。目前尚不清楚这种替换是否限制了所得架构的表现力或干扰平移等变性。我们用 $\prod^{\text{p.s.d.}}$ 对 2 的实现进行了调查。为以后的工作。

【源通道】：架构 (6) 的一个新颖方面是源通道 $\mathbf{H}_{::3} = \mathbf{I}$，它只是单位矩阵，不存在于 ConvDeepSet 架构中。 直观地说，源通道允许架构从协方差为 $\mathbf{I}$ 的平稳先验“开始”，对应于白噪声，然后通过 CNN 对其进行调制，然后引入从上下文集推断出的相关性。 C.f.，任何高斯过程都可以通过首先采样白噪声然后与适当的滤波器进行卷积来采样；核架构是此过程的非线性推广。

【高斯神经过程】：用于均值映射 $m$ 的 ConvDeepSet 和上述用于核映射 $k$ 的架构形成了一个模型，我们称之为高斯神经过程 (GNP)。高斯神经过程取决于一些参数 $θ$，例如 CNN 的权重和偏差。为了训练这些参数 $θ$，我们最大化 (5)。有关更多详细信息，请参阅 附录 E.3。

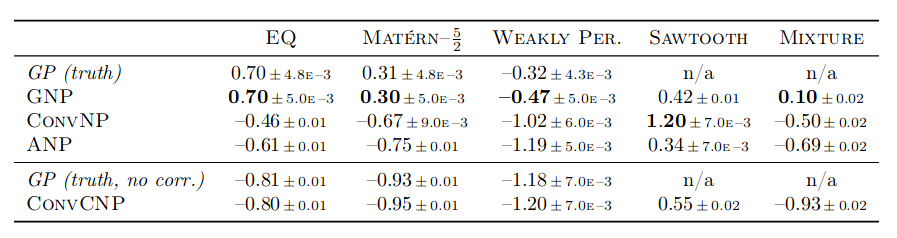
表 1：训练范围内插值的一维回归实验的似然。突出最佳性能。只有 ConvCNP 不对相关性建模。误差为 95% 置信区间。参见附录 F。

图 1：一维实验中学习的和真正的平稳先验协方差函数。先验协方差函数可以通过取 $D^{(c)} = ∅$ 从模型中提取。

4 实验

我们在合成一维回归实验中评估高斯神经过程。我们遵循 Foong 等(2020)的实验设置。有关详细信息，请参阅 附录 F。与第 2 节的理论分析一致，但与 Foong 等 (2020) 不同，我们用 $\mathcal{N}(0, 0.052)$-噪声污染了所有数据样本。可以在 https://github.com/wesselb/NeuralProcesses.jl 找到实现高斯神经过程和重现所有实验的代码。

表 1 显示了真实 GP（如果适用）、没有相关性的真实 GP、GNP、ConvCNP（Gordon 等人，2020）、ConvNP（Foong 等人，2020）和 ANP 的性能(Kim 等, 2019 ^[9]) 在插值设置中；图 2 显示了学习模型的样本。高斯神经过程在除 Sawtooth 之外的所有任务上都明显优于所有其他模型。在 EQ 和 Matérn–$\frac{5}{2}$ 上，GNP 甚至与真实 GP 持平。此外，GNP 是 Mixture 上表现最好的模型，它是高度非高斯的，表明高斯神经过程可以成功地近似非高斯过程。

图 1 显示了通过高斯神经过程学得的平稳先验协方差函数，在高斯过程任务上接近 ground-truth；这与似然数一起，凭经验验证了高斯神经过程恢复真值高斯过程预测图的能力。请注意，学习到的协方差函数也与非高斯任务 Sawtooth 和 Mixture 的真实情况相匹配。对于 Sawtooth，GNP 的似然比 ConvCNP 更差，并且仅比 ANP 有所提高，这表明，在某些非高斯任务上，非高斯近似（如 ConvNP）可以提供更好的性能。在最昂贵的任务（Sawtooth 和 Mixture）上，GNP 的一个 epoch 花费的时间大约是任何其他模型的六倍；参见 表 F.2。更多结果在 附录 F 中，包括测试泛化和外推性能的设置结果；与 ConvCNP 和 ConvNP 一样，由于平移等变性，这些结果表明高斯神经过程表现出出色的泛化能力。

图 2：在一维实验中训练的模型的样本预测。灰色区域表示模型的训练位置；紫色虚线表示根据基本事实做出的最佳预测。

5 结论

我们对用于训练神经过程的标准最大似然目标进行了严格的分析。此外，我们向神经过程家族提出了一个新成员，称为高斯神经过程 (GNP)，它结合了平移等方差，提供通用近似保证，并在初步实验中展示了令人鼓舞的性能。在未来的工作中，我们的目标是研究将 $\prod^{\text{p.s.d.}}$ （第 3 节）直接纳入架构。

参考文献

• [1] A. G. d. G. Matthews, J. Hensman, R. E. Turner, and Z. Ghahramani. On sparse variational methods and the Kullback-Leibler divergence between stochastic processes. In Aarti Singh and Jerry Zhu, editors, International Conference on Artificial Intelligence and Statistics 22, volume 54 of Proceedings of Machine Learning Research. Proceedings of Machine Learning Research, Apr 2016.
• [2] James Dugundji. An extension of Tietze’s theorem. Pacific Journal of Mathematics, 1(3): 353–367, 1951.
• [3] Aasa Feragen. Characterization of equivariant ANEs, 2006.
• [4] Andrew Y. K. Foong, Wessel P. Bruinsma, Jonathan Gordon, Yann Dubois, James Requeima, and Richard E. Turner. Meta-learning stationary stochastic process prediction with convolutional neural processes. In H. Larochelle, M. Ranzato, R. Hadsell, M.F. Balcan, and H. Lin, editors, Advances in Neural Information Processing Systems 33. Curran Associates, Inc., Jul 2020.
• [5] M. Garnelo, D. Rosenbaum, C. J. Maddison, T. Ramalho, D. Saxton, M. Shanahan, Y. Whye Teh, D. J. Rezende, and S. M. A. Eslami. Conditional neural processes. In Jennifer Dy and Andreas Krause, editors, International Conference on Machine Learning 35, volume 80 of Proceedings of Machine Learning Research. Proceedings of Machine Learning Research, Jul 2018a.
• [6] M. Garnelo, J. Schwarz, D. Rosenbaum, F. Viola, D. J. Rezende, S. M. A. Eslami, and Y. Whye Teh. Neural processes. arXiv preprint arXiv:1807.01622, Jul 2018b.
• [7] Jonathan Gordon, Wessel P. Bruinsma, Andrew Y. K. Foong, James Requeima, Yann Dubois, and Richard E. Turner. Convolutional conditional neural processes. International Conference on Learning Representations (ICLR), 8th, Oct 2020.
• [8] Nicholas J. Higham. Computing a nearest symmetric positive semidefinite matrix. Linear Algebra and Its Applications, 103:103–118, 1988.
• [9] H. Kim, A. Mnih, J. Schwarz, M. Garnelo, A. Eslami, D. Rosenbaum, O. Vinyals, and Y. Whye Teh. Attentive neural processes. In International Conference on Learning Representations 7, Jan 2019.
• [10] D. P. Kingma and J. Ba. ADAM: A method for stochastic optimization. In International Conference on Learning Representations 3, Dec 2015.
• [11] Chao Ma, Yingzhen Li, and José Miguel Hernández-Lobato. Variational implicit processes. In Yarin Gal, José Miguel Hernández-Lobato, Christos Louizos, Andrew G. Wilson, Zoubin Ghahramani, Kevin Murphy, and Max Welling, editors, Advances in Neural Information Processing Systems 31, Dec 2018.
• [12] Edward C. Posner. Random coding strategies for minimum entropy. IEEE Transactions on Information Theory, 21(4), Jul 1975.
• [13] Carl Edward Rasmussen and Christopher K. I. Williams. Gaussian Processes for Machine Learning. MIT Press, 2006.
• [14] Sachin Ravi and Hugo Larochelle. Optimization as a model for few-shot learning. In International Conference on Learning Representations 5, Apr 2017.
• [15] J. Shi, M. Emtiyaz Khan, and J. Zhu. Scalable training of inference networks for Gaussianprocess models. In Kamalika Chaudhuri and Ruslan Salakhutdinov, editors, International Conference on Machine Learning 36, volume 97 of Proceedings of Machine Learning Research. Proceedings of Machine Learning Research, May 2019.
• [16] Shengyang Sun, Guodong Zhang, Jiaxin Shi, and Roger Grosse. Functional variational Bayesian neural networks. In Yarin Gal, José Miguel Hernández-Lobato, Christos Louizos, Andrew G. Wilson, Zoubin Ghahramani, Kevin Murphy, and Max Welling, editors, Advances in Neural Information Processing Systems 31, Dec 2018.
• [17] Oriol Vinyals, Charles Blundell, Timothy Lillicrap, Koray Kavukcuoglu, and Daan Wierstra. Matching networks for one shot learning. In D. D. Lee, M. Sugiyama, U. V. Luxburg, I. Guyon, and R. Garnett, editors, Advances in Neural Information Processing Systems 29. Curran Associates, Inc., Jun 2016.
• [18] D. Yarotsky. Universal approximations of invariant maps by neural networks. arXiv preprint arXiv:1804.10306, Apr 2018.