数据驱动地球系统科学的深度学习和过程理解
【摘 要】机器学习方法越来越多地用于从不断增长的地理空间数据流中提取模式和见解,但是当系统行为受空间或时间上下文支配时,当前的方法可能不是最优的。在这里,我们认为应该将这些上下文线索用作深度学习( 一种能够自动提取时空特征的方法 )的一部分,而不是仅仅对经典机器学习方法做修补,以获得对地球系统科学问题更进一步的过程理解。例如,改善季节性预报的预测能力、跨多个时间尺度的远距离空间连接性建模。下一个阶段将会是将 物理过程模型 与 数据驱动的机器学习多功能性 相结合的混合建模方法时代。
【原 文】 M. Reichstein, G. Camps-Valls, B. Stevens, M. Jung, J. Denzler, and N. Carvalhais, “Deep learning and process understanding for data-driven earth system science,” Nature, vol. 566, no. 7743, pp. 195–204, 2019.
【阅后感】2019年,德国马克斯普朗克研究所、美国劳伦斯伯克利实验室等机构的研究者,合作发表于 Nature。系统阐述了大数据时代,地球系统科学所面临的挑战与机遇,深度学习方法在该领域的应用案例、存在的问题以及未来的发展方向。作者认为,深度学习为地球科学提供了有前景的方法,但需要与地球科学中的物理模型进行有效结合。作者为地学领域的深度学习研究提出了以下四点建议:(1) 认识到地球科学数据的特殊性,建模的时候要充分考虑到数据的多源、多尺度、高维、复杂时空依赖性;(2) 模型推断不仅要准确,还要具有合理性和可解释性,要充分考虑物理规律;(3) 贝叶斯、概率推断等不确定性估计应该被整合到模型中,模型要给出它们的置信度和可信度;(4) 机器学习方法应当能够够经得起地球系统物理模型合成数据的检验。机器学习的空间和时间预测能力,至少应该与物理模型中观测到的模式一致。鉴于实际地球数据的获取可能代价较高,因此,根据地球系统物理模型生成的合成数据来检验机器学习方法的性能是必要的。 总之,作者建议未来的模型应该整合基于过程的物理模型与机器学习方法,数据驱动方法并不是替代,而是对物理模型的补充与增强。
1 背景
人类一直在努力预测和了解世界,做出更好预测的能力为不同领域(如天气、疾病或金融市场)赋予了竞争优势。然而,随着时间推移,预测工具发生了巨大变化,从古希腊哲学推理,到中世纪的占卜等非科学方法,再到现代科学法则(包括假设检验、理论发展和以统计和物理关系为基础的计算机建模)[1] 。地球科学的一个成功案例是天气预报,它通过整合更好的理论、增强的计算能力和强大的观测系统得到了极大改进,这些系统允许将大量数据同化到建模系统中[2]。我们可以准确地预测天气的演变,但时间尺度是几天,而不是几个月。目前为止, 季节性气象预测(prediction)、极端事件预报(forecasting,如洪水、火灾等)、长期气候变化预测(projections)仍然是重要挑战。 这对于预测生物圈动态非常重要,因为该动态由生物介导过程(如生长或繁殖)控制,并受到火灾和山体滑坡等看似随机的干扰强烈控制。在过去的几十年中,此类预测问题并未取得太大进展[3]。
与此同时,大量的地球系统数据已经可用,存储量已经远远超过数十 PB,并且传输速率迅速增加,每天超过数百 TB [4]。这些数据来自大量与时间/空间集成的、用于测量状态、通量、密度等变量的传感器,可以表示 或更多阶时间和空间量级。它们包括:地球上空几米到数百公里的遥感、地表和地表以下以及大气中的原位观测(越来越多地来自自主传感器),其中许多进一步得到了民间科学观测的补充。模型的模拟输出增加了这股洪流;气候模型比对项目 的 CMIP-5 数据集,已经被广泛用于周期气候评估的科学基础工作,其大小超过 PB,下一代 CMIP-6 估计将达到 PB [5]。来自模型的数据共享了观测数据的许多挑战和统计特性,包括多种形式的不确定性。总之,地球系统数据包含 “大数据” 的 “四个 V” 中的所有四个情况:数量、速度、多样性和准确性(见 图 1 )。一个关键挑战是从这些大数据中提取出可解释的信息和知识(有时需要实时的),并且可以在多学科之间进行整合。

图 1: 大数据时代地球科学所面临的挑战。数据大小现在超过 PB,并且呈准指数增长(图中向右逐渐变细表示数据大小正在减小)。变化速度超过每年 PB;以高达 Hz 或更高的频率采集数据;再处理和版本控制是常见的挑战。数据源可以是一维到四维的、空间整合的,从器官级别(如叶)到全球级别。地球有多种观测系统,从遥感到现场观测。数据的不确定性可能源于观测误差或概念的不一致。
总而言之,我们收集和创建数据的能力远远超过了我们明智地吸收它的能力,更不用说理解它了。过去几十年的预测能力并没有随着数据可用性的提高而迅速提高。为了充分利用地球系统数据的爆炸式增长和多样性,我们将在未来几年面临两项主要任务:
-
(1) 从海量数据中提取知识;
-
(2) 开发能够从数据中比传统数据同化方法获得更多知识的模型,并且模型要尊重人类对自然规律的理解(正在不断进步的)。
前所未有的数据源、增强的计算能力、统计建模、机器学习的最新进展相结合,为我们从数据中扩展关于地球系统的知识提供了令人兴奋的新机会。特别是, **机器学习和人工智能领域有许多工具可用,但它们需要进一步开发并适应地球科学分析。**地球系统科学提供了新的机遇、挑战和方法要求,特别是对于那些关注时空上下文和不确定性的研究方向(方框 1;参见 机器学习词汇表 和 深度学习词汇表)。
框 1: 术语定义

在以下部分中,我们回顾了地球科学背景下机器学习的发展,并强调深度学习有可能克服阻碍机器学习更广泛使用的许多限制。我们进一步提出了将机器学习与物理模型相结合的最有前途但也最具挑战性的方法。
2 地球科学领域的机器学习
在涉及大气、地表和海洋等几个研究驱动的、可操作的地球科学处理计划中,机器学习现在是比较成功的部分;并且在过去十年间,与数据的可用性协同发展。
近 30 年前,高分辨率卫星数据的出现和神经网络的第一次复兴 [6][7],推动了云和土地覆盖分类等早期里程碑。在相关方法适用的数据可用时,大多数主要的机器学习方法发展随后都被应用到了地球科学和遥感问题(如 “核方法” 或 “随机森林”)[8]。机器学习已成为地球科学处理分类、变化检测、异常检测等问题的普遍方法 [9][10][11][12]。在过去的几年里,地球科学已经开始使用深度学习来更好地开发和利用数据中的空间和时间结构,这些特征通常是传统机器学习方法难以提取的(见 表 1 及下文)。
表 1 地球科学任务的常规方法和深度学习方法

机器学习能够成功的另一类问题是回归。例如土壤调查,我们在空间中稀疏分布的测点处有土壤特性和协变量的测量值,可以使用 “随机森林” 的机器学习方法,来预测土壤特性或土壤类型的空间密集估计[13][14]。在过去的十年中,机器学习在局部和全球尺度的遥感反射率反演生物地球物理参数方面,取得了突出的成果[15][16][17]。这些方法强调空间预测,即预测在观测时间段内相对静态的属性。 然而,地球系统的有趣之处在于它不是静态的,而是动态的。机器学习回归技术也被用于研究这些动态,方法是将时变特征变量映射到陆地、海洋和大气领域的时变目标变量上。
由于无法在任何地方得到诸如 “陆地-大气碳吸收” 或 “海洋-大气碳吸收” 等观测,因此建立将气候和遥感等协变量关联到目标变量的模型,以便从点观测推断出对陆地和全球的估计,就成为了一个挑战。在这种情况下,机器学习方法已被证明比以前的机制或半经验建模方法更强大、更灵活。例如,
- 具有一个隐藏层的人工神经网络能够滤除噪声,预测二氧化碳 ( ) 通量的昼夜和季节变化,并提取诸如春季根系生长期间呼吸增加等模式,这在以前是无法被量化的,并且在碳循环模型中没有得到很好体现 [18]。
- 进一步的发展使我们能够以纯数据驱动的方式量化全球陆地光合作用和水的蒸发蒸腾 [19][20]。这种通过机器学习预测的空间、季节、年际或十年际通量变化,甚至被用作物理地表和气候模型评估的重要基准 [21][22][23][24]。
- 同样,海洋二氧化碳浓度和通量已通过神经网络进行时空映射,其中分类和回归方法已结合起来,用于对数据进行分层和预测[25]。
- 最近,随机森林方法也被用于预测时空变化的降水 [26]。
总的来说,我们得出结论: 各种有影响力的机器学习方法已经应用于地球系统科学的所有主要子领域,并且越来越多地被整合到操作方案中,并被用于发现模式、提高我们的理解和评估综合物理模型。
尽管机器学习在地球科学领域取得了成功,但重要的注意事项和限制阻碍了其更广泛的采用和影响。一些陷阱需要通过最佳实践和专家干预来避免,例如, 过于简单的外推/采样或其他数据偏差、 无法区分混淆变量、 将统计关联解释为因果关系、 多重假设检验 (‘P-fishing’) 等缺陷[27][28][29] 等。不过,目前机器学习方法的应用尚存在一些固有的局限性,恰恰正是深度学习技术有望取得突破的领域。
经典机器学习方法受益于面向领域的、人工制作或选用的特征,以解释时间或空间依赖性(例如,从每日时间序列得出的累积降水),但很少详尽地利用时空依赖性。例如,在海洋-大气(或陆地-大气) 通量预测 [19][25] 中,会执行瞬时局部环境条件(如辐射、温度和湿度)到瞬时通量的映射。实际上,特定时间和空间点的过程几乎总是受到某些系统状态的附加影响,而这些系统状态通常无法(或不能)被观测到,进而无法被用作预测变量。此时,之前的时间步和相邻的网格单元中或多或少包含了有关系统状态的一些隐藏信息(例如,长时间没有降雨加上持续的晴天意味着干旱)。例如:火灾发生 以及 燃烧面积 和 微量气体排放 等特征的预测。火灾发生和蔓延不仅取决于瞬时气候驱动因素和火源(例如人类、闪电或两者),还取决于状态变量(例如状态和可用燃料的数量)[3]。火势蔓延和燃烧面积不仅取决于每个像素的局部条件,还取决于燃料的空间排列和连通性、水分、地形特性,当然还有风速和风向。同样,将某种大气情况分类为飓风或温带风暴需要了解空间上下文,例如由像素构成的风暴几何形状、数值和拓扑。举个例子,检测对称性的外流和 “风眼” ,对于识别飓风和评估其强度非常重要,而这不能仅通过局部单像素值来确定。
当然,时间动态性质(“记忆效应”)可以通过机器学习中的手工设计和特定领域的特征来表示。例如,用于预测植被物候阶段的每日温度的累积总和,以及将过去几个月的降水异常总结为干旱状态的气象指标的标准化降水指数 [30]。在大多数时候,这些方法只考虑了单变量中的记忆,而忽略了几个变量的交互影响(虽然也有些例外)[22][31]。
机器学习可以使用人工设计的特征,例如来自卫星图像的地形形状、地形、纹理特征,以结合空间上下文[6]。这类似于计算机视觉中的早期方法,其中对象通常由一组描述边缘、纹理、形状和颜色的特征来表征。然后将这些特征输入到标准机器学习算法中,用于图像中对象的定位、分类或检测。几十年来,遥感图像分类[8][9][10] 都采用了类似方法。手工设计的功能既可以被视为优势(解释性驱动程序的控制),但也可以被视为劣势(繁琐的临时过程,可能不是最佳的)。可以肯定的是,关于使用 “受限和主观选择的特征” 还是使用 “广泛和通用的特征” 的忧虑仍然有效和重要。不过,深度学习的新发展使我们不再局限于这些方法。
3 深度学习应用的机遇
深度学习在计算机视觉、语音识别和控制系统领域 [32] 以及物理学 [33][34][35]、化学[36]和生物学[37]的相关科学领域对有序序列和具有空间上下文的数据进行建模方面取得了显著成功(另见参考文献 [38])。不过在地球科学方面的应用尚处于起步阶段,但在关键问题(分类、异常检测、回归、空间或时间相关状态预测)中,有一些很有前景的例子(见 表 1 和附件的 图 2 )[39][40]。最近的两项研究展示了深度学习在极端天气问题中(例如飓风检测[41][42])的应用,并且提到了传统机器学习方法存在的问题。
这些研究成功地应用深度学习架构提取空间特征,以在数值天气预报模型输出中定义和分类极端情况(例如风暴、大气河流)。此类方法能够快速检测事件并预测模拟,而无需使用主观的人工注释或依赖于风速或其他变量的预定义任意阈值的方法。特别是,这种方法使用了事件的空间形状信息,例如典型的飓风螺旋。同样,对于城市地区的分类,从遥感数据中自动提取多尺度特征极大地提高了分类准确度(几乎总是大于 95%)[43]。
虽然经典的深度学习方法分为空间学习(例如,用于对象分类的卷积神经网络)和序列学习(例如,语音识别),但人们对融合这两种观点的兴趣越来越大。一个典型例子是视频和运动预测[44][45],这个问题与许多动态地球科学问题有着惊人的相似之处。在地球科学领域,我们面临着随时间演变的多维结构,例如主导热带降雨模式的有组织的降水对流,以及影响碳流动和蒸散的植被状态。研究开始将 卷积-循环组合方法 应用于地球科学问题,例如降水临近预报( 表 1 )[46]。对大气和海洋运输、火灾蔓延、土壤运动或植被动力学进行建模也是时空动力学很重要的问题,但尚未从这些新方法的协同努力中受益。
简而言之,经典深度学习应用处理的数据类型与地球科学数据之间的相似性,为深度学习与地球科学的整合提供了令人信服的论据( 图 2 )。图像类似于包含特定变量的二维数据场,类似于照片中的颜色三元组(RGB 值),而视频可以链接到一系列图像,因此可以链接到随时间演变的二维场。类似地,自然语言和语音信号具有相同的地球系统变量动态时间序列的多分辨率特征。此外,分类、回归、异常检测和动态建模是计算机视觉和地球科学中的典型问题。

图 2 典型深度学习方法(左图)及其可应用的地球科学问题(右图)。a)图像中的对象识别与使用气候模拟数据上的统一卷积神经网络对极端天气模式进行分类相关联。 b)超分辨率应用与气候模型输出的统计降尺度有关。 c)视频预测类似于地球系统变量的短期预测。右图由马克斯普朗克生物地球化学研究所的 Sujan Koirala 和 Paul Bodesheim 提供。 d)语言翻译链接到动态时间序列的建模。
4 深度学习面临的挑战
上述经典深度学习应用和地球科学应用之间的相似之处是惊人的。然而,也存在许多差异。 例如:
-
虽然经典计算机视觉应用处理具有三个通道(红色、绿色、蓝色)的照片,但高光谱卫星图像扩展到数百个光谱通道,远远超出可见范围,这通常会导致与自然图像不同的统计特性。其中包括变量的空间依赖性和交叉依赖性,这与深度学习领域中常用的独立同分布数据假设相违背。
-
集成多传感器数据并非易事,因为不同的传感器表现出不同的成像几何形状、空间和时间分辨率、物理意义、内容和统计数据。 (多传感器)卫星观测序列还伴随着各种噪声源、不确定性水平、缺失数据和(通常是系统性的)差距(由于云或雪的存在、采集、存储和传输的失真等)。
-
光谱、空间和时间维度带来了计算挑战。数据量正在增加,很快就有必要在全球范围内处理每天 PB 的数据。目前,最大的气象机构每天必须近乎实时地处理 TB 级数据,而且精度通常非常高(32 位、64 位)。
-
虽然典型的计算机视觉应用使用的图像大小为 像素,但中等分辨率(约 公里)的全球视野大小约为 像素,即三个数量级以上。
-
与 ImageNet(人类标记图像的数据库,具有诸如“猫”或“狗”等标签 [47] 不同,大型、标记的地球科学数据集并不总是存在于地球科学中,不仅是因为所涉及的数据集大小,也在于标记数据集的困难;例如,确定一幅图像描绘了一只猫比确定一个数据集反映了干旱要容易得多,因为干旱取决于强度和程度,可以根据收集和分析数据的方法而变化,并且没有足够的标记样本来训练机器学习系统。
-
除了训练集有限的挑战之外,地球科学问题通常是有约束的,这会导致模型过于自信,这些模型在训练甚至测试数据集上表现良好,但对于超出其范围的数据则存在很大偏差(分布外数据、外推问题等),不过,这一点即便是复杂的物理地球系统模型也会发生。
总体而言,我们确定了在地球科学中成功采用深度学习方法的五个主要挑战和途径,如下所示。
4.1 可解释性
提高预测准确性很重要,但还不够。当然,可解释性和理解力至关重要,包括可视化结果以供人类分析。可解释性已被确定为深度神经网络的潜在弱点,实现它是深度学习的当前焦点。该领域距离实现不言自明的模型还有很长的路要走,也远未从观测数据中发现因果关系[50][51]。然而我们应该注意到,鉴于其复杂性,在实际工作中现代地球系统模型通常很难追溯其假设,这也限制了它们的可解释性。
4.2 物理一致性
深度学习模型可以很好地拟合观测结果,但预测可能在物理上存在不一致或不可信,例如,由于外推或观测偏差。通过让模型学习有关地球系统物理规则的模型,来整合领域知识并获得物理一致性,可以在观测数据基础之上提供非常强大的理论约束。
4.3 不确定性
需要深度学习方法来应对复杂的统计数据、多输出、不同的噪声源和高维空间。迫切需要不仅利用局部邻域(即使在不同尺度上),而且利用远距离关系(例如,远程连接)的新网络拓扑。不过,变量之间的确切因果关系事先并不清楚,需要被发现。对不确定性建模是一个重要方面,需要整合来自贝叶斯/概率推断的概念,来直接解决这些不确定性问题(见 框 1 和参考文献 [52])。
4.4 受限的标签
需要深度学习方法从少数标记示例中学习,同时利用相关未标记观测中的大量信息。这些方法包括无监督密度建模、特征提取、半监督学习和域适应 [53](见框 1)。
4.5 计算需求
当前地球科学问题的高计算成本是一个巨大的技术挑战,解决此类问题的一个例子是谷歌地球引擎,它可以解决从森林砍伐 [54] 到湖泊监测 [55]的实际问题,并有望跟进深度学习未来的应用。
4.6 机会
通过解决这些挑战,深度学习可以在地球科学中产生比经典计算机视觉更大的差异。
在计算机视觉中,人工特征来自于人们对世界的清晰理解,以及二维图像上真实世界点的某种外观假设。这种成功假设包括朗伯曲面假设,这也导致随着时间推移三维点观测强度恒定的经典假设。此外,世界的变化在大多数情况下被建模为刚性变换,或由物理假设产生并且仅在局部有效的非刚性变换。即使是计算机视觉中的复杂问题也已通过手工制作的特征得到了解决,这些特征反映了来自共同世界知识的假设和期望。
但是,在地球科学和气候科学中,这种全球性的、一般性的知识仍然部分缺失,而实际上这正是我们在研究中所寻求的。目前所有地球科学问题(从遥感图像分割到某些变量的回归分析)都有某些已知有效的假设或至少是良好近似。
不过, 对过程的了解越少,用于建模的高质量人工选择特征就越少。因此,深度学习方法(特别是由于其从数据中找到良好表示的能力)代表了解决地球科学和气候研究问题的机会。
最有前途的近期应用包括:(1)短时预报(即预测非常近的未来,气象学中最多两个小时)和预报;(2)基于空间和时间上下文信息的异常检测和分类等(参见 表 1 中的示例)。
长期愿景包括:(1)数据驱动的季节性预测;(2)跨多个时间尺度的空间长期相关性建模;(3)空间环境要素(例如火灾、飓风)相对比较重要的空间动态建模;(4)人类可能尚不知道或没想到的变量之间的远程连接检测等。
我们推断:深度学习将很快成为地球科学中时空结构分类和预测的主要方法。其中更具挑战性的事是: 不仅要获得最佳预测,还要获得理解;不仅要得到从数据中最大程度学习到的模型,同时还要考虑物理和生物学知识。实现此目标的一种有前途但很大程度上未知的方法是: 将机器学习与物理建模相结合。
5 与物理建模融合
从历史上看,物理建模和机器学习经常被视为两个不同的领域,具有非常不同的科学范式(理论驱动与数据驱动)。然而,实际上这些方法是互补的,物理方法原则上可以直接解释并提供超出观测条件的外推潜力,而数据驱动方法在适应数据方面具有高度灵活性,并且易于发现意想不到的模式。两种方法之间的协同作用已引起关注 [56][57][58],这体现在一些和 评测 [59][60] 和 约束 等有关的概念中 [27][61][62]。
5.1 在系统建模中引入机器学习
在这里,我们认为机器学习以及地球科学中观测和模拟能力的进步,为以多种方式更密集地整合模拟和数据科学方法提供了机会。从系统建模的角度来看,有五个潜在的协同作用点(见 图 3 ,其中编号的圆圈对应于以下编号列表)。

图 3:物理模型与机器学习模型的耦合方式。此处描述了物理系统的一部分(例如地球系统模型)的抽象。该模型由子模型组成;每个子模型都有参数和强制变量作为输入并产生输出,这些输出可以输入(强制)到另一个子模型。如圆圈数字所示,数据驱动的学习方法在各种情况下都有帮助。例如,标记为 2 的圆圈代表混合建模。
(1)改进参数化方法
参见 图 3➀ 。
物理模型需要参数化,但其中许多参数并不容易从第一性原理推导出来。机器学习可以学习参数化,以最优地描述可以通过第一性原理从详细和高分辨率模型中观测或生成的基本事实。例如,不将地球系统模型中的植被参数直接分配给植物功能类型(大多数全球地表模型中常见的方法),而是允许从适当的统计协变量集合中学习这些参数,允许其更具动态性、相互依存性和上下文关联性。已经在水文学中采用了一种原型方法,其中环境变量(例如降水和地表坡度)与集水区参数(例如平均、最小和最大流量)的映射,已经从几千个集水区学习并在全球范围内,应用于水文模型 [63]。全球大气建模的另一个例子是从数据或高分辨率模型 [64][65](高分辨率模型运行起来成本太高,这就是需要粗略参数化的原因)。这些学习到的参数化可以更好地表示热带对流[66][67]。
(2)将机器学习模型用于 “物理” 子模型
参见 图 3➁ 。
如果子模型的公式是半经验性质的,其中函数形式几乎没有理论基础(例如,生物过程),如果有足够数量的观测可用,则可以用机器学习模型替换该子模型。这导致了一个混合模型,它结合了物理建模(理论基础、可解释的隔间)和机器学习(数据适应性)的优势。例如,可以将已建立的用于植物中水分运输的物理(微分)扩散方程与机器学习结合起来,以了解对水分运输电导的生物调节知之甚少。这导致了一个更 “物理” 的模型,它遵循公认的质量和能量守恒定律,但其调节(生物)是灵活的,并且可以从数据中学习。这些原理最近已被用于有效地模拟海洋中水的运动,并专门预测海面温度。在这里,运动场是通过深度神经网络学习的,然后通过对运动场隐含的运动进行物理建模来更新热量和温度。此外,许多大气科学家已经开始试验相关方法,以规避大气对流物理参数化中长期存在的偏差[65][69]。
虽然 “探索–>形成假设->检验” 的一般循环保持不变,但现代数据驱动的科学和机器学习可以 “在观测数据中提取任意复杂的模式”,以挑战复杂的理论和地球系统模型(附件 图 3 )。例如,由空间显式全球数据驱动的、基于机器学习的光合作用估计结果,表明气候模型高估了热带雨林的光合作用[86]。这种不匹配会导致科学家们提出新的假设,以便更好地描述植被冠层中的辐射转移,从而更好地估计其他地区的光合作用,并与叶片水平的观测更好地保持一致。相关数据驱动的碳循环估计,使植被模型的校准成为可能;并有助于解释高纬度地区二氧化碳浓度季节性幅度增加的难题 [87],这是由高纬度地区的植被更加旺盛引起的.
(3)模型-观测失配分析
参见 图 3➂ 。
假设没有观测偏差,物理模型与观测的偏差可以被视为导致模型错误的不完善知识。机器学习可以帮助识别、可视化和理解模型错误的模式,这使我们还可以相应地纠正模型输出。
例如,机器学习可以自动从数据中提取模式并识别那些未在物理模型中明确表示的模式。这种方法有助于改进物理模型和理论。
在实践中,它还可以用于纠正动态变量的模型偏差,或者与繁琐和临时手工设计的方法相比,它可以促进改进缩小到更精细的空间尺度[71][72]。
(4)约束子模型
参见 图 3➃ 。
除了数据驱动的理论和模型构建之外,这种提取的模式越来越多地被用作探索地球系统模型中改进参数化的一种方式[65][69],并且模型模拟器越来越多地被用作模型校准的基础[88]。这样,理论与观测之间、假设生成与理论驱动的假设检验之间的科学相互作用将继续下去。由于通过强大的机器学习技术从数据中推断出的假设、检验的复杂性、假设生成的速度正在以数量级的速度增加,我们可以期待复杂地球系统科学在质和量方面取得前所未有的进步。
(5)代理建模或仿真
参见 图 3➄ 。
图 3 中的一些概念已经被广泛采用。例如,链接 (3) 涉及模型基准测试和统计降尺度以及模型输出统计 [77][78]。在这里,我们认为采用深度学习方法将大大改善时空上下文信息在模型输出修改中的使用。仿真 (5) 已在工程和地球科学的多个分支中广泛采用,主要是为了高效建模,但尚未深入探讨易处理性问题。其他途径,例如混合建模(链接(2)),似乎很少探索。
从概念上讲,上面讨论的混合方法可以解释为加深神经网络以使其在物理上更加逼真( 图 4 ),其中物理模型位于神经网络层之上(参见 图 4 b、图 4 c 中的示例)。它与上面讨论的反向方法形成对比,后者产生物理模型输出,然后使用额外的机器学习方法层进行校正。我们认为,将物理建模和机器学习相结合的两种途径都值得追求。
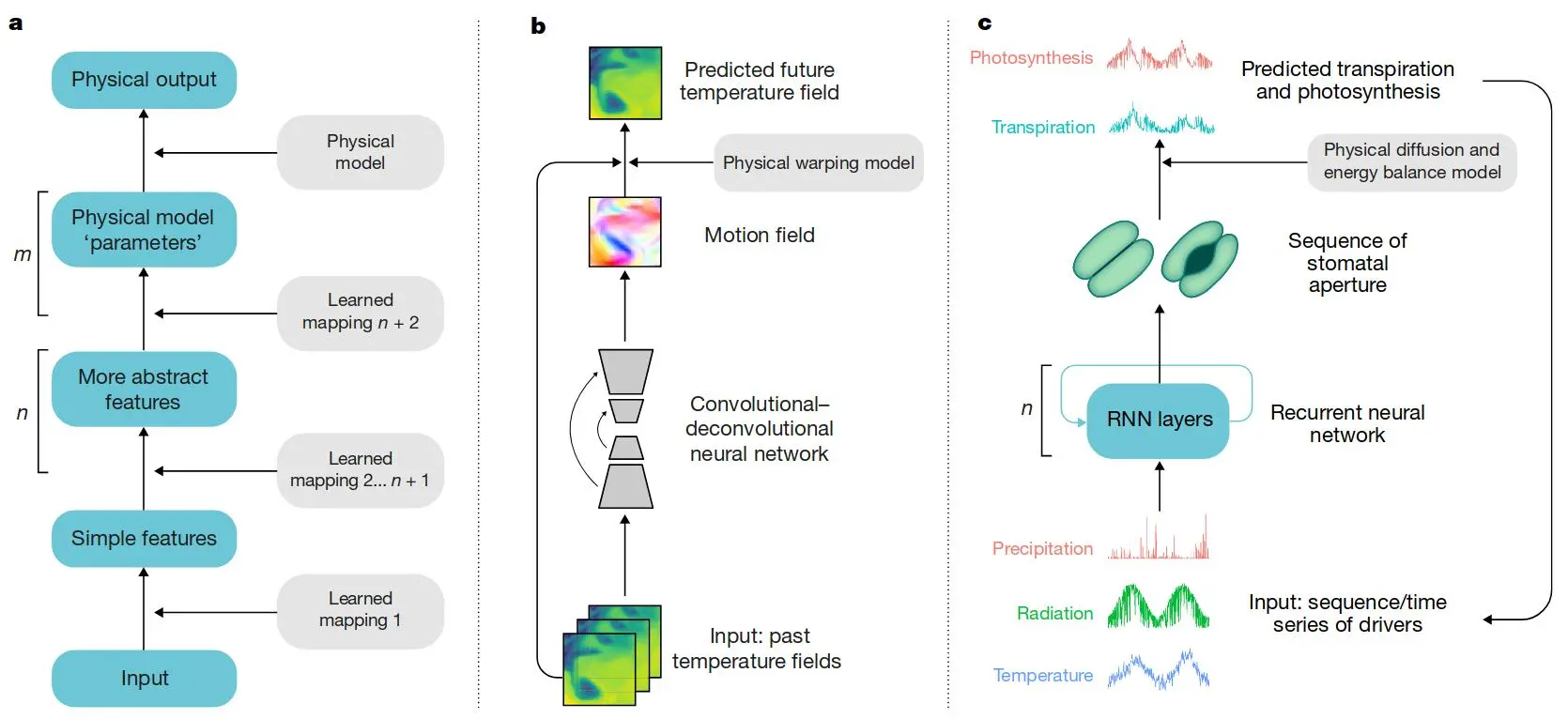
图 4:将混合建模解释为通过在多层神经网络之后添加一个或多个物理层来加深深度学习架构,使模型在物理上更加逼真。a)多层神经网络,n 为神经层数,m 为物理层数。 b 和 c 是混合建模的具体示例(
图 3中的圆圈 2)。 b)海面温度预测,通过卷积-反卷积神经网络学习水的运动场,并用物理模型进一步处理运动场以预测未来状态。 c)一个生物调节过程(气孔“阀门”的打开控制来自叶子的水蒸气通量)用递归神经网络建模。然后使用物理扩散模型来估计蒸腾作用,而蒸腾作用又会影响一些驱动因素,例如土壤水分。
5.2 将系统知识集成到机器学习框架
图 3 展示了一个系统建模视图,旨在将机器学习集成到系统模型中。作为另一种视角,系统知识可以被集成到机器学习框架中。这可能包括 网络架构的设计 [36][79]、 成本函数中的物理约束 [58]、扩展欠采样域的训练数据集(基于物理的数据增强)[80]。例如,虽然像普通最小二乘法之类的代价函数会惩罚模型-数据的不匹配,但可以对其进行修改,以避免对湖泊温度建模做出物理上不可信的预测[58]。物理和机器学习模型的整合不仅可以提高性能和泛化能力,而且可能更重要的是,结合了机器学习模型的一致性和可信度。作为副产品,混合具有有趣的正则化效果,因为物理学丢弃了不合理的模型。因此,物理感知机器学习模型应该更好地对抗过拟合,尤其是在中低样本大小的数据集中。这个概念也与获得可解释和可解释的机器学习模型(“可解释的 AI” [82])的方向有关,并将逻辑规则与深度神经网络相结合 [83]。
5.3 最新的方法学支持: 概率编程与微分编程
方法学的两个领域的最新进展有可能以一种合理的方式促进机器学习和物理模型的融合:概率编程 [52] 和 可微分编程。
-
概率编程:允许以正式但灵活的方式考虑各种不确定性方面。正确考虑数据和模型的不确定性以及通过先验和约束整合知识对于优化组合数据驱动和理论驱动的范式(包括逻辑规则)至关重要,就像在统计关系学习中所做的那样。此外,误差传播在概念上是无缝的,有助于模型输出的有根据的不确定性裕度。到目前为止,这种能力在很大程度上是缺失的,但对于科学目的至关重要,尤其是对于管理或政策决策。
-
微分编程:由于自动微分的实现[84][85],可微分编程允许有效优化。这有助于使大型、非线性和复杂反演问题在计算上更易于处理,此外还允许进行明确的敏感性评估,从而有助于可解释性。
6 推进科学发展
毫无疑问,正如本文所展示的那样,现代机器学习方法极大地提高了分类和预测能力,仅此一项就具有很大的价值。然而,除了统计预测之外,数据驱动的方法如何能够提高对基础科学的理解呢?尤其是考虑到复杂统计模型的结果通常难以解释。
一个基本的答案是: 观测几乎一直是科学进步的基础。例如,哥白尼的发现,是通过对行星轨迹的精确观测来推断和验证其运行规律的。
7 结论
地球科学需要处理大量且快速增长的数据,以预测、建模和理解复杂地球系统的形式提供更准确、更少不确定性和物理一致的推论。总体而言,机器学习,尤其是深度学习,提供了有前景的工具,可以为地球系统的组成部分构建新的数据驱动模型,从而建立我们对地球的理解。地球系统特有的挑战将进一步促进方法论的发展,我们提出以下四项主要建议。
(1) 对数据特殊性的认识
多源、多尺度、高维、复杂的时空关系,包括变量之间的非平凡和滞后的长距离关系(遥连接)需要充分建模。深度学习能够很好地解决这些数据挑战,需要开发网络架构和算法来产生解决不同尺度空间和时间上下文的方法(见 图 4 )。
(2) 推理的合理性和可解释性
模型不仅应该准确而且可信,并结合了控制地球系统的物理学。如果模型变得更加透明和可解释,将促进机器学习在地球科学中的广泛采用:它们的参数和特征排名应该有最小的物理解释,并且模型应该可以简化为一组规则、描述符和关系或可以解释.
(3) 不确定性估计
模型应该定义他们的信心和可信度。贝叶斯/概率推断应该集成到模型中,因为这种推断允许明确表示和传播不确定性。此外,识别和处理外推是一个优先事项。
(4) 针对复杂物理模型进行测试
机器学习的空间和时间预测能力至少应该与物理模型中观测到的模式一致。因此,我们建议根据来自地球系统物理模型的合成数据测试机器学习方法的性能。例如,应用于真实数据的 图 4 b、c 中的模型应在复杂物理模型模拟的广泛动力学范围内进行测试。这在训练数据有限的条件下和评估外推问题时特别重要。
总的来说,我们建议未来的模型应该整合基于过程和机器学习的方法。地球科学研究的数据驱动机器学习方法不会取代物理建模,而是有力地补充和丰富它。具体来说,我们设想了物理模型和数据驱动模型之间的各种协同作用,其最终目标是混合建模方法:它们应该遵循物理定律,具有概念化且因此可解释的结构,同时在理论存在的情况下完全适应数据虚弱的。重要的是,机器学习研究将受益于源自自然科学的合理的基于物理的关系。其中,最近几乎没有取得进展的两大地球系统挑战——大气对流的参数化和生态系统对气候和相互作用的地理因素的时空依赖性的描述——可以使用此处讨论的混合方法来解决.
参考文献
- [1] Howe, L. & Wain, A. Predicting the Future Vol. V, 1–195 (Cambridge Univ. Press, 1993).
- [2] Bauer, P., Thorpe, A. & Brunet, G. The quiet revolution of numerical weather prediction. Nature 525, 47–55 (2015).
- [3] Hantson, S. et al. The status and challenge of global fire modelling. Biogeosciences 13, 3359–3375 (2016).
- [4] Agapiou, A. Remote sensing heritage in a petabyte-scale: satellite data and heritage Earth Engine applications. Int. J. Digit. Earth 10, 85–102 (2017).
- [5] Stockhause, M. & Lautenschlager, M. CMIP6 data citation of evolving data. Data Sci. J. 16, 30 (2017).
- [6] Lee, J., Weger, R. C., Sengupta, S. K. & Welch, R. M. A neural network approach to cloud classification. IEEE Trans. Geosci. Remote Sens. 28, 846–855 (1990).
- [7] Benediktsson, J. A., Swain, P. H. & Ersoy, O. K. Neural network approaches versus statistical methods in classification of multisource remote sensing data. IEEE Trans. Geosci. Remote Sens. 28, 540–552 (1990).
- [8] Camps-Valls, G. & Bruzzone, L. Kernel Methods for Remote Sensing Data Analysis 434 (John Wiley & Sons, Chichester, 2009).
- [9] Gómez-Chova, L., Tuia, D., Moser, G. & Camps-Valls, G. Multimodal classification of remote sensing images: a review and future directions. Proc. IEEE 103, 1560–1584 (2015).
- [10] Camps-Valls, G., Tuia, D., Bruzzone, L. & Benediktsson, J. A. Advances in hyperspectral image classification: Earth monitoring with statistical learning methods. IEEE Signal Process. Mag. 31, 45–54 (2014). This paper provides a comprehensive overview of machine learning for classification.
- [11] Gislason, P. O., Benediktsson, J. A. & Sveinsson, J. R. Random forests for land cover classification. Pattern Recogn. Lett. 27, 294–300 (2006). This paper is one of the first machine learning papers for land-cover classification, a method now operationally used.
- [12] Muhlbauer, A., McCoy, I. L. & Wood, R. Climatology of stratocumulus cloud morphologies: microphysical properties and radiative effects. Atmos. Chem. Phys. 14, 6695–6716 (2014).
- [13] Grimm, R., Behrens, T., Märker, M. & Elsenbeer, H. Soil organic carbon concentrations and stocks on Barro Colorado Island—digital soil mapping using Random Forests analysis. Geoderma 146, 102–113 (2008).
- [14] Hengl, T. et al. SoilGrids250m: global gridded soil information based on machine learning. PLoS ONE 12, e0169748 (2017). This paper describes machine learning used for operational global soil mapping.
- [15] Townsend, P. A., Foster, J. R., Chastain, R. A. & Currie, W. S. Application of imaging spectroscopy to mapping canopy nitrogen in the forests of the central Appalachian Mountains using Hyperion and AVIRIS. IEEE Trans. Geosci. Remote Sens. 41, 1347–1354 (2003).
- [16] Coops, N. C., Smith, M.-L., Martin, M. E. & Ollinger, S. V. Prediction of eucalypt foliage nitrogen content from satellite-derived hyperspectral data. IEEE Trans. Geosci. Remote Sens. 41, 1338–1346 (2003).
- [17] Verrelst, J., Alonso, L., Camps-Valls, G., Delegido, J. & Moreno, J. Retrieval of vegetation biophysical parameters using Gaussian process techniques. IEEE Trans. Geosci. Remote Sens. 50, 1832–1843 (2012).
- [18] Papale, D. & Valentini, R. A new assessment of European forests carbon exchanges by eddy fluxes and artificial neural network spatialization. Glob. Change Biol. 9, 525–535 (2003).
- [19] Jung, M. et al. Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite and meteorological observations. J. Geophys. Res. Biogeo. 116, G00j07 (2011).
- [20] Tramontana, G. et al. Predicting carbon dioxide and energy fluxes across global FLUXNET sites with regression algorithms. Biogeosciences 13, 4291–4313 (2016).
- [21] Jung, M. et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 467, 951–954 (2010). This paper describes the first data-driven machine-learning-based spatio-temporal estimation of global water fluxes on land.
- [22] Jung, M. et al. Compensatory water effects link yearly global land CO2 sink changes to temperature. Nature 541, 516–520 (2017).
- [23] Bonan, G. B. et al. Improving canopy processes in the Community Land Model version 4 (CLM4) using global flux fields empirically inferred from FLUXNET data. J. Geophys. Res. Biogeosci. 116, G02014 (2011).
- [24] Anav, A. et al. Spatiotemporal patterns of terrestrial gross primary production: a review. Rev. Geophys. 53, 785–818 (2015).
- [25] Landschützer, P. et al. A neural network-based estimate of the seasonal to inter-annual variability of the Atlantic Ocean carbon sink. Biogeosciences 10, 7793–7815 (2013). This paper describes the first data-driven machine-learning-based carbon fluxes in the ocean.
- [26] Kühnlein, M., Appelhans, T., Thies, B. & Nauss, T. Improving the accuracy of rainfall rates from optical satellite sensors with machine learning—a random forests-based approach applied to MSG SEVIRI. Remote Sens. Environ. 141, 129–143 (2014).
- [27] Caldwell, P. M. et al. Statistical significance of climate sensitivity predictors obtained by data mining. Geophys. Res. Lett. 41, 1803–1808 (2014).
- [28] Reichstein, M. & Beer, C. Soil respiration across scales: the importance of a model-data integration framework for data interpretation. J. Plant Nutr. Soil Sci. 171, 344–354 (2008).
- [29] Wright, S. Correlation and causation. J. Agric. Res. 20, 557–585 (1921).
- [30] Guttman, N. B. Accepting the standardized precipitation index: a calculation algorithm. J. Am. Water Resour. Assoc. 35, 311–322 (1999).
- [31] Vicente-Serrano, S. M., Beguería, S. & López-Moreno, J. I. A multiscalar drought index sensitive to global warming: the standardized precipitation evapotranspiration index. J. Clim. 23, 1696–1718 (2010).
- [32] LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).
- [33] Lore, K. G., Stoecklein, D., Davies, M., Ganapathysubramanian, B. & Sarkar, S. Hierarchical feature extraction for efficient design of microfluidic flow patterns. Proc. Machine Learning Res. 44, 213–225 (2015).
- [34] Baldi, P., Sadowski, P. & Whiteson, D. Searching for exotic particles in high-energy physics with deep learning. Nat. Commun. 5, 4308 (2014).
- [35] Bhimji, W., Farrell, S. A., Kurth, T., Paganini, M. & Racah, E. Deep neural networks for physics analysis on low-level whole-detector data at the LHC. Preprint at https://arxiv.org/abs/1711.03573 (2017).
- [36] Schütt, K. T., Arbabzadah, F., Chmiela, S., Muller, K. R. & Tkatchenko, A. Quantum-chemical insights from deep tensor neural networks. Nat. Commun. 8, 13890 (2017).
- [37] Alipanahi, B., Delong, A., Weirauch, M. T. & Frey, B. J. Predicting the sequence specificities of DNA- and RNA-binding proteins by deep learning. Nat. Biotechnol. 33, 831–838 (2015).
- [38] Prabhat. A look at deep learning for science. O’Reilly Blog https://www.oreilly. com/ideas/a-look-at-deep-learning-for-science (2017).
- [39] Zhang, L. P., Zhang, L. F. & Du, B. Deep learning for remote sensing data: a technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 4, 22–40 (2016).
- [40] Ball, J. E., Anderson, D. T. & Chan, C. S. Comprehensive survey of deep learning in remote sensing: theories, tools, and challenges for the community. J. Appl. Remote Sens. 11, 042609 (2017).
- [41] Racah, E. et al. ExtremeWeather: a large-scale climate dataset for semisupervised detection, localization, and understanding of extreme weather events. Adv. Neural Inform. Process. Syst. 30, 3405–3416 (2017).
- [42] Liu, Y. et al. Application of deep convolutional neural networks for detecting extreme weather in climate datasets. In ABDA'16-International Conference on Advances in Big Data Analytics 81–88 https://arxiv.org/abs/1605.01156 (2016). This paper is the first approach to detecting extreme weather automatically without any prescribed thresholds, using deep learning.
- [43] Zhao, W. Z. & Du, S. H. Learning multiscale and deep representations for classifying remotely sensed imagery. ISPRS J. Photogramm. Remote Sens. 113, 155–165 (2016).
- [44] Mathieu, M., Couprie, C. & LeCun, Y. Deep multi-scale video prediction beyond mean square error. Preprint at https://arxiv.org/abs/1511.05440 (2015).
- [45] Oh, J., Guo, X., Lee, H., Lewis, R. L. & Singh, S. Action-conditional video prediction using deep networks in Atari games. Adv. Neural Inf. Process. Syst. 28, 2863–2871 (2015).
- [46] Shi, X. et al. Convolutional LSTM network: a machine learning approach for precipitation nowcasting. Adv. Neural Inf. Process. Syst. 28, 802–810 (2015).
- [47] Deng, J. et al. ImageNet: a large-scale hierarchical image database. In 2009 IEEE Conference on Computer Vision and Pattern Recognition 248–255 (IEEE, 2009).
- [48] Friedlingstein, P. et al. Uncertainties in CMIP5 climate projections due to carbon cycle feedbacks. J. Clim. 27, 511–526 (2014).
- [49] Montavon, G., Samek, W. & Müller, K.-R. Methods for interpreting and understanding deep neural networks. Digit. Signal Process. 73, 1–15 (2017).
- [50] Runge, J. et al. Identifying causal gateways and mediators in complex spatio-temporal systems. Nat. Commun. 6, 8502 (2015).
- [51] Chalupka, K., Bischoff, T., Perona, P. & Eberhardt, F. in UAI'16 Proceedings of the Thirty-Second Conference on Uncertainty in Artificial Intelligence 72–81 (AUAI Press, 2016).
- [52] Ghahramani, Z. Probabilistic machine learning and artificial intelligence. Nature 521, 452–459 (2015).
- [53] Goodfellow, I. J. et al. Generative Adversarial Nets. Adv. Neural. Inf. Process. Syst. 27, 2672–2680 (2014). This is a fundamental paper on a deep generative modelling approach, allowing possible futures to be modelled from data.
- [54] Hansen, M. C. et al. High-resolution global maps of 21st-century forest cover change. Science 342, 850–853 (2013).
- [55] Pekel, J.-F., Cottam, A., Gorelick, N. & Belward, A. S. High-resolution mapping of global surface water and its long-term changes. Nature 540, 418–422 (2016).
- [56] Karpatne, A. et al. Theory-guided data science: a new paradigm for scientific discovery from data. IEEE Trans. Knowl. Data Eng. 29, 2318–2331 (2017).
- [57] Camps-Valls, G. et al. Physics-aware Gaussian processes in remote sensing. Appl. Soft Comput. 68, 69–82 (2018).
- [58] Karpatne, A., Watkins, W., Read, J. & Kumar, V. Physics-guided Neural Networks (PGNN): an application in lake temperature modeling. Preprint at https:// arxiv.org/abs/1710.11431 (2017).
- [59] Luo, Y. Q. et al. A framework for benchmarking land models. Biogeosciences 9, 3857–3874 (2012).
- [60] Eyring, V. et al. Towards improved and more routine Earth system model evaluation in CMIP. Earth Syst. Dyn. 7, 813–830 (2016).
- [61] Klocke, D., Pincus, R. & Quaas, J. On constraining estimates of climate sensitivity with present-day observations through model weighting. J. Clim. 24, 6092–6099 (2011).
- [62] Cox, P. M. et al. Sensitivity of tropical carbon to climate change constrained by carbon dioxide variability. Nature 494, 341–344 (2013).
- [63] Beck, H. E. et al. Global-scale regionalization of hydrologic model parameters. Wat. Resour. Res. 52, 3599–3622 (2016).
- [64] Schirber, S., Klocke, D., Pincus, R., Quaas, J. & Anderson, J. L. Parameter estimation using data assimilation in an atmospheric general circulation model: from a perfect toward the real world. J. Adv. Model. Earth Syst. 5, 58–70 (2013).
- [65] Gentine, P., Pritchard, M., Rasp, S., Reinaudi, G. & Yacalis, G. Could machine learning break the convection parameterization deadlock? Geophys. Res. Lett. 45, 5742–5751 (2018).
- [66] Becker, T., Stevens, B. & Hohenegger, C. Imprint of the convective parameterization and sea-surface temperature on large-scale convective self-aggregation. J. Adv. Model. Earth Syst. 9, 1488–1505 (2017).
- [67] Siongco, A. C., Hohenegger, C. & Stevens, B. Sensitivity of the summertime tropical Atlantic precipitation distribution to convective parameterization and model resolution in ECHAM6. J. Geophys. Res. Atmos. 122, 2579–2594 (2017).
- [68] de Bezenac, E., Pajot, A. & Gallinari, P. Deep learning for physical processes: incorporating prior scientific knowledge. Preprint at https://arxiv.org/abs/ 1711.07970 (2017).
- [69] Brenowitz, N. D. & Bretherton, C. S. Prognostic validation of a neural network unified physics parameterization. Geophys. Res. Lett. 45, 6289–6298 (2018).
- [70] Willis, M. J. & von Stosch, M. Simultaneous parameter identification and discrimination of the nonparametric structure of hybrid semi-parametric models. Comput. Chem. Eng. 104, 366–376 (2017).
- [71] McGovern, A. et al. Using artificial intelligence to improve real-time decision making for high-impact weather. Bull. Am. Meteorol. Soc. 98, 2073–2090 (2017).
- [72] Vandal, T. et al. Generating high resolution climate change projections through single image super-resolution: an abridged version. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence (IJCAI-18) https://www.ijcai.org/proceedings/2018/0759.pdf (2018).
- [73] Verrelst, J. et al. Emulation of leaf, canopy and atmosphere radiative transfer models for fast global sensitivity analysis. Remote Sens. 8, 673 (2016).
- [74] Chevallier, F., Chéruy, F., Scott, N. & Chédin, A. A neural network approach for a fast and accurate computation of a longwave radiative budget. J. Appl. Meteorol. 37, 1385–1397 (1998).
- [75] Castruccio, S. et al. Statistical emulation of climate model projections based on precomputed GCM runs. J. Clim. 27, 1829–1844 (2014).
- [76] Fer, I. et al. Linking big models to big data: efficient ecosystem model calibration through Bayesian model emulation. Biogeosci. Disc. 2018, 1–30 (2018).
- [77] Glahn, H. R. & Lowry, D. A. The use of model output statistics (MOS) in objective weather forecasting. J. Appl. Meteorol. 11, 1203–1211 (1972).
- [78] Wilks, D. S. Multivariate ensemble model output statistics using empirical copulas. Q. J. R. Meteorol. Soc. 141, 945–952 (2015).
- [79] Tewari, A. et al. in Proc. IEEE Conf. on Computer Vision and Pattern Recognition 2549–2559 (IEEE, 2018).
- [80] Xie, Y., Franz, E., Chu, M. & Thuerey, N. tempoGAN: a temporally coherent, volumetric GAN for super-resolution fluid flow. Preprint at https://arxiv.org/ abs/1801.09710 (2018).
- [81] Stewart, R. & Ermon, S. in Proc. Thirty-First AAAI Conf. on Artificial Intelligence (AAAI-17) 2576–2582 (2017).
- [82] Gunning, D. Explainable Artificial Intelligence (XAI) https://www.cc.gatech. edu/~alanwags/DLAI2016/(Gunning)%20IJCAI-16%20DLAI%20WS.pdf (2017).
- [83] Hu, Z., Ma, X., Liu, Z., Hovy, E. & Xing, E. in Proc. 54th Annual Meeting of the Association for Computational Linguistics Vol. 1, 2410–2420 (Association for Computational Linguistics, 2016).
- [84] Pearlmutter, B. A. & Siskind, J. M. Reverse-mode AD in a functional framework: lambda the ultimate backpropagator. ACM Trans. Progr. Lang. Syst. 30, 7 (2008).
- [85] Wang, F. & Rompf, T. in ICLR 2018 Workshop https://openreview.net/pdf?id =SJxJtYkPG (2018).
- [86] Beer, C. et al. Terrestrial gross carbon dioxide uptake: global distribution and covariation with climate. Science 329, 834–838 (2010).
- [87] Forkel, M. et al. Enhanced seasonal CO2 exchange caused by amplified plant productivity in northern ecosystems. Science 351, 696–699 (2016).
- [88] Bellprat, O., Kotlarski, S., Lüthi, D. & Schär, C. Objective calibration of regional climate models. J. Geophys. Res. Atmos. 117, D23115 (2012).
- [89] Reichstein, M. et al. in AGU Fall Meeting Abstracts 2016AGUFM.B2044A.2007R (AGU, 2016).
- [90] Rußwurm, M. & Körner, M. Multi-temporal land cover classification with long short-term memory neural networks. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 42, 551–558 (2017). This paper describes the first use of the LSTM deep learning model for multi-temporal land-cover classification.
- [91] Nash, J. E. & Sutcliffe, J. V. River flow forecasting through conceptual models. Part I—a discussion of principles. J. Hydrol. 10, 282–290 (1970).
- [92] Shi, X. et al. Deep learning for precipitation nowcasting: a benchmark and a new model. Adv. Neural. Inf. Process. Syst. 30, 5617–5627 (2017). This paper describes the first approach to data-driven modelling of near-term precipitation using a combination of deep-learning concepts, that is, LSTMs and convolutional neural networks.
- [93] Isola, P., Zhu, J.-Y., Zhou, T. & Efros, A. A. Image-to-image translation with conditional adversarial networks. Preprint at https://arxiv.org/abs/ 1611.07004 (2016). This paper is a geoscience-related extension application of ref. 53, in which, for example, remote sensing images are transferred to thematic maps.
- [94] Tompson, J., Schlachter, K., Sprechmann, P. & Perlin, K. Accelerating Eulerian fluid simulation with convolutional networks. Proc. Machine Learning Res. 70, 3424–3433 (2017).
- [95] University Corporation for Atmospheric Research (UCAR). Short-Term Explicit Prediction (STEP) Program Research Applications Laboratory 2013 Annual Report https://nar.ucar.edu/2013/ral/short-term-explicit-prediction-stepprogram (NCAR/UCAR, 2013).
- [96] Ren, S., He, K., Girshick, R. & Sun, J. Faster R-CNN: towards real-time object detection with region proposal networks. Adv. Neural Inf. Process. Syst. 28, 91–99 (2015).
- [97] Zaytar, M. A. & El Amrani, C. Sequence to sequence weather forecasting with long short term memory recurrent neural networks. Int. J. Comput. Appl. 143, 7–11 (2016).
- [98] Goodfellow, I., Bengio, Y. & Courville, A. Deep Learning Vol. xxii, 1–775 (MIT Press, Cambridge, 2016).
- [99] Hochreiter, S. & Schmidhuber, J. Long short-term memory. Neural Comput 9, 1735–1780 (1997).
- [100] Schmidhuber, J. Deep learning in neural networks: an overview. Neural Netw. 61, 85–117 (2015).
- [101] Requena-Mesa, C., Reichstein, M., Mahecha, M., Kraft, B. & Denzler, J. Predicting landscapes as seen from space from environmental conditions. In IEEE International Geoscience and Remote Sensing Symposium (IGARSS) 1768–1771 (IEEE, 2018).
补充材料
Efficient modelling a dynamic non-linear system with recurrent neural networks
Aforementioned state-of-the-art examples of mapping sequences of driving variables (e.g. meteorological conditions) onto target variables such as CO2 fluxes from ocean or land have considered instantaneous mapping without representation of state dynamics. Dynamic effects have either been considered by directly using observed states as predictors (e.g. vegetation state represented by reflectance) or by introducing hand-designed features. The general problem is depicted in the figure below, where the input acts on an unknown, unobservable system state, while the observable is both influenced by the past state and the current input. It is not a problem of forecasting a time series a few steps ahead, because the whole output sequence has to be predicted by the model.
As an example, in the synthetic dynamic system below (one realization in Figure Box 1) we have three forcing variables x_1, x_2, x_3 where two of them influence one (unobserved) state r according to
with
being a parameter determining the inertia of the dynamics of , here set to . A target state to be predicted evolves as a logistic map well known from ecology and chaos theory[1].
where (contrary to the standard logistic map) the parameter is not fixed but dynamic and dependent on as
where simply scales onto the interval which implies dynamics varying with time between dampened oscillations, limit cycles and chaos. In the synthetic example realizations of and as Gaussian i.i.d. variables are generated, while is always a seasonal variable as in the Figure below. Obviously and are mimicking a stochastic forcing, whereas represents a deterministic forcing (e.g. solar radiation varying diurnally and seasonally).
The lower panel shows the performance of different approaches to model the sequence given the sequences of With a feed-forward ANN or random forests it is hard to model the sequence , even with including intuitive features which represent lagged or memory effects, such as lagged or cumulated variables over the last time steps. On the contrary, being turing-complete[2] a recurrent NN has the potential to describe any dynamic system, and the challenge is the parameter estimation or training. In the specific case a simple LSTM[3] with cells was trained on of the realizations and the results are shown here for the test set. Certainly, other modelling approaches such as dynamic Bayesian approaches (e.g. hidden Markov models) exist as well for state estimation, and the relation to recurrent neural networks and deep learning is under research[4].

Supplementary Figure 1: Concept of modelling a dynamic system, i.e. mapping an input sequence to an output sequence, where a (hidden) dynamic state is involved.


Supplementary Figure 2: Data-driven modelling of a synthetic geoscientific time-series depicted in (a) with dynamic effects. Shown are predictor variables , , , the resulting time-series of the system state (“observed” and modelled with an LSTM), and the parameter of the logistic map. (b) While classical approaches including typical feature design fail to explain the dynamics (grey bars, RF = Random Forest, ANN = feedforward ANN), a deep learning approach, long-short-term-memory neural network (LSTM) is able to explain almost all variance (red), without designing any features.

Supplementary Figure 3: Cycle of hypothesis generation and testing in complex systems involving process-based models and extraction of patterns from observations. Such patterns are only a surprise, and constitute an puzzle, if state-of-the-art theory and models do not predict them. Machine learning allows to extract hidden and complex patterns, which should be confronted with modelled patterns.
[References]
- 1.May, R. M. Simple mathematical models with very complicated dynamics. Nature 261, 459-467 (1976). ↩
- 2.Siegelmann, H. T. & Sontag, E. D. On the computational power of neural nets. Journal of computer and system sciences 50, 132-150 (1995). ↩
- 3.Hochreiter, S. & Schmidhuber, J. Long short-term memory. Neural computation 9, 1735-1780 (1997). ↩
- 4.Schmidhuber, J. Deep learning in neural networks: An overview. Neural networks 61, 85-117 (2015). ↩






