一种地理加权人工神经网络 -- GWANN

一种地理加权人工神经网络

【摘 要】 虽然最近的发展在许多方向上扩展了地理加权回归( GWR )，但通常假设因变量和自变量之间的关系是线性的。然而，在实践中，变量往往是非线性关联的。为解决该问题，荷兰乌特勒支大学 Hagenauer 等提出了一种地理加权人工神经网络( $GWANN$ )。 $GWANN$ 将地理加权与人工神经网络相结合，能够在无假设情况下以数据驱动方式学习复杂的非线性关系。通过已知空间特征的合成数据和真实世界案例研究，作者将 $GWANN$ 和 GWR 进行了比较。合成数据的结果表明，当数据之间关系是非线性且空间方差较大时， $GWANN$ 算法的性能要好于 GWR 算法，而基于真实数据的结果表明， $GWANN$ 算法在实际应用中也可以取得更好的性能。

【原 文】 Hagenauer, J. and M. Helbich ( 2021 ). “A geographically weighted artificial neural network.” International Journal of Geographical Information Science: 1-21. https://doi.org/10.1080/13658816.2021.1871618

【阅后感】 地理加权回归在计量经济学、地理空间统计学等方向具有重要作用，是 Goodchild 所提出的地理学第二定律（即空间异质性）的一种量化表征方式，同时也是一种空间线性的回归模型。前一段时间，在阅读地理空间统计学资料时，就曾经思考过是否可以采用神经网络来代替地理加权回归，但没有深入研究，未曾想竟然有人在 IJGIS 上发表了一篇类似的文章，于是整理出来供参考。

1 引言

变量关系之间的空间异质性( 即空间非平稳性 )是空间数据分析中的一个重要问题( Anselin，1989 )。它指的是这样一个概念：对于一个空间过程，变量之间的关系在某种程度上取决于观察到这些关系的位置( Fotheringham 等，2002 年 )。如果在校准模型时没有适当考虑空间异质性，对系数的估计很可能是有偏差的，这可能导致不适当的结论( Páez 等，2008 年；LeSage 和 Pace，2009 )。

已经提出了几种方法来模拟空间变化的关系。典型例子包括扩展方法( Casetti， 1972 )、加权空间自适应滤波( Gorr 和 Ollicschlaeger， 1994 )、特征向量空间滤波( Griffith，2003 )和地理加权回归( GWR)( Brunsdon 等，1999 年 )。其中 GWR 受到了最多关注，并被应用于许多学科，例如房地产经济学( Bitt et al.，2007 年；Helbich 和 Griffith， 2016 )，生态学( Nelson 等，2007 年 )，犯罪学( Waller 等，2007 年；Troy 等，2012 年 )、健康( Choi 和 Kim，2017 年 )、土地利用科学( Yu 等人，2011 年；Hagenauer 和 Helbich，2018 年 )。

GWR 是普通最小二乘法的扩展，它估计每个位置的加权最小二乘回归，其中离回归位置较近的观测值被赋予比距离较远的观测值更高的权重，加权由距离衰减核函数和带宽参数确定。在基础 GWR 基础上，又发展出一些变种。如：

在基本 GWR 中，假设所有关系在空间上不同，而在混合 GWR 中 ( Brunsdon 等，1999 )仅对系数的子集进行地理加权；每个空间变化的系数的核函数和带宽是相同的。后一种限制是由 Fotheringham 等人提出的( 2017 )，他提出了一个多尺度 GWR ，使用系数的单独带宽来对不同尺度的空间异质性进行建模。此外，虽然基本 GWR 是基于观测之间欧几里得距离的，但已经提出了不同距离度量的应用。例如，Lu 等( 2011 )表明非欧几里德距离度量可以改善 GWR 的拟合，而 Fotheringham 等( 2015 )建议使用时空距离度量。Lu 等( 2017 )将多尺度 GWR 与每个系数的单个距离度量相结合。

GWR 还因人为在系数对之间引入多重共线性而受到批评( Wheeler 和 Tiefelsdorf，2005 年 )，该点最近被驳斥( Fotheringham 和 Osan，2016 )。为了反驳这种批评，提出了惩罚形式的 GWR ， 例如：地理加权套索( Wheeler， 2009 )、岭( Wheeler， 2009 )、岭( Wheeler，2007；Bárcena 等，2014 人）和弹性净回归( Li 和 Lam，2018 )。

另一个扩展是地理神经网络加权回归( Du 等，2020 )，它利用人工神经网络( $ANN$ )在估计 GWR 模型的系数时找到合适的地理权重。

尽管做出了这些努力，但 GWR 的一些局限性尚未得到解决。例如：由于 GWR 类似于被重复使用的局部模型的集合，其推理特性被认为不如单个非平稳模型( Comber 等，2020 )。同样，与最小二乘法类似，在使用最简单形式的 GWR 时，通常假设因变量和自变量之间的关系是线性的。而该假设通常不适用于复杂空间预测任务( Anselin，1989；Leuenberger 和 Kanevski， 2015 )。

为解决该问题，我们提出了一种地理加权人工神经网络( $GWANN$ )，它将地理加权与人工神经网络相结合。与 GWR 相似， $GWANN$ 在建立模型时使用距离衰减核函数和带宽参数对观测数据进行地理加权。然而，与 GWR 不同的是， $GWANN$ 还能够以数据驱动的方式对非线性函数进行建模，而不需要做任何假设。

本文的其余部分结构如下。第二节介绍了 GWR 和 $ANN$，并介绍了 $GWANN$ 。接下来，第三节介绍了对 $GWANN$ 和 GWR 进行比较的实验。最后，第四部分对全文进行了总结，并对下一步的工作提出了建议。

2 方法

2.1 人工神经网络

人工神经网络( $ANN$ )由一组神经元和它们之间的单向连接组成，能够模仿大脑检测模式和学习数据中关系的能力( Haykin， 2008 )。与每个神经元 i 相关联的是激活函数 $\phi_i$ ，并且两个神经元 $i$ 、$ j$ 之间的每个连接具有分配的权重 $W_{ij}$ ，该权重 $W_{ij}$ 控制神经元 $i$ 对神经元 $j$ 的影响。虽然神经元表示 $ANN$ 的基本计算单元，但它们之间的加权连接允许对复杂关系进行建模。

神经元通常是按层组织的，一层中的每个神经元都与后续层中的神经元有直接连接( 图 1 )。第一层被称为“输入层”，最后一层被称为“输出层”，而这两层之间的所有层都是“隐藏层”。输入数据从输入层传递到第一个隐藏层，在那里进行聚合和转换，如下所示：

$$net_{j}=\sum\limits_{i \in P_{j}} w_{i j} o_{i}$$

其中 $w_{ij}$ 是神经元 $i$ 和 $j$ 之间的连接的权重，$o_i$ 是神经元 $i$ 的输出， $P_j$ 是与神经元 $j$ 有传出连接的神经元集合。神经元 $i$ 的输出计算如下：

$$o_{i}=\phi\left(n e t_{i}\right)$$

其中 $ϕ$ 是神经元 $i$ 的激活函数。一个常见的激活函数是双曲正切函数，定义为 $ f( x )=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} $ 。这个函数特别有用，因为它是连续的和可微的；这两者都是计算网络误差梯度的必要条件( Rojas,2013 )。

然后，每个神经元的输出被传递到下一层的神经元。对于后续的每一层，重复此过程，直到到达网络的输出层。输出层的输出代表网络的总输出。

为了对非线性关系进行建模，必须调整神经网络的连接权。这通常是使用两个步骤的过程来完成的。在第一步中，使用反向传播计算给定观测的每个神经元的误差信号( Rumelhart 等，1986 )。误差信号取决于误差函数。在回归的情况下，误差函数定义为 $E=\frac{1}{2} \sum*{i=1}^{n}\left( t*{i}-o\_{i}\right )^{2}$ 。其中 $t_i$ 是目标值，$o_i$ 是输出神经元 $i$ 的输出， $n$ 是目标值的数目。给定误差函数，误差信号计算如下：

$$\delta_{j}=\left\{\begin{array}{lc}\phi^{\prime}\left(\text { net }_{j}\right)\left(o_{j}-t_{j}\right) & \text { if } j \text { is an output neuron } \\ \phi^{\prime}\left(\text { net }_{j}\right) \sum_{k} \delta_{k} w_{j k} & \text { otherwise }\end{array}\right.$$

其中 $o_j$ 是神经元 $j$ 的输出，$t_j$ 是神经元 $j$ 的目标值，$w_{jk}$ 是神经元 $j$ 和 $k$ 之间的连接权重，$δ_k$ 是神经元 $k$ 的误差信号， $ϕ_j$ 是神经元 $j$ 的网络输入，而 $\phi '$是激活函数的导数。

在第二步中，使用梯度下降来调整连接权重：

$$\Delta w_{i j}=-\eta \frac{\partial E}{\partial w_{i j}}=-n \delta_{j} o_{i}$$

其中 $w_{ij}$ 是神经元 $i$ 和 $j$ 之间的连接权重，$E$ 是神经元 $i$ 输出的误差函数，$δ_j$ 是神经元 $j$ 的误差信号。重复这两个步骤，直到达到终止条件( 例如，误码率低于预定阈值 )。

有几种梯度下降的扩展和变体来改进网络的训练。为了使训练对噪声更加健壮，实际上将误差梯度求和到被称为“小批量”的观测子集上。然后使用累积的更改更新连接权重。此外，当调整连接权重时，使用 Nesterov 的加速梯度( Nesterov, 1983 )可以显著提高训练性能( Sutskever 等人，2013 年 )。

2.2 地理加权回归

地理加权回归( GWR )( Brunsdon 等，1996 年 )假设每个地点都有一个单独的局部模型。假设有 $n$ 个位置，并且每个位置都分配了一个观测值，则位置 $i \in 1,2,...,n$ 的 GWR 模型为：

$$y_{i}=\sum_{j=0}^{m} \beta_{i j} x_{i j}+\epsilon_{i}$$

其中，$y_i$ 是因变量，$x_{ij}$ 是第 $j$ 个自变量 ，${\beta}_{ij}$ 是第 $j$ 个自变量的系数，$\epsilon_i$ 是误差项，假设误差项是独立同分布的。

在估计局部系数时， GWR 根据观测之间的空间距离对观测进行加权；较近的观测比较远的观测被赋予更大的权重。通常使用地理加权最小二乘进行估计，加权最小二乘的矩阵表达式为：

$$\hat{\beta}_{i}=\left(X^{\top} W_{i} X\right)^{-1} X^{\top} W_{i} y$$

其中 $X$ 是样本支撑的自变量矩阵，$y$ 是因变量，$W_i$ 是位置 $i$ 的空间权重矩阵 $W$ 。为了计算 $W$ ，引入基于观测和回归位置之间距离的核函数。广泛使用的核有高斯核、双二次核、三次核和箱形核( Brunsdon 等，1999 年 )等。

例如，高斯核被定义为 $v_{i j}=\exp({-0.5\left( \frac{d_{i j}}{b}\right)^{2})}$ ，其中 $d_{ij}$ 是位置 $i$ 和 $j$ 之间的距离，$b$ 是核带宽。带宽决定了局部系数估计的变化程度，并且带宽的选择对 GWR 性能的影响比核函数的选择更重要( Fotheringham 等，2002 年 )。带宽可以是固定的，也可以是自适应的，其中后者指的是到每个观测值的 $k$ 个最近邻居的距离( Brunsdon 等，2007 年；Guo 等，2008 年 )。

2.3 地理加权人工神经网络

地理加权人工神经网络( $GWANN$ )是包含在权重中嵌入了地理加权的神经网络变体。神经网络由输入层、隐藏层和输出层组成。其中从隐层到输出层的连接可被视为隐藏层输出（非线性模型的输出）到输出层的线性模型的权重系数。因此，当利用地理加权误差函数来估计隐藏层和输出层之间的连接权重时，这些权重可以被解释为 GWR 模型。

$GWANN$ 的结构与基本神经网络结构相同，只是 $GWANN$ 的每个输出神经元都被分配到地理空间中的一个位置( 图 2 )。这允许计算观测数据和输出神经元位置之间的空间距离。

除了网络结构之外， $GWANN$ 和基本神经网络之间的主要区别是 $GWANN$ 使用地理加权误差函数而不是基本的二次误差函数来计算误差信号。在回归情况下，地理加权误差函数定义为 $E=\frac{1}{2} \sum*{i=1}^{n} v*{i}\left( t*{i}-o*{i}\right )^{2}$ ，其中 $t_i$ 是目标值，$o_i$ 是输出神经元 $i$ 的输出， $v_i$ 是观测值和输出神经元 $i$ 的位置之间的地理加权距离，$n$ 是目标值/输出神经元的数量。根据这个定义，输出神经元的输出与目标值之间的差值由输出神经元位置与观测之间的空间距离来加权；当输出神经元的位置与观测距离较近时，输出神经元的输出与目标值之间的差值比它们之间相距较远时的差值被赋予更大的权重。请注意，目标值的数量必须与输出神经元的数量相同。具体地说，在想要计算单个目标值但具有典型不同位置的多个输出神经元的地理误差函数值的实际示例中，需要为每个输出神经元复制目标值。

根据地理加权误差函数的定义，反向传播误差信号的计算修改如下：

$$\delta_{j}= \left( \begin{array}{lc} \phi^{\prime}\left(n e t_{j}\right) v_{j}\left(o_{j}-t_{j}\right) & \text { if } j \text { is an output neuron } \\ \phi^{\prime}\left(\text { net }_{j}\right) \sum_{k} \delta_{k} w_{j k} & \text { otherwise } \end{array} \right.$$

其中 $o_j$ 是神经元 $j$ 的输出，$t_j$ 是神经元 $j$ 的目标值，$w_{jk}$ 是神经元 $j$ 和 $k$ 之间的连接权重，$\sigma_k$ 是神经元 $k$ 的误差信号，$net_j$ 是神经元 $j$ 的网络输入，$\phi^\prime$ 是激活函数的导数， $v_j$ 是观测值和输出神经元 $j$ 的位置之间的地理加权距离。地理加权只用于计算输出神经元的误差信号，而所有其他神经元向后传播下一层神经元的误差信号。与 $ANN$ 一样， $GWANN$ 的连接权重也是使用梯度下降来调整的( 公式( 4 ) )。

3 实验

为了比较 GWR 和 $GWANN$ ，我们使用了四个合成数据集和一个来自房地产经济学的真实数据集。合成数据集使我们能够完全控制数据的特征，特别是关系的性质和空间异质性，这有助于更好地理解模型的不同属性。真实世界的数据使我们能够在实际使用案例中评估模型。

对于所有实验，我们将输入变量调整为零均值和单位方差，以使它们具有可比性。在调整连接权时，我们使用动量系数为 $0.900$ 的 Nesterov 加速梯度。我们将 $GWANN$ 的学习率 $\eta$ 设置为 $0.010$，将小批量大小设置为 $50$。虽然原则上 $ANN$ 的隐含层数是任意的，但我们选择了具有单一隐含层的网络。给定足够多的隐层神经元，具有单一隐层的人工神经网络能够很好地逼近 $n$ 维欧氏闭空间有界子集上的任意连续函数( Cybenko 1989 )。对于每个实验，我们测试了不同数量的隐藏神经元。偏置神经元总是被添加到输入和隐层，但我们在报告神经元数量时没有包括它们。采用双曲正切函数作为隐含神经元的激活函数。

我们使用具有 GWR 和 $GWANN$ 的高斯核进行地理加权。当使用自适应带宽时，执行网格搜索以确定合适的带宽。当使用固定带宽时，使用以下局部搜索方法来确定合适带宽：首先选择两个观测间最大距离的一半作为当前带宽；然后，在当前带宽附近执行网格搜索，以获得更好的平均性能带宽；当找到一个带宽时，在新发现的带宽的较小邻域内重复该过程，直到收敛。

带宽搜索内的性能使用 $10$ 倍交叉验证( CV )进行估计。此过程将数据随机划分为 $10$ 个互不相交的子集。然后，一次一个子集用于测试模型，而其他子集用于构建模型。然后，报告了所有 fold 的平均性能。我们使用均方根误差( RMSE )作为性能衡量标准。

$GWANN$ 的训练迭代次数也是使用 $10$ 倍 CV 来确定的。在每个文件夹中，对模型进行训练，直到当前文件夹的测试数据的性能在 1,000 次迭代中没有改善。额外迭代的目的是给网络一个摆脱局部极小值的机会。这种方法通常被称为“耐心地提前停止”，大大降低了训练数据过度拟合的风险( Bengio 2012 )。然后，给出了在所有 fold 上获得最佳平均性能的迭代以及获得的性能值。

3.1 实验 1：合成数据

本实验的目的是考察 GWR 和 $GWANN$ 在模拟具有不同空间特征的过程时的差异。特别是，我们感兴趣的是模型的性能如何依赖于关系的线性和空间变化。我们还研究了 $GWANN$ 将隐藏神经元和输出神经元之间的连接权重作为曲面的可视化。

3.1.1 数据生成过程

我们创建了四个人工数据集。数据集的空间布局由大小为 25x25 的网格给出。以下函数用于创建数据集：

$$\begin{align} y_{i}=\beta_{0}+\beta_{1}\left(u_{i}, v_{i}\right) x_{i 1}+\beta_{2}^{1}\left(u_{i}, v_{i}\right) x_{i 2}+\epsilon_{i}\\ y_{i}=\beta_{0}+\beta_{1}\left(u_{i}, v_{i}\right) x_{i 1}+\beta_{2}^{2}\left(u_{i}, v_{i}\right) x_{i 2}+\epsilon_{i}\\ y_{i}=\beta_{0}+4 \tanh \left(\frac{\beta_{1}\left(u_{i}, v_{i}\right) x_{i 1}}{3}\right)+4 \tanh \left(\frac{\beta_{2}^{1}\left(u_{i}, v_{i}\right) x_{i 2}}{3}\right)+\epsilon_{i}\\ y_{i}=\beta_{0}+4 \tanh \left(\frac{\beta_{1}\left(u_{i}, v_{i}\right) x_{i 1}}{3}\right)+4 \tanh \left(\frac{\beta_{2}^{2}\left(u_{i}, v_{i}\right) x_{i 2}}{3}\right)+\epsilon_{i} \end{align}$$

对于所有函数， $\left( u*i,v_i\right )$ 表示网格单元 $i$ 的位置， $\epsilon_i$ 是服从 $N( 0,0.25 )$ 的误差项， $x_i$ 是服从 $N( 0,1 )$ 的随机变量 （自变量）， $\beta*{0}$ ， $\beta*{1}\left( u*{i}, v*{i}\right )$ ， $\beta*{2}^{1}\left( u*{i}, v*{i}\right )$ 和 $\beta*{2}^{2}\left( u*{i}, v\_{i}\right )$ 分别表示网格单元 $i$ 的权重系数。前两个函数( 方程式( 8 )和( 9 ) )模拟因变量和自变量之间的线性关系，而第三和第四个函数( 方程式( 10 )和( 11 ) ) 使用双曲正切函数来表示非线性关系。

这些系数被设计成代表空间异质性的不同特征。它们的计算方法如下：

$$\beta_{0}=1$$

$$\beta_{1}\left(u_{i}, v_{i}\right)=1+\frac{u_{i}+v_{i}}{12}$$

$$\beta_{2}^{1}\left(u_{i}, v_{i}\right)=1+2\left(\cos \left(\frac{\pi u_{i}}{24}\right) \cos \left(\frac{\pi v_{i}}{24}\right)\right)$$

$$\beta_{2}^{2}\left(u_{i}, v_{i}\right)=1+2\left(\cos \left(\frac{\pi u_{i}}{12}\right) \cos \left(\frac{\pi v_{i}}{12}\right)\right)$$

对于所有的系数，$(u_i，v_i)$ 表示网格单元 i 的位置。${\beta}_0$ 表示没有空间异质性的常量曲面。${\beta}_1$ 是一个线性趋势面。${\beta}^1_ 2$ 和 ${\beta}^2_2$ 随地理位置的变化呈非线性变化， ${\beta}_2^2$ 的空间变异大于 ${\beta}^1_2$ 。从尺度上看，${\beta}^1_2$ 代表小尺度空间异质性， ${\beta}^2_2$ 代表大尺度空间异质性。图 3 显示了系数的曲面。

在系数的定义之后，第一和第三函数( 方程式( 8 )和( 10 ) )表示具有低空间方差的过程，而第二和第四函数( 方程式( 9 )和( 11 ) )表示具有较高的系数空间方差的过程。

3.1.2 实验设置

对于所有数据集，我们使用变量 $y$ 作为因变量，变量 $x1$ 和 $x2$ 作为自变量。我们对 GWR 和 $GWANN$ 使用固定带宽。当观测均匀排列在格网中时，这允许对带宽进行更精细的控制，因此只存在几个距离类。

为了研究 GWR 和 $GWANN$ 的性能，我们使用 10 倍 CV 和 90% 的数据来确定 GWR 和 $GWANN$ 的合适带宽以及 $GWANN$ 的合适迭代次数。然后，我们使用相同的数据建立了 GWR 和 $GWANN$ 模型，确定了超参数，并使用剩余数据来获得对其性能的独立估计。我们重复了该过程，对四个数据集中的每一个都进行了 100 次随机复制，并报告了平均结果。

可以将 GWR 的估计系数可视化为曲面，以探索这些关系的空间变化。与 GWR 类似，也可以将 $GWANN$ 在隐藏神经元和输出神经元之间的连接权重可视化为曲面。然后，每个曲面指的是一个隐藏神经元的输出，它是输入变量的非线性变换的线性组合。

为了研究和比较 GWR 的系数曲面和 $GWANN$ 的连接权重曲面的可视化，我们使用使用公式( 11 )创建的数据集的示例性复制来构建 GWR 和 $GWANN$ 模型。由于关系的非线性和系数的高度空间方差，该数据集是最复杂的。 $GWANN$ 的隐藏神经元的数量被设置为 5 个，因为这可以在提供良好的模型拟合的同时实现全面的可视化。因为我们想要可视化每个观察的系数权重，所以输出神经元的数量等于观察的总数，并且每个输出神经元都被分配了观察的位置。由于 $GWANN$ 在数据生成过程和训练过程中的随机性，对于大多数重复，确定了不同的带宽和不同的训练迭代次数。我们选择了与已获得所有复制的均方根中值的复制相对应的带宽和迭代次数。

3.1.3 结果与讨论

图 4 显示了直到收敛的平均训练迭代次数 $GWANN$ 。在非线性关系和系数空间方差较小的情况下， $GWANN$ 算法的平均训练迭代次数不随隐含神经元个数的增加而变化；否则， $GWANN$ 的平均训练迭代次数随隐含神经元个数的增加而减少。

图 5 显示了获得的平均带宽。 $GWANN$ 的平均带宽总是随着隐含神经元数目的增加而减小，但当这种关系是非线性时，减小的幅度很小。在线性关系下， $GWANN$ 的平均带宽大于 GWR 的平均带宽，而在非线性关系下， $GWANN$ 的平均带宽小于 GWR 的平均带宽。此外，当系数的空间方差较小时， $GWANN$ 和 GWR 的平均带宽通常较高

图 6 显示了独立坚持测试数据集的模型的平均均方根误差( 有关解释方差的比例，请参见补充资料中的图 S1 )。当两者呈线性关系时， GWR 的平均 RMSE 低于 $GWANN$ 的平均 RMSE 。然而，当这些关系是非线性时， GWR 的平均 RMSE 显著高于 $GWANN$ 的平均 RMSE。这并不出人意料，因为与 $GWANN$ 不同， GWR 本身并不具备建模非线性关系的能力。当这些关系是非线性的，且系数的空间方差较大时， $GWANN$ 的平均均方根显著低于 GWR 的平均均方根。在线性关系下， $GWANN$ 的平均均方根误差一般随隐含神经元数目的增加而减小，但当系数的空间方差较大时，其减小幅度更大。当这些关系是非线性的，并且系数的空间方差较低时， $GWANN$ 的平均均方根误差仅在该数目较低时才随隐含神经元数目的增加而减小；否则，均方根误差保持不变。当隐层神经元个数与均方根误差呈非线性关系且系数的空间方差较大时，两者之间不存在相关性。

通常，所有测试模型的性能取决于底层流程的性质。当数据中的关系是非线性的，并且系数的空间方差较高( 即大尺度空间异质性 )时， $GWANN$ 的性能明显好于 GWR 。然而，在实践中，数据生成过程的特征通常是事先不知道的，因此有必要对竞争模型的性能进行经验评估。

使用使用公式( 11 )创建的数据集的示例性复制，我们训练 $GWANN$ 进行 $5,610$ 次迭代，带宽为 $1,801$，并拟合带宽为 $2,000$ 的 GWR 模型。图 7 显示了 GWR 的系数曲面。系数曲面大致类似于原始数据集的系数( 参见图 3 )。我们计算了 GWR 曲面与数据集系数之间的 Pearson 相关系数，以量化它们之间的相似性。${\beta}_1$ 的线性趋势是从左下角到右上角， $\hat{\beta}^{1}( r=0.871, p \leq 0.05 )$ 以及 ${\beta}_2^ 2$ 的丘陵和谷地图案曲面 $\hat{\beta}\_{2}^{2}( r=0.708, p \leq 0.05 )$ 都可以观察到。然而，估计系数的所有曲面都显示出不规则性和噪声。

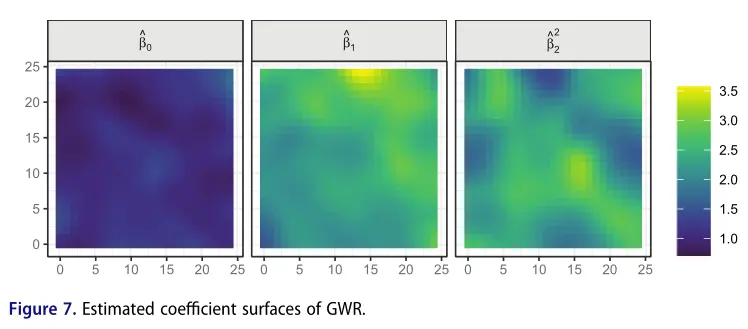
图 8 将隐藏神经元( 包括偏置神经元 )和 $GWANN$ 的输出神经元之间的连接权重显示为曲面。 $GWANN$ 的某些曲面显示与原始数据集的系数相对应的图案。神经元 2( 皮尔逊相关系数 $r=-0：906，p \leq 0.05$ )和神经元 5( $r=-0：779，p \leq 0.05$ )曲面 ${\beta}-1$ 的线性趋势从左下到右上可见，而神经元 4 的曲面则有明显的丘状和谷状分布( $r=-0：960，p \leq 0.05$ )。然而，神经元 1 和 3 以及偏置神经元的曲面与任何系数曲面都不相似。此外，没有一个神经元的曲面显示出 ${\beta}_0$ 的图案，所有的 $GWANN$ 曲面都显示出明显的不规则和噪声的痕迹。除了 GWR 0 之外，我们可以为每个系数识别至少一个与 ${\beta}$ 的估计系数的任何曲面更相关的 $GWANN$ 的连接权重曲面

此外，输入和隐藏的神经元越多，在网络中执行的计算就越不容易跟踪，这进一步限制了 $GWANN$ 曲面在实际环境中用于探索性空间数据分析的有用性

3.2 实验二：奥地利的房价

在这个实验中，我们使用真实世界的数据评估了 GWR 和 $GWANN$ 在预测性能上的差异。我们还考察了不同的距离矩阵对 GWR 和 $GWANN$ 预测的影响，并评估了残差的空间分布。

我们选择住房作为案例研究，因为在房地产经济学中，基于回归的房价评估至关重要( Sopranzetti， 2010 )。享乐主义理论假设，一种财产代表一种可分解为其效用承载特征的异质商品，由此产生的利益反映在财产价格中( Rosen，1974 )。房产的物理特征( 例如建筑面积 )和邻里特征( 即住宅的环境 )都会影响整体价格。在住房研究中，交易价格在空间上是不同的，因此，考虑空间异质性的享乐房价模型被越来越多地应用( 例如，Bitt 等，2007；Sunding 和 Swoboda，2010；Lu 等，2011；Helbich 和 Griffith 2016 )。

3.2.1 数据

奥地利联合信贷银行( UniCredit Bank )奥地利股份公司( Helbich et al.，2014 年 )提供了有关奥地利 3887 套经地理编码的独栋房屋的数据。以欧元记录的购房个人交易价格是从 1998 年到 2009 年收集的，还有 11 套房屋的结构属性和两个时间变量。补充材料中的表 S1 列出了描述性统计数据。

3.2.2 实验设置

我们使用对数变换的交易价格作为因变量，结构属性和时间变量作为自变量。由于住房位置分布不均，我们对 $GWANN$ 和 GWR 使用了自适应带宽( 图 12 )。我们对地理权重采用了两种不同的距离度量，即欧几里德距离( ED )和乘车旅行时间距离( TTD )。使用 Open Source Routing Machine( Huber And Rust 2016 )和 OpenStreetMap 数据计算 TTD。

为了考察 GWR 和 $GWANN$ 的性能，我们使用 10 倍 CV 来获得模型性能的稳健估计( 外部 10 倍 CV )。请注意，在每个折叠中，10 倍 CV 还用于确定 GWR 和 $GWANN$ 的合适带宽以及 $GWANN$ 的迭代次数( 内部 10 倍 CV )。

为了详细研究预测和残差，我们使用完整的数据集建立了模型。根据平均均方根误差最低的隐含神经元个数选择网络的隐含神经元个数。因为我们想要预测整个数据集的房价，所以 $GWANN$ 的输出神经元的数量等于观察的总数，并且每个输出神经元都被分配了观察的位置。由于( 外部 )10 倍 CV 过程和 $GWANN$ 的训练中的随机性，对于大多数折叠，确定了不同的带宽和不同的训练迭代次数。我们选择了与已获得所有折叠的中值均方根误差的折叠相对应的带宽和迭代次数。

如果模型不能考虑数据的空间属性，则其残差往往是空间自相关的。我们使用 Moran‘s I 检验模型的残差空间自相关性。我们使用逆 ED 计算检验统计量，并通过 999 次 Monte-Carlo 模拟运行来评估显著性。

3.2.3 结果与讨论

图 9 显示了 $GWANN$ 在收敛之前的平均训练迭代次数。当使用 TTD 而不是 ED 时， $GWANN$ 通常需要较少的迭代才能收敛。 $GWANN$ 在使用 EDS 和 TTDS 时的平均训练迭代次数随着隐含神经元数目的增加而减少，但隐含神经元数目越多，减少的幅度越小。

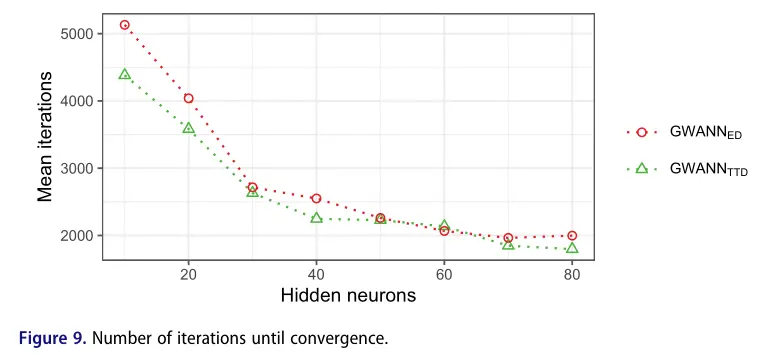
图 10 显示了所获得的 $GWANN$ 和 GWR 的平均带宽。虽然 $GWANN$ 的平均带宽与隐藏神经元的数量无关，但当它使用 TTD 而不是 ED 时，平均带宽要小得多。类似地，当使用 TTD 而不使用 ED 时， GWR 的平均带宽较小。一般来说， $GWANN$ 的平均带宽比 GWR 的小得多，与所使用的距离度量和隐含神经元的数量无关。该结果表明， $GWANN$ 通常能够在比 GWR 更小的尺度上对数据中的空间变化进行建模。

图 11 显示了通过( 外部 ) 10 倍 CV( 解释方差的比例，请参见图 S2 )获得的模型的平均均方根( RMSE )。当使用 EDS 而不是 TTD 时， $GWANN$ 的平均 RMSE 较低，但 GWR 的距离度量之间的平均 RMSE 几乎看不到差异。这证实了 Lu 等人的结果( 2017 )，他还发现在 EDS 和 TTD 之间 GWR 的拟合优度没有实质性差异，还指出 $GWANN$ 的预测性能更多地取决于距离度量的选择，而不是 GWR 的情况。此外，除了由少于 30 个隐含神经元组成的 $GWANN$ 和使用 TTDS 外， $GWANN$ 的平均均方根误差总是低于 GWR 的，与用于建模的距离无关。当使用 ED 和 60 个隐含神经元时， $GWANN$ 获得了总体最低的 RMSE 。结果表明，在实际应用中， $GWANN$ 算法在处理空间异构关系时比 GWR 算法能做出更好的预测。

使用完整的数据集，我们使用以下超参数构建了 GWR 和 $GWANN$ 。当使用 EDS 时， GWR 的带宽为 53， $GWANN$ 的训练带宽为 50 个隐藏神经元，带宽为 27 ，重复 2304 次。当使用 TTDS 时， GWR 的带宽被拟合为 36， $GWANN$ 被训练了 60 个隐藏神经元，带宽为 15 ，进行了 2478 次迭代

为了比较所选距离度量对预测的影响，图 12 显示了使用 $GWANN$ 和 GWR 的 TTD 和 EDS 时预测房价的差异。当使用 EDS 而不是 TTD 时， $GWANN$ 预测林兹市的房价会更高。对于格拉茨地区，这座城市与其周围环境之间的鲜明对比是显而易见的： $GWANN$ 预测，当使用 EDS 而不是 TTD 时，城市本身的房价会更高，但周围地区的房价会更低。对于维也纳的大都市地区，可以看出，当使用 EDS 而不是 TTD 时， $GWANN$ 预测城市东部地区的价格会更高，西部地区的价格会更低。对于萨尔茨堡市来说，预测房价没有明显差异。然而，在萨尔茨堡北部地区，当 $GWANN$ 使用 EDS 而不是 TTD 时，预计房价会大幅下降。对于 GWR 来说，使用 EDS 或 TTD 导致的预测房价差异通常很小，而且没有观察到空间模式。这些结果表明，与 GWR 相比，对于 $GWANN$ 来说，距离度量的选择对预测的空间分布有很大的影响。

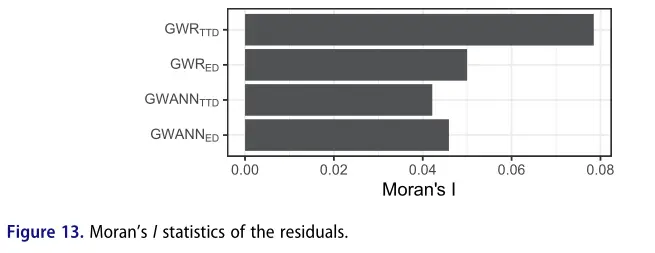
图 13 显示了模型残差的 Moran‘s I 统计数据。对于 GWR ，当使用 EDS 而不是 TTD 时， Moran‘s I 值更小，而对于 $GWANN$ ，当使用 TTDS 而不是 EDS 时，它们更小。与距离度量无关， $GWANN$ 的 Moran‘s I 值小于 GWR 的。然而，两种模型的残差均未达到统计学意义( p>0：05 )，表明两种模型都适当地考虑了数据的空间属性。

4 结论

我们介绍了 $GWANN$ -一种结合人工神经网络和地理权重的方法来建模空间异构关系。我们使用合成数据和真实数据对 $GWANN$ 和 GWR 进行了比较。综合数据的结果表明，当数据之间的关系是非线性的且空间方差较大时， $GWANN$ 比 GWR 具有更好的预测性能。基于真实世界数据的结果表明， $GWANN$ 的预测性能在实际设置中也可以优于竞争模型。

尽管有这些令人振奋的结果，但这项研究在解释研究结果或应用 $GWANN$ 时仍有一些局限性需要考虑。

首先，结果取决于模型超参数的选择。虽然我们在选择超参数时遵循了常规做法并进行了仔细的敏感度分析，但不能保证我们选择了最合适的超参数。综合敏感性分析是未来分析的一部分。

其次，虽然 GWR 的系数对于分析建模的关系很有用，但 $GWANN$ 网络中执行的计算的复杂性使得解释其面即使不是不可能的话也是困难的。

第三，在大多数实际应用中， $GWANN$ 由多个输出神经元组成( 即每个要预测的位置对应一个输出神经元 )。因此，由于每个输出神经元都连接到每个隐含神经元，因此连接权重的数量可能非常大，并且在训练过程中调整连接权重需要大量的计算资源。当搜索合适的带宽时，这是一个特别需要关注的问题，这涉及到训练和比较大量具有不同带宽的 $GWANN$ 。寻找合适带宽的更有效的启发式方法有可能缓解该问题。

第四，在全球水资源研究的背景下，Fotheringham 等，( 2017 )表明，通过对系数使用单独的带宽来建模不同尺度上的空间异质性是有用的。虽然这样的方法也有可能提高 $GWANN$ 的预测性能，但对于是否以及如果可以，如何将其转移到 $GWANN$ 仍然有待进一步研究。

5 数据和代码可用性声明

提供 $GWANN$ 实现、源代码和合成数据集的 R 包可从 https://github.com/jhagenauer/GWANN 下载。由于数据保护限制，房地产数据集不能公开共享。

参考文献

1. Anselin, L., 1989. What is special about spatial data? Alternative perspectives on spatial data analysis. Technical report. Santa Barbara: National Center for Geographic Information and Analysis.
2. Bárcena, M.J., et al., 2014. Alleviating the effect of collinearity in geographically weighted regression. Journal of Geographical Systems, 16 ( 4 ), 441–466. doi:10.1007/s10109-014-0199-6
3. Bengio, Y., 2012. Practical recommendations for gradient-based training of deep architectures. In: G. Montavon, G. B. Orr and K.-R. Müller, eds. Neural networks: tricks of the trade. Berlin: Springer, 437–478.
4. Bitter, C., Mulligan, G.F., and Dall’erba, S., 2007. Incorporating spatial variation in housing attribute prices: a comparison of geographically weighted regression and the spatial expansion method. Journal of Geographical Systems, 9 ( 1 ), 7–27. doi:10.1007/s10109-006-0028-7
5. Brunsdon, C., Fotheringham, A.S., and Charlton, M., 1999. Some notes on parametric significance tests for geographically weighted regression. Journal of Regional Science, 39 ( 3 ), 497–524. doi:10.1111/0022-4146.00146
6. Brunsdon, C., Fotheringham, A.S., and Charlton, M.E., 1996. Geographically weighted regression: a method for exploring spatial nonstationarity. Geographical Analysis, 28 ( 4 ), 281–298. doi:10.1111/j.1538-4632.1996.tb00936.x
7. Brunsdon, C., Fotheringham, S., and Charlton, M., 2007. Geographically weighted discriminant analysis. Geographical Analysis, 39 ( 4 ), 376–396. doi:10.1111/j.1538-4632.2007.00709.x
8. Casetti, E., 1972. Generating models by the expansion method: applications to geographical research. Geographical Analysis, 4 ( 1 ), 81–91. doi:10.1111/j.1538-4632.1972.tb00458.x
9. Choi, H. and Kim, H., 2017. Analysis of the relationship between community characteristics and depression using geographically weighted regression. Epidemiology and Health, 39, e2017025. doi:10.4178/epih.e2017025
10. Comber, A., et al., 2020. Distance metric choice can both reduce and induce collinearity in geographically weighted regression. Environment and Planning B: Urban Analytics and City Science, 47 ( 3 ), 489–507.
11. Cybenko, G., 1989. Approximation by superpositions of a sigmoidal function. Mathematics of Control, Signals, and Systems, 2 ( 4 ), 303–314. doi:10.1007/BF02551274
12. Du, Z., et al., 2020. Geographically neural network weighted regression for the accurate estimation of spatial non-stationarity. International Journal of Geographical Information Science, 34 ( 7 ), 1353–1377.
13. Fotheringham, A.S., Brunsdon, C., and Charlton, M., 2002. Geographically weighted regression: the analysis of spatially varying relationships. Chichester, UK: Wiley.
14. Fotheringham, A.S., Crespo, R., and Yao, J., 2015. Geographical and temporal weighted regression ( GTWR ). Geographical Analysis, 47 ( 4 ), 431–452. doi:10.1111/gean.12071
15. Fotheringham, A.S. and Oshan, T.M., 2016. Geographically weighted regression and multi- collinearity: dispelling the myth. Journal of Geographical Systems, 18 ( 4 ), 303–329. doi:10.1007/s10109-016-0239-5
16. Fotheringham, A.S., Yang, W., and Kang, W., 2017. Multiscale geographically weighted regression ( M GWR ). Annals of the American Association of Geographers, 107 ( 6 ), 1247–1265. doi:10.1080/24694452.2017.1352480
17. Gorr, W.L. and Olligschlaeger, A.M., 1994. Weighted spatial adaptive filtering: monte Carlo studies and application to illicit drug market modeling. Geographical Analysis, 26 ( 1 ), 67–87. doi:10.1111/j.1538-4632.1994.tb00311.x
18. Griffith, D.A., 2003. Spatial autocorrelation and spatial filtering: gaining understanding through theory and scientific visualization. Berlin, Heidelberg: Springer Science & Business Media.
19. Guo, L., Ma, Z., and Zhang, L., 2008. Comparison of bandwidth selection in application of geographically weighted regression: a case study. Canadian Journal of Forest Research, 38 ( 9 ), 2526–2534. doi:10.1139/X08-091
20. Hagenauer, J. and Helbich, M., 2018. Local modelling of land consumption in Germany with RegioClust. International Journal of Applied Earth Observation and Geoinformation, 65, 46–56. doi:10.1016/j.jag.2017.10.003
21. Haykin, S., 2008. Neural networks: a comprehensive foundation. 3rd ed. Upper Saddle River, NJ: Prentice Hall.
22. Helbich, M., et al., 2014. Spatial heterogeneity in hedonic house price models: the case of Austria. Urban Studies, 51 ( 2 ), 390–411. doi:10.1177/0042098013492234
23. Helbich, M. and Griffith, D.A., 2016. Spatially varying coefficient models in real estate: eigen- vector spatial filtering and alternative approaches. Computers, Environment and Urban Systems, 57, 1–11. doi:10.1016/j.compenvurbsys.2015.12.002
24. Huber, S. and Rust, C., 2016. Calculate travel time and distance with OpenStreetMap data using the open source routing machine ( OSRM ). The Stata Journal, 16 ( 2 ), 416–423. doi:10.1177/1536867X1601600209
25. LeSage, J.P. and Pace, R.K., 2009. Introduction to spatial econometrics. Statistics: A Series of Textbooks and Monographs. CRC Press.
    Leuenberger, M. and Kanevski, M., 2015. Extreme learning machines for spatial environmental data. Computers & Geosciences, 85, 64–73. doi:10.1016/j.cageo.2015.06.020
26. Li, K. and Lam, N.S., 2018. Geographically weighted elastic net: A variable-selection and modeling method under the spatially nonstationary condition. Annals of the American Association of Geographers, 108 ( 6 ), 1582–1600. doi:10.1080/24694452.2018.1425129
27. Lu, B., et al., 2017. Geographically weighted regression with parameter-specific distance metrics. International Journal of Geographical Information Science, 31 ( 5 ), 982–998. doi:10.1080/13658816.2016.1263731
28. Lu, B., Charlton, M., and Fotheringhama, A.S., 2011. Geographically weighted regression using a non-Euclidean distance metric with a study on london house price data. Procedia Environmental Sciences, 7, 92–97. doi:10.1016/j.proenv.2011.07.017
29. Nelson, A., Oberthür, T., and Cook, S., 2007. Multi-scale correlations between topography and vegetation in a hillside catchment of Honduras. International Journal of Geographical Information Science, 21 ( 2 ), 145–174. doi:10.1080/13658810600852263
30. Nesterov, Y.E., 1983. A method for solving the convex programming problem with convergence rate O( 1/k2 ). Doklady Akademii Nauk SSSR, 269, 543–547.
31. Páez, A., Long, F., and Farber, S., 2008. Moving window approaches for hedonic price estimation: an empirical comparison of modelling techniques. Urban Studies, 45 ( 8 ), 1565–1581. doi:10.1177/0042098008091491
32. Rojas, R., 2013. Neural networks: a systematic introduction. Berlin, Heidelberg: Springer Science & Business Media.
33. Rosen, S., 1974. Hedonic prices and implicit markets: product differentiation in pure competition. Journal of Political Economy, 82 ( 1 ), 34–55. doi:10.1086/260169
34. Rumelhart, D.E., Hinton, G.E., and Williams, R.J., 1986. Learning representations by back- propagating errors. Nature, 323 ( 6088 ), 533–536. doi:10.1038/323533a0
35. Sopranzetti, B.J., 2010. Hedonic regression analysis in real estate markets: a primer. In: Handbook of quantitative finance and risk management. Berlin, Heidelberg: Springer, 1201–1207.
36. Sunding, D.L. and Swoboda, A.M., 2010. Hedonic analysis with locally weighted regression: an application to the shadow cost of housing regulation in Southern California. Regional Science and Urban Economics, 40 ( 6 ), 550–573. doi:10.1016/j.regsciurbeco.2010.07.002
37. Sutskever, I., et al. 2013. On the importance of initialization and momentum in deep learning. In: Proceedings of the 30thInternational conference on machine learning. Atlanta, Georgia. 1139–1147.
38. Troy, A., Grove, J.M., and O’Neil-Dunne, J., 2012. The relationship between tree canopy and crime rates across an urban-rural gradient in the greater Baltimore region. Landscape and Urban Planning, 106 ( 3 ), 262–270. doi:10.1016/j.landurbplan.2012.03.010
39. Waller, L.A., et al., 2007. Quantifying geographic variations in associations between alcohol distribution and violence: a comparison of geographically weighted regression and spatially varying coefficient models. Stochastic Environmental Research and Risk Assessment, 21 ( 5 ), 573–588. doi:10.1007/s00477-007-0139-9
40. Wheeler, D.C., 2007. Diagnostic tools and a remedial method for collinearity in geographically weighted regression. Environment & Planning A, 39 ( 10 ), 2464–2481. doi:10.1068/a38325
41. Wheeler, D.C., 2009. Simultaneous coefficient penalization and model selection in geographically weighted regression: the geographically weighted lasso. Environment & Planning A, 41 ( 3 ), 722–742. doi:10.1068/a40256
42. Wheeler, D.C. and Tiefelsdorf, M., 2005. Multicollinearity and correlation among local regression coefficients in geographically weighted regression. Journal of Geographical Systems, 7 ( 2 ), 161–187. doi:10.1007/s10109-005-0155-6
43. Yu, W., et al., 2011. Analyzing and modeling land use land cover change ( LUCC ) in the Daqing City, China. Applied Geography, 31 ( 2 ), 600–608. doi:10.1016/j.apgeog.2010.11.019