空间数据的贝叶斯分层建模

【摘 要】由于空间数据的复杂性，使其统计建模非常困难。分层建模方法由于能够对模型进行分解，从而使建模和推断变得更具可操作性，因此在空间统计学领域得到快速应用和发展。而本文正是围绕空间数据的分层建模方法展开的。文中涉及通用分层建模方法、地统计中的分层建模、广义线性模型的分层建模等内容，以及相应的推断问题。本文内容摘自 Gelfand 的 《空间统计手册》第七章。

【原 文】 Gelfand, A.E. et al. (2010)， Handbook of spatial statistics (chapter 7). CRC press.

7.1 简介

在空间统计中，人们通常必须在存在复杂过程、多个数据源、参数化不确定性和不同程度的科学知识的情况下开发统计模型。人们可以从联合或条件的角度来处理这些复杂的问题。虽然从联合角度考虑过程可能很直观，但这种方法可能对统计建模提出严重挑战。例如，可能很难为相关空间数据集指定联合多元依赖结构。将此类联合分布分解为一系列条件模型可能会容易得多。例如，考虑以近地表环境空气温度为条件的近地表臭氧过程（尤其是在夏季）比同时考虑臭氧和温度过程更简单（也是一个合理的科学假设）。事实上，通常可以简化建模指定、考虑不确定性并在一系列条件模型中使用科学知识，这些模型通过简单的概率规则连贯在一起。这就是分层建模的本质。

原则上，可以从经典或贝叶斯角度考虑层次模型。然而，随着复杂程度的增加，贝叶斯范式成为必需。事实上，这种方法的使用增加与贝叶斯计算的革命相吻合，马尔可夫链蒙特卡罗 (MCMC) 模拟方法的采用和进一步发展就是例证 (Gelfand and Smith, 1990 ^[9])。使用这种模拟方法的事实要求，在某些情况下，必须做出建模选择以促进计算。当然，对于更传统的建模/估计方法也是如此，但是分层建模者在构建模型时必须明确考虑这些挑战，并且此类选择通常是特定于问题（如果不是数据集）的。

本章的其余部分将考虑空间数据的层次模型。本讨论无意全面回顾有关空间统计中层次模型的全部文献。相反，它旨在介绍和瞥见层次模型如何用于以及如何用于促进空间过程的建模。分层建模的基本原则已经确立，引用的参考资料可以提供额外的视角和更多的技术细节。 第 7.2 节 将从简单示意图的角度描述分层方法。然后将在 第 7.3 节 和 第 7.4 节 中具体讨论层次模型，因为它们分别与高斯和非高斯地统计空间过程有关。鉴于本手册的这一部分关注的是连续的空间变化，我们将把层次模型的讨论限制在此类模型上，尽管这些想法可以推广到其他类型的空间支持和过程。最后， 第 7.5 节 包含一个简短的概述和讨论。

7.2 分层建模概述

分层建模的基本思想源于简单的概率规则。尽管这个概念本质上不是贝叶斯的，但随着时间的推移，大多数文献都是在这种背景下发展起来的，最好的教学描述最常出现在贝叶斯文献中（例如，Gelman、Carlin、Stern 和 Rubin，2004 ^[13]）。我们在这里的目的不是重现此类一般描述，而是在与空间建模相关的框架背景下描述层次模型。这些想法遵循 Berliner (1996 ^[4]) 和 Wikle (2003 ^[24]) 的想法。

分层建模基于概率论的基本事实，即随机变量集合的联合分布可以分解为一系列条件分布和边缘分布。也就是说，如果 $A$ 、 $B$ 、 $C$ 是随机变量，则那我们可以写出其联合分布的分解形式：如 $[ A, B , C ] = [A|B,C][B|C][C]$ ，其中方括号符号 $[C]$ 表示 $C$ 的概率分布，符号 $[B|C]$ 表示给定 $C$ 时 $B$ 的条件概率分布。

对于空间过程而言，联合分布描述了具有空间参考的观测数据、真实（隐）空间过程以及模型参数的随机表现。对于许多问题，直接指定联合分布可能很难（如果不是不可能），但指定相关的条件模型的分布相对容易（例如，以真实过程和参数为条件的观测数据）。在此情况下，一系列相对简单的条件模型的乘积就可以产生复杂的联合分布。

对于存在观测数据的复杂过程，将其分为三个主要阶段（逻辑分层而非实际分层，实际分层可能更多）有助于解决问题（例如，Berliner，1996 ^[4]）：

• 阶段 1： 数据模型： $[数据 |过程,参数]$
• 阶段 2： 过程模型： $[过程|参数]$
• 阶段 3： 参数模型： $[参数]$

第一阶段与 “观测过程” 或 “数据模型” 有关，它指定了在给定感兴趣过程和参数时，观测数据的条件分布。
第二阶段描述了给定其他参数时，过程的条件分布。
第三个阶段赋予参数以概率分布，用于解释参数的不确定性。

通常，这些阶段中的每一个都可能有多个子阶段。例如，如果某个过程模型是多变量和空间的，它可能根据物理原理被建模为给定某些随机过程时，目标过程的条件分布（如以温度为条件的臭氧浓度）。类似的分解在数据模型和参数模型阶段也都是可能的。

我们最终感兴趣的是被观测数据更新后的过程分布和参数分布，也被称为 “后验” 分布。这可以通过贝叶斯规则获得，其中后验分布与数据、过程和参数分布的乘积成正比：

$$[过程,参数|数据] \propto [数据|过程,参数][过程|参数][参数]$$

其中归一化常数被表示为公式右侧关于过程分布和参数分布的积分。上述公式是分层贝叶斯分析的基础。

上面简单概述了分层建模思想和框架，下面将更详细地讨论分层模型的三个主要组成部分。

7.2.1 数据模型

在给定真实过程的情况下对数据的条件分布进行建模，其主要优点是可以对模型形式进行实质性简化。

令 $Y$ 为某个（空间）过程 $\eta$ 的观测数据（含有误差），令 $\theta_{y}$ 表示模型参数，则数据模型的分布可以记为： $[\mathbf{Y} |\eta, \theta_{y}]$ 。此条件分布通常比 $[Y]$ 的无条件分布要简单很多，因为大多数复杂的依赖结构都来自于过程 $\eta$。一般情况下，数据模型的误差结构仅表示测量误差（和/或空间过程中无法建模的小尺度空间变异性）。在这个通用框架中，误差不必是可加的。此外，此框架还能容纳与过程 $\eta$ 处于不同支撑和/或对齐的数据（参见 Gelfand、Zhu 和 Carlin，2001 ^[11]；Wikle、Milliff、Nychka 和 Berliner，2001 ^[27]；Wikle 和 Berliner , 2005 ^[25])。

分层数据模型还提供了一种组合数据集的自然方式。例如，假设 $Y_a$ 和 $Y_b$ 代表来自两个不同来源的数据。同样，设 $\eta$ 为感兴趣的过程， $\theta_{y_a}$ 和 $\theta_{y_b}$ 为参数。在这种情况下，数据模型通常写为

$$[Y_a ,Y_b|\eta, \theta_{y_a} , \theta_{y_b} ] = [Y_a |\eta, \theta_{y_a} ][Y_b|\eta, \theta_{y_b} ] \tag{7.1}$$

也就是说，以真实过程为条件，假设数据是独立的。这并不意味着这两个数据集是无条件独立的，而是数据集之间的依赖主要是由于过程 $\eta$ 。必须针对每个问题评估和/或证明这种独立性假设。

条件独立性假设也可以应用于多变量模型。也就是说，如果感兴趣的过程分别表示为 $\eta_a$ 和 $\eta_b$ ，以及相关的观测值 $Y_a$ 和 $Y_b$ ，则可以假定：

$$[Y_a ,Y_b |\eta_a , \eta_b , \theta_{y_a} , \theta_{y}c ] = [Y_a |\eta_a , \theta_{y_a} ][ Y_b |\eta_b , \theta_{y_b} ] \tag{7.2}$$

同样，必须评估此假设在特定问题中的有效性。在适当的时候，这可以导致估计的显著简化。

7.2.2 过程模型

通常情况下，开发过程模型是构建层次模型最关键的步骤。

如前所述，过程模型的分布有时可以进一步分层为一系列子模型。例如，假设感兴趣的过程由两个子过程组成， $\eta_a$ 和 $\eta_b$ （例如， $\eta_a$ 可能代表较低的对流层臭氧，而 $\eta_b$ 可能代表同一区域的地表温度，如 Royle 和 Berliner (1999 ^[19]) 中所述）。此外，令参数 $\theta_{\eta} = \{ \theta_{\eta_a} , \theta_{\eta_b} \}$ 与这两个过程相关联。然后，可以考虑分解，

$$[\eta_a , \eta_b|\theta_{\eta}] = [\eta_a |\eta_b, \theta_{\eta}][\eta_b|\theta_{\eta}] \tag{7.3}$$

对参数的进一步假设导致了简化，因此 式（7.3） 的右侧通常可以写成 $[\eta_a |\eta_b, \theta_{\eta_a} ][\eta_b|\theta_{\eta_b} ]$ 。

此阶段最大的建模挑战在于如何指定这些组件的概率分布。人们对感兴趣过程的科学理解能够促进此模型的效用和实施，但层次分解的合理性和有效性并不依赖于这种理解。

7.2.3 参数模型

与数据模型和过程模型分布的情况类似，参数分布通常被分解为一系列分布。例如，给定数据模型 式（7.2） 和过程模型 式（7.3） ，需要指定参数分布 $[\theta_{y_a} , \theta_{y_b} , \theta_{\eta_a} , \theta_{\eta_b} ]$ 。通常，人们可以对这些分布做出合理的独立性假设，例如 $[\theta_{y_a} , \theta_{y_b} , \theta_{\eta_a} , \theta_{\eta_b} ] = [\theta_{y_a} ][\theta_{y_b} ][\theta_{\eta_a} ][\theta_{\eta_b} ]$ 。当然，这样的假设是特定于问题的。

通常也有适当的参数子模型，从而导致模型层次结构的其他级别。对于复杂过程，可能会存在可用的科学洞察力来开发多层次的参数模型（例如，Wikle 等，2001 ^[27]）。但在其他情况下，人们对参数分布知之甚少，建议使用 “无信息先验” 或使用数据集估计超参数。 在许多情况下，参数分布的选择主要（或部分）是为了便于计算。

从历史上看，参数分布的指定有时因其固有 “主观性” 而成为被反对的焦点。数据模型和过程模型的指定其实也相当主观，但这些选择并没有引起太多注意。事实上，这些阶段的主观性也是经典推断的一部分。分层（贝叶斯）方法的一个优势是对这种主观判断的量化。分层模型提供了一个连贯的框架，在该框架中，可以将与判断、科学推断、实用主义和经验相关的不确定性明确地纳入模型中。然而，如果选择尽可能多地消除主观性，则可以考虑先验分布的各种 “客观” 选择。在分层建模框架中必须小心，这样的选择会导致相应的后验分布。有关贝叶斯统计中主观和客观先验发展问题的更具哲学性的讨论，请参阅 Berger (2006 ^[2]) 和 Goldstein (2006 ^[14]) 以及随附的讨论。

7.2.4 层次空间模型

分层框架可应用于本书中描述的大多数标准空间统计建模方法。

我们没有单独开发另外一个通用框架来包含所有这些内容，而是在以下部分中说明了高斯和非高斯地统计问题的层次空间模型。贯穿始终的共同主题是：上述的 三阶段层次结构 、对该框架内 隐高斯空间过程的依赖 以及 相关的贝叶斯实现 。这些示例并非旨在详尽无遗。更详细和完整的描述可以在文献中找到，例如 Banerjee、Carlin 和 Gelfand (2004 ^[1])、Diggle 和 Ribeiro (2007 ^[7])，以及其中的参考文献。

7.3 层次高斯地统计模型

假设有 $m$ 个空间过程观测值，用 $\mathbf{Y} = (Y(\tilde{\mathbf{s}}_1),\ldots ,Y(\tilde{\mathbf{s}}_m))'$ 表示，我们定义一个隐空间向量， $\boldsymbol{ \eta} = (\eta(\mathbf{s}_1),\ldots , \eta(\mathbf{s}_n))'$ ，其中 $\eta(\mathbf{s}_i )$ 来自高斯空间过程，其中 $\mathbf{s}_i$ 是一个空间位置（这里假设在二维实空间的某个子集中，尽管推广到更高维度并不困难原则）。通常，对应于隐向量 $\boldsymbol{\eta}$ 的位置 $\{\mathbf{s}_1,\ldots , \mathbf{s}_n\}$ 可能与观测位置 $\{\tilde{\mathbf{s}}_1,\ldots ,\tilde{\mathbf{s}}_m\}$ 不重合。此外，大多数情况下，观测位置和预测位置的支持不必相同，尽管我们在这里假设观测和隐空间过程都具有点级支持。

就通用层次框架而言，我们必须指定数据模型、过程模型和参数模型。例如，分层空间模型可能由下式给出：

$$\begin{align*} 数据模型：&\mathbf{Y} | \boldsymbol{\beta}, \boldsymbol{\eta} , \sigma^2_{\epsilon} \sim \operatorname{Gau}(\mathbf{X} \boldsymbol{\beta} + \mathbf{H} \boldsymbol{\eta}, \sigma^2 I) \tag{7.4}\\ 过程模型：&\boldsymbol{\eta} | \boldsymbol{\theta} \sim \operatorname{Gau}(\mathbf{0}, \boldsymbol{\Sigma} (\boldsymbol{\theta})) \tag{7.5} \\ 参数模型：&[\boldsymbol{\beta}, \sigma^2_{\epsilon} , \boldsymbol{\theta}] \tag{7.6} \end{align*}$$

其中 $\mathbf{X}$ 是 $m × p$ 的协变量矩阵，通常与大尺度空间均值有关， $\boldsymbol{\beta}$ 是相关的 $p × 1$ 参数向量， $\mathbf{H}$ 是一个 $m × n$ 矩阵，它将观测值 $\mathbf{Y}$ 与隐过程 $\mathbf{\boldsymbol{\eta}}$ 相关联， $\sigma^2_{\epsilon}$ 对应于一个独立的、小尺度（块金）空间效应和/或测量误差过程 $\varepsilon$ ， $\boldsymbol{\theta}$ 是用于与空间隐过程相关的空间协方差函数的参数向量（例如，方差、空间范围参数、平滑度参数等）。请注意，特定参数分布的选择通常取决于估计方法和/或所考虑的特定过程。值得注意的是， “映射矩阵” $\mathbf{H}$ 非常灵活。例如，在其最简单的形式中，如果观测和隐过程位置重合，$\mathbf{H}$ 就是单位矩阵。或者，如果部分（但不是全部）观测位置直接对应于隐过程位置，则 $\mathbf{H}$ 可能是 $1$ 和 $0$ 的关联矩阵。或者， $\mathbf{H}$ 在某些情况下可能是加权或平均矩阵（例如，参见 Wikle、Berliner 和 Cressie，1998 ^[26]；Wikle 等，2001 ^[27]；Wikle 和 Berliner，2005 ^[25] ）。

人们可能会考虑另一种层次参数化，其中空间平均值（趋势）向下移动层次结构的一个级别。在这种情况下，数据模型为 $\mathbf{Y}|\boldsymbol{ \eta}, \sigma^2_{\epsilon} \sim \operatorname{Gau}(\mathbf{H} \boldsymbol{ \eta}, \sigma^2_{\epsilon} \mathbf{I})$ ，过程模型由 $\boldsymbol{ \eta}|\boldsymbol{\beta,\theta} \sim \operatorname{Gau}(\mathbf{X} \boldsymbol{\beta,\Sigma} (\boldsymbol{\theta}))$ 给出，参数分布与 式（7.6） 中一样不变。原则上，这种 “分层居中” 可以改进贝叶斯估计（Gelfand、Sahu 和 Carlin，1995 ^[10]）。

如果将隐空间过程积分出来，就会出现另一种表示形式，本质上是将数据模型和过程模型阶段合并为一个。具体来说，

$$[\mathbf{Y}|\boldsymbol{\beta}, \sigma^2_{\epsilon} , \boldsymbol{\theta}] = \int [\mathbf{Y}|\boldsymbol{ \eta}, \boldsymbol{\beta}, \sigma^2_{\epsilon}][\boldsymbol{ \eta}|\boldsymbol{\theta}] d \boldsymbol{ \eta} \tag{7.7}$$

对于 式（7.4） 和 式（7.5） 中的模型，积分在 $\boldsymbol{ \eta}$ 的支持下，给出

$$\begin{align*} 数据模型：&\mathbf{Y}|\boldsymbol{\beta}, \sigma^2_{\epsilon}, \boldsymbol{\theta} \sim \operatorname{Gau}(\mathbf{X}\boldsymbol{\beta}, \boldsymbol{\Sigma} (\boldsymbol{\theta}) + \sigma^2 \mathbf{I}) \tag{7.8}\\ 参数模型：&[\boldsymbol{\beta}, \sigma^2_{\epsilon} , \boldsymbol{\theta}] \tag{7.9} \end{align*}$$

式（7.4） 、 式（7.5） 和 式（7.6） 建议的完全分层公式与 式（7.8） 和 式（7.9） 中的边缘化形式在传统线性混合模型分析（例如，纵向数据分析，Verbeke 和 Molenberghs (2000 ^[22])）中本质上时一致的。在这种情况下，当推断与参数 $\boldsymbol{\beta}$ 有关时（例如 “空间回归分析” ），通常可以方便地根据边缘化模型进行，而不需要对随机效应进行具体预测（即示例中的空间隐过程）。对于大多数传统的地统计应用程序，人们对空间过程的预测感兴趣，而分层公式似乎更合适。但如下所述，给定参数 $[\boldsymbol{\beta}, \sigma^2_{\epsilon} , \boldsymbol{\theta}|\mathbf{Y}]$ 的后验分布时，可以轻松获得过程模型的后验分布 $[\boldsymbol{ \eta}|\mathbf{Y}]$ 。此外，无论最终预测目标如何，经典估计和贝叶斯估计都存在使用边缘化形式来促进参数估计的情况。

7.3.1 后验分析

选择 式（7.6） 中参数的先验分布后，我们寻求的使其后验分布，它正比于 式（7.4） 、 式（7.5） 和 式（7.6） 的乘积：

$$[\boldsymbol{\eta}, \boldsymbol{\beta}, \boldsymbol{\theta}, \sigma^2_{\epsilon} |\mathbf{Y}] \propto [\mathbf{Y} |\boldsymbol{\eta}, \boldsymbol{\beta}, \sigma^2_{\epsilon} ][\boldsymbol{\eta}|\boldsymbol{\theta}][\boldsymbol{\beta}, \sigma^2_{\epsilon} , \boldsymbol{\theta}] \tag{7.10}$$

在这种情况下，人们无法获得归一化常数的解析表示，因此，蒙特卡洛方法被广泛用于估计、推断和预测（参见 Robert 和 Casella (2004 ^[18]) 的概述）。

或者，可以直接使用 式（7.8） 的边缘化形式来获得参数的后验分布：

$$[\boldsymbol{\beta}, \sigma^2_{\epsilon} , \boldsymbol{\theta}|\mathbf{Y}] \propto [\mathbf{Y} |\boldsymbol{\beta}, \sigma^2_{\epsilon} , \boldsymbol{\theta}][\boldsymbol{\beta}, \sigma^2_{\epsilon} , \boldsymbol{\theta}] \tag{7.11}$$

同样， 式（7.11） 的归一化常数在解析上不可用，必须使用蒙特卡罗方法从后验分布中获取样本。此外，请注意由于

$$[\boldsymbol{\eta}|\mathbf{Y}] = \int [\boldsymbol{\eta}|\boldsymbol{\theta}][\boldsymbol{\theta}|\mathbf{Y}]d\boldsymbol{\theta} \tag{7.12}$$

如果我们有来自边缘后验分布 $[\boldsymbol{\theta}|\mathbf{Y}]$ 的样本，则只要知道 $[\boldsymbol{\eta}|\boldsymbol{\theta}]$ 的封闭表达形式，我们就可以通过蒙特卡洛直接从 $[\boldsymbol{\eta} | \mathbf{Y}]$ 中采样，。因此，在分层高斯地统计模型中，确实没有必要直接考虑 式（7.10） 的完全联合后验。事实上，正如 Banerjee 等 (2004 ^[1])所讨论的那样， 式（7.8） 的边缘模型中的协方差结构在计算上更稳定（由于边缘协方差矩阵对角线上的附加常数），并且在 MCMC 实现时，估计越有效，越能解析地边缘化层次模型。

在地统计分析中，典型做法是区分对应于观测数据的隐空间过程向量 $\boldsymbol{\eta}$ 的元素，比如 $\boldsymbol{\eta}_d$ （一个 $m×1$ 向量），以及那些需要预测的非观测位置，比如 $\boldsymbol{\eta}_0$ (一个 $(n − m) × 1$ 向量）。在这种情况下， $\boldsymbol{\eta} = (\boldsymbol{\eta}'_d , \boldsymbol{\eta}'_0)'$ 并且 式（7.5） 的过程模型可以分解为

$$[\boldsymbol{\eta}_0, \boldsymbol{\eta}_d |\boldsymbol{\theta}] = [\boldsymbol{\eta}_0|\boldsymbol{\eta}_d , \boldsymbol{\theta}][\boldsymbol{\eta}_d |\boldsymbol{\theta}] \tag{7.13}$$

然后可以从

$$[\boldsymbol{\eta}_0|\mathbf{Y}, \boldsymbol{\theta}] = \int [\boldsymbol{\eta}_0|\boldsymbol{\eta}_d , \boldsymbol{\theta}][\boldsymbol{\eta}_d |\mathbf{Y}]d\boldsymbol{\eta}_d \tag{7.14}$$

中获得后验预测分布 $[\boldsymbol{\eta}_0|\mathbf{Y}, \boldsymbol{\theta}]$，其中 $[\boldsymbol{\eta}_d |\mathbf{Y}]$ 是那些对应于观测位置的隐过程位置的后验分布，在这种情况下， $[\boldsymbol{\eta}_0|\boldsymbol{\eta}_d , \boldsymbol{\theta}]$ 是一个多元高斯分布，很容易从条件多元正态分布的基本属性中（分析地）获得。但是请注意，此后验预测分布等同于 $\mathbf{H}\boldsymbol{\eta}$ 的后验分布，其中 $\mathbf{H} = [\mathbf{I}_{m×m} \cdot \mathbf{0}_{m×(n−m)}]$。也就是说，可以预测完整的空间向量 $\boldsymbol{\eta}$ ，然后简单地 “挑选” 与预测位置对应的元素。考虑 式（7.13） 和 式（7.14） 中分解的优点是计算性的。具体来说，对于与 式（7.5） 的基本过程模型相关的推断，必须考虑完整的 $n × n$ 协方差矩阵 $\boldsymbol{\Sigma} (\boldsymbol{\theta})$ 的逆矩阵。然而，通过分解隐过程，只需要计算 $m × m$ 协方差矩阵的逆。这对于经典估计和贝叶斯估计都是正确的。应该注意的是，在预测完整的 $\boldsymbol{\eta}$ 时也可能具有计算优势，特别是在非常高维的问题中，其中 $\boldsymbol{\eta}$ 可以在网格上定义和/或考虑 $\boldsymbol{\eta}$ 的降秩表示。

7.3.2 参数模型的注意事项

与分层模型的通用情况一样，通常指定参数分布的特定选择以及方差和协方差参数的替代参数化以促进计算。通常情况下，参数被认为是相互独立的， $[\boldsymbol{\beta}, \sigma^2_{\epsilon} , \boldsymbol{\theta}] = [\boldsymbol{\beta}][\sigma^2_{\epsilon} ][\boldsymbol{\theta}]$。显然，还有其他选择，并且应该验证后验推断对参数分布的选择并不过分敏感。在进行贝叶斯分层分析时，此类敏感性分析至关重要。

可以从为地统计建模开发的任何有效空间协方差函数中选择包含 $\boldsymbol{\Sigma} (\boldsymbol{\theta})$ 的空间协方差函数。然而，对于层次模型，空间过程通常被认为是平稳的、均匀的和各向同性的，通常遵循众所周知的空间协方差函数类之一，例如 Matérn 或幂指数类。因此，我们可以写成 $\boldsymbol{\Sigma}(\boldsymbol{\theta}) = \sigma^2_{\eta} \mathbf{R}(\phi, \kappa)$ ，其中 $\mathbf{R}(\phi, \kappa)$ 是空间相关矩阵，$\sigma^2_{\eta}$ 是方差， $\phi$ 和 $\kappa$ 是空间范围和平滑度参数。这些参数的先验选择再次取决于建模者。在某些情况下，假定平滑参数是已知的（例如，指数相关模型）。有时使用方差的逆伽马或均匀先验和空间相关参数的信息伽马先验。此外，为了简化计算，通常为空间相关参数指定离散（均匀）先验。这种简单性的出现是因为在 MCMC 分析中总是可以从相关的离散分布中生成随机样本（例如，参见 Robert 和 Casella，2004 ，第 2 章）。在实践中，可能必须在足够精细的分辨率之前调整离散化区间以允许马尔可夫链移动。有关详细信息，请参阅上述参考资料以及 第 7.3.4 节 和 第 7.4.2 节 中的示例以及 第 7.5 节 中的讨论。此外，请注意，如 Browne 和 Draper (2006 ^[5]) 以及 Gelman (2006 ^[12]) 中所讨论的，在某些情况下，为方差分量选择非信息先验先验可能很困难。

在计算上，重新参数化边缘模型方差通常很有帮助。例如，Diggle 和 Ribeiro (2007 ^[7]) 建议边缘模型参数化：

$$\mathbf{Y} |\boldsymbol{\beta}, \phi, \kappa, \sigma^2_{\eta} , \tau^2 \sim \operatorname{Gau}(\mathbf{X}\boldsymbol{\beta}, \sigma^2_{\eta} [\mathbf{R}(\phi, \kappa) + \tau^2 \mathbf{I}]) \tag{7.15}$$

其中 $\tau^2 \equiv \sigma^2_{\epsilon} /\sigma^2_{\eta}$ 是块金变化与过程变化的比率，具有无标度的优点。或者，Yan、Cowles、Wang 和 Armstrong (2007 ^[28]) 提出了一种不同的边缘重新参数化：

$$\mathbf{Y} |\boldsymbol{\beta}, \phi, \kappa, \sigma^2, \xi \sim \operatorname{Gau}(\mathbf{X}\boldsymbol{\beta}, \sigma^2[(1 − \xi ) \mathbf{R} (\phi, \kappa) + \xi \mathbf{I}]) \tag{7.16}$$

,其中 $\sigma^2 = \sigma^2_{\epsilon} + \sigma^2_{\eta}$ 和 $\xi = \sigma^2_{\epsilon} /\sigma^2$ 。在这种情况下， $\xi$ 可以很好地解释为由块金效应贡献的 $Y$ 总变化的分数.参数 $\xi$ 有界支持 $(0, 1)$ ，这有助于某些类型的 MCMC 实现（例如，切片采样）。

7.3.3 贝叶斯计算

分层空间模型的贝叶斯估计、预测和推断必须通过蒙特卡罗方法进行。蒙特卡洛算法的具体选择取决于参数模型的选择。通常，可以按照 Banerjee 等 (2004 ^[1]) 的描述使用 MCMC 算法。在某些情况下，可以使用直接蒙特卡洛模拟，如 Diggle 和 Ribeiro (2007 ^[7]) 中所述。在具有大量数据和/或预测位置的问题中，必须特别注意计算方面的考虑。在这种情况下，考虑各种降维或去相关方法来对空间过程进行建模通常会更有效。本书第八章（ 《空间过程的低秩表示》 ）有部分相关模型的介绍。

越来越多的专业计算软件可用于适应越来越复杂的分层空间模型。感兴趣的读者可以参考上述文本作为起点。

7.3.4 高斯地统计示例：美国中西部温度

为了便于说明，请考虑 图 7.1 中显示的以爱荷华州为中心的美国中部平原地区的月平均最高温度观测值。这些数据来自美国历史气候网络 (USHCN) 1941 年 11 月的 131 个站点。

在此示例中，假设我们有兴趣预测（插值）该区域点网格处的真实（无噪声）月平均最高温度。网格化数据集有助于气候学分析，并且在将观测数据用作数值天气和气候模型的输入时是必要的。在这两种情况下，与网格化相关的不确定性与网格化场本身一样重要。

我们假设模型的边缘形式如 式（7.15） 所示，其中 $\mathbf{X}$ 具有三列，分别对应于截距、经度趋势和纬度趋势。因此，在这样一个相对均匀且较小的地理区域上，假设空间相关模型是平稳且各向同性的是合理的。特别是，我们在这里假设一个指数相关函数，具有空间相关参数 $\phi$ （即 $r (d, \phi) = \exp(−d/\phi)$ ，其中 $d$ 是两个空间位置之间的距离）。我们为 $\boldsymbol{\beta}$ 选择一个相对无信息的先验， $\boldsymbol{\beta} \sim N(0, \boldsymbol{\Sigma}_{\boldsymbol{\beta}})$ ，其中 $\boldsymbol{\Sigma}_{\boldsymbol{\beta}}$ 是对角线，每个方差等于 $1000$ 。我们还考虑了 $\beta$ 参数的无信息（均匀）先验，后验概率对这个选择。我们为 $\sigma^2_{\eta}$ 选择了一个比例逆卡方先验，先验均值为 $2.7$ ，自由度 $= 2$ ，对应于相当模糊的先验。先验均值的选择基于初步回归分析，其中没有空间相关误差项的空间趋势占温度变化的约 $83\%$ 。由于温度数据的总体方差约为 $16 deg^2$ ，我们假设空间误差过程可以解释大约 $2.7 deg^2$ 。应该注意的是，我们确实考虑了先验均值的其他几个值，以及非信息性先验 $p(\sigma^2_{\eta}) \propto 1/\sigma^2_{\eta}$ ，后验概率对这些选择不是很敏感。假设 $\phi$ 的先验是从 $0.1$ 到 $4.0$ 的离散均匀分布，增量为 $0.1$ 。该选择基于以下事实：指数模型的实际范围（点之间的最小距离，空间相关性可忽略不计）被定义为 $3\phi$ （参见 Schabenberger 和 Pierce，2002，第 583 页）。基于 $0.3$ （度）和 $12$ （度）之间的实际范围，它涵盖了我们预测域的范围，这对应于 0.1 和 4.0 之间的 $\phi$ 选择。类似地， $\tau^2$ 的先验由从 0.05 到 2.0 的离散均匀分布给出，增量为 0.05。这允许空间变化在比块金大 20 倍到小 2 倍之间。对于此空间尺度上的温度数据，块金方差远大于空间变化在科学上是不可信的。后验分布对此上限不敏感。尽管对于大的地理区域，在计算距离和选择有效的协方差函数时需要考虑地球的曲率，但这里考虑的区域足够小，不需要这样的考虑。如 Diggle 和 Ribeiro (2007 ^[7]) 所述，使用带有 geoR 包的贝叶斯直接模拟进行估计。

图 7.2 中的直方图总结了模型参数的后验分布样本。此外，还显示了这部分参数空间的先验分布以供比较。我们从这些直方图中注意到的第一件事是，相对于它们各自的先验，这些边缘后验分布肯定存在贝叶斯学习。毫不奇怪，鉴于 11 月该地区的温度普遍随着纬度的增加而降低，因此大尺度空间平均值中的纬度效应 ( $\boldsymbol{\beta}_2$ ) 比经度效应 ( $\boldsymbol{\beta}_1$ ) 更 “显著” 。鉴于强烈的空间依赖性（ $\phi$ 的后验中位数（均值）为 2.0 式（2.2） ）和过程方差的后验中位数（均值）$\sigma^2_{\eta}$ 为 3.0 式（3.2） ，隐空间过程相当重要。请注意，有证据表明 $\tau^2$ 的后验中位数（均值）为 0.25 式（0.31） ，表明中位数（均值）块方差为 0.75 式（1.0） 。尽管 USHCN 台站经常得到志愿观测员的支持，这可能会导致测量误差，但通常认为当考虑月平均值时此类误差非常小，进一步支持 $\sigma^2_{\epsilon}$ 反映小尺度空间变异性的解释。

最后， 图 7.3 显示了点网格上预测过程的后验均值和方差图。请注意，预测位置对应于每个网格框的中心，提供的图像图仅用于帮助可视化；我们并没有根据与我们的数据不同的支持进行预测。从北到南的空间趋势在预测中非常明显，但除了趋势之外，还有空间依赖性的证据。后验预测方差显示观测位置附近的预测方差小得多的预期模式，而数据位置以外的区域（地图的边缘）的方差大得多。

7.4 层次广义线性地统计模型

在 第 7.3 节 介绍的基本高斯地统计模型的背景下，分层方法的优势主要在于它考虑了参数估计的不确定性，这与经典地统计方法不同。如需使用传统克里金法和贝叶斯克里金法对此进行很好的说明，请参阅 Diggle 和 Ribeiro（2007 ^[7] ，第 7.4 章）中的示例。这个例子清楚地表明贝叶斯预测方差通常（但不总是）大于相应的插件预测方差。尽管这很重要，但当考虑非高斯数据模型时，分层方法的真正优势和力量就会变得显而易见。有许多现实世界的过程，其中数据显然不是高斯分布，但表现出空间依赖性。例如，计数数据在许多生物、生态和环境问题中很常见。在此类数据集中，通常存在可辨别的均值-方差关系，并且数据明显离散且具有正值。在这些情况下自然要考虑泊松和二项式模型，而忽略这种结构而盲目地应用高斯地统计模型会导致估计和预测效率低下。正如上面介绍的高斯地统计模型可以被认为是线性混合模型的特例，非高斯空间数据问题可以在广义线性混合模型（GLMM，例如，参见 McCulloch 和 Searle (2001 ^[15]) 的概述）由 Diggle、Tawn 和 Moyeed (1998 ^[7]) 提出。下面从分层的角度描述这种方法。有关详细信息，请参阅 Diggle 和 Ribeiro (2007 ^[7])、Banerjee 等 (2004 ^[1])，以及其中的参考文献。

GLMM 的公式化需要指定与空间数据关联的随机变量 $Y(\mathbf{s})$ 的似然。人们假设这有一个数据模型是指数家族的一员。与经典广义线性模型一样，有一个对应于该分布的指定参数，名义上是该分布的位置参数的函数 $g()$ （链接函数）。为了结合空间过程 $\boldsymbol{\eta}$ （如上所述），我们假设 $[Y(\mathbf{s}_i )|\boldsymbol{\eta}, \boldsymbol{\beta}]$， $i = 1,\ldots ,m$ 对于感兴趣域中的任何位置 $\mathbf{s}_i$ 是有条件独立的，有条件的均值 $E(Y(\mathbf{s}_i )|\boldsymbol{\eta}, \boldsymbol{\beta}) = \boldsymbol{\mu}(\mathbf{s}_i )$ ，其中该均值 $\boldsymbol{\mu}(\mathbf{s}_i )$ 是空间协变量和隐空间随机过程的线性函数。具体来说，空间相关的隐过程通过链接函数合并到线性预测器中：

$$g(\boldsymbol{\mu}) = X\boldsymbol{\beta} + H\boldsymbol{\eta} + \varepsilon$$

其中， $\boldsymbol{\mu} = (\mu(\mathbf{s}_1),\ldots , \mu(\mathbf{s}_m))'$ ，并且与高斯地统计模型一样， $\mathbf{X}\boldsymbol{\beta}$ 解释了空间协变量效应， $\mathbf{H}\boldsymbol{\eta}$ 解释了隐的空间过程效应，以及额外的噪声项 $\varepsilon$ ，解释了特定地点的随机变化，可能包括也可能不包括在内，取决于应用程序。例如，可能需要此项来解释由于小尺度空间效应导致的过度分散。增加这样一个词有些争议，有拥护者也有反对者。虽然不能直接解释为测量误差，但小尺度空间过程解释在许多情况下都是有效的。但是，如果不在观测和/或先验知识中进行适当的复制，则可能无法识别这种影响。和以前一样，层次模型的过程阶段需要指定，例如 $\boldsymbol{\eta} \sim \operatorname{Gau}(\mathbf{0}, \boldsymbol{\Sigma} (\boldsymbol{\theta}))$ 和 $\varepsilon \sim \operatorname{Gau}(\mathbf{0}, \sigma^2 \mathbf{I})$，空间协方差矩阵由 $\boldsymbol{\theta}$ 参数化。要完成层次结构，必须为参数 $[\boldsymbol{\beta}, \sigma^2_{\epsilon} , \boldsymbol{\theta}]$ 指定分布。请注意，我们可能还需要指定与指数族数据模型相关联的色散参数的分布，例如 $\gamma$ 。参数分布的具体选择将取决于上下文和计算考虑因素，就像高斯数据模型的情况一样。因此，此类 GLMM 空间模型与 第 7.3 节 中介绍的分层高斯地统计模型之间的主要区别在于数据阶段。在这种情况下，考虑到高斯隐空间过程和协变量，数据观测是条件独立的是至关重要的。

7.4.1 计算考虑

基于上述分层模型，我们对后验分布感兴趣：

$$[\boldsymbol{\eta}, \boldsymbol{\beta}, \sigma^2_{\epsilon} , \boldsymbol{\theta}, \gamma |\mathbf{Y}] \propto [\mathbf{Y} |\boldsymbol{\eta}, \boldsymbol{\beta}, \sigma^2_{\epsilon} , \gamma ][\boldsymbol{\eta}|\boldsymbol{\theta}][\boldsymbol{\beta} , \sigma^2_{\epsilon} , \boldsymbol{\theta}, \gamma ] \tag{7.18}$$

与分层高斯数据地统计模型一样，无法通过解析找到 式（7.18） 的归一化常数，必须使用 MCMC 方法。然而，与高斯数据案例不同，我们无法在分析上边缘化空间隐过程以促进计算。因此，MCMC 采样程序必须直接包括 $\boldsymbol{\eta}$ （或其组件）的更新。

必须特别注意分层广义线性空间模型的 MCMC 采样的特定计算方法。一个主要问题是空间隐过程 $\boldsymbol{\eta}$ 的有效更新，这通常通过 Gibbs 采样器中的 Metropolis-Hastings 更新来完成。在这种情况下，主要关注的是算法在对相关进程进行采样时的效率。在这种情况下，一种可能有用的方法是朗之万更新方案，正如 Diggle 和 Ribeiro（2007 ^[7] ）在空间上下文中所讨论的那样。或者，当在模型中保留小规模过程项 $\varepsilon$ 时，可以通过共轭多元正态 Gibbs 更新来完成 $\boldsymbol{\eta}$ 过程的更新（例如，参见 Wikle，2002 ^[23]；Royle 和 Wikle，2005 ^[20]），这可以大大增加比 Metropolis 更新更高效。当然，在这种情况下，必须估计与 $\varepsilon$ 误差过程相关的参数。如果没有重复观测和/或大量的先验知识，这可能会有问题。在某些情况下，将这些参数视为 “讨厌的参数” （例如，假设它们是已知的或具有非常严格的先验分布）是合理的，只是为了便于 $\boldsymbol{\eta}$ 的计算和预测。

第二个问题是隐空间过程协方差参数 $\boldsymbol{\theta}$ 的更新。如 Christensen、Roberts 和 Sköld (2006 ^[6])、Palacios 和 Steel (2006 ^[16]) 以及 Zhang (2004 ^[29]) 所述，重新参数化通常是必要的。这是当前研究的一个活跃领域，并且最先进的技术正在迅速发展。经验表明，成功实施这些模型可能很困难，而且肯定是特定于模型和数据集的。

7.4.2 非高斯数据示例：鸟类数量制图

作为说明性示例，请考虑从年度北美鸟类繁殖调查（BBS，参见 Robbins、Bystrak 和 Geissler 1986 ^[17]）收集的数据。在每年 5 月和 6 月进行的这项调查中，志愿观测员穿越了 39.2 公里长的路边采样路线，每条路线包含 50 个站点。在每一站，观测员记录在三分钟内看到和听到的鸟类数量（按物种分类）。北美有数千条 BBS 路由。我们重点关注 2007 年观测到的密苏里州 45 条航线中的哀鸽 (Zenaida macroura) 数量，如 图 7.4 所示。给定 BBS 路线上分配给路线质心空间位置的鸽子总数（在 50 个停靠点上汇总），我们的目标是制作该州内鸽子相对丰度的地图，并描述与相关的不确定性这些相对丰度的预测。此类地图用于研究鸟类/栖息地关系以及物种范围。

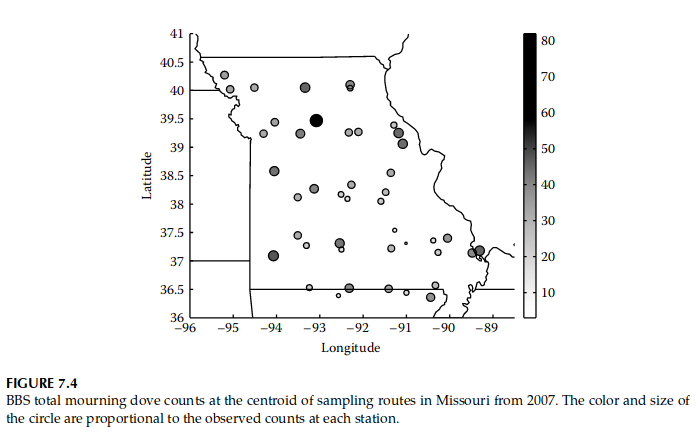
遵循前面描述的分层广义线性空间建模框架，我们首先指定质心位置 $\mathbf{s}_i$ 和 $Y(\mathbf{s}_i )$ 处的鸽子相对丰度（计数）的泊松数据模型，条件是泊松均值 $\lambda(\mathbf{s}_i )$ :

$$Y(\mathbf{s}_i )| \lambda(\mathbf{s}_i ) \stackrel{ind} \sim \operatorname{ Poisson}(\lambda(\mathbf{s}_i )),\quad i= 1,\ldots ,m \tag{7.19}$$

请注意，我们假设以空间相关的平均过程 ( $\lambda$ ) 为条件，BBS 计数是独立的。如果在多条路线上对同一只鸟进行计数，虽然在技术上可能违反这种独立性假设，但考虑到 BBS 采样协议的性质，这不太可能（例如，Robbins 等，1986 ^[17]）。鉴于我们预计由于鸟类隐栖息地偏好的空间依赖性而导致计数依赖，我们采用高斯空间过程模型来描述 $\lambda(\mathbf{s}_i)$ 的空间变化并使用指定对数链接函数：

$$\log( \lambda(\mathbf{s}_i )) = \beta + \eta(\mathbf{s}_i )$$

其中 $\beta$ 是均值，假设在空间上是常数，它可以被推广以适应有趣的协变量，而 $\eta(\mathbf{s}_i )$ 是隐的空间过程。具体而言， $\eta(\mathbf{s}_i )$ 是均值为 $0$ 、方差为 $\sigma^2_{\eta}$ 且相关函数为 $r (\mathbf{s}_i , \mathbf{s}_j ; \phi)$ 的高斯函数。像往常一样，人们可能会考虑许多不同的相关模型。鉴于我们关注的地理区域相对较小，我们将 $r_{\eta}(\mathbf{s}_i , \mathbf{s}_j ; \phi)$ 指定为单参数各向同性指数模型： $r_{\eta}(\mathbf{s}_i , \mathbf{s}_j ; \phi) = \exp(− \|\mathbf{s}_i − \mathbf{s}_j \|/ \phi)$ 其中 $\phi$ 控制随着位点之间距离的增加相关性的衰减率。请注意，在这种情况下，我们不包括额外的小规模可变性过程 $\varepsilon$ 。有关包含此类术语的 BBS 计数模型的示例，请参见 Wikle (2002 ^[23]) 以及 Royle 和 Wikle (2005 ^[20])。他们包含该术语的主要原因是他们在一个网格上进行预测，其中有多个 BBS 计数与特定网格位置相关联，从而在小尺度上提供足够的复制来估计与 $\varepsilon$ 相关的参数。此外，他们需要一种非常有效的估计和预测算法，因为他们正在考虑对美国大陆进行预测，并且可以利用模型中具有额外误差项的好处，如前所述。

参数 $\beta$ 、$\sigma^2_{\eta}$ 和 $\phi$ 的估计、位置网格处 $\eta(\mathbf{s})$ 的预测以及这些位置处 $Y(\mathbf{s})$ 的预测是在贝叶斯框架内使用 MCMC 技术进行的（例如，参见 Diggle 等，1998 ^[8] ；Wikle，2002 ^[23] ；Banerjee 等，2004 ^[1] ）。特别是，我们使用了 geoRglm 包，如 Diggle 和 Ribeiro (2007) 中所述。在这种情况下，我们假设程序默认的 $\beta$ 的先验平坦和 $\sigma^2_{\eta}$ 的默认统一先验。对于空间依赖参数，我们考虑了 $0$ 到 $1.7$ 之间的离散统一先验，增量为 $0.005$ 。 $1.7$ 的上限是由实际范围决定的，对于指数模型来说，它是 $3\phi$ ，我们假设在我们的有限域内，该范围的合理上限约为 $5$ 度，这意味着 $\phi$ 的上限接近 $1.7$。 图 7.5 显示了模型参数的后验分布和相关先验样本的直方图。请注意，在每种情况下似乎都存在贝叶斯学习。

图 7.6 的左面板显示了一张地图，显示了点网格上预测的 BBS 相对丰度（鸟类数量）的中位数。在这种情况下，预测位置实际上是网格框中心指定的一个点。在这种情况下，网格框被填充，仅用于说明目的，因为我们没有预测与我们的数据（假设）不同的支持。请注意这些预测中明显的相对大规模的空间依赖性。此外，我们注意到该州东南部较低的预测相对丰度对应于密苏里奥扎克山脉的较高海拔。不确定性通过基于 $95\%$ 预测区间长度四分之一的稳健方法进行量化。这显示在 图 7.6 的右侧面板中。这些地图中明显的主要特征是预测的相对丰度（鸟类数量）与其不确定性之间的密切关系——泊松框架内建模的结果。此外，请注意在密苏里州以外有不少预测位置，这些位置显然是外推位置。如果我们真的对当前分析的这些区域感兴趣，我们将使用来自与密苏里州接壤的州的路线的 BBS 计数。显然，如果没有这样的观测，我们预计这些位置的预测会有很大的不确定性，这已通过预测不确定性图得到验证。

7.5 讨论

本章概述了一个通用的层次框架，可以促进复杂空间过程的建模。该框架的主要优点是它允许将复杂的数据集分解为三个主要部分，所有这些部分都通过简单的概率规则联系起来。也就是说，有一个以真实过程和相关参数为条件的数据模型，一个以不同参数为条件的过程模型，最后是参数模型。这种层次划分可以在每个阶段产生相对简单的模型，但当结合起来时，描述了一个非常复杂的联合数据、过程和参数分布。除了考虑每个阶段的不确定性外，这种方法还有助于容纳多个数据集、多个过程和复杂的参数结构以及科学信息的包含。分层模型通常在贝叶斯范式中构建，估计和预测通常基于蒙特卡罗方法。

在空间模型的背景下，分层方法在传统高斯数据、地统计设置以及非高斯数据、广义线性混合空间模型框架中得到了证明。这些分层模型的主要区别在于数据阶段，因为它们都依赖于空间随机过程的条件来诱导观测中的空间依赖性。此外，还有与计算问题相对应的差异。例如，分析边缘化可以促进高斯数据模型的估计和预测，但非高斯数据模型不允许这种边缘化。对于这两种类型的模型，计算问题可以建议方差分量和空间相关参数的特定参数化。

尽管在 第 7.3 节 和 第 7.4 节 中简要讨论了参数化和先验选择的几种方法，但对于分层空间模型而言，这些选择并不总是那么容易。例如，即使在简单的（非空间）分层线性混合模型中，方差参数的先验分布选择也可能非常棘手（例如，参见 Browne 和 Draper，2006 ^[5] ，以及 Gelman，2006 ^[12] 的讨论等）。经验表明，这个问题因添加空间相关过程而变得复杂。最重要的是，在做出这些选择时必须非常小心，无论是使用相对常见的统计软件，还是编写特定问题的程序。尽管已经完成了一些工作来寻找空间过程的 “客观” 先验（例如，Berger、De Oliveira 和 Sanso，2001 ^[3] ），但这些并不总是适用于更大层次框架中的子组件。

另一种思想流派认为，人们通常对是否存在空间依赖性有一些概念（至少对于有观测的过程），因此在这些情况下使用更多信息先验是合理的。当然，必须注意所选择的先验（无论它们是否 “提供信息” ）相对于感兴趣的过程和数据具有意义。例如，用于哀鸽计数的分层模型的简单模拟表明，当 $\beta$ （对应于均值的对数）远远超出大约 $3$ 到 $4$ 的范围时，模拟的计数很快变得不切实际。同样，模拟的当过程方差 $\sigma^2_{\eta}$ 远远超出大约 $0.05$ 到 $2$ 的范围时，计数是非常不现实的。相比之下，模拟计数对空间相关参数 $\phi$ 的敏感度并不高。那么一个自然的问题是，为这些参数选择的所谓 “模糊” 先验（回想一下，我们选择先验 $\beta \sim N(0, 100)$ ）是否合理，因为它们将质量分配给永远无法给出的参数空间部分一个有意义的模型？使用这种预测结果驱动的、基于科学的方法来进行先验启发并没有被所有贝叶斯统计学家普遍接受为最佳贝叶斯程序，但它提供了一个很好的 “现实检查” 。有关贝叶斯模型中先验的更多有趣讨论（请参阅 Berger (2006 ^[2]) 和 Goldstein (2006 ^[14]) 以及相关讨论）。

最后，当考虑非常复杂的过程时，层次建模的真正力量会更加明显（并且先验启发通常更为关键）。在这种情况下，此处讨论的层次空间模型可能是某些较大层次结构的相对较小的组成部分。例如，在多变量时空建模问题中，空间过程的演化参数可能由一组空间相关参数表示，而这些参数可能与其他过程的空间参数相关等。似然是无限的，算法开发和优先选择问题很多。回答科学问题并在考虑此类情况下的不确定性的同时做出预测的能力正在增加高级统计建模在广泛学科中的实用性。

参考文献

• [1] Banerjee, S., Carlin, B.P., and A.E. Gelfand (2004). Hierarchical Modeling and Analysis for Spatial Data. Boca Raton, FL: Chapman & Hall/CRC. 452 pp.
• [2] Berger, J. (2006). The case for objective Bayesian analysis. Bayesian Analysis, 1, 385–402.
• [3] Berger, J., De Oliveira, V., and Sanso, B. (2001). Objective Bayesian analysis of spatially correlated data. Journal of the American Statistical Association, 96, 1361–1374.
• [4] Berliner, L.M. (1996). Hierarchical Bayesian time series models. In Maximum Entropy and Bayesian Methods, K. Hanson and R. Silver, Eds., Kluwer Academic Publishers, Dordrecht, the Netherlands, 15–22.
• [5] Browne, W.J. and Draper, D. (2006). A comparison of Bayesian and likelihood-based methods for fitting multilevel models. Bayesian Analysis, 1, 473–514.
• [6] Christensen, O.F., Roberts, G.O., and Sköold, M. (2006). Robust Markov chain Monte Carlo methods for spatial generalized linear mixed models. Journal of Computational and Graphical Statistics, 15, 1–17.
• [7] Diggle, P.J. and Ribeiro Jr., P.J. (2007). Model-Based Geostatistics. Springer Science+Business Media, New York, 228 pp.
• [8] Diggle, P.J., Tawn, J.A., and Moyeed, R.A. (1998). Model-based geostatistics (with discussion). Applied Statistics, 47, 299–350.
• [9] Gelfand, A.E. and Smith, A.F.M. (1990). Sampling based approaches to calculating marginal densities. Journal of the American Statistical Association, 85, 398–409.
• [10] Gelfand, A.E., Sahu, S.K., and Carlin, B.P. (1995). Efficient parameterization for normal linear mixed models. Biometrika, 82, 479–488.
• [11] Gelfand, A.E., Zhu, L., and Carlin, B.P. (2001). On the change of support problem for spatial-temporal data. Biostatistics, 2, 31–45.
• [12] Gelman, A. (2006). Prior distributions for variance parameters in hierarchical models. Bayesian Analysis, 1, 515–533.
• [13] Gelman, A., Carlin, J.B., Stern, H.S., and Rubin, D.B. (2004). Bayesian Data Analysis, 2nd ed. Chapman & Hall/CRC. Boca Raton, FL. 668 pp.
• [14] Goldstein, M. (2006). Subjective Bayesian analysis: Principles and practice. Bayesian Analysis, 1, 403420.
• [15] McCulloch, C.E. and Searle, S.R. (2001) Generalized, Linear and Mixed Models. John Wiley & Sons. New York. 325 pp.
• [16] Palacios, M.B. and Steel, M.F.J. (2006). Non-Gaussian Bayesian geostatistical modeling. Journal of the American Statistical Association, 101, 604–618.
• [17] Robbins, C.S., Bystrak, D.A., and Geissler, P.H. (1986). The Breeding Bird Survey: Its First Fifteen Years, 1965–1979. USDOI, Fish and Wildlife Service Resource Publication 157. Washington, D.C.
• [18] Robert, C.P. and Casella, G. (2004). Monte Carlo Statistical Methods, 2nd ed. Springer Science+Business Media, New York, 645 pp.
• [19] Royle, J.A. and Berliner, L.M. (1999). A hierarchical approach to multivariate spatial modeling and prediction. Journal of Agricultural, Biological, and Environmental Statistics, 4, 29–56.
• [20] Royle, J.A. and Wikle, C.K. (2005). Efficient statistical mapping of avian count data. Environmental and Ecological Statistics, 12, 225–243.
• [21] Schabenberger, O. and Pierce, F.J. (2002). Contemporary Statistical Models for the Plant and Soil Sciences. Taylor & Francis. Boca Raton, FL.
• [22] Verbeke, G. and Molenberghs, G. (2000). Linear Mixed Models for Longitudinal Data. Springer-Verlag. New York. 568 pp.
• [23] Wikle, C.K. (2002). Spatial modeling of count data: A case study in modeling breeding bird survey data on large spatial domains. In Spatial Cluster Modeling. A. Lawson and D. Denison, eds. Chapman & Hall/CRC, Boca Raton, FL. 199–209.
• [24] Wikle, C.K. (2003). Hierarchical models in environmental science. International Statistical Review, 71, 181–199.
• [25] Wikle, C.K. and Berliner, L.M. (2005). Combining information across spatial scales. Technometrics, 47, 80–91.
• [26] Wikle, C.K., Berliner, L.M., and Cressie, N. (1998). Hierarchical Bayesian space-time models. Journal of Environmental and Ecological Statistics, 5, 117–154.
• [27] Wikle, C.K., Milliff, R.F., Nychka, D., and Berliner, L.M. (2001). Spatiotemporal hierarchical Bayesian modeling: Tropical ocean surface winds. Journal of the American Statistical Association, 96, 382397.
• [28] Yan, J., Cowles, M., Wang, S., and Armstrong, M. (2007). Parallelizing MCMC for Bayesian spatialtemporal geostatistical models. Statistics and Computing, 17, 323–335.
• [29] Zhang, H.Z. (2004). Inconsistent estimation and asymptotically equal interpolations in model-based geostatistics. Journal of the American Statistical Association, 99, 250–261.