GeoAI 中的位置编码：方法和应用

【阅读建议】 本文是空间位置嵌入的第一篇比较全面的综述，涉及新概念、新方法和未来可能的新应用，比较有想象空间。但阅读后感觉将必要性简单地表述为机器学习的需要，似乎并不充分（第 2 节）；另外该概念到底带来了那些提升、对未来哪些冲击、影响和改变，似乎可以更进一步提炼，目前尚难以感觉到值得深入研究的价值。

【原文摘要】 地球科学对人工智能模型的共同需求，是在潜在的嵌入空间中表示点、线、多边形、网络、栅格等多种类型的空间数据，以便能够很容易地将这些数据融入到深度学习模型中去。一个基本做法是通过编码过程将位置转换到嵌入空间中，而这种嵌入表示对于下游机器学习模型（例如支持向量机和神经网络）来说是学习友好的，我们将此过程称为位置编码。目前，对于位置编码的概念、潜在应用以及需要解决的关键挑战，尚缺乏系统的回顾，而本文旨在填补这一空白。本文首先提供了位置编码的形式化定义，并从机器学习角度讨论了位置编码对于 GeoAI 研究的必要性，然后对位置编码研究的现状进行了较为全面地调查和讨论。依据输入和编码方法，我们将位置编码模型分为了不同类别，并根据其是否参数模型、多尺度性、距离保持和方向感知等性质进行了比较。我们证明了现有位置编码模型可以在一个共享的形式化框架下实现统一。文中还讨论了位置编码对不同类型空间数据的应用。最后，指出了位置编码研究中需要在未来解决的几个挑战。

【引文信息】 Gengchen Mai, Krzysztof Janowicz,Yingjie Hu, Song Gao, Bo Yan, Rui Zhu, Ling Cai, Ni Lao. A review of location encoding for GeoAI: methods and applications. International Journal of Geographical Information Science, 2021

【Eprint】 arXiv:2111.04006

1 背景和动机

新型深度学习和表征学习技术的快速发展以及多样化、大规模地理空间数据的日益普及，推动了地理空间人工智能 (GeoAI) 研究的实质性发展 ^{[69][15][58][32]}，其中包括广泛且具有挑战性的任务，例如地形特征检测和提取^[41]、土地利用分类^[94]、城市环境导航^[55]、图像地理定位 ^[82][31]、地名识别和消歧 ^[16][80]、 地理知识图谱补全和摘要 ^[62][88]、流量预测 ^[42] 等。 尽管这些模型在设计上非常不同，但它们有一个共同特点：**需要在潜在的嵌入空间中表示（或编码）不同类型的空间数据**，例如：点（如兴趣点 (POI)）、线（如轨迹）、多边形（如行政区划）、图/网络（如交通网络）或栅格（如卫星图像），以便这些数据能够被机器学习模型（例如深度神经网络、支持向量机）使用。对于栅格数据，此编码过程似乎很容易理解，因为常规 grid 结构可以直接用现有的卷积神经网络 ^[37] 来处理。但对于矢量数据（例如点集、线、多边形和网络），其表示问题变得更加复杂。这些数据具有更不规则的空间组织格式，而位置、距离和方向等在现有神经网络中没有直接对应的概念，并且为不规则结构的数据设计神经网络运算（例如卷积）也并非易事^[76]。 前期有些工作执行数据转换运算，将底层空间数据转换为现有神经网络模块可以处理的格式^[81]。然而，这种转换过程往往会导致信息丢失。例如，许多关于点云分类和分割的早期研究，首先将 `3D` 点云转换为体积表示（如体素化的形状）^[54][60]，或将它们渲染为 `2D` 图像 ^[70][60]。然后，再将 `3D` 或 `2D` 卷积神经网络应用于这些转换后的数据，执行后续分类或分割等任务。这些做法有一个主要限制：为体积表示选择合适的空间分辨率是一项挑战^[59] ，更精细的空间分辨率会导致数据稀疏和更高的计算成本，而更粗的空间分辨率会提供较差的预测结果。本作作者认为：**执行此类数据转换的原因是缺乏在深度神经网络中直接处理矢量数据的方法**。 另一种研究思路是直接对上述空间数据模型进行编码（ Encoding ）。其中第一步是将普遍使用的点位置转换到高维度嵌入空间中，生成嵌入编码，然后就可以在下游神经网络模块中使用。这就是**位置编码（Location Encoding）**的思想。 位置编码 ^{[47][51][93][48][22][87][14]} 指一个基于神经网络的**编码过程**，该过程将一个点/位置表示为一个高维向量/嵌入，而这种高维向量/嵌入不仅能够保留一定的空间信息（如距离、方向等），而且对下游机器学习模型（如神经网络、支持向量机等）而言还是**学习友好**的。所谓学习友好，是指下游模型不需要非常复杂，也不需要大量训练数据来防止过拟合。此编码过程输出的结果被称为**位置嵌入（ Location Embedding ）**，而对应的神经网络架构被称为**位置编码器（ Location Encoder ）** 。位置编码器应当是一种通用模型，可以与下游任务中的不同 GeoAI 模型相结合。 > 注：作者在此处似乎有意表达点和位置并不相同。 `点（point）` 是数学上的抽象定义，通常指一个更大整体中的一个元素，在本文中侧重于物理空间中的 `点`；而 `位置（location）` 是地理名词，除了表达物理空间概念外，更突出人类意识中的空间语义，例如物理空间存在的某个`place`。When used as nouns, location means a particular point or place in physical space, whereas point means an individual element in a larger whole. `图 1` 是位置编码过程的示意图。我们将 “基于位置的物种分类” 作为下游任务的示例，其目的是根据给定位置 $\mathbf{x}$ 来预测物种 $y$。训练目标是学习一个条件分布 $P(y|\mathbf{x})$，即在给定 $\mathbf{x}$ 时，观测到 $y$ 的概率，本例假设这是一种高度非线性的情况。 可以将位置编码的思想理解为一个 *特征分解过程* ，即将位置 $\mathbf{x}$（如经纬度表示的二维向量）解构成一个对学习友好的高维向量（例如，$100$ 维的向量），使得高度非线性的分布 $P(y|\mathbf{x})$ 在高维嵌入空间中，能够通过相对简单的学习器 $M()$ 来学习，例如`线性支持向量机`或`浅层神经网络模型`。 位置编码器架构的潜在好处是： - 更简单的学习器以及更少的训练数据； - 利用无监督训练来更好地学习位置表示的可能性。 最近，位置编码的有效性已在多个 GeoAI 任务中得到证明，包括地理感知图像分类 ^{[91][14][47][51]}、POI 分类^[51]、地点标注 ^[91]、轨迹预测 ^[87][91]、位置隐私保护 ^[63]、地理问答 ^[52][48]、3D 蛋白质分布重建 ^[93]、点云分类和分割 ^[59][61][44] 等。尽管有这些成功的案例，但仍然缺乏对此类主题的系统评估。本文通过对不同位置编码模型进行比较调查来填补这一空白。我们给出了一个通用的形式化框架，它统一了几乎所有现有的位置编码方法。 值得一提的是：本文讨论的位置编码不同于传统位置编码系统（即 [地理编码系统](https://gogeomatics.ca/location-encoding-systems-could-geographic-coordinates-be-replaced-and-at-what-cost)），后者使用 `Geohash` 、 `Open Location Code` 、 `what3words` 等分块位置代码将地理坐标转换为编码形式，旨在支持导航和空间索引，而本文展示的（神经）位置编码器则主要用于支持下游机器学习模型。 本文的主要贡献如下： （1）虽然已有多个位置编码成果，但设计这样一个模型的必要性尚不清楚。在本文工作中，我们正式定义了位置编码问题，并从机器学习的角度讨论了其必要性。 （2）对现有位置编码研究进行了系统回顾，提出了位置编码器的分类系统，所有模型都在统一框架下进行了重新制定。这使我们能够识别不同位置编码模型之间的共性和差异。据我们所知，这是对此类主题的第一次系统性回顾。 （3）将位置编码的思想扩展到了对线、多边形、图和栅格等更广泛类型空间数据的编码，讨论了可能的解决方案和挑战。 （4）为了强调位置编码的普遍适用性，我们讨论了它在不同地球科学领域的潜在应用，希望这些讨论能够开辟新的研究领域。 本文其余部分结构如下： - 在`第 2 节`中，介绍了位置编码的正式定义。 - 在`第 3 节`中，讨论位置编码的必要性。 - 在`第 4 节`中，提供了一个通用框架来理解各种位置编码，并调查一系列代表性工作。 - 在`第 5 节`中，讨论了如何将位置编码应用于不同类型的空间数据。 - 在`第 6 节`中，总结了本文主要工作并讨论了未来研究方向。  > 图 1：位置编码示意图。使用基于位置的物种分类作为下游任务的示例。二维空间中的 $20$ 个点代表物种出现的观测记录。每次出现都可以写成 $p_i = (\mathbf{x}_i,y_i)$ ，其中 $\mathbf{x}_i$ 表示二维空间中的位置， $y_i$ 表示相应的物种类型，即观测标签。 $\mathcal{N}(\mathbf{x}_i)$ 表示 $\mathbf{x}_i$ 的空间邻域。位置编码器 $Enc(\cdot)$ 将位置 $\mathbf{x}_i$ 作为输入，将位置嵌入作为高维向量输出。这种位置嵌入被进一步送入下游的神经网络模型 $M()$ 中，以进行物种预测。整个模型架构支持以监督学习方式进行端到端的训练。 # 2 概念定义 ## 2.1 位置编码的定义 **定义 2.1（位置编码 Location Encoding）**。 给定一组点 $\mathcal{P}=\{p_i\}$，例如，传感器位置、物种出现位置等，其中每个点 $p_i=(\mathbf{x}_i,\mathbf{v}_i)$ 与 $L$ 维空间（ $L=2,3$ ）中的位置 $\mathbf{x}_i \in \mathbb{R}^L$ （如传感器位置）和属性 $\mathbf{v}_i \in \mathbb{R}^E$ （如空气质量测量值）相关联。我们将位置编码器定义为由 $\theta$ 参数化的函数 $Enc^{(\mathcal{P},\theta)}(\mathbf{x}) : \mathbb{R}^L \rightarrow \mathbb{R}^d (L \ll d)$，它将 $L$ 维空间中的任何坐标 $\mathbf{x}$ 映射成 $d$ 维向量表示。上述编码过程被称为**位置编码 （Location Encoding）**，其结果被称为**位置嵌入（Location Embedding）**。 该定义中，$Enc^{(\mathcal{P},\theta)}(\mathbf{x})$ 表示 $\mathbf{x}$ 的编码结果可能依赖于 $\mathcal{P}$ 中的其他位置。当 $Enc^{(\mathcal{P},\theta)}(\mathbf{x})$ 独立于 $\mathcal{P}$ 中的其他点时，也可以将其简化为 $Enc^{(\theta)}(\mathbf{x})$。请注意，有时位置编码器的输入可以同时包含位置 $\mathbf{x}$ 和属性 $\mathbf{v}$，此时可以将编码函数表示为 $Enc^{(\mathcal{P},\theta)}(\mathbf{x},\mathbf{v}) ：\mathbb {R}^{L+E} \rightarrow \mathbb{R}^d$ 。 `图 1` 说明了`定义 2.1` 中位置编码的思想。采用 $20$ 个二维点作为点集 $\mathcal{P}=\{p_i\}$ 的示例，其中 $L=2$ 和 $n= \mid \mathcal{P} \mid =20$ 。注意 $Enc^{(\mathcal{P},\theta)}(\mathbf{x})$ 不仅可以用于编码全局位置 $\mathbf{x}$，还可以用于编码两个空间位置之间的关系，即空间相似向量 $\Delta_{AB}=\mathbf{x}_A - \mathbf{x}_B$ 。 我们可能会问的一个问题是位置编码器是否可以在编码过程之后保留空间信息，例如距离和方向信息。从空间信息保持的角度来看，我们期望位置编码器具有两个性质：**距离保持性**和**方向感知性**。 ## 2.2 距离保持性 **性质 2.1（距离保持性）**。 距离保持性要求两个邻近的位置具有相似的位置嵌入。更具体地说，给定任何一对位置 $(\mathbf{x}_A,\mathbf{x}_B)$，当 $\mathbf{x}_A$ 与 $\mathbf{x}_B$ 之间的空间距离（ 即 $\| \mathbf{x}_A - \mathbf{x}_B \|$ ）增加时，它们在嵌入空间中对应的位置嵌入之间的内积（可理解为相似性） $\langle Enc^{(\mathcal{P },\theta)}(\mathbf{x}_A),Enc^{(\mathcal{P},\theta)}(\mathbf{x}_B)\rangle$ 会单调递减。 `性质 2.1` 可以看作是 `Tobler 第一地理定律` ^[73] 在位置编码中的体现。多个已有的位置编码研究工作已经采用了距离保持要求。例如，`Gao 等人 ` ^[22] 提出了一个可学习的位置表示模型 $v(\mathbf{x})$，它由向量矩阵乘法、放大的局部等势、全局邻接核三个子模型组成。全局邻接核假设 $\langle v(\mathbf{x}_a),v(\mathbf{x}_b) \rangle = (Kd)f(\| \mathbf{x}_a - \mathbf{x}_b \|)$，其中 $K, d$ 是预定义常数，$f(r)$ 是随着 $r$ 增加而单调减少的邻接核。可以看出，该模型满足`性质 2.1`。`Mai 等人` ^[51] 也表明，他们提出的多尺度位置编码器具有相似的距离保持能力。 ## 2.3 方向感知性 **性质 2.2（方向感知性）**。 指向相似方向的位置比指向不同方向的位置具有（相对）更相似的位置嵌入。更具体地说，如 `图 2` 所示，给定 $\mathbf{x}_O$ 作为参考点，$y$ 轴作为全局的北方向，$\mathbf{x}_A$ 、$\mathbf{x}_B$ 和 $\mathbf{x}_C$ 在以 $\mathbf{x}_O$ 为中心的同一个圆上，因此到 $\mathbf{x}_O$ 的距离相同。 $\mathbf{x}_A$ 和 $\mathbf{x}_O$ 之间的相对空间关系定义为向量 $\Delta_{AO} = \mathbf{x}_A - \mathbf{x}_O$， $\Delta_{AO}$ 的方向，记为 $\angle_{AO}$ ，定义为 $y$ 轴与 $\Delta_{AO}$ 之间的顺时针角度。 同样的逻辑适用于 $\mathbf{x}_B$ 和 $\mathbf{x}_C$。我们说位置编码器是方向感知的，如果它满足以下性质：内积 $\langle Enc^{(\mathcal{P},\theta)}(\Delta_{AO}),Enc^{(\mathcal{ P},\theta)}(\Delta_{BO}) \rangle < \langle Enc^{(\mathcal{P},\theta)}(\Delta_{AO}),Enc^{(\mathcal{P} ,\theta)}(\Delta_{CO})\rangle$ , 如果 $|\angle \Delta_{AO} - \angle \Delta_{BO}| < |\angle \Delta_{AO} - \angle \Delta_{CO}|$。 `性质 2.2` 反映了`广义地理学第一定律` ^[98]，其中包括方向相似性的考虑。在本文中，当方向改变时，如果位置嵌入只保留了空间邻近性但忽略了方差的变化，则我们称位置编码器为具有**各向同性**的位置编码器。当各向同性假设不再成立时，我们需要开发方向感知的、所谓的**各向异性**位置编码器。事实上，在传统的空间分析中，各向同性是大多数时候的“默认”假设。尽管已经开发了 `定向克里金法` ^[72]、`各向异性聚类` ^[49] 等许多具有各向异性的地理空间分析技术，但方向问题大多仍然停留在事后考虑的水平上 ^[98]。在当前的位置编码研究或一般性的 GeoAI 研究中也可以看到类似的情况。 与具有距离保持性的位置编码器研究相比，有关使位置编码器具备方向感知能力的研究工作要少得多。`Mai 等人` ^[51] 的经验表明，其开发的多尺度位置编码器以及许多基线模型都是方向感知的。但这些只是他们对其位置编码响应图进行可视化分析时的副产品（即经验感觉），并没有提供理论证明。据我们所知，目前还没有旨在有意开发方向感知位置编码器的研究。  > 图 2：位置编码的方向感知性示意图 除了上述两种空间信息保持的性质外，位置编码器 $Enc^{(\mathcal{P},\theta)}()$ 还应考察以下两个性质，以保证其通用性。 ## 2.4 归纳性 **性质 2.3（归纳学习方法）**。 位置编码器 $Enc^{(\mathcal{P},\theta)}()$ 是一种归纳学习方法，也就是说不依赖于样本而存在，即便某个位置没有出现在训练集中，经过预训练的位置编码器也能够用于对其编码，而无需再次训练。 `性质 2.3` 使得 $Enc^{(\mathcal{P},\theta)}()$ 不同于许多现有的基于传导的位置表示学习方法，例如 `Location2Vec` ^[97]、 `POI2Vec` ^[20]，以及 ^[34]。例如， ^[34] 将一组 GeoNames 位置转换为 $k$ 近邻图，其中所有位置（即节点）通过距离加权的边链接到邻近的位置，并采用一种基于随机游走的方法来学习每个位置的图嵌入。该方法本质上是一种传导学习模型：当将新位置添加到训练集中时，图会发生改变，因此必须重新训练整个模型以获得新的位置嵌入。 ## 2.5 任务无关性 **性质 2.4（任务独立性）**。 位置编码器 $Enc^{(\mathcal{P},\theta)}()$ 是任务独立的或任务不可知的，即相同的模型架构无需任何修改即可用于不同的下游任务。 `性质 2.4` 将 $Enc^{(\mathcal{P},\theta)}()$ 与一些现有的任务相关位置表示方法区分开来。例如， `Location2Vec` ^[97] 和 `POI2Vec` ^[20] 通过采用 `Word2Vec` 风格的训练目标来学习基于轨迹的位置（例如，手机基站、POI）的嵌入。这种位置表示难以迁移到人类移动性之外的其他任务中。同样，`Gao 等人` ^[23] 将研究区域离散化为 $N \times N$ 的网格，并通过基于长短期记忆 (LSTM) 的人工代理在研究区域中的导航，来学习每个位置的嵌入。学习到的位置嵌入仅用于模拟目的，而很难用于其他地理空间任务。 ## 2.6 参数模型 **性质 2.5（参数模型）**。 参数模型具有有限的参数集合 $\theta$ 。参数模型不是很灵活，但模型复杂度有界。相反，非参数模型假设数据分布不能用数量有限的参数集 $\theta$ 来定义，而且 $\theta$ 的数量可以随着数据量的增长而增长 ^[66]。因此，非参数模型更灵活，但模型复杂度是无界的。 尽管我们希望位置编码器具有`性质 2.1`、`性质 2.2` 和 `性质 2.5`，但并非所有位置编码器都能同时具有这三项性质，参见即将在`第 4 节`中讨论的模型，其各种性质的详细对比见 `表 1`。不过经验主义的观察告诉我们，似乎所有的位置编码器都满足`性质 2.3` 和 `性质 2.4`，所以我们不会为每个模型特别讨论这两个性质。 为简单起见，我们将使用缩略符号 $Enc()$ 和 $Enc^{(\mathcal{P})}()$ 来分别表示 $Enc^{(\theta)}()$ 和 $Enc^{(\mathcal{ P},\theta)}()$ 。 > 表 1：位置编码方法的概述。单点位置编码器 $Enc(\mathbf{x})$ 和聚合位置编码器 $Enc^{(\mathcal{P})}(\mathbf{x})$ 根据 $PE(\mathbf{x})$ 或 $N(\mathbf{x})$ 进一步做了分类（见图 1）。 $(M)$ 表示多尺度表征。$\star$ 表示所引用原始模型的通用版本。我们考虑了位置编码器的多个指标：1）$L$：$\mathcal{P}$ 的空间维度； 2）$Parametric$：位置编码器是参数模型（Yes）还是非参数模型（No）； 3）$Mul.S.$：位置编码是否支持多尺度 4) $Dist.P.$：位置编码器是否具有距离保持性； 5) $Dir.A.$：位置编码器是否具有方向感知性。对于 $Dist.P.$ 和 $Dir.A.$ ，`Yes` 或 `No` 表示该性质是否可以通过经验主义证明（ 通过训练后位置编码器的响应图来判断 ^[51] ）， `-` 表示性质未知，`Yes+` 表示该性质在理论和经验上都可以证明。  # 3 GeoAI 中空间表征的重要性 在本节中，我们提出了将位置 $\mathbf{x} \in \mathbb{R}^L$ 嵌入到高维向量 $Enc^{(\mathcal{P},\theta)}(\mathbf{x}) \in \mathbb{R}^d$ 中的需求，这乍一看似乎违反直觉，但我们会从机器学习的角度来探讨这个问题。 统计机器学习的一个关键概念是**偏差-方差之间的权衡** ^[29]。 - 一方面，当一个学习系统需要从一个大的假设空间中选择某个特定假设时（例如为一个 $24$ 层的大型神经网络选择一组权重参数），这个学习系统可能足够灵活，以至于能够逼近几乎任何非线性分布（即低偏差）。但它需要大量训练数据来防止过拟合。这种情况被称为 “低偏差/高方差”。 - 另一方面，当假设空间受限时（例如，线性回归或单层神经网络之类的简单模型），这个学习系统几乎没有机会过拟合，但可能不适合对底层的数据分布进行充分建模，并导致在训练集和测试集上都表现出较低性能（即高偏差）。这种情况被称为 “低方差/高偏差”。 对于许多应用而言，数据分布是复杂且高度非线性的。大多数情况下，我们缺乏足够的领域知识，来设计一个同时具有低方差（有效模型复杂度）和低偏差（模型数据匹配的好）的模型。此外，有时我们可能更希望避免在模型设计中采用过多的领域知识，因为这会使生成的模型变得过于具有针对性。例如，植物物种的分布（ `图 1` 中的 $P(y \mid \mathbf{x})$ ）可能会受到多种地理空间因素和物种间交互作用的、高度不规律性的影响^[47]。 `核（平滑）方法`（如径向基函数）和`神经网络`（如前馈网络）是两种比较成功的、不需要太多领域知识的模型，而且都有自身完善的方法来控制模型的复杂度。 - 核方法更适合于低维输入数据，采用较低的模型复杂度对高度非线性的数据分布建模，但核方法需要在推断阶段存储核数据，内存使用效率不高。 - 神经网络具有更强的表示能力，意味着深度网络可以在无偏差的情况下逼近任意复杂的函数，但同时需要更多领域知识来进行模型设计以实现更低的方差和偏差。 从统计机器学习的角度来看，位置编码的主要目的是为下游任务生成**学习友好**的地理位置表示。所谓学习友好，是指下游模型不需要过于复杂或者需要大量训练样本即可完成任务。例如，位置编码过程可能会执行特征分解运算（$\mathbb{x} \in \mathbb{R}^L \rightarrow Enc^{(\mathcal{P},\theta)}(\mathbf{x}) \in \mathbb{R}^d$，其中 $L 图 3：位置编码如何为下游模型生成便于学习的地理位置表示。使用`图 1` 中相同的 $20$ 个点作为 $\mathcal{P}={p_i}$ 的示例。红点和蓝点表示它们分别属于两个不同的类别。 $M_1$ 和 $M_2$ 分别是在原始地理空间和位置嵌入空间中训练好的二元分类器示意图。 # 4 当前位置编码方法概览 在本节中，我们将全面回顾现有的位置编码技术。我们不是列举每个现有的位置编码方法，而是以自上而下的方式组织讨论，先根据`输入`和`操纵空间特征的方式`将位置编码模型分成不同的组。 - 根据输入，可以将现有的位置编码器分为两类： **单点位置编码器** $Enc(\mathbf{x})$ 和**聚合位置编码器** $Enc^{(\mathcal{P})}(\mathbf{x})$。 $Enc(\mathbf{x})$ 只考虑当前的点位置，而 $Enc^{(\mathcal{P})}(\mathbf{x})$ 则需要考虑其邻域 $\mathcal{N}(\mathbf{x}) \subseteq \mathcal{P}$ 中的其他点。 - 在`第 4.1 节`中，$Enc(\mathbf{x})$ 被进一步根据点位编码器 $PE(\mathbf{x})$ 的类型划分为子类别。 - 在`第 4.2 节`中，$Enc^{(\mathcal{P})}(\mathbf{x})$ 被进一步根据所使用的邻域 $\mathcal{N}(\mathbf{x})$ 不同而划分为子类别。 上述两大类位置编码模型的调查结果，汇总于`表 1`中。在 `4.3 节`中，我们将对不同模型做比较。 ## 4.1 单点位置编码器 $Env(\mathbf{x})$ 大多数现有的单点位置编码器，即 $Enc(x)$ ，都具有相似的结构 ^{[71][22][87][14][47][51][93][63]} ： $$ Enc(x) =NN(PE(\mathbf{x})) \tag{1} $$ 这里，$NN(\cdot) : \mathbb{R}^W \rightarrow \mathbb{R}^d$ 是一个可学习的神经网络组件，它将输入的点位嵌入（Position Embedding） $PE(\mathbf{x}) \in \mathbb{R}^W$ 映射到位置嵌入（Location Embedding ） $Enc(\mathbf{x}) \in \mathbb{R}^d$ 。 一种常见的做法是将 $NN(\cdot)$ 定义为多层感知机，而 `MacAodha` 等人 ^[47] 采用了更复杂的 $NN(\cdot)$，其中包括一个初始的`全连接层`，然后是一系列`残差块（Residual Blocks）`。 $NN(\cdot)$ 的目的是为位置编码器提供一个可学习的组件，它可以捕获输入位置和目标标签之间的复杂交互。 点位嵌入 $PE(\cdot)$ 是区分不同 $Enc(\mathbf{x})$ 的最重要的部分。通常，$PE(\cdot)$ 是一个将 $\mathbf{x}$ 转换为 $W$ 维向量的确定性函数。 $PE(\cdot)$ 的目的是实现位置特征的归一化 ^[14][47][63] 和/或特征分解 ^[51][93] ，以便输出的点位嵌入对 $NN(\cdot)$ 更友好。 在 `表 1` 中，我们根据 $PE(\cdot)$ 的不同将 $Enc(x)$ 进一步分为四个子类别：`基于离散化的位置编码器`、`直接位置编码器`、`正弦位置编码器`、`正弦多尺度位置编码器`。 ### 4.1.1 基于离散化的位置编码器 早期的研究者 ^[71] 认为 GPS 坐标是相当精确的位置测度，分类器很难使用。因此，他们没有使用坐标，取而代之，将整个研究区域离散化为网格瓦片，使用每个点所属的网格来指示其位置。 **定义 4.1（基于离散化的位置编码器）**。基于离散化的位置编码器将研究区域（例如地球表面）划分为规则区域单元，例如网格、六边形或三角形。$Enc_{discretize}(x) = NN(PE_{discretize}(x))$ ， 其中 $PE_{discretize }(\cdot)$ 通常是一个瓦片查找函数，它将 $\mathbf{x}$ 映射到一个指示其所属瓦片标识的独热向量。 #### Onehot-位置编码器 位置编码的早期工作实际上并没有特定于位置编码器的可学习组件。例如，Tang 等人 ^[71] 将研究区域（毗邻的美国）划分为 $M$ 个矩形网格。给定一个位置 $\mathbf{x}$（图像的地理标签），$PE_{onehot}(\mathbf{x}) \in \mathbb{R}^{M}$ 是一个独热向量，表示 $\mathbf{x}$ 落入了哪个网格，而 $\mathbf{NN}(\cdot)$ 则为恒等函数，即 $Enc_{onehot }(\mathbf{x })=\mathbf{NN}\left(PE_{onehot}(\mathbf{x})\right)=PE_{onehot }(\mathbf{x})$。 #### Tile-位置编码器（ Tile ） 后来 Mai 等人 ^[51] 引入了 Tile 作为一种 $Enc_{discretize}(\mathbf{x})$，该编码器使用可训练的位置嵌入矩阵作为 $NN(\cdot)$，这使得模型可以从无监督训练中受益。 虽然 $Enc_{discretize}(\mathbf{x})$ 在带有地理感知的图像分类等任务上显示出了有希望的结果，但它存在几个固有的局限： 1）每个瓦片嵌入都是单独训练的，瓦片之间的空间依赖性被忽略了，即该编码器不具有距离保持性； 2）只有一个固定的空间尺度，不能有效处理不同密度的点； 3）选择正确的离散化本身非常具有挑战性 ^[57][21]，错误的选择会显著地影响模型性能和效率 ^[39]。 上述问题存在一些可能的解决方案： - 对于`问题 1`，可以在损失函数中添加一个正则化项，以使附近的瓦片嵌入具有更高的余弦相似度。 - 对于`问题 2` 和 `问题 3`，可以采用自适应离散化 ^[82] 或多层级离散化策略 ^[38] ，使较深的层次（即较小的瓦片）用于较高的点密度区域，而较浅的层次（即较大的瓦片）用于稀疏区域。但更精细的空间划分或多级离散化意味着更多的瓦片和更多需要学习的参数，这很容易导致过拟合。 ### 4.1.2 直接定位编码器 最近，研究人员采用了一种相当简单的方法，将神经网络直接应用于（归一化的）坐标 ^[87][14][63]。 **定义 4.2（直接位置编码器）**。直接位置编码器定义为 $Enc_{direct}(\mathbf{x})=\mathbf{NN}\left(PE_{direct}(\mathbf{x}) \right)$ ，其中 $PE_{direct}(\mathbf{x})$ 通常是对输入位置特征 $\mathbf{x}$ 实施标准化或归一化的函数，而 $\mathbf{NN}( \cdot)$ 通常是一个多层感知机。 #### Direct-位置编码器 $Enc_{direct}(\mathbf{x})$ 模型有许多细微的变化。`Chu 等人` ^[14] 通过除法将输入的经度和纬度（即图像的 $\mathbf{x}=[\lambda, \phi]^{T}$）标准化为 $[-1,1)$ 范围内的恒定值。同样，在轨迹综合研究中，`Rao 等人` ^[63] 使用了一个 $PE_{direct}(\mathbf{x})$ ，其通过所有轨迹点的质心对每一个轨迹点坐标 $\mathbf{x}=[\lambda, \phi]^{T}$ 实施了标准化 。为了进行行人轨迹预测，`Xu 等人` ^[87] 还设计了一个简单的位置编码器，其 $PE_{direct}(\mathbf{x})$ 将 $\mathbf{x}$ 归一化到区间 $[0,1]$ 内。 如果没有特征分解的步骤，直接位置编码器模型通常无法捕获数据分布的精细细节，并且在特定任务上的预测准确性比 `tile-位置编码器` 差。 ### 4.1.3 正弦位置编码器 **定义 4.3（正弦位置编码器）**。正弦位置编码器定义为 $Enc_{sinu}(\mathbf{x})=\mathbf{NN}\left(PE_{sinu}(\mathbf{x})\right )$ 。其中 $PE_{sinu}(\mathbf{x})$ 是一个确定性函数，它通常在位置特征完成归一化之后， 对 $\mathbf{x}$ 实施正弦函数运算（例如 $\sin()$）。 #### Wrap-位置编码器 MacAodha 等人 ^[47] 开发了 $Enc_{wrap}(\mathbf{x})=\mathbf{NN}\left(PE_{sinu}(\mathbf{x})\right)$。它使用正弦函数包裹了地理坐标。在 `式 2` 中，经度 $\lambda$ 和纬度 $\phi$ 首先通过除以 $180^{\circ}$ 和 $90^{\circ}$ 被归一化至范围 $[-1,1]$，然后是输入到 $\sin (\pi x)$ 和 $\cos (\pi x)$ 函数中。 $$ PE_{wrap}(\mathbf{x})=\left[\sin \left(\pi \frac{\lambda}{180^{\circ}}\right), \cos \left( \pi \frac{\lambda}{180^{\circ}}\right), \sin \left(\pi \frac{\phi}{90^{\circ}}\right), \cos \left( \pi \frac{\phi}{90^{\circ}}\right)\right]，其中 \mathbf{x}=(\lambda, \phi) \tag{2} $$ 使用正弦函数的目的是将全球的地理坐标都包裹在内 ^[47]。这保证了经度 $\lambda_{1}=-180^{\circ}$ 和 $\lambda_{2}=180^{\circ}$ 具有相同的编码结果。但在纬度上存在问题。对于 $\phi_{1}=-90^{\circ}$ 和$\phi_{2}=90^{\circ}$，即南极和北极，存在编码结果相同的问题。此外，即使能够解决这个问题，Wrap-位置编码器依然不具备球面距离保持性。 ### 4.1.4 正弦多尺度位置编码器 到目前为止，我们讨论的所有位置编码器都存在一个限制：它们无法处理不均匀的点密度 ^[59] 或特征非常不同的若干分布的混合分布 ^[51]。例如，给定一组 POI，某些 POI 类型倾向于聚集在一起，例如夜总会、女装、餐馆，而其他 POI 类型则分布相当均匀，例如邮局、学校和消防局。同样，在物种出现方面，一些物种倾向于聚集在一起，如角马和斑马，而另外一些物种的个体则倾向于独行并保护自己的领地，如老虎和熊。这导致物种之间出现不同的空间分布模式。为了对这些空间分布进行联合建模，需要一种支持多尺度表示的位置编码方法。 受 Transformer 中位置编码架构的启发 ^[78]，研究人员通过使用不同频率的正弦函数开发了多尺度位置编码器 ^[51][93]。 **定义 4.4（正弦多尺度位置编码器）**。正弦多尺度位置编码器定义为 $Enc_{sinmul}(\mathbf{x})=\mathbf{NN}\left(PE_{sinmul}(\mathbf{x} )\right)$ 。其中 $PE_{sinmul}(\mathbf{x})$ 将 $\mathbf{x}$ 分解为具有不同频率的不同正弦函数的多尺度表示： $$ PE_{sinmul}(\mathbf{x})=\left[PE_{0}^{(S)}(\mathbf{x}) ; \ldots ; PE_{s}^{(S)}(\mathbf{x}) ; \ldots ; PE_{S-1}^{(S)}(\mathbf{x})\right] \tag{3} $$ 其中 $S$ 是尺度的总数。 $PE_{s}^{(S)}(\mathbf{x})$ 用于处理具有不同正弦函数的位置特征，正弦函数的频率由尺度 $s$ 决定。 #### Transformer-位置编码器 Zhong 等人 ^[93] 对 `Transformer` ^[78] 做了轻微改动，构造了一种新的点位置编码架构，并将其应用于高维数据点（例如： `3D` 笛卡尔坐标）。 **定义 4.5（基于 `Transformer` 的位置编码器）**。基于 `Transformer` 的位置编码器 $Enc_{TF}(\mathbf{x})=\mathbf{NN}\left(PE_{TF}(\mathbf{x})\right)$ 遵循`定义 4.4`。对于每个尺度 $s \in$ $\{0,1, \ldots, S-1\}$， 通过 `式 4` 定义了 $PE_{s}^{(S)}(\mathbf{x})=PE_{s}^{ TF}(\mathbf{x})$ ： $$ PE_{s}^{T F}(\mathbf{x})=\left[PE_{s, 1}^{T F}(\mathbf{x}) ; \ldots ; PE_{s, l}^{T F}(\mathbf{x}) ; \ldots ; PE_{s, L}^{T F}(\mathbf{x})\right] \tag{4a} $$ 其中： $$ PE_{s, l}^{TF}(\mathbf{x})=\left[\cos \left(\frac{2 \pi S \mathbf{x}^{[l]} }{S^{(s+1) / S}}\right) ; \sin \left(\frac{2 \pi S \mathbf{x}^{[l]}}{S^{(s+1) / S}}\right)\right], \forall l=1, 2, \ldots, L \tag{4b} $$ 这里，$\mathbf{x}^{[l]}$ 表示 $\mathbf{x}$ 的第 $l$ 维。 Zhong 等人 ^[93] 表明： $Enc_{TF}(\mathbf{x})$ 适用于无噪声数据，但对于噪声数据，需要排除 `式 3` 中前 $10 \%$ 最高频率分量（ 即最小的几个 $s$ )。这表明我们需要另一个参数来控制在正弦函数中考虑的最小尺度。这就是将在下面讨论的 `theory` 和 `grid` 编码器对 $\lambda_{\min }$ 的使用。 #### Theory-位置编码器 `Space2Vec` ^[51] 通过使用不同频率的正弦函数，引入 `theory` 作为 `2D` 多尺度位置编码器。 **定义 4.6（ theory 位置编码器）**。令 $\mathbf{a}_{1}=[1,0]^{T}, \mathbf{a}_{2}=$ $[-1 / 2, \sqrt{3} / 2]^{ T}, \mathbf{a}_{3}=[-1 / 2,-\sqrt{3} / 2]^{T} \in \mathbb{R}^{2}$ 是三个相互之间相差 $120^{\circ}$ 的单位向量。 $\lambda_{\min }, \lambda_{\max }$ 是最小和最大网格尺度，$s \in\{0,1, \ldots, S-1\}$ ， $PE_{s}^{ (S)}(\mathbf{x})=PE_{s}^{theory}(\mathbf{x})$ 遵循`定义 4.4`， 其中在每个尺度 $s \in\{0,1 , \ldots, S-1\}$ ，在 `式 5` 中定义了 $PE_{s}^{(S)}(\mathbf{x})=PE_{s}^{theory}(\mathbf{x})$ 。这里 $\langle\cdot, \cdot\rangle$ 表示向量内积。 $$ PE_{s}^{theory}(\mathbf{x}) =\left[PE_{s, 1}^{theory}(\mathbf{x}) ; PE_{s, 2}^{theory}(\mathbf{x}) ; PE_{s, 3}^{theory}(\mathbf{x})\right] \tag{5a} $$ 其中： $$ PE_{s, j}^{theory}(\mathbf{x}) =\left[\cos \left(\frac{\left \langle \mathbf{x}, \mathbf{a}_{j}\right\rangle}{\lambda_{\min } \cdot g^{s /(S-1)}}\right) ; \sin \left(\frac{\left\langle\mathbf{x}, \mathbf{a}_{j}\right\rangle}{\lambda_{\min } \cdot g^{s /(S-1 )}}\right)\right], \forall j=1,2,3 \tag{5b} $$ $Enc_{theory}(\cdot)$ 和 `Gao 等人`^[22]的灵感来自神经科学领域的网格细胞研究^{[27][7][35][2]}。事实上，`Gao 等人` ^[22] 启发并奠定了 $Enc_{theory}(\mathbf{x})$ 的理论基础。正如在`第 2 节`中讨论的那样，`Gao 等` ^[22] 提出了一个位置表示模型 $v(\mathbf{x})$，它由三个子模型组成。他们还提出了一种基于复数值的位置编码器 $\boldsymbol{\Psi}(\mathbf{x})$ 作为 $v(\mathbf{x})$ 的解析解，这启发了 $Enc_ {theory}(\cdot)$。更具体地说，给定两个位置 $\mathbf{x}_{a}，\mathbf{x}_{b}$，`Gao 等人` ^[22] 证明了 $\left\langle\boldsymbol{\Psi}\left(\mathbf{x}_{a}\right), \boldsymbol{\Psi}\left(\mathbf{x}_{b} \right)\right\rangle=3\left(1-\frac{\beta}{4}\left\|\mathbf{x}_{b}-\mathbf{x}_{a}\right\| ^{2}\right)$ ，其中 $\beta=\left\|\mathbf{a}_{j}\right\|_{2}^{2}=1$。这意味着当 $\left\|\mathbf{x}_{b}-\mathbf{x}_{a}\right\|^{2}$ 减少时，它们的位置嵌入之间的内积增加，这满足`性质 2.1`。`Mai 等人` ^[51] 表明 $Enc_{\text{theory }}(\cdot)$ 在理论和经验上满足`性质 2.1`。 #### Grid-位置编码器 grid 是 `Space2Vec` ^[51] 提出的另一种类型的 $Enc_{sinmul}(\mathbf{x})$ 。 **定义 4.7（ grid-位置编码器）**。 $Enc_{grid}(\mathrm{x})$ 遵循`定义 4.4`，其在每个尺度 $s \in\{0,1, \ldots, S-1\}$ 上，$PE_{s}^{(S)} (\mathbf{x}) = PE_{s}^{grid}(\mathbf{x})$ ，由 `式 6` 定义。$\lambda_{\min }$ ，$\lambda_{\max }$ 和 $g$ 均遵循与`定义 4.6`相同的定义。 $$ PE_{s}^{g r i d}(\mathbf{x}) =\left[PE_{s, 1}^{g r i d}(\mathbf{x}) ; \ldots ; PE_{s, l}^{g ri d}(\mathbf{x}) ; \ldots ; PE_{s, L}^{g ri d}(\mathbf{x})\right] ]\tag{6a} $$ 其中： $$ PE_{s, l}^{grid}(\mathbf{x}) =\left[\cos \left(\frac{\mathbf{x}^{[l]}}{\lambda_ {\min } \cdot g^{s /(S-1)}}\right) ; \sin \left(\frac{\mathbf{x}^{[l]}}{\lambda_{\min } \cdot g^{s /(S-1)}}\right)\right], \forall l=1,2, \ldots, L 。 \tag{6b} $$ `Mai 等人` ^[51] 表明，对于 `theory` 和 `grid` ，$\lambda_{\max }$ 可以直接根据研究区域的大小确定，而 $\lambda_{\min}$ 是决定 $Enc(\mathbf{x})$ 可以处理的最高空间分辨率的关键参数。 ### 4.1.5 不同单点位置编码器之间的比较 与为落入同一瓦片的 $x$ 产生相同嵌入的 `discretize` 相比， `direct` 可以区分邻近的位置，即：如果 $\mathbf{x}_a \neq \mathbf{x}_b$，则 $Enc_{direct}(\mathbf{x}_a) \neq Enc_{direct}(\mathbf{x }_b)$。`Mai 等人` ^[51] 在不同任务中对它们进行了比较，发现如果没有适当的位置特征归一化 $PE_{direct}(\mathbf{x})$， `direct` 的性能将低于 `tile` 。这表明了 $PE_{direct}(\mathbf{x})$ 的重要性。 `direct` 的一个优点是架构简单、超参数更少。但与 $PE_{sinu}(\mathbf{x})$ 和 $PE_{sinmul}(\mathbf{x})$ 相比，$PE_{direct}(\mathbf{x})$ 对于 $NN(\cdot)$ 来说是很难学习的，并且可能产生过度泛化的分布。 与 `TF` 和 `grid` 相比， `theory` 有保证 `性质 2.1` 的理论基础。但 `theory` 只能应用于二维空间中的点集。相比之下， `TF` 和 `grid` 缺乏对`性质 2.1` 的理论保证，但它们可以用于任何 $L$ 维空间中的点。 `TF` 和 `grid` 思路类似，而 `grid` 多了一个参数 $λ_{min}$，对于不同特征的数据集来说更加灵活。 ## 4.2 聚合位置编码器 **定义 4.8（聚合位置编码器）**。聚合位置编码器 $Enc^{(\mathcal{P})}(\mathbf{x})$ 联合考虑位置特征 $\mathbf{x}$ 和来自 $\mathbf{x}$ 邻域的聚合特征，记为 $\mathcal{N}(\mathbf{x})$。受 `Xu 等人`图神经网络 (GNN) 框架的启发 ^[86]，$Enc^{(\mathcal{P})}(\mathbf{x})$ 的通用模型设置可以定义为 $$ \mathbf{h}_{\mathbf{x}}^{(0)} =Enc(\mathbf{x}) \tag{7a} $$ $$ \mathbf{g}_{\mathbf{x}}^{(m)} =Agg_{\mathbf{x}_{\mathbf{i}} \in \mathcal{N}(\mathbf{x})}\left\{\mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}\right\} \tag{7b} $$ $$ \mathbf{h}_{\mathbf{x}}^{(m)} =Cmb\left(\mathbf{h}_{\mathbf{x}}^{(m-1)}, \mathbf{g}_{\mathbf{x}}^{(m)}\right) \tag{7c} $$ $$ Enc^{(\mathcal{P})}(\mathbf{x}) =Rdt\left(\mathbf{h}_{\mathbf{x}}^{(M)}\right) \tag{7d} $$ 它由 $M$ 个 `位置编码聚合层 (LEA)` 组成，多个层迭代地更新并生成最终的位置表示。 `式 7a` 为初始位置嵌入 $\mathbf{h}_{\mathrm{x}}^{(0)}$ ，其可以来自于 `第 4.1 节`中讨论的任何单点位置编码器。 每个 `LEA 层` 由一个邻域聚合运算 $Agg_{\mathbf{x}_{i} \in \mathcal{N}(\mathbf{x})}\{\cdot\}$（`式 7b`） 和一个特征组合运算 $Cmb(\cdot, \cdot)$ （`式 7c`) 构成。$Agg_{\mathbf{x}_{\mathbf{i}} \in \mathcal{N}(\mathbf{x})}\{\cdot\}$ 运算的输入对象，是来自前一个 `LEA 层` 中 $\mathcal{N}(\mathbf{x})$ 邻域内 $\mathbf{x}_{i}$ 的特征 $\mathbf{h}_{\mathbf{x}_{i}}^{ (m-1)}$ ，这与卷积神经网络对点集的卷积运算有些相似。其中： - ${Agg}_{\mathbf{x}_{i} \in \mathcal{N}(\mathbf{x})}\{\cdot\}$ 聚合运算：可以对输入的元素集合做 $max / min / mean$ 池化、求和或其他与排列无关的计算 ^{[92][59][79][50]}。 - $Cmb(\cdot, \cdot)$ 特征组合运算：逐点地将上一层特征 $\mathbf{h}_{\mathbf{x}}^{(m-1)}$ 与本层聚合特征 $\mathbf{g}_{\mathrm{x}}^{(m)}$ 组合在一起得到本层特征，组合方式可以是向量的 `concatenation` 或逐元素计算 $max / min / mean$ 值。 最后一层为读出函数 $Rdt(\cdot)$，它可以是一个恒等函数或一个多层感知机，产生 $\mathbf{x}$ 的最终聚合位置嵌入（ `式 7d` )。 `式 7` 可以被视为 GNN 框架^[5][86][84]的类比，这是一个可以应用于不同神经网络架构（例如 GCN ^[36], GraphSAGE ^[28], GG-NN ^[45], GAN ^[79], MPNN ^[24]、R-GCN ^[67]、TransGCN ^[11] 等）的通用框架。 邻域 $\mathcal{N}(\mathbf{x})$ 可以用不同的方式定义，例如 $k$ 近邻位置 ^[4][51]，缓冲区半径内的位置^[61]，或与 $\mathbf{x}$ 相同体素内的位置^[95]。根据邻域 $\mathcal{N}(\mathbf{x})$ 的定义不同，我们将 $Enc^{(\mathcal{P})}(\mathbf{x})$ 分为不同的类别：`核`、`全局邻域`、`局部邻域`和`分层邻域`聚合位置编码器，如`表 1` 所示。我们将在下一节中详细讨论每一个。 ### 4.2.1 基于核的位置编码器 基于核的位置编码器需要两个预定义的组件：核函数 $k(\cdot, \cdot)$ 、核中心点的集合 $\mathcal{Q}=\left\{p_{j}\right\}$。 核函数 $k(\cdot, \cdot)$ 的选择取决于数据集的性质，比较流行的是 `RBF 核` 和 `Mercer 核`（或 `正定核` ）^[77]。 中心点集合 $\mathcal{Q}$ 可以是训练集或其子集，即 $\mathcal{Q} \subseteq \mathcal{P}$ ，也可以是预定义的点集，例如预定义规则网格的中心点 ^[91]。 **定义 4.9（Kernel-Based 位置编码器）。** 给定核函数 $k(\cdot, \cdot)$ 和核中心点集 $\mathcal{Q}=\left\{p_{j} \right\}$，我们将`Kernel-Based 位置编码器`定义为 `式 8` ，遵循`定义 4.8`，其中 $M=1$。 $$ \mathbf{h}_{\mathbf{x}}^{(0)} = \mathbf{x} \tag{8a} $$ $$ \mathbf{g}_{\mathbf{x}}^{(1)} = Agg_{p_{i} \in \mathcal{N}(\mathbf{x})}^{(k e r n e l)}\left\{\mathbf{h}_{\mathbf{x}_{i}}^{(0)}\right\}=\Psi(\mathbf{x})=\left[k\left(\mathbf{x}, \mathbf{x}_{1}\right) ; \ldots ; k\left(\mathbf{x}, \mathbf{x}_{|\mathcal{Q}|}\right)\right] \tag{8b} $$ $$ \mathbf{h}_{\mathbf{x}}^{(1)} = Cmb\left(\mathbf{h}_{\mathbf{x}}^{(0)}, \mathbf{g}_{\mathbf{x}}^{(1)}\right)=\mathbf{g}_{\mathbf{x}}^{(1)} \tag{8c} $$ $$ Enc_{kernel}^{(\mathcal{P})}(\mathbf{x}) = Rdt\left(\mathbf{h}_{\mathbf{x}}^{(1)}\right)=\mathbf{N N}\left(\mathbf{h}_{\mathbf{x}}^{(1)}\right) \tag{8d} $$ 在此类编码器中，每个 $\mathbf{x}$ 都有一个固定的“邻域”—— $\mathcal{Q}$，即 $\mathcal{N}(\mathbf{x})=\mathcal{Q}=\left\{p_{j}=\left(\mathbf{x}_{i}\right)\right\}$；`式 8b` 中的 $[\cdot;\cdot ]$ 表示向量连接； $|\mathcal{Q}|$ 表示核的总数；$\mathbf{N N}(\cdot)$ 是一个多层感知机。 从位置特征分解的角度来看，$Enc_{kernel}^{(\mathcal{P})}(\mathbf{x})$ 可以看作是使用核技巧将 $\mathbf{x}$ 分解成了另一个希尔伯特空间中的多个核特征（参见`第 3 节`）。从位置编码聚合的角度来看，它可以被看作是聚合了从 $\mathbf{x}$ 和每个核之间的交互中得出的核特征。 由于每一个位置 $\mathbf{x} \in \mathcal{P}$ 共享相同的 $\mathcal{N}(\mathbf{x})=\mathcal{Q}$，因此 $Agg_{p_{i} \in \mathcal{N}(\mathbf{x})}^{(kernel)}\{\cdot\}$ 不需要是与排列无关的函数。这里我们使用 $\mathbf{x}$ 的 $|\mathcal{Q}|$ 个核特征的 `concatenation` 。 $Enc_{kernel}^{(\mathcal{P})}(\mathbf{x})$ 的例子有 `GPS2Vec` ^[91] 和 `Space2Vec` ^[51]。它们之间的主要区别在于 $\mathcal{Q}$ 和 $k(\cdot, \cdot)$ 的定义不同。 #### GPS2Vec-聚合位置编码器 `GPS2Vec` ^[91] 将地球划分为多个 UTM 区域，并分别训练不同的 $Enc_{kernel}^{(\mathcal{P})}(\mathbf{x})$ 。每个区域进一步划分为 $q$ 个网格，其网格中心点构成 $\mathcal{Q}$， 核函数 $k\left(\mathbf{x}, \mathbf{x}_{j}\right)=\exp \left(-\frac{\left\|\mathbf{x}-\mathbf{x}_{j}\right\|_{2}}{\zeta}\right)$ 。这里 $\|\cdot\|_{2}$ 表示 $L_2$ 范数，$\zeta$ 是一个衰减系数常数。为标识其唯一性，我们将此模型标记为 $Enc_{GPS2Vec}^{(\mathcal{P})}(\cdot)$。 #### RBF-聚合位置编码器 `Mai 等人`^[51] 提出了一种基于 RBF 核的位置编码器作为他们的基线之一，并称其为 $rbf$ 。 在该方案中， $\mathcal{Q}$ 是从 $\mathcal{P}$ 中随机抽取的 $q$ 个点，即 $\mathcal{Q} \subseteq \mathcal{P}$。核函数 $k\left(\mathbf{x}, \mathbf{x}_{j}\right)=\exp \left(-\frac{\left\|\mathbf{x}-\mathbf{x }_{j}\right\|_{2}^{2}}{2 \sigma^{2}}\right)$ 是 RBF 核。我们将其唯一地标记为 $Enc_{rbf}^{(\mathcal{P})}(\cdot)$。 #### 自适应核聚合位置编码器 `Berg 等人`^[6]没有使用恒定的核宽，而是提出了一种自适应核，以模拟鸟类时空分布的先验知识。他们将此先验预先计算为固定尺度的核密度估计 (KDE) 图。 在本文中，我们不制作预先计算的 KDE 图，而是利用其思想设计一个基于自适应核的位置编码器 $Enc_{ak}(\mathbf{x})$，其中 $k\left(\mathbf{x}, \mathbf{x}_{j}\right)=\exp \left(-\frac{\left\|\mathbf{x}-\mathbf{x}_{j}\right\|_{2}^ {2}}{2 h_{\sigma}(\mathbf{x})^{2}}\right)$ 。$h_{\sigma}(\mathbf{x})$ 是位置 $\mathbf{x}$ 的核带宽函数，例如可以将其定义为从 $\mathbf{x}$ 到其第 $K$ 个最近邻之间距离的一半。这里我们使用 $*$ 将 $Enc_{ak}(\mathbf{x})$ 与 `Berg 等人`提出的原始模型做了区分。 > **小结：** 尽管设计简单并且能够处理非线性分布，$Enc_{kernel}(\mathbf{x})$ 有几个缺点。 > - $Enc_{kernel}(\mathbf{x})$ 必须在测试时记住 $\mathcal{Q}$，这会影响内存效率。 > - 由于 $\mathbf{h}_{\mathrm{x}}^{(1)} \in \mathbb{R}^{|\mathcal{Q}|}$，$\mathcal{Q }$ 的大小直接决定 $\mathbf{NN}(\cdot)$ 中可学习参数的数量，这产生了性能效率权衡问题。 > - 当 $|\mathcal{Q}|$ 较小时，$Enc_{kernel}(\mathbf{x})$ 的内存负担小，$\mathbf{N N}(\cdot)$ 的可学习参数也较少，需要较少的训练数据并且不太可能过拟合，但 $\mathcal{Q}$ 在研究区域内的分布相当稀疏，最终可能影响编码结果的质量。 > - 当 $|\mathcal{Q}|$ 较大时，编码结果更准确，但需要大量内存来存储 $\mathcal{Q}$ 和 $\mathbf{NN}(\cdot)$ 需要的更多学习参数。 > - $Enc_{kernel}(\mathbf{x})$ 的预测还取决于 $\mathcal{Q}$ 的分布情况，并且在数据稀疏区域上表现不佳。 ### 4.2.2 全局聚合位置编码器 全局聚合位置编码器 $Enc_{\text{global}}^{(\mathcal{P})}(\mathbf{x})$ 将 $\mathcal{N}(\mathbf{x})$ 定义为 $\mathcal{P}$ 中的所有位置，即 $\mathcal{N}_{\text{global}}(\mathbf{x})=\mathcal{P}$。全局聚合位置编码器的代表是 `PointNet`。 #### PointNet-聚合位置编码器 `PointNet` ^[59] 最初是针对 `3D` 点云分类和分割提出的。其点云分割架构可以表述为一个全局聚合位置编码器，如 `式 9` 所示。 $$ \mathbf{h}_{\mathbf{x}}^{(0)}=Enc_{\text{pnet }}(\mathbf{x})=\mathbf{N N}\left(PE_{\text{pnet }}(\mathbf{x})\right)=T N_{2}\left(MLP_{1}\left(T N_{1}\left(PE_{\text{pnet }}(\mathbf{x})\right)\right)\right. \tag{9a} $$ $$ \mathbf{g}_{\mathbf{x}}^{(1)}=Agg_{\mathbf{x}_{i} \in \mathcal{N}_{\text{pnet }}(\mathbf{x})}^{(\text{pnet })}\left\{\mathbf{h}_{\mathbf{x}_{i}}^{(0)}\right\}=\operatorname{MaxPool}_{\mathbf{x}_{i} \in \mathcal{N}_{\text{pnet }}(\mathbf{x})}\left\{MLP_{2}\left(\mathbf{h}_{\mathbf{x}_{i}}^{(0)}\right)\right\}\tag{9b} $$ $$ \mathbf{h}_{\mathbf{x}}^{(1)}=Cmb^{(p n e t)}\left(\mathbf{h}_{\mathbf{x}}^{(0)}, \mathbf{g}_{\mathbf{x}}^{(1)}\right)=MLP_{3}\left(\left[\mathbf{h}_{\mathbf{x}}^{(0)} ; \mathbf{g}_{\mathbf{x}}^{(1)}\right]\right)\tag{9c} $$ $$ Enc_{\text{pnet }}^{(\mathcal{P})}(\mathbf{x})=Rdt^{(p n e t)}\left(\mathbf{h}_{\mathbf{x}}^{(1)}\right)=\mathbf{h}_{\mathbf{x}}^{(1)} \tag{9d} $$ `式 9a` 首先使用单点位置编码器 $Enc_{pnet}(\mathbf {x})$ 将每个点转换到初始嵌入中，例如 `Direct-位置编码器`。在输入到神经网络 $\mathbf{NN}(.)$ 之前，PointNet 首先将输入的 $3 \mathrm{D}$ 点特征 $\mathbf{x}=[x, y, z]^{T} \in \mathbb{R}^{3}$ 归一化为单位球体，记为 $PE_{\text{pnet }}(\cdot)$。 $\mathbf{NN}(.)$ 由两个仿射变换 $T N_{1}(\cdot)$ 和 $T N_{2}(\cdot)$ 组成，两者之间为一个多层感知机 $MLP_{1}(\cdot)$ 。这些仿射变换有助于在几何变换过程中保持点云语义标签的不变性 ^[59]。 注意 `PointNet` 只有一个 `LEA 层`，即 $M=1$。 $Agg_{\mathbf{x}_{i} \in \mathcal{N}(\mathbf{x})}^{(pnet)}\{\cdot\}$ 是为每个 $\mathbf{x}_{i} \in \mathcal{N}_{pnet}(\mathbf{x})=\mathcal{P}$ 提供的多层感知机 $MLP_{2}(\cdot)$，后接一个逐元素的最大池化 $MaxPool_{\mathbf{x}_{i} \in \mathcal{N}_{pnet}(\mathbf{x})}\{\cdot\} $，见 `式 9b`。 $Cmb(\cdot,\cdot)$ 是一个向量连接运算，后接一个多层感知机 $MLP_{3}(\cdot)$ ，见 `式 9c`。 $Rdt(\cdot)$ 读出函数是如 `式 9d` 所示的恒等函数。 ### 4.2.3. 局部聚合编码器 局部聚合位置编码器 $Enc_{local }^{(\mathcal{P})}(\mathbf{x})$ 仅考虑局部邻域 $\mathcal{N}(\mathbf{x})$ 内的所有位置，例如， $\mathbf{x}$ 半径为 $r$ 的缓冲区内的所有位置，即 $\mathcal{N}_{\text{buffer }}(\mathbf{x})=\left\{\mathbf{x}_{i} \mid \|\right.$ $\left.\mathbf{x}-\mathbf{x}_{i} \|_{2} \leqslant r, \forall \mathbf{ x}_{i} \in \mathcal{P} \wedge \mathbf{x}_{i} \neq \mathbf{x}\right\}$。 #### VoxelNet-聚合位置编码器 `Zhou and Tuzel` ^[95] 将 `3D` 空间离散化为单位体素。对于任意位置 $\mathbf{x}$，其邻域定义为 $\mathcal{N}_{vox}(\mathbf{x})=\left\{\mathbf{x}_{i } \mid \iota(\mathbf{x})=\iota\left(\mathbf{x}_{i}\right), \forall \mathbf{x}_{i} \in \mathcal{P}\right\}$，其中 $\iota(\mathbf{x})$ 是一个体素查找函数，它返回 $\mathbf{x}$ 所在体素的标识 ID。 $$ \mathbf{h}_{\mathbf{x}}^{(0)} = Enc_{vox}(\mathbf{x})=\mathbf{N N}\left(PE_{vox}(\mathbf{x})\right)=PE_{vox}(\mathbf{x}) \tag{10a} $$ $$ \mathbf{g}_{\mathbf{x}}^{(m)} = Agg_{\mathbf{x}_{i} \in \mathcal{N}_{vox}(\mathbf{x})}\left\{\mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}\right\}=M a x P o o l_{\mathbf{x}_{i} \in \mathcal{N}_{vox}(\mathbf{x})}\left\{F C N^{(m)}\left(\mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}\right)\right\} \tag{10b} $$ $$ \mathbf{h}_{\mathbf{x}}^{(m)} = Cmb^{(v o x)}\left(\mathbf{h}_{\mathbf{x}}^{(m-1)}, \mathbf{g}_{\mathbf{x}}^{(m)}\right)=\left[\mathbf{h}_{\mathbf{x}}^{(m-1)} ; \mathbf{g}_{\mathbf{x}}^{(m)}\right] \tag{10c} $$ $$ Enc_{vox}^{(\mathcal{P})}(\mathbf{x}) = Rdt^{(v o x)}\left(\mathbf{h}_{\mathbf{x}}^{(M)}\right)=\mathbf{h}_{\mathbf{x}}^{(M)} \tag{10d} $$ 在 `式 10a` 中，首先采用一个类 `Direct-位置编码器` $Enc_{vox}(\cdot)$（），将 $\mathbf{x}=[x, y, z ]^{T}$ 转化为 $PE_{vox}(\mathbf{x})=[x, y, z, x-\bar{x}, y-\bar{y}, z- \bar{z}]^{T}$。$\mathbf{NN}(\cdot)$ 是一个恒等函数，而 $(\bar{x}，\bar{y }, \bar{z})$ 是 $\mathcal{N}_{vox}(\mathbf{x})$ 中所有点的质心。 在 `式 10b` 中，聚合运算通过一个逐点的全连接层 $FCN^{(m)}(\cdot)$ 后接逐元素的最大池化层 $MaxPool_{\mathbf{x}_{i} \in \mathcal{N}_{\text{vox } }(\mathbf{x})}\{\cdot\}$ 实现。$\mathbf{g}_{\mathrm{x}}^{(m)}$ 编码了包含在当前体素中的所有形状 $\mathcal{N}_{vox}(\mathbf{x})$ 。 在 `式 10c` 中，组合运算 $Cmb(\cdot, \cdot)$ 只是一个向量 `concatenation` 运算。读出函数 $Rdt_{vox}(\cdot)$ 是一个恒等函数（见 `式 10d` ）。 #### SAGAT-聚合位置编码器 `Mai 等人` ^[51] 提出了一种改进的图注意力网络 ^[79] 来对邻近位置（例如 POI）之间的空间交互进行建模。 $\mathcal{N}_{knn}(\mathbf{x})$ 被定义为位置 $\mathbf{x}$ 的 $k$ 个最近邻。原始模型聚焦在为每一个位置的特征信息 $\mathbf{v}$ （如 POI 的类型）做编码，而本文将其概括为一个通用的局部聚合位置编码器（Spatial-Aware Graph Attention Network，简称 SAGAT）： $$ \mathbf{h}_{\mathbf{x}}^{(0)} = Enc_{sagat}(\mathbf{x}) \tag{11a} $$ $$ \mathbf{g}_{\mathbf{x}}^{(m)} = Agg_{\mathbf{x}_{i} \in \mathcal{N}_{knn}(\mathbf{x})}^{(\text{sagat })}\left\{\mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}\right\}=\sigma\left(\frac{1}{U} \sum_{u=1}^{U} \sum_{\mathbf{x}_{i} \in \mathcal{N}_{knn}(\mathbf{x})} \alpha_{iu}^{(m)} \mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}\right)\tag{11b} $$ $$ \mathbf{h}_{\mathbf{x}}^{(m)} = Cmb^{(\text{sagat })}\left(\mathbf{h}_{\mathbf{x}}^{(m-1)}, \mathbf{g}_{\mathbf{x}}^{(m)}\right)=\mathbf{g}_{\mathbf{x}}^{(m)} \tag{11c} $$ $$ Enc_{sagat}^{(\mathcal{P})}(\mathbf{x}) =Rdt^{(\text{sagat })}\left(\mathbf{h}_{\mathbf{x}}^{(M)}\right)=\mathbf{h}_{\mathbf{x}}^{(M)} \tag{11d} $$ 其中： $$ \alpha_{iu}^{(m)} = \frac{\exp \left(\sigma_{iu}^{(m)}\right)}{\sum_{\mathbf{x}_{o} \in \mathcal{N}_{knn}(\mathbf{x})} \exp \left(\sigma_{o u}^{(m)}\right)} \tag{11e} $$ $$ \sigma_{iu}^{(m)} = \operatorname{LeakyReLU}\left(\left(\mathbf{a}_{u}^{(m)}\right)^{T}\left[\mathbf{h}_{\mathbf{x}}^{(m-1)} ; \mathbf{h}_{\mathbf{x}_{i}}^{(m-1)} ; Enc\left(\mathbf{x}-\mathbf{x}_{i}\right)\right]\right) \tag{11f} $$ 在`式 11a` 中， `SAGAT` 首先使用 $Enc_{sagat}(\mathbf{x})$ 将每个位置转换到嵌入空间。在原作中，`Mai 等人` ^[51] 使用特征编码器 $Enc_{sagat}(\mathbf{x})$ 生成特征嵌入 $\mathbf{v}$。在本文中，我们将 $Enc_{\text{sagat}}(\mathbf{x})$ 泛化为 `第 4.1 节` 中讨论的任何一种单点位置编码器。 `式 11b` 是最重要的邻域聚合步骤，采用多头注意力来聚合来自上一层 $\mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}$ 的近邻 $\mathbf{x}_{i} \in \mathcal{N}_{knn}(\mathbf{x})$ 的位置嵌入 。 $U$ 是注意力头的总数。 $\alpha_{iu}^{(m)}$ 是 $\mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}$ 在第 $m$ 层内的第 $u$ 个注意力头，根据`式 11e`， $\alpha_{iu}^{( m)}$ 是在 $\mathcal{N}_{knn}$ 上归一化的，而 $\sigma_{iu}^{( m)}$ 是其非归一化的对应物。 在`式 11f` 中，$\mathbf{h}_{\mathbf{x}}^{(m-1)}$ 和 $\mathbf{h}_{\mathbf{x}_{i}} ^{(m-1)}$ 表示第 $m-1$ 层中中心位置 $\mathbf{x}$ 及其邻居 $\mathbf{x}_{i}$ 。与 `GAT` ^[79] 相比，$Enc\left(\mathbf{x}-\mathbf{x}_{i}\right)$ 被添加到注意力分数的计算中，因此在聚合步骤中考虑了空间相似度 $\Delta \mathbf{x}_{i}=\mathbf{x}-\mathbf{x}_{i}$ 。这种做法使 `SAGAT` 具有“空间感知性”。 $\mathbf{a}_{u}^{(m)}$ 是第 $u$ 个注意头的可学习注意力向量，$LeakyReLU(·) $ 是 `LeakyReLU` 激活函数。 $Enc(\cdot)$ 是空间关系的编码器，可以是任何一种单点位置编码器，如：`tile`、`rbf`、`direct`、`theory`、`grid`、 `TF` 等。`Mai等人` ^[51] 仅使用了一个聚合层，即 $M=1$。而在这里，我们将其泛化为多个层，即 $M \geqslant 1$。此外，组合函数和读出函数都是恒等函数。 `图 4` 说明了 `SAGAT` 的第 $m$ 个聚合层。在这个例子中仅考虑三个邻居。三个黄色向量 $\mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}(i=1,2,3)$ 分别是三个邻居的隐嵌入。三个绿色向量 $Enc\left(\mathbf{x}-\mathbf{x}_{i}\right)$ 分别是空间位移嵌入，用于实现空间感知的图注意力。红色向量是下一层中心位置 $\mathbf{x}$ 的隐嵌入。  > 图 4 ： `SAGAT` 的第 $m$ 个聚合层示意图。 #### DGCNN-聚合位置编码器 `Wang` ^[81] 提出了`动态图卷积神经网络（简称 DGCNN）`，用于在点云上学习时联合考虑全局形状结构和局部邻域信息。 `DGCNN` 也有 $M$ 个 `LEA 层`。与其他位置编码器相比， `DGCNN` 有两个关键区别（见 `式 12`）： 1）动态图邻域 $\mathcal{N}_{dgcnn}^{(m)}(\mathbf{x})$ 2）边缘卷积模块 ${ EdgeConv}_{\mathbf{x}_{i} \in \mathcal{N}_{dgcnn}^{(m)}(\mathbf{x})}^{(m)}\{\cdot\}$ 。 前者意味着 `DGCNN` 不是像 `VoxelNet` 和 `SAGAT` 那样使用固定邻域，而是为每个 `LEA 层`重新计算 $\mathbf{x}$ 的邻域。在第 $m$ 层，给定来自前一层的所有位置嵌入 $\mathcal{H}^{(m-1)}=\left\{\mathbf{h}_{\mathbf{x}_ {j}}^{(m-1)} \mid \forall \mathbf{x}_{j} \in \mathcal{P}\right\}$。邻域 $\mathcal{N}_{dgcnn}^{(m )}(\mathbf{x})$ 被定义为嵌入空间（不是欧几里得空间） $\mathcal{H }^{(m-1)}$ 中的元素 $\mathbf{h}_{\mathbf{x}}^{(m-1)}$ 的 $top-K$ 最近邻。 由于 $\mathcal{H}^{(m-1)}$ 在每个 `LEA 层`之后会更新，因此 $\mathcal{N}_{dgcnn}^{(m)}(\mathbf{x})$ 被称为动态邻居。边缘卷积$EdgeConv_{\mathbf{x}_{i} \in \mathcal{N}_{d g c n n}^{(m)}(\mathbf{x})}^{(m)}\{\cdot\}$ 是一个能够捕获局部几何结构、同时又能保持与排列无关的聚合算子。 $$ \mathbf{g}_{\mathbf{x}}^{(m)} = Agg_{\mathbf{x}_{i} \in \mathcal{N}_{d g c n n}^{(m)}(\mathbf{x})}^{(d g c n)}\left\{\mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}\right\}=E d g e C o n v_{\mathbf{x}_{i} \in \mathcal{N}_{d g e n n}^{(m)}(\mathbf{x})}^{(m)}\left\{\mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}\right\} \tag{12a} $$ $$ = \operatorname{MaxPool}_{\mathbf{x}_{i} \in \mathcal{N}_{\mathbf{d}_{c m n}}^{(m)}(\mathbf{x})}\left\{MLP_{e}^{(m)}\left(\left[\mathbf{h}_{\mathbf{x}}^{(m-1)} ; \mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}-\mathbf{h}_{\mathbf{x}}^{(m-1)}\right]\right)\right\}\tag{12b} $$ $$ \mathbf{h}_{\mathbf{x}}^{(m)} = Cmb^{(d g c n n)}\left(\mathbf{h}_{\mathbf{x}}^{(m-1)}, \mathbf{g}_{\mathbf{x}}^{(m)}\right)=\mathbf{g}_{\mathbf{x}}^{(m)} \tag{12c} $$ `式 12` 主要展示了边缘卷积的工作方式，省略了位置嵌入初始化、读出函数等其他步骤。 $EdgeConv_{\mathbf{x}_{i} \in \mathcal{N}_{d_{g c n}}^{(m)}(\mathbf{x})}^{(m)}\{\cdot\}$ 连接了 $\mathbf{h}_{\mathbf{x}}^{(m-1)}$ 及其与邻居的相似度 $\mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}-\mathbf{h}_{\mathbf{x}}^{(m-1)}$，然后将结果输入到一个多层感知机 $MLP_{e}^{(m)}(\cdot)$ 中，最后是逐点最大池化。 `式 12c` 的组合算子是一个恒等函数。虽然 $\mathcal{N}_{dgcnn}^{(m)}(\mathbf{x})$ 是动态的，但我们只考虑每个 $\mathbf{x}$ 的单一尺度邻域。因此将 `DGCNN` 归类为局部聚合位置编码器。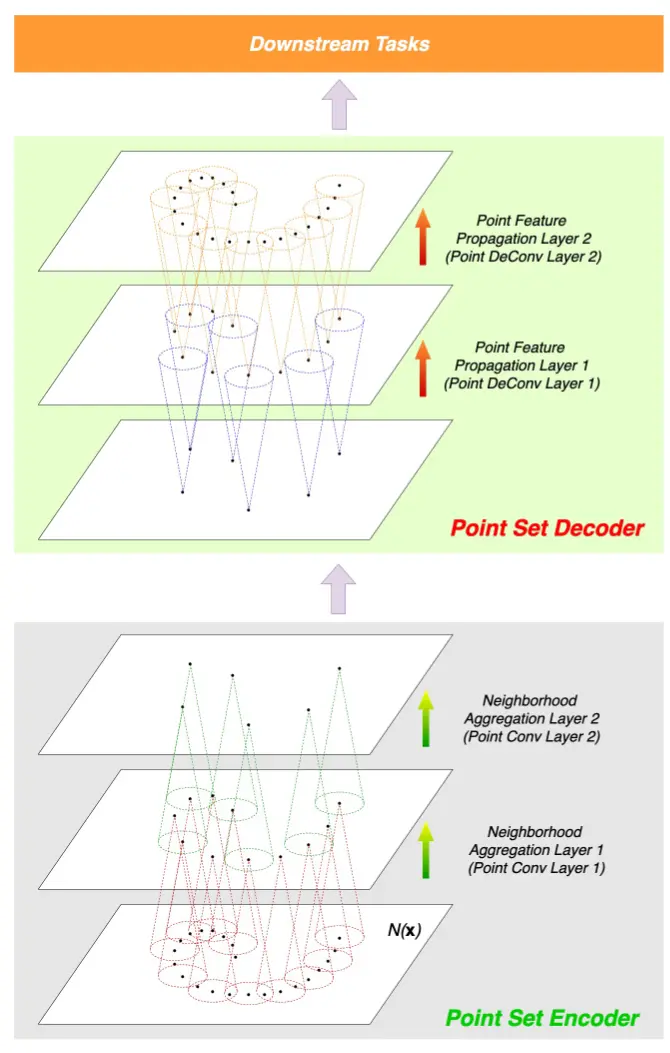  > 图 5：$Enc_{\text{hieagg}}^{(\mathcal{P})}(\mathbf{x})$ 的 `Conv-DeConv` 架构图展示 ^[56]，例如 `PointNet++`^[61]、 `PointCNN` ^[44] 和 `Graph-Conv GAN` ^[76]。 ### 4.2.4 分层聚合位置编码器 `分层聚合位置编码器` $Enc_{hieagg}^{(\mathcal{P})}(\mathbf{x})$ 为每一个位置 $\mathbf{x}$ 定义了一个多尺度的邻域，而不是为每个位置仅定义一个邻域，即 $\mathcal{N}_{hieagg}(\mathbf{x})=\left\{\mathcal{N}_{hieagg}^{(1)}(\mathbf{x}), \mathcal{N}_{hieagg}^{(2)}(\mathbf{x}), \ldots, \mathcal{N }_{hieagg}^{(m)}(\mathbf{x}), \ldots, \mathcal{N}_{hieagg}^{(M)}(\mathbf{x })\right\}$，该邻域可以按照分层方式聚合，如 `图 5` 所示。 **定义 4.10（分层聚合位置编码器）**。$Enc_{hieagg}^{(\mathcal{P})}(\mathbf{x})$ 首先从这些邻域分层地聚合位置特征，然后再将聚合后的特征传播回每个位置。$Enc_{hieagg}^{(\mathcal{P})}(\mathbf{x})$ 通常采用类似 `Conv-DeConv` ^[56] 的架构，由两个模块组成： 1）**点集编码器 $PTConv_{hieagg}^{(\mathcal{P})}(\cdot)$** ： 点集编码器是 $M$ 个邻域聚合层的堆叠（或称为 `PointConv 层` ^[44] ），其中第 $m$ 层中的每个位置嵌入都是从其上一层的邻居 $\mathcal{N}_{hieagg}^{(m-1)}(\mathrm{x})$ 聚合而来； 2）**点集解码器 ${PTDeConv }_{hieagg}^{(\mathcal{P})}(\cdot)$** ： 点集解码器是 $M$ 个点特征传播层的堆叠（或称为 `PointDeConv 层`），其中每个类似 `DeConv` 的架构都将位置嵌入从前一层传播到更密集的位置集合。其整个架构遵循 `U-Net` 设计 ^[65] $$ Enc_{hieagg}^{(\mathcal{P})}(\mathbf{x})=PTDeConv_{hieagg}^{(\mathcal{P})}\left(PTConv_{hieagg}^{(\mathcal{P})}(\mathbf{x})\right) \tag{13} $$ 其中 $PTConv_{hieagg}^{(\mathcal{P})}(\cdot)$ 遵循 `式 7` 中的模型设置。有时，$PTDeConv_{hieagg}^{( \mathcal{P})}(\cdot)$ 也遵循 `式 7` ，例如 `PointCNN` ^[44]。 `图 5` 展示了 $Enc_{hieagg}^{(\mathcal{P})}(\mathbf{x})$ 的这种 `Conv-DeConv` 架构示意图。 #### PointNet++ 聚合位置编码器 作为 `PointNet` 的扩展，`PointNet++` ^[61] 遵循 `图 5` 中类似 `Conv-DeConv` 的架构，以实现分层地特征聚合和传播。点集编码器 $PTConv_{pnet+}^{(\mathcal{P})}(\mathbf{x})$ 由 $M$ 个 `PointConv` 层组成（原文中称为 `集合抽象层（SAL)` ），每一个 `PointConv` 层都由三个关键层组成： (1) **采样层**：在第 $m$ 个 `SAL` 中，从前一个 `SAL` 层 $\mathcal{P}^{(m- 1)}$ 中采样得到一个子集 $\mathcal{P}^{(m)}$ ，即 $\mathcal{P}^{(m)} \subset \mathcal{P}^{(m-1)}$ 并且 $\mathcal{P}^{(0)} =\mathcal{P}$。 (2) **分组层**：在第 $m$ 个 `SAL` 中，将 $\mathcal{P}^{(m-1)}$ 中的点分组到点 $\mathbf{x} \in \mathcal{P}^{(m)}$ 的邻域 $\mathcal{N}_{pne t+}^ {(m)}(\mathbf{x}) \subseteq \mathcal{P}^{(m-1)}$ 中 。$\mathcal{N}_{\text{pnet }+}^{(m)}(\mathbf{x})$ 定义为在半径 $r^{(m)}$ 内的所有点 $\mathbf{x}_{i} \in \mathcal{ P}^{(m-1)}$ 。 (3) **聚合层**：在第 $m$ 个 `SAL` 中，为每个 $\mathbf{x}$ 生成新的位置嵌入 $\mathbf{h}_{\mathbf{x}}^{(m)} \in \mathcal{P}^{(m)}$。其方法是对 $\mathbf{x}$ 的邻域 $\mathcal{N}_{\text{pnet+ }}^{(m)}(\mathbf{x})$ 中每一个 $\mathbf{x} _{i}$ 的嵌入 $\mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}$ 做聚合。 $$ \mathbf{h}_{\mathbf{x}}^{(0)} = Enc_{direct}(\mathbf{x}) \tag{14a} $$ $$ \mathbf{g}_{\mathbf{x}}^{(m)} = Agg_{\left.\mathbf{x}_{i} \in \mathcal{N}_{pnet+}^{(m)}(\mathbf{x})^{(s s g}\right)}\left\{\mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}\right\} \tag{14b} $$ $$ =MaxPool_{\mathbf{x}_{i} \in \mathcal{N}_{\text{pnet+}}^{(m)}(\mathbf{x})}\left\{MLP^{(m)}\left(\mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}\right)\right\} \tag{14c} $$ $$ \mathbf{h}_{\mathbf{x}}^{(m)} = Cmb^{(s s g)}\left(\mathbf{h}_{\mathbf{x}}^{(m-1)}, \mathbf{g}_{\mathbf{x}}^{(m)}\right)=\mathbf{g}_{\mathbf{x}}^{(m)} \tag{14d} $$ $$ P T C o n v_{s s g}^{(\mathcal{P})}(\mathbf{x}) = \operatorname{Rdt}{ }^{(s s g)}\left(\mathbf{h}_{\mathbf{x}}^{(M)}\right)=\mathbf{h}_{\mathbf{x}}^{(M)} \tag{14e} $$ Qi ^[61] 提出了 `PointNet++` 的好几个版本：**SSG** （逐层单尺度分组 `PointNet++`)、**MSG** （多尺度分组 `PointNet++`) 和 **MRG**（多分辨率分组 `PointNet++` ）。根据`定义 4.10`，它们都属于分层聚合编码器范畴。 `式 14` 展示了 **SSG** 的点集编码器是如何工作的。在第 $m$ 个 `SAL` 中， `PointNet` 层使用一个`类 PointNet` 函数 $Agg_{\mathbf{x}_{i} \in \mathcal{N}_{\text{pnet+}}^{(m)}(\mathbf{x})}^{(s s g)}\{\cdot\}-MLP^{(m)}(\cdot)$ 后接一个最大池化，来聚合 $\mathcal{N}_{\text{pnet +}}^{(m)}(\mathbf{x})$ 中的特征（见`式 14c`）。 由于 $\mathcal{P}^{(M)} \subset \mathcal{P}^{(M-1)} \subset \ldots \subset \mathcal{P}^{(0)}=\mathcal{P }$，因此 $\mathcal{P}^{(M)}$ 是 $\mathcal{P}$ 的一个很小的子集，我们可以将其视为 $\mathcal{P}$ 的骨架点。 $PTConv_{ssg}^{(\mathcal{P})}(\cdot)$ 只能为 $\mathbf{x} \in \mathcal{P}^{(M)}$ 生成嵌入。为了获得每个 $\mathbf{x} \in \mathcal{P}$ 的嵌入，需要使用 $PTDeConv_{ssg}^{(\mathcal{P})}(\cdot)$ 通过反距离加权插值，将位置特征传播回每个 $\mathrm{x} \in \mathcal{P}$ 。这可以被视为 $PTConv_{ssg}^{(\mathcal{P})}(\cdot)$ 的逆过程。 采样点集合 $\left\{\mathcal{P}^{(0)}=\mathcal{P}, \mathcal{P}^{(1)}, \mathcal{P}^{(2)} , \ldots, \mathcal{P}^{(m)}, \ldots, \mathcal{P}^{(M)}\right\}$ 以相反的方式逐步将位置特征内插回更大的采样点集，直到得到所有 $\mathbf{x}\in\mathcal{P}$ 的位置嵌入。这个想法遵循 `式 13` 中的 `Conv-DeConv` 思路。 与 **SSG** 相比，**MSG** 串接了从具有不同空间尺度的邻域获得的同一个点的多个位置嵌入，来形成点集编码器。 **MSG** 在计算上相当昂贵，因为它为每个质心点聚合了更大尺度邻域中的特征。 **MRG** 连接了具有不同数量 `SAL` 层的不同 **SSG** 点集编码器输出的多个位置嵌入，来解决此问题。详情请参阅 ^[61]。 #### PointCNN 聚合位置编码器 与`PointNet++` 类似， `PointCNN` ^[44] 也使用了一个带有 $M$ 个 `PointConv` 层的点集编码器（被称为 `PointCNN` 层）。每个 `PointCNN` 层包含三个关键步骤：采样层、分组层、聚合层（ `PointNet` 层）。 其与 **SSG** 的区别主要在于分组层和聚合层。 第 $m$ 个 `PointCNN 分组层` 将邻域 $\mathcal{N}_{ptcnn}^{(m)}(\mathbf{x}) \subset \mathcal{P}^{(m-1)}$ 定义为从 $\mathcal{P}^{(m-1)}$ 获得的 $\mathbf{x}$ 的 $K \mathcal{D}$ 最近邻中均匀采样的 $K$ 个点。这可以被视为对传统 CNN 模型`空洞卷积`思想的近似，$\mathcal{D}$ 为空洞率。 第 $m$ 个 `PointCNN 聚合层` 在 $\mathcal{N}_{ptcnn}^ {(m)}(\mathbf{x})$ 上定义了一个卷积运算 $Conv^{(ptcnn)}\left(\kappa^{(m)}, \cdot\right)$ ，类似于图像上的卷积。 $\kappa^{(m)}$ 是第 $m$ 层的卷积核。 $$ \mathbf{h}_{\mathbf{x}_{i}, \delta}^{(m)} = MLP_{\delta}^{(m)}\left(\mathbf{x}_{i}-\mathbf{x}\right), \forall \mathbf{x}_{i} \in \mathcal{N}_{ptcnn}^{(m)}(\mathbf{x}) \tag{15a} $$ $$ \mathcal{X}^{(m)} = MLP^{(m)}\left(\Gamma_{\mathcal{N}_{ptcnn}^{(m)}(\mathbf{x})}\left(\mathbf{x}_{i}-\mathbf{x}\right)\right) \tag{15b} $$ $$ \mathbf{g}_{\mathbf{x}}^{(m)} = Agg_{\mathbf{x}_{i} \in \mathcal{N}_{ptcnn}^{(m)}(\mathbf{x})}^{\left(ptcnn\right)} \{\mathbf{h}_i^{(m-1)} \} \tag{15c} $$ $$ = C o n v^{(ptcnn)}\left(\kappa^{(m)}, \mathcal{X}^{(m)} \times \Gamma_{\mathcal{N}_{ptcnn}^{(m)}(\mathbf{x})}{\left(\left[\mathbf{h}_{\mathbf{x}_{i},\delta}^{(m)};h_{\mathbf{x}_i}^{(m-1)}\right]\right)}\right) \tag{15d} $$ $$ \mathbf{h}_{\mathbf{x}}^{(m)} = Cmb^{(ptcnn)}\left(\mathbf{h}_{\mathbf{x}}^{(m-1)}, \mathbf{g}_{\mathbf{x}}^{(m)}\right)=\mathbf{g}_{\mathbf{x}}^{(m)} \tag{15e} $$ $$ PTConv_{ptcnn}^{(\mathcal{P})}nn(\mathbf{x}) = Rdt^{(ptcnn)}\left(\mathbf{h}_{\mathbf{x}}^{(M)}\right)=\left[\mathbf{h}_{\mathbf{x}}^{(M)} ; MLP_{g}(\mathbf{x})\right] \tag{15f} $$ `式 15` 描述了 `PointCNN` 点集编码器的工作方式。 在`式 15a` 中，一个多层感知机 $MLP_{\delta}^{(m)}(\cdot)$ 分别将每个邻居的空间相似度 $\mathbf{x}_{i}-\mathbf{x}$ 转化为 $\mathbf{h}_{\mathbf{x}_{i }, \delta}^{(m)} \in \mathbb{R}^{C_{\delta}}$，其中邻居 $\mathbf{x}_{i} \in \mathcal{N}_{ptcnn}^{(m)}(\mathbf{x})$ 是一个 $C_{\delta}$ 维的嵌入。 在 `式 15b` 中， $\Gamma_{\mathcal{N}_{\text{ptcnn }}^{(m)}(\mathbf{x})}\left(\mathbf{x}_ {i}-\mathbf{x}\right) \in \mathbb{R}^{K \times L}$ 表示所有 $\mathbf{x}_{i} \in \mathcal{N}_{ptcnn}^{(m)}(\mathbf{x})$ 的空间相似度向量 $\mathbf{x}_{i}-\mathbf{x } \in \mathbb{R}^{L}$ 构成的堆叠，这会产生一个 $K \times L$ 矩阵。多层感知机 $MLP^{(m)}(\cdot)$ 将此矩阵转换为 $K \times K$ 的 $\mathcal{X}$-变换矩阵 $\mathcal{X}^{(m)}$ 。 在`式 15d` 中，点卷积算子 $Conv^{(ptcnn)}\left(\kappa^{(m)}, \cdot\right)$ 聚合了串接 $\left[\mathbf{h}_{\mathbf{x}_{i}, \delta}^{(m)} ; \mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}\right] \in \mathbb{R}^{C_{\delta}+d^{(m-1 )}}$ 。$\mathcal{X}^{(m)}$ 在此用于排列该 $K \times\left(C_{\delta}+d^{(m-1)}\right)$ 矩阵，因此并且必须知道所有 $\mathbf{x}_{i} \in \mathcal{N}_{ptcnn}^{(m)}(\mathbf{x})$ 的排序。 在`式 15f` 的读出函数中，另一个多层感知机 $MLP_{g}(\cdot)$ 用于直接将 $\mathbf{x}$ 提升至由 $\mathbf{h}_{\mathbf{x}}^{(M)} \in \mathbb{R}^{d^{(M)}}$ 串接形成的高维嵌入。这可以被看作传统 CNN 中的 `skip-connection`。 在`式 15d`中，当 $m=1$ 时，$\mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}=\mathbf{h}_{ \mathbf{x}_{i}}^{(0)}$ 需要被初始化。给定 $p_{i}=\left(\mathbf{x}_{i}, \mathbf{v}_{i}\right)$（参见`定义 2.1`），`Li 等人` ^[44] 令 $\mathbf{h}_{\mathbf{x}_{i}}^{(0)}=\mathbf{v}_{i}$ 。我们也可以选择 $\mathbf{h}_{\mathbf{x}_{i}}^{(0)}=\mathbf{x}_{i}$ 。 在点集解码器 ${PTDeConv }_{ptcnn}^{(\mathcal{P})}(\mathbf{x})$ 中可以部署类似的 `PointCNN 层`，以形成类似 `Conv-DeConv` 的架构。也可以采用类似的 ${Conv}^{(ptcnn)}\left(\kappa^{(m)}, \cdot\right)$ 运算符，唯一的区别是 $PTDeConv_{ptcnn}^{(\mathcal{P})}(\mathbf{x})$ 的输出与输入相比，有更多的点和更少的特征通道，并且 $\left\{\mathcal{P}^{(m)}\right\}$ 来自 $PTConv_{ptcnn}^{(\mathcal{P})}(\mathbf{x})$ 。 #### Graph-Conv GAN 聚合编码器 `Valsesia 等人` ^[76] 为 $3D$ 点云数据生成提出了一种基于图卷积的分层聚合编码器，该编码器采用了对抗生成网络（GAN） ^[25] 。我们将该位置编码器标记为 $Enc_{gcgan}^{(\mathcal{P})}(\mathbf{x})$。该模型使用了相同的 `Conv-DeConv` 思想（参见 `定义 4.10` ），并且点集编码器 $PTConv_{gcgan}^{(\mathcal{P})}(\mathbf{x})$ 由 $M$ 个 `PointConv 层` 组成，每个层由一个采样层、分组层和聚合层组成： $$ \mathbf{h}_{\mathbf{x}}^{(0)} = Enc(\mathbf{x}) \tag{16a} $$ $$ \mathbf{g}_{\mathbf{x}}^{(m)} = Agg_{\mathbf{x}_{i} \in \mathcal{N}_{knn}^{(m)}(\mathbf{x})}^{(g c g a n)}\left\{\mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}\right\}=\sum_{\mathbf{x}_{i} \in \mathcal{N}_{knn}^{(m)}(\mathbf{x})} \frac{F^{(m)}\left(\mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}-\mathbf{h}_{\mathbf{x}}^{(m-1)}\right) \mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}}{\left|\mathcal{N}_{knn}^{(m)}(\mathbf{x})\right|} \tag{16b} $$ $$ \mathbf{h}_{\mathbf{x}}^{(m)} = Cmb^{(g c g a n)}\left(\mathbf{h}_{\mathbf{x}}^{(m-1)}, \mathbf{g}_{\mathbf{x}}^{(m)}\right)=\sigma\left(\mathbf{g}_{\mathbf{x}}^{(m)}+\mathbf{W}^{(m)} \mathbf{h}_{\mathbf{x}}^{(m-1)}+\mathbf{b}^{(m)}\right) \tag{16c} $$ $$ PTConv_{g c g a n}^{(\mathcal{P})}(\mathbf{x}) = Rdt^{(g c g a n)}\left(\mathbf{h}_{\mathbf{x}}^{(M)}\right)=\mathbf{h}_{\mathbf{x}}^{(M)} \tag{16d} $$ 我们将 $\mathbf{x}$ 在第 $m$ 层的位置嵌入表示为 $\mathbf{h}_{\mathbf{x}}^{(m)} \in \mathbb{R}^{ d^{(m)}}$。`式 16a` 中的 $Enc(\mathbf{x})$ 可以是任一单点位置编码器。 在`式 16b` 中，$Agg_{\mathbf{x}_{i} \in \mathcal{N}_{knn}^{(m)}(\mathbf{x})}^{(gcgan)}\left\{\mathbf{ h}_{\mathbf{x}_{i}}^{(m-1)}\right\} \in \mathbb{R}^{d^{(m)}}$ 在第 $m$ 层的聚合邻域 $\mathcal{N}_{knn}^{(m)}(\mathbf{x})$ 上使用了一个图卷积算子。 $\mathcal{N}_{knn}^{(m)}(\mathbf{x})$ 被定义为 $\mathbf{x}$ 的 $K$ 最近邻，即 $\mathcal{N}_{knn}^{(m )}(\mathbf{x})=$ $KNN\left(\mathbf{x}, K, \mathcal{P}^{(m-1)}\right)$ 。$\mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}-\mathbf{h}_{\mathbf{x}}^{(m-1)} \in \mathbb{R}^{d^{(m-1)}}$ 捕获相邻位置 $\mathbf{x}_{i}$ 和 $\mathbf{x}$ 之间的空间相似度。 $F^{(m)}(\cdot)$ 表示一个全连接网络，它将 $\mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}-\mathbf{ h}_{\mathbf{x}}^{(m-1)}$ 转化为矩阵 $F^{(m)}\left(\mathbf{h}_{\mathbf{x}_{i}}^{(m-1)}-\mathbf{h}_{\mathbf{x}}^{(m-1)}\right) \in \mathbb{R}^{d^{(m)} \times d^{(m-1)}}$。 `式 16c` 展示了如何将邻域特征 $\mathbf{g}_{\mathbf{x}}^{(m)} \in \mathbb{R}^{d^{(m)}}$ 与 $\mathbf{x}$ 自身来自前一层的特征 $\mathbf{h}_{\mathbf{x}}^{(m-1)} \in \mathbb{R}^{d^ {(m-1)}}$ 进行结合。 $\mathbf{W}^{(m)} \in \mathbb{R}^{d^{(m)} \times d^{(m-1)}}$ 和 $\mathbf{b}^{(m)} \in \mathbb{R}^{d^{(m)}}$ 分别表示可学习的矩阵和偏置向量。 值得一提的是，`SSG`、 `PointCNN` 和 `GraphConv GAN` 之间的主要区别在于点集编码器中使用的聚合层不同（参见 `式 14` ，`式 15` 和 `式 16` ）。`图 5` 显示了它们共享相同的 `Conv-DeConv` 架构。 ## 4.3 现有方法比较 在介绍了单点位置编码器 $Enc(\mathbf{x})$ 和聚合位置编码器 $Enc^{(\mathcal{P})}(\mathbf{x})$ 后，值得从不同的方面对其进行比较。首先，我们提供 $Enc(\mathbf{x})$ 和 $Enc^{(\mathcal{P})}(\mathbf{x})$ 之间的一般性比较： - $Enc(\mathbf{x})$ 独立编码 $\mathbf{x}$ 而不考虑其空间上下文。相比之下，$Enc^{(\mathcal{P})}(\mathbf{x})$ 联合考虑 $\mathbf{x}$ 及其邻域 $\mathcal{N}(\mathbf{x})$。 $Enc^{(\mathcal{P})}(\mathbf{x})$ 可以看作是 $Enc(\mathbf{x})$ 的泛化，而任一 $Enc(\mathbf{x})$ 都可用于计算 $\mathbf{h}_{\mathrm{x}}^{(0)}$（参见 `式 7` ）。 - 当一个新位置 $\mathbf{x}^{\prime}$ 被添加到 $\mathcal{P}$ 中时，$Enc\left(\mathbf{x}_{i}\right)$ 对于所有 $\mathbf{x}_{i} \in \mathcal{P}$ 来说都不受影响。而相反，对于 $Enc^{(\mathcal{P})}(\mathbf{x})$，对于所有 $\mathbf{x}_{i} \in\left\{\mathbf{x} _{i} \mid \mathbf{x}_{i} \in \mathcal{P} \wedge \mathbf{x}^{\prime} \in \mathcal{N}\left(\mathbf{x}_ {i}\right)\right\}$, $Enc^{(\mathcal{P})}\left(\mathbf{x}_{i}\right)$ 将被更新，因为邻域 $\mathcal{N}\left(\mathbf{x}_{i}\right)$ 被修改了。其中有个特例：基于核的编码器 $Enc_{kernel}^{(\mathcal{P})}(\mathbf{x})$ 不受影响，因为 $\mathcal{N}(\mathbf{x})=\mathcal{Q}$ 对于所有 $\mathbf{x} \in \mathcal{P}$ 都相同而且不变的。 - $Enc(\mathbf{x})$ 具有较高的推断速度，而 $Enc^{(\mathcal{P})}(\mathbf{x })$ 很耗时。 - 由于 $Enc^{(\mathcal{P})}(\mathbf{x})$ 额外考虑了 $\mathcal{N}(\mathbf{x})$，因此，与 $Enc(\mathbf{x})$ 相比，模型预测具有更丰富的特征和更高的潜在性能。 我们可以看到 $Enc(\mathbf{x})$ 和 $Enc^{(\mathcal{P})}(\mathbf{x})$ 都有优点和缺点。尽管两者都能做到与任务无关，但它们分别擅长不同的任务，模型选择时应根据实际任务做选择： - 第一个准则是考虑模型预测的输入，是一个位置 $\mathbf{x}$（如带地理感知的图像分类）还是整个点集 $\mathcal{P}$（如点云分割）。鉴于其快速的推理速度，前着更倾向于 $Enc(\mathbf{x})$，而后者更倾向于 $Enc^{(\mathcal{P})}(\mathbf{x})$，因为它可以额外捕获空间上下文信息。此外，有些任务需要为整个点集 $\mathcal{P}$ 或其子集生成一个嵌入，例如点云分类、对象识别等，此类任务的唯一选择是$Enc^{(\mathcal{P})}(\mathbf{x})$ 。 - 第二个准则是考虑需要更快的推断速度还是更高的预测精度。移动应用可能更倾向于 $Enc(\mathbf{x})$ 擅长的推断速度，而企业应用可能更倾向于 $Enc^{(\mathcal{P})}(\mathbf{x})$ 的预测精度。 下面，我们从五个不同的角度对不同子类别位置编码器做一比较。下面将详细讨论`表 1` 所示结果。 **（1）位置编码器支持的维度 $L$** 就位置编码器可处理的 $\mathbf{x}$ 的空间维度而言，除了 `GPS2Vec`、`Wrap` 和 `Theory` 外，几乎所有模型都能够处理不同的 $L$，例如$L=2,3$。GPS2Vec 和 `Wrap` 是专门为 GPS 坐标设计的，可以由 $\phi$ 和 $\lambda$ 唯一标识。`Theory` 仅针对 $2 \mathrm{D}$ 坐标设计，因为它受到有关网格单元的神经科学研究启发，这些网格单元对于哺乳动物在 $2 \mathrm{D}$ 空间中的自我运动整合和导航至关重要。 **（2）是否参数化模型** 如 `表 1` 所示，除 `rbf-编码器` 和 `自适应核编码器` 外，其他所有模型都是参数化模型，这意味着它们具有固定数量的可学习参数。 `rbf-编码器` 和 `自适应核编码器` 可以是参数模型，也可以是非参数模型。由于 $\mathbf{h}_{\mathbf{x}}^{(1)} \in \mathbb{R}^{|\mathcal{Q}|}$（见 `式 8b`、 `式 8c` )，核中心点的集合 $\mathcal{Q}$ 的大小决定了 $NN(\cdot)$ 中 $Enc_{kernel}^{(\mathcal{P})}(\mathbf{x})$ 的可学习参数数量。如果 $\mathcal{Q}=\mathcal{P}$，则 `rbf-编码器` 和 `自适应核编码器` 都成为非参数模型。否则，如果 $\mathcal{Q}$ 具有固定大小，则它们都是参数模型。 **（3）是否支持多尺度** $Enc_{sinmul}(\mathbf{x})$ 和 $Enc_{hieagg}^{(\mathcal{P})}(\mathbf{x })$ 使用了多尺度方法。因此，它们更擅长于捕获那些密度分布不均匀的位置或具有不同特征混合分布的位置。但它们采用了不同的多尺度方法。前者基于 $PE(\mathbf{x})$ 设计多尺度表示，使用了不同频率的正弦函数；而后者以分层方式聚合了 $\mathbf{x}$ 的邻域。从实际角度来看，许多研究表明，多尺度位置编码器在各种任务上都优于单尺度模型和没有尺度相关参数的模型。例如，`Qi 等` ^[61] 表明 `PointNet++` 在点云分类和分割任务上都可以胜过`PointNet`。 `Mai 等` ^[51] 表明，多尺度模型（ `theory` 和 `grid`）在 POI 分类任务和地理感知的图像分类任务上都可以胜过 `tile`、`direct`、`wrap` 和 `rbf`。 `Mai 等` ^[48] 表明 `theory` 在地理问答任务上的表现优于 `direct`。 **（4）是否具有距离保持性** 对于位置编码器是否能够保持距离的问题（`性质 2.1`），我们主要从经验角度考虑，例如，位置编码器的响应图表现为`空间连续模式`还是`空间异质模式`。前者意味着模型是距离保持的，而后者则表明相反。例如，`Mai 等` ^[51] 在 POI 分类任务训练后，系统比较了 `tile`、`direct`、`wrap`、`theory`、`grid` 和 `rbf` 等不同位置编码器的响应图（见 ^[51] 的 `图 2` ）。结果表明，`direct`、`wrap`、`theory` 和 `rbf` 能够保持距离，而 `tile` 和 `direct` 则不行。此外，正如在 `第 4.1.4 节` 中讨论的，`theory` 有距离保持的理论性证明，所以在 `表 1` 中填了 `Yes`。对于其他位置编码器，由于没有做过实验或理论证明，是否具有距离保持性尚是未知数。 **（5）是否具有方向感知性** 这里使用了类似的经验逻辑。`Mai 等` ^[51] 生成的响应图表明，`direct` 和 `theory` 能够感知方向信息，而 `rbf` 则不行。其他模型尚无法得出结论。 **（6）与众不同的 `SAGAT`** `SAGAT` 的性质取决于 `式 11f` 中使用的 $Enc(\cdot)$ 。 `SAGAT` 可以是参数模型或非参数模型（ 如使用 `rbf` 作为 $Enc(\cdot)$ ） 模型。如果 $Enc(\cdot)$ 使用多尺度表示，则它又能够成为一种多尺度方法。 `SAGAT` 是否具有距离保持和方向感知性质也取决于所使用的 $Enc(\cdot)$。 # 5. 不同类型空间数据的编码方法 位置编码器可以直接用于多个基于点集的 GeoAI 任务，例如地理感知的图像分类、POI 分类和点云分割。但还有许多任务是在线、多边形、图（网络）等其他类型的空间数据上定义的。本节讨论位置编码器对更广泛类型空间数据的建模潜力。 ## 5.1 线 位置-折线关系可以看作是词-句关系的类比。在 NLP 中，句子作为单词的有序序列，可以通过不同的顺序神经网络进行编码，例如不同的循环神经网络 (RNN) ^[30][12] 和 Transformer ^[78]。他们的想法是在每个时间步将每个 `word token` 的嵌入输入到一个顺序模型中，以将整个单词序列编码为一个单独的隐状态或一系列隐状态。 类似地，我们可以通过使用这些顺序神经网络模型将折线编码为有序的位置序列。在每个时间步，我们将当前位置编码为位置嵌入，并将其输入序列模型。 事实上，最近几项关于人类流动性的工作直接使用了这个想法。 Xu ^[87] 利用 `Direct-位置编码器` 将每个轨迹点表示为位置嵌入。然后，由 LSTM 为一系列位置嵌入的轨迹进行编码，用于行人轨迹预测。同样，Rao ^[63] 提出了一个 LSTM-TrajGAN 框架来生成保护隐私的合成轨迹数据，其中每个轨迹点都由 `Direct-位置编码器` 编码。 ## 5.2 多边形 将多边形几何编码到嵌入空间，对于需要比较多边形几何形状的地理空间任务非常有用，例如地理实体对齐 ^[74] 、空间拓扑推理 ^[64] 和地理问答 ^[53][48][52] 。 但与可以由位置的有序序列表示的折线不同，多边形应该由其包含的所有位置表示。在多边形编码之后，多边形内部的所有位置 $x$ 和多边形之间的拓扑关系都应该被保留。也就是说，多边形编码器应该要考虑**拓扑感知性**。 据我们所知，多边形编码仍然是一个持续中的研究问题，没有令人满意的解决方案。`Mai 等人`^[48] 提出了一种地理实体边界框编码模型，通过从地理实体的边界框内统一采样位置并将其送入位置编码器。尽管具有创新性，但该模型无法处理细粒度的多边形几何形状。`Yan 等人` ^[89] 提出了一种`图卷积自编码器（GCAE）`，它可以编码简单多边形（即不相交且无孔的多边形）。 `GCAE` 将简单多边形的轮廓线转换为图，然后将该图编码到嵌入空间。 `GCAE` 的缺点是：它不能处理带孔的多边形和多-多边形；它也不能保存拓扑信息。因此，一个有趣的未来研究方向是开发一种具备拓扑感知性的多边形编码器，最好既能够处理简单多边形，也能处理复杂多边形。 ## 5.3 图数据 图（或网络）也是一种重要的空间数据模型，用于多种地理空间数据集，如交通网络^[42] ，^[10] 、空间社交网络^[3] 和地理知识图谱（GeoKG）^[48] 。一个图可以定义为 $\mathcal{G}=(\mathcal{V},\mathcal{E})$ ，其中 $\mathcal{V}$ 和 $\mathcal{E}$ 是图中的节点集合和边集合。在地理空间域中，每个节点 $e \in \mathcal{V}$ 或 $\mathcal{V}$ 中节点的子集都与位置 $\mathbf{x}$ 相关联，例如传感器网络中的传感器位置、空间社交网络中的用户位置或 GeoKG 中地理实体的位置。我们进一步称这种图为 `空间嵌入图`。 编码空间嵌入图的早期实践是将其视为普通的非空间图，并使用一些现有的 GNN 模型或（知识）图嵌入模型^[26] 、^[8] 、^[75] 。为了在不显著修改现有架构的情况下添加空间信息作为附加特征，可以通过使用`表 1` 中的某个 $Enc(x)$ 作为节点编码器或作为一个组件在保持其他组件不变的情况下来修改节点编码器。该模型可以使用相同的损失函数进行训练。 `Mai 等` ^[48] 正是采用这种做法开发了一种空间显式的知识图谱嵌入模型。类似想法可以应用于其他空间嵌入图。 有趣的是，除了普通的图数据之外，许多先前的研究工作把点集转换成图模型，而后使用图神经网络。他们首先基于空间关系将点集 $\mathcal{P}$ 转换图，如 $k$ 近邻空间图，其中节点表示点，而边与基于成对的距离权重相关联。转换后，在该图上应用图神经网络模型，不仅可以基于节点自身的特征，还可以基于它们的空间上下文来进行节点属性预测。许多 GeoAI 研究采用这种做法来处理不同的任务，包括空气质量预测^[46] 、地点特征预测^[96] 、GeoNames 实体嵌入学习^[34] 以及不同的空间插值问题^[4] 、^[83] 。 我们认为这种距离加权图方法不足以捕捉相对空间关系，因为它必然会丢失有关点的空间布局的信息。当没有各向同性假设时，一些重要的空间信息会丢失，例如对某些任务很重要的方向关系。 我们鼓励将 `4.2 节`中讨论的 $Enc^{(\mathcal{P})}(x)$ 用于此类任务的想法，因为 $Enc^{(\mathcal{P})}(x)$ 更擅长捕获位置之间的空间关系。 ## 5.4 栅格 卷积神经网络 (CNN) ^[40] 是许多处理栅格数据（如图像分类、图像生成和图像理解）的成功模型的核心。这一巨大成功归功于卷积操作利用局部性、平稳性和组合性原则的能力。局部性归因于局部连通性，平稳性归因于移位不变性，组合性源于栅格数据的多分辨率结构^[9] 。由于其特征局部性和跨数据域的权重共享，可学习参数的数量大大减少^[76] 。由于矢量数据上位置编码的成功，思考如何将位置编码技术应用于栅格以及有什么好处的问题特别有趣。 有趣的是，随着 `Transformer` ^[78] 架构的日益普及，已经做出了一些用类 `Transformer` 架构来代替 CNN 的尝试。其想法是，不使用 CNN 卷积核，而是首先使用类似位置编码器的架构将像素特征和像素位置一起编码到嵌入空间中，即所谓的`像素位置编码`，然后将`自注意力`应用于这些像素嵌入以用于不同的视觉任务。 然而，这种方法的问题是基于逐像素的自注意力具有非常高的计算成本。 `Vision Transformer (ViT)` ^[18] 提出了一种新的解决方案，其中一种解决方案使用 `per-image-patch`（而不是 `per-pixel` ）的自我注意力，显著降低了计算成本。 `Dosovitskiy` 表明，`ViT` 在多个图像分类基准上的表现优于传统的基于 CNN 的模型。但 `patch` 大小又成了一个重要的超参数，会显著影响模型性能。 在栅格数据上应用位置编码器是一个非常新的研究方向。现有工作主要集中在对图像上像素的位置进行编码。当一个像素代表地球表面的某个区域（如卫星图像中的像素）时，编码像素的地理位置而不是图像位置可能更加有益。地理位置作为一个通道，可以将大量未标记数据（地理数据、地理标签图像或地理标签文本）中学到的知识，迁移到监督学习任务中。 # 6 结论、愿景和未来工作 在这项工作中，我们将位置编码形式化为一种基于归纳学习的、与任务无关的地理位置编码技术。我们提供了位置编码的正式定义，并从地理信息科学角度讨论了两个期望的性质： 距离保持性和方向感知性。 我们从统计机器学习角度说明了 GeoAI 位置编码的必要性，并提供了一个通用分类框架来了解位置编码研究的现状（见`表 1`）。我们将现有位置编码器分为两类：`单点位置编码器` $Enc(\mathbf{x})$ 和 `聚合位置编码器` $Enc^{(\mathcal{P})}(\mathbf{x})$ 。对于两种类别，我们分别将位置编码器统一到了相同的形式化框架中（参见 `式 1` 和 `式 7` ），同时根据各种性质比较了各种位置编码器之间的区别。最后，我们展示了位置编码对不同类型空间数据的可能用法。 位置编码有几个有趣的未来研究方向： **(1) 区域表征学习** 正如我们在 `第 5.2 节` 中所讨论的，多边形编码没有令人满意的解决方案（即所谓的`区域表征学习`），但这在地理实体对齐和拓扑关系推理等任务中又非常有用。因此，如何设计一个能够同时处理`简单多边形`、`带孔多边形`和`多多边形`，有能够实现拓扑感知的多边形编码器，是未来一个有趣的研究方向。 **(2) 时空点编码** 到目前为止，我们讨论的所有方法都集中在位置信息上，而地理空间数据的时间因素也非常重要。几个重要的相关问题是： - 1）如何在 GeoAI 模型中利用时间信息？ - 2）能否以与空间信息类似的方式对时间信息进行编码？ - 3）在进行时间编码时，需要保留哪些重要性质？ - 4）如何在一个统一框架中结合时间编码和位置编码？ 对于同步发生（即定期采样）的事件序列^[33]，时间信息可以通过 RNN 隐式建模，或者在将时间转换为手工特征后作为输入维度送入 RNN^[19] （ Li 2017）（ Rao 2020)。最新进展不是使用手工设计的时间特征，而是建议将时间编码为可学习的向量表征，例如 `Time2Vec` ^[33] 和 ^[10]。这些时间编码器有望保留重要的性质，如：周期性、时间连续性、时间重缩放的不变性等。但这些时间编码方法之间缺少系统地比较研究。至于如何结合位置和时间编码，一种明显的方法是添加时间信息作为位置特征的附加维度。`MacAodha 等人` ^[47] 采用了这种做法，在 `式 2` 中添加了时间来作为 $PE_{wrap}(\mathbf{x})$ 的附加特征，并导致了小的性能提升（$0.25\%-1.37\%$）。但是，他们没有考虑上述时间的那些重要性质。未来需要研究不同时间编码方法的优缺点以及如何将其与位置编码相结合。 **(3) 球面位置编码** 正如我们在 `5.4 节`中所讨论的，目前还没有现有的可以保持球面距离的位置编码器。当我们在处理某些 “地图失真问题不能被忽略” 的大尺度地理空间数据集时（如：全球 SST 数据、世界各地的物种出现），需要一个球面感知的位置编码器，使我们能够直接在球面上做计算 ^[13]。 **(4) 位置编码的无监督学习** `表 1` 中列出的大多数位置编码器都是以监督学习方式训练的，这使得训练后的位置嵌入比较难于应用到其他任务上。相比之下，一些文本编码方法（例如 `BERT` ）从大量未标记的数据中以无监督方式进行训练，并且预训练的模型可用于不同的下游任务 ^[17]。如何设计一个用于位置编码的无监督学习框架是一个非常有吸引力的研究方向。 最近，已经提出了多个点云生成模型，例如 `r-GAN/l-GAN` ^[1]、`Graph-Conv GAN` ^[76]、`tree-GAN` ^[68]、 `PointFlow` ^[90] 和 `Generative PointNet` ^[85]。他们的主要目标是重建点云。这为未标记点（没有性质值的点）提供了一种可能的位置编码无监督学习框架。 另一个有趣的想法是对有标记点（有属性值的点）的空间分布进行无监督学习。 ## 参考文献

• [1] Achlioptas, P., , 2018. Learning representations and generative models for 3d point clouds. In: International Conference on Machine Learning. 40–49.
• [2] Agarwal, A., , 2015. A boon in studies of cognitive functions: brain and grid cells. Current Science, 108 (12), 2142–2144.
• [3] Andris, C., 2016. Integrating social network data into gisystems. International Journal of Geographical Information Science, 30 (10), 2009–2031.
• [4] Appleby, G., Liu, L., and Liu, L.P., 2020. Kriging convolutional networks. In: AAAI 2020.
• [5] Battaglia, P.W., , 2018. Relational inductive biases, deep learning, and graph networks. arXiv preprint arXiv:1806.01261.
• [6] Berg, T., , 2014. Birdsnap: Large-scale fine-grained visual categorization of birds. In: CVPR 2014. 2011–2018.
• [7] Blair, H.T., Welday, A.C., and Zhang, K., 2007. Scale-invariant memory representations emerge from moire interference between grid fields that produce theta oscillations: a computational model. Journal of Neuroscience, 27 (12), 3211–3229.
• [8] Bordes, A., , 2013. Translating embeddings for modeling multi-relational data. In: Advances in neural information processing systems. 2787–2795.
• [9] Bronstein, M.M., , 2017. Geometric deep learning: going beyond euclidean data. IEEE Signal Processing Magazine, 34 (4), 18–42.
• [10] Cai, L., , 2020. Traffic transformer: Capturing the continuity and periodicity of time series for traffic forecasting. Transactions in GIS.
• [11] Cai, L., , 2019. TransGCN: Coupling transformation assumptions with graph convolutional networks for link prediction. In: ACM K-CAP 2019. 131–138.
• [12] Cho, K., , 2014. Learning phrase representations using rnn encoder–decoder for statistical machine translation. In: EMNLP 2014. 1724–1734.
• [13] Chrisman, N.R., 2017. Calculating on a round planet. International Journal of Geographical Information Science, 31 (4), 637–657.
• [14] Chu, G., , 2019. Geo-aware networks for fine-grained recognition. In: Proceedings of the IEEE International Conference on Computer Vision Workshops. 0–0.
• [15] Couclelis, H., 1986. Artificial intelligence in geography: Conjectures on the shape of things to come. The professional geographer, 38 (1), 1–11.
• [16] DeLozier, G., Baldridge, J., and London, L., 2015. Gazetteer-independent toponym resolution using geographic word profiles. In: AAAI 2015. 2382–2388.
• [17] Devlin, J., , 2018. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805.
• [18] Dosovitskiy, A., , 2021. An image is worth 16x16 words: Transformers for image recognition at scale. In: ICLR 2021.
• [19] Du, N., , 2016. Recurrent marked temporal point processes: Embedding event history to vector. In: ACM SIGKDD 2016. 1555–1564.
• [20] Feng, S., , 2017. POI2Vec: Geographical latent representation for predicting future visitors.In: AAAI 2017.
• [21] Fotheringham, A.S. and Wong, D.W., 1991. The modifiable areal unit problem in multivariate statistical analysis. Environment and planning A, 23 (7), 1025–1044.
• [22] Gao, R., , 2019. Learning grid cells as vector representation of self-position coupled with matrix representation of self-motion. In: ICLR 2019.
• [23] Gao, R., , 2020. A representational model of grid cells based on matrix lie algebras. arXiv preprint arXiv:2006.10259.
• [24] Gilmer, J., , 2017. Neural message passing for quantum chemistry. In: ICML 2017.
• [25] Goodfellow, I., , 2014. Generative adversarial nets. In: Advances in Neural Information Processing Systems. 2672–2680.
• [26] Grover, A. and Leskovec, J., 2016. node2vec: Scalable feature learning for networks. In: ACM SIGKDD 2016. 855–864.
• [27] Hafting, T., , 2005. Microstructure of a spatial map in the entorhinal cortex. Nature, 436 (7052), 801–806.
• [28] Hamilton, W., Ying, Z., and Leskovec, J., 2017. Inductive representation learning on large graphs. In: Advances in neural information processing systems. 1024–1034.
• [29] Hastie, T., Tibshirani, R., and Friedman, J., 2009. The elements of statistical learning: Data mining, inference, and prediction. Springer.
• [30] Hochreiter, S. and Schmidhuber, J., 1997. Long short-term memory. Neural computation, 9 (8), 1735–1780.
• [31] Izbicki, M., Papalexakis, E.E., and Tsotras, V.J., 2019. Exploiting the earth’s spherical geometry to geolocate images. In: Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Springer, 3–19.
• [32] Janowicz, K., , 2020. GeoAI: Spatially explicit artificial intelligence techniques for geographic knowledge discovery and beyond. International Journal of Geographic Information Science.
• [33] Kazemi, S.M., , 2019. Time2vec: Learning a vector representation of time. arXiv preprint arXiv:1907.05321.
• [34] Kejriwal, M. and Szekely, P., 2017. Neural embeddings for populated geonames locations. In: International Semantic Web Conference. Springer, 139–146.
• [35] Killian, N.J., Jutras, M.J., and Buffalo, E.A., 2012. A map of visual space in the primate entorhinal cortex. Nature, 491 (7426), 761–764.
• [36] Kipf, T.N. and Welling, M., 2017. Semi-supervised classification with graph convolutional networks. In: ICLR 2017.
• [37] Krizhevsky, A., Sutskever, I., and Hinton, G.E., 2012. Imagenet classification with deep convolutional neural networks. In: Advances in neural information processing systems.1097–1105.
• [38] Kulkarni, S., , 2020. Spatial language representation with multi-level geocoding. arXiv preprint arXiv:2008.09236.
• [39] Lechner, A.M., , 2012. Investigating species–environment relationships at multiple scales: Differentiating between intrinsic scale and the modifiable areal unit problem. Ecological Complexity, 11, 91–102.
• [40] Lecun, Y. and Bengio, Y., 1995. Convolutional networks for images, speech and time series. The MIT Press, 255–258.
• [41] Li, W. and Hsu, C.Y., 2020. Automated terrain feature identification from remote sensing imagery: a deep learning approach. International Journal of Geographical Information Science, 34 (4), 637–660.
• [42] Li, Y., , 2018a. Diffusion convolutional recurrent neural network: Data-driven traffic forecasting. In: ICLR 2018.
• [43] Li, Y., Du, N., and Bengio, S., 2017. Time-dependent representation for neural event sequence prediction. arXiv preprint arXiv:1708.00065.
• [44] Li, Y., , 2018b. PointCNN: Convolution on x-transformed points. In: Advances in neural information processing systems. 820–830.
• [45] Li, Y., , 2016. Gated graph sequence neural networks. In: ICLR 2016.
• [46] Lin, Y., , 2018. Exploiting spatiotemporal patterns for accurate air quality forecasting using deep learning. In: ACM SIGSPATIAL 2018. 359–368.
• [47] MacAodha, O., Cole, E., and Perona, P., 2019. Presence-only geographical priors for fine-grained image classification. In: ICCV 2019. 9596–9606.
• [48] Mai, G., , 2020a. SE-KGE: A location-aware knowledge graph embedding model for geographic question answering and spatial semantic lifting. Transactions in GIS, 24, 623–655.
• [49] Mai, G., , 2018. ADCN: An anisotropic density-based clustering algorithm for discovering spatial point patterns with noise. Transactions in GIS, 22 (1), 348–369.
• [50] Mai, G., , 2019a. Contextual graph attention for answering logical queries over incomplete knowledge graphs. In: ACM K-CAP 2019. 171–178.
• [51] Mai, G., , 2020b. Multi-scale representation learning for spatial feature distributions using grid cells. In: ICLR 2020.
• [52] Mai, G., , 2021. Geographic Question Answering: Challenges, Uniqueness, Classification, and Future Directions. AGILE 2021: GIScience Series, 2, 1–21.
• [53] Mai, G., , 2019b. Relaxing unanswerable geographic questions using a spatially explicit knowledge graph embedding model. In: AGILE 2019. Springer, 21–39.
• [54] Maturana, D. and Scherer, S., 2015. Voxnet: A 3d convolutional neural network for real-time object recognition. In: 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 922–928.
• [55] Mirowski, P., , 2018. Learning to navigate in cities without a map. In: Advances in Neural Information Processing Systems. 2419–2430.
• [56] Noh, H., Hong, S., and Han, B., 2015. Learning deconvolution network for semantic segmentation.In: Proceedings of the IEEE international conference on computer vision. 1520–1528.
• [57] Openshaw, S., 1981. The modifiable areal unit problem. Quantitative geography: A British view, 60–69.
• [58] Openshaw, S. and Openshaw, C., 1997. Artificial intelligence in geography. John Wiley & Sons, Inc.
• [59] Qi, C.R., , 2017a. PointNet: Deep learning on point sets for 3d classification and segmentation. In: CVPR 2017. 652–660.
• [60] Qi, C.R., , 2016. Volumetric and multi-view cnns for object classification on 3d data. In: CVPR 2016. 5648–5656.
• [61] Qi, C.R., , 2017b. PointNet++: Deep hierarchical feature learning on point sets in a metric space. In: Advances in neural information processing systems. 5099–5108.
• [62] Qiu, P., , 2019. Knowledge embedding with geospatial distance restriction for geographic knowledge graph completion. ISPRS International Journal of Geo-Information, 8 (6), 254.
• [63] Rao, J., , 2020. LSTM-TrajGAN: A deep learning approach to trajectory privacy protection. In: GIScience 2020. 12:1–12:17.
• [64] Regalia, B., Janowicz, K., and McKenzie, G., 2019. Computing and querying strict, approximate, and metrically refined topological relations in linked geographic data. Transactions in GIS, 23 (3), 601–619.
• [65] Ronneberger, O., Fischer, P., and Brox, T., 2015. U-net: Convolutional networks for biomedical image segmentation. In: International Conference on Medical image computing and computer- assisted intervention. Springer, 234–241.
• [66] Russell, S. and Norvig, P., 2015. Artificial Intelligence: a modern approach. Pearson.
• [67] Schlichtkrull, M., , 2018. Modeling relational data with graph convolutional networks. In: European Semantic Web Conference. Springer, 593–607.
• [68] Shu, D.W., Park, S.W., and Kwon, J., 2019. 3d point cloud generative adversarial network based on tree structured graph convolutions. In: ICCV 2019. 3859–3868.
• [69] Smith, T.R., 1984. Artificial intelligence and its applicability to geographical problem solving. The Professional Geographer, 36 (2), 147–158.
• [70] Su, H., , 2015. Multi-view convolutional neural networks for 3d shape recognition. In: ICCV 2015. 945–953.
• [71] Tang, K., , 2015. Improving image classification with location context. In: ICCV 2015. 1008–1016.
• [72] Te Stroet, C.B. and Snepvangers, J.J., 2005. Mapping curvilinear structures with local anisotropy kriging. Mathematical geology, 37 (6), 635–649.
• [73] Tobler, W.R., 1970. A computer movie simulating urban growth in the detroit region. Economic geography, 46 (sup1), 234–240.
• [74] Trisedya, B.D., Qi, J., and Zhang, R., 2019. Entity alignment between knowledge graphs using attribute embeddings. In: AAAI 2019. vol. 33, 297–304.
• [75] Trouillon, T., , 2017. Knowledge graph completion via complex tensor factorization. The Journal of Machine Learning Research, 18 (1), 4735–4772.
• [76] Valsesia, D., Fracastoro, G., and Magli, E., 2019. Learning localized generative models for 3d point clouds via graph convolution. In: ICLR 2019.
• [77] Vapnik, V., 2013. The nature of statistical learning theory. Springer science & business media.
• [78] Vaswani, A., , 2017. Attention is all you need. In: Advances in neural information processing systems. 5998–6008.
• [79] Veličković, P., , 2018. Graph attention networks. In: ICLR 2018.
• [80] Wang, J., Hu, Y., and Joseph, K., 2020. Neurotpr: A neuro-net toponym recognition model for extracting locations from social media messages. Transactions in GIS.
• [81] Wang, Y., , 2019. Dynamic Graph CNN for learning on point clouds. Acm Transactions On Graphics (tog), 38 (5), 1–12.
• [82] Weyand, T., Kostrikov, I., and Philbin, J., 2016. Planet-photo geolocation with convolutional neural networks. In: European Conference on Computer Vision. Springer, 37–55.
• [83] Wu, Y., , 2020a. Inductive graph neural networks for spatiotemporal kriging. arXiv preprint arXiv:2006.07527.
• [84] Wu, Z., , 2020b. A comprehensive survey on graph neural networks. IEEE Transactions on Neural Networks and Learning Systems.
• [85] Xie, J., , 2021. Generative pointnet: Deep energy-based learning on unordered point sets for 3d generation, reconstruction and classification. In: CVPR 2021. 14976–14985.
• [86] Xu, K., , 2019. How powerful are graph neural networks? In: ICLR 2019.
• [87] Xu, Y., Piao, Z., and Gao, S., 2018. Encoding crowd interaction with deep neural network for pedestrian trajectory prediction. In: CVPR 2018. 5275–5284.
• [88] Yan, B., , 2019. A spatially explicit reinforcement learning model for geographic knowledge graph summarization. Transactions in GIS, 23 (3), 620–640.
• [89] Yan, X., , 2021. Graph convolutional autoencoder model for the shape coding and cognition of buildings in maps. International Journal of Geographical Information Science, 35 (3), 490–512.
• [90] Yang, G., , 2019. Pointflow: 3d point cloud generation with continuous normalizing flows. In: ICCV 2019. 4541–4550.
• [91] Yin, Y., , 2019. GPS2Vec: Towards generating worldwide gps embeddings. In: ACM 31 SIGSPATIAL 2019. 416–419.
• [92] Zaheer, M., , 2017. Deep sets. In: Advances in neural information processing systems. 3391–3401.
• [93] Zhong, E.D., , 2020. Reconstructing continuous distributions of 3d protein structure from cryo-em images. In: ICLR 2020.
• [94] Zhong, L., Hu, L., and Zhou, H., 2019. Deep learning based multi-temporal crop classification. Remote sensing of environment, 221, 430–443.
• [95] Zhou, Y. and Tuzel, O., 2018. Voxelnet: End-to-end learning for point cloud based 3d object detection. In: CVPR 2018. 4490–4499.
• [96] Zhu, D., , 2020. Understanding place characteristics in geographic contexts through graph convolutional neural networks. Annals of the American Association of Geographers, 110 (2), 408–420.
• [97] Zhu, M., , 2019a. Location2Vec: a situation-aware representation for visual exploration of urban locations. IEEE Transactions on Intelligent Transportation Systems, 20 (10), 3981–3990.
• [98] Zhu, R., Janowicz, K., and Mai, G., 2019b. Making direction a first-class citizen of tobler’s first law of geography. Transactions in GIS, 23 (3), 398–416.