【摘 要】 尽管可扩展模型取得了进步，但用于高斯过程 (GP) 的推断工具尚未充分利用计算硬件的发展。我们提出了一种基于黑盒矩阵-矩阵乘法 (BBMM) 的高斯过程推断的有效通用方法。 BBMM 推断使用修改后的共轭梯度算法的批处理版本在一次调用中导出用于训练和推断的所有项。 BBMM 将精确高斯过程推断的渐近复杂度从 \mathcal{O}(n3) 降低到 \mathcal{O}(n2)。使该算法适用于可扩展的近似值和复杂的高斯过程模型只需要一个程序即可与核及其导数进行高效的矩阵-矩阵乘法。此外，BBMM 使用专门的预处理器来大大加快收敛速度。在实验中，我们表明 BBMM 有效地使用 GPU 硬件来显著加速精确的高斯过程推断和可扩展的近似。此外，我们还提供了 GPyTorch，这是一个基于 PyTorch 构建的通过 BBMM 进行可扩展高斯过程推断的软件平台。

【原 文】 Gardner, Jacob, Geoff Pleiss, Kilian Q Weinberger, David Bindel, and Andrew G Wilson. “GPyTorch: Blackbox Matrix-Matrix Gaussian Process Inference with GPU Acceleration.” In Advances in Neural Information Processing Systems, edited by S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett, Vol. 31. Curran Associates, Inc., 2018. https://proceedings.neurips.cc/paper/2018/file/27e8e_17134dd7083b050476733207ea1-Paper.pdf.

1 简介

过去几年见证了深度学习前所未有的创新。这一进展涉及网络设计的创新 [18][20][24][26][30]，但它也极大地受益于优化 [6] 的改进以及 PyTorch、MXNet、TensorFlow 和 Caffe [1][8][28][38]。从广义上讲，优化的收益在很大程度上源于对随机梯度优化 [6][7][23][27][29][31] 的见解，有效地牺牲了不必要的准确性以换取速度，在某些情况下还可以进行正则化。此外，现代深度学习软件框架的优势包括快速原型制作、轻松访问专用计算硬件（如 GPU）以及通过自动微分进行黑盒优化。 同样，高斯过程研究近年来经历了重大创新 [9][21][45][49][50][51]——特别是在提高对大型数据集的可扩展性方面。然而，最常用于高斯过程推断的工具并没有有效地利用现代硬件，新模型需要大量的实施工作。实际上，模型和推断引擎通常是紧密耦合的，因此许多复杂模型（如多输出高斯过程和可扩展高斯过程近似）需要自定义推断过程 [5][22]。模型规范和推断过程的这种纠缠阻碍了不同模型类型的快速原型制作，并阻碍了该领域的创新。 在本文中，我们通过引入一个高效的高斯过程推断框架来弥补这一差距。鉴于以前的推断方法要求用户提供用于计算足够复杂模型的完整高斯过程边缘对数似然的程序，而我们的框架只需要访问一个黑盒程序，该程序使用核矩阵及其导数执行矩阵-矩阵乘法。因此，我们将我们的方法称为黑盒矩阵-矩阵 (BBMM) 推断。 与许多现有推断引擎的核心 Cholesky 分解相反，矩阵-矩阵乘法可以充分利用 GPU 加速。我们将证明，这种矩阵-矩阵方法还可以显著简化大量现有高斯过程模型的实施。特别是，我们做出以下贡献： - （1） 受基于矩阵-向量乘法 (MVM) 的迭代式推断方法 [9][13][43][50][51] 启发，我们提供了一种线性共轭梯度的改进批处理版本 (mBCG) ，它能够提供边缘似然及其导数计算所需的所有计算。mBCG 能够使用大型矩阵-矩阵乘法，因此可以比现有基于 Cholesky 和 MVM 的推断策略更有效地利用 GPU。此外，该方法还规避了现有推断方法中存在的几个空间复杂性和数值稳定性问题。最值得注意的是，黑盒矩阵-矩阵乘法（BBMM） 将精确高斯过程推断的时间复杂度从 $\mathcal{O}(n^3)$ 降低到 $\mathcal{O}(n^2)$。 - （2） 我们为这种改进的共轭梯度算法设计了一种基于 pivoted Cholesky 分解 [4][19] 的预处理方法。此预处理的所有必需运算都是高效的，并且在实践中所需的时间可以忽略不计。我们在实证和理论上都证明了这种预处理能够显著加速推断。 - （3） 我们介绍一个使用 BBMM 推断进行可扩展高斯过程的新软件平台 `GPyTorch`。它建立在 PyTorch 之上：https://gpytorch.ai 。在多达 $3000$ 个数据点的数据集上（填满了 GPU 内存，意即如果 GPU 内存足够大则还能够扩展），我们证明了使用 BBMM 的精确高斯过程比使用基于 Cholesky 的方法的高斯过程快 $20$ 倍。此外，在高达 $500,000$ 个数据点的数据集上，带有 BBMM 的 SKI 结构化插值方法 [50] 和 SGPR 变分推断方法 [45] 分别实现了高达 $15$ 倍和 $4$ 倍的加速。此外，SKI、SGPR 以及其他可扩展近似只需要不到 $50$ 行代码即可实现，其实核心只需要一个高效的矩阵-矩阵乘法程序。 ## 2 相关工作 **（1）共轭梯度、Lanczos 对角化算法及相关算法** 共轭梯度、Lanczos 对角化算法及相关算法是数值线性代数中用于求解线性系统和求解特征值问题的常用方法，其特点是无需显式地计算一个矩阵。这些技术已经存在了几十年，并在流行的书籍和论文中有所介绍 [11][12][17][32][36][37][42]。总的来说，此类算法属于被称为 _Krylov 子空间方法_ 的一大类迭代方法，它仅通过矩阵-向量乘法 (MVM) 访问矩阵。从历史上看，此类方法已被广泛应用于解决大型数值线性代数问题，特别是那些能够提供快速 MVM 计算的稀疏矩阵问题。 最近，许多论文将这些 MVM 方法用于高斯过程推断 [9][13][15][34][39][43][49][50]。一个关键优势是 MVM 方法可以利用代数结构来提高计算效率。其中值得注意的成果有： - 结构化核插值 (SKI) 方法 [50] ，该方法使用具有快速 MVM 的结构化核矩阵来实现显著的渐近复杂性。 - Dong 等 [13] 提出使用基于 Lanczos 对角化 [16][46] 技术来计算对数行列式及其导数的随机估计的 MVM 方法。 在本文中，我们将使用与 Dong 等[13]相同的对数行列式估计器，不过，我们明确避免了使用具有存储和数值稳定性问题的 Lanczos 对角化算法 [17]。 **（2）预处理** 预处理是加速共轭梯度收敛的有效工具。此类技术太多了，无法在这里充分回顾。下面是一些推荐文献： - Saad [42] 中有两个章节讨论各种预处理技术。 - Cutajar 等 [10] 探索了使用预处理的共轭梯度进行精确高斯过程推断，他们使用了各种稀疏高斯过程方法作为预处理器。不过，Cutajar 等 [10] 并不提供通用的预处理器。例如，Jacobi 预处理方法在使用平稳核 [10][51] 时没有效果。此外，许多预处理具有 $\mathcal{O}(n^2)$ 的复杂度，而这会限制大多数可扩展高斯过程方法的复杂度（注：此处指无法超越此复杂度约束）。 **（3）Pivoted Cholesky 分解** Pivoted Cholesky 分解是一种计算正定矩阵低秩分解的高效算法 [4][19] ，我们将在预处理中使用该算法。 - Harbrecht 等 [19] 在科学计算环境中探索了 Pivoted Cholesky 分解作为低秩近似的方法。在证明我们的预处理器的收敛边界时，我们明确地使用了 Harbrecht 等[19] 中的一些理论结果（参见附录 D）。 - Bach [4] 考虑使用随机列采样以及 Pivoted Cholesky 分解作为核矩阵的低秩近似， Bach [4] 将这种分解视为一种近似训练方法。 在本文中，我们主要将 Pivoted Cholesky 分解用作预处理器，这避免了低秩近似造成的任何精度损失以及计算导数的复杂性。 ## 3 背景 **（1）符号** $X$ 将表示一组 $d$ 维的 $n$ 个训练示例，或者等效地表示一个 $n × d$ 矩阵，其中第 $i$ 行（表示为 $\mathbf{x}_i$）是第 $i$ 个训练示例。 $\mathbf{y}$ 表示训练标签。 $k(\mathbf{x,x'})$ 表示核函数 $K_{XX}$ 表示包含所有核元素配对的核矩阵，也就是说， $[K_{XX} ]_{ij} = k(\mathbf{x}_i,\mathbf{x}_j)$。 $\mathbf{k}_{X \mathbf{x}^*}$ 表示训练示例和测试点 $\mathbf{x}^*$ 之间的核值，例如 $[\mathbf{k}_{X \mathbf{x}^*}]_i = k(\mathbf{x}_i, \mathbf{x}^*)$。帽子符号表示加了对角线的核矩阵： $\hat{K}_{XX} = K_{XX} + \sigma^2 I$。 **（2）高斯过程 (GP)** 高斯过程是一种核方法，它定义了被建模函数的完整分布，$f(x) \sim \mathcal{GP}(μ(\mathbf{x}), k(\mathbf{x,x'}))$。 高斯过程中流行的核包括 RBF 核，$k(\mathbf{x,x'}) = s \exp(−( \|\mathbf{x-x'} \|)/(2 \ell^2))$ 和 Matérn 核系列 [41]。 **（3）高斯过程预测** 高斯过程的预测对应于一个分布，即预测后验分布： $p(f(\mathbf{x}^*) | X, \mathbf{y})$。如果有两个测试输入 $\mathbf{x}^*$ 和 $\mathbf{x}^{*'}$，则 $\mathbf{x}^*$ 的预测均值以及 $\mathbf{x}^*$ 和 $\mathbf{x}^*'$ 之间的预测协方差可以由下式给出： $$ \begin{align*} \mu_{f|\mathcal{D}}(\mathbf{x}^*) &= μ(\mathbf{x}^*) + \mathbf{k}^{\top}_{X \mathbf{x}^*} \hat{K}^{-1}_{XX} \mathbf{y}\\ k_{f|\mathcal{D}}\mathbf{x}^*, \mathbf{x}^{*}′) &= k_{\mathbf{x}^*\mathbf{x}^{*}′} − \mathbf{k}^{\top}_{X\mathbf{x}^*} \hat{K}^{−1}_{XX} \mathbf{k}_{X \mathbf{x}^{*}′} \end{align*} \tag{1} $$ **（4）高斯过程的训练** 高斯过程取决于超参数 $θ$。超参数可能包括似然的噪声、长度尺度、归纳点位置 [45] 或用于深度核学习的神经网络参数 [52] 等。这些参数通常是通过最小化或采样 **负对数边缘似然** 来进行学习的，见下式（带导数）： $$ \begin{align*} L(θ | X, \mathbf{y}) &\propto \log |\hat{K}_{XX}| − \mathbf{y}^{\top} \hat{K}^{-1}_{XX} \mathbf{y}\\ dL dθ &= \mathbf{y}^{\top} \hat{K}^{-1}_{XX} \frac{d \hat{K}_{XX}}{dθ} \hat{K}^{-1}_{XX} \mathbf{y} + \text{Tr} \left(\hat{K}^{-1}_{XX} \frac{d \hat{K}_{XX}}{dθ} \right) \end{align*} \tag{2} $$ 在训练和预测过程中，计算复杂度最高的运算有两个：求逆运算 $\hat{K}^{-1}_{XX}$ 和求对数行列式 $\log |\hat{K}_{XX}|$。 ## 4 通过黑盒矩阵乘法进行高斯过程推断 本文的目标是 **用能够有效利用现代硬件的新框架取代原有的传统推断策略**。此外，我们还希望可以在没有额外推断规则的情况下，以黑盒方式使用更为复杂的高斯过程模型。为此，我们将大量高斯过程推断缩减为 “矩阵-矩阵乘法” 运算，并且称我们的方法为 “黑盒矩阵-矩阵推断 (Blackbox Matrix-Matrix inference，BBMM)” 方法，因为它只需要用户为 $\hat{K}_{XX} M$ 及其导数 $\frac{d \hat{K}_{XX}}{dθ} M$ 指定矩阵乘法的程序即可使用。 **（1） 必需的运算**。 推断引擎是一种用于计算 `式 (1)` 预测分布、`式 (2)` 损失及其导数的方案。这些公式涉及三个共同运算，决定了其时间复杂度： - 1) **线性求解**： $\hat{K}^{-1}_{XX} \mathbf{y}$， - 2) **对数行列式**： $\log | \hat{K}_{XX} |$， - 3) **迹项**： $\text{Tr}( \hat{K}^{-1}_{XX} \frac{d \hat{K}_{XX}}{dθ})$。 在大部分实现中，上述三个量是使用 $\hat{K}_{XX}$ 矩阵的 Cholesky 分解来计算的，但这在计算上非常昂贵，需要 $\mathcal{O}(n^3)$ 运算，并且无法有效地利用并行硬件。 近年来，越来越多的研究倾向于使用 “矩阵-向量乘法 (MVM)” 的迭代程序来计算上述运算。其中： - **线性求解** $\hat{K}^{-1}_{XX} \mathbf{y}$ 可以使用共轭梯度 (CG) [9][10][43][50] 计算; - **对数行列式** 和 **迹** 可以使用迭代的 Lanczos 对角化算法 [13][46] 计算。 基于 MVM 的方法比基于 Cholesky 的方法渐近速度更快且空间效率更高 [13][50]。此外，这些方法能够利用数据中的代数结构进一步提高效率 [9][43][50]。但它们也有缺点：这些量是通过多次独立调用共轭梯度和随机 Lanczos 正交子程序来计算的，这些子程序本质上是顺序的，并没有充分利用并行硬件。此外，Lanczos 对角化算法需要 $\mathcal{O}(np)$ 空间进行 $p$ 次迭代，并且会由于失去正交性而存在数值稳定性问题 [17]。 **（2）改进后的共轭梯度**。 我们的目标是利用 MVM 类方法的优势（空间效率、利用结构的能力等），同时利用针对现代并行计算硬件优化的高效程序。为此，使用了改进的批量共轭梯度算法 (mBCG) 算法。标准共轭梯度将向量 $\mathbf{y}$ 视为输入，计算 “矩阵-向量积” $\hat{K}_{XX} \mathbf{y}$，并在 $p$ 次迭代后输出近似解 $\mathbf{u}_p \approx \hat{K}^{-1}_{XX} \mathbf{y}$（当 $p = n$ 时完全相等）。我们将 `式(1)` 的共轭梯度修改为同时对多个右侧执行线性求解；对于 `式 (2)` 的共轭梯度返回 $\hat{K}_{XX}$ 相对于每个右侧的部分 Lanczos 三对角。具体来说，mBCG 将矩阵 $[ \mathbf{y \quad z_1 \quad \dots \quadz_t} ]$ 作为输入，并输出： $$ [ \mathbf{u_0 \quad u_1 \quad \ldots \quad u_t} ] = \hat{K}^{-1}_{XX} [ \mathbf{y \quad z_1 \ldots \quad z_t} ] \text{ and } \tilde{T}_1,\ldots,\tilde{T}_t \tag{3} $$ 其中 $\tilde{T}_1,\ldots , \tilde{T}_t$ 是 $\hat{K}_{XX}$ 关于向量 $\mathbf{z}_1, \ldots, \mathbf{z}_t$ 的偏 Lanczos 三对角化。 接下来，我们将展示如何使用对 mBCG 的单次调用来计算三个高斯过程推断项: $\hat{K}^{−1}_{XX} \mathbf{y}$、$\text{Tr}(\hat{K}^{-1}_{XX} \frac{\partial \hat{K}_{XX}}{\partial θ})$ 和 $\log | \hat{K}_{XX} |$。 $\hat{K}^{-1}_{XX} \mathbf{y}$ 等于 `式 (3)` 中的 $\mathbf{u}_0$，可以直接从 mBCG 返回。因此下面主要描述其他两个项。 **（3）迹的估计** 从共轭梯度估计 $\text{Tr}( \hat{K}^{-1}_{XX} \frac{\partial \hat{K}_{XX}}{\partial \theta})$ 依赖于随机迹估计 [3][14][25]，这允许我们将此项视为线性解的和。给定 i.i.d. 的随机变量 $\mathbf{z}_1, \ldots , \mathbf{z}_t$，使得 $\mathbb{E}[\mathbf{z}_i] = 0$ 且 $\mathbb{E}[\mathbf{z}_i \mathbf{z}_i^{\top}] = I$, (e.g., $\mathbf{z}_i \sim \mathcal{N}(0, I)$ ）， 矩阵迹 $\text{Tr}(A)$ 可以写为 $\text{Tr}(A) = \mathbb{E}[\mathbf{z}_i^{\top} A \mathbf{z}_i ]$ , 这样： $$ \begin{align*} \text{Tr}( \hat{K}^{-1}_{XX} \frac{d \hat{K}_{XX}}{d \theta} ) &=\mathbb{E}[ \mathbf{z}_i^{\top} \hat{K}^{-1}_{XX} \frac{d \hat{K}_{XX}}{d \theta} \mathbf{z}_i ] \\ &\approx \frac{1}{t} \sum^{t}_{i=1} ( \mathbf{z}_i^{\top} \hat{K}^{-1}_{XX} ) \left( \frac{d \hat{K}_{XX}}{d \theta} \mathbf{z}_i \right ) \tag{4} \end{align*} $$ 迹项是导数的一种无偏估计量。该计算激发了 `式 (3)` 中的 $\mathbf{z}_1, \ldots ,\mathbf{z}_t$ 项： mBCG 调用返回 $\hat{K}^{-1}_{XX} [\mathbf{z}_1 \quad \ldots \quad \mathbf{z}_t]$ 的解，这会产生 $\mathbf{u}_i = \mathbf{z}_i^{\top} \hat{K}^{-1}_{XX}$。单个矩阵与导数的乘法 $\frac{d \hat{K}_{XX}}{dθ} [\mathbf{z}_1 \quad \ldots \quad \mathbf{z}_t]$ 产生右侧的剩余项。然后，如 (4) 中所示，可以通过逐个元素地将这些项相乘并求和来估计完整迹。 **（4）对数行列式的估计** 估计 $\log | \hat{K}_{XX} |$ 可以使用来自 mBCG 的 $T_1,\ldots , T_t$ 矩阵来完成。如果 $\hat{K}_{XX} = Q T Q^{\top}$，且 $Q$ 正交，则因为 $\hat{K}_{XX}$ 和 $T$ 具有相同的特征值： $$ \log | \hat{K}_{XX} | = \text{Tr}(\log T ) = \mathbb{E}[\mathbf{z}_i^{\top}(\log T)\mathbf{z}_i ]\approx \sum^{t}_{i=1} \mathbf{z}_i^{\top} (\log T ) \mathbf{z}_i \tag{5} $$ 这里的 $\log T$ 表示矩阵对数，近似值来自用于 $式 (4)$ 相同的随机迹估计技术。获得分解 $\hat{K}_{XX} = QT Q^{\top}$ 的一种方法是使用 Lanczos 三对角化算法。该算法采用矩阵 $\hat{K}_{XX}$ 和探测向量 $\mathbf{z}$ 并输出 $Q T Q^{\top}$ 分解（其中 $\mathbf{z}$ 是 $Q$ 的第一列）。然而，我们也可以运行 $t$ 次算法的 $p$ 次迭代，而不是运行完整算法，每次迭代都有一个向量 $\mathbf{z}_1,\ldots , \mathbf{z}_t$ 以获得 $t$ 个分解 $\tilde{Q}_1 \tilde{T}_1 \tilde{Q}_1^{\top},\ldots , \tilde{Q}_t\tilde{T}_t \tilde{Q}_t^{\top}$ 其中 $\tilde{Q}_i \in \mathbb{R}^{n \times p}$ 和 $\tilde{T}_i \in \mathbb{R}^{p \times p}$。我们可以使用这些部分分解来估计 `式 (5)`： $$ \mathbb{E}[\mathbf{z}_i^{\top}(\log T )\mathbf{z}_i ] = \mathbb{E}[ \mathbf{z}_i^{\top} \tilde{Q}_i(\log \tilde{T}_i) \tilde{Q}_i^{\top}\mathbf{z}_i ] \approx \frac{1}{t} \sum^{t}_{i=1} \mathbf{z}_i^{\top} \tilde{Q}_i(\log \tilde{T}_i) \tilde{Q}_i^{\top}\mathbf{z}_i = \frac{1}{t} \sum^{t}_{i=1} e_1^{\top}(\log \tilde{T}_i)e_1 \tag{6} $$ 其中 $e_1$ 是单位矩阵的第一行。使用起始向量 $\mathbf{z}_i$ 运行 Lanczos 确保 $\tilde{Q}_i$ 的所有列都与 $\mathbf{z}_i$ 正交，除了第一列，所以 $\tilde{Q}_i \mathbf{z}_i = e_1$ [13][16][46]。 在 mBCG 中，我们采用了 Saad [42] 中的一项技术，该技术允许我们计算 $\tilde{T}_1,\ldots ,\tilde{T}_t$ 对应于输入向量 $\mathbf{z}_1,\ldots , \mathbf{z}_t$ 从共轭梯度的系数到 mBCG 在每次迭代的 $\mathcal{O}(1)$ 额外工作中。这种方法允许我们在不运行 Lanczos 算法的情况下计算与 `式 (6)` 相同的对数行列式估计。因此，我们避免了与 Lanczos 迭代相关的额外计算、存储和数值不稳定性。我们在附录 A 中描述了这种改进的细节。 **（5） 运行时间和空间**。 如上所示，我们能够通过对 mBCG 的单次调用来近似所有推断项。这些近似值随着 mBCG 迭代次数的增加而提高。每次迭代都需要一个矩阵-矩阵与 $\hat{K}_{XX}$ 相乘，而推导这些推断项的后续工作所花费的额外时间可以忽略不计（附录 B）。因此，mBCG 的 $p$ 次迭代需要 $\mathcal{O}(nt)$ 空间（参见附录 B）和 $\mathcal{O}(p Ξ( \hat{K}_{XX} ))$ 时间，其中 $Ξ( \hat{K}_{XX} )$ 是将 $\hat{K}_{XX}$ 乘以 $n × t$ 矩阵的时间。对于标准矩阵，此乘法需要 $\mathcal{O}(n^2t)$ 时间。值得注意的是，这是一个比标准的基于 Cholesky 的推断更低的渐近复杂度，即 $\mathcal{O}(n^3)$。因此，BBMM 为精确的高斯过程推断提供了计算加速。正如我们将在第 5 节中展示的那样，可以使用结构化数据或稀疏高斯过程近似进一步降低时间复杂度。 ### 4.1 预处理 虽然 mBCG 的每次迭代都执行可有效利用硬件的大型并行矩阵-矩阵运算，但迭代本身是顺序的。更好地利用硬件的一个自然目标是用更少的顺序步骤换取每一步稍微多一点的努力。我们使用预处理 [12][17][42][47] 来实现这个目标，它引入了一个矩阵 $P$ 来求解相关的线性系统 $$ P^{-1} \hat{K}_{XX} \mathbf{u} = P^{-1} \mathbf{y} $$ 而不是 $\hat{K}^{-1}_{XX} \mathbf{y}$。两个系统都保证有相同的解，但预处理系统的收敛取决于 $P^{-1} \hat{K}_{XX}$ 的条件而不是 $\hat{K}_{XX}$ 的条件。 我们观察到一般用于高斯过程推断的预处理器的两个设计要求： - 首先，为了确保在使用可扩展高斯过程方法时预处理运算不会支配运行时间，预条件器应提供大致线性的时间求解和空间。 - 其次，我们应该能够有效地计算预处理器矩阵的对数行列式，$\log |P |$。这是因为应用于预处理系统的 mBCG 算法估计 $\log |P^{-1} \hat{K}_{XX}|$ 而不是 $\log | \hat{K}_{XX} |$。因此必须计算 $\log |\hat{K}_{XX}| = \log |P^{-1} \hat{K}_{XX}| + \log |P|$。 **（1） Pivoted Cholesky 分解。** 对于一种可能的预处理器，我们转向 Pivoted Cholesky 分解。 Pivoted Cholesky 算法允许我们计算正定矩阵的低秩近似，$K_{XX} \approx L_kL_k^{\top}$ [19]。我们用 $(L_kL_k^{\top} + \sigma^2 I)^{-1}$ 对 mBCG 进行预处理，其中 $\sigma^2$ 是高斯似然的噪声项。直观地说，如果 $P_k = L_kL_k^{\top}$ 是 $K_{XX}$ 的良好近似，则 $(P_k + \sigma^2 I)^{-1} \hat{K}_{XX} \approx I$。 虽然我们在附录 C 中全面回顾了 Pivoted Cholesky 算法，但我们想强调三个关键属性。 - 首先，它可以在 $\mathcal{O}(ρ(K_{XX} )k^2)$ 时间内计算，其中 $ρ(K_{XX} )$ 是访问一行的时间（名义上这是 $\mathcal{O}(n)$）。 - 其次，可以在 $\mathcal{O}(nk^2)$ 时间内执行 $\hat{P} = L_kL_k^{\top} + \sigma^2 I$ 的线性求解。 - 最后，可以在 $\mathcal{O}(nk^2)$ 时间内计算出 $\hat{P}$ 的对数行列式。 在 `图 6` 中，我们凭实证表明该预处理器显著加速了共轭梯度收敛。此外，在 `附录 D` 中，我们针对单变量 RBF 核证明了以下引理和定理： **【引理 1】** 设 $K_{XX} \in \mathbb{R}^{n \times n}$ 为单变量 RBF 核矩阵。令 $L_kL_k^{\top}$ 为 $K_{XX}$ 的秩 $k$ pivoted Cholesky 分解，并令 $\hat{P}_k = L_kL_k^{\top} + \sigma^2 I$，则存在常数 $b > 0$ 使得条件数 $κ(\hat{P}^{-1} \hat{K}_{XX})$ 满足以下不等式： $$ κ \left( \hat{P}^{-1}_k \hat{K}_{XX} \right) \triangleq \| \hat{P}^{-1}_k \hat{K}_{XX} \|_2 \| \hat{K}^{-1}_{XX} \hat{P}_k \|_2 \leq (1 + \mathcal{O}(n \exp(−bk)))^2 \tag{7} $$ **【定理 1】（ Pivoted Cholesky 预处理共轭梯度的收敛性）**。令 $K_{XX} \in \mathbb{R}^{n \times n}$ 为 $n × n$ 单变量 RBF 核，令 $L_kL_k^{\top}$ 为其秩 $k$ pivoted Cholesky 分解。假设我们使用预条件共轭梯度求解系统 $\hat{K}^{-1}_{XX} \mathbf{y} = (K_{XX} + \sigma^2 I)^{-1} \mathbf{y}$，预条件 $\hat{P} = (L_kL_k^{\top} + \sigma^2 I)$。令 $\mathbf{u}_p$ 为共轭梯度的第 $p$ 个解，令 $\mathbf{u}^* = \hat{K}^{-1}_{XX} \mathbf{y}$ 为精确解。然后存在一些 $b > 0$，这样： $$ \| \mathbf{u}^* − \mathbf{u}_p \|_{\hat{K}_{XX}} \leq 2 (1/(1 + \mathcal{O}(\exp(kb)/n))^p \| \mathbf{u}^* − \mathbf{u}_0 \|_{\hat{K}_{XX}} \tag{8} $$ `定理 1` 意味着我们应该期望共轭梯度的收敛性随着用于 RBF 核的 Pivoted Cholesky 分解的等级呈指数级提高。在我们的实验中，我们观察到其他核的收敛性也得到了显著改善（`图 6`）。此外，我们可以利用 `引理 1` 和 [46] 中的现有理论来论证预处理改进了我们的对数行列式估计。特别是，我们重述了 Ubaru 等的定理 4.1。 [46] 这里： **【定理 2】**（Ubaru 等的定理 4.1 [46]）。令 $K_{XX} \in \mathbb{R}^{n \times n}$，并令 $L_kL_k^{\top}$ 为其秩 $k$ pivoted Cholesky 分解。假设我们运行 $p \geq \frac{1}{4} \sqrt{κ \left( \hat{P}^{-1}_k \hat{K}_{XX} \right)} \log \frac{D}{\epsilon}$ 次 mBCG 迭代，其中 $D$ 是一个涉及相同条件数的项，它随着 $k \rightarrow n$ 消失（见 [46]），我们使用 $t \geq \frac{24}{\epsilon^2} \log (2/δ)$ 向量 $\mathbf{z}_i$ 用于求解。令 $Γ$ 为 `式(6)` 中的对数行列式估计。则： $$ \text{Pr}[ | \log |\hat{P}^{-1} \hat{K}_{XX}| − Γ| \leq \epsilon | \log |\hat{P}^{-1} \hat{K}_{XX} || ] \geq 1 − δ \tag{9} $$ 因为`引理 1` 指出条件数 $κ \hat{P}^{-1}_k \hat{K}_{XX} )$ 随着 $L_k$ 的秩呈指数衰减，`定理 2` 意味着我们应该期望准确估计 $\log |\hat{P}^{-1} \hat{K}_{XX}|$ 随着 $k$ 的增加而迅速减小所需的共轭梯度迭代次数。此外，在 $k \rightarrow n$ 的极限中，我们有 $\log | \hat{K}_{XX} | = \log |\hat{P}|$。这是因为 $\log |\hat{P}^{-1} \hat{K}_{XX} | \rightarrow 0$（因为 $\hat{P}^{-1} \hat{K}_{XX}$ 收敛于 $I$）并且我们有那个 $\log | \hat{K}_{XX} | =\log|\hat{P}^{-1} \hat{K}_{XX} | + \log |\hat{P} |$。由于我们计算 $\log |\hat{P} |$ 是准确的，我们对 $\log | K_{XX} |$ 的最终估计̂随着 $k$ 的增加变得更加精确。在未来的工作中，我们希望得到一个更通用的结果，涵盖多变量设置和其他核。 ## 5 BBMM 的可编程性 我们已经讨论了 BBMM 框架如何比现有推断引擎更高效的硬件，并避免了 Lanczos 的数值不稳定性。 BBMM 的另一个关键优势是它可以轻松适应复杂的高斯过程模型或结构化高斯过程近似。 事实上，BBMM 本质上是黑盒，只需要一个程序来执行与核矩阵及其导数的矩阵乘法。在这里，我们提供了如何在此框架中轻松实现现有高斯过程模型和可扩展近似的示例。模型的矩阵乘法程序最多需要 50 行 Python 代码。我们所有的软件，包括以下使用 BBMM 的高斯过程实现，都可以通过我们的 GPyTorch 库获得：https://gpytorch.ai 。 **（1）贝叶斯线性回归** 贝叶斯线性回归可以看作是具有特殊核矩阵 $\hat{K}_{XX} = XX^{\top} + \sigma^2 I$ 的高斯过程回归。一个矩阵乘以这个核与一个 $n × t$ 矩阵 $V$ , $(XX^{\top} + \sigma^2 I)V$ 需要 $\mathcal{O}(tnd)$ 时间。因此，BBMM 需要 $\mathcal{O}(ptnd)$ 时间，并且精确到 $\mathcal{O}(tnd^2)$ 时间。这种运行时间复杂度与贝叶斯线性回归的现有高效算法相匹配，无需额外推导。多任务高斯过程 [5] 可以采用相同的方式 [15]。 **（2）稀疏高斯过程** 变分稀疏高斯过程回归 (SGPR) [45] 和许多其他稀疏高斯过程 [21][40][44] 使用核的回归子集 (SoR) 近似: $$ \hat{K}_{XX} \approx (K_{XU} K^{-1}_{UU} K_{UX} + \sigma^2 I) $$ 通过正确地分配向量乘法和对项进行分组，可以在 $\mathcal{O}(tnm + tm^3)$ 时间内执行矩阵-矩阵乘法。此计算渐近地快于 Cholesky 推断方法的 $\mathcal{O}(nm^2 + m^3)$ 时间。 使用对角线校正来增强 SoR 的一些技术（如 FITC [44]），也很容易实现。 **（3）结构化核插值 (SKI)** 结构化核插值 (SKI) [50]，也称为 KISS-GP，是一种归纳点方法，旨在提供与 Krylov 子空间方法一起使用的快速矩阵向量乘法 (MVM)。因此，SKI 是 BBMM 的天然候选者，并且可以从硬件加速中受益匪浅。SKI 是 SoR 的推广，它指定 $K_{XU} \approx W K_{UU}$，其中 $W$ 是稀疏矩阵。例如 $W$ 可以对应稀疏局部三次卷积插值的系数。应用于训练协方差矩阵的 SKI 近似给我们 $\hat{K}_{XX} \approx (W K_{UU} W ^{\top} +\sigma^2 I)$。假设 $K_{UU}$ 中没有结构，矩阵乘法需要 $\mathcal{O}(tn+tm^2)$ 时间。在 KISS-GP [50][51] 中，矩阵 $K_{UU}$ 也被选择为具有代数结构，例如 Kronecker 或 Toeplitz 结构，这进一步加速了 MVM。例如，具有 Toeplitz $K_{UU}$ 的 MVM 只需要 $\mathcal{O}(m \log m)$ 时间。因此 KISS-GP 提供 $\mathcal{O}(tn+tm \log m)$ 矩阵-矩阵乘法 [50]。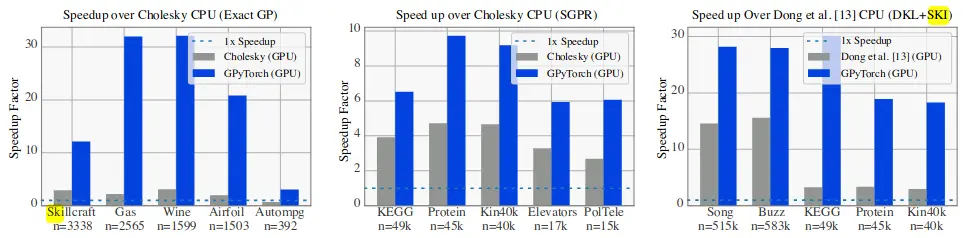 ![Fig01](https://xishansnowblog.oss-cn-beijing.aliyuncs.com/images/images/stats-20230310123615-94fa..webp) > 图 1：GPU 加速推断引擎的加速。 BBMM 为蓝色，竞争 GPU 方法为灰色。左：精确的 GP。中间：SGPR [21][45] – 加速基于 CPU Cholesky 的推断引擎。右图：SKI+DKL [50][52] – 比 Dong 等的 CPU 推断加速。 [13]. **（4）组合核** 核的组合通常可以自动进行处理。例如，给定 $K_1$、$K_2$、$K_3$ 的 BBMM 程序，我们可以自动执行 $(K_1K_2 + K_3)M = K_1(K_2M ) + K_3M$ 。 SGPR 和 KISS-GP 就是以这种方式实现的。给定一些预定义的基本组合策略，SGPR 中的核矩阵乘法 $KM$ 简化为定义如何执行 $K^{-1}_{UU} M$ ，类似地，对于 KISS-GP，它简化为执行与 Toeplitz 矩阵 $K_{UU} M$ 的乘法。对于积核，可以遵循 Gardner 等 [15]。 ## 6 结果 我们评估了 BBMM 框架，证明了： - (1) BBMM 推断引擎比基于 Cholesky 的推断和基于标准 MVM 的共轭梯度推断提供了显著的速度优势，特别是对于 GPU 计算； - (2) 与 Cholesky 推断相比，BBMM 实现了相当或更好的最终测试误差，即使没有核近似； - (3) 预处理大大提高了我们方法的效率。 **（1） 基线方法**。 我们在三种类型的高斯过程上测试 BBMM： - 1. 精确高斯过程模型， - 2. SGPR 归纳点模型 [21][45]， - 3. 具有 Toeplitz K_{UU} 和深度核的 SKI 模型 [50][52]。 对于 Exact 和 SGPR，我们将 BBMM 与 GPFlow [33] 中实现的基于 Cholesky 的推断引擎进行比较。 GPFlow 是目前使用 Cholesky 推断引擎最快实现这些模型的方法。由于 SKI 不适用于 Cholesky 推断，我们将 BBMM 与 Dong 等 [13] 的推断过程进行了比较。在我们的 GPyTorch 包中实现。此过程与 BBMM 的不同之处在于它计算 $\hat{K}^{-1}_{XX} \mathbf{y}$ 时不使用预处理器并计算 $\log | \hat{K}_{XX}|$ 及其与 Lanczos 算法的导数。 **（2）数据集**。 我们在来自 UCI 数据集存储库 [2] 的五个数据集上测试了 Exact 模型，其中包含多达 $3500$ 个训练示例（在所有实施耗尽 GPU 内存之前的最大可能）：Skillcraft、Gas、Airfoil、Autompg 和 Wine。我们在更大的数据集（$n$ 高达 $50000$）上测试 SGPR：KEGG、Protein、Elevators、Kin40k 和 PoleTele。对于 SKI，我们测试了五个最大的 UCI 数据集（$n$ 高达 $515000$）：Song、Buzz、Protein、Kin40k 和 KEGG。 **（3） 实验细节。** 所有方法都使用具有相同超参数的相同优化器 (Adam)。在 BBMM 实验中，除非另有说明，否则我们使用等级 $k = 5$ 的 Pivoted Cholesky 预处理器。我们对每个求解使用最多 $p = 20$ 次共轭梯度迭代，并且我们使用 $t = 10$ 个充满 Rademacher 随机变量的探测向量来估计对数行列式和迹项。 SGPR 模型使用 $300$ 个归纳点。 SKI 模型使用 $10,000$ 个归纳点和 [52] 中描述的深层核。 BBMM 推断引擎在我们的 GPyTorch 包中实现。 ![Fig02](https://xishansnowblog.oss-cn-beijing.aliyuncs.com/images/images/stats-20230310123644-2da2..webp) > 图 2：求解 mBCG 和 Cholesky 的错误。 所有速度实验均在 Intel Xeon E5-2650 CPU 和 NVIDIA Titan Xp GPU 上运行。 ![Fig03](https://xishansnowblog.oss-cn-beijing.aliyuncs.com/images/images/stats-20230310123703-39f2..webp) > 图 3：比较使用 BBMM 与基于 Cholesky 的推断时的最终测试 MAE。左边的两个图比较了使用具有 RBF 和 Matern-5/2 核的精确高斯过程的误差，最后一个图比较了在明显更大的数据集上使用 SGPR 和 Matern-5/2 核的误差。 ![Fig04](https://xishansnowblog.oss-cn-beijing.aliyuncs.com/images/images/stats-20230310123723-e641..webp) > 图 4：预处理对求解误差 $\| K \mathbf{x}^* − y\|/ \|y\|$ 的影响通过使用深度 RBF 和深度 Matern 的 $2$ 个 UCI 基准数据集上不使用预处理的线性共轭梯度与等级 2、5 和 9 Pivoted Cholesky 预条件器实现核。 $K$ 的超参数是通过最大化每个数据集上的边缘对数似然来学习的。 **（4） 速度比较。** `图 1` 显示了 GPU 加速的 BBMM 相对于领先的基于 CPU 的推断引擎（Cholesky for Exact/SGPR，Dong et al. [13] for SKI）获得的加速。正如预期的那样，GPU 加速的 BBMM 比基于 CPU 的推断更快。在 Exact 和 SKI 上，BBMM 比 CPU 推断快 32 倍，在 SGPR 上快 10 倍。最大的加速发生在最大的数据集上，因为较小的数据集会经历较大的 GPU 开销。值得注意的是，BBMM 比 GPU 加速的 Cholesky 方法（Exact，SGPR）实现了更大的加速，后者仅实现了大约 4 倍的加速。这一结果强调了 Cholesky 方法不太适合 GPU 加速的事实。此外，BBMM 在 SKI 上的性能优于 [13] 的 GPU 加速版本。这种加速是因为 BBMM 能够并行计算所有推断项，而 [13] 计算序列项。 **（5） 误差比较**。 在 `图 3` 中，我们报告了 Exact 和 SGPR 模型的测试平均误差 (MAE)。我们使用 RBF 核和 Matern-5/2 核演示了结果。在所有数据集中，我们的方法至少在最终测试 MAE 方面同样准确。在一些数据集（例如 Gas、Airfoil 和 Wine with Exact GPs）上，BBMM 甚至改善了最终测试错误。共轭梯度具有正则化效果，可以改进涉及 Cholesky 分解的精确核的方法，其中忽略了由核矩阵的极小特征值引起的数值问题。例如，Cholesky 方法经常将噪声（或“抖动”）添加到核矩阵的对角线以实现数值稳定性。可以用双精度减少数值不稳定性（见 `图 2`）；然而，这需要增加计算量。另一方面，BBMM 避免添加这种噪音，而不需要双精度。 **（6） 预处理**。 为了证明预处理在加速共轭梯度收敛方面的有效性，我们首先在两个数据集 Protein 和 KEGG 上训练一个深度 RBF 核模型，并根据相对残差 $\| \hat{K}_{XX} \mathbf{u} − \mathbf{y}\| / \|\mathbf{y}\|$ 计算执行 $\hat{K}^{-1}_{XX}\mathbf{y}$ 的解误差，作为执行的共轭梯度迭代次数的函数。我们在不使用预处理器以及使用等级 2、5 和 9 预处理器时查看此错误。为了证明预处理器不限于与 RBF 核一起使用，我们评估了在蛋白质上使用深度 RBF 核和在 KEGG 上使用深度 Matern-5/2 核。结果在`图 4` 的顶部。正如基于我们对该预处理器的理论直觉所预期的那样，增加预处理器的等级会大大减少实现收敛所需的共轭梯度迭代次数。 在 `图 4` 的底部，我们确认这些更准确的求解确实对最终测试 MAE 有影响。作为计算预测所需的总挂钟时间的函数，我们绘制了不使用预处理器和使用 5 级预处理器产生的测试 MAE。通过更改用于计算预测平均值的共轭梯度迭代次数来改变挂钟时间。我们观察到，因为如此低秩的预处理器就足够了，所以使用预调节可以显著提高求解的准确性，同时对每个共轭梯度迭代的运行时间几乎没有影响。因此，我们建议始终将 Pivoted Cholesky 预条件器与 BBMM 一起使用，因为它几乎没有挂钟开销并且可以快速加速收敛。 ## 7 讨论 在本文中，我们讨论了一种新的高斯过程推断 (BBMM) 框架，该框架基于带有核矩阵的黑盒矩阵-矩阵乘法程序。我们已经在我们新的公开可用的 GPyTorch 包中实现了这个框架和几个最先进的高斯过程模型。 **（1）非高斯似然** 尽管本文主要关注回归设置，但 BBMM 与变分技术完全兼容，例如 [22][53]，GPyTorch 也支持这些技术。这些方法需要计算变分下界（或 ELBO）而不是 `式(2)` 高斯过程边缘对数似然 。我们将 ELBO 推导的确切细节留给其他论文（例如 [22]）。然而，我们注意到对 mBCG 的一次调用可用于计算两个多元高斯分布之间的 KL 散度，这是 ELBO 中计算量最大的一项。 **（2）避免 Cholesky 分解** 本文的一个令人惊讶且重要的收获是，即使在精确的高斯过程设置中，避免高斯过程推断的 Cholesky 分解也是有益的。 Cholesky 分解的基本算法（在附录 C 中描述）涉及一种分而治之的方法，这种方法可能不适合并行硬件。此外，当快速近似方法足够时，Cholesky 分解执行大量计算以获得线性求解。最终，全矩阵的 Cholesky 分解需要 $\mathcal{O}(n^3)$ 时间，而共轭梯度需要 $\mathcal{O}(n^2)$ 时间。实际上，如`图 2` 所示，共轭梯度甚至可以提供比 Cholesky 分解更好的线性解。虽然我们使用了 Cholesky 算法的 Pivoted 版本进行预处理，但我们只计算该分解的前五行。通过尽早终止算法，我们避免了计算瓶颈和许多数值不稳定性。 我们希望这项工作能显著降低实现新高斯过程模型的复杂性，同时允许尽可能高效地执行推断。 ## 参考文献

  • [1] M. Abadi, P. Barham, J. Chen, Z. Chen, A. Davis, J. Dean, M. Devin, S. Ghemawat, G. Irving, M. Isard, et al. Tensorflow: A system for large-scale machine learning. In OSDI, volume 16, pages 265–283, 2016.
  • [2] A. Asuncion and D. Newman. Uci machine learning repository. https://archive.ics.uci.edu/ ml/, 2007. Last accessed: 2018-05-18.
  • [3] H. Avron and S. Toledo. Randomized algorithms for estimating the trace of an implicit symmetric positive semi-definite matrix. Journal of the ACM (JACM), 58(2):8, 2011.
  • [4] F. Bach. Sharp analysis of low-rank kernel matrix approximations. In COLT, 2013.
  • [5] E. V. Bonilla, K. M. Chai, and C. Williams. Multi-task Gaussian process prediction. In NIPS, 2008.
  • [6] L. Bottou. Large-scale machine learning with stochastic gradient descent. In COMPSTAT, pages 177–186. Springer, 2010.
  • [7] P. Chaudhari, A. Choromanska, S. Soatto, Y. LeCun, C. Baldassi, C. Borgs, J. Chayes, L. Sagun, and R. Zecchina. Entropy-sgd: Biasing gradient descent into wide valleys. arXiv preprint arXiv:1611.01838, 2016.
  • [8] T. Chen, M. Li, Y. Li, M. Lin, N. Wang, M. Wang, T. Xiao, B. Xu, C. Zhang, and Z. Zhang. Mxnet: A flexible and efficient machine learning library for heterogeneous distributed systems. arXiv preprint arXiv:1512.01274, 2015.
  • [9] J. P. Cunningham, K. V. Shenoy, and M. Sahani. Fast Gaussian process methods for point process intensity estimation. In ICML, 2008.
  • [10] K. Cutajar, M. Osborne, J. Cunningham, and M. Filippone. Preconditioning kernel matrices. In ICML, 2016.
  • [11] B. N. Datta. Numerical linear algebra and applications, volume 116. Siam, 2010.
  • [12] J. W. Demmel. Applied numerical linear algebra, volume 56. Siam, 1997.
  • [13] K. Dong, D. Eriksson, H. Nickisch, D. Bindel, and A. G. Wilson. Scalable log determinants for Gaussian process kernel learning. In NIPS, 2017.
  • [14] J. K. Fitzsimons, M. A. Osborne, S. J. Roberts, and J. F. Fitzsimons. Improved stochastic trace estimation using mutually unbiased bases. arXiv preprint arXiv:1608.00117, 2016.
  • [15] J. R. Gardner, G. Pleiss, R. Wu, K. Q. Weinberger, and A. G. Wilson. Product kernel interpolation for scalable Gaussian processes. In AISTATS, 2018.
  • [16] G. H. Golub and G. Meurant. Matrices, moments and quadrature with applications. Princeton University Press, 2009.
  • [17] G. H. Golub and C. F. Van Loan. Matrix computations, volume 3. JHU Press, 2012.
  • [18] R. H. Hahnloser, R. Sarpeshkar, M. A. Mahowald, R. J. Douglas, and H. S. Seung. Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit. Nature, 405(6789):947, 2000.
  • [19] H. Harbrecht, M. Peters, and R. Schneider. On the low-rank approximation by the pivoted cholesky decomposition. Applied numerical mathematics, 62(4):428–440, 2012.
  • [20] K. He, X. Zhang, S. Ren, and J. Sun. Deep residual learning for image recognition. In CVPR, 2016.
  • [21] J. Hensman, N. Fusi, and N. D. Lawrence. Gaussian processes for big data. In UAI, 2013.
  • [22] J. Hensman, A. G. d. G. Matthews, and Z. Ghahramani. Scalable variational Gaussian process classification. In ICML, 2015.
  • [23] S. Hochreiter and J. Schmidhuber. Flat minima. Neural Computation, 9(1):1–42, 1997.
  • [24] G. Huang, Z. Liu, K. Q. Weinberger, and L. van der Maaten. Densely connected convolutional networks. In CVPR, 2017.
  • [25] M. F. Hutchinson. A stochastic estimator of the trace of the influence matrix for laplacian smoothing splines. Communications in Statistics-Simulation and Computation, 19(2):433–450, 1990.
  • [26] S. Ioffe and C. Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In ICML, 2015.
  • [27] P. Izmailov, D. Podoprikhin, T. Garipov, D. Vetrov, and A. G. Wilson. Averaging weights leads to wider optima and better generalization. In Uncertainty in Artificial Intelligence (UAI), 2018.
  • [28] Y. Jia, E. Shelhamer, J. Donahue, S. Karayev, J. Long, R. Girshick, S. Guadarrama, and T. Darrell. Caffe: Convolutional architecture for fast feature embedding. In ACMMM, pages 675–678. ACM, 2014.
  • [29] N. S. Keskar, D. Mudigere, J. Nocedal, M. Smelyanskiy, and P. T. P. Tang. On large-batch training for deep learning: Generalization gap and sharp minima. arXiv preprint arXiv:1609.04836, 2016.
  • [30] A. Krizhevsky, I. Sutskever, and G. E. Hinton. Imagenet classification with deep convolutional neural networks. In NIPS, 2012.
  • [31] A. Krizhevsky, I. Sutskever, and G. E. Hinton. Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems, pages 1097–1105, 2012.
  • [32] C. Lanczos. An iteration method for the solution of the eigenvalue problem of linear differential and integral operators. United States Governm. Press Office Los Angeles, CA, 1950.
  • [33] A. G. d. G. Matthews, M. van der Wilk, T. Nickson, K. Fujii, A. Boukouvalas, P. León-Villagrá, Z. Ghahramani, and J. Hensman. Gpflow: A Gaussian process library using TensorFlow. Journal of Machine Learning Research, 18(40):1–6, 2017.
  • [34] I. Murray. Gaussian processes and fast matrix-vector multiplies. In ICML Workshop on Numerical Mathematics in Machine Learning, 2009.
  • [35] D. P. O’Leary. The block conjugate gradient algorithm and related methods. Linear algebra and its applications, 29:293–322, 1980.
  • [36] C. Paige. Practical use of the symmetric Lanczos process with re-orthogonalization. BIT Numerical Mathematics, 10(2):183–195, 1970.
  • [37] B. N. Parlett. A new look at the Lanczos algorithm for solving symmetric systems of linear equations. Linear algebra and its applications, 29:323–346, 1980.
  • [38] A. Paszke, S. Gross, S. Chintala, G. Chanan, E. Yang, Z. DeVito, Z. Lin, A. Desmaison, L. Antiga, and A. Lerer. Automatic differentiation in PyTorch. 2017.
  • [39] G. Pleiss, J. R. Gardner, K. Q. Weinberger, and A. G. Wilson. Constant-time predictive distributions for Gaussian processes. In ICML, 2018.
  • [40] J. Quiñonero-Candela and C. E. Rasmussen. A unifying view of sparse approximate Gaussian process regression. Journal of Machine Learning Research, 6(Dec):1939–1959, 2005.
  • [41] C. E. Rasmussen and C. K. Williams. Gaussian processes for machine learning, volume 1. MIT press Cambridge, 2006.
  • [42] Y. Saad. Iterative methods for sparse linear systems, volume 82. siam, 2003.
  • [43] Y. Saatçi. Scalable inference for structured Gaussian process models. PhD thesis, University of Cambridge, 2012.
  • [44] E. Snelson and Z. Ghahramani. Sparse Gaussian processes using pseudo-inputs. In NIPS, 2006.
  • [45] M. K. Titsias. Variational learning of inducing variables in sparse Gaussian processes. In AISTATS, pages 567–574, 2009.
  • [46] S. Ubaru, J. Chen, and Y. Saad. Fast estimation of tr (f (a)) via stochastic Lanczos quadrature. SIAM Journal on Matrix Analysis and Applications, 38(4):1075–1099, 2017.
  • [47] H. A. Van der Vorst. Iterative Krylov methods for large linear systems, volume 13. Cambridge University Press, 2003.
  • [48] A. J. Wathen and S. Zhu. On spectral distribution of kernel matrices related to radial basis functions. Numerical Algorithms, 70(4):709–726, 2015.
  • [49] A. G. Wilson. Covariance kernels for fast automatic pattern discovery and extrapolation with Gaussian processes. PhD thesis, University of Cambridge, 2014.
  • [50] A. G. Wilson and H. Nickisch. Kernel interpolation for scalable structured Gaussian processes (KISS-GP). In ICML, 2015.
  • [51] A. G. Wilson, C. Dann, and H. Nickisch. Thoughts on massively scalable Gaussian processes. arXiv preprint arXiv:1511.01870, 2015.
  • [52] A. G. Wilson, Z. Hu, R. Salakhutdinov, and E. P. Xing. Deep kernel learning. In AISTATS, 2016.
  • [53] A. G. Wilson, Z. Hu, R. R. Salakhutdinov, and E. P. Xing. Stochastic variational deep kernel learning. In NIPS, 2016.