无监督之聚类与降维任务--线性模型(Clusting、PCA、NMF)
无监督学习之线性模型(clustering、PCA、MF)
1 无监督学习总览
我们都知道,有监督数据是十分宝贵的。一般来说我们获取data很容易,但获取label却比较困难。因此,无监督学习在机器学习中十分关键。如何利用好大量的无监督数据,对于业务冷启动和持续迭代运行,都至关重要。
无监督学习大致分为
- 化繁为简。又包括
- 聚类,将无监督数据合并为一个个cluster。cluster内数据相似,cluster间数据不相似。
- 降维,特征提取。对无监督数据,比如图像、文本,提取特征。比如PCA、Auto-Encoder、MF
- 无中生有,主要就是各种生成模型。
本文主要讲无监督中的线性模型。包括clustering、PCA、MF等
2 聚类 Clustering
2.1 聚类种类
聚类在实际业务中十分重要,特别是业务冷启动的时候。可以用来做意图类别挖掘、知识库生产、话题挖掘等。还可以结合打标数据,实现标注数据噪声发现。聚类算法很多,如下
- 划分聚类 k-means、k-medoids、k-modes、k-medians、kernel k-means
- 层次聚类 Agglomerative 、divisive、BIRCH、ROCK、Chameleon、HAC
- 密度聚类 DBSCAN、OPTICS、HDBScan
- 网格聚类 STING
- 模型聚类 GMM
- 图聚类 Spectral Clustering(谱聚类)
2.2 聚类算法步骤(k-means、DBScan)
其中k-means步骤为:
- 随机选取k个值作为初始均值向量(冷启动)
- 将样本放入距离最近的均值向量簇中
- 簇构造好后,重新计算均值向量
- 迭代第二步
- 直到两次迭代的结果簇完全相同,则停止
DBScan步骤:
先基于邻域参数,最小距离,最小簇size,计算所有可能的core
从core中选一个,计算器密度可达的所有样本,将包含的core从core集合中去掉
剩余core集合中继续执行第二步
core集合为空,或无法产生新聚类,则结束
2.3 聚类评价指标
聚类评价指标分为如下,sklearn均实现了它们,直接调用即可
- 无验证集,DBI,DB指数
- 有验证集,rand兰德系数,NMI互信息,homogeneity同质性等
3 PCA 主成分分析
PCA(Principe Component Analysis),利用降维的思想,将多指标转化为少数几个指标。比如对于人脸识别,转化为识别眼睛、鼻子、嘴巴等。这就是为啥叫主成分分析的意思了。
PCA是一个线性变换,它将数据变换到新的坐标系中,任何数据投影的第一大方差在第一个坐标上(第一主成分),第二大方差在第二个坐标上(第二主成分),以此类推。PCA的思想是,降维的同时,保留对数据方差贡献大的特征。这些特征就是数据的主要特征,称为主成分。
如下图是在一维空间上的PCA,数据投影方差最大的方向,即为第一主成分,也就是最重要的特征。
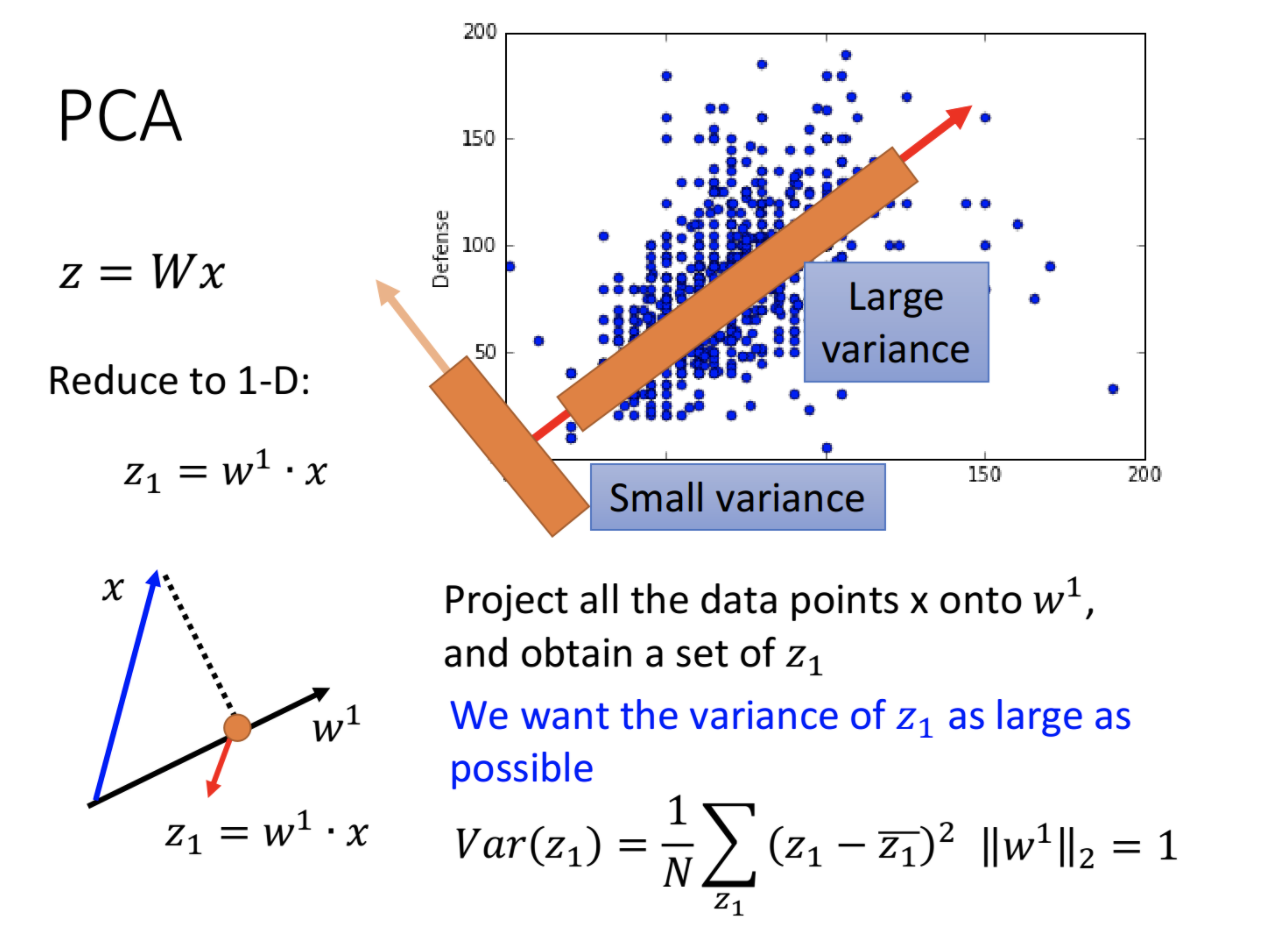
通过PCA可以找到数据的主要特征,如下图可以找到数字7,由三个最主要特征构成。
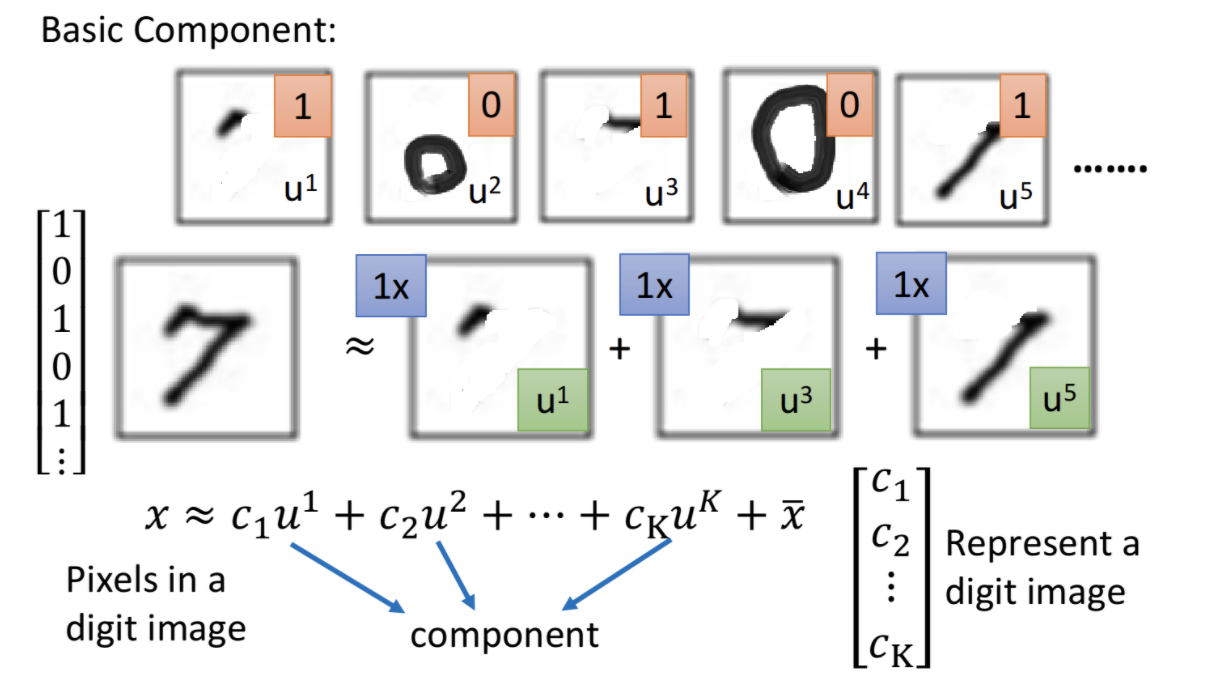
PCA的缺点有
- 无监督的,准确性差一些。基于有监督的LDA效果更好,但需要监督数据。
- 线性模型,捕获的特征还是太浅层了。相比可以基于深度模型的Auto-Encoder,特征提取能力要弱很多。
4 MF 矩阵分解
矩阵分解也可以得到基础组件和特征。利用SVD可实现矩阵分解。下面是通过MF提取的手写字识别的特征。可以看到,基本的笔画可以被提取出来。







