大型空间数据分析方法案例及评测

【摘 要】 高斯过程是空间数据分析人员不可或缺的工具。然而，“大数据” 时代的到来导致传统高斯过程在计算上对现代空间数据不可行。因此，已经提出了更适合处理大空间数据的完全高斯过程的多种替代方案。这些现代方法通常利用低秩结构和/或多核和多线程计算环境来促进计算。本研究首先介绍性地概述了几种分析大型空间数据的方法。然后，阐述了由不同组实施的方法之间的预测评测结果。具体来说，每个研究组都得到了两个训练数据集（一个模拟数据集和一个观测数据集）以及一组预测位置。然后，各组实现自己的方法，并在给定位置处生成预测，每组的成果都在公共计算环境中运行。然后根据各种预测诊断对这些方法进行了比较。有关方法和代码的实现细节的补充材料可在线。

【原 文】 M. J. Heaton et al., “A Case Study Competition Among Methods for Analyzing Large Spatial Data,” Journal of Agricultural, Biological and Environmental Statistics, vol. 24, no. 3, pp. 398–425, Sep. 2019, doi: 10.1007/s_13253-018-00348-w.

【补充材料】https://static-content.springer.com/esm/art%3A10.1007%2Fs13253-018-00348-w/MediaObjects/13253_2018_348_MOESM1_ESM.pdf

【参考】

• 大数据时代的可扩展高斯过程综述

1 引言

（1）背景

几十年来，高斯过程 (GP) 一直是用于分析点参考空间数据的主要工具（Schabenberger 和 Gotway 2004 ^[70]；Cressie 1993 ^[9]；Cressie 和 Wikle 2015 ^[12]；Banerjee 等 2014 ^[2]）。当空间过程 $\mathbf{Y}(\mathbf{s}), \mathbf{s} \in \mathcal{D} \subset \mathbb{R}^2$ 在有限数量的位置 $\mathbf{s}_1,\ldots,\mathbf{s}_N$ 上的任意实现 $\mathbf{Y}=(Y(\mathbf{s}_1),\ldots,Y(\mathbf{s}_N))$ 服从 $N$ 元高斯分布时，我们称其服从高斯过程。 更具体地说，令 $\mu (\mathbf{s}) : \mathcal{D} \rightarrow \mathbb{R}$ 表示能够返回位置 $\mathbf{s}$ 处均值的均值函数，$\mu(\mathbf{s})$ 通常其被建模为协变量 $\mathbf{X}(\mathbf{s}) = (1, X_1(\mathbf{s}),\ldots,X_P (\mathbf{s}))^T )$ 的线性函数；令 $\mathbb{C}(\mathbf{s}_1, \mathbf{s}_2) : \mathcal{D}^2 \rightarrow \mathbb{R}^+$ 表示正定的协方差函数。当空间过程 $Y(\mathbf{s})$ 服从高斯过程时，所有采样点处的区域化变量构成的向量 $\mathbf{Y}$ 应当具有如下形式的多元高斯密度函数： $$ f_{\boldsymbol{Y}}(\boldsymbol{y})=\left(\frac{1}{\sqrt{2 \pi}}\right)^N|\boldsymbol{\Sigma}|^{-1 / 2} \exp \left\{-\frac{1}{2}(\boldsymbol{y}-\boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1}(\boldsymbol{y}-\boldsymbol{\mu})\right\} \tag{1} $$ 其中 $\boldsymbol{\mu} = (\mu (\mathbf{s}_1), \ldots , \mu (\mathbf{s}_N ))^T$ 为均值向量，${\boldsymbol{\Sigma}}=\{\mathbb{C}(\mathbf{s}_i , \mathbf{s}_j)\}_{ij}$ 是由协方差函数 $\mathbb{C}(\mathbf{s}_i ,\mathbf{s}_j)$ (如 Matérn 函数）控制的协方差矩阵。多元高斯分布吸引人的特性（如高斯边缘分布和高斯条件分布等）是使高斯过程成为空间数据分析人员执行克里金法（空间预测）和不确定性量化等任务时不可或缺的工具。 然而，随着现代越来越大的空间数据集出现，高斯过程在科学发现中的使用遇到了计算难处理的瓶颈。具体来说，估值 `式(1)` 中的密度需要 $\mathcal{O}(N^3)$ 运算和 $\mathcal{O}(N^2)$ 内存，当 $N$ 相当大时，这会很快压倒计算系统。 **（2）前期解决方案** 此问题的早期解决方案包括： - **精度矩阵稀疏化**： - `条件分解法`：将 `式(1)` 分解为一系列条件分布（Vecchia 1988 ^[83]；Stein 等 2004 ^[76]）， - `组合似然法`：使用组合似然（Varin 等 2011 ^[82]；Eidsvik 等 2014 ^[18]） - `多分辨率法`：Katzfuss 2017,^[47]，Katzfuss 2017a,^[49] - `最近邻高斯过程`：Datta 等 2016b ^[15] - `随机偏微分方程`：Lindgren 等 2011 年^[58]。 - **协方差矩阵稀疏化**： - `空间分区法`： - `协方差函数锥化`：Furrer 等 2006 年^[26]；Kaufman 等 2008 年^[51]；Stein 2013 年^[73]。 - **低秩近似方法**：从 2000 年代末开始，业内开发（或流行）了几种基于高斯过程的低秩近似方法，包括： - `固定秩克里金法`：Cressie 和 Johannesson 2008 ^[11]；Kang 和 Cressie 2011 年^[46]；Katzfuss 和 Cressie 2011 年^[48] - `预测过程`（Banerjee 等 2008 年^[3]；Finley 等 2009 年^[22]） - `格子克里金法`：Nychka 等 2015 年^[64] - **其他重要方法** - `谱域转换法`：在谱域计算 (Fuentes 2007 ^[23]) - `离散过程卷积`：Higdon 2002 ^[42]；Lemos 和 Sansó 2009 ^[56] Sun 等 (2012) ^[77]、Bradley 等(2016)^[6] 和 Liu 等 (2018)^[60] 对这些方法进行了特别的综述，并证明了它们对空间数据建模的有效性。 **（3）近期趋势** 但在经过几年使用后，科学家们开始观察到上述近似高斯过程方法的缺点，例如：过度平滑的倾向（Simpson 等，2012 年^[71]；Stjin，2014 年^[74]），甚至有一些方法还存在可建模数据集大小的上限。因此， **该领域最近的科学研究，主要集中在现代计算平台的高效使用和可并行化方法的开发上**。例如： - Paciorek 等 (2015)^[65] 表明 `式 (1)` 可以使用并行计算计算 - Katzfuss 和 Hammerling (2017)^[50] 以及 Katzfuss (2017)^[47] 开发了一种适用于分布式计算的基函数方法。 - Barbian 和 Assunção (2017)^[4] 以及 Guhaniyogi 和 Banerjee (2018)^[36] 建议将数据划分为大量子集后，并行地对子集进行推断，然后再组合推断。 - Datta 等 (2016a,2016c) ^[14][16] 在 Vecchia (1988)^[83] 的基础上，开发了将 `式 (1)` 分解为一系列仅基于最近邻条件分布的新方法。 鉴于分析大型空间相关数据的选择过多，在本文中，我们不仅寻求提供关于海量空间数据分析现代方法的概述，还将对这些方法进行简单比较。具体来说，本研究实施了 Wikle 等 (2017)^[87] 的公共任务框架，描述了全球各研究组案例评测的结果（参与评测的研究组参见 `表 1` ）。各研究组都实现了自己的方法，并用于分析相同的空间数据集。 我们向几个研究组提供了两个空间数据集，其中一个是模拟的，另一个是真实的。每个数据集的一部分被预留出来以验证预测效果（没有向研究组提供预留部分，因此本研究是 “摸黑” 评测）。模拟数据代表了高斯过程假设有效的场景（即正确指定了的模型），而真实数据集则面向模型可能由于固有非平稳性或非高斯错误而被错误指定的场景。每个组都实施了自己独特的方法，并在预留位置处提供了空间过程的预测结果（包括预测区间或标准差）。这些预测由第三方进行了比较，并在本文中进行了总结。 本文描述的案例研究评测独特而新颖，因为通常情况下，各种方法的比较/审查是由实施该方法的研究组自行完成的（参见 Sun 等 2012 年^[77]；Bradley 等 2016 年^[6]）。然而，单个研究组可能或多或少熟悉某些方法，导致对不太熟悉的方法进行了可能不公平的比较。相比之下，对于本文的比较/评测，每种方法都由一个研究组实施的，该研究组对于该方法具有丰富的专业知识，并且精通与使用相关的任何可能的复杂性。此外，与 Sun 等 (2012)^[77]、Bradley 等 (2016)^[6] 的评论不同，我们还比较了每种方法对预测不确定性的量化能力。 **（4）论文贡献** 本文的主要科学贡献在于： - (1) 一个有价值的综述； - (2) 讨论了大型数据集空间分析方法的一个独特案例比较研究； - (3) 为从业者提供了实施每种方法的代码（参见补充材料)； - (4) 提供了与每种方法相关的不确定性量化的比较； - (5) 建立了未来研究在比较各种分析方法时要服从的框架。 **（5）论文结构** 本文的其余部分安排如下。 - 第 2 节简要介绍了每种方法的背景。 - 第 3 节提供了比较设置以及数据集的背景。 - 第 4 节总结了预测准确性、不确定性量化和计算时间方面的比较结果。 - 第 5 节得出结论，并强调了海量空间数据分析的未来研究领域。 ## 2 大空间数据分析方法概述 本节简要概述了本案例研究评测中的参赛者。为方便起见，我们将方法分为以下类别： - **降秩方法**：降低 $N × N$ 矩阵的秩，从而减少计算所需时间 - **稀疏协方差矩阵法**：通过在协方差矩阵中引入大量 “0” 来加速计算 - **稀疏精度矩阵法**：通过在精度矩阵中引入引入大量 “0” 以加速计算 - **算法**：这可能是定义最模糊的类别，更侧重于拟合算法，而不是模型构建。 上述类别是我们的主观分类，纯粹是为了便于说明。与其他任何主观分组一样，某些方法可能包括各种类别的片段。因此，我们强烈鼓励将方法作为一个整体来看待，而不是仅仅依从于我们的主观分类。

注解： Liu 等在 综述文献 ^[60] 中，根据模型的局部性将方法分为 全局近似 和 局部近似 两种大类。 在 Huang 等的 评测文章 中，将参与比赛的方法分为 组合似然法、降秩方法、稀疏协方差矩阵（或精度矩阵）法 和 其他组合或扩展方法。

### 2.1 降秩方法 #### 2.1.1 固定秩克里金法 固定秩克里金法（ FRK ）（Cressie 和 Johannesson，2006 年^[10]、2008 年^[11] ）是围绕空间随机效应模型的概念构建的。在 FRK 中，空间过程 $\tilde{Y}(\mathbf{s}), s \in \mathcal{D}$, 被建模为 $$ \tilde{Y}(\mathbf{s}) = \mu (\mathbf{s}) + w(\mathbf{s}) + ξ(\mathbf{s}), \mathbf{s} \in \mathcal{D} \tag{2} $$ 其中： - $\mu (\mathbf{s})$ 是均值函数，它本身被建模为已知协变量的线性组合，即 $\mu (\mathbf{s}) = \mathbf{X}^T (\mathbf{s}) \boldsymbol{\beta}$，其中 $\mathbf{X}(\mathbf{s})$ 是在位置 $\mathbf{s}$ 处评估的协变量向量，$\boldsymbol{\beta}$ 是相应的系数 - $w(\mathbf{s})$ 是一个平滑尺度过程 - $ξ(\mathbf{s})$ 是一个精细尺度的过程，其方差 $\sigma^2_ξ v(\mathbf{s})$ 被建模为与空间无关， $v(\mathbf{s})$ 是已知加权函数。 `式 (2)` 中的过程 $ξ(\mathbf{s})$ 旨在容纳 $\tilde{Y}(\mathbf{s})$ 中未被 $w(\mathbf{s})$ 考虑到的可变性。 FRK 的主要假设是： 空间过程 $w(·)$ 可以通过 $K$ 个基函数 $\mathbf{h}(\mathbf{s}) = (h_1(\mathbf{s}),\ldots,h_K (\mathbf{s}))^T, \mathbf{s} \in \mathcal{D}$ 和 $K$ 个基函数系数 $\boldsymbol{w}^* = (w^*_1,\ldots,w^*_K )^T$ 的线性组合来近似得到： $$ w(\mathbf{s}) \approx \tilde{w} (\mathbf{s}) = \sum^K_{k=1} h_k(\mathbf{s}) w^*_k,\quad \mathbf{s} \in \mathcal{D} \tag{3} $$ 使用 $K$ 个基函数，可以确保所有估计和预测方程中仅包含大小为 $K × K$ 的矩阵和逆矩阵，而 $K \ll N$。实际上，`式 (3)` 中的基函数集合 $\{h_k(·)\}$ 可以由 $R$ 个不同分辨率的函数组成，因此 `式 (3)` 也可以写成： $$ \tilde{w}(\mathbf{s})= \sum^R_{r=1} \sum^K_{k=1} h_{rk}(\mathbf{s}) w^*_{rk},\quad \mathbf{s} \in \mathcal{D} \tag{4} $$ 其中 $h_{rk}(\mathbf{s})$ 是第 $r$ 个分辨率下的第 $k$ 个基函数，其系数为 $w^*_{rk}$。令 $K_r$ 是第 $r$ 个分辨率下基函数的数量，则 $K = \sum^R_{r=1} K_r$ 是使用的总基函数数量。在本次实验中，我们使用了 $r = 3$ 个分辨率的 `双平方基函数`，总共有 $K = 475$ 个基函数。 系数向量 $\boldsymbol{w}^* = (w^*_{rk}: \, r = 1,\ldots,R; k = 1,\ldots,K_r)^T$ 被视为随机的，具有协方差矩阵 $\operatorname{Var}(\boldsymbol{w}^*) = {\boldsymbol{\Sigma}}_{w^*}(\boldsymbol{\theta})$，其中参数 $\boldsymbol{\theta}$ 是需要估计的。在这项工作中，${\boldsymbol{\Sigma}}_{w^*}(\boldsymbol{\theta})$ 是由 $R$ 个稠密矩阵组成的块对角矩阵，其中第 $r$ 个块的第 $(i, j)$ 个元素为 $\sigma^2_r \exp(−d_r (i, j)/\phi_r)$，其中 $d_r (i, j)$ 是第 $r$ 个分辨率下第 $i$ 个和第 $j$ 个基函数的质心之间的距离； $\sigma^2_r$ 为第 $r$ 个分辨率的方差； $\phi_r$ 为指数族的相关函数在第 $r$ 个分辨率下的参数； $\boldsymbol{\theta} = (\sigma^2_1 ,\ldots,\sigma^2_R,\phi_1,\ldots,\phi_R)^T$。请注意，${\boldsymbol{\Sigma}}_{w^*}(\boldsymbol{\theta})$ 也可以是非结构化的，在这种情况下需要估计 $K (K + 1)/2$ 个参数；但是，这里不考虑这种情况。 FRK 有多种变体。在这项工作中，我们使用 Zammit-Mangion 和 Cressie (2018) ^[88] 的实现，它以 R 包的形式出现，可从 CRAN 获得。在本文中，我们使用该软件包的 v0.1.6 版本。在 FRK 中，假设在 $\mathbf{s}_i$ 处评估的过程 $\tilde{Y}(\mathbf{s}_i)$ 具有测量误差 $ε(\mathbf{s}_i )$。因此，数据模型由下式给出： $$ Y (\mathbf{s}_i ) = \mu (\mathbf{s}_i ) + \tilde{w} (\mathbf{s}_i ) + ξ(\mathbf{s}_i ) + ε(\mathbf{s}_i ), i = 1,\ldots,N \tag{5} $$ 其中 $ε(\mathbf{s}_i)$ 表示独立同正态分布的测量误差，均值为 $0$，测量误差方差为 $\sigma^2_ε$ 。在此模型规格下，在所有 $N$ 个观测位置评估的 $Y (·)$ 的联合模型是： $$ \mathbf{Y} = \mathbf{X} \boldsymbol{\beta} + \mathbf{H} \boldsymbol{w}^* + \boldsymbol{ξ} + \boldsymbol{ε} \tag{6} $$ 其中 $\mathbf{X}$ 是设计矩阵； $\boldsymbol{\beta}$ 是回归系数； $\mathbf{H}$ 是具有相关随机系数 $\boldsymbol{w}^* \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{\Sigma}_{w^*}(\boldsymbol{\theta}))$ 的空间基函数的 $N × K$ 矩阵； $\boldsymbol{ξ} \sim \mathcal{N} (0,σ^2_ξ \mathbf{D})$ 其中 $\mathbf{D}$ 是由用户指定的已知对角权重矩阵（这里我们只使用等方差设置 $\mathbf{D} = \mathbf{I}$，但实际工作中不一定全是这种情况）；$\boldsymbol{ε} \sim \mathcal{N}(\boldsymbol{0},σ^2_ε \mathbf{I})$。 FRK 包首先使用半变异函数和最大似然技术的组合来估计参数 $\boldsymbol{\theta}$ 、$σ^2_ξ$ 和 $\sigma^2_ε$（参见 Kang 等，2009 年），然后使用 “plugged-in” 的估计参数进行预测。更多关于本研究中 FRK 实施的信息参见补充材料。

延续了克里金的经验贝叶斯方法。首先根据观测数据估计半变异函数，然后将半变异函数引入克里金预测方程，得到预测值和预测方差。详情参见 点参考数据与克里金法。

#### 2.1.2 预测过程法

个人理解：预测过程法本质上就是稀疏高斯过程在空间领域的推广。该方法不使用原始测点数据，而是引入 归纳点 的概念，然后基于构建高斯过程，由于数量该大大小于原始测点数量，所以能够显著减少参与计算的测点数量，实现了协方差矩阵的降秩。 参见《稀疏高斯过程及其变分推断方法》

对于 `预测过程 (Predictive-processss, PP)` 法 ^[3] ，让 $\mathbf{s}^*_1,\ldots,\mathbf{s}^*_K$ 表示一组很好地分散在空间域 $\mathcal{D}$ 上的 “结（knots）” 位置。假设 `式 (2)` 的空间随机效应 $w(\mathbf{s})$ 服从协方差函数为 $\mathbb{C}(\mathbf{s},\mathbf{s}^\prime) = \sigma^2_w ρ(\mathbf{s},\mathbf{s}^\prime)$ 的零均值高斯过程，其中 $ρ(·,·)$ 是正定相关函数。在这个高斯过程假设下，空间随机效应 $\boldsymbol{w}^*= (w^*(\mathbf{s}^*_1),\ldots, w(\mathbf{s}^*_K))^T \sim \mathcal{N}(0, \boldsymbol{\Sigma}_{w^*})$ 其中 $\boldsymbol{\Sigma}_{w^*}$ 是 $K × K$ 协方差矩阵，其中第 $ij$ 个元素为 $\mathbb{C}(\mathbf{s}^*_i ,\mathbf{s}^*_j)$。预测过程法利用了空间随机效应的高斯过程假设，并将 `式 (2)` 中的 $w(\mathbf{s})$ 替换为： $$ \tilde{w}(\mathbf{s})= \mathbb{C}^T(\mathbf{s},\mathbf{s}^*) \boldsymbol{\Sigma}^{−1}_{w^*} \boldsymbol{w}^* \tag{7} $$ 其中 $\mathbb{C}(\mathbf{s},\mathbf{s}^* ) = (\mathbb{C}(s, \mathbf{s}^*_1),\ldots,\mathbb{C}(\mathbf{s},\mathbf{s}^*_K ))$。注意， `式 (7)` 可以等效地写成上面在 `式 (3)` 中给出的基函数表达式，其中基函数是 $\mathbb{C}^T(\mathbf{s},\mathbf{s}^* ) \boldsymbol{\Sigma}^{-1}_{w^*}$，而 $\boldsymbol{w}^*$ 有效地起到基函数系数的作用。 在 `第 4 节` 的后续分析中，我们应用了一个相当粗糙的 $14×14$ 个结的网格，以平衡计算时间和预测性能。将结数增加到超过 $196$ 可以进一步改进推断结果，但其代价是运行时间更长。 Finley 等 (2009)^[22] 注意到 `式 (7)` 中的基函数扩展方式会系统地低估原始过程的边缘方差 $\sigma^2_w$。即 $\operatorname{Var}(\tilde{w} (\mathbf{s})) = \mathbb{C}^T(\mathbf{s}，\mathbf{s}^*) \boldsymbol{\Sigma}^{-1}_{w^*} \mathbb{C}^T (\mathbf{s},\mathbf{s}^*) \leq \sigma^2_w$。为了克服该问题，Finley 等 (2009) ^[22] 使用 `式 (5)` 中的结构， $$ Y (\mathbf{s}) = \mu (\mathbf{s}) + \tilde{w} (\mathbf{s}) + ξ(\mathbf{s}) + ε(\mathbf{s})a \tag{8} $$ 其中 $ξ(\mathbf{s})$ 在空间上独立，且服从分布 $\mathcal{N}(0,\sigma^2_w − \mathbb{C}^T (\mathbf{s},\mathbf{s}^*) \boldsymbol{\Sigma^{-1}_{w^*}} \mathbb{C}^T (\mathbf{s},\mathbf{s}^*))$，进而有 $\operatorname{Var}( \tilde{w} (\mathbf{s}) + ξ(\mathbf{s})) = \sigma^2_w$ ，与原始父进程保持一致。 `式 (8)` 中的这种优化调整被称为 “改进的预测过程”，是本次评测中使用的方法。 与 FRK 一样， `式 (8)` 的似然只需要计算 $K × K$ 密集矩阵和 $N × N$ 对角矩阵的逆与行列式，这在 $K \ll N$ 时会节省大量计算。与 FRK 或 LatticeKrig 相比，预测过程法的一个技术优势是： **基函数完全由协方差函数 $\mathbb{C}(·,·)$ 决定**。因此，即使在考虑建模复杂性（例如各向异性、非平稳性甚至多变量过程）时，预测过程法也不会有太大改变。但与此同时，当 $\mathbb{C}(·,·)$ 由未知参数控制时（几乎总是如此），预测过程法的基函数需要迭代计算，而不是像 FRK 或 LatticeKrig 那样一次性计算，这将增加计算时间。 #### 2.1.3 格子克里格 LatticeKrig（ Nychka 等，2015 年^[64]）使用与 FRK 几乎相同的设置。 具体来说，LatticeKrig 假设 `式 (6)` 的模型但省略了精细尺度过程 $ξ(·)$。对于矩阵 $\mathbf{H}$，LatticeKrig 也服从 `式 (4)` 中的多分辨率方法，但 LatticeKrig 使用与 FRK 不同的结构和约束。 首先，每个分辨率的边缘方差表示为 $\mathbf{h}^T_r(\mathbf{s}) \boldsymbol{w}^*_r$，其中 $\mathbf{h}^T_r (\mathbf{s}) = (h_{r1}(\mathbf{s}),\ldots,h_{rK_r}(\mathbf{s}))^T$ 是第 $r$ 个分辨率的基函数，具有系数 $\boldsymbol{w}^*_r = (w^*_{r1} ,\ldots,w^*_{rK_r})^T$，这些系数被约束为 $\sigma^2_{w^*} \alpha r$ ，其中 $\sigma^2_{w^*}, \alpha_r > 0$ 并且 $\sum^R_{r=1} \alpha_r = 1$。为了进一步减少参数数量，LatticeKrig 令 $\alpha_r \sim r^{−ν}$，其中 $ν$ 是一个自由参数。 LatticeKrig 通过以下方式平移和缩放径向函数来得到多分辨率的径向基函数。对于 $r = 1,\ldots,R$ 和 $k = 1,\ldots,Kr$，令 $u_{rk}$ 表示 $D$ 上对应于分辨率 $r$ 的、包含 $Kr$ 个点的规则网格。对于本文试验，LatticeKrig 定义 $$ h_{rk}(\mathbf{s}) = \psi ( \| \mathbf{s} − \mathbf{u}_{rk} \| / \lambda_r ) \tag{11} $$ 其中距离被认为是欧几里德距离，因为在这种情况下空间区域的地理范围很小并且 $\lambda_r = 2^{−r}$ 。此外，LatticeKrig 定义 $$ \psi(d) \propto \left\{ \begin{array}{ll} \frac{1}{3}(1-d)^{6} \left( 35 d^{2} + 18 d +3 \right) & \text { if } d \leq 1 \\ 0 & \text { otherwise } \end{array} \right. \tag{12} $$ 这是 Wendland 多项式并且是正定的（当基用于插值时，这是一个有吸引力的属性）。最后，在每个分辨率下将 `式(12)` 中的基函数做归一化，以便所有 $\mathbf{s}$ 处的过程边缘方差为 $\sigma^2_{w^*} \alpha_r$ 。这减少了边缘效应，并有助于更好地逼近平稳协方差函数。 LatticeKrig 假设每个分辨率的系数 $\boldsymbol{w}^*_r = (w^*_{r1} ,\ldots,w^*_{rK_r} )^T$ 是独立的（类似于 FRK 中使用的块对角线结构）并服从协方差为 $\mathbf{Q}^{-1}_r (\phi_r)$ 的多元正态分布，其中协方差被单个参数 $\phi_r$ 参数化。因为位置 $\{\mathbf{u}_{rk}\}^{K_r}_{k=1}$ 被规定为规则网格，LatticeKrig 可以为协方差矩阵 $\mathbf{Q}^{-1}_r (\phi_r)$ 使用空间自回归/马尔可夫随机场结构（参见 Banerjee 等，2014 年 ^[2]，第 4.4 节），进而产生了稀疏性和计算易处理性。此外，由于精度矩阵 $\mathbf{Q}_r (\phi_r)$ 是稀疏的，LatticeKrig 可以将 $K$ 设置得非常大（如本次评测中 $K = 136, 000 > N$ ），而无需太多额外的计算成本。本文的补充材料包含有关本案例研究中使用的 LatticeKrig 实施的其他信息。 ### 2.2 稀疏协方差矩阵法 #### 2.2.1 空间分区 设空间域 $\mathcal{D} = \cup^D_{d=1} \mathcal{D}_{d}$，其中 $\mathcal{D}_1,\ldots,\mathcal{D}_D$ 是构成了某种区域剖分的子区域（即对于所有 $d1 = d2$，有 $\mathcal{D}_{d_1} ⋂ \mathcal{D}_{d_2} =∅$）。基于空间剖分的建模方法再次使用了 `式（6）` 的模型，但假设不同子区域的观测值之间相互独立。更具体地说，如果令 $\mathbf{Y}_d =\{Y (\mathbf{s}_i ) : \mathbf{s}_i \in \mathcal{D}_d \}$，其中 $d = 1,\ldots,D$，则有： $$ \mathbf{Y}_d = \mathbf{X}_d \boldsymbol{\beta} + \mathbf{H}_d \boldsymbol{w}^* + \boldsymbol{ξ}_d + \boldsymbol{ε}_d \tag{9} $$ 其中 $\mathbf{X}_d$ 是与 $\mathbf{Y}_d$ 对应的协变量构成的设计矩阵，$\mathbf{H}_d$ 是空间基函数矩阵（类似于预测过程法、FRK 或 LatticeKrig ），$\boldsymbol{ξ}_d$ 和 $\boldsymbol{ε}_d$ 是关于区域 $d$ 的 $\boldsymbol{ξ}$ 和 $\boldsymbol{ε}$ 的子向量。需要注意的是：在 `式 (9)` 中，所有子区域共享相同的 $\boldsymbol{\beta}$ 和 $\boldsymbol{w}^*$ 参数，而不考虑独立性假设，以允许跨子区域的平滑。更进一步，跨子区域的独立性假设为协方差矩阵 $\boldsymbol{\Sigma}$ 创建了一个块对角矩阵结构，同时使该方法具备了并行计算的可能性（每个子区域一个计算节点）。 这种空间方法本质上不同于 “分而治之” 的方法（Liang 等，2013 年^[57]；Barbian 和 Assunção，2017 年^[4]）。因为在分而治之的方法中，整个数据集被二次采样，模型适用于所有子集，并且所有子样本的结果会被合并。相比之下，空间分区方法在估计时同时使用所有数据，没有二次采样过程，不同子区域的模型也不相同，只是跨区域的独立性有利于降低计算成本。 实施空间分区方法的关键是分区方案，现有文献中充斥着各种选择。定义空间分区的先验方法包括将区域划分为相等的区域 (Sang et al. 2011 ^[69])、基于质心聚类的分区 (Knorr-Held and Raßer 2000 ^[54]; Kim et al. 2005 ^[52]) 和基于空间梯度的层次聚类 ( Anderson 等 2014 年^[1]；Heaton 等 2017 年^[41]）。或者，基于模型的空间分区方法包括：树回归（Konomi 等，2014 年 ^[55]）和混合建模（Neelon 等，2014 年 ^[63]），但这些方法通常需要更多计算。 本文中的分析考虑了几种不同的分区方案，但每种方案都会产生与训练数据近似等效的模型。因此，根据训练数据的结果，对于下面的评测，我们使用了每个子区域包含大约 $6000$ 个观测值的等面积分区。 #### 2.2.2 协方差锥化 协方差椎化的想法基于这样一个事实，即 `式 (1)` 中的协方差矩阵中的许多条目都接近于零，并且相应位置对可以被认为本质上是独立的。协方差锥化将协方差函数 $\mathbb{C}(\mathbf{s}_i , \mathbf{s}_j )$ 与紧支撑协方差函数相乘，得到另一个具有紧支撑的正定协方差函数。从理论角度来看，协方差椎化（在渐近内插框架内）使用了 “高斯等效度量” 的概念，以及 “被错误指定的协方差函数”（例如，参见 Stein 1999 ^[72] 和其中的参考文献）。随后，Furrer 等 (2006) ^[26] 假设了二阶平稳和各向同性的 Matérn 协方差，以显示在锥化情况下预测的渐近最优性。这个想法已经扩展到不同的协方差结构 (Stein 2013) ^[73]、非高斯响应 (Hirano and Yajima 2013)^[43] 和多元和/或时空设置 (Furrer et al. 2016)^[24]。 从计算角度来看，紧支撑协方差函数节省了采用稀疏矩阵算法有效求解线性方程组的计算复杂度。更准确地说，为了估值密度 `式 (1)` ，对 $\boldsymbol{\Sigma}$ 执行 Cholesky 分解，并对三角矩阵进行两次求解。对于典型的空间数据设置来说，这种求解算法关于观测数量是线性的。 对于似然框架中的参数估计，存在单锥和双锥两类方法（参见 Kaufman，2008 ^[51]；Du，2009 ^[17]；Wang 和 Loh 2011 ^[84]；Bevilacqua 等 2016 ^[5] ）。为了区分这两种方法，请注意 `式(1)` 中的似然可以重写为： $$ f_{\mathbf{Y}}(\mathbf{y}) = \left (\frac{1}{\sqrt{2 \pi}} \right)^N | \boldsymbol{\Sigma} |^{−1/2} \operatorname{etr} \left \{ − \frac{1}{2} (\mathbf{y} − \boldsymbol{\mu}) (\mathbf{y} − \boldsymbol{\mu})^T \boldsymbol{\Sigma}^{−1} \right\} \tag{10} $$ 其中 $\operatorname{etr}(A) = \exp(\operatorname{trace}(A))$。 在单锥设置中，只有协方差是锥化的，使得 `式(10)` 中的 $\boldsymbol{\Sigma}$ 值被 $\boldsymbol{\Sigma} \odot \boldsymbol{T}$ 替换，其中 “$\odot$” 表示 Hadamard 积，$\boldsymbol{T}$ 是 $N × N$ 的锥化矩阵。 在双锥化方法中，协方差和经验协方差都受到影响，不仅 $\boldsymbol{\Sigma}$ 被 $\boldsymbol{\Sigma} \odot \boldsymbol{T}$ 取代，而且 $(\mathbf{y} − \boldsymbol{\mu })(\mathbf{y} − \boldsymbol{\mu })^T$ 也被 $(\mathbf{y} − \boldsymbol{\mu })(\mathbf{y} − \boldsymbol{\mu })^T \odot \boldsymbol{T}$ 取代。 单锥化方程导致模型参数的估计有偏差，而双锥化方法基于估计方程（因此是无偏的），但代价是计算效率严重下降。如果使用模型参数的单锥化有偏估计进行预测，则偏差会导致预测准确性的损失（Furrer 等，2016 年^[24]）。 尽管可以调整锥化以更好地考虑密度不均匀和各向异性，但我们在本次评测中使用了一种简单直接的方法。这里的实现几乎完全依赖于 R 包 `spam`（Furrer 和 Sain 2010 ^[27]；Furrer 2016 ^[24]）。作为似然法的替代方案，并且考虑到计算成本，我们最小化了经验协方差和参数化协方差函数之间的差平方。评测利用了数据的网格化结构，仅针对一组特定位置估计经验协方差，其结果接近于经典变异函数估计和拟合 (Cressie 1993 ^[9])。 ### 2.3 稀疏精度矩阵法 #### 2.3.2 多分辨率近似 多分辨率近似(MRA) 可以看作是前面描述的几种方法的组合。与 FRK 或 LatticeKrig 类似，多分辨率近似也使用 `式 (4)` 中的基函数方法，但在不同的分辨率下使用紧支撑的基函数。与 FRK 或 LatticeKrig 相比，多分辨率近似基函数和相应系数的先验分布使用了 `预测过程法` 的方法，以自动适应任何给定的协方差函数 $\mathbb{C}(·)$，因此 多分辨率近似可以灵活地调整到所需的空间平滑度和依赖结构。 多分辨率近似的可扩展性得到保证，因为为了增加分辨率，基函数的数量增加，而每个函数的支持（即空间域中非零的部分）减少，允许基函数的数量近似为和数据一样。减少支撑度（并增加相应权重的协方差矩阵的稀疏性）是通过协方差函数锥化 MRA-Taper（ Katzfuss 和 Gong 2017 ^[49]）或递归划分空间域 MRA-Block（Katzfuss 2017,^[47]）来实现的。这可能导致（几乎）精确的近似与拟线性计算复杂性 虽然 MRA-Taper 具有一些有吸引力的平滑特性，但我们在这里关注 MRA-Block，它基于将域 $\mathcal{D}$ 递归划分为越来越小的子区域，直到某个级别 $M$。在每个（子）区域内，每个分辨率，有少量的基函数，比如 $r_0$。在分辨率为 $M$ 的每个区域中，过程的最终近似值（包括其方差和平滑度）是精确的。此外，将大量预测位置的联合后验协方差矩阵（即不仅仅是其与相关方法的逆矩阵）计算和存储为两个稀疏矩阵的乘积是可行的（Jurek 和 Katzfuss 2018 ^[44]）。 多分辨率近似块旨在充分利用高性能计算系统，因为推断非常适合大规模分布式计算，通信开销有限。通过将计算节点分配给递归分区的每个区域，将计算任务分成小部分。然后节点并行处理与其指定区域相对应的基函数，从而导致多对数计算复杂性。对于这个项目，我们使用 $M = 9$ 层，将每个域划分为 $2$ 个部分，并将每个分区中的基函数数设置为 $r_0 = 64$。 #### 2.3.3 随机偏微分方程 随机偏微分方程方法 (SPDE) 基于 Matérn 协方差场和随机偏微分方程之间的等价性，结合二维域上适用于 Matérn 系列中整数值平滑参数的马尔可夫性质。起点是 `式 (3)` 的 $w(\mathbf{s})$ 的基扩展，其中选择基函数 $h_k(\mathbf{s})$ 在域的三角剖分上是分段线性的（Lindgren 等，2011 年 ^[58]）。 $w^*_k$ 个系数的最优联合分布通过有限元构造获得，这导致稀疏的逆协方差矩阵（精度矩阵）$\mathbf{Q}_{\boldsymbol{\theta}} (\boldsymbol{\phi})$。精度矩阵元素是精度和反范围参数（$1/\phi^2_\sigma$ 和 $1/\phi_r$ ）的多项式，稀疏矩阵系数仅由三角剖分的选择决定。这不同于最近邻高斯过程方法的顺序马尔可夫构造，后者构造其结果精度矩阵的无平方根 $\mathbf{LDL}^T$ Cholesky 分解（以元素的逆序排列）。 空间过程通过 $\mathbf{z} = (\boldsymbol{w}^* , \boldsymbol{\beta})$ 的联合高斯模型指定，先验均值为 $\mathbf{0}$ 且块对角线精度为 $\mathbf{Q}_z = \operatorname{Diag}(\mathbf{Q}_{w^*}, \mathbf{Q}_{\beta} )$，其中 $\mathbf{Q}_{\beta} = \mathbf{I} \cdot 10^{−8}$ 给出了 $\boldsymbol{\beta}$ 的模糊先验。引入具有元素 $H_{ij} = h_j(\mathbf{s}_i)$ 和协变量矩阵 $\mathbf{X} = X_j(\mathbf{s}_i)$ 的稀疏基评估矩阵 $\mathbf{H}$，则观测模型为 $\mathbf{Y} = \mathbf{X} \boldsymbol{\beta} + \mathbf{H} \boldsymbol{w}^* + \boldsymbol{ε}= \mathbf{A} \mathbf{z} + \boldsymbol{ε}$ 其中 $\mathbf{A} = (\mathbf{H,X})$ , $\boldsymbol{ε}$ 是零均值观测噪声向量，对角精度为 $\mathbf{Q}_\varepsilon = \mathbf{I}/\sigma^2_ε$。 使用多元正态分布的基于精度的方程，$\mathbf{z}$ 的条件精度和期望由 $\mathbf{Q}_{z|y} = \mathbf{Q}_z + \mathbf{A}^T \mathbf{Q}_\varepsilon \mathbf{A}$ 和 $\boldsymbol{\mu}_{ z|y} = \mathbf{Q}^{−1}_{ z|y} \mathbf{A}^T \mathbf{Q}_\varepsilon \mathbf{Y}$ 给出，其中稀疏 Cholesky 分解 $\mathbf{Q}_{z|y}$ 用于线性求解。 $\mathbf{z}$ 的元素会自动重新排序，以使 Cholesky 因子尽可能稀疏。这种具有 $K$ 基函数的空间高斯马尔可夫随机场的后验预测和多元高斯似然的计算和存储成本为 $O(K^{3/2})$。由于直接求解器不利用模型的平稳性，因此相同的预测成本将适用于非平稳模型。对于较大的问题，可以应用更容易并行化的迭代稀疏求解器（例如，多重网格），但对于这里相对较小的问题，直接求解器的直接实现可能更可取 此处使用的随机偏微分方程方法的实现基于 R 包 INLA（Rue 等，2017 年 ^[67]），它旨在使用集成嵌套拉普拉斯对潜在高斯模型（特别是贝叶斯广义线性、加法和混合模型）进行贝叶斯推断近似值 (Rue et al. 2009 ^[66])。 $\boldsymbol{\phi} = (\phi_r ,\phi_σ ,σ^2_ε)$ 的参数优化使用一般数值对数似然导数，因此完全贝叶斯推断因此被关闭，导致协方差参数的经验贝叶斯估计。大部分运行时间仍然花在参数优化上，但使用与 LatticeKrig 相同的参数估计技术，结合纯高斯实现，即使没有专门的导数代码也能显著减少总运行时间。 #### 2.3.4 最近邻过程 Datta 等开发的最近邻高斯过程 (NNGP)。 (2016a,b) ^[14][15] 是根据 `式 (2)` 中空间随机效应的联合分布的条件规范定义的。令 `式 (2)` 中的 $w(\mathbf{s})$ 服从均值零高斯过程，其中 $\mathbb{C}(\mathbf{s},\mathbf{s}^\prime) = \sigma^2_w ρ(\mathbf{s},\mathbf{s}^\prime)$，其中 $ρ(·)$ 是正定相关函数。将 $w(\mathbf{s}_1),\ldots,w(\mathbf{s}_N)$ 的联合分布分解为一系列条件分布，得到 $w(\mathbf{s}_1) = 0 + η(\mathbf{s}_1)$ 和 $$ w(\mathbf{s}_i) | \boldsymbol{w}_{1:(i−1)} = \mathbb{C}' (\mathbf{s}_1, \mathbf{s}_{1:(i−1)}) \boldsymbol{\Sigma}^{−1}_{1:(i−1)} \boldsymbol{w}_{1:(i−1)} + η(\mathbf{s}_i ) \tag{13} $$ 其中 $\boldsymbol{w}_{1:(i-1)} = (w(\mathbf{s}_1), \ldots , w(\mathbf{s}_{i−1}))^T$, $\mathbb{C}(\mathbf{s}_1, \mathbf{s}_{1:(i−1)}) = (\mathbb{C}(\mathbf{s}_i , \mathbf{s}_1),\ldots,\mathbb{C}(\mathbf{s}_i , \mathbf{s}_{i−1}))^T$，$\boldsymbol{\Sigma}_{1:(i−1)} = \operatorname{Var}(\boldsymbol{w}_{1:(i-1)})$ 和 $η$ 是独立的、均值为零、正态分布的随机变量。`式 (13)` 等价于 $\boldsymbol{w} = \mathbf{A} \boldsymbol{w} + \boldsymbol{η}$ 其中 $\mathbf{A}= (a_{ij})$ 是下三角矩阵，对角线为零且 $\boldsymbol{η} = (η(\mathbf{s}_1),\ldots,η(sn))^T \sim \mathcal{N}(0, \mathbf{D})$ 具有对角线项 $\mathbb{C}(\mathbf{s}_i , \mathbf{s}_i ) − \mathbb{C}' (\mathbf{s}_1, \mathbf{s}_1:(i−1)) \boldsymbol{\Sigma}^{−1}_{1:(i−1)} \mathbb{C}(\mathbf{s}_1, \mathbf{s}_{1:(i−1)})$ 。这实现了联合分布 $\boldsymbol{w} \sim \mathcal{N}(\mathbf{0}, \boldsymbol{\Sigma} )$ 其中 $\boldsymbol{\Sigma}^{−1} = (\mathbf{I} − \mathbf{A})^T \mathbf{D}^{−1}(\mathbf{I} − \mathbf{A})$。此外，当预测任何 $\mathbf{s} \notin \{\mathbf{s}_1,\ldots,\mathbf{s}_N \}$ 时，可以定义 $$ w(\mathbf{s}) | w_{1:N} = \mathbf{a}^T(\mathbf{s})\boldsymbol{w}_{1:N} + η(\mathbf{s}) $$ 类似于 `式（13）`。 $A$ 的稀疏公式确保评估 $\boldsymbol{w}$ 的可能性（以及 $Y$ 的可能性）在计算上是可扩展的，因为 $\boldsymbol{\Sigma}^{−1}$ 是稀疏的。由于空间协方差随着距离的增加而减小，Vecchia (1988) 证明用 $\mathbf{s}_i$ 的较小的 $m$ 个最近邻（根据欧几里得距离）集合替换条件集 $\boldsymbol{w}_{1:(i-1)}$ 提供了对条件密度的极好近似在（13）中。Data 等 (2016a) 证明这相当于 $A$ 在每行中最多有 $m$ 个非零条目（在本研究中我们取 $m = 25$），因此对应于适当的概率分布。类似地，对于在新位置 $\mathbf{s}$ 的预测，基于 $\mathbf{s}_1,\ldots,\mathbf{s}_N$ 中 $\mathbf{s}$ 的 $m$ 个最近邻构造 `式(14)` 中的稀疏 $\mathbf{a}(\mathbf{s})$。将生成的高斯过程称为最近邻高斯过程 (NNGP)。这使最近邻方法得到了广泛使用，从 Vecchia (1988) ^[83]和 Stein 等(2004) ^[76] 的权宜似然估计，到在整个域上可以实现完全贝叶斯推断和隐空间随机效应相干恢复的最近邻高斯过程，。 使用最近邻高斯过程，模型可以写为 $\mathbf{Y} \sim \mathcal{N}(\mathbf{X} \boldsymbol{\beta}, \tilde{\boldsymbol{\Sigma}}(\boldsymbol{\phi}))$，其中 $\tilde{\boldsymbol{\Sigma}}$ ̃是从完整高斯过程导出的最近邻高斯过程协方差矩阵。通过为参数 $\boldsymbol{\beta}$ 和 $\boldsymbol{\phi}$ 指定先验来完成贝叶斯规范。对于此应用，协方差函数 $m\mathbb{C}$ 由方差为 $\sigma^2$ 和范围为 $\phi$ 的平稳指数高斯过程和方差为 $\sigma^2_ε$ 的块过程组成（参见 `式 (5)` ）。我们为 $\boldsymbol{\beta}$ 分配一个正常先验，为 $\sigma^2_w$ 和 $σ^2_ε$ 分配一个反伽马先验，为 $phi$ 分配一个均匀先验。该模型的 Gibbs 采样器涉及 $\boldsymbol{\beta}$ 的共轭更新和 $b\boldsymbol{\phi}= (\sigma^2_w ,σ^2_ε ,\phi )^T$ 的都市随机游走更新。 设 $α = \sigma^2_ε /\sigma^2_w$，模型也可以表示为 $\mathbf{Y} \sim \mathcal{N}(\mathbf{X} \boldsymbol{\beta}, \sigma^2_w \tilde{\mathbf{R}}(\phi,\alpha))$ 其中 $\tilde{\mathbf{R}}$ 是从 $\mathbf{C}(\phi ) + α \mathbf{I}$ 导出的最近邻高斯过程矩阵, $\mathbf{C}(\phi)$ 是指数高斯过程的相关矩阵。固定 $α$ 和 $phi$ 给出 $\boldsymbol{\beta}$ 和 $\sigma^2_w$ 的共轭正态-逆 Gamma 后验分布。 $y(\mathbf{s})$ 在新位置的预测分布也可以作为 $t$ 分布获得。 $α$ 和 $phi$ 的固定值可以通过最小化基于 $K$ 折交叉验证的均方根预测误差分数从网格搜索中选择。这种混合方法通过使用超参数调整背离了完全贝叶斯哲学。但是，它为海量空间数据集提供了实用的解决方案。我们将此模型称为共轭最近邻高斯过程模型，并将作为此计算中使用的模型。 Finley 等 (2018) ^[21]提供了这两种模型的详细算法。用于分析海量空间数据的最近邻高斯过程模型在 CRAN 上作为 R 包 `spNNGP` 提供（Finley 等，2017 年^[20]）。 #### 2.3.5 周期嵌入 当观测位置形成规则网格且模型静止时，使用离散傅里叶变换 (DFT) 的方法（也称为谱方法）在统计和计算上可能是有益的，因为 DFT 是近似去相关变换，并且可以使用快速傅立叶变换 (FFT) 算法快速计算且内存负担低。对于二维或更高维度的空间网格数据，有两个突出的问题需要解决。第一个是边缘效应，第二个是缺失值。通过投影到三角函数基上，谱方法假设空间过程在观测域上是周期性的，这导致谱估计中的偏差（Guyon 1982 ^[40]；Dahlhaus 和 Künsch 1987 ^[13]）。 Guinness 和 Fuentes (2017)^[39] 以及 Guinness (2017) ^[38]提出使用小域的扩展并以周期性方式在扩展格上插补数据。基于插补的方法还解决了缺失值的问题，因为缺失观测值也可以插补。 此处介绍的方法服从 Guinness (2017)^[38] 中的迭代半参数方法。 Guinness 和 Fuentes (2017) ^[39] 提供了另一种参数化方法。对于本节，让 $\mathbf{N} = (N_1, N_2)$ 给出观测网格的维度 [在 $N = (300, 500)$ 以下的案例研究数据集中]。令 $τ$ 表示扩展因子，$m = \lfloor τ N \rfloor$ 表示扩展格的大小。我们在所有示例中使用 $τ = 1.2$，因此表面温度数据集中的 $m = (360, 600)$。令 $\mathbf{U}$ 为观测向量，$\mathbf{V}$ 为大小为 $m$ 的网格上缺失值的向量，使得完整向量 $\mathbf{Y} = (\mathbf{U}^T, \mathbf{V}^T)^T$。整个向量的离散傅立叶变换为： $$ J (\boldsymbol{ω}) = \frac{1}{\sqrt{m_1m_2}} \sum_{\mathbf{s}} Y(\mathbf{s}) \exp(−i \boldsymbol{ω}^T \mathbf{s}), $$ $\boldsymbol{ω} = (ω_1,ω_2)^T$ 是空间频率，$ω_j \in [0, 2 \pi]，i = \sqrt{−1}$，并且 $\boldsymbol{ω}^T \mathbf{s} = ω_1\mathbf{s}_1 + ω_2\mathbf{s}_2$。 该过程是迭代的。在第 $k$ 次迭代中，频谱 $f_k$ 更新为 $$ f_{k+1}(ω) = \sum_{\boldsymbol{ν}} E_k(|J (\boldsymbol{ν})|^2 | U) α (\boldsymbol{ω} − \boldsymbol{ν}) \tag{15} $$ 其中 $α$ 为平滑核，$Ek$ 为协方差函数平稳的多元正态分布下的期望值 $$ R_k(\mathbf{h}) = \frac{1}{m_1m_2} \sum_{\boldsymbol{ω} \in \mathbb{F}_m } f_k(\boldsymbol{ω}) \exp(i \boldsymbol{ω}^T \mathbf{h}) $$ 其中 $\mathbb{F}_m$ 是大小为 $m$ 的网格上的傅里叶频率集。这很关键，因为它确保 $R_k$ 在扩展网格上是周期性的。在实践中，(15) 中的预期值被替换为使用估算向量 $V$ 计算的 $|J (\boldsymbol{ν})|^2$，这是在协方差函数 $R_k$ 下给定 $U$ 的缺失值的条件模拟。这确保了插补向量 $V$ 在扩展格上是周期性的，并减少了边缘效应。迭代过程也可以与中间参数步骤一起运行，其中 Whittle 似然 (Whittle 1954)^[86] 用于估计参数谱密度，该密度用于在平滑谱之前过滤估算数据。有关更精细的均值方案和迭代方法收敛监控的详细信息，请参阅 Guinness (2017) ^[38]。 ### 2.4 算法方法 #### 2.4.1 元克里金法 空间元克里金法是一种近似贝叶斯方法，不依赖于任何特定模型，本质上是部分算法。特别是，上述任何空间模型都可用于从子集中得出推论（如下所述）。根据 `式 (1)` ，让 $N × N$ 协方差矩阵由一组协方差参数 $\boldsymbol{\phi}$ 确定，使得 $\boldsymbol{\Sigma} = \boldsymbol{\Sigma}(\boldsymbol{\phi})$（例如，$\boldsymbol{\phi}$ 可以表示来自 Matérn 协方差函数的衰减参数）和 $\mu (\mathbf{s}) = \mathbf{X}^T (\mathbf{s})\boldsymbol{\beta}$ 其中 $\mathbf{X}(\mathbf{s})$ 是一组具有未知系数 $\boldsymbol{\beta}$ 的已知协变量。此外，将采样位置 $\mathcal{S} =\{\mathbf{s}_1,\ldots,\mathbf{s}_N \}$ 划分为集合 $\{\mathcal{S}_1,\ldots,\mathcal{S}_K \}$ 使得 $\mathcal{S}_i \cap \mathcal{s}_j =∅$ 对于 $i \neq j$ , $\cup^K_{ i=1} \mathcal{S}_i = \mathcal{S}$ 和数据的相应分区由 $\{\mathbf{y}_k, \mathbf{X}_k\}$ 给出，对于 $k = 1, 2,\ldots,K$ ，其中每个 $\mathbf{y}_k$ 为 $n_k × 1$，$\mathbf{X}_k$ 为 $n_k × p$。假设我们能够从 `式 (1)` 中获得 $=\{\boldsymbol{\beta}, \boldsymbol{\phi} \}$ 的后验样本，独立应用于不同核上的 $K$ 个数据子集。具体来说，假设 $\boldsymbol{\Omega}_k =\{ \boldsymbol{\Omega}^{(1)}_k , \boldsymbol{\Omega}^{(2)}_k ,\ldots, \boldsymbol{\Omega}^{(M)}_k \}$ 是来自 $p( \boldsymbol{\Omega} | \mathbf{y}_k)$ 的 $M$ 个后验样本的集合。我们将每个 $p(\boldsymbol{\Omega} | \mathbf{y}_k )$ 作为“后验子集”。我们在下面概述的元克里金方法试图以最佳方式和有意义的方式组合这些后验子集以达到合理的概率密度。我们将此称为“元后验”。 Metakriging 依赖于后验子集的唯一几何中位数 (GM)（Minsker 等 2014；Minsker 2015）。对于正定核 $h(·)$，定义两个分布 $π_1(·)$ 和 $π_2(·)$ 之间的范数为 $d_h(π_1(·), π_2(·)) = \| \int h(\boldsymbol{\Omega} , ·)d( π_1 − π_2)(\boldsymbol{\Omega}) \|$。我们设想个体后验密度 $p_k ≡ p(\boldsymbol{\Omega} | \mathbf{y}_k)$ 位于配备范数 $d_h(·,·)$ 的 Banach 空间 $\mathcal{H}$ 上。GM 被定义为 $$ π^∗(\boldsymbol{\Omega} | \mathbf{y}) = \arg \min_{\pi \in \mathcal{H}} \sum^K_{k=1} d_h( p_k,\pi) \tag{16} $$ w 其中 $\mathbf{y} = ( \mathbf{y}^T_1, \mathbf{y}^T_2,\ldots, \mathbf{y}^T_K )^T$。在下文中，我们假设 $h(z_1, z_2) = \exp(− \| z_1 − z_2 \|^2)$。 GM 是独一无二的。此外，几何中位数位于各个后验概率的凸包中，因此 $\pi^*(\boldsymbol{\Omega} | \mathbf{y})$ 是合法的概率密度。具体来说，$\pi^*(\boldsymbol{\Omega} | \mathbf{y}) = \sum^K_{k=1} ξ_{h,k} ( \mathbf{y}) p_k$ , $\sum^K_{k=1} ξ_{h,k}(\mathbf{y}) = 1$，每个 $ξ_{h,k}(\mathbf{y})$ 都是 $h, \mathbf{y}$ 的函数, 所以 $\int_{\boldsymbol{\Omega}} \pi^*(\boldsymbol{\Omega} | \mathbf{y})d \boldsymbol{\Omega} = 1$。 几何中位数 $\pi^* ≡ \pi^*(\boldsymbol{\Omega} | \mathbf{y})$ 的计算通过使用流行的 Weiszfeld 迭代算法进行，该算法从子集后验概率 $p_k$ 中估计每个 $k$ 的 $ξ_{h,k}(y)$。为了进一步说明，我们使用一个众所周知的结果，即几何中位数 $\pi^*$ 满足 $\pi^* = \left[\sum^K_{ k=1} p_k/d_h ( p_k ,π^∗) \right] \left[\sum^{K}_{k=1} 1/d_h(p_k ,\pi^*) \right]^{−1}$ 使得 $ξ_{h,k}(\mathbf{y}) = (1/d_h( p_k ,\pi^*))/ \sum^K_{j=1}(1/d_h( p_j ,\pi^*))$。由于不存在满足该方程的 $ξ_{h,k}(\mathbf{y})$ 的明显封闭形式解，因此需要求助于 Minsker 等 (2014) 概述的 Weiszfeld 迭代算法。为所有 $k = 1, .., K$ 生成 $ξ_{h,k}( \mathbf{y})$ 的经验估计。 Guhaniyogi 和 Banerjee (2018) 表明，对于大样本，$\pi^*(·| \mathbf{y})$ 在某些限制性设置中提供了完整后验分布的理想近似值。因此，通过子集后验预测分布 $p(y(s_0) | \mathbf{y}_k)$ 来近似后验预测分布 $p(y(s_0) | \mathbf{y})$ 是很自然的。令 $\{y(s_0)^{(j,k)}\}^M_{ j=1}$， $k = 1,\ldots,K$ ，是从第 $k$ 个后验子集的后验预测分布 $p(y(s_0)| \mathbf{y}_k)$ 中获得的样本。然后， $$ p(y(s_0) | \mathbf{y}) \approx \sum^K_{k=1} ξ_{h,k} (\mathbf{y}) p(y(s_0) | \mathbf{y}_k ) = \sum^K_{k=1} ξ_{h,k} (\mathbf{y}) \int p(y(s_0) | \boldsymbol{\Omega} , \mathbf{y}_k) p(\boldsymbol{\Omega} | \mathbf{y}_k)d \boldsymbol{\Omega} $$ 因此，后验的经验后验预测分布由 $\sum^{K}_{k=1} \sum^M_{j=1} \frac{ξ_{h,k}(\mathbf{y})}{M} I_{y(s_0)}(j,k)$ 给出，从中后验预测中位数和 $95\%$ 未观测到的 $y(s_0)$ 的后验预测区间很容易获得。 与 Minsker 等 (2014) 相比，空间元克里金方法具有额外的优势。 Minsker 等 (2014) 建议计算每个子集的随机近似后验，这限制了用户使用标准 R 包从中提取后验样本。相反，metakriging 允许使用流行的 R 包进行子集后验计算。此外，Minsker 等 (2014) 主要关注预测并将其适用性限制在 i.i.d.设置。相反，Guhaniyogi 和 Banerjee（2018）对空间高斯过程的参数估计、残差表面插值和预测进行了综合分析。 Guhaniyogi 和 Banerjee（2018 年）的补充材料中介绍了在限制性假设下支持拟议方法的理论结果。 空间元克里金法 (SMK) 的一个重要组成部分是将数据集划分为子集。对于本文，我们采用随机分区方案，将数据随机划分为 $K = 30$ 个详尽且互斥的子集。随机划分方案有助于每个子集成为整个域的合理代表，因此每个后验子集充当完整后验的“弱学习者”。我们探索了更复杂的分区方案并发现了类似的预测推断。 为了明确起见，本文对每个子集推断都使用平稳的高斯过程模型，这可能会导致更高的运行时间。实际上，当在每个子集中安装固定高斯过程模型时，此处介绍的元克里金方法版本会产生更准确的结果。然而，当在每个子集中使用上述任何模型时，元克里金方法提供了更大的可扩展性。事实上，空间元克里金法的扩展，称为分布式空间克里金法 (DISK)（Guhaniyogi 等，2017 年），将非平稳修正预测过程扩展到数百万个观测值。正在进行的关于元克里金法的更一般扩展的研究，被称为聚合蒙特卡洛 (AMC)，涉及将时空变化系数模型扩展到大数据集 #### 2.4.2 gapfill gapfill 方法 (Gerber et al. 2018) 与此处介绍的其他方法的不同之处在于它是纯算法的、无分布的，特别是不基于高斯过程。与卫星成像界流行的其他预测方法一样（参见 Gerber 等 2018 年；Weiss 等 2014 年的评论），gapfill 方法因其低计算工作量而很有吸引力。 gapfill 的一个关键方面是它专为并行处理而设计，允许用户利用不同规模的计算资源，包括大型服务器。通过仅基于数据的一个子集分别预测每个缺失值来启用并行化。 为了预测位置 $\mathbf{s}_0$ 处的值 $Y(\mathbf{s}_0)$，gapfill 首先选择一个合适的子集 $\mathbf{A} = {Y (\mathbf{s}_i ) : \mathbf{s}_i \in \mathcal{N}(\mathbf{s}_0)}$，其中 $\mathcal{N}(\mathbf{s}_0)$ 定义了 $\mathbf{s}_0$ 周围的空间邻域。发现 $\mathbf{A}$ 是用规则形式化的，这些规则确保 $\mathbf{A}$ 很小但包含足够的观测值来为预测提供信息。在本研究中，我们要求 $\mathbf{A}$ 的范围至少为 $5×5$ 像素，并且至少包含 $25$ 个非缺失值。随后，$Y(\mathbf{s}_0)$ 的预测基于 $A$ 并依赖于排序算法和分位数回归。此外，预测区间是使用排列参数构建的（有关预测和不确定区间的更多详细信息，请参阅 Gerber 等 2018 年）。 gapfill 方法最初是为时空数据设计的，在这种情况下，邻域 $\mathcal{N}(\mathbf{s}_0)$ 是根据数据的空间和时间维度定义的。因此，R 包 gapfill (Gerber 2017) 中 gapfill 的实现需要多个图像才能正常工作。为了模拟这种情况，我们将给定图像沿 $x$ 轴和 $y$ 轴在两个方向上移动一个、两个和三个像素。然后将算法应用于总共这 $13$ 张图像（一张原始图像和通过原始图像平移获得的 $12$ 张图像）。 #### 2.4.3 局部近似高斯过程 局部近似高斯过程（laGP、Gramacy 和 Apley 2015）通过采用所谓的转导学习方法解决了高斯过程回归中的大 $N$ 问题，其中拟合方案是针对预测问题量身定制的（Vapnik 1995），而不是通常的归纳法首先拟合，然后以拟合为条件进行预测。基于最近邻的 laGP 的一个特例很容易描述。为了在 $\mathbf{s}$ 处进行预测，只需在 $\mathbf{s}$ 最近的 $m$ 个邻居上训练一个高斯过程预测器；即，使用数据子集 $\mathcal{Y}_m ={Y (\mathbf{s}_i ) : \mathbf{s}_i \in \mathcal{N}_m(\mathbf{s})}$，其中 $\mathcal{N}_m(\mathbf{s})$ 是就欧几里得距离而言最接近 $\mathbf{s}$ 的 $m$ 个观测位置。如果数据生成机制与建模假设不矛盾（例如，具有明确指定的协方差结构），则可以选择 $m$ 尽可能大，直到计算限制，以获得准确的近似值。请注意，这种使用最近邻 (NN) 进行预测更类似于经典的统计/机器学习变体，这与它们在确定全局（逆）协方差结构中的使用形成鲜明对比，如 `第 2.3 节` 中所述。 有趣的是，NN 不包含根据均方误差等常用标准进行预测的最佳数据子集。然而，从 $N !/(m!(N − m)!)$ 可能的选择中找到最好的 $m$ 代表了一个巨大的组合搜索。 laGP 方法通过使用贪心启发法近似搜索来概括这种所谓的最近邻预测算法（空间统计文献中的现代形式由 Emery 2009 描述）。首先，从 NN 集合 $\mathcal{Y}_{m_0} (\mathbf{s}) =\{Y(\mathbf{s}_i) : \mathbf{s}_i \in \mathcal{N}_{m_0} (\mathbf{s}))$ 开始，其中 $m_0 < m$ ，然后对于 $j = m_0 + 1,\ldots,m$ 连续选择 $\mathbf{s}_j$ 来扩充 $\mathcal{Y}_{m_0}$ 根据与均方预测误差相关的几个简单客观标准之一，一次建立一个局部设计数据集。想法是这样重复，直到 $\mathcal{Y}_m(\mathbf{s})$ 中有 $m$ 个观测值。 Gramacy 和 Apley 的首选变异目标 $\mathbf{s}_j$ 最大限度地减少了 $\mathbf{s}$ 处的预测方差。为了识别称为主动学习 Cohn (Cohn 1996) 的类似全局设计标准，他们将此标准称为 ALC。定性地，这些本地 ALC 设计往往具有一组邻居和“卫星”点，并且已被证明可以提供比 NN 甚至全数据替代方案更好的预测特性，尤其是当数据生成机制与建模假设不一致时。原因是局部拟合提供了一种方法来应对一定程度的非平稳性，这在许多真实数据设置中很常见 ALC 搜索迭代和高斯过程更新注意事项随着设计的建立，经过精心设计，以产生一种计算复杂度为 $\mathcal{O}(N^3)$ 的方法（即，与更简单的 NN 替代方案相同）。 $m = 50$ 的相对适中的本地设计大小通常效果很好。此外，每个 $\mathbf{s}$ 的计算在统计上独立于下一个，这意味着它们可以简单地并行化。通过多核、多节点和 GPU 并行化的级联，Gramacy 等 (2014) 以及 Gramacy 和 Haaland (2016) 说明了如何在不到一个小时的计算时间内处理训练和测试数据大小的数百万 N（并产生准确的预测变量）。 laGP 方法已为 R 包，可在 CRAN (Gramacy 2016) 上使用。对称多核并行化（通过 OpenMP）和多节点自动化（通过内置并行包）开箱即用。源代码中提供了 GPU 扩展，但需要自定义编译。 这种方式的局部建模的缺点是全局预测协方差不可用。事实上，计算的统计独立性使得该过程在计算上高效且可并行化。事实上，在连续的预测 $\mathbf{s}$ 位置上产生的全局预测表面甚至不需要是平滑的。然而，在大多数预测表面的视觉表示中，很难区分真正光滑的表面和通过 laGP 预测方程绘制的表面。最后，值得注意的是，虽然 laGP 在这里应用于空间建模设置（即，具有两个输入变量），但它是为计算机模拟建模而设计的，并且已被证明在高达 $10$ 的输入维度上工作良好。 ## 3 对比 在本次评测的初始规划阶段，我们希望比较各种方法：从常客到贝叶斯，从成熟的到现代的发展。根据该计划，我们努力联系在分析数据集的方法方面具有丰富专业知识的各种研究组。外展期结束后，表 1 中列出的研究团队同意参与并实施其相关方法。 表 1 中列出的每个组都提供了两个训练数据集：一个真实的和一个模拟的。模拟数据集表示正确指定协方差函数的情况，而真实数据集表示错误指定协方差函数的情况。两个数据集都包含在相同的 $500×300$ 网格上的观测值，经度值从 $−95.91153$ 到 $−91.28381$，纬度值从 $34.29519$ 到 $37.06811$。真实数据集包括 2016 年 8 月 4 日 MODIS 卫星上的 Terra 仪器测量的白天地表温度（3 级数据）。数据是从 MODIS 重投影工具网络界面 (MRTweb) 下载的。虽然这个确切的工具在这个项目开始后不久就停止了，但数据在 [GitHub](https://github.com/finnlindgren/heatoncomparison) 上依然提供。选择纬度和经度范围以及日期是因为这一天该地区的云层稀疏（而不是出于对日期本身的科学兴趣）。也就是说，只有 $1.1\%$ 的 3 级 MODIS 数据被云覆盖破坏，留下 $148,309/150,000$ 个观测值供我们使用。 > 表 1. 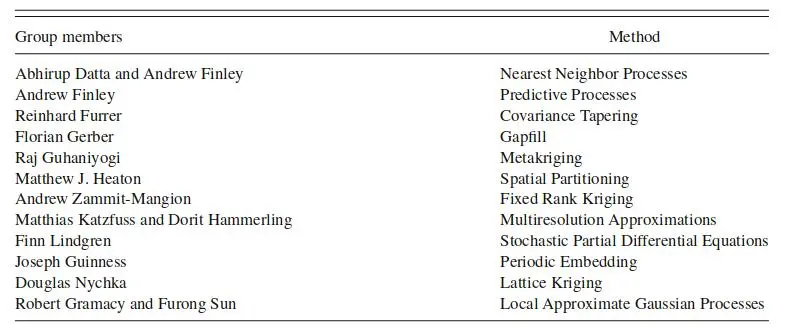参加评测的研究组及其选择的方法  模拟数据集的创建方法是： 首先，将具有常量均值、指数协方差函数和块金效应的高斯过程模型拟合到来自上述 MODIS 数据的 $2500$ 个观测值的随机样本。空间范围、空间方差、块金方差和常量均值的参数估计值分别为 $4/3$、$16.40$、$0.05$ 和 $44.49$。 $4/3$ 的空间范围参数相当于大约 $210$ 英里（$338$ 公里）的近似有效空间范围（相关性等于 $0.05$ 的距离）。然后使用这些参数在与 MODIS 数据相同的网格上模拟 $150,000$ 个观测值。 为定义测试集和训练集，使用同一 MODIS 卫星数据产品 2016 年 8 月 6 日的缺失数据模式将每个数据集分成训练集和测试集。拆分后，MODIS 数据的训练集包含 $105,569$ 个观测值，在测试集中留下 $42,740$ 个观测值。模拟数据的训练集也包括 $105,569$ 个观测值，但测试集大小为 $44,431$（测试集大小的差异是由于原始 MODIS 数据中的云覆盖导致数据丢失）。向研究团队提供了训练集和测试集的位置（但不是测试集中的实际观测）。`图 1` 显示了完整的数据集以及提供给每个研究组的相应训练集。本文中使用的所有数据集均在[公共 GitHub 存储库](https://github.com/finnlindgren/heatoncomparison) 上提供。  > 图 1. 顶行显示 a 完整和 b 训练卫星数据集。底行显示 c 完整 和 d 训练模拟数据 每个组独立编写代码（也包含在随附的 GitHub 页面上），提供： - (1) 测试集中每个位置的点预测 - (2) 测试集中位置的 $95\%$ 预测区间或相应的标准误差预测 - (3) 实施该方法所需的总时钟时间。 为了尽量减少本次评测中混杂因素的数量，指示每个组使用指数相关函数（如果适用于他们选择的方法）和块金方差。对于模拟数据，组被指示仅使用常数均值（因为这是最初模拟数据的方式）。然而，对于卫星数据，这些组对纬度和经度使用了线性效应，因此残差过程更接近于指数相关。然后每个团队的代码在 Becker 计算环境（256 GB RAM 和 2 个 Intel Xeon E5-2680 v4 2.40GHz CPU，每个 14 个内核和每个内核 2 个线程 - 总共 56 个可能的线程用于并行计算）上运行在杨百翰大学 (BYU)。每个团队的代码都是单独运行的，没有其他进程同时运行，以提供计算时间的准确测量 每种方法都根据`均绝对误差 (MAE)`、`均方根误差 (RMSE)`、`连续等级概率得分 (CRPS）`（参见 Gneiting 和 Raftery 2007 ^[31]；Gneiting 和 Katzfuss 2014 ^[30])、`区间得分（INT）`（参见 Gneiting和 Raftery 2007）和 `预测区间覆盖率（CVG）`（包含真实值的区间百分比）。为了计算 CRPS，我们假设相关的预测分布很好地近似于高斯分布，其均值以预测值为中心，标准差等于预测标准误差。在仅提供预测区间的情况下，预测标准误差取为 $(U − L)/(2 × \Phi^{−1}(0.975))$，其中 $U$ 和 $L$ 分别是区间的上限和下限。 ## 4 对比结果 ### 4.1 模拟数据的结果 模拟数据评测的数值结果显示在 `表 2` 中。首先，考虑 `表 2` 中 MAE 和 RMSE 测量的预测精度。在预测精度方面，最好的 MAE 为 $0.61$，而最差的 MAE 仅为 $1.03$（相差 $68\%$ ）。同样，最佳 RMSE 为 $0.83$，而最差 RMSE 仅为 $1.31$（相差 $57\%$）。然而，值得注意的是，对于只有一个模拟数据集的情况，这些结果具有启发性，但对于哪种方法给出始终如一的更好预测而言并不是决定性的。 考虑到不确定性量化 (UQ)，一些方法比其他方法表现更好。例如，LatticeKrig、LAGP、metakriging、多分辨率近似、periodic embedding、最近邻高斯过程和预测过程都达到了接近标称的 $95\%$ 的覆盖率。相比之下，FRK、Gapfill 和分区实现的覆盖率低于标称覆盖率，而随机偏微分方程和 tapering 的覆盖率高于标称覆盖率。进一步考虑不确定量化，Gapfill 具有较大的区间分数，表明除了因丢失真实值而招致的惩罚外，还可能存在较宽的预测区间。在这方面，重要的是要记住 LAGP、metakriging、多分辨率近似、最近邻高斯过程和预测过程都可以指定 “正确的” 指数相关函数。此外，LatticeKrig 和随机偏微分方程具有可以很好地逼近指数相关函数的设置。相比之下，一些方法如 FRK 和 Gapfill 不太适合模拟具有指数相关函数的字段，这可能部分解释了它们在这种情况下相对较差的预测或覆盖性能。 为了进一步探索这些方法之间的差异，我们计算了 5 个类别的预测的 RMSE 和 CRPS，其中类别是从距离到最近的训练点创建的。从最短距离到最长距离类别，每类的观测次数分别为 $36106$、$5419$、$1918$、$729$ 和 $259$（即，有 $36106$ 个预测被归类为“短距离”）。图 2 显示了每个预测距离类别的前 5 个执行方法（就整体 RMSE 而言）的 RMSE 和 CRPS。虽然短距离预测的方法之间几乎没有差异，但在更远距离的方法中有更多的传播。也就是说，多分辨率近似、随机偏微分方程和最近邻高斯过程似乎比空间分区和 LatticeKrig 更适合最长距离预测。当考虑不确定性 (CRPS) 而不仅仅是预测准确性 (RMSE) 时，这些方法之间的差异更大。 > 表 2. 模拟数据上每种参与评测方法的数值评分   > 图 2. （a） RMSE 和 （b） CRPS （根据与模拟数据集上表现最佳者的最近观测值距离） ### 4.2 真实数据的结果 `表 3` 显示了真实 MODIS 数据的结果，并在很大程度上重申了模拟数据的结果。也就是说，每种方法在预测准确性方面都表现得非常好。最大的 RMSE 仅为 $2.52$，考虑到 $55.41−24.37 = 31.04$ 的数据范围时，这个值非常小。相对于模拟数据，对于归因于模型指定错误的所有方法，观察到的 RMSE 都相当高。我们注意到，在比赛的设置下，一些方法被迫逼近具有各向同性指数协方差函数的高斯过程，这是模拟数据的真实协方差函数，但对于真实数据肯定不是。因此，那些恰好与数据拟合良好的近似值的分数最低，而那些最接近指数协方差的方法的分数不一定最低。这也可以解释为什么多分辨率近似在模拟示例中对远距离预测表现良好，但对远距离卫星预测表现不佳。此外，由于许多表现最好的方法都在努力逼近指数协方差，因此在模拟数据和真实数据上表现最好的方法之间的细微差别不应归因于模型错误指定的鲁棒性。 > 表 3. 卫星数据上每种竞争方法的数值评分  评测方法之间最大的差异再次出现在不确定性量化方面。 Lattice kriging、metakriging、多分辨率近似、最近邻高斯过程和周期性嵌入再次以小区间分数和 CRPS 实现了接近标称的覆盖率。随机偏微分方程和逐渐减少的方法在覆盖率方面做得更好，因为经验率接近标称值（回想一下，对于这些方法的模拟数据，相应的覆盖率太高了）。相比之下，FRK、Gapfill、LAGP、分区和预测过程的 MODIS 数据覆盖率太小，导致区间得分较大。 `图 3` 显示了卫星案例研究中 5 种表现最好的方法（就整体 RMSE 而言）和一种低等级方法 (FRK) 的 RMSE 和 CRPS 作为距离类别函数的结果。在考虑预测距离时，与模拟数据应用程序相比，实际数据应用程序中的方法之间存在更明显的差异。最近邻高斯过程和随机偏微分方程在模拟数据和卫星数据的所有距离类别中均表现良好。此外，从该图中可以明显看出，低秩方法的预测性能较差（见表 3），因为它们在短期预测方面表现不佳（这在 FRK 中是预期的，其中使用的基函数数量相对较少小的）。然而，相对而言，它们在预测大差距时仍然做得很好。  >图 3： （a） RMSE 和 （b） CRPS （根据到卫星数据集上表现最好的最近观测的距离） ## 5 结论 本文的贡献有四方面： (1) 概述了可用于分析大型空间数据集的大量方法； (2) 通过在研究组之间实施案例研究评测，对这些方法进行了简要比较； (3) 使向更广泛的科学界提供分析数据的代码； (4) 提供一个公共任务框架的例子，供未来研究在比较各种分析方法时使用。 就比较而言，每种方法在预测准确性方面表现得都非常好，这表明上述任何一种方法都非常适合预测任务。各种方法之间最大的区别，主要体现在对与预测相关的不确定性量化能力上。 虽然一些方法在模拟数据和真实数据的预测性能和指标覆盖率方面始终表现良好，但一般来说，我们可以预期任何方法的性能都会随数据集大小、测量误差方差和属性缺失等因素而变化。此外，虽然 `表 1` 中的结果具有启发性，但由于只有一个模拟数据集和一个真实数据集，我们无法明确声称任何一种方法提供的预测始终比其他方法更好。不过，本文考虑的数据场景相对代表了典型的空间分析场景，因此我们的结果可以用作从业者的指南。 对于本文考虑的两种情况，上述每种方法都表现良好。然而，每种方法表现不佳的情况也很有趣。例如 - `FRK` 和 `预测过程` 等低秩方法在高信噪比和过程空间范围小的情况下挣扎（如本文模拟数据所示；参见 Zammit-Mangion 和 Cressie 2018；Zammit-Mangion 等 2018）。 - 如果数据不在规则网格上，则 `gapfill` 方法可能会遇到困难。 - 根据参数和数据中缺失值的模式，`Gapfill`、LAGP 和空间分区的预测可能会显示不连续性。 - 众所周知，当每个子集使用非固定高斯过程而不是固定高斯过程时，`Meta-克里金方法` 不太准确，但最近的研究试图解决该问题（Guhaniyogi 等，2017 年）。 在本研究之初，我们最感兴趣的是运行时间和计算时间。然而，由于有许多方法在使用和实施方面还很不成熟，导致运行时可变性太大，无法用做进行比较的衡量标准。 例如，一些方法是在 $R$ 中实现的，而另一些是在 MATLAB 中实现的。尽管如此，其他人仍然使用 $R$ 作为前端来调用 $C$ 优化的函数。因此，虽然我们在结果部分汇报了运行时间，但提供的更像是 “现成的” 运行时间估计，而不是优化后的运行时间。在时间允许进一步开发每种方法并且软件可用之前，比较运行时间可能会产生误导。 重要的是，我们没有标准化每个组在本项目上花费的时间。一些组能够从现有 $R$ 或 MATLAB 库快速编写其分析代码。而其他组不得不花费更多时间编写特定于此分析的代码。毫无疑问，一些组可能会花更多时间运行 “内部” 交叉验证研究，以在 BYU 服务器上最终运行之前验证其模型预测，而其他组则没有。由于这种差异，我们可以注意一些结果差异可能是由不同组付出的不同努力所致。不过，我们仍然认为此处显示的结果对了解每种方法的优缺点提供了宝贵的见解。 本研究研究虽然比较彻底，但在其他大型空间数据方法方面并不全面（例如，Sang 和 Huang 2012；Stein 等 2013 年；Kleiber 和 Nychka 2015 年；CastrillonCandás 等 2016 年；Sun 和 Stein 2016 年；Litvinenko 等 2017）不包括在内。此外，未来肯定会开发出适用于大型空间数据建模的新方法（参见 Ton 等，2017 年；Taylor-Rodriguez 等，2018 年）。我们尝试邀请尽可能多的团体参与此案例研究，但由于时间和其他限制因素，并非所有团体都能参与。不过，此处比较的方法代表了撰写本文时大型空间数据最常用的方法。 本案例研究中考虑的数据场景并未涵盖与空间数据相关的一系列问题。也就是说，空间数据可能表现出各向异性、非平稳性、大范围和小范围的空间依赖性以及各种信噪比。因此，未来可以针对这些不同空间数据场景的适用性进一步区分参评的方法。但此处包含的比较可作为方法性能的一个很好的基准案例。进一步的研究可以为这些更复杂的场景开发案例研究评测。 值得注意的是，每种方法仅在预测准确性方面进行了比较。进一步的比较可能包括基础模型参数的估计。但比较估计的困难在于，并非所有方法都使用相同的模型结构。例如，`最近邻高斯过程` 使用指数协方差，而 `Gapfill` 不需要指定的协方差结构。因此，我们将参数估计值的比较留给未来研究。 这种比较只关注空间数据。因此，我们强调此处发现的结果仅适用于空间设置。然而，时空数据通常比空间数据大得多且复杂得多。上述许多方法都对时空设置进行了扩展（例如，`Gapfill` 是直接针对时空设置构建的）。需要进一步研究在时空环境中比较这些方法。 ## 参考文献

• [1] Anderson, C., Lee, D., and Dean, N. (2014), “Identifying clusters in Bayesian disease mapping,” Biostatistics, 15, 457–469.
• [2] Banerjee, S., Carlin, B. P., and Gelfand, A. E. (2014), Hierarchical modeling and analysis for spatial data,Crc Press.
• [3] Banerjee, S., Gelfand, A. E., Finley, A. O., and Sang, H. (2008), “Gaussian predictive process models for large spatial data sets,” Journal of the Royal Statistical Society: Series B (Statistical Methodology), 70, 825–848.
• [4] Barbian, M. H. and Assunção, R. M. (2017), “Spatial subsemble estimator for large geostatistical data,” Spatial Statistics, 22, 68–88.
• [5] Bevilacqua, M., Faouzi, T., Furrer, R., and Porcu, E. (2016), “Estimation and Prediction using Generalized Wendland Covariance Function under Fixed Domain Asymptotics,” arXiv:1607.06921v2.
• [6] Bradley, J. R., Cressie, N., Shi, T., et al. (2016), “A comparison of spatial predictors when datasets could be very large,” Statistics Surveys, 10, 100–131.
• [7] Castrillon-Candás, J. E., Genton, M. G., and Yokota, R. (2016), “Multi-level restricted maximum likelihood covariance estimation and kriging for large non-gridded spatial datasets,” Spatial Statistics, 18, 105–124.
• [8] Cohn, D. A. (1996), “Neural Network Exploration Using Optimal Experimental Design,” in Advances in Neural Information Processing Systems, Morgan Kaufmann Publishers, vol. 6(9), pp. 679–686.
• [9] Cressie, N. (1993), Statistics for spatial data, John Wiley & Sons.
• [10] Cressie, N. and Johannesson, G. (2006), “Spatial prediction for massive data sets,” in Mastering the Data Explosion in the Earth and Environmental Sciences: Proceedings of the Australian Academy of Science Elizabeth and Frederick White Conference, Canberra, Australia: Australian Academy of Science, pp. 1–11.
• [11] Cressie, N. and Johannesson, G. (2008), “Fixed rank kriging for very large spatial data sets,” Journal of the Royal Statistical Society: Series B (Statistical Methodology), 70, 209–226.
• [12] Cressie, N. and Wikle, C. K. (2015), Statistics for spatio-temporal data, John Wiley & Sons.
• [13] Dahlhaus, R. and Künsch, H. (1987), “Edge effects and efficient parameter estimation for stationary random fields,” Biometrika, 74, 877–882.
• [14] Datta, A., Banerjee, S., Finley, A. O., and Gelfand, A. E. (2016a), “Hierarchical nearest-neighbor Gaussian process models for large geostatistical datasets,” Journal of the American Statistical Association, 111, 800–812.
• [15] Datta, A., Banerjee, S., Finley, A. O., and Gelfand, A. E. (2016b), “On nearest-neighbor Gaussian process models for massive spatial data,” Wiley Interdisciplinary Reviews: Computational Statistics, 8, 162–171.
• [16] Datta, A., Banerjee, S., Finley, A. O., Hamm, N. A., Schaap, M., et al. (2016c), “Nonseparable dynamic nearest neighbor Gaussian process models for large spatio-temporal data with an application to particulate matter analysis,” The Annals of Applied Statistics, 10, 1286–1316.
• [17] Du, J., Zhang, H., and Mandrekar, V. S. (2009), “Fixed-domain asymptotic properties of tapered maximum likelihood estimators,” Ann. Statist., 37, 3330–3361.
• [18] Eidsvik, J., Shaby, B. A., Reich, B. J., Wheeler, M., and Niemi, J. (2014), “Estimation and prediction in spatial models with block composite likelihoods,” Journal of Computational and Graphical Statistics, 23, 295–315.
• [19] Emery, X. (2009), “The kriging update equations and their application to the selection of neighboring data,” Computational Geosciences, 13, 269–280.
• [20] Finley, A., Datta, A., and Banerjee, S. (2017), spNNGP: Spatial Regression Models for Large Datasets using Nearest Neighbor Gaussian Processes, r package version 0.1.1.
• [21] Finley, A. O., Datta, A., Cook, B. C., Morton, D. C., Andersen, H. E., and Banerjee, S. (2018), “Efficient algorithms for Bayesian Nearest Neighbor Gaussian Processes,” arXiv:1702.00434.
• [22] Finley, A. O., Sang, H., Banerjee, S., and Gelfand, A. E. (2009), “Improving the performance of predictive process modeling for large datasets,” Computational statistics & data analysis, 53, 2873–2884.
• [23] Fuentes, M. (2007), “Approximate likelihood for large irregularly spaced spatial data,” Journal of the American Statistical Association, 102, 321–331.
• [24] Furrer, R. (2016), spam: SPArse Matrix, r package version 1.4-0.
• [25] Furrer, R., Bachoc, F., and Du, J. (2016), “Asymptotic Properties of Multivariate Tapering for Estimation and Prediction,” J. Multivariate Anal., 149, 177–191.
• [26] Furrer, R., Genton, M. G., and Nychka, D. (2006), “Covariance tapering for interpolation of large spatial datasets,” Journal of Computational and Graphical Statistics, 15, 502–523.
• [27] Furrer, R. and Sain, S. R. (2010), “spam: A Sparse Matrix R Package with Emphasis on MCMC Methods for Gaussian Markov Random Fields,” J. Stat. Softw., 36, 1–25.
• [28] Gerber, F. (2017), gapfill: Fill Missing Values in Satellite Data, r package version 0.9.5.
• [29] Gerber, F., Furrer, R., Schaepman-Strub, G., de Jong, R., and Schaepman, M. E. (2018), “Predicting missing values in spatio-temporal satellite data,” IEEE Transactions on Geoscience and Remote Sensing, 56, 2841–2853.
• [30] Gneiting, T. and Katzfuss, M. (2014), “Probabilistic forecasting,” Annual Review of Statistics and Its Application, 1, 125–151.
• [31] Gneiting, T. and Raftery, A. E. (2007), “Strictly proper scoring rules, prediction, and estimation,” Journal of the American Statistical Association, 102, 359–378.
• [32] Gramacy, R. and Apley, D. (2015), “Local Gaussian Process Approximation for Large Computer Experiments,” Journal of Computational and Graphical Statistics, 24, 561–578.
• [33] Gramacy, R., Niemi, J., and Weiss, R. (2014), “Massively Parallel Approximate Gaussian Process Regression,” Journal of Uncertainty Quantification, 2, 564–584.
• [34] Gramacy, R. B. (2016), “laGP: Large-Scale Spatial Modeling via Local Approximate Gaussian Processes in R,” Journal of Statistical Software, 72, 1–46.
• [35] Gramacy, R. B. and Haaland, B. (2016), “Speeding up neighborhood search in local Gaussian process prediction,” Technometrics, 58, 294–303.
• [36] Guhaniyogi, R. and Banerjee, S. (2018), “Meta-kriging: Scalable Bayesian modeling and inference for massive spatial datasets,” Technometrics.
• [37] Guhaniyogi, R., Li, C., Savitsky, T. D., and Srivastava, S. (2017), “A Divide-and-Conquer Bayesian Approach to Large-Scale Kriging,” arXiv preprint arXiv:1712.09767.
• [38] Guinness, J. (2017), “Spectral Density Estimation for Random Fields via Periodic Embeddings,” arXiv preprint arXiv:1710.08978.
• [39] Guinness, J. and Fuentes, M. (2017), “Circulant embedding of approximate covariances for inference from Gaussian data on large lattices,” Journal of Computational and Graphical Statistics, 26, 88–97.
• [40] Guyon, X. (1982), “Parameter estimation for a stationary process on a d-dimensional lattice,” Biometrika, 69, 95–105.
• [41] Heaton, M. J., Christensen, W. F., and Terres, M. A. (2017), “Nonstationary Gaussian process models using spatial hierarchical clustering from finite differences,” Technometrics, 59, 93–101.
• [42] Higdon, D. (2002), “Space and space-time modeling using process convolutions,” in Quantitative methods for current environmental issues, Springer, pp. 37–56.
• [43] Hirano, T. and Yajima, Y. (2013), “Covariance tapering for prediction of large spatial data sets in transformed random fields,” Annals of the Institute of Statistical Mathematics, 65, 913–939.
• [44] Jurek, M. and Katzfuss, M. (2018), “Multi-resolution filters for massive spatio-temporal data,” arXiv:1810.04200.
• [45] Kang, E., Liu, D., and Cressie, N. (2009), “Statistical analysis of small-area data based on independence, spatial, non-hierarchical, and hierarchical models,” Computational Statistics & Data Analysis, 53, 3016–3032.
• [46] Kang, E. L. and Cressie, N. (2011), “Bayesian inference for the spatial random effects model,” Journal of the American Statistical Association, 106, 972–983.
• [47] Katzfuss, M. (2017), “A multi-resolution approximation for massive spatial datasets,” Journal of the American Statistical Association, 112, 201–214.
• [48] Katzfuss, M. and Cressie, N. (2011), “Spatio-temporal smoothing and EM estimation for massive remote-sensing data sets,” Journal of Time Series Analysis, 32, 430–446.
• [49] Katzfuss, M. and Gong, W. (2017), “Multi-resolution approximations of Gaussian processes for large spatial datasets,” arXiv:1710.08976.
• [50] Katzfuss, M. and Hammerling, D. (2017), “Parallel inference for massive distributed spatial data using low-rank models,” Statistics and Computing, 27, 363–375.
• [51] Kaufman, C. G., Schervish, M. J., and Nychka, D. W. (2008), “Covariance tapering for likelihood-based estimation in large spatial data sets,” Journal of the American Statistical Association, 103, 1545–1555.
• [52] Kim, H.-M., Mallick, B. K., and Holmes, C. (2005), “Analyzing nonstationary spatial data using piecewise Gaussian processes,” Journal of the American Statistical Association, 100, 653–668.
• [53] Kleiber, W. and Nychka, D. W. (2015), “Equivalent kriging,” Spatial Statistics, 12, 31–49.
• [54] Knorr-Held, L. and Raßer, G. (2000), “Bayesian detection of clusters and discontinuities in disease maps,” Biometrics, 56, 13–21.
• [55] Konomi, B. A., Sang, H., and Mallick, B. K. (2014), “Adaptive bayesian nonstationary modeling for large spatial datasets using covariance approximations,” Journal of Computational and Graphical Statistics, 23, 802–829.
• [56] Lemos, R. T. and Sansó, B. (2009), “A spatio-temporal model for mean, anomaly, and trend fields of North Atlantic sea surface temperature,” Journal of the American Statistical Association, 104, 5–18.
• [57] Liang, F., Cheng, Y., Song, Q., Park, J., and Yang, P. (2013), “A resampling-based stochastic approximation method for analysis of large geostatistical data,” Journal of the American Statistical Association, 108, 325–339.
• [58] Lindgren, F., Rue, H., and Lindström, J. (2011), “An explicit link between Gaussian fields and Gaussian Markov random fields: the stochastic partial differential equation approach,” Journal of the Royal Statistical Society: Series B (Statistical Methodology), 73, 423–498.
• [59] Litvinenko, A., Sun, Y., Genton, M. G., and Keyes, D. (2017), “Likelihood Approximation With Hierarchical Matrices For Large Spatial Datasets,” arXiv preprint arXiv:1709.04419.
• [60] Liu, H., Ong, Y.-S., Shen, X., and Cai, J. (2018), “When Gaussian Process Meets Big Data: A Review of Scalable GPs,” arXiv preprint arXiv:1807.01065.
• [61] Minsker, S. (2015), “Geometric median and robust estimation in Banach spaces,” Bernoulli, 21, 2308–2335.
• [62] Minsker, S., Srivastava, S., Lin, L., and Dunson, D. B. (2014), “Robust and scalable Bayes via a median of subset posterior measures,” arXiv preprint arXiv:1403.2660.
• [63] Neelon, B., Gelfand, A. E., and Miranda, M. L. (2014), “A multivariate spatial mixture model for areal data: examining regional differences in standardized test scores,” Journal of the Royal Statistical Society: Series C (Applied Statistics), 63, 737–761.
• [64] Nychka, D., Bandyopadhyay, S., Hammerling, D., Lindgren, F., and Sain, S. (2015), “A multiresolution Gaussian process model for the analysis of large spatial datasets,” Journal of Computational and Graphical Statistics, 24, 579–599.
• [65] Paciorek, C. J., Lipshitz, B., Zhuo, W., Kaufman, C. G., Thomas, R. C., et al. (2015), “Parallelizing Gaussian Process Calculations In R,” Journal of Statistical Software, 63, 1–23.
• [66] Rue, H., Martino, S., and Chopin, N. (2009), “Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations,” Journal of the Royal Statistical Society: Series B (Statistical Methodology), 71, 319–392.
• [67] Rue, H., Martino, S., Lindgren, F., Simpson, D., Riebler, A., Krainski, E. T., and Fuglstad, G.-A. (2017), INLA: Bayesian Analysis of Latent Gaussian Models using Integrated Nested Laplace Approximations, r package version 17.06.20.
• [68] Sang, H. and Huang, J. Z. (2012), “A full scale approximation of covariance functions for large spatial data sets,” Journal of the Royal Statistical Society: Series B (Statistical Methodology), 74, 111–132.
• [69] Sang, H., Jun, M., and Huang, J. Z. (2011), “Covariance approximation for large multivariate spatial data sets with an application to multiple climate model errors,” The Annals of Applied Statistics, 2519–2548.
• [70] Schabenberger, O. and Gotway, C. A. (2004), Statistical methods for spatial data analysis, CRC press.
• [71] Simpson, D., Lindgren, F., and Rue, H. (2012), “In order to make spatial statistics computationally feasible, we need to forget about the covariance function,” Environmetrics, 23, 65–74.
• [72] Stein, M. L. (1999), Interpolation of Spatial Data, Springer-Verlag, some theory for Kriging.
• [73] Stein, M. L. (2013), “Statistical properties of covariance tapers,” Journal of Computational and Graphical Statistics, 22, 866–885.
• [74] Stein, M. L. (2014), “Limitations on low rank approximations for covariance matrices of spatial data,” Spatial Statistics,8, 1–19.
• [75] Stein, M. L., Chen, J., Anitescu, M., et al. (2013), “Stochastic approximation of score functions for Gaussian processes,” The Annals of Applied Statistics, 7, 1162–1191.
• [76] Stein, M. L., Chi, Z., and Welty, L. J. (2004), “Approximating likelihoods for large spatial data sets,” Journal of the Royal Statistical Society: Series B (Statistical Methodology), 66, 275–296.
• [77] Sun, Y., Li, B., and Genton, M. G. (2012), “Geostatistics for large datasets,” in Advances and challenges in space-time modelling of natural events, Springer, pp. 55–77.
• [78] Sun, Y. and Stein, M. L. (2016), “Statistically and computationally efficient estimating equations for large spatial datasets,” Journal of Computational and Graphical Statistics, 25, 187–208.
• [79] Taylor-Rodriguez, D., Finley, A. O., Datta, A., Babcock, C., Andersen, H.-E., Cook, B. D., Morton, D. C., and Baneerjee, S. (2018), “Spatial Factor Models for High-Dimensional and Large Spatial Data: An Application in Forest Variable Mapping,” arXiv preprint arXiv:1801.02078.
• [80] Ton, J.-F., Flaxman, S., Sejdinovic, D., and Bhatt, S. (2017), “Spatial Mapping with Gaussian Processes and Nonstationary Fourier Features,” arXiv preprint arXiv:1711.05615.
• [81] Vapnik, V. (1995), The Nature of Statistical Learning Theory, New York: Springer Verlag.
• [82] Varin, C., Reid, N., and Firth, D. (2011), “An overview of composite likelihood methods,” Statistica Sinica, 5–42.
• [83] Vecchia, A. V. (1988), “Estimation and model identification for continuous spatial processes,” Journal of the Royal Statistical Society. Series B (Methodological), 297–312.
• [84] Wang, D. and Loh, W.-L. (2011), “On fixed-domain asymptotics and covariance tapering in Gaussian random field models,” Electron. J. Statist., 5, 238–269.
• [85] Weiss, D. J., Atkinson, P. M., Bhatt, S., Mappin, B., Hay, S. I., and Gething, P. W. (2014), “An effective approach for gap-filling continental scale remotely sensed time-series,” ISPRS J. Photogramm. Remote Sens., 98, 106–118.
• [86] Whittle, P. (1954), “On stationary processes in the plane,” Biometrika, 434–449.
• [87] Wikle, C. K., Cressie, N., Zammit-Mangion, A., and Shumack, C. (2017), “A Common Task Framework (CTF) for Objective Comparison of Spatial Prediction Methodologies,” Statistics Views.
• [88] Zammit-Mangion, A. and Cressie, N. (2018), “FRK: An R Package for Spatial and Spatio-Temporal Prediction with Large Datasets,” arXiv preprint arXiv:1705.08105.
• [89] Zammit-Mangion, A., Cressie, N., and Shumack, C. (2018), “On statistical approaches to generate Level 3 products from satellite remote sensing retrievals,” Remote Sensing, 10, 155.