海量空间数据集的多分辨率近似（MRA ）

【摘 要】 卫星和飞机上的自动传感仪器能够收集大空间区域空间场的大量高分辨率观测数据。如果可以有效地利用这些数据集，它们可以为各种问题提供新的见解。然而，传统的空间统计技术（如克里金法）在计算上对于大数据集不可行。我们提出了在空间不规则位置观测到的高斯过程的多分辨率近似 (M-RA)。 M-RA 过程被指定为多个空间分辨率级别的基函数的线性组合，它可以捕获从非常精细到非常大尺度的空间结构。自动选择基函数来近似给定的协方差函数，该协方差函数可以是非平稳的。所有涉及 M-RA 的计算，包括参数推断和预测，对于海量数据集都是高度可扩展的。至关重要的是，推断算法也可以并行化，以充分利用大型分布式内存计算环境。在使用模拟数据和大型卫星数据集进行比较时，M-RA 优于相关的最新技术

【原 文】 Katzfuss, M. (2017) ‘A Multi-Resolution Approximation for Massive Spatial Datasets’, Journal of the American Statistical Association, 112(517), pp. 201–214. Available at: https://doi.org/10.1080/01621459.2015.1123632.

1 简介

卫星和飞机上的自动传感仪器已经能够收集大型和非均匀空间域上空间场的大量高分辨率观测数据。如果可以有效地利用这些类型的数据集，它们可以为各种各样的问题提供新的见解，例如气候变化的温室气体浓度、精准农业的土壤特性以及天气预报的大气状态。基于（隐式或显式）高斯过程，空间统计领域为分析此类数据提供了丰富的工具包，包括估计未知参数，预测未观测到的位置的空间场，以及适当量化预测和参数中的不确定性（例如, Cressie 和 Wikle, 2011 ^[7])。

然而，传统的空间统计技术（如克里金法）在计算上对于大数据集不可行，因为需要分解密集的 $n \times n$ 矩阵，其中 $n$ 是测量的数量。

（1）纯数值计算方法

通用方法，例如预处理共轭梯度算法（例如，Golub 和 Van Loan，2012 年 ^[15]）或概率预测（例如，Halko 等，2011 年 ^[17]；Stein 等，2013 年 ^[45]）可以求解大型线性系统。但是，对于此类算法来说，计算基于似然推断所需的数据协方差矩阵的行列式具有挑战性，因为此类协方差矩阵很大，通常很密集，并且可能具有缓慢衰减的频谱。

（2）近似推断方法

文献中提出了更专门的近似空间推断方法，这些方法明确尝试利用数据中的空间信息，但其中:

• 大多数方法都需要对协方差函数进行限制性假设（例如，Fuentes，2007 年 ^[12]；Lindgren 等，2011 年 ^[32]）
• 或者忽略了很多精细尺度的依赖性（例如，Higdon，1998 年 ^[20]；Mardia 等，1998 年 ^[33]；Calder，2007 年 ^[3]；Cressie 和 Johannesson，2008 年 ^[6]；Katzfuss 和 Cressie，2009 年 ^[24]；Lemos 和 Sans o，2009 年 ^[31]；Katzfuss and Cressie, 2011 ^[25], 2012 ^[26])
• 大规模依赖（例如，Furrer 等，2006 年 ^[13]；Kaufman 等，2008 年 ^[29]；Shaby 和 Ruppert，2012 年 ^[40]）。
• 复合似然法（例如，Vecchia，1988 年 ^[47]；Curriero 和 Lele，1999 年 ^[8]；Stein 等，2004 年 ^[46]；Caragea 和 Smith，2007 年 ^[4]；Bevilacqua 等，2012 年 ^[2]；Eidsvik 等，2014 年 ^[9]）通过处理观测块作为条件独立的，但不清楚如何为不同块中的位置获得适当的联合预测分布。

（3）本文方法

我们在这里提出了在空间中不规则（即非网格）位置观测到的高斯过程的多分辨率近似（M-RA）。

在模型结构方面:

M-RA 过程被定义为多个空间分辨率级别基函数的线性组合，它可以捕获从非常精细到非常大尺度的空间结构。

• 与多分辨率模型的关系：多分辨率模型（例如 Chui，1992 年；Johannesson 等，2007 年；Nychka 等，2015 年 ^[35]）在空间统计方面非常成功，因为它们能够灵活地捕捉多个空间尺度的依赖性，同时在计算上是可行的。 与这些多分辨率模型方法相比， M-RA 中的基函数及其权重分布是通过对指定协方差函数的 “预测过程” 递归优化选择的，而多分辨率模型则大多事先选定基函数的形式。具体来说，每一级分辨率的每一个子区域的基函数，都是根据预测过程（Quinonero Candela 和 Rasmussen，2005 年 ^[36]；Banerjee 等，2008 年 ^[1]）的规则递归选择的，其基本方法是将空间域递归划分为越来越小的子区域，每个区域内有一组 “结点” 。
• 与全尺度近似方法的关系：M-RA 是全尺度近似的泛化（Snelson 和 Ghahramani，2007 年 ^[42]；Sang 等，2011 年 ^[38]；Sang 和 Huang，2012 年 ^[37]），全尺度近似是目前最先进的面向大数据的协方差近似方法，它只有一个层级的域划分和一种分辨率的基函数。我们将在后文中广泛比较这两种方法。

注：

多分辨率模型：将空间过程分解为在多个多分辨率上的子过程，每个子过程进一步根据 KL 展开分解为该分辨率层级上若干 “结点” 位置处的基函数组合，由于超参数会随着分辨率层级的变化而相应变化，因此使得空间过程能够反映多个分辨率上的空间模式。参见 Nychka 等 2015 年提出的 《格子克里金法》。

全尺度近似 ： 是 Sang 和 Huang （2012 年 ^[37]） 提出的一种空间过程协方差函数近似方法。该方法使用降秩过程捕获大尺度空间变化，使用具有紧支撑协方差函数的空间过程来捕获小尺度的局部变化。其中，紧支撑协方差函数来自于 “对降秩过程的残差过程逐渐细化”。该方法利用大尺度的降秩表示和小尺度的稀疏矩阵技术，降低了与超大数据集相关的计算负担。

预测过程： 是 Banerjee 等 2008 年提出的一种近似方法。该方法是一种更接近空间几何的方法，采用某种策略在研究区域内选择 $m$ 个 “结点” 构成网格（原则上可以是不规则网格，但通常会用规则网格简化），然后用这些 “结点” 定义的新空间过程（被成为 预测过程）来近似原始空间过程，显然 “结点” 的选择策略是一个重要环节。参见 《高斯预测过程》。

降秩过程：代表作是 Cressie 等 2008 年提出的 《固定秩克里金法》。该方法采是纯数学方法，将满秩的 $n \times n$ 矩阵降秩为 $r \times r$ 的低秩矩阵，其技巧在于协方差函数类应当满足 $cov(\mathbf{s,t}) = S(\mathbf{s})^{\top} \mathbf{K} S(\mathbf{t})$。式中 $\mathbf{K}$ 为 $r \times r$ 的固定秩矩阵，而 $S(\mathbf{s})$ 则被定义为由 $r$ 个基函数构成的 $r \times 1$ 向量。作者认为在基函数的选择上没有特殊要求，但建议考虑多尺度的基函数。在推断方面，固定秩克里金法将 $\mathbf{K}$ 视为待估计的协方差超参数，并利用已观测数据用矩量法进行估计。

在模型推断方面:

基于基函数的模型推断，本质上包含对基函数权重（注：被视为随机变量）后验分布的推断。在之前的方法中:

• 通过将基函数的数量限制在较小范围内（例如，Higdon，1998 年 ^[20]；Quinonero Candela 和 Rasmussen，2005 年 ^[36]；Cressie 和 Johannesson，2008 年 ^[6]）
• 或指定权重随机向量的协方差矩阵为对角矩阵或稀疏矩阵（例如，Higdon，1998 年 ^[20]；Lindgren 等，2011 年^[32]；Nychka 等，2015 年 ^[35]）。

M-RA 结合了这两种方法：它产生了多分辨率（块）的稀疏精度矩阵，但每个区域内的空间基函数数量很少，允许重复应用 Sherman-Morrison-Woodbury 公式（Sherman 和 Morrison，1950 年^[41]；Woodbury，1950 年 ^[48]）(注： 参见 《固定秩克里金法》 的 第 2.3 节)。这导致 M-RA 的高度可扩展推断算法（注：该算法也可以应用于任何具有类似结构的多分辨率基函数模型）。至关重要的是，基于之前工作（Katzfuss 和 Hammerling，2014 ^[27]）中描述的特殊情况下的 M-RA 并行算法，我们推导出可以在多个节点之间有效拆分计算任务的算法。这样，可以对大量空间数据集在多个节点上进行并行空间推断，每个节点只处理数据集的一个子集。如果有足够计算节点可用，这能够确保 M-RA 的可扩展性，即使对于具有数百万个观测值的数据集也是如此。

这篇文章的结构安排如下：

• 在 第 2 节 中，我们介绍了 M-RA 并讨论了它的一些属性。
• 在 第 3 节 中，我们介绍了参数推断和空间预测的算法，并描述了 M-RA 的计算复杂度。
• 在 第 4 节 中，我们将 M-RA 应用于大型模拟数据集和真实数据示例，并将 M-RA 与全面近似进行比较。
• 在 第 5 节 总结。所有证明都在附录 A 中给出。

2 多分辨率近似（M-RA）

我们从描述要近似的真实高斯过程开始本节（ 第 2.1 节 ）。经过一些准备工作（ 第 2.2 节 ），我们介绍了多分辨率近似 (M-RA)（ 第 2.3 节 ）并讨论了它的属性（ 第 2.4 节 和 第 2.5 节 ）。

2.1 真正的高斯过程

令 $\{y_0(\mathbf{s}) : \mathbf{s} \in \mathcal{D}\}$ 或 $y_0(·)$ 为连续（非网格）域 $\mathcal{D} \subset \mathbb{R}^d$, $d \in \mathbb{N}^+$ 上的真实空间场或感兴趣过程。我们假设 $y_0(·) \sim \mathcal{GP}(0, C_0)$ 是一个具有协方差函数 $C_0$ 的零均值高斯过程。我们对 $C_0$ 没有任何限制，只是假设它是 $\mathcal{D}$ 上的正定函数，直到参数向量 $\boldsymbol{\theta}$ 为已知。在实际应用中，$y_0(·)$ 的均值通常不为零，但估计和减去均值通常不是太大的问题。一旦在一组 $n$ 个空间位置 $\mathcal{S} = \{\mathbf{s}_1,\ldots , \mathbf{s}_n\}$ 处观测到 $y_0(·)$, 则数据的分布由下式给出：

$$y_0(\mathcal{S}) := (y_0(\mathbf{s}_1), \ldots , y_0(\mathbf{s}_n))^{\prime} \sim \mathcal{N}_n(\mathbf{0}, \mathbf{C}_0(\mathcal{S,S}))$$

一个具有协方差矩阵 $C_0(\mathcal{S,S}) = (C_0(\mathbf{s}_i, \mathbf{s}_j))_{i,j=1,\ldots ,n}$ 的 $n$ 元高斯分布。

空间统计的基本目标是（基于似然的）对参数 $\boldsymbol{\theta}$ 进行推断，并在一组新位置 $\mathcal{S}^P$ 处获得 $\mathbf{y}_{\boldsymbol{\theta}}(·)$ 的空间预测，即获得 $\mathbf{y}_0(\mathcal{S}^P)$ 的后验分布。这需要对观测的协方差矩阵 $\mathbf{C}_0(\mathcal{S, S})$ 进行多次 Cholesky 分解，一般具有 $\mathcal{O}(n^3)$ 的时间复杂度和 $\mathcal{O}(n^2)$ 内存复杂度。当 $n = 10^5$ 或更大时，这在计算上是不可行的。此外，推断计算也很难并行化，因为密集的巨大协方差矩阵的计算，需要大量通信开销。因此，计算挑战不能通过强力使用高性能计算系统来解决，需要近似或简化假设。

2.2 域划分和节点

（1）空间域的划分

为了定义 M-RA，我们要对空间域 $\mathcal{D}$ 进行递归划分，即对于其 $J$ 个区域（ $\mathcal{D}_1，\ldots, \mathcal{D}_J$）, 进一步划分成 $J$ 个更小的子区域，依此类推，直到层级 $M$：

$$\mathcal{D}_{j_1,\ldots ,j_{m-1}} =\dot{\cup}_{j_m=1,\ldots ,J} \mathcal{D}_{j_1,\ldots ,j_m},\qquad \text{where} \quad j_1,\ldots , j_{m-1} = 1,\ldots,J ; m = 1,\ldots,M$$

对于高斯过程 $x(·) \sim \mathcal{GP}(0, C)$，我们将 $[x(·)]_{[m]}$ 定义为 $x(·)$ 的分辨率为 $m$ 的区域之间的 “块独立” 版本；也就是说，将高斯过程定义为 $[x(·)]_{[m]} \sim \mathcal{GP}(0, [C]_{[m]})$ 的分块协方差矩阵版本，其中如果 $\mathbf{s}_1$, $\mathbf{s}_2$ 位于分辨率为 $m$ 的同一区域 $\mathcal{D}_{j_1,\ldots,j_m}$ 中，则 $[C]_{[m]}(\mathbf{s}_1, \mathbf{s}_2) = C(\mathbf{s}_1, \mathbf{s}_2)$ ，否则 $[C]_{[m]}(\mathbf{s}_1, \mathbf{s}_2) = 0$。

（2）结点的设置

我们还需要一组多多分辨率 “结点”，例如 $\mathcal{Q}_{j_1,\ldots ,j_m}$ 是一组 $r$ 个 “结点”（$r \ll n$），它们都位于子区域 $\mathcal{D}_{j_1,\ldots ,j_m}$ 中。为了便于标记，我们假设分辨率为 $M$ 的每区域中的节点，由其观测位置给出：$\mathcal{Q}_{j_1,\ldots ,j_M} = \mathcal{S}_{j_1,\ldots ,j_M}$ 。此外，对于分辨率为 $m$，我们记 $\mathcal{Q}^{(m)} = \{\mathcal{Q}_{j_1,\ldots ,j_m} : j_1,\ldots , j_m = 1,\ldots , J \}$ 为该分辨率中所有 $rJ^{m}$ 个结点构成的集合。

对于一维玩具示例， 图 1 的顶行显示了 $M = 1$ 和 $M = 3$ 的 M-RA 的 “分区” 和节点。节点是基函数达到最大值的位置。请注意，我们假设子区域数 ($J$) 和节点数 ($r$) 在各 “分区” 之间保持一致，不过这只是为了符号方便，并非必需。此后，我们将假设域划分和节点是固定已知的。 第 2.5 节 给出了他们选择的进一步讨论。

图 1：在 $n = 54$ 个观察（从指数协方差函数生成）的一维空间域 $\mathcal{D} = [0, 1]$ 的玩具示例中，当具有相同的计算复杂度（两种模型的 $M r = 6$）时，全尺度近似 (1-RA) 与具有 $3$ 个分辨率的多分辨率近似 (3-RA) 之间的比较。图 © 和 (d) 显示协方差近似使用的基函数达到分辨率 $m$，其中 $m = 0, \ldots, M$。随着 $m$ 的增加，真实协方差和近似协方差之间的偏差只会出现在越来越小的尺度（距离）上。当 $m = M$ 时，3-RA 的协方差和预测与 0-RA 的真实协方差和预测完全相同，而使用 1-RA 的协方差近似和预测与真实值不同。请注意，对于其他协方差函数或更高维度，M-RA 通常不准确（请参阅 第 2.5 节）。

2.3 多分辨率近似（M-RA）的定义

回忆 第 2.1 节 中的真实高斯过程 $y_0(·) \sim \mathcal{GP}(0, C_0)$。我们暂时假设协方差函数 $C_0$ 已知（超参数的推断将在 第 3.3 节 中讨论）。 M-RA 过程以分辨率 $m = 0,\ldots , M$ 迭代地近似 $y_0(·)$ 及其协方差 $C_0$，基于 第 2.2 节 中指定的 “结点” 和 “分区” 。在每个分辨率 $m$ 处，各区域 $\mathcal{D}_{j_1,\ldots ,j_m}$ 之间相互独立地使用预测过程（Banerjee 等，2008 年 ^[1]）来近似 “残余” 项（ 即 $y_0(·)$ 和较低分辨率下的近似之间的差异 ）。如 图 1(d) 所示，低 M-RA 分辨率捕获低频（即远距离）的可变性，导致随着 $m$ 的增加， “残余项” 在越来越小的尺度上表现出可变性，因此近似 “残余项” 在更精细的 “分区” 中产生更小的近似误差。

更具体地说，我们从 $y_0(·)$ 的预测过程近似 $\tau_0(\mathbf{s}) := \mathbb{E}(y_0(\mathbf{s}) \mid \mathbf{y}_0(\mathcal{Q}^{(0)}))$, $\mathbf{s} \in \mathcal{D}$ 开始，在假设区域 $\mathcal{D}_1,\ldots , \mathcal{D}_J$ 独立的情况下，得到分辨率 $1$ 的近似 “残余项” 过程 $\delta_1(·) = [y_0(·) − \tau_0(·)]_{[1]}$ (Sang 等, 2011 ^[38])。然后，我们再将此 “残余项” 过程近似为其预测过程 $\tau_1(\mathbf{s}) = \mathbb{E}(\delta_1(\mathbf{s}) | \delta_1(\mathcal{Q}^{(1)}))$，$\mathbf{s} \in \mathcal{D}$ 与近似 “残余项” $\delta_2(·) = [ \delta_1(·) − \tau_1(·)]_{[2]}$ 之和。依此类推，直到 $M$ 级。这导致 M-RA 的以下表达式：

$$y_M(·) = \tau_0(·) + \tau_1(·) + \ldots + \tau_{M-1}(·) + \delta_M(·) \tag{1}$$

其中预测过程 $\tau_m(\mathbf{s}) = \mathbb{E}(\delta_m(\mathbf{s}) | \delta_m(\mathcal{Q}^{(m)}))$, $\mathbf{s} \in \mathcal{D}$；“残余项” 为 $\delta_m(·) = [\delta_{m−1}(·) − \tau_{m−1}(·)]_{[m]} \sim \mathcal{GP}(0, v_m)$。

注意到，对于 $m = 0，\ldots , M − 1$, 我们可以将 $\mathbf{s} \in \mathcal{D}_{j_1,\ldots ,j_m}$ 的每个预测过程写成基函数的线性组合 (参考 Katzfuss, 2013 ^[23]) 形式：, $\tau_m(\mathbf{s}) = \mathbf{b}_{j_1,\ldots ,j_m}(\mathbf{s})^{\prime} \boldsymbol{η}_{j_1,\ldots ,j_m}$ ，其中 $\boldsymbol{η}_{j_1,\ldots ,j_m} \sim \mathcal{N}_r(\mathbf{0}, \mathbf{K}_{j_1,\ldots ,j_m})$, 和

$$\begin{align*} \mathbf{b}_{j_1,\ldots ,j_m} (\mathbf{s}) &:= v_m({\mathbf{s}}, \mathcal{Q}_{j_1,\ldots ,j_m}), \mathbf{s} \in \mathcal{D}_{j_1,\ldots ,j_m} \\ \mathbf{K}^{-1}_{j_1,\ldots ,j_m} &:= v_m(\mathcal{Q}_{j_1,\ldots ,j_m}, \mathcal{Q}_{j_1,\ldots ,j_m})\\ v_{m+1}(\mathbf{s}_1, \mathbf{s}_2) &:= v_m(\mathbf{s}_1, \mathbf{s}_2) − \mathbf{b}_{j_1,\ldots ,j_m} (\mathbf{s}_1)^{\prime} \mathbf{K}_{j_1,\ldots ,j_m} \mathbf{b}_{j_1 ,\ldots ,j_m}(\mathbf{s}_2), \quad \mathbf{s}_1, \mathbf{s}_2 \in \mathcal{D}_{j_1,\ldots ,j_m} \end{align*} \tag{2}$$

其中如果 $\mathbf{s}_1$ 和 $\mathbf{s}_2$ 在第 $m$ 个分辨率下位于不同区域，则 $v_{m+1}(\mathbf{s}_1, \mathbf{s}_2) = 0$ ，并且我们设置 $v_0 = C_0$。

因此，式（1） 的 M-RA 也可以写成分辨率 $0,\ldots , M − 1$ 中基函数的线性组合, 再加上 $M$ 分辨率处的 “残余项” ：

$$\mathbf{y}_M(\mathbf{s}) = \mathbf{b}(\mathbf{s})^{\prime} \boldsymbol{η} + \mathbf{b}_{j_1}(\mathbf{s})^{\prime} \boldsymbol{η}_{j_1} + \ldots + \mathbf{b}_{j_1,\ldots ,j_{M−1}}(\mathbf{s})^{\prime} \boldsymbol{η}_{j_1,\ldots ,j_{M−1}} + \delta_M(\mathbf{s}), \qquad \mathbf{s} \in \mathcal{D}_{j_1,\ldots ,j_M} \tag{3}$$

其中权重向量相互独立且与 $\delta_M(·) \sim \mathcal{GP}(0, v_M )$ 无关。 图 1 (a) 和 图 1 (c) 显示了玩具示例中的基函数。一旦我们在位置 $\mathcal{S}$ 处观测到数据，我们也可以将 式 (3) 中的 “残余项” $\delta_M(·)$ 写为基函数的线性组合，如 式 (2) 中 $\delta_M(\mathbf{s}) = \mathbf{b}_{j_1,\ldots ,j_M}(\mathbf{s})^{\prime} \boldsymbol{η}_{j_1,\ldots,j_M}$, $\mathbf{s} \in \mathcal{D}_{j_1,\ldots ,j_M}$，其中 $\mathcal{Q}_{j_1,\ldots,j_M} = \mathcal{S}_{j_1,\ldots ,j_M}$。

2.4 M-RA 的特性

（1）许多基函数

与依赖于少量或中等数量基函数的所谓低秩方法（参见如，Stein，2014 ^[44]，此类方法通常难以捕获小尺度变化）相比， $M > 0$ 的 M-RA 模型的基函数总数 $r_{total}$ 大于测量次数 $n$： $r_{total} = r \sum^{M}_{m=0} J^M = rJ^M + r \sum^{M-1}_{m=0} J^m = n + r \frac{ J^M −1}{J−1} > n$。这使得 M-RA 能够捕获所有空间尺度的变化，包括非常小的尺度。

（2）正交分解

因为预测过程是一个条件期望，也是一个投影运算，对于所有 $m = 0,\ldots , M − 1$，预测过程 $\tau_m(·)$ 均独立于 “残余项” $\delta_m(·) − \tau_m(·)$。因此，我们将 式 (1) 中的 M-RA 定义为正交分量之和。在 式 (3) 中，M-RA 是空间基函数的加权和，其权重 $\boldsymbol{η}_{j_1,\ldots ,j_m}$ 在概率空间上是块正交的（注：根据 KL 定理，权重被视为随机变量），但如果 $\mathcal{D}_{j_1,\ldots ,j_{m_1}} \cap D_{i_1,\ldots ,i_{m_2}} = \emptyset$，则两组基函数 \mathbf{b}_{j_1,\ldots, j_{m_1} 和 \mathbf{b}_{i_1,\ldots,i_{m_2} 仅在物理空间中是块正交的。

（3）有效的高斯过程

【命题 1】 M-RA 是具有非负定协方差函数 $C_M$ 的有效高斯过程

（4）“最优” 的基函数

在每个分辨率 $m = 0,\ldots , M −1$ 和在每个区域 $\mathcal{D}_{j_1,\ldots ,j_m}$ 内，式 (1) 中 M-RA 的目标是尽可能接近地近似 “残余项” 过程 $\delta_m(·)$，其中

$$\delta_m(·) = [\delta_{m−1}(·) − \tau_{m−1}(·)]_{[m]} = [y_0(·) − \sum^{m-1}_{l=0} \tau_l(·)]_{[m]} \tag{4}$$

因此，在每个区域中，式 (1) 中的 $\delta_m(·)$ 是真实过程 $y_0(·)$ 与较低分辨率下的 “先前” 项 $\sum^{m-1}_{l=0} \tau_l(·)$ 之间的差异。我们选择 $\tau_m(·)$ 作为 $\delta_m(·)$ 的预测过程近似。由于这是一个条件期望，$\tau_m(·)$ 是以 $\delta_m(\mathcal{Q}^{(m)})$ 为条件，最小化 $\delta_m(\mathbf{s})$ 和$\delta_m(\mathcal{Q}^{(m)})$ 之间期望平方差的一个函数（Banerjee 等，2008 年^[1]）。此外，$\tau_m(·)$ 可以被视为每个区域 $\mathcal{D}_{j_1,\ldots ,j_m}$ 内 $\delta_m(·)$ 的最佳秩 $r$ 表示的近似，因为 $\tau_m(·)$ 是 $\delta_m(·)$ 的 Karhunen–Loeve 展开中前 $r$ 项的 Nystrom 近似（Sang 和 Huang，2012 ^[37]）。这进一步证明，在每个分辨率下，预测过程都会捕获低频的可变性，而大部分较高频率的可变性将在较小的子区域内以较高分辨率捕获。随着 $r$ 的增加，$\tau_m(·)$ 将越来越接近 $\delta_m(·)$。事实上，如果 $\mathcal{Q}_{j_1,\ldots ,j_m}$ 等于 $\mathcal{S}_{j_1,\ldots ,j_m}$，即 $\mathcal{D}_{j_1,\ldots ,j_m}$ 中的观测位置集，那么可以直接证明 $\tau_m(\mathcal{S}_{j_1,\ldots ,j_m}) = \delta_m(\mathcal{S}_{j_1,\ldots ,j_m})$。从这个意义上说，$\tau_m(·)$ 及其基函数表示是 $\delta_m(·)$ 的 “最优” 近似。

与空间数据的许多其他多分辨率方法相比，M-RA 因此自动提供基函数表示来近似给定的协方差函数 $C_0$（基于特定的域划分和节点集），而对 $C_0$ 没有任何限制.这在 图 2 中进行了说明，它显示了高度非平稳协方差函数 $C_0$ 的 3-RA 的基函数。

图 2：对于在一维域 $\mathcal{D} = [0, 1]$ 上具有范围为 $0.15$ 和空间变化（增加）平滑度 $ν(s) = 0.2+0.7s$ 的非平稳 Matern 协方差函数的空间过程，基函数和 $J = 2$ 和 $r = 3$ 的 M -RA 的划分。请注意基函数如何适应真实协方差函数的平滑度增加以及根据基函数在较低分辨率下的设置。

（5）协方差近似的质量

在分辨率为 $m$ 时，M-RA 尝试通过预测过程基函数分量 $\mathbf{b}_{j_1,\ldots ,j_m}(·)^{\prime} \boldsymbol{η}_{j_1,\ldots ,j_m}$。 M-RA 的协方差 $C_M(\mathbf{s}_1, \mathbf{s}_2)$ 与真实协方差 $C_0(\mathbf{s}_1, \mathbf{s}_2)$ 的接近程度取决于 $\mathbf{s}_1$ 和 $\mathbf{s}_2$ 处于同一区域的分辨率。如果 $\mathbf{s}_1$ 和 $\mathbf{s}_2$ 在分辨率为 $M$ 的同一区域中，则 $C_M(\mathbf{s}_1, \mathbf{s}_2) = C_0(\mathbf{s}_1, \mathbf{s}_2)$。 （要证明这一点，只需将 式 (1) 与 式 (4) 结合起来。）这也意味着 $y_0(·)$ 和 $y_M(·)$ 的方差相同。如果 $\mathbf{s}_1$ 和 $\mathbf{s}_2$ 在分辨率为 $m<M$ 的同一区域 $\mathcal{D}_{j_1,\ldots ,j_m}$ 中，但不在分辨率 $m + 1$ 中，则 $C_0(\mathbf{s}_1, \mathbf{s}_2)$ 仅由分辨率为 $m$ 的基函数近似：$C_M (\mathbf{s}_1, \mathbf{s}_2) = \sum^{m}_{l=0} \mathbf{b}_{j_1,\ldots ,j_l}(\mathbf{s}_1)^{\prime} \mathbf{K}_{j_1,\ldots ,j_l} \mathbf{b}_{j_1,\ldots ,j_l}(\mathbf{s}_2)$。

（6）与全尺寸近似的比较

M-RA 的重要特例是 $M = 0$ 的原始过程 $y_0$ 和 $M = 1$ 的全尺度近似（Snelson 和 Ghahramani，2007 年 ^[42]；Sang 等，2011 年 ^[38]）。全尺度近似（或 1-RA）只有一个分辨率下的基函数（ $r^F$ 个 “结点” 集 $\mathcal{Q}^F$ ），以及单一层的域划分 $\mathcal{D} =\dot{\cup}_{j=1,\ldots ,J^F} \mathcal{D}^F_j$ 。对于海量数据集，子区域 $\mathcal{D}^F_j$ 需要非常小才能保持计算可行性。

比较 M-RA（$M > 1$）模型和 $\mathcal{Q}^F = Q$ 、$\{\mathcal{D}^F_j : j = 1,\ldots , J^F\} = \{\mathcal{D}_{j_1,\ldots ,j_M} : j_1,\ldots , j_M = 1,\ldots , J\}$ 的全尺度近似（1-RA）模型，对于同一（最精细）子区域 $\mathcal{D}^F_j$ 中的位置对和分辨率为 $1$ 的、$i \neq j$ 的不同（最粗略）子区域 $\mathcal{D}_i$ 和 $\mathcal{D}_j$ 中的位置对来说，其协方差近似是相同的。对于所有其他位置对，M-RA 有额外的基函数来捕获其依赖性，如果 $r$ 足够大以至于 $\tau_m(·)$ 捕获子区域 $\mathcal{D}_{j_1,\ldots ,j_{m+1}}$ 之间的 $\delta_m(·)$ 的依赖性，则 M-RA 将提供比 1-RA 更好的 $y_0(·)$ 近似。

如稍后在 第 3.6 节 中所述，具有 $r$ 个节点的 M-RA 与具有 $M r$ 个节点的 1-RA 具有相同的计算复杂度。如 图 1 所示，M-RA 可以产生相当好的近似。进一步的比较在 第 4 节 中介绍。

2.5 更多关于节点和 “分区” 的选择

为了获得良好的近似，我们建议在 $rJ^M \leq n$ 的约束条件下，在计算资源允许的范围内选择尽可能小的 $M$ 和 $J$，以及尽可能大的 $r$（见后面的 表（1a） ）。

如果观测位置近似均匀分布在域 $\mathcal{D}$ 上，则可以简单地通过递归地将每个区域划分为等面积的 $J$ 个子区域来获得 “分区” 。如果观测位置远非统一，则可能需要更复杂的 “分区” 方案才能实现快速推断。

剩下的问题是每个区域内 $r$ 个节点的放置。一个简单的解决方案是在每个区域 $\mathcal{D}_{j_1,\ldots,j_m}$ 上使用等距网格，但在每个区域内靠近边界放置更多节点也可能是有利的。要了解原因，请记住 式（4） 和 第 2.3 节 中每个区域 $\mathcal{D}_{j_1,\ldots,j_m}$ 内的目标是近似 $\delta_m(·) \sim \mathcal{GP}(0, v_m)$。考虑 $J = 2$ 个包含观测位置 $\mathcal{S} = \{\mathcal{S}_1, \mathcal{S}_2\}$ 和 $\mathcal{S}_j = \{\mathcal{S}^B_j , \mathcal{S}^I_j \}$ 的子区域的情况，其中 $\mathcal{S}^B_j$ 是距离边界 $c$ 内的位置，$\mathcal{S}^I_j$ 是次区域 $j$ 内部的其余位置。选择节点 $\mathcal{Q}_{j+1,\ldots,j_m} = \mathcal{S}^B := \{\mathcal{S}^B_1 , \mathcal{S}^B_2 \}$，可以证明 $\operatorname{var}(\delta_m(\mathcal{S}I)|\delta_m(\mathcal{S}B))$，后者是只有一个非零块的矩阵，$\operatorname{var}(\delta_m(\mathcal{S}^I)|\delta_m(\mathcal{S}^B))$。该矩阵中唯一被 M-RA 忽略的部分是 $\operatorname{cov}(\delta_m(\mathcal{S}I 1 ), \delta_m(\mathcal{S}I 2 )|\delta_m(\mathcal{S}B))$，如果 $c$ 很大和/或屏蔽效应，它应该非常小（例如，Stein，2011 ^[43]）适用于 $v_m$。

图 1 说明了该策略的一个极端情况。对于在一个空间维度上没有块块的指数协方差函数，筛选效果完全成立，因为在给定第三个观测值将两者分开的情况下，两个观测值是条件独立的。因为 图 1 中特定分辨率的节点位于下一个更高分辨率的 “分区” 之间的边界上，所以 M-RA 在这种情况下是精确的。对于没有屏蔽效应或更高维度的协方差函数，M-RA 通常不准确。

虽然 第 4.1 节 中的（有利的）数值结果是通过最简单的等面积 “分区” 和等距节点选择获得的，但可以采用更复杂的策略，例如基于聚类选择节点和 “分区” （例如，Snelson 和Ghahramani, 2007 ^[42]) 或使用可逆跳跃马尔可夫链蒙特卡洛 (例如, Gramacy and Lee, 2008 ^[16]; Katzfuss, 2013 ^[23])。通过使用不同的移动 “分区” 执行多个 M-RA 并使用贝叶斯模型平均合并结果（例如，Hoeting 等，1999 ^[21]），可以减轻由于 “分区” 选择引起的任何潜在边界效应。

3 推断

在本节中，我们描述了 M-RA 的推断。对于参数向量 $\boldsymbol{\theta}$ 的特定值，协方差函数 $C_0$ 以及 式 (3) 中的基函数 $\mathbf{b}_{j_1,\ldots ,j_m}$ 和协方差矩阵 $\mathbf{K}_{j_1,\ldots ,j_m}$ 是固定的。推断的先决条件是计算总结 M-RA 在选定节点和观测位置处诱导的先验分布的数量（ 第 3.1 节 ）。然后，推断的主要任务是获得未知权重向量 $\mathcal{E}^{M-1}$ 的后验分布（ 第 3.2 节 ），其中我们定义 $\mathcal{E}_m := \{ \boldsymbol{η}_{j_1,\ldots ,j_l} : j_1,\ldots , j_l = 1,\ldots , J; l = 0,\ldots , m \}$ 对于所有 $m = 0,\ldots , M − 1$ 是分辨率为 $m$ 和所有较低分辨率的所有基函数权重的集合（我们设 $\mathcal{E}_{-1} = \emptyset$ 为空集）。一旦获得此后验分布，就可以使用它来评估可能性（ 第 3.3 节 ）和获得空间预测（ 第 3.4 节 ）。通过利用权重的先验和后验精度矩阵的块稀疏多多分辨率 “结点”构，我们获得了具有出色时间和内存复杂度的推断（ 第 3.6 节 ），可以充分利用具有大量的分布式内存系统节点（ 第 3.5 节 ），因此可扩展到海量空间数据集。

3.1 计算先验

令 $\mathcal{S}_{j_1,\ldots ,j_m}$ 为位于 $\mathcal{D}_{j_1,\ldots ,j_m}$ 区域的观测点，定义

$$\begin{align*} \mathbf{B}^l_{j_1,\ldots ,j_m} &:= \mathbf{b}_{j_1,\ldots ,j_l}(\mathcal{S}_{j_1,\ldots , j_m}), l = 0, 1,\ldots , m,\\ \boldsymbol{\Sigma}_{j_1,\ldots ,j_m} &:= \operatorname{var}(\mathbf{y}_M(\mathcal{S}_{j_1,\ldots ,j_m} ) | \mathcal{E}_{m−1}) = \mathbf{B}^m_{j_1,\ldots ,j_m} \mathbf{K}_{j_1,\ldots ,j_m} {\mathbf{B}^{m}_{j_1,\ldots ,j_m}}^{\prime} + \mathbf{V}_{j_1,\ldots ,j_m} \\ \mathbf{V}_{j_1,\ldots ,j_m} &:= \operatorname{var}(\mathbf{y}_M(\mathcal{S}_{j_1,\ldots ,j_m}) | \mathcal{E}_m) = \operatorname{blockdiag}\{ \boldsymbol{\Sigma}_{j_1,\ldots ,j_m,1},\ldots , \boldsymbol{\Sigma}_{j_1,\ldots ,j_m,J} \} \end{align*} \tag{5}$$

对于 $m = 0, 1,\ldots , M − 1$, 和 $\boldsymbol{\Sigma}_{j_1,\ldots ,j_M} := v_M (\mathcal{S}_{j_1,\ldots ,j_M} , \mathcal{S}_{j_1,\ldots ,j_M} )$ 。

对于推断，我们明确需要计算矩阵 $\{\mathbf{K}^{-1}_{j_1,\ldots ,j_m}: j_1,\ldots , j_m = 1,\ldots , J ; m = 0,\ldots , M −1\}$, $\{\mathbb{B}^l_{j_1,\ldots ,j_M}: j_1,\ldots , j_M = 1,\ldots , J ; l = 0,\ldots , M −1 \}$, 和 $\{\boldsymbol{\Sigma}_{j_1,\ldots ,j_M}: j_1,\ldots , j_M = 1,\ldots , J \}$。定义 $\mathbf{W}^l_{j_1,\ldots ,j_m} := v_l(\mathcal{Q}_{j_1,\ldots ,j_m} , \mathcal{Q}_{j_1,\ldots ,j_l} )$，我们可以通过计算

$$\mathbf{W}^l_{j_1,\ldots ,j_m} = C_0(\mathcal{Q}_{j_1,\ldots ,j_m} , \mathcal{Q}_{j_1,\ldots ,j_l} ) − \sum^{l-1}_{k=0} \mathbf{W}^k_{j_1,\ldots ,j_m} \mathbf{K}_{j_1,\ldots ,j_k} {\mathbf{W}^k_{j_1,\ldots ,j_l}}^{\prime} \tag{6}$$

对于 $m = 0,\ldots , M$ , $j_1,\ldots , j_m = 1,\ldots,J$ 和 $l = 0,\ldots,m$。然后我们有 $\mathbf{K}^{-1}_{j_1,\ldots ,j_m} = \mathbf{W}^m_{j_1,\ldots ,j_m}$ 对于 $m < M$ , $\mathbb{B}^l_{j_1,\ldots ,j_M} = \mathbf{W}^l_{j_1,\ldots ,j_M}$ 其中 $l < M$ , 且 $\boldsymbol{\Sigma}_{j_1,\ldots ,j_M} = \mathbf{W}^M_{j_1,\ldots ,j_M}$ 。

顺便说一句，这些矩阵的其他参数化（以及 式（3） 中的数量）也是可能的，并且将导致类似的推断算法，如下所述，只要权重向量是先验独立的并且基函数具有相同的限制支持。

3.2 基函数权重的后验分布

式 (3) 中 M-RA 的定义，连同 式(5) 中的定义，意味着

$$\mathbf{y}_M(\mathcal{S}_{j_1,\ldots ,j_m}) | \mathcal{E}_m \sim \mathcal{N}(\sum^{m}_{l=0} \mathbb{B}^l_{j_1,\ldots ,j_m} \boldsymbol{η}_{j_1,\ldots ,j_l} , \mathbf{V}_{j_1,\ldots ,j_m})$$

使用 Katzfuss 和 Hammerling（2014 年， 第 3 节 ）中的结果，可以证明所有 $m = 0，\ldots , M − 1$ 的权重向量的条件后验分布由下式给出。

$$\mathbf{η}_{j_1,\ldots ,j_m} | \mathbf{y}_M(\mathcal{S}), \mathcal{E}_{m−1} \stackrel{ind.} \sim \mathcal{N}_r(\tilde{\boldsymbol{ν}}_{j_1,\ldots ,j_m} ,\tilde{\mathbf{K}}_{j_1,\ldots ,j_m}), j_1,\ldots , j_m = 1,\ldots J \tag{7}$$

具有后验精度和均值分别为：

$$\begin{align*} \tilde{\mathbf{K}}^{-1}_{j_1,\ldots ,j_m} = \mathbf{K}^{-1}_{j_1,\ldots ,j_m} + {\mathbf{B}^m_{j_1,\ldots ,j_m}}^{\prime} \mathbf{V}^{−1}_{j_1,\ldots ,j_m} \mathbf{B}^m_{j_1,\ldots ,j_m} = \mathbf{K}^{-1}_{j_1,\ldots ,j_m} + \mathbf{A}^{m,m}_{j_1,\ldots ,j_m}\\ \tilde{\boldsymbol{ν}}_{j_1,\ldots ,j_m} = \tilde{\mathbf{K}}_{j_1,\ldots ,j_m} ({\mathbf{B}^m_{j_1,\ldots ,j_m}}^{\prime} \mathbf{V}^{−1}_{j_1,\ldots ,j_m} (\mathbf{y}_M(\mathcal{S}_{j_1,\ldots ,j_m} ) − \sum^{m-1}_{l=0} \mathbb{B}^l_{j_1,\ldots ,j_m} \boldsymbol{η}_{j_1,\ldots ,j_l})) \\ = \tilde{\mathbf{K}}_{j_1,\ldots ,j_m} \boldsymbol{ω}^m_{j_1,\ldots ,j_m} − \sum^{m-1}_{l=0} \mathbf{K}_{j_1,\ldots ,j_m} \mathbf{A}^{m,l}_{j_1,\ldots ,j_m} \boldsymbol{η}_{j_1,\ldots ,j_l} \end{align*} \tag{8}$$

其中：

$$\begin{align*} \mathbf{A}^{k,l}_{j_1,\ldots ,j_m} &:= {\mathbf{B}^k_{j_1,\ldots ,j_m}}^{\prime} \mathbf{V}^{-1}_{j_1,\ldots ,j_m} \mathbb{B}^l_{j_1,\ldots ,j_m} = \sum^{J}_{j_{m+1}=1} \tilde{\mathbf{A}}^{k,l}_{j_1,\ldots ,j_{m+1}} \\ \boldsymbol{ω}^k_{j_1,\ldots ,j_m} &:= {\mathbf{B}^k_{j_1,\ldots ,j_m}}^{\prime} \mathbf{V}^{-1}_{j_1,\ldots ,j_m} \mathbf{y}_M(\mathcal{S}_{j_1,\ldots ,j_m}) = \sum^{J}_{j_{m+1}=1} \tilde{\boldsymbol{ω}}^k_{j_1,\ldots ,j_{m+1}}\\ &k \leq l = 0,\ldots , m \end{align*} \tag{9}$$

对于 $m = M − 1, M − 2,\ldots , 0$ 可以迭代地得到，使用

$$\begin{align*} &\tilde{\mathbf{A}}^{k,l}_{j_1,\ldots ,j_m} := {\mathbf{B}^k_{j_1,\ldots ,j_m}}^{\prime} \boldsymbol{\Sigma}^{−1}_{j_1,\ldots ,j_m} \mathbb{B}^l_{j_1,\ldots ,j_m} = \mathbf{A}^{k,l}_{j_1,\ldots ,j_m} − \mathbf{A}^{k,m}_{j_1,\ldots ,j_m} \tilde{\mathbf{K}}_{j_1,\ldots ,j_m} \mathbf{A}^{m,l}_{j_1,\ldots ,j_m}\\ &\tilde{\boldsymbol{ω}}^k_{j_1,\ldots ,j_m} := {\mathbf{B}^k_{j_1,\ldots ,j_m}}^{\prime} \boldsymbol{\Sigma}^{-1}_{j_1,\ldots ,j_m} \mathbf{y}(\mathcal{S}_{j_1,\ldots ,j_m} ) = \boldsymbol{ω}^k_{j_1,\ldots ,j_m} − \mathbf{A}^{k,m}_{j_1,\ldots ,j_m} \tilde{\mathbf{K}}_{j_1,\ldots ,j_m} \boldsymbol{ω}^m_{j_1,\ldots ,j_m} \end{align*} \tag{10}$$

在实践中，式 (10) 中的数量直接根据 $m = M$ 的定义（第一个等式）计算，并使用 $m = M − 1,\ldots , 0$ 的递归表达式（第二个等式）。结果 式 (9)–(10) 的证明使用 Sherman-Morrison-Woodbury 公式 很简单（Sherman 和 Morrison，1950；Woodbury，1950；Henderson 和 Searle，1981）：

$$\boldsymbol{\Sigma}^{-1}_{j_1,\ldots ,j_m} = \mathbf{V}^{-1}_{j_1,\ldots ,j_m} − \mathbf{V}^{-1}_{j_1,\ldots ,j_m} \mathbf{B}^m_{j_1,\ldots ,j_m} \tilde{\mathbf{K}}_{j_1,\ldots ,j_m} {\mathbf{B}^m_{j_1,\ldots ,j_m}}^{\prime} \mathbf{V}^{-1}_{j_1,\ldots ,j_m} \tag{11}$$

3.3 参数推断

M-RA 的推断基于 $L_M(\boldsymbol{\theta})$，观测值 $\mathbf{y}_M(\mathcal{S}) \sim \mathcal{N}_n(\mathbf{0}, \boldsymbol{\Sigma})$ 的似然，其中 $\boldsymbol{\Sigma} = \boldsymbol{\Sigma}(\boldsymbol{\theta})$ 是 式 (5) 中给出的 M-RA 协方差矩阵 $m = 0$ 基于参数向量 $\boldsymbol{\theta}$：

$$−2 \log L_M(\boldsymbol{\theta}) = \log |\boldsymbol{\Sigma}| + {\mathbf{y}_M(\mathcal{S})}^{\prime} \boldsymbol{\Sigma}^{-1} \mathbf{y}_M(\mathcal{S})$$

这种可能性可以使用 第 3.2 节 中的数量来计算。我们有 $−2 \log L_M(\boldsymbol{\theta}) = d + u$，其中

$$\begin{align*} &d_{j_1,\ldots ,j_m} := \log |\boldsymbol{\Sigma}_{j_1,\ldots ,j_m} |\\ &u_{j_1,\ldots ,j_m} := \mathbf{y}_M(\mathcal{S}_{j_1,\ldots ,j_m})^{\prime} \boldsymbol{\Sigma}^{-1}_{j_1,\ldots ,j_m} \mathbf{y}_M(\mathcal{S}_{j_1,\ldots ,j_m})\\ &m = 0, 1,\ldots , M \end{align*}$$

对于 $m = M$ ，这些量是使用定义计算的。对于 $m = M − 1,\ldots , 0$, 递归表达式

$$\begin{align*} &d_{j_1,\ldots ,j_m} = \log |\tilde{\mathbf{K}}^{-1}_{j_1,\ldots ,j_m} | − \log |\mathbf{K}^{-1}_{j_1,\ldots ,j_m} | + \sum^{J}_{j_{m+1}=1} d_{j_1,\ldots ,j_{m+1}} \\ &u_{j_1,\ldots ,j_m} = − {\boldsymbol{ω}^m_{j_1,\ldots ,j_m}}^{\prime} \tilde{\mathbf{K}}_{j_1,\ldots ,j_m} \boldsymbol{ω}^m_{j_1,\ldots ,j_m} + \sum^{J}_{j_{m+1}=1} u_{j_1,\ldots ,j_{m+1}} \end{align*}$$

可以使用矩阵行列式引理（例如，Harville, 1997, Thm. 18.1.1）和 Sherman-Morrison-Woodbury 公式导出 式(11)。

总之，M-RA 对数似然可以写成对数行列式和仅涉及 $r\times r$ 矩阵的二次形式的总和。该结果支持对似然进行快速且可扩展的评估，进而允许对未知参数向量 $\boldsymbol{\theta}$ 进行广泛的基于似然的推断技术，例如最大似然估计、马尔可夫链蒙特卡罗或空间粒子滤波时间上下文。

3.4 空间预测

空间预测可以在参数推断完成后单独进行。在频率论者的背景下，预测只需要进行一次，就可以得到最终的参数估计值。在贝叶斯框架中，只能对细化的 MCMC 链进行参数推断，或者在粒子采样器的情况下对具有相当大重量的粒子进行参数推断。

隐式调节参数向量 $\boldsymbol{\theta}$ 的特定值，空间预测相当于在一组预测位置 $\mathcal{S}^P$ 处找到后验预测分布 $\mathbf{y}_M(\mathcal{S}^P) | \mathbf{y}_M(\mathcal{S})$。我们用 $\mathcal{S}^P_{j_1,\ldots ,j_M}$ 表示区域 $\mathcal{D}_{j_1,\ldots ,j_M}$ 中的预测位置。作为第一步，我们需要计算类似于 式(6) 的先验预测量，

$$\mathbf{U}^l_{j_1,\ldots ,j_M} := v_l(\mathcal{S}^P_{j_1,\ldots ,j_M}, \mathcal{Q}_{j_1,\ldots ,j_l} ) = C_0(\mathcal{S}^P_{j_1,\ldots ,j_M}, \mathcal{Q}_{j_1,\ldots ,j_l}) − \sum^{l-1}_{k=0} \mathbf{U}^k_{j_1,\ldots ,j_M} \mathbf{K}_{j_1,\ldots ,j_k} {\mathbf{W}^k_{j_1,\ldots ,j_l}}^{\prime}$$

对于 $l = 0,\ldots , M$ ，然后我们设置 $L^M_{j_1,\ldots ,j_M} := v_M (\mathcal{S}^P_{j_1,\ldots ,j_M} , \mathcal{S}_{j_1,\ldots ,j_M} ) = \mathbf{U}^M_{j_1,\ldots ,j_M}$ 和

$$\mathbf{V}^P_{j_1,\ldots,j_M} := v_M (\mathcal{S}^P_{j_1,\ldots ,j_M} , \mathcal{S}^P_{j_1,\ldots ,j_M} ) = C_0(\mathcal{S}^P_{j_1,\ldots ,j_M} , \mathcal{S}^P_{j_1,\ldots ,j_M}) − \sum^{l −1}_{k=0} \mathbf{U}^k_{j_1,\ldots ,j_M} \mathbf{K}_{j_1,\ldots ,j_k} {\mathbf{U}^k_{j_1,\ldots ,j_M}}^{\prime}$$

然后可以使用以下命题获得空间预测。

【命题 2】 后验预测分布可以写成:

$$\mathbf{y}_M(\mathcal{S}^P_{j_1,\ldots ,j_M}) | \mathbf{y}_M(\mathcal{S}) = \sum^{M-1}_{m=0} \tilde{\mathbf{B}}^{m+1,m}_{j_1,\ldots ,j_M} \tilde{\boldsymbol{η}}_{j_1,\ldots ,j_m} + \tilde{\boldsymbol{\delta}}_{j_1,\ldots ,j_M} \tag{12}$$

其中

$$\begin{align*} &\tilde{\boldsymbol{η}}_{j_1,\ldots ,j_m} \stackrel{ind.} \sim \mathcal{N}_r(\tilde{\mathbf{K}}_{j_1,\ldots ,j_m} \boldsymbol{ω}^m_{j_1,\ldots ,j_m}, \tilde{\mathbf{K}}_{j_1,\ldots ,j_m})\\ &\tilde{\boldsymbol{\delta}}_{j_1,\ldots ,j_M} \stackrel{ind.} \sim \mathcal{N}(\mathbf{L}^M_{j_1,\ldots ,j_M} \boldsymbol{\Sigma}^{-1}_{j_1,\ldots ,j_M} \mathbf{y}_M(\mathcal{S}_{j_1,\ldots ,j_M}), \mathbf{V}^P_{j_1,\ldots ,j_M} − \mathbf{L}^M_{j_1,\ldots ,j_M} \boldsymbol{\Sigma}^{-1}_{j_1,\ldots ,j_M} {\mathbf{L}^M_{j_1,\ldots ,j_M}}^{\prime}) \end{align*}$$

and the “posterior basis-function matrices” are given by

$$\tilde{\mathbf{B}}^{l,k}_{j_1,\ldots ,j_M} := \mathbf{b}_{j_1,\ldots ,j_k} (\mathcal{S}^P_{j_1,\ldots ,j_M}) − \mathbf{L}^l_{j_1,\ldots ,j_M} \boldsymbol{\Sigma}^{-1}_{j_1,\ldots ,j_l} \mathbf{B}^k_{j_1,\ldots ,j_l} = \tilde{\mathbf{B}}^{l+1,k}_{j_1,\ldots ,j_M} − \tilde{\mathbf{B}}^{l+1,l}_{j_1,\ldots ,j_M} \tilde{\mathbf{K}}_{j_1,\ldots ,j_l} \mathbf{A}^{l,k}_{j_1,\ldots ,j_l} \tag{13}$$

对于 $k = 0, 1,\ldots , l − 1$。

因此，式 (12) 中的后验预测分布与 式 (3) 中的（先验）M-RA 过程具有相同的形式。这允许计算和存储联合后验预测分布。通常，人们感兴趣的是这种联合后验预测分布的摘要，例如每个预测位置的边际后验预测分布。实际上，式 (13) 中的后验基函数矩阵直接根据 $l = M$ 的定义（第一个方程）计算，并使用 $l = M − 1, \ldots,0$ 的递归关系（第二个方程）。

3.5 分布式计算

M-RA 的一个主要优点是它非常适合现代计算环境，因为计算可以以分布式方式进行，在大量节点上几乎没有通信开销，每个节点只处理一小部分数据。

更具体地说，假设我们有节点 $\{\mathcal{N}_{j_1,\ldots ,j_m} : j_1,\ldots , j_m = 1,\ldots , J; m = 0, 1,\ldots , M \}$ 在树状结构中，如 图 3 所示。每个节点 $\mathcal{N}_{j_1,\ldots ,j_m}$ 持有 $r$ 个节点或观测位置 $\mathcal{Q}_{j_1,\ldots ,j_m}$ 位于子区域 $\mathcal{D}_{j_1,\ldots ,j_m}$,它只需要使用大小为 $r \times r$ 的矩阵（意味着出色的负载平衡）。节点 $\mathcal{N}_{j_1,\ldots ,j_m}$ 的主要计算工作是计算 $r \times r$ 矩阵 $\tilde{\mathbf{K}}_{j_1,\ldots ,j_m}$ 的 Cholesky 分解并计算 式 (10) 中的数量，后者可以并行化，如果该节点有多个核心。与每个节点 $\mathcal{N}_{j_1,\ldots ,j_m}$ 的通信是 $\mathcal{O}(Jm^2r^2)$，因为它从其子节点接收矩阵来计算 式 (9) 中的数量。每个分辨率的节点/子区域的计算可以完全并行进行。

对于位置 $\mathcal{S}^P$ 的空间预测，每个（终端）节点 $\mathcal{N}_{j_1,\ldots ,j_M}$ 执行涉及 $\mathcal{S}^P_{j_1,\ldots ,j_M}$ 的并行计算，区域 $\mathcal{D}_{j_1,\ldots ,j_M}$ 中的预测位置，以获得 式(13) 中的 “后验基函数矩阵”。

图 3：$J = 2$ 和 $r = 5$ 的 2-RA 分布式推断的计算设置图示，用于一维空间域中的玩具示例。如匹配颜色所示，节点 $\mathcal{N}_{j_1,\ldots,j_m}$ 与节点 $Q_{j_1,\ldots,j_m}$ 一起工作，$j_m = 1, 2$； $m = 0, 1, 2$。只需要连接节点之间的通信。

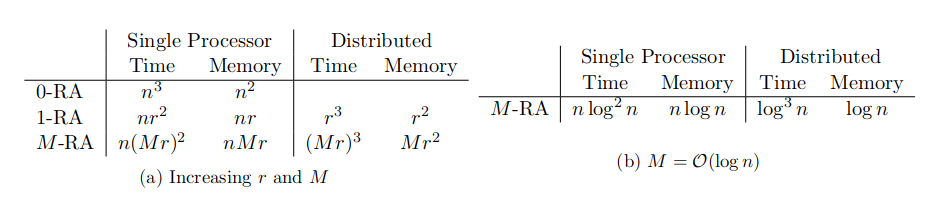
3.6 计算复杂度

请记住，为了简单起见，我们在此假设每个区域 $\mathcal{D}_{j_1,\ldots ,j_m}$ 中有相等数量的 $r = \frac{n}{J^M}$ 结或观测位置，并且我们将 $J$ 视为固定（小）数。对于 $\sum^{M}_{m=0} J^m < 2J^M$ 区域中的每一个，推断的主要计算工作是在 式 (10) 中获得矩阵 $\tilde{\mathbf{A}}^{k,l}_{j_1,\ldots ,j_m}$，这需要对 $r \times r$ 矩阵 $\tilde{\mathbf{K}}_{j_1,\ldots ,j_m}$ 并计算大小为 $r \times r$ 的 $\mathcal{O}(m^2)$ 二次形式。因此，M-RA 推断具有 $\mathcal{O}(J^M M^2r^3) = \mathcal{O}(nr^2M^2)$ 时间复杂度和 $\mathcal{O}(nrM)$ 内存复杂度。

当 M-RA 在具有大量节点的分布式环境中实现时（如上文 第 3.5 节），整体时间复杂度为 $\mathcal{O}(M^3r^3)$，每个节点的内存复杂度为 $\mathcal{O}(M r2)$，假设通信（每个节点的 $\mathcal{O}(M^2r^2)$）不支配计算时间。

因此，具有 $r$ 个节点的 M-RA 与具有 $M r$ 个节点的 1-RA 具有相同的计算复杂度，但 M-RA 可以提供更好的近似（参见 图 1 ）。正如下面 第 4.1 节 中进一步探讨的那样，随着 $n$ 的增加，1-RA 的性能会降低，除非允许 $r$ 增加为 $n$ 的某个分数，而对于 M-RA，我们可以保持 $r$ 固定，而不是让 $M$ 随着 $n$ 增加因为 $M = \mathcal{O}(\log_J n)$。这是递增域渐近下的自然假设，域和数据大小增加 $J$ 倍允许对结果域进行额外拆分（即，将 $M$ 增加一），而不会降低 $J$ 子区域内的近似在第一个决议。在这种情况下，在非分布式设置中，M-RA 的时间和内存复杂度分别为 $\mathcal{O}(n \log^2 n)$ 和 $\mathcal{O}(n \log n)$。在分布式设置中，整体时间复杂度为 $\mathcal{O}(\log^3 n)$，每个节点的内存和通信复杂度分别为 $\mathcal{O}(\log n)$ 和 $\mathcal{O}(\log^2 n)$。

只要每个终端区域的预测位置数量与观测到的位置数量（即 $|\mathcal{S}^P_{j_1,\ldots ,j_M} | = \mathcal{O}(r)$ ）的数量级相同，预测也具有相同的复杂性。此外，M-RA 允许我们将整个联合预测分布存储在 $\mathcal{O}(M r^2J^M ) = \mathcal{O}(nM r)$ 内存中（分布式情况下每个节点 $\mathcal{O}(M r^2)$ ）。如果 $M = \mathcal{O}(\log n)$，则这是 $\mathcal{O}(n \log n)$（或每个节点的 $\mathcal{O}(\log n)$ ）。

如 表 1(b) 中总结的那样，如果我们让 $M$ 随着 $\log n$ 增加，则 M-RA 的时间和内存复杂度都是 $n$ 的拟线性，甚至在具有许多节点的分布式设置中是多对数的。因此，M-RA 具有高度可扩展性，如果有足够的计算节点可用，则可以处理真正庞大的空间数据集。

表 1：M -RA 的时间和内存复杂度及其特殊情况、常规克里金法 (0-RA) 和全尺度近似 (1-RA)，在单台计算机和第 3.5 节的分布式设置中

4 数值比较与说明

4.1 模拟研究

4.2 总可降水量分析

5 结论和未来工作

我们提出了多分辨率近似 (M-RA)，这是一种用任何协方差函数近似高斯过程的新技术。 M-RA 本质上是多种分辨率下许多空间基函数的线性组合。基函数权重的精度矩阵具有多分辨率块稀疏结构，允许可扩展的推断和分布式计算。因为我们的方法中的基函数是针对给定的协方差函数最佳选择的，所以这可以提供对其他多分辨率方法的进一步了解，在这些方法中，基函数是以更特别的方式选择的。

M-RA 与 Sang 等 (2011 ^[38])的全尺度近似相比具有优势。这是目前用于大型空间数据的最先进方法，可以看作是 M-RA（M = 1）的特例。使用理论结果、玩具示例、大型模拟数据集和真实数据应用程序，我们已经证明 M-RA 可以在与 1-RA 相同的计算复杂度和计算时间下提供更好的近似，或者它可以提供计算时间的一小部分类似的近似。还应该注意的是，我们对 M = 1 的推断结果提供了一种并行分布式计算算法，用于在全尺度近似中进行推断

我们正计划提供用户友好的软件，为 M-RA 提供良好的默认选择，并且可以在台式计算机和高性能计算环境中运行。利用后者的分布式内存架构，原则上应该允许将 M-RA 应用于具有数亿个观测值的数据集，因为许多卫星仪器现在能够每天生成。

M-RA 不仅近似于数据协方差矩阵，而且它本身就是一个有效的高斯过程。因此，通过将 M-RA 过程嵌入分层模型中，可以扩展到更复杂的场景（例如，Cressie 和 Wikle，2011 ^[7]）。当数据测量过程复杂时，M-RA 可以嵌入到层次模型中，该模型明确地对测量过程进行建模，并允许例如对非高斯数据建模，或融合来自不同测量仪器的数据。

同样令人感兴趣的是 M-RA 的时空版本。因为可以存储和传播整个联合后验预测分布，所以可以扩展 M-RA 以允许在大规模时空状态空间模型中进行卡尔曼滤波器类型的推断（这对其他稀疏精度方法具有挑战性，例如正如 Lindgren 等，2011 年 ^[32]）。从这个意义上讲，在某些情况下，M-RA 还可以提供整体卡尔曼滤波器的替代方案（Evensen，1994 ^[10]；Katzfuss 等，2015 ^[28]）。

参考文献

• [1] Banerjee, S., Gelfand, A. E., Finley, A. O., and Sang, H. (2008). Gaussian predictive process models for large spatial data sets. Journal of the Royal Statistical Society, Series B, 70(4):825–848.
• [2] Bevilacqua, M., Gaetan, C., Mateu, J., and Porcu, E. (2012). Estimating space and space-time covariance functions for large data sets: A weighted composite likelihood approach. Journal of the American Statistical Association, 107(497):268–280.
• [3] Calder, C. A. (2007). Dynamic factor process convolution models for multivariate space-time data with application to air quality assessment. Environmental and Ecological Statistics, 14(3):229–247.
• [4] Caragea, P. C. and Smith, R. L. (2007). Asymptotic properties of computationally efficient alternative estimators for a class of multivariate normal models. Journal of Multivariate Analysis, 98(7):1417–1440.
• [5] Chui, C. (1992). An Introduction to Wavelets. Academic Press.
• [6] Cressie, N. and Johannesson, G. (2008). Fixed rank kriging for very large spatial data sets. Journal of the Royal Statistical Society, Series B, 70(1):209–226.
• [7] Cressie, N. and Wikle, C. K. (2011). Statistics for Spatio-Temporal Data. Wiley, Hoboken, NJ.
• [8] Curriero, F. and Lele, S. (1999). A composite likelihood approach to semivariogram estimation. Journal of Agricultural, Biological, and Environmental Statistics, 4(1):9–28.
• [9] Eidsvik, J., Shaby, B. A., Reich, B. J., Wheeler, M., and Niemi, J. (2014). Estimation and prediction in spatial models with block composite likelihoods using parallel computing. Journal of Computational and Graphical Statistics, 23(2):295–315.
• [10] Evensen, G. (1994). Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. Journal of Geophysical Research, 99(C5):10143–10162.
• [11] Forsythe, J. M., Dodson, J. B., Partain, P. T., Kidder, S. Q., and Haar, T. H. V. (2012). How total precipitable water vapor anomalies relate to cloud vertical structure. Journal of Hydrometeorology, 13(2):709721.
• [12] Fuentes, M. (2007). Approximate likelihood for large irregularly spaced spatial data. Journal of the American Statistical Association, 102(477):321–331.
• [13] Furrer, R., Genton, M. G., and Nychka, D. W. (2006). Covariance tapering for interpolation of large spatial datasets. Journal of Computational and Graphical Statistics, 15(3):502–523.
• [14] Gneiting, T. and Katzfuss, M. (2014). Probabilistic forecasting. Annual Review of Statistics and Its Application, 1(1):125–151.
• [15] Golub, G. H. and Van Loan, C. F. (2012). Matrix Computations. JHU Press, 4th edition.
• [16] Gramacy, R. and Lee, H. (2008). Bayesian treed Gaussian process models with an application to computer modeling. Journal of the American Statistical Association, 103(483):1119–1130.
• [17] Halko, N., Martinsson, P., and Tropp, J. (2011). Finding structure with randomness: Probabilistic algorithms for constructing approximate matrix decompositions. SIAM Review, 53(2):217–288.
• [18] Harville, D. A. (1997). Matrix Algebra From a Statistician’s Perspective. Springer, New York, NY.
• [19] Henderson, H. and Searle, S. (1981). On deriving the inverse of a sum of matrices. SIAM Review, 23(1):53–60.
• [20] Higdon, D. (1998). A process-convolution approach to modelling temperatures in the North Atlantic Ocean. Environmental and Ecological Statistics, 5(2):173–190.
• [21] Hoeting, J. A., Madigan, D., Raftery, A. E., and Volinsky, C. T. (1999). Bayesian model averaging: A tutorial. Statistical Science, 14(4):382–417.
• [22] Johannesson, G., Cressie, N., and Huang, H.-C. (2007). Dynamic multi-resolution spatial models. Environmental and Ecological Statistics, 14(1):5–25.
• [23] Katzfuss, M. (2013). Bayesian nonstationary spatial modeling for very large datasets. Environmetrics, 24(3):189–200.
• [24] Katzfuss, M. and Cressie, N. (2009). Maximum likelihood estimation of covariance parameters in the spatialrandom-effects model. In Proceedings of the Joint Statistical Meetings, pages 3378–3390, Alexandria, VA. American Statistical Association.
• [25] Katzfuss, M. and Cressie, N. (2011). Spatio-temporal smoothing and EM estimation for massive remotesensing data sets. Journal of Time Series Analysis, 32(4):430–446.
• [26] Katzfuss, M. and Cressie, N. (2012). Bayesian hierarchical spatio-temporal smoothing for very large datasets. Environmetrics, 23(1):94–107.
• [27] Katzfuss, M. and Hammerling, D. (2014). Parallel inference for massive distributed spatial data using low-rank models. arXiv:1402.1472.
• [28] Katzfuss, M., Stroud, J. R., and Wikle, C. K. (2015). Understanding the ensemble Kalman filter. The American Statistician, forthcoming.
• [29] Kaufman, C. G., Schervish, M., and Nychka, D. W. (2008). Covariance tapering for likelihood-based estimation in large spatial data sets. Journal of the American Statistical Association, 103(484):1545–1555.
• [30] Kidder, S. Q. and Jones, A. S. (2007). A blended satellite total precipitable water product for operational forecasting. Journal of Atmospheric and Oceanic Technology, 24(1):74–81.
• [31] Lemos, R. T. and Sans ́o, B. (2009). A spatio-temporal model for mean, anomaly, and trend fields of North Atlantic sea surface temperature. Journal of the American Statistical Association, 104(485):5–18.
• [32] Lindgren, F., Rue, H., and Lindstr ̈om, J. (2011). An explicit link between Gaussian fields and Gaussian Markov random fields: the stochastic partial differential equation approach. Journal of the Royal Statistical Society, Series B, 73(4):423–498.
• [33] Mardia, K., Goodall, C., Redfern, E., and Alonso, F. (1998). The kriged Kalman filter. Test, 7(2):217–282.
• [34] McLeod, A. I., Yu, H., and Krougly, Z. (2007). Algorithms for linear time series analysis: With R package. Journal of Statistical Software, 23(5).
• [35] Nychka, D. W., Bandyopadhyay, S., Hammerling, D., Lindgren, F., and Sain, S. R. (2015). A multi-resolution Gaussian process model for the analysis of large spatial data sets. Journal of Computational and Graphical Statistics, in press.
• [36] Quinonero Candela, J. and Rasmussen, C. (2005). A unifying view of sparse approximate Gaussian process regression. Journal of Machine Learning Research, 6:1939–1959.
• [37] Sang, H. and Huang, J. Z. (2012). A full scale approximation of covariance functions. Journal of the Royal Statistical Society, Series B, 74(1):111–132.
• [38] Sang, H., Jun, M., and Huang, J. Z. (2011). Covariance approximation for large multivariate spatial datasets with an application to multiple climate model errors. Annals of Applied Statistics, 5(4):2519–2548.
• [39] Schlather, M., Malinowski, A., Menck, P. J., Oesting, M., and Strokorb, K. (2015). Analysis, simulation and prediction of multivariate random fields with package RandomFields. Journal of Statistical Software, 63(8):1–25.
• [40] Shaby, B. A. and Ruppert, D. (2012). Tapered Covariance: Bayesian Estimation and Asymptotics. Journal of Computational and Graphical Statistics, 21(2):433–452.
• [41] Sherman, J. and Morrison, W. (1950). Adjustment of an inverse matrix corresponding to a change in one element of a given matrix. Annals of Mathematical Statistics, 21(1):124–127.
• [42] Snelson, E. and Ghahramani, Z. (2007). Local and global sparse Gaussian process approximations. In Artificial Intelligence and Statistics 11 (AISTATS).
• [43] Stein, M. L. (2011). 2010 Rietz lecture: When does the screening effect hold? Annals of Statistics, 39(6):2795–2819.
• [44] Stein, M. L. (2014). Limitations on low rank approximations for covariance matrices of spatial data. Spatial Statistics, 8:1–19.
• [45] Stein, M. L., Chen, J., and Anitescu, M. (2013). Stochastic approximation of score functions for Gaussian processes. The Annals of Applied Statistics, 7(2):1162–1191.
• [46] Stein, M. L., Chi, Z., and Welty, L. (2004). Approximating likelihoods for large spatial data sets. Journal of the Royal Statistical Society: Series B, 66(2):275–296.
• [47] Vecchia, A. (1988). Estimation and model identification for continuous spatial processes. Journal of the Royal Statistical Society, Series B, 50(2):297–312.
• [48] Woodbury, M. (1950). Inverting modified matrices. Memorandum Report 42, Statistical Research Group, Princeton University.