生成模型概览 | 西山晴雪的知识笔记

〖摘要〗生成模型（Generative Model）是概率统计和机器学习中的一类重要模型，泛指一系列用于随机生成可观测数据的模型。生成模型应用十分广泛，可以用于对不同类型的数据建模，如图像、文本、声音等。如果假设上述某类型的数据对象都服从一个未知分布，则生成模型通常希望通过一些观测样本来学习（估计）该分布，并能够利用该分布随机地生成未观测过的新样本。生成模型有很多种，本文是此类模型的一个简单概览，其中大部分内容来自 Murphy 的《Machine Learning: Advanced Topics》第 20 章。

〖参考〗 J. M. Tomczak, Deep Generative Modeling. ch.1 / Murphy, 《Machine Learning: Advanced Topics》ch. 20 / Deep Generative Modelling: A Comparative Review of VAEs, GANs, Normalizing Flows, Energy-Based and Autoregressive Models / An Introduction to Deep Generative Modeling

〖模型导引〗

0️⃣ 概率图生成模型

1️⃣ 受限玻尔兹曼机

2️⃣ 变分自编码器

3️⃣ 自回归模型

4️⃣ 归一化流

5️⃣ 基于能量的模型

6️⃣ 生成式对抗网络

7️⃣ 扩散模型

1 概述

生成模型 旨在模拟数据在现实世界中的生成方式，从数学上表述，就是学习一个概率分布 $p(\mathbf{x})$，其中 $\mathbf{x} \in \mathcal{X}$。例如，通过大量无监督图像数据集学得数据分布后，可以随机生成一张图像。除了上述无条件的生成模型外，在某些情况下，也可能以输入（或协变量） $\boldsymbol{c} \in \mathcal{C}$ 为条件，产生形式为 $p(\mathbf{x}|\boldsymbol{c})$ 的 有条件生成模型。例如，通过大量图像与标引文本数据集学得数据分布后，根据一段文字描述生成一幅图像。

符号表示

在生成模型和判别模型的各类文档中，首先数学公式中的符号 $\mathbf{x}$ 、$\mathrm{y}$、$\mathbf{z}$ 都代表了随机变量（或向量），其中 $\mathbf{x}$ 常代表可观测变量（向量）、$\mathrm{y}$ 常代表被预测变量、而 $\mathbf{z}$ 常被用于表示隐变量。

此外，模型 $\mathcal{M}$ 和数据 $\mathcal{D}$ 通常都在公式中被隐含表示了。也就是说：

$p(\mathrm{y} \mid \mathbf{x}) = p(\mathrm{y} \mid \mathbf{x},\mathcal{M},\mathcal{D})$
$p(\mathbf{x}) = p(\mathbf{x} \mid \mathcal{M},\mathcal{D})$
$p(\mathbf{x},\mathrm{y}) = p(\mathbf{x},\mathrm{y} \mid \mathcal{M},\mathcal{D})$

当模型 $\mathcal{M}$ 为可参数化（相对于非参数模型而言）时，通常可以用一组用希腊字母表示的参数来代替。例如：

$p(\mathrm{y} \mid \mathbf{x}) = p(\mathrm{y} \mid \mathbf{x},\boldsymbol{\theta},\mathcal{D})$ —> 由 $\boldsymbol{\theta}$ 表示模型
$p(\mathbf{x}) = p(\mathbf{x} \mid \boldsymbol{\phi},\mathcal{D})$ —> 由 $\boldsymbol{\phi}$ 表示模型
$p(\mathbf{x},\mathrm{y}) = p(\mathbf{x},\mathrm{y} \mid \boldsymbol{\theta},\boldsymbol{\phi},\mathcal{D})$ —> 由 $\boldsymbol{\theta}$ 和 $\boldsymbol{\phi}$ 共同表示模型，但两者分别表示不同的内涵

生成模型与判别模型的关系

生成模型（此处特指无条件生成模型）与判别模型本身要解决的问题不同。

判别建模的目标是在给定观测的情况下学习如何预测变量，用数学描述是为了得到预测分布 $p(y \mid \mathbf{x})$
生成模型的目标是学习变量的联合分布以服务于更广泛的任务，因此有时被视为一种辅助任务。生成模型用数学描述是为了得到数据的分布 $p(\mathbf{x})$

本来两种模型之间并没有什么可比性，但由于两者都可以用于实现预测任务，因此产生了一些联系。两者用于预测任务的工作原理如下：

判别模型：在已知数据 $\mathcal{D}$ 和模型偏好 $\mathcal{M}$ 的条件下，学习一个由可观测变量 $\mathbf{x}$ 到可观测变量 $\mathrm{y}$ 的映射 $f(\mathrm{y} \mid \mathbf{x})$ 。对于参数模型而言，该映射由模型参数 $\boldsymbol{\theta}$ 定义。也就是说，判别模型会通过训练学得对模型参数 $\boldsymbol{\theta}$ 的估计，其中频率派方法会给出 $\boldsymbol{\theta}$ 的点估计，而贝叶斯方法会给出 $\boldsymbol{\theta}$ 的概率分布。相应的，在预测输出方面，频率派方法会通过映射 $f(\mathrm{y} \mid \mathbf{x})$ 直接给出 $\mathrm{y}$ 的点估计，即忽略了不确定性，可以理解为 $p(\mathrm{y} \mid \mathbf{x}) = 1$；而贝叶斯方法则会给出 $\mathrm{y}$ 的预测分布 $p(\mathrm{y} \mid \mathbf{x})$，其中描述了所有可能的 $\mathrm{y}$ 值及其概率。
生成模型：在已知数据 $\mathcal{D}$ 和模型偏好 $\mathcal{M}$ 的条件下，不仅要学习由 $\mathbf{x}$ 到 $\mathrm{y}$ 的映射 $y \mid \mathbf{x}$，还要学习输入变量 $\mathbf{x}$ 的分布，进而可以利用贝叶斯原理，即 $p(\mathbf{x},\mathrm{y}) = p(\mathrm{y} \mid \mathbf{x})p(\mathbf{x})$ ，得出更具有解释力的预测 $p(\mathbf{x},\mathrm{y})$。下图展示了其与 $p(\mathrm{y} \mid \mathbf{x})$ 之间的在解释能力和不确定上的显著区别：生成模型通过学习 $\mathbf{x}$ 的分布，可以有效降低分布外数据的确定性程度，从而给出更为科学合理的预测（这也是预训练能够有效果的原因之一）。

数据样本（左）和两种决策方法。（中）判别方法：在使用判别方法训练模型（即条件分布 $p(\mathrm{y}|\mathbf{x})$）后，我们获得了清晰的决策边界；但黑色十字离橙色区域更远；因此，分类器给蓝色标签分配了更高的概率。输出结果为蓝色！（右）生成方法：如果我们额外学习分布 $p(\mathbf{x})$ ，就会观察到黑色十字不仅离决策边界更远，而且离蓝色数据点所在的区域也很远。也就是说，黑点远离了高概率质量区域（深蓝色椭圆区域）。因此，黑十字 $p(x = \text{黑叉})$ 的（边缘）概率很低，联合分布 $p(x = \text{黑叉}, \mathrm{y} = \text{蓝色})$ 并不高，因此，黑十字是蓝色的决策不确定！

其实真正需要与判别模型区分开的是条件生成模型，因为判别模型的符号表示 $p(\mathrm{y} \mid \mathbf{x})$ 与条件生成模型的符号表示 $p(\mathbf{x} \mid \mathbf{c})$ 非常相似。不过两者之间还是有一些显著区别的：

在判别模型中，通常假设仅有一个正确输出
在条件生成模型中，通常假设可能存在多个正确输出。

生成建模具有吸引力的原因有很多：

首先，我们可以在生成建模过程中表达物理规律和约束，而忽略那些不必关心的细节，或将其视为噪声。
其次，生成模型通常非常直观、可解释，并且根据观测数据可以对模型做出检验，帮助我们接受或拒绝所作出的假设。
再次，生成模型天然具备表达因果关系的能力，而从统计学意义上来说，因果关系比相关关系更能泛化到新情况。例如，一旦我们了解了地震的生成过程，就可以在地震多发地使用该模型。

生成模型的复杂之处在于：

学习变量 $\mathbf{x}$ 的分布本身构成了无监督学习的一个大邻域。不过这也会带来额外的好处，那就是如果能够得到足够精确的 $p(\mathbf{x})$，则可以通过对其采样，生成 $\mathbf{x}$ 的新样本 $\boldsymbol{x’}$，而这正是生成模型名字的由来。

在学习 $p(\mathbf{x})$ 时需要注意的是：$p(\mathbf{x})$ 自身可能也存在特殊性，需要一套学习方法。例如：

当 $\mathbf{x}$ 呈单峰的多元高斯分布性状时，可以用平均场来近似
当 $\mathbf{x}$ 呈现多峰的多元高斯分布性状时，可以用多个标准分布的混合来近似，此时可能需要引入离散型隐变量 $c$ 等等

本文所阐述的生成任务，主要指对 $p(\mathbf{x})$ 的学习和应用；如果没有特殊声明，本文中所指生成模型均指无条件生成模型 $p(\mathbf{x})$，但相关结论完全可以应用在条件生成模型 $p(\mathbf{x}|\boldsymbol{c})$ 之上。

根据上述分析，也可以知道生成模型的两个最关键的用途了：

密度估计：为了给具体实例 $\boldsymbol{x}$ 作出更为可信的预测 $p(\boldsymbol{x},y)$，计算该实例的密度估值 $p(\boldsymbol{x})$；
生成数据：利用一些方法（如采样算法等），从 $p(\mathbf{x})$ 中获得新样本 $\boldsymbol{x’}$

当然生成模型还有很多其他用途，详情见 第 3 节。

2 生成模型的类型

2.1 类型划分

在顶层上，我们可以将生成模型区分为『深度生成模型（DGM）』和『经典概率图模型（PGM）』。

深度生成模型（DGM）：使用深度神经网络来学习从单个隐向量 $\mathbf{z}$ 到可观测数据 $\mathbf{x}$ 的复杂非线性映射。这部分包括近年十分火热的变分自编码器、生成对抗网络、能量模型、归一化流、扩散模型等
概率图模型（PGM） ：使用简单的（通常是线性的）关系来学习一组相互关联的隐变量 $\mathbf{z}_1, \ldots, \mathbf{z}_L$ 到可观测变量 $\mathbf{x}_1, \ldots , \mathbf{x}_D$ 的映射。这部份包含高斯混合模型、隐马尔可夫模型、条件随机场等非常有名的传统模型。

当然，两者之间存在许多的混合体。例如，PGM 可以使用神经网络，而 DGM 可以使用结构化状态空间。我们在贝叶斯方法的概率图模型部分一般性地讨论概率图生成模型，而 在本部分主要关注深度生成模型。

2.2 主要深度生成模型及其特征

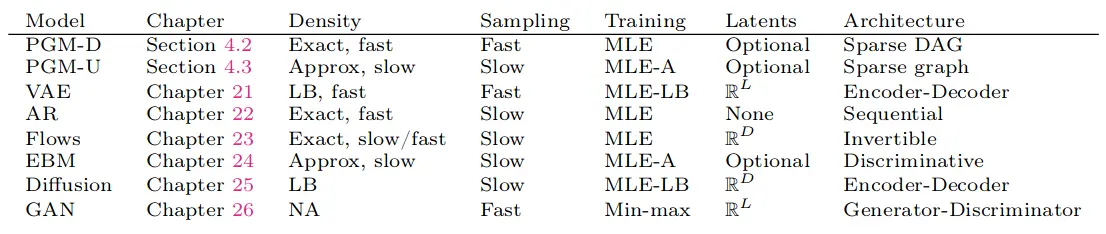
主要生成模型类型

表 1：常见生成模型的特征。

上表中， $D$ 代表可观测变量 $\mathbf{x}$ 的维度，$L$ 代表隐变量 $\mathbf{z}$ 的维度（如果存在的话，通常假设 $L \ll D$，尽管过完备表示也可能存在 $L \gg D$ 的情况）。缩写：Approx = 近似，AR = 自回归，EBM = 基于能量的模型，GAN = 生成对抗网络，MLE = 最大似然估计，MLE-A = 最大似然估计（基于近似），MLE-LB = 最大似然估计（基于变分下界），NA = 不可用，PGM = 概率图模型，PGM-D = 有向概率图模型，PGM-U = 无向概率图模型，VAE = 变分自编码器。

目前，深度生成模型的主要类型是： **变分自编码器 (VAE)、自回归 (AR) 模型、归一化流、扩散模型、基于能量的模型 (EBM) 和生成对抗网络 (GAN)**。我们可以根据以下标准对这些模型进行区分（参见 表 1 的汇总）：

密度计算能力：该模型的密度估计所采用的方法（精确或近似）和效率（快或慢）
- 对于隐式模型（如 GAN），通常没有明确定义的 $p(\mathbf{x})$
- 对于 VAE 模型，只能计算 $p(\mathbf{x})$ 的下限
- 对于 EBM、UPGM，只能计算 $p(\mathbf{x})$ 的近似值
样本生成效率：该模型的样本生成效率（快或慢）
- 有向 PGM、VAE 和 GAN 都支持快速采样。
- 无向 PGM、EBM、AR、扩散模型和流模型的采样速度很慢。
训练方法：该模型训练采用的目标函数、是否有显式似然？
- 对于某些模型（如 AR、流和有向 PGM），可以执行精确最大似然估计 (MLE)，由于目标通常是非凸的，所以只能达到局部最优。
- 在 VAE 的情况下，最大化似然的下界；
- 在 EBM 和 UGM 的情况下，最大化似然的近似值。
- 对于 GAN，必须使用 min-max 训练，这可能不稳定，并且没有明确的目标函数来监控。
隐变量情况：该模型中是否存在隐变量，隐变量的维度有什么特点？
- AR 模型不使用隐变量；
- 流模型和扩散模型使用隐变量，但没有压缩。
- 概率图模型（包括 EBM ）可能使用也可能不使用隐变量。
神经网络架构：该模型采用何种架构，此特征没有统一归类法？
- 对于流，仅限于使用可逆神经网络，其中每一层都有一个可处理的雅可比行列式。
- 对于 EBM，可以使用我们喜欢的任何模型。
- 其他模型有不同的限制。

2.3 各深度生成模型的优缺点

下表从优略势方面给出了简洁的总结：

几种深度生成模型的比较

表 2：几种常见的深度生成模型征比较。

2.4 各深度生成模型的架构特征

下图从顶层抽象，给出了几种深度生成模型的结构特征。

主要深度生成模型

图 1：各种深度生成模型的结构特征。

注：图中 $\boldsymbol{x}$ 是可观测数据，$\boldsymbol{z}$ 是隐编码，$\boldsymbol{x}^\prime$ 是来自模型的一个新样本。 AR 模型没有隐编码 $\boldsymbol{z}$。对于扩散模型和流模型，$\boldsymbol{z}$ 的大小与 $\boldsymbol{x}$ 相同。对于 AR 模型，$\boldsymbol{x}^d$ 指 $\boldsymbol{x}$ 的第 $d$ 个样本点。 $\mathrm{R}$ 代表实数值输出，$0/1$ 代表二进制输出。

3 生成模型的用途

3.1 生成数据

生成模型的主要目标之一是生成（创建）新的数据样本。例如，如果能够将模型 $p(\mathbf{x})$ 拟合到人脸图像的数据集，则我们可以从 $p(\mathbf{x})$　中随机采样，获得新的人脸，如图 2 所示。

生成脸图像示例

图 2：合成人脸，来自基于分数的生成模型。来自 [Son+21] 的图 12。

类似的方法可以用于创建文本、音频等样本。当这种技术被滥用来制作虚假内容时，它们被称为 深度伪造（ Deep Fakes）。有关该主题的评论，请参见 Ngu+19。

为了控制生成的内容，使用形式为 $p(\mathbf{x}|\boldsymbol{c})$ 的 条件生成模型 非常有用。以下是一些示例：

$\boldsymbol{c}$ = 文本提示，$\mathbf{x}$ = 图像。这是一个文本到图像的模型（示例见图 3 和图 8 ）。
$\boldsymbol{c}$ = 图像，$\mathbf{x}$ = 文本。这是一个图像到文本的模型，对图像字幕很有用。
$\boldsymbol{c}$ = 图像，$\mathbf{x}$ = 图像。这是一个图像到图像的模型（示例见图 4 ）。
$\boldsymbol{c}$ = 声音序列，$\mathbf{x}$ = 单词序列。这是一个语音到文本的模型，对自动语音识别 (ASR) 很有用。

请注意，从符号表示上，有时也会采用 $\mathbf{x}$ 表示输入，用 $\mathbf{y}$ 表示输出。此时模型具有我们非常熟悉的形式 $p(\mathbf{y}|\mathbf{x})$ 。在 $\mathbf{y}$ 表示低维量的特殊情况下，例如整数类标签，$\mathrm{y} \in {1, . . . , C}$，我们将得到一个预测（判别）模型。

判别模型和条件生成模型的主要区别在于：

在判别模型中，假设仅有一个正确输出
在条件生成模型中，假设可能存在多个正确输出。

正是因为生成模型的这种假设，使得对生成模型的能力评估更加困难。

文本到图像

图 3：Imagen 扩散模型从文本提示生成的一些 1024 × 1024 图像。来自 [Sah+22] 的图 1。

图 4：使用条件 GAN 将灰度图像（左）转换为彩色图像（中）; 右列显示了原始图像。由 https://github.com/jantic/DeOldify 生成。

3.2 估计密度

密度估计被广泛用于计算某个被观测到的数据向量的概率，即计算某个实例的 $p(\boldsymbol{x})$ 值。这对于异常值检测、数据压缩、生成式分类器、模型比较等针对特定实例的应用场景非常有用。

在低维度时，解决此问题的一种简单方法是使用核密度估计（ KDE ），其形式为：

$$
p(\mathbf{x} \mid \mathcal{D}） = \frac{1}{N}\sum\limits^{N}_{n=1} \mathcal{K}(\mathbf{x}-\mathbf{x}_n)
$$

这里 $\mathcal{D} = { x_1, \ldots , x_N }$ 是数据，$\mathcal{K}h$ 是带宽为 $h$ 的密度核，它是一个函数 $\mathcal{K} : \mathbb{R} \rightarrow \mathbb{R}+$ ，满足 $\int \mathcal{K}(x)dx = 1$ 和 $\int x \mathcal{K}(x)dx = 0$ 。 图 5 中给出密度估计的一维示例，在顶行中，使用了均匀核，在底部行中，使用了高斯核。

在高维度时，KDE 会面临维度灾难问题，此时需要使用某些参数化的密度模型 $p_{\boldsymbol{\theta}}(\mathbf{x})$ 来对密度做近似。

密度估计

图 5：从 6 个数据点估计的一维非参数 (Parzen) 密度估计器。

上图中，随机变量用 $x$ 表示。顶行：均匀核。底行：高斯核。左栏：带宽参数 $h = 1$。右栏：带宽参数 $h = 2$。由 parzen_window_demo.ipynb 生成。

3.3 数据填充

填充任务是指 “插补” 数据向量或矩阵中的缺失值。例如，假设 $\mathbf{X}$ 是一个 $N × D$ 的数据矩阵（想象一个电子表格），其中一些条目（表示为 $\mathbf{X}_m$ ）可能会缺失，而其余的条目（表示为 $\mathbf{X}_o$ ）则能够被观测到。

填充缺失数据的一种简单方法是使用所有特征的平均值 $\mathbb{E} [x_d]$；这被称为平均值填充，如 图 6 所示。但是，这种方式忽略了每行中变量之间的依赖关系，并且不返回任何不确定性度量。

我们可以通过将生成模型拟合到可观测数据 $p(\mathbf{X}_o)$，然后从 $p(\mathbf{X}_m \mid \mathbf{X}_o)$ 中抽取样本来泛化这个问题，这被称为 多样本填充（multiple imputation）。

生成模型可用于填充更复杂的数据类型，例如在图像中修复被遮挡的像素（见 图 7）。

数据填充

图 6：使用每列的平均值进行缺失数据插补。

复杂填充任务示例

图 7：一些复杂图像填充示例。来自 [Sah+21] 的图 1。

3.4 发现结构

某些类型的生成模型具有隐变量 $\mathbf{z}$，它们被假定为生成可观测数据 $\mathbf{x}$ 的 “原因”。在这种场景中，可以使用贝叶斯规则实现模型反转，以推断隐变量的后验分布 $p(\mathbf{z}|\mathbf{x}) ∝ p(\mathbf{z})p(\mathbf{x}|\mathbf{z})$，这对于发现数据中隐藏的低维模式很有用。

例如，假设我们扰乱细胞中的各种蛋白质，并使用称为流式细胞术的技术测量产生的磷酸化状态，如 [Sac+05]。图 8(a) 显示了此类数据集的一个示例。每行代表一个数据样本 $\mathbf{x}_n \sim p(·|\boldsymbol{a}n, \mathbf{z})$，其中 $\mathbf{x} \in \mathbb{R}^{11}$ 是输出向量（磷酸化），$\boldsymbol{a} \in {0, 1}^6$ 是输入动作向量（扰动），$\mathbf{z}$ 是未知的蜂窝信号网络结构。我们可以使用概率图模型的结构学习技术来推断图结构 $p(\mathbf{z}|\mathcal{D})$。特别是，我们可以使用[EM07]中描述的动态规划方法得到如图 7（b）所示的结果。在这里，我们绘制了中值图，其中包括 $p(\mathbf{z}{ij} = 1|\mathcal{D}) > 0.5$ 的所有边。（有关此问题的更新方法，请参见例如 [Bro+20b]。）

结构发现

图 8: 细胞中蛋白质之间结构关系的发现

上图中， (a) 由 $5400$ 个数据点（行）组成的设计矩阵，测量 $11$ 种蛋白质（列）在不同实验条件下的状态（使用流式细胞术）。数据已离散化为 $3$ 个状态：低（黑色）、中（灰色）和高（白色）。使用激活或抑制化学物质明确控制一些蛋白质。（ b ）表示各种蛋白质（蓝色圆圈）和各种实验干预（粉红色椭圆）之间的依赖关系的有向图形模型，这是从数据中推断出来的。我们绘制 $p(G_{ij} = 1 \mid \mathcal{D}) > 0.5$ 的所有边。虚线边被认为存在于自然界中，但算法并未发现（$1$ 个假阴性）。实线边是真正的阳性。浅色边代表了干预的效果。来自 [EM07] 的图 6d。

3.5 隐空间插值

隐变量模型最有趣的能力之一是：能够在隐空间中的已有数据点之间，通过插值来生成具有某些所需属性的样本。

让 $\boldsymbol{x}_1$ 和 $\boldsymbol{x}_2$ 代表两个输入（例如图像），让 $\boldsymbol{z}_1 = e(\boldsymbol{x}_1)$ 和 $\boldsymbol{z}_2 = e(\boldsymbol{x}_2)$ 代表它们在隐空间中的编码。我们可以将 $\boldsymbol{z}_1$ 和 $\boldsymbol{z}_2$ 视为在隐空间中的两个 “锚点” ，现在可以通过计算 $\boldsymbol{z} = λ\boldsymbol{z}_1 + (1 − λ) \boldsymbol{z}_2$ 生成在这些锚点之间插值的新图像，其中 $0 ≤ λ ≤ 1$，然后通过计算 $\boldsymbol{x}^\prime = d(\boldsymbol{z})$ 进行解码，其中 $d(\cdot)$ 代表解码器。

上述过程被称为隐空间插值，将生成能够结合 $\boldsymbol{x}_1$ 和 $\boldsymbol{x}_2$ 语义特征的数据。

（注：此处采用线性插值的理由是学习的流形通常具有近似为零的曲率，如 [SKTF18] 所示。然而，有时使用非线性插值效果会更好 [Whi16; MB21; Fad+20]。）

我们可以在 图 9 中看到此过程的一个示例，其中使用了适合 MNIST 数据集的 $β$ -VAE 模型。我们看到该模型能够在数字 $7$ 和数字 $2$ 之间产生合理的插值。作为一个更有趣的例子，我们可以将 $β$ -VAE 拟合到 CelebA 数据集 [Liu+15]。结果显示在 图 10 中，看起来似乎也很合理。如果我们使用在更多数据上训练更长时间的更大模型，我们可以获得更好的质量。

隐空间插值 1

图 9：在 β -VAE 隐空间中的两个 MNIST 图像之间做插值（ β = 0.5 ）。

由 mnist_vae_ae_comparison.ipynb 生成。

隐空间插值 2

图 10：两个 CelebA 图像在 β -VAE 隐空间中的插值（ β = 0.5 ）。

由 celeba_vae_ae_comparison.ipynb 生成。

也可以在文本模型的隐空间中执行插值，如 图 11 所示。

文本隐空间插值

图 11：在文本隐空间中插值生成新样本

(a) 来自 VAE 文本模型隐空间的样本，我们在两个句子之间进行了插值（第一行和最后一行）。请注意，中间句子是语法的，但其在语义上与其邻居相关。来自 [Bow+16b] 的表 8。 (b) 与 (a) 相同，但使用了确定性的 RNN 自编码器。来自 [Bow+16b] 的表 1。

3.6 隐空间算术

在某些情况下，我们可以超越插值，并且执行隐空间算术，在其中我们可以增加或减少所需的 “语义变化因子” 的量值。这首先显示在 word2vec 模型 [Mik+13] 中，但在其他隐变量模型中也是可能的。

例如，考虑我们的 VAE 模型适合 CelebA 数据集，其中包含名人的面孔和一些对应的属性。令 $X^+_i$ 是一组具有属性 $i$ 的图像，而 $X^-_i$ 是一组不具有该属性的图像。设 $Z^+_i$ 和 $Z^-_i$ 是对应的嵌入，$\bar{z}^+_i$ 和 $\bar{z}^-_i$ 是这些嵌入的平均值。我们将偏移向量定义为 $\Delta_i = \bar{z}^+_i − \bar{z}^−_i$ 。如果我们将 $\Delta_i$ 的某个正倍数添加到新点 $z$，则增加属性 $i$ 的值；如果减去 $\Delta_i$ 的某个倍数，则减少属性 $i$ 值。

我们在 图 12 中给出了一个例子。我们考虑戴太阳镜的属性。第 $j$ 次重建是使用 $\hat{\mathbf{x}}_j = d(z + s_j\Delta)$ 计算的，其中 $z = e(\mathbf{x})$ 是原始图像的编码，$s_j$ 是比例因子。当 $s_j > 0$ 时，我们在脸上添加太阳镜。当 $s_j < 0$ 时，我们移除太阳镜。这会产生使脸部看起来更年轻、更女性化的副作用，但这可能是数据集偏差的结果。

隐空间算术

图 12：β -VAE 隐空间中的算术（ β = 0.5 ）。

第一列是输入图像，带有嵌入 $\mathbf{z}$。随后的列显示了 $\mathbf{z} + s\Delta$ 的解码，其中 $s ∈ {−2, −1, 0, 1, 2}$ 和 $\Delta = \bar{\mathbf{z}}^+ − \bar{\mathbf{z}}^−$ 是具有（或不具有特定属性）的图像的平均嵌入之间的差（本例中的属性是墨镜）。由 celeba_vae_ae_comparison.ipynb 生成。

3.7 生成式设计

（深度）生成模型的另一个有趣用例是生成设计，我们使用该模型来生成候选对象，例如具有所需属性的分子（参见例如 [RNA22]）。一种方法是将 VAE 拟合到未标记的样本，然后在其隐空间中执行贝叶斯优化。

3.8 基于模型的强化学习

迄今为止，强化学习 RL 的主要成功案例是在计算机游戏中，其中存在模拟器且数据丰富。然而，在机器人技术等其他领域，获取数据的成本很高。在这种情况下，学习模型生成的 “世界” 可能很有用，也就是说，学习代理可以 “在头脑中” 进行规划和学习。有关详细信息，请参阅 强化学习 相关章节。

3.9 表示学习

表示学习是指学习产生可观测数据 $\mathbf{x}$ 的隐因子（可能无法解释的） $\mathbf{z}$。其主要目标是将这些功能用于 “下游” 监督任务。相关内容请参见 表示学习 的章节。

3.10 数据压缩

能够将高概率分配给频繁出现的数据向量（例如，图像、句子）而将低概率分配给稀有向量的模型，可以被用于数据压缩；因为我们能够将较短的代码分配给更常见的要素。实际上，根据香农定理，来自某个随机源 $p(\mathbf{x})$ 的向量 $\mathbf{x}$ 的最佳编码长度是 $l(\mathbf{x}) = − \log p(\mathbf{x})$。有关详细信息，请参阅 信息论 相关章节。

4 生成模型的能力评估

评估生成模型的能力需要衡量以下因素：

生成样本的质量 ：模型生成的样本是数据分布的一部分吗？
生成样本的多样性：来自模型分布的样本是否捕获了数据分布的所有模式？
模型泛化能力：模型泛化是否超出了训练数据？

目前尚没有同时满足所有这些要求的度量手段，但是已经提出了各种度量来捕获其中的不同方面，我们将在下面讨论其中的一些。

4.1 基于似然做模型评估

4.1.1 对数似然的计算

衡量模型 $q$ 与真实分布 $p$ 之间接近程度的标准方法是利用信息论，计算两者之间的 $\mathbb{KL}$ 散度：

$$
D_{\mathbb{KL}}(p | q)=\int p(\mathbf{x}) \log \frac{p(\mathbf{x})}{q(\mathbf{x})}=-\mathbb{H}(p)+\mathbb{H}_{c e}(p, q)
$$

式中，$H (p)$ 可被视为一个常数，$H_{ce} (p, q)$ 是分布 $p$ 和 $q$ 之间的 交叉熵。如果用经验分布来近似真实分布 $p(x)$，那么利用最大似然法，就可以根据数据集上的经验 负对数似然（NLL） 来评估交叉熵（当然，通常我们关心的是在一个预留测试集上的负对数似然）：

$$
\mathbb{NLL}=-\frac{1}{N} \sum_{n=1}^N \log q\left(\mathbf{x}_n\right)
$$

（1）离散型变量似然的计算

对于离散数据的模型（如语言模型），很容易根据上式计算负对数似然。不过通常会使用一个被称为 perplexity 的量来衡量性能，该量定义为 $2^H$， $H=\text{NLL}$ 为交叉熵或负对数似然。

（2）连续性变量似然的计算

对于图像和音频等数据的模型，则存在一个复杂问题：模型通常为连续型的密度函数 $p(\mathbf{x}) \geq 0$ ，但数据 $\mathbf{x}$ 却表现为离散值（如，$\mathbf{x} \in{0 , \ldots, 255}^D$ ）。根据定义，连续型随机变量的概率密度可以大于 $1$，这导致 $\mathbb{NLL}$ 有可能任意大。为了避免这种情况，标准做法是对其实施 均匀去量化 处理，具体操作是：将均匀的随机噪声添加到离散数据中，然后将数据 $\mathbf{x}$ 视为连续值。此方法能够为原始数据的离散模型的平均对数似然设定一个下界。

数学细节

为了展示这一点，让 $\mathbf{z}$ 代表一个连续隐变量， $\mathbf{x}$ 是一个通过舍入计算的可观测二进制向量，即逐个元素的计算 $p(\mathbf{x} \mid \boldsymbol{ z})=\delta(\mathbf{x}-\operatorname{round}(\mathbf{z}))$，则有 $p(\mathbf{x})=\int p(\mathbf{x} \mid \mathbf{z}) p(\mathbf{z}) d \mathbf{z}$。

如果令 $q(\mathbf{z} \mid \mathbf{x})$ 是 $\mathbf{x}$ 的概率逆，也就是说，它只有在 $p(\mathbf{x} \mid \mathbf{z})=1$ 时值才成立。在这种情况下，Jensen 不等式给出

$$
\begin{align*}
\log p(\mathbf{x}) & \geq \mathbb{E}{q(\mathbf{z} \mid \mathbf{x})}[\log p(\mathbf{x} \mid \mathbf{z})+\log p(\mathbf{z})-\log q(\mathbf{z} \mid \mathbf{x})] \
&=\mathbb{E}{q(\mathbf{z} \mid \mathbf{x})}[\log p(\mathbf{z})-\log q(\mathbf{z} \mid \mathbf{x})]
\end{align*}
$$

上式表明，如果我们对密度 $\mathbf{z} \sim q(\mathbf{z} \mid \mathbf{x})$ 建模， $\mathbf{z}$ 是离散型随机变量 $\mathbf{x}$ 的一个去量化版本，则我们将能够得到 $p(\mathbf{x})$ 的下界。

4.1.2 似然评估法存在的问题

使用似然法来评估生成模型存在一些挑战：

（1）似然计算非常困难

对于许多模型，计算似然的成本非常高，因为它需要知道概率模型的归一化常数。实践中常用两种方法来近似地计算似然：

一种是使用 变分推断，该方法提供了一种有效计算对数似然下界的方法。
另一种是使用 退火重要性采样，该方法提供了一种使用蒙特卡罗采样来估计对数似然的方法。

需要注意的是：在某些隐式生成模型中（例如 GAN ）并没有定义似然，显然基于似然的评估方法更无法使用，需要找到替代评估方法。

（2）似然大小与生成的样本质量无关

似然方法还存在一个令人担忧的地方： 似然大小与生成样本的质量似乎没有太大关系 ，一个模型可能似然很大，但生成的样本却非常差；相反的情况也可能出现。

要了解为什么模型具有良好的似然却会生成不良样本，请考虑 [TOB16] 中的讨论。

具体示例

示例一：

假设 $q_0$ 是 $D$ 维数据 $x$ 的密度模型，该模型在平均对数似然评估时表现非常好，同时假设 $q_1$ 是一个相对差的模型，例如白噪声。现在考虑从混合模型生成的样本：

$$
q_2(\mathbf{x})=0.01 q_0(\mathbf{x})+0.99 q_1(\mathbf{x})
$$

显然 $99%$ 的样品会很差。但是，当维数 $D$ 很大时，每个像素的对数似然几乎不会在 $q_2$ 和 $q_0$ 之间变化，因为：

$$
\log q_2(\mathbf{x})=\log \left[0.01 q_0(\mathbf{x})+0.99 q_1(\mathbf{x})\right] \geq \log \left[0.01 q_0(\mathbf{x})\right]=\log q_0(\mathbf{x})-100
$$

对于高维数据，$|\log q_0(x) | \sim D \gg 100$，因此 $\log q_2(x) \approx \log q_0(x)$，也就是说，在比较差的采样器中做混合，并不一定会显著影响对数似然。

示例二：

现在考虑一个相反的案例，即模型有很好的样本但似然却很差的情况。假设 $q$ 是以训练图像为中心的高斯混合模型 GMM：

$$
q(\mathbf{x})= \frac{1}{N}\sum\limits^N_{n=1} \mathcal{N}(\mathbf{x}|\mathbf{x}_n,\epsilon^2\mathbf{I})
$$

如果 $\epsilon$ 足够小以至于高斯噪声难以察觉，那么来自该模型的样本看起来会很好，因为它们对应于真实图像的训练集。但是由于存在过拟合，该模型在测试集上几乎肯定具有很小的似然（在这种过拟合情况下，模型实际上只是记住了训练集）。

4.2 基于特征空间中的距离与散度做模型评估

在高维空间中比较分布非常具有挑战，同时人们希望能够以对语义有帮助的方式来比较分布；因此，人们通常会使用特定领域的 感知距离 指标来衡量数据向量彼此之间或与训练数据之间的相似程度。

然而，大多数用于评估生成模型的指标并不直接比较原始数据（例如像素），而是比较神经网络从原始数据中提取的特征。也就是将 “从模型生成的样本中提取的特征分布” 与 “从数据集中提取的特征分布” 进行比较。需要注意的是用于提取特征的神经网络，该网络既可以出于评估目的而专门训练，也可以直接使用预训练网络，例如，一个常见选择是直接使用预训练的分类器（参见 [Sal+16; Heu+17b; Bin+18; Kyn+19; SSG18a] ）。

下面我们看一下在原始空间和特征空间中测量距离，其效果有何区别：

（1）原始空间中的 Inception 评分

Inception 得分 [Sal+16] 是一种在原始空间中测量距离（散度、相似度）的度量。它测量 “标签的边缘分布 $p_{\boldsymbol{\theta}}(y) = ∫ p(y|x)p_{\boldsymbol{\theta}}(x)$” 和 “样本 $\mathbf{x} \sim p_{\boldsymbol{\theta}}(\mathbf{x})$ 对应的标签条件概率 $p(y|\mathbf{x})$” 之间的 平均 $\mathbb{KL}$ 散度。评分规则定义为：

$$
\text{IS} = \exp\left[ \mathbb{E}{p{\boldsymbol{\theta}}(\mathbf{x})} D_{\mathbb{KL}}(p(y \mid \mathbf{x}) | p_{\boldsymbol{\theta}}(y))\right]
$$

如果一个模型能够从数据集中的所有类别中产生高质量样本，那么 $p_{\boldsymbol{\theta}}(y)$ 通常会接近于均匀，而 $p(y|\mathbf{x})$ 应该是一个对应于 $\mathbf{x}$ 类别的尖锐分布；这会导致较高的 $D_{\mathbb{KL}} (p(y|\mathbf{x}) | p_{\boldsymbol{\theta}}(y))$，进而产生较高的 Inception 分数。同时， Inception 得分仅依赖于类标签，因此不会考虑预定义类别之外的过拟合或样本多样性。例如，一个为每个类都生成完美样本的模型，尽管并没有捕获到类内各种样本的差异性，但仍将获得完美的 Inception 分数，如 图 13a 所示。

(2) 特征空间中的 FID 评分

为了克服此缺点，有人设计了在特征空间中进行距离测量的新测度指标：Fréchet Inception Distance ，简称 FID 分数 [Heu+17b]。

该指标在预训练分类器的特征集上测量两个高斯分布之间的 Fréchet 距离。其中一个高斯通过将模型生成的样本传递给预训练分类器获得，另一个高斯则通过将数据集样本传递给同一分类器来获得的。如果从模型生成样本中得到的特征均值和协方差是 $\mu_m$ 和 $\sum_m$，而从数据集中得到的均值和协方差是 $\mu_d$ 和 $\sum_d$，那么 FID 分数定义为：

$$
\mathrm{FID}=\left|\boldsymbol{\mu}_m-\boldsymbol{\mu}_d\right|_2^2+\operatorname{trace}\left(\boldsymbol{\Sigma}_d+\boldsymbol{\Sigma}_m-2\left(\boldsymbol{\Sigma}_d \boldsymbol{\Sigma}_m\right)^{1 / 2}\right)
$$

可以看出，FID 使用了特征，而没有使用类的 logits，因此 FID 捕获的模式多于类标签捕获的模式，如 图 13b 所示。与 Inception 分数不同，该分数越低越好，因为我们希望两个分布尽可能接近。

FID 评分的缺点： Fréchet 距离已被证明具有很高的偏差，在计算分数的样本基础上，其结果往往存在很大差异。为了缓解此问题，有人引入了 Kernel Inception Distance [Bin+18]，它测量 “从数据集获得的特征” 和 “从模型生成样本中获得的特征” 之间的平方质量中值半径（MMD）。

Inception Distance

图 13：Inception 得分与 FID 得分的对比

（a）具有高 Inception 得分的模型，其生成的样本在视觉上比较真实。 (b) 具有低 FID 得分的模型，其生成的样本在视觉上不仅真实而且多样。

4.3 基于精度与召回率指标做模型评估

由于 FID 仅测量数据分布和模型分布之间的距离，因此很难将其用作诊断工具：不良 FID 可能表明模型无法生成高质量数据，但这可能由于模型将太多概率质量在数据分布上，也可能是由于模型仅捕获了数据的某些子集。为了解开这两种失败模式之间的纠缠，人们一直在生成模型背景下寻求个体的精度（样本质量）指标和召回（样本多样性）指标 [LPO17; Kyn+19]。多样性问题在 GAN 的场景中尤为重要，其中 峰值坍塌(Mode Collapse) 可能是一个问题。

定义精度合找回的一种常见方法是：使用预训练分类器特征空间中的最近邻 [Kyn+19]。首先定义一个函数：

$$
f_k(\phi, \Phi)= \begin{cases}1 & \text { if } \exists \phi^{\prime} \in \Phi \text { s.t. }\left|\phi-\phi^{\prime}\right|_2^2 \leq\left|\phi^{\prime}-\mathrm{NN}_k\left(\phi^{\prime}, \Phi\right)\right|_2^2 \ 0 & \text { otherwise }\end{cases}
$$

其中 $\Phi$ 是一组特征向量，$\mathrm{NN}_k\left(\phi^{\prime}, \Phi\right)$ 是一个函数，返回 $\Phi$ 中的第 $k$ 个最近邻 $\phi^{\prime}$。

现在可以定义精度和召回率如下：

$$
\begin{aligned}
\operatorname{precision}\left(\Phi_{\text {model }}, \Phi_{\text {data }}\right) &=\frac{1}{\left|\Phi_{\text {model }}\right|} \sum_{\phi \in \Phi_{\text {model }}} f_k\left(\phi, \Phi_{\text {data }}\right) \
\operatorname{recall}\left(\Phi_{\text {model }}, \Phi_{\text {data }}\right) &=\frac{1}{\left|\Phi_{\text {data }}\right|} \sum_{\phi \in \Phi_{\text {data }}} f_k\left(\phi, \Phi_{\text {model }}\right)
\end{aligned}
$$

精度和召回率始终介于 $0$ 和 $1$ 之间。直观地说， 精度指标衡量了模型生成的样本与数据点之间，是否像相邻数据点之间一样接近；而 召回率指标则衡量数据点与模型生成的样本之间，是否与相邻的模型生成样本之间一样接近。公式中的参数 $k$ 控制着指标的宽松程度：$k$ 越高，精度和召回率都越高。与分类问题一样，生成模型中的 精度 和 召回率 可用于构建不同模型之间的权衡曲线，使人们能够做出明智的决定。

4.4 基于统计检验方法做模型评估

统计检验长期以来一直被用于确定两组样本是否来自同一分布；此类型的统计检验被称为双样本检验。

让我们将零假设定义为两组样本来自同一分布。然后，从数据中计算一个统计量并将其与阈值进行比较，并基于此，决定是否拒绝原假设。在评估隐式生成模型（如 GAN）时，已经有人使用了基于分类器 [Saj+18] 和 MMD [Liu+20b] 的统计量。为了在深度学习时代无处不在的高维输入空间场景中使用，双样本检验已经逐步从使用原始数据，转变为使用学得的特征。

与生成模型的所有其他评估指标一样，统计检验有其自身的优点和缺点：虽然用户可以指定 类型 1 错误 （代表用户允许零假设被错误拒绝的机会），统计检验往往计算量大，因此通常无法用于包含监视进程的训练过程；统计检验更适合用于比较已经训练好的模型。

4.5 使用预训练模型的挑战

虽然流行且方便，但依赖于预训练分类器（如 IS、FID、特征空间中的最近邻、特征空间中的统计检验等）的评估指标具有明显的缺点。人们手头上可能没有可用于数据集的预训练分类器，因此会使用在其他数据集上训练得到的分类器。鉴于神经网络泛化存在的挑战，从某个数据集的图像上训练得到的分类器，其提取的特征可能不够可靠，无法为在另一个数据集上训练的模型的样本提供细粒度的质量信号。

如果生成模型是在与预训练分类器相同的数据集上训练的，但模型无法完美地捕捉数据分布，我们将向预训练分类器提供分布外数据，并依靠其特征来获得评估模型的分数。远非纯粹的理论问题，这些问题已被广泛研究，并已被证明会影响实践中的评估效果 [RV19; BS18]。

4.6 使用模型生成的样本训练分类器

人们也可以在来自条件生成模型的样本上训练分类器，而无需使用预训练的分类器来评估样本，然后看看这些分类器在分类数据方面的表现如何。例如，将合成（采样）数据添加到真实数据有帮助吗？这更接近于对生成模型生成的样本的可靠评估，因为最终，生成模型的性能取决于它们所训练的下游任务。如果用于半监督学习，应该评估将样本添加到分类器数据集对测试准确性有多大帮助。如果用于基于模型的强化学习任务，应该评估生成模型对学习代理性能的帮助程度。有关此方法的示例，请参见例如 [SSM18; SSA18; RV19；SS20b]。