Contents

第一章：贝叶斯推断

第一章：贝叶斯推断

现代贝叶斯统计主要使用计算机代码来运行，这极大地改变了贝叶斯统计的执行方式。我们能够建立的模型的复杂性越来越大，必要的数学和计算技能障碍逐步降低。而且 迭代式建模过程 也变得比以往更容易实施和更有价值。计算机方法的普及和流行确实很棒，但也需要更大的责任心。现在表达统计方法比以往任何时候都容易，但统计是一个微妙的领域，强大的计算方法并不会使统计神奇地消失。因此，具有良好理论知识背景（尤其是与实践相关的知识），对于有效应用统计方法非常重要。在本章中，我们会介绍了其中一些基础概念和方法，还有很多内容将在本书其余部分进一步探索和扩展。

1.1 贝叶斯建模

概念模型是对一个系统的表征，它由若干概念组成，用于帮助人们了解、理解或者模拟该模型所代表的对象或过程 [6]。此外，模型是人为设计的表示，具有非常具象的目标，因此，讨论某个（些）模型对于指定问题的充分性，通常比讨论模型内在的正确性更方便。模型的存在仅仅是为了帮助人们实现进一步的目标。

在设计新车时，汽车公司会制作物理模型，以帮助人们理解产品在制造时的外观。此时，一位具有汽车先验知识并且对如何使用模型具有很好估计的雕刻家，会寻找所需粘土等原材料，并使用手工工具雕刻物理模型。此物理模型能够帮助其他人了解设计的方方方面，例如：外观是否美观、形状是否符合空气动力学等。这样的模型需要同时结合汽车设计专业知识和雕刻知识才能得到想要的结果。此外，建模过程通常需要构建多个模型，这样做是为了探索不同的选择，或者是因为需要与其他汽车设计团队成员互动，来获得迭代式的改进和扩展。

现如今，除了上述实体汽车模型外，通过计算机辅助设计软件制作数字模型也很常见。计算机模型相比物理模型存在一些优势。例如：与在实体汽车模型上进行测试相比，使用数字模型进行碰撞模拟更简单、成本更低，与团队内的同事共享模型也更加容易。

贝叶斯建模思想与上述汽车建模非常相似。构建一个贝叶斯模型，需要结合领域专业知识和统计技能，将知识整合到一些可计算的目标中，并确定结果的可用性。在贝叶斯建模场景中，所使用的“原材料” 是 数据 ，而“雕刻模型”的主要数学工具是 统计分布 。人们需要同时结合领域专业知识和统计知识，才能获得有用的结果。此外，贝叶斯实践者同样会以迭代方式构建多个模型，往往其中的第一个基础模型，主要用于帮助自身识别与思想的差距或模型存在的缺陷，然后将这些模型用于构建后续的改进模型和扩展模型。

此外，使用一种推断机制并不意味着阻碍其他推断机制发挥作用，就像汽车的物理模型不会阻碍数字模型发挥效用一样。现代贝叶斯实践者也有很多方式来表达想法、生成结果和分享输出，从而允许实践者及其同行能够更广泛地推广其积极成果。

1.1.1 贝叶斯模型及其工作流程

贝叶斯模型，无论其是否可计算，都有两个基本概念特征：

  • 一是使用概率分布来描述未知量 1 ，通常我们称这些未知量为参数 2。

  • 二是采用贝叶斯定理，以数据为已知条件来更新参数的值，此过程也可以被视为概率的重新分配。

在高层次上，可以将贝叶斯模型的构建过程分为三个步骤：

  1. 模型设计：给定一些数据，以及关于这些数据如何生成的一些假设，我们通过对随机变量的 组合（ Combing ） 和 转换（ Transforming ） 来设计模型。

  2. 模型推断：利用贝叶斯定理，使所设计的模型能够拟合数据，我们称此过程为 推断（ Inference ） 。推断的结果是获得了参数的后验分布。我们希望已有的数据能够减少所有可能参数值的不确定性，尽管这并不是任何贝叶斯模型都能够保证的。

  3. 模型评判：我们会根据不同标准来检查模型是否有意义，进而对模型进行评判。这些标准包括数据以及专业领域知识等。由于模型来自于人类的设计，因此其天然具有不确定性，通过比较多个模型，在理论上会减少模型设计带来的不确定性。

如果你熟悉其他形式的建模工作，就会认识到模型评判的重要性，以及迭代式地执行上述三个步骤的必要性。例如：我们可能需要在任何给定点回溯历史步骤。这也许是因为我们引入了一个愚蠢的编程错误，或者在一些挑战之后我们找到了改进模型的方法，或者我们发现数据不像最初想象的那样可用，以至于需要收集更多数据甚至是不同类型的数据。

在本书中，我们会讨论这三个步骤中每一步的实施方法，并将学习如何将上述的简单流程扩展到更为复杂的贝叶斯工作流（ Bayesian Workflow ）。我们认为 “贝叶斯工作流” 非常重要，因此用了完整的一章（ 第 9 章 ）来审视和讨论此主题。

1.1.2 贝叶斯推断 （ Bayesian Inference ）

通俗地说，推断 与 “根据证据和推理得出结论” 有关。贝叶斯推断是一种特殊形式的统计推断，它通过组合概率分布来获得其他概率分布。当我们已经观测到一些数据 \(\boldsymbol{Y}\) 时，贝叶斯定理提供了用于估计参数 \(\boldsymbol{\theta}\) 的通用方法：

(1)\[\underbrace{p(\boldsymbol{\theta} \mid \boldsymbol{Y})}_{\text{posterior}} = \frac{\overbrace{p(\boldsymbol{Y} \mid \boldsymbol{\theta})}^{\text{likelihood}}\; \overbrace{p(\boldsymbol{\theta})}^{\text{prior}}}{\underbrace{{p(\boldsymbol{Y})}}_{\text{marginal likelihood}}}\]

上式中，似然函数（ 简称似然， likelihood ） 将观测数据（ \(\boldsymbol{Y}\) ）与未知参数（ \(\boldsymbol{\theta}\) ）连接起来；先验分布（ 简称先验，prior ） 表示在观测到数据之前参数的不确定性 3；通过将两者相乘，可以得到 后验分布（ 简称后验， posterior ），即给定观测数据的条件下，模型中所有未知参数的联合分布。

Fig. 1 展示了一个任意的先验分布、似然函数，以及两者产生的后验分布 4 。

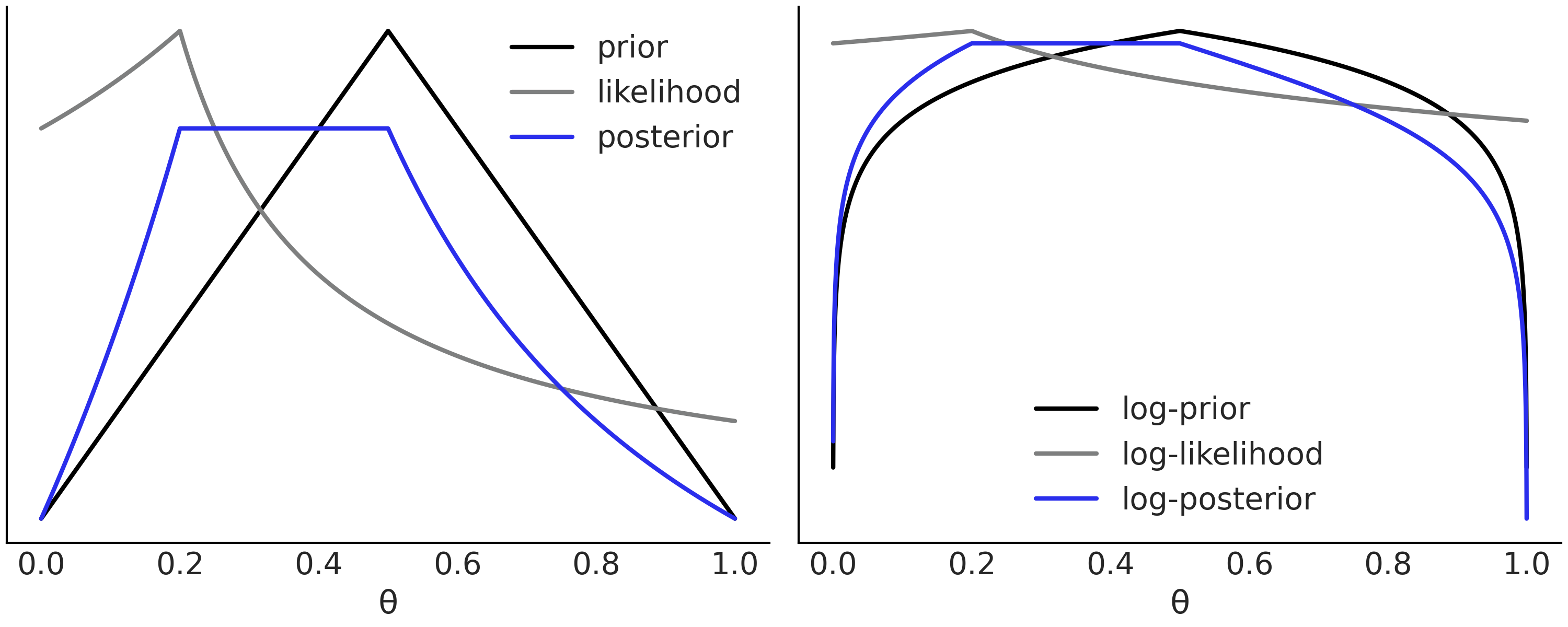
../_images/bayesian_triad.png

Fig. 1 左图为一个假想的先验分布（黑色曲线），其中 \(\theta = 0.5\) 的可能性更大，而其余值则呈现出线性对称的下降趋势；似然函数（灰色曲线）则表明， \(\theta = 0.2\) 的值能更好地解释数据；而两者相乘后的后验分布（蓝色曲线），则是先验和似然之间的折衷。图中省略了 \(y\) 轴的值和刻度，因为我们只关心相对值。右图的功能与左图相同，但 \(y\) 轴采用了对数尺度。可以发现对数尺度能够保留概率的相对性质，例如，两个图中最大值和最小值所在位置并没有改变。正是由于对数尺度具备此优点而且计算稳定，很多贝叶斯软件包都将其作为首选。

注意：虽然 \(\boldsymbol{Y}\) 是观测数据，但会被视为一个随机向量，因为其值取决于包含不确定性的特定生成过程或实验结果 5。为了获得后验分布，我们会将随机向量 \(\boldsymbol{Y}\) 的值固定在实际观测值上不变，因此一个常见的替代表示符号是 \(y_{obs}\) 。

正如公式和图中所示，在某个特定点上计算后验的值，从概念层面来说非常简单，只需将 一个先验值 乘以 一个似然值 即可。但这不足以告诉我们后验概率的全部，因为我们不仅想要特定点处的绝对后验值，还想要其与周围点的相对后验值。后验分布的这种全局信息由 边缘似然（ marginal likelihood ） （或者 归一化常数） \(p(\boldsymbol{Y})\) 来表示。贝叶斯定理中最不幸的事情就在于，计算这个全局信息异常困难。把边缘似然写成如下形式可能更容易理解这一点：

(2)\[{p(\boldsymbol{Y}) = \int_{\boldsymbol{\Theta}} p(\boldsymbol{Y} \mid \boldsymbol{\theta})p(\boldsymbol{\theta}) d\boldsymbol{\theta}}\]

其中 \(\Theta\) 表示我们需要对 \(\theta\) 的所有可能值做积分。

计算这样的积分非常难（ 参见 11.7 边缘似然 和一个有趣的 XKCD 漫画 6 ）。对于大多数问题而言，可能压根儿无法给出边缘似然的封闭形式解，进而更难得到积分结果了。好在有一些数值方法可以应对这一挑战，我们会在后面章节中做一些介绍。

另外，实践中的很多问题并不需要计算边缘似然，此时将贝叶斯定理表示为比率形式比较常见：

(3)\[\underbrace{p(\boldsymbol{\theta} \mid \boldsymbol{Y})}_{\text{posterior}} \propto \overbrace{p(\boldsymbol{Y} \mid \boldsymbol{\theta})}^{\text{likelihood}}\; \overbrace{p(\boldsymbol{\theta})}^{\text{prior}}\]

关于符号的说明

在本书中，我们使用相同的符号 \(p(\cdot)\) 来表示不同的量，例如：似然函数和先验分布。这其实是对符号的轻微滥用，因为似然函数并非一定是某种概率分布。不过这样做有一些好处：一是为贝叶斯公式中的所有量都提供了相同的认识论地位；二是反映出：即便似然函数不是严格意义上的概率密度函数，我们也能接受，因为我们只关心先验背景下的似然，反之亦然。

换句话说，为了计算后验分布，我们将这似然函数和先验分布视为模型中同等必要的元素。

贝叶斯统计的特点之一是：后验总是一个概率分布，这使我们能够给参数做出概率性的表述。例如参数 \(\boldsymbol{\tau}\) 为正的概率是 \(0.35\) 。或者 \(\boldsymbol{\phi}\) 最可能的值是 \(12\)，而且有 \(50\%\) 的机会介于 \(10\) 和 \(15\) 之间等。

此外，还可以将后验分布视为将模型与数据相结合的逻辑结果，因此由其得出的概率陈述保证了在数学上的一致性。我们只需记住，所有这些好的数学性质只在柏拉图式的内在理想世界中有效。当我们从 “理想世界中数学的纯粹性” 转向 “现实世界中应用数学的混杂性” 时，必须始终牢记：结果不仅取决于数据，还取决于模型。在实际问题中，有时候即便在数学上具有一致性，不良数据和/或不良模型也有可能导致毫无意义的结果。因此，必须始终对数据、模型和结果保持健康的怀疑精神。

为了使这一点更明确，可以更准确地表示贝叶斯定理如下：

\[p(\boldsymbol{\theta} \mid \boldsymbol{Y}, M) \propto p(\boldsymbol{Y} \mid \boldsymbol{\theta}, M) \; p(\boldsymbol{\theta}, M)\]

式中显式地强调了：推断总是依赖于对问题的某个模型假设 \(M\) 。

1.1.3 三种类型的预测

（1）后验用于计算积分

一旦有了后验分布，就可以基于它推导出有关参数的其他感兴趣量。而这通常以计算期望的方式实现，例如：

(4)\[J = \int f(\boldsymbol{\theta}) \; p(\boldsymbol{\theta} \mid \boldsymbol{Y}) \; d\boldsymbol{\theta}\]

该公式中最为常见的一个量是：当 \(f\) 为恒等函数时， 积分 \(J\) 就是参数 \(\boldsymbol{\theta}\) 的期望（均值） 7：

\[\bar{\boldsymbol{\theta}} = \int_{\boldsymbol{\Theta}} \boldsymbol{\theta} p(\boldsymbol{\theta} \mid \boldsymbol{Y}) d\boldsymbol{\theta}\]

（2）先验用于计算预期分布

后验分布是贝叶斯统计的核心对象，但不是唯一重要的。在大部分场景中，除了可以对参数值进行推断外，我们更需要对数据做出推断。这可以通过计算 先验预测分布 来完成：

(5)\[p(\boldsymbol{Y}^\ast) = \int_{\boldsymbol{\Theta}} p(\boldsymbol{Y^\ast} \mid \boldsymbol{\theta}) \; p(\boldsymbol{\theta}) \; d\boldsymbol{\theta}\]

上式根据模型（即先验和似然）得出了预期的数据概率分布。但要注意：这是在看到任何实际观测数据 \(\boldsymbol{Y}^\ast\) 之前的预期数据。

公式 (2)（边缘似然）和公式 (5)（先验预测分布）看起来有些相似，但两者的含义截然不同。在边缘似然公式中，我们有已知的观测数据 \(Y\) 作为前提条件，最终积分结果一个数字；而在先验预测分布的公式中，并没有观测数据作为已知前提，只是求结果为 \(\boldsymbol{Y}^\ast\) 的可能性有多大，最终表现为一个表达不确定性的概率分布。

我们可以使用先验预测分布的样本作为评估和校准模型的一种手段。例如，我们可能会问 “人类身高的模型能否将人类身高预测为 \(-1.5\) 米？” 之类的问题。而此类问题通常在实施身高测量这个实验之前，我们就能认识到其荒谬性。在本书后面章节中，会看到许多 “使用先验预测分布进行模型评估” 或者 “使用先验预测分布为后续建模选择提供有效或无效信息” 的案例。

作为生成式模型的贝叶斯模型

采用概率视角建模导致了一个常见表述：模型生成数据 [4]。我们认为此概念至关重要。一旦你将它内化，所有统计模型都会变得更加清晰，甚至包括非贝叶斯模型。

此表述可以指导我们创建新的模型。如果我们认可数据是由模型生成的，那么通过思考如何生成数据，就有可能为数据创建适合的模型！

此外，此表述并非一个抽象概念，我们可以用先验预测分布作为其具体表现形式。

如果重新审视贝叶斯建模的三个步骤，我们可以将它们重新调整为：编写先验预测分布 –> 添加数据以对其进行约束 —> 检查结果是否有意义。当然，必要时同样需要进行迭代。

（3）后验用于预测

另一个需要计算的量是 后验预测分布：

(6)\[p(\tilde{\boldsymbol{Y}} \mid \boldsymbol{Y}) = \int_{\boldsymbol{\Theta}} p(\tilde{\boldsymbol{Y}} \mid \boldsymbol{\theta}) \, p(\boldsymbol{\theta} \mid \boldsymbol{Y}) \, d\boldsymbol{\theta}\]

这是根据后验 \(p(\boldsymbol{\theta} \mid \boldsymbol{Y})\) 预测的未来数据 \(\tilde{\boldsymbol{Y}}\) 的分布，而后验是模型（先验和似然）和观测数据的结果。因此，后验预测分布是模型在看到数据集 \(\boldsymbol{Y}\) 后预期看到的未来数据，即该分布是模型的预测结果。从公式 (6) 可以看到，预测是通过对参数的后验分布进行积分（边缘化）来计算的。因此，该预测包含了不确定性估计。

频率主义者眼中的贝叶斯后验

因为后验仅来自于模型和观测数据，所以我们并不是基于未观测到的事情做出陈述，而是对 “基于内蕴数据生成过程得到潜在观测” 做出陈述。对未观测的事物做出推断通常是频率主义者常用的方法。但在使用后验预测样本来检查模型这方面，贝叶斯主义者其实（部分）接受了频率主义者关于 “未观测但潜在可观测的数据” 的思想。

我们不仅对该想法满意，而且将在本书中看到此过程的多处示例。这真是一个很棒的主意！

1.2 一个自制的采样器

公式 (2) 中的积分很多情况下没有封闭形式的解析解，因此现代贝叶斯推断大多使用被称为 通用推断引擎（ Universal Inference Engines ） 的数值方法来实现推断（ 参见 11.9 推断方法 ) 。有许多经过良好测试的 Python 软件包能够提供此类数值方法，因此一般来说，贝叶斯实践者不太可能需要编写自己的通用推断引擎。

当前编写自己的推断引擎通常只有两个理由：一是为了设计一个能够改进旧引擎的新引擎；二是为了学习某个引擎的工作原理。本章出于学习目的，将编写一个简易的引擎代码，但本书其余部分会主要使用 Python 库中的可用推断引擎。

（1）Metropolis-Hastings 采样器

可用于通用推断引擎的算法很多，其中使用最广泛、功能最强的算法是马尔可夫链蒙特卡洛方法（ MCMC ） 。所有 MCMC 方法 几乎都使用样本来近似后验分布，而这些样本大多通过接受或拒绝来自某个 提议分布 （部分数据称之为 状态转移矩阵 ） 的样本来生成。我们有理论上的保证，即通过遵循某些规则和假设能够获得非常近似后验分布的样本 8 。因此，MCMC 方法也称为 采样器 （ Sampler ）。所有这些 MCMC 方法都需要具备在给定参数值时计算先验和似然的能力。也就是说，即使不知道完整的后验形态，通过逐点计算，我们也能够获取其概率密度。

此类算法之一是 Metropolis-Hastings [7, 8, 9]。这并不是一个非常现代且有效的算法，但很容易被理解，因此为理解更复杂、更强大的其他方法奠定了基础 9 。

Metropolis-Hasting 算法定义如下：

  1. 在 \(x_i\) 处初始化参数 \(\boldsymbol{X}\) 的值

  2. 使用提议分布 \(q(x_{i + 1} \mid x_i)\) 从旧值 \(x_i\) 生成新值 \(x_{i + 1}\) 10。

  3. 计算新值被接受的概率：

    (7)\[p_a (x_{i + 1} \mid x_i) = \min \left (1, \frac{p(x_{i + 1}) \; q(x_i \mid x_{i + 1})} {p(x_i) \; q (x_{i + 1} \mid x_i)} \right)\]

  4. 如果 \(p_a > R\) 其中 \(R \sim \mathcal{U}(0, 1)\) ，则保留新值，否则保留旧值。

  5. 迭代 \(2\) 到 \(4\) 直到生成 足够多 的样本点。

Metropolis 算法 非常通用，而且可以在非贝叶斯应用中使用，但对于本书内容，\(p(x_i)\) 是参数在 \(x_i\) 处的后验密度。如果提议分布 \(q\) 是一个对称分布 （或矩阵），则公式中的 \(q(x_i \mid x_{i + 1})\) 和 \(q(x_{i + 1} \mid x_i)\) 将被消掉（这在概念上意味着从 \(x_{i+1}\) 转移到 \(x_i\) 与从 \(x_{i}\) 转移到 \(x_{i+1}\) 具有相同的可能性），只留下在两个点处估计的概率密度之比。从公式 (7) 可以看到，该算法始终接受从低概率区到较高概率区的转移，并按照一定概率接受从高概率区到低概率区的转移。

采样方法不同于最优化方法

需要说明的是：Metropolis-Hastings 算法 并不是一种优化方法！我们不关心概率密度最大的点在哪儿，而是想探索整个 \(p\) 分布（ 在贝叶斯统计中主要指后验分布 ）。如果你深入洞察和分析，就会发现此方法在达到最大概率区域后并不会停止，而是在后续步骤中继续转移到概率较低的区域。

（2）基础的 Beta-Binomial 模型

为了使事情更具象，让我们尝试求解一个 Beta-Binomial 模型。这可能是贝叶斯统计中最常见的示例，它用于对二值的、互斥的事件进行建模，例如 0 或 1、正或负、正面或反面、垃圾邮件或正常邮件、热狗或非热狗、健康或不健康等。 Beta-Binomial 模型 经常被用作介绍贝叶斯统计基础知识的第一个示例，因为它足够简单，而且可以轻松求解和计算。在统计符号系统中， Beta-Binomial 模型 记为：

(8)\[\begin{split}\begin{split} \theta \sim &\; \text{Beta}(\alpha, \beta) \\ Y \sim &\; \text{Bin}(n=1, p=\theta) \end{split}\end{split}\]

在公式 (8) 中，未知参数为 \(\theta\) ，其先验为Beta 分布 \(\text{Beta}(\alpha, \beta)\) ；我们假设数据的似然函数为二项分布 \(\text{Bin}(n=1, p=\theta)\) 。在此模型中，成功的次数 \(\theta\) 可以代表抛硬币时的正面比例、病亡率等量。

Beta-Binomial 模型实际上存在封闭形式的解（ 参见 1.4.1 共轭先验 了解详细信息 ），但这里为了方便讲解，我们假设不知道如何计算该模型的后验。因此需要在 Python 代码中实现 Metropolis-Hastings 算法来以获得近似的数值解。在 SciPy 软件包的统计函数支持下，可以实现为：

Listing 1 Metropolis_Hastings_采样器的实现
def post(θ, Y, α=1, β=1):
    if 0 <= θ <= 1:
        prior = stats.beta(α, β).pdf(θ)
        like  = stats.bernoulli(θ).pmf(Y).prod()
        prob = like * prior
    else:
        prob = -np.inf
    return prob

推断后验分布需要引入观测数据，为此我们生成了一些合成数据（也称伪数据，Fake Data）。

Listing 2 metropolis_hastings_sampler_rvs
Y = stats.bernoulli(0.7).rvs(20)

运行 Metropolis-Hastings 算法的代码：

Listing 3 metropolis_hastings 的采样过程
 1n_iters = 1000
 2can_sd = 0.05
 3α = β =  1
 4θ = 0.5
 5trace = {"θ":np.zeros(n_iters)}
 6p2 = post(θ, Y, α, β)
 7
 8for iter in range(n_iters):
 9    θ_can = stats.norm(θ, can_sd).rvs(1)
10    p1 = post(θ_can, Y, α, β)
11    pa = p1 / p2
12
13    if pa > stats.uniform(0, 1).rvs(1):
14        θ = θ_can
15        p2 = p1
16
17    trace["θ"][iter] = θ

在代码 metropolis_hastings 中，第 \(9\) 行从标准差为 can_sd 的高斯分布中采样来生成提议分布。第 \(10\) 行在参数值 θ_can 处估计后验，第 \(11\) 行计算接受概率。第 \(17\) 行在轨迹数组 trace 中保存了 θ 的值。该值是一个新值还是重复上一次的值，取决于第 \(13\) 行的比较结果。

模棱两可的 MCMC 术语

当使用马尔可夫链蒙特卡洛方法进行贝叶斯推断时，我们通常将其称为MCMC 采样器。在每次迭代中，我们从采样器中抽取一个随机样本，因此很自然地将 MCMC 的结果称为 样本（ Samples ） 或 抽取（Draws）。有些人喜欢将 样本 视为由一组 抽取 组成，而另外一些人则倾向于两个概念可以互换。

由于 MCMC 是按迭代顺序抽取样本的，因此也会说：我们得到了一个采样结果的 链（ Chain ），或者简称为 MCMC 链 。出于计算和诊断的原因，通常需要抽取许多链。所有输出的链，无论是单条还是多条，通常都被称为 轨迹、迹（ Trace ） 或直接称为 后验。

无论怎么定义这些名词，口语总是不精确的。如果需要精确，最好的方法还是查看代码以准确了解正在发生的事。

请注意，代码 metropolis_hastings 中的实现方式并非旨在提高效率，实际上生产级代码中会出现许多优化，例如会改为计算对数尺度的概率，以避免溢出问题、提高计算稳定性等（ 参见 10.4.1 对数概率 ），或预先计算提议分布值。这些优化都是需要改变数学纯粹性以适应计算机实现的地方，也能解释为什么最好让专家来构建推断引擎。

同样， can_sd 的值是 Metropolis-Hastings 算法 的参数，而不是贝叶斯模型的参数。理论上该参数不应该影响算法的正确行为，但在实践中它又非常重要，因为方法的效率肯定会受到该值的影响（ 参阅 11.9 推断方法 ）。

（3）推断结果的诊断

回到示例，现在有了 MCMC 样本，我们想了解其形态。检查贝叶斯推断结果的一种常用方法是：将每次迭代得到的采样值通过直方图或其他可视化工具绘制出来，以表示分布。例如，可以使用代码 diy_trace_plot 中的代码来绘制 Fig. 2 11：

Listing 4 diy_trace_plot
_, axes = plt.subplots(1,2, sharey=True)
axes[1].hist(trace["θ"], color="0.5", orientation="horizontal", density=True)
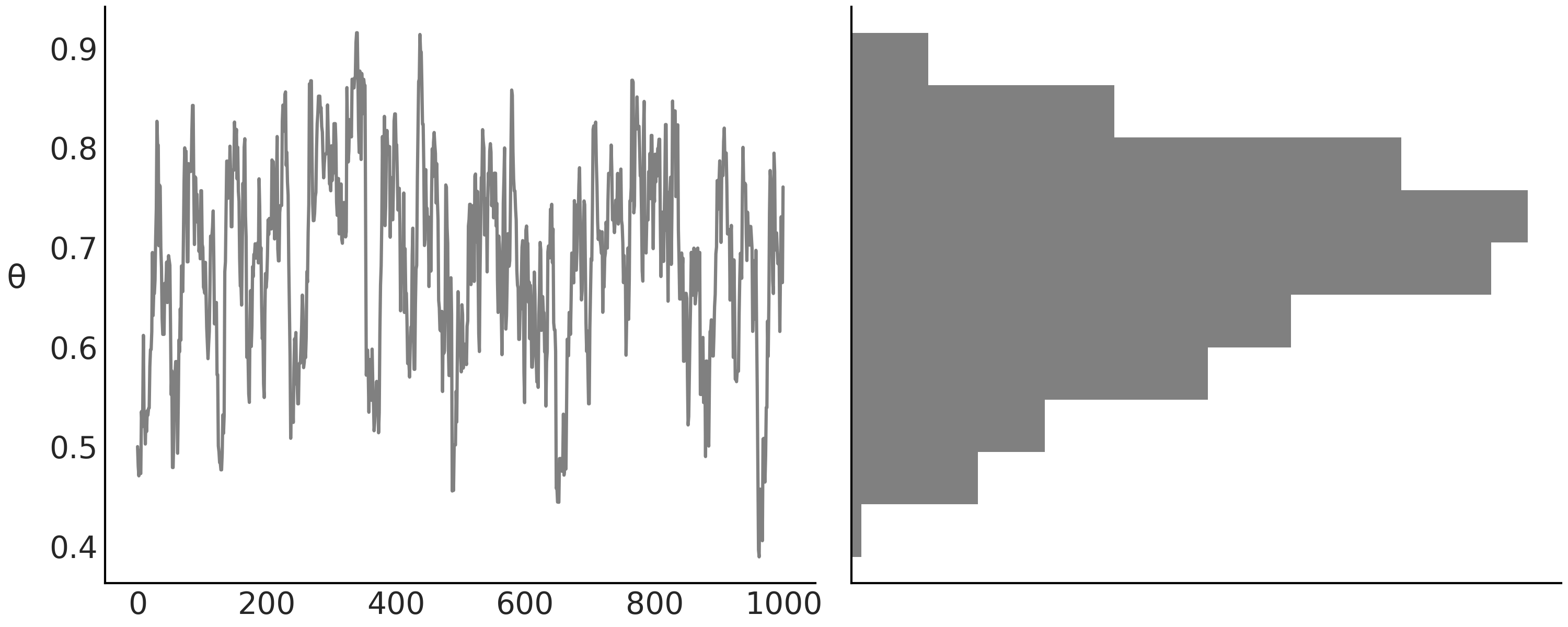
../_images/traceplot.png

Fig. 2 左图中，每次迭代都会产生参数 \(\theta\) 的采样值。右图为 \(\theta\) 采样值的直方图。该直方图经过了旋转，以便更容易看出两个图之间的密切关系。左图显示了采样值的顺序序列，该序列其实就是所谓的马尔可夫链，而右图则显示了采样值的分布情况。

通常，计算一些数字汇总信息也很有用。我们将使用名为 ArviZ 的 Python 软件包 [3] 来计算这些统计信息：

az.summary(trace, kind="stats", round_to=2)
Table 1 后验分布的汇总信息

mean

sd

hdi_3%

hdi_97%

\(\theta\)

0.69

0.01

0.52

0.87

ArviZ 的函数 summary 计算参数 \(\theta\) 的均值、标准差和 \(94\%\) 最高密度区间 (HDI)。 最高密度区间（ HDI ）是包含给定概率密度（此处为 \(94\%\) ）的最短区间 12 。 Fig. 3 为 az.plot_posterior(trace) 生成，其与 Table 1 中的汇总信息非常相似。我们可以在代表整个后验分布的曲线顶部看到均值和最高密度区间。该曲线使用 核密度估计（ Kernel Density Estimator, KDE ） 计算，类似于直方图的平滑版本。

ArviZ 在许多绘图函数中都会使用 KDE，甚至在内部进行一些计算。

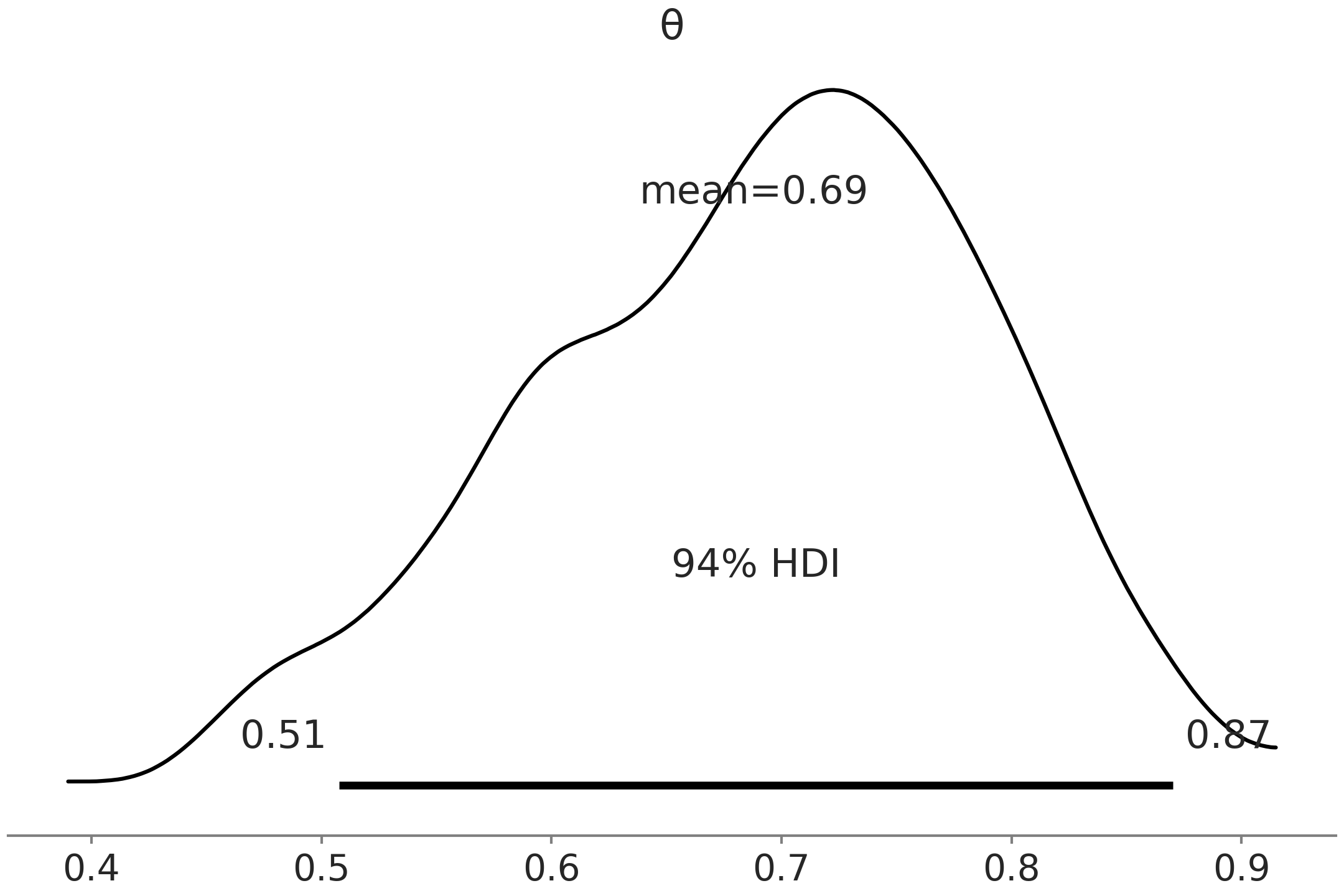
../_images/plot_posterior.png

Fig. 3 用后验图对代码 metropolis_hastings 生成的样本进行可视化。后验分布使用核密度估计曲线表示，均值和 \(94\%\) 最高密度区间均在图中有所展示。

最高密度区间（ HDI ）是贝叶斯统计中的常见选择，像 \(50\%\) 或 \(95\%\) 这样的边界值也很常见。但 ArviZ 的默认值为 \(94\%\)（ 或 \(0.94\) ），如 Table 1 和 Fig. 3 中所示。这种选择的原因是 \(94\) 接近广泛使用的 \(95\)，而同时这种微小的区别可以提醒观众，边界值的选择并没有特别之处 [10] 。理想情况下，你应该选择一个满足需要的值 [11]，或者至少承认你使用的是默认值。

1.3 人工建模与自动推断

我们可以在 概率编程语言 ( Probabilistic Programming Languages, PPL ) 的帮助下定义和推断模型，而不是编写自己的采样器从头定义自己的模型。概率编程语言允许用户使用代码表达贝叶斯模型，然后借助 通用推断引擎 以自动化的方式执行贝叶斯推断。简而言之，概率编程语言能够帮助贝叶斯实践者将注意力更多地聚焦在模型构建本身，而不是数学和计算细节。

在过去的几十年中，此类工具的可用性大大提升了贝叶斯方法的普及度和实用性。不幸的是，这些通用推断引擎方法并不是真正通用的，因为它们无法有效地求解所有贝叶斯模型。现代贝叶斯实践者的部分工作是理解这些局限性并给出解决方法。

在本书中，我们使用的概率编程语言是 PYMC3 [1] 和 TensorFlow Probability(TFP) [2]。例如用 PYMC3 为公式 (8) 编写模型：

Listing 5 beta_binom
# Declare a model in PyMC3
with pm.Model() as model:
   # Specify the prior distribution of unknown parameter
    θ = pm.Beta("θ", alpha=1, beta=1)
   # Specify the likelihood distribution and condition on the observed data
    y_obs = pm.Binomial("y_obs", n=1, p=θ, observed=Y)

# Sample from the posterior distribution
idata = pm.sample(1000, return_inferencedata=True)

你可以自己检查这段代码的结果是否与之前自制采样器的结果一致。在概率编程语言支持下，工作量要少得多。如果你不熟悉 PYMC3 语法，现阶段只需关注代码注释中表达的每一行的意图。

在 PYMC3 语法中定义了模型后，可以利用 pm.model_to_graphviz(model) 在代码 beta_binom 中生成模型的概率图表示（参见 Fig. 4）。

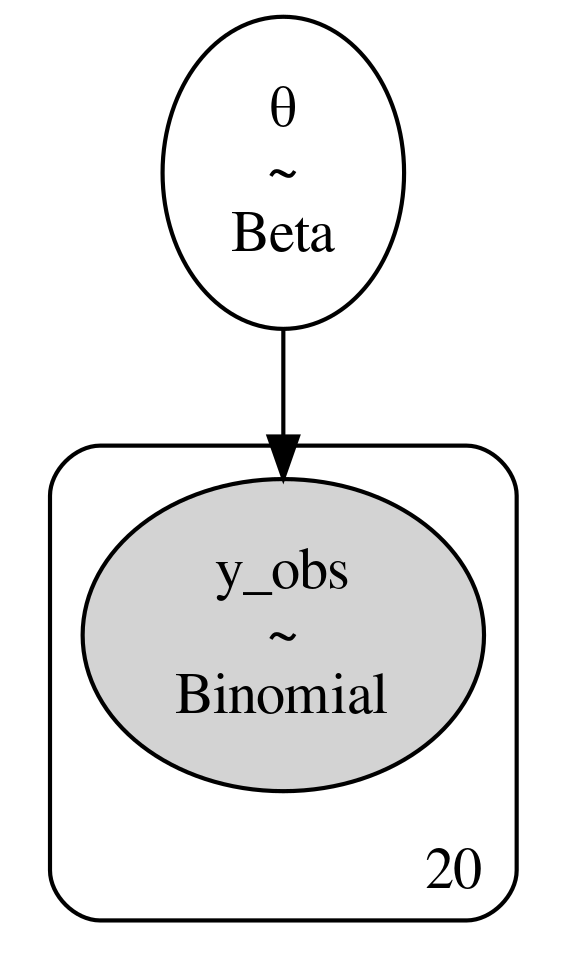
../_images/BetaBinomModelGraphViz.png

Fig. 4 公式 (8) 和代码 beta_binom 中定义的贝叶斯模型的概率图表示。椭圆代表先验和似然，而 \(20\) 表示观测次数。

概率编程语言不仅可以计算随机变量的对数概率以获得后验分布，还可以模拟前面提到的两种预测分布：先验预测分布 和 后验预测分布。例如，代码 predictive_distributions 展示了如何使用 PYMC3 分别获得先验预测分布和后验预测分布的 \(1000\) 个样本。请注意，第一个函数仅有 model 参数，而第二个函数必须同时传递 model 和 trace 参数，这反映了先验预测分布仅需要知道模型，而后验预测分布不仅需要模型还需要后验分布。两种预测分布的样本分别在绘制在 Fig. 5 的上下子图中。

Listing 6 predictive_distributions
pred_dists = (pm.sample_prior_predictive(1000, model)["y_obs"],
              pm.sample_posterior_predictive(idata, 1000, model)["y_obs"])

公式 (1) 、 (5) 和 (6) 清楚地将后验分布、先验预测分布和后验预测分布定义为三个不同的数学对象。显然后面两个是数据的概率分布，而第一个是参数的概率分布。Fig. 5 帮助我们可视化了这种区别，为了完整，图中还包含了先验分布。

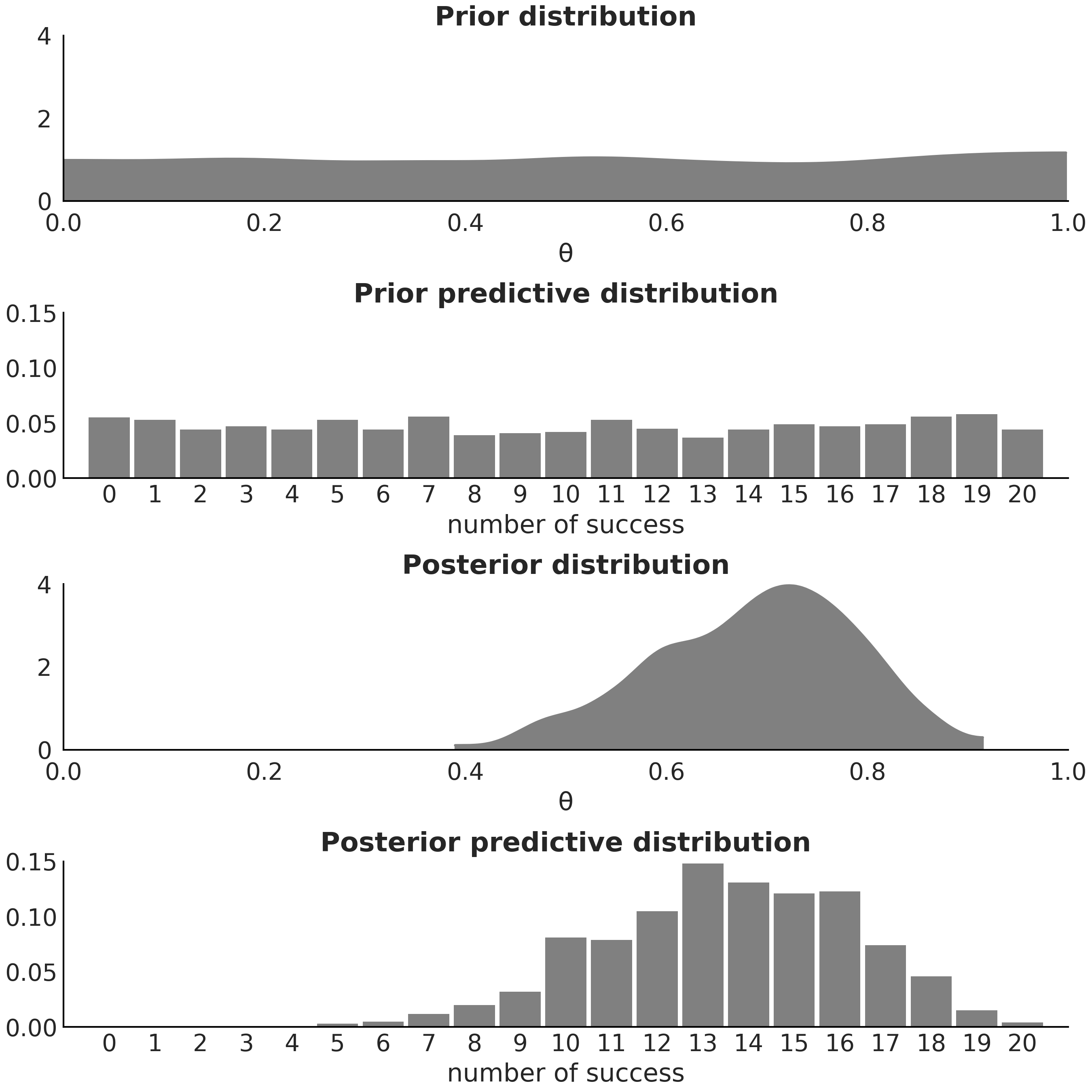
../_images/Bayesian_quartet_distributions.png

Fig. 5 自上至下，我们展示了：（1）参数 \(\theta\) 的先验分布样本； (2) 成功总数的先验预测分布样本； (3) 参数 \(\theta\) 的后验分布样本； (4) 成功总数的后验预测分布样本。在第一个和第三个图、第二个和第四个图之间分别共享 \(x\) 轴和 \(y\) 轴的坐标尺度。

应当熟练掌握的几种统计模型表达方式

有许多方法可以表示统计模型的架构。以下没有特定的顺序：

  • 口语和书面语言

  • 概念图：例如 Fig. 4。

  • 数学符号：例如公式 (8)

  • 源代码：例如代码 beta_binom

对于现代贝叶斯实践者来说，所有这些媒介都很有用。它们是在会谈、科学论文、与同事讨论时的手绘草图、互联网上的代码示例等中经常看到的格式。熟练地使用这些媒介，你能够更好地理解以某种形式呈现的概念，然后将其应用到其他形式中。例如，阅读一篇论文然后实现一个模型，或者在演讲中听到一种技术，然后能够为其写一篇博客。对个人而言，熟练程度会加快你的学习速度并提高与他人交流的能力。

正如已经提到的，后验预测分布考虑了估计结果的不确定性。Fig. 6 表明：根据后验均值计算得到的预测结果，比后验预测分布（根据完整的后验分布计算得到）中的预测结果范围更窄。此现象不仅对均值有效，对于其他任何点估计，都会得到类似的图。

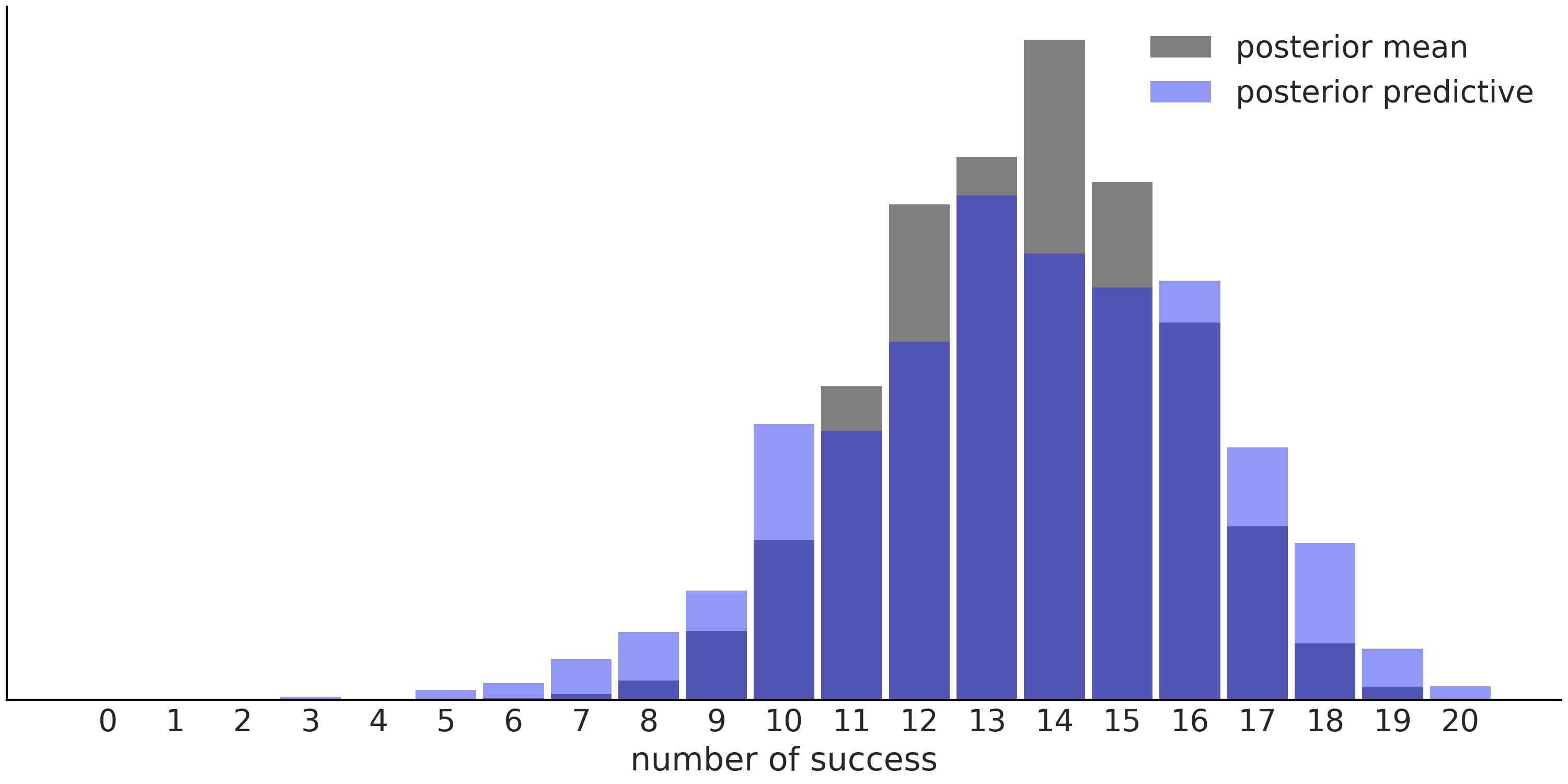
../_images/predictions_distributions.png

Fig. 6 Beta-Binomial 模型的预测结果对比，使用后验均值所做的预测表示为灰色直方图，使用完整后验所做的预测（ 即后验预测分布 ）表示为蓝色直方图。

1.4 先验分布的选择方法

在贝叶斯统计中，必须要选择先验分布这件事，既是一种负担又是一种祈福，而我们认为这是必要的。如果你没有选择先验，那么最大可能是别人已经为你做这件事。当然，让别人替你做决定并不总是坏事。如果在正确的场景中应用并且意识到其局限性，许多非贝叶斯方法会非常有用和有效。然而，我们坚信：了解模型假设并灵活调整这些假设是有优势的，而先验是假设的形式之一。

我们也明白，对于许多实践者来说，先验选择可能是怀疑、焦虑甚至沮丧的根源，尤其是对于新手。寻找给定问题的最佳先验，是一个常见且有效的问题。但是除了没有最佳先验这个结论之外，很难给出一个令人满意的答案。好在我们有一些默认值，可以作为迭代式建模工作流的起点。

在本节中，我们将讨论一些选择先验的一般性方法。此讨论或多或少遵循一个信息性的阶梯，从不包含任何信息的“空白”先验，到信息丰富的、信息尽可能多的先验。本章关于先验的讨论更多是在理论方面的。在后续章节中，我们将讨论如何在更实际的环境中选择先验。

1.4.1 共轭先验

如果后验与先验属于同一分布族，则先验与似然共轭，或称其为似然的共轭先验。例如，如果似然是 Poisson 分布并且先验为 Gamma 分布，那么后验也会是 Gamma 分布。

从纯数学角度来看，共轭先验是最有利的选择，因为共轭先验和似然能够得到后验的封闭形式解，这允许我们用“纸笔”就可以分析和计算后验分布 14。但从现代计算角度来看，共轭先验通常并不比其他方法好，主要原因是现代计算方法允许我们使用几乎任何先验进行推断，而不仅仅是那些在数学上方便的有限选择。尽管如此，共轭先验在学习贝叶斯推断时、以及在某些需要对后验使用解析表达式的情况下，可能仍然非常有用（ 参阅 10.2.2 示例：近实时推断 中的示例 ）。因此，我们会简要地讨论 Beta-Binomial 模型 中解析形式的共轭先验。顾名思义，该模型的似然为 Binomial 分布，而其共轭先验为 Beta 分布：

\[p(\theta \mid Y) \propto \overbrace{\frac{N!}{y!(N-y)!} \theta^y (1 - \theta)^{N-y}}^{\text{binomial-likelihood}} \: \overbrace{\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}\, \theta^{\alpha-1}(1-\theta)^{\beta-1}}^{\text{beta.prior}}\]

式中所有不包含 \(\theta\) 的项关于 \(\theta\) 都是不变的，可以省略它们，进而得到：

\[p(\theta \mid Y) \propto \overbrace{\theta^y (1 - \theta)^{N-y}}^{\text{binomial-likelihood}} \: \overbrace{ \theta^{\alpha-1}(1-\theta)^{\beta-1}}^{\text{beta.prior}}\]

重新组织公式，得到：

(9)\[p(\theta \mid Y) \propto \theta^{\alpha-1+y}(1-\theta)^{\beta-1+N-y}\]

如果想确保后验是一个正确的概率分布函数，还需要添加一个归一化常数，以确保密度函数的积分为 \(1\)（参见 11.1.5 连续型随机变量及其分布 ）。请注意，公式 (9) 看起来与Beta 分布的核一致，由此，在添加Beta 分布的归一化常数后，得出 Beta-Binomial 模型 的后验分布为：

(10)\[p(\theta \mid Y) \propto \frac{\Gamma(\alpha_{post}+\beta_{post})}{\Gamma(\alpha_{post})\Gamma(\beta_{post})} \theta^{\alpha_{post}-1}(1-\theta)^{\beta_{post}-1} = \text{Beta}(\alpha_{post}, \beta_{post})\]

其中 \(\alpha_{post} = \alpha+y\) 和 \(\beta_{post} = \beta+N-y\)。

Beta-Binomial 模型的后验也是Beta 分布，因此我们可以使用其作为下一步贝叶斯分析的先验。这意味着，一次使用完整的数据集 和 一次使用一个数据点 将获得相同的结果。例如，Fig. 7 的前四个子图显示了从 \(0\) 次到 \(1\)次、 \(2\) 次和 \(3\) 次试验时，不同的先验更新情况。遵循此顺序，或者直接从 \(0\) 次试验跳到 \(3\) 次试验（ 或 \(n\) 次试验 ）最终会得到一致的结果。

从 Fig. 7 中还可以看到很多其他有趣的事情。例如，随着试验次数增加，后验的宽度越来越小，不确定性越来越低。子图 \(3\) 和 \(5\) 分别显示了“ \(2\) 次试验成功 \(1\) 次” 和“ \(12\) 次试验成功 \(6\) 次” 的结果。两种情况根据样本得到的成功比例估计值 \(\hat \theta = \frac{y}{n}\)（ 黑点 ）相同，均为 \(0.5\)（ 后验分布的众数也是 \(0.5\) ），不过子图 \(5\) 中的后验相对更加集中，反映出观测数量更大，不确定性更低。最后可以观察到：随着观测次数增加，不同先验最终可以收敛到同样的后验。在无限数据的条件下，后验与先验的选择无关，根据不同的先验推断得到的后验，最终将在点 \(\hat \theta = \frac{y}{n}\) 处具有几乎所有密度。

Listing 7 binomial_update
_, axes = plt.subplots(2,3, sharey=True, sharex=True)
axes = np.ravel(axes)

n_trials = [0, 1, 2, 3, 12, 180]
success = [0, 1, 1, 1, 6, 59]
data = zip(n_trials, success)

beta_params = [(0.5, 0.5), (1, 1), (10, 10)]
θ = np.linspace(0, 1, 1500)
for idx, (N, y) in enumerate(data):
    s_n = ("s" if (N > 1) else "")
    for jdx, (a_prior, b_prior) in enumerate(beta_params):
        p_theta_given_y = stats.beta.pdf(θ, a_prior + y, b_prior + N - y)

        axes[idx].plot(θ, p_theta_given_y, lw=4, color=viridish[jdx])
        axes[idx].set_yticks([])
        axes[idx].set_ylim(0, 12)
        axes[idx].plot(np.divide(y, N), 0, color="k", marker="o", ms=12)
        axes[idx].set_title(f"{N:4d} trial{s_n} {y:4d} success")
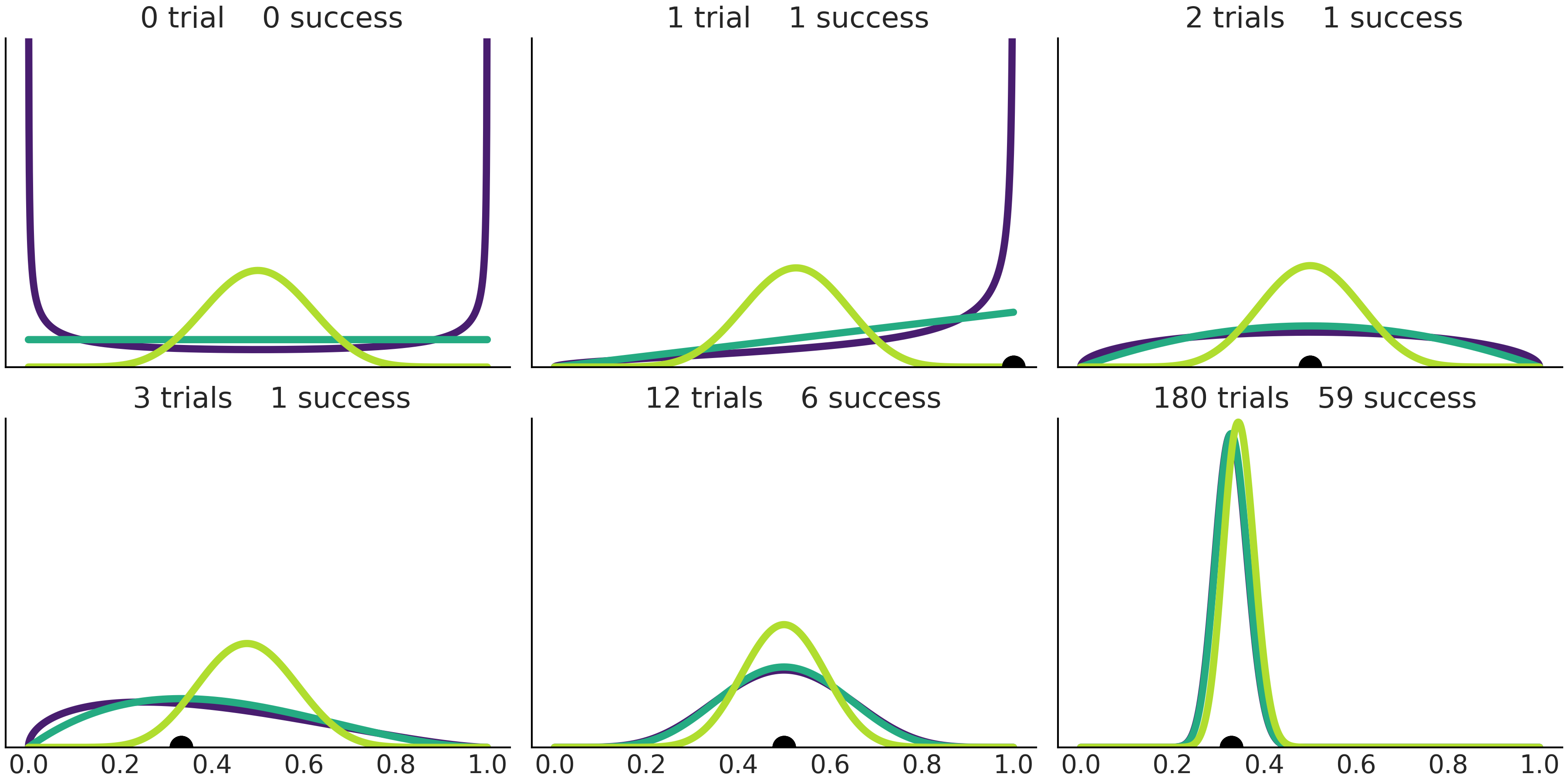
../_images/beta_binomial_update.png

Fig. 7 从 \(3\) 种不同的先验开始连续更新先验并增加试验次数。黑点代表根据样本得到的成功比例估计值 \(\hat \theta = \frac{y}{n}\)。

Beta 分布的均值为 \(\frac{\alpha}{\alpha + \beta}\) ，因此先验均值为：

\[\mathbb{E}[\theta] = \frac{\alpha}{\alpha + \beta}\]

后验均值为：

(11)\[\mathbb{E}[\theta \mid Y] = \frac{\alpha + y}{\alpha + \beta + n}\]

可以看到，如果 \(n\) 的值相对于 \(\alpha\) 和 \(\beta\) 的值较小，那么后验均值更接近于先验均值。也就是说，先验对结果的贡献大于数据。如果 \(n\) 的值相对于 \(\alpha\) 和 \(\beta\) 的值较大，则后验均值将更接近成功比例的估计值 \(\hat \theta = \frac{y}{n}\) ，实际上在 \(n \rightarrow \infty\) 的情况下，后验均值将与 \(\alpha\) 和 \(\beta\) 的先验无关，最终都会完美地匹配根据样本得到的成功比例。

对于 Beta-Binomial 模型，后验众数为：

(12)\[\operatorname*{argmax}_{\theta}{[\theta \mid Y]} = \frac{\alpha + y - 1}{\alpha + \beta + n - 2}\]

可以看到，当先验为 \(\text{Beta}(\alpha\!=\!1, \beta\!=\!1)\) ( 即均匀分布 ) 时，后验众数在数值上等于根据样本计算的成功比例估计值 \(\hat \theta = \frac{y}{n}\)。后验众数通常被称为最大后验( MAP ) 值。此结果并非 Beta-Binomial 模型独有。事实上，许多非贝叶斯方法的结果都可以被理解为贝叶斯方法在特定先验条件下的最大后验 15。

将公式 (11) 与样本得到的成功比率估计值 \(\frac{y}{n}\) 进行比较。贝叶斯估计器将成功次数增加了 \(\alpha\) ，将试验次数增加了 \(\alpha + \beta\) 。这使得 \(\beta\) 成为失败的次数。从此意义上说，我们可以将先验参数视为 伪计数 。先验 \(\text{Beta}(1, 1)\) 等价于进行两次试验，\(1\) 次成功，\(1\) 次失败。从概念上讲，Beta 分布的形状由参数 \(\alpha\) 和 \(\beta\) 控制，观测数据会更新先验，从而使Beta 分布的形状更接近、更窄地移动到大多数观测值。对于 \(\alpha < 1\) 和/或 \(\beta < 1\) 的值，先验的解释变得有点奇怪，因为字面解释会说先验 \(\text{Beta}(0.5, 0.5)\) 对应于一次试验，半次失败，半次成功，或者可能是一次结果未定的试验。

一些比较常见的似然及其共轭先验，可参见 维基百科。

1.4.2 无信息先验（ 或客观先验 ）

在没有先验信息的情况下，遵循 无差别原则 听起来似乎更合理。此原则基本上是说：如果你没有关于某个问题的信息，那么你就没有任何理由相信一个结果会比任何其他结果更有可能发生。

在贝叶斯统计背景下，这一原则推动了 客观先验（ Objective Priors ） 的研究和应用。这是一种“生成对给定分析影响最小的先验”的系统方法。有些统计学者偏爱客观先验，因为他们认为此类先验消除了先验的主观性。但其实这种想法是立不住脚的，因为采用客观先验并没有消除其他来源的主观性，例如：似然的选择、数据的选择、问题的选择等等。

一种获得客观先验的方法是著名的 Jeffreys 先验。此类先验通常被称为 无信息先验 ，尽管它总是以某种方式提供了信息。 Jeffreys 先验具有在 重参数化 时保持不变性的特点（ 重参数化指以形式不同但在数学上等效的方式重写表达式 ）。让我们用例子来解释一下这是什么意思。

假设 Alice 具有参数为 \(\theta\) 的 Binomial 似然，她选择了某种先验并计算得到后验。而她的朋友 Bob，也对同一问题感兴趣，但并不关心成功次数 \(\theta\) ，而是关心另外一个参数：成功的赔率（ odds ），即关心参数 \(\kappa\) ，\(\kappa = \frac{\theta}{1-\theta}\) 。 此时 Bob 有两种选择：一是使用 Alice 在 \(\theta\) 上的后验来计算 \(\kappa\) ，二是在 \(\kappa\) 上选择先验来计算自己的后验 16。

Jeffreys 先验 的不变性是指：

在针对同一问题的两种参数化表示中，如果 Alice 模型 和 Bob 模型都为各自的参数设置了 Jeffreys 先验，那么无论 Bob 用 \(\theta\) 的后验推导出 \(\kappa\) 的后验，还是自己用 \(\kappa\) 的先验推断出其后验，最终都会得到相同的结果。也就是说，最终的后验推断结果对于所选择的参数而言具有不变性。此解释的一个推论是，除非使用 Jeffreys 先验，否则无法保证模型的两种或多种参数化必然会导致一致的后验。

对于一维 \(\theta\) 的情况， Jeffreys 先验 为：

(13)\[p(\theta) \propto \sqrt{I(\theta)}\]

其中 \(I(\theta)\) 为 Fisher 信息的期望：

(14)\[I(\theta) = - \mathbb{E_{Y}}\left[\frac{d^2}{d\theta^2} \log p(Y \mid \theta)\right]\]

此式意味着：一旦建模者确定了似然函数 \(p(Y \mid \theta)\) ，Jeffreys 先验 就自动被确定了。也就是说，消除了对先验选择的任何讨论。

有关 Alice 和 Bob 问题的 Jeffreys 先验 推导，请参阅 11.6 Jeffreys 先验的推导 。这里跳过细节，Alice 的 Jeffreys 先验 为：

\[\begin{aligned} p(\theta) \propto \theta^{-0.5} (1-\theta)^{-0.5} \end{aligned}\]

这就是 \(\text{Beta}(0.5, 0.5)\) 分布的核，是一个 \(U\) 形分布，就像 Fig. 8 的左上图所示。

而对于 Bob 来说， Jeffreys 先验 为：

(15)\[p(\kappa) \propto \kappa^{-0.5} (1 + \kappa)^{-1}\]

这是一个半 \(U\) 形分布，定义在 \([0, \infty)\) 区间中，参见 Fig. 8 中的右上角图。称其为半 \(U\) 形似乎有些奇怪，但实际上它是 Beta-prime 分布 （ Beta 分布的一个近亲 ）在参数为 \(\alpha=\beta=0.5\) 时的核。

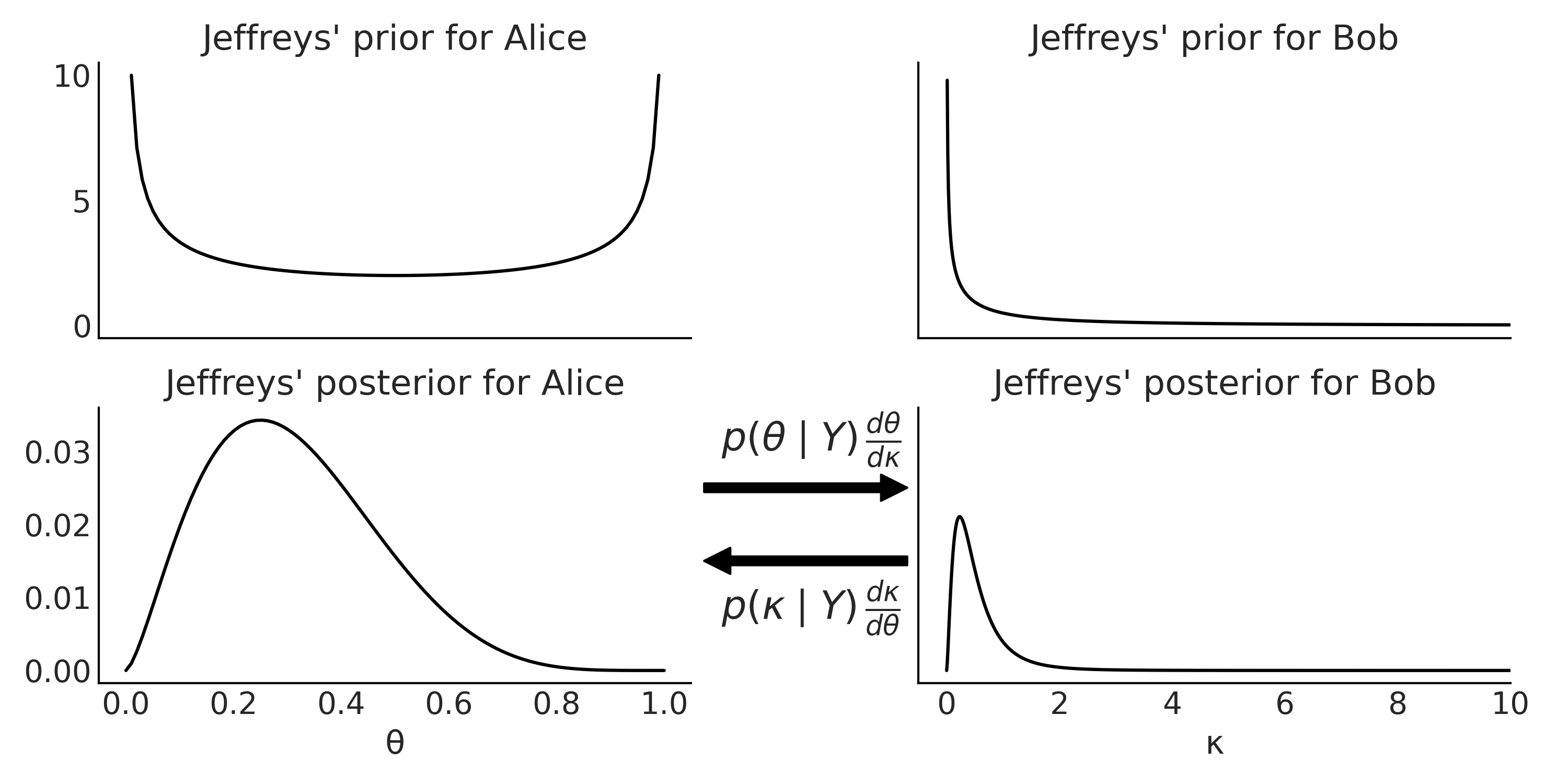
../_images/Jeffrey_priors.png

Fig. 8 上图：二项似然的两种参数化形式对应的 Jeffreys 先验（ 未归一化 ），左图根据成功次数 \(\theta\) 参数化，右图根据成功赔率 \(\kappa\) 参数化。下图：根据成功次数 \(\theta\)（ 左 ）或成功赔率 \(\kappa\)（ 右 ）参数化的二项似然的 Jeffreys 后验（ 未归一化 ）。后验之间的箭头表示，通过应用一些变量规则的调整，两个后验之间可相互转换（ 详细信息参阅 11.1.9 变换 ）。

注意，公式 (14) 中的期望是关于观测 \(Y \mid \theta\) 的，这是在样本空间上的期望。这意味着为了获得 Jeffreys 先验，我们需要对所有可能的实验结果求平均，这违反了似然原则 17，因为关于 \(\theta\) 的推断不仅取决于手头数据，还取决于潜在（但尚未）观测的数据集。

Jeffreys 先验 可以是不恰当的先验，即它的积分可能不会为 \(1\) 。例如，已知方差的高斯分布，其均值参数的 Jeffreys 先验 在整个实数轴上均匀分布。但只要能够验证，这些不恰当的先验与似然组合后，能够产生恰当（ 即积分为 \(1\) ）的后验，则这些不恰当的先验就是可用的。

另外还要注意，我们不能从不恰当的先验中抽取随机样本（ 即此类先验是非生成式的 ），这会造成许多模型推断工具失效。

Jeffreys 先验 并不是获得客观先验的唯一方法。另一种途径是通过最大化先验和后验之间KL 散度的期望来获得先验（ 参见 11.3 KL 散度 ）。此类先验被称为 Bernardo 参考先验，之所以是客观性先验，是因为它们 “允许数据将最大量的信息带入后验”。 另外，Bernardo 参考先验和 Jeffreys 先验 不必一致。

此外，对于某些复杂模型，可能不存在客观先验或难以推导出客观先验。

1.4.3 最大熵先验

另一种证明先验选择合理性的方法是选择具有最大熵的先验。

如果我们对参数的可取值完全无区别对待，那么此先验就是可取值范围内的均匀分布 18。但当我们对可取值并非无动于衷呢？例如，我们可能知道参数必须位于 \([0, \infty)\) 区间，那我们能得到既有最大熵又能满足约束的先验吗？这个先验是什么呢？这正是最大熵先验背后的思想。在文献中谈论最大熵原理时，通常会找到 MaxEnt 这个词。

为了获得最大熵先验，需要求解包含一组约束条件的优化问题。在数学上，这可以使用拉格朗日乘数来实现。但这里我们不会采用形式化方法去推导和证明最大熵先验，而是使用几个代码案例来感性认识它。

Fig. 9 展示了通过最大化熵获得的 \(3\) 个分布。紫色分布是在没有约束条件下获得的，这确实是 11.2 熵 中所预期的均匀分布，如果我们对问题一无所知，那么所有事件都是同等可能的。第二个青色分布是在知道分布均值为 \(1.5\) 的约束下获得的最大熵先验，这是一个类似指数的分布。最后一个黄绿色的分布是在已知 \(3\) 和 \(4\) 的概率为 \(0.8\) 的约束下获得的最大熵先验。

注意：如果检查代码 max_ent_priors，你会看到所有的最大熵先验都是在两个基本约束条件下计算的，一是概率只能在 \([0, 1]\) 区间中取值，二是总概率必须为 \(1\) 。它们是有效概率分布的共同约束，因此可以被视为固有约束，我们经常默认它们，进而称 Fig. 9 中的紫色分布是在无约束条件下获得的。

Listing 8 max_ent_priors
 1cons = [[{"type": "eq", "fun": lambda x: np.sum(x) - 1}],
 2        [{"type": "eq", "fun": lambda x: np.sum(x) - 1},
 3         {"type": "eq", "fun": lambda x: 1.5 - np.sum(x * np.arange(1, 7))}],
 4        [{"type": "eq", "fun": lambda x: np.sum(x) - 1},
 5         {"type": "eq", "fun": lambda x: np.sum(x[[2, 3]]) - 0.8}]]
 6
 7max_ent = []
 8for i, c in enumerate(cons):
 9    val = minimize(lambda x: -entropy(x), x0=[1/6]*6, bounds=[(0., 1.)] * 6,
10                   constraints=c)['x']
11    max_ent.append(entropy(val))
12    plt.plot(np.arange(1, 7), val, 'o--', color=viridish[i], lw=2.5)
13plt.xlabel("$t$")
14plt.ylabel("$p(t)$")
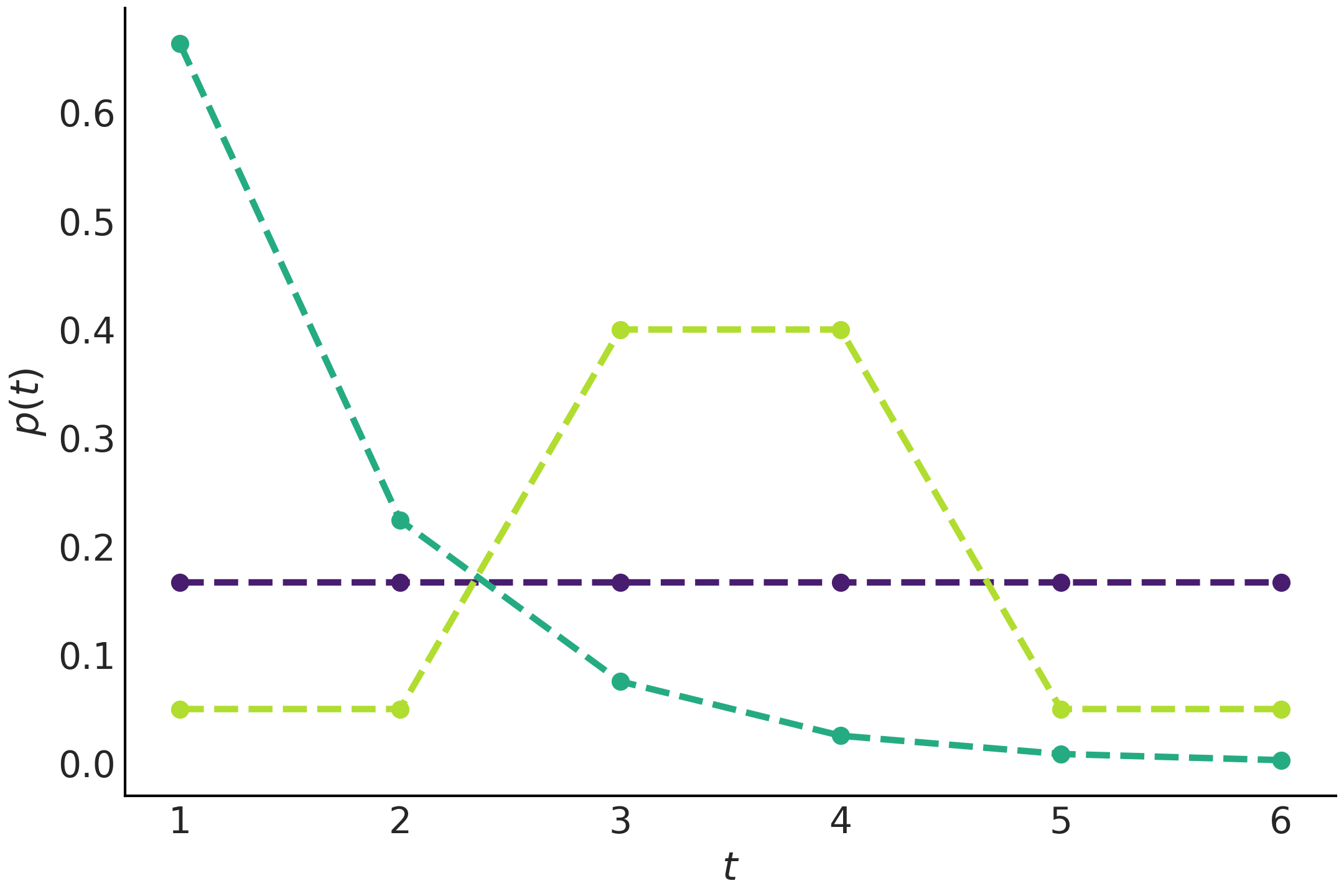
../_images/max_entropy.png

Fig. 9 在不同约束下通过最大化熵获得的离散分布。我们使用了 scipy.stats 的 entropy 函数来估计这些分布。注意观察，在添加约束后分布发生了较大变化。

我们可以将最大熵原理理解为在给定约束下选择最平坦分布的过程，在贝叶斯统计中可以被延伸为在给定约束下选择最平坦先验分布的过程。在 Fig. 9 中，均匀分布是最平坦的分布，但请注意，一旦引入 “ \(3\) 和 \(4\) 的出现概率为 80% ” 的约束，黄绿色分布就变成了最平坦的分布。

注意：本例中 \(3\) 和 \(4\) 的出现概率都为 \(0.4\) ，以获得 \(0.8\) 的总概率值。但其实有很多种选择，例如： \(0+0.8\) 、 \(0.7+0.1\) 、 \(0.312+0.488\) 等。与之相反， 值 \(1\) 、 \(2\) 、 \(5\) 和 \(6\) 也有类似情况，它们的总概率值为 \(0.2\) ，而本例中也仅采用了其中的均匀分布（ 每个值的概率均为 \(0.05\) ）。

现在看一下类似指数的曲线，它看起来肯定不是很平坦，但应注意到，其他选择将更不平坦且更集中。例如，分别以 \(50\%\) 的概率获得 \(1\) 和 \(2\)（ 因此 \(3\) 至 \(6\) 的概率为 \(0\) ），这也满足均值为 \(1.5\) 的约束，但更不平坦。

ite = 100_000
entropies = np.zeros((3, ite))
for idx in range(ite):
    rnds = np.zeros(6)
    total = 0
    x_ = np.random.choice(np.arange(1, 7), size=6, replace=False)
    for i in x_[:-1]:
        rnd = np.random.uniform(0, 1-total)
        rnds[i-1] = rnd
        total = rnds.sum()
    rnds[-1] = 1 - rnds[:-1].sum()
    H = entropy(rnds)
    entropies[0, idx] = H
    if abs(1.5 - np.sum(rnds * x_)) < 0.01:
        entropies[1, idx] = H
    prob_34 = sum(rnds[np.argwhere((x_ == 3) | (x_ == 4)).ravel()])
    if abs(0.8 - prob_34) < 0.01:
        entropies[2, idx] = H

Fig. 10 显示了在与 Fig. 9 中 \(3\) 个分布满足完全相同约束时，随机生成的分布及熵，垂直虚线表示了 Fig. 9 中曲线的熵所在位置，显然是最大熵。虽然这不是一个证明，但实验似乎表明没有分布会比 Fig. 9 中的分布具有更高的熵，这与理论完全一致。

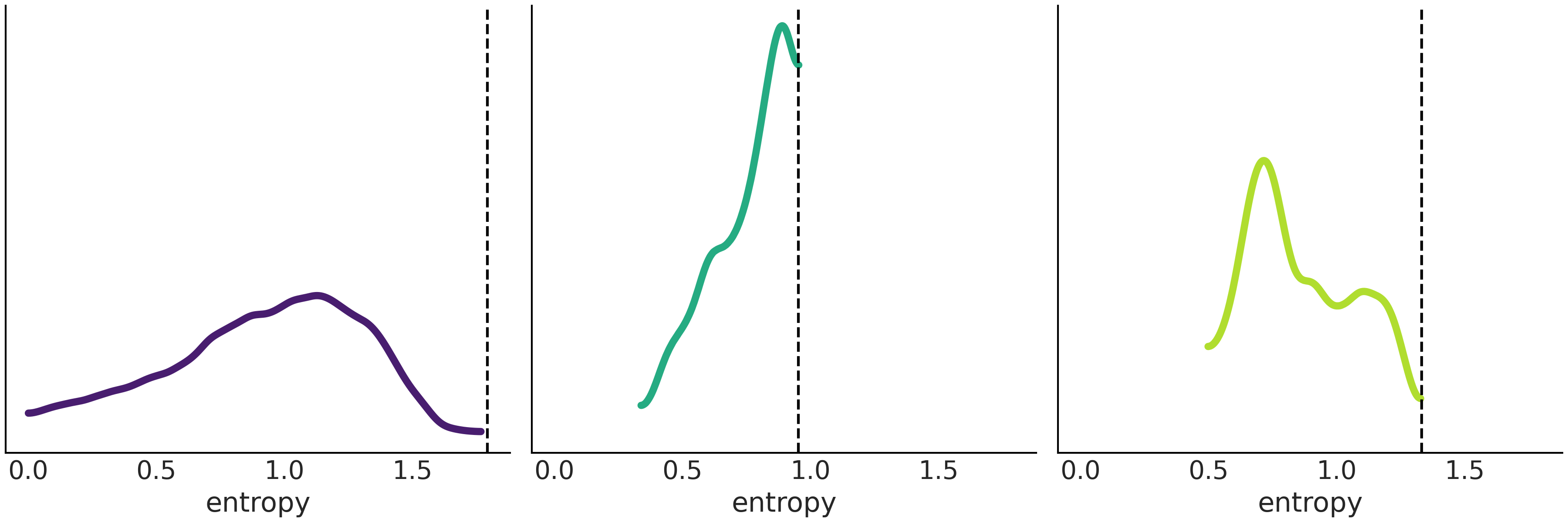
../_images/max_entropy_vs_random_dist.png

Fig. 10 一组随机生成的分布的熵的分布。垂直虚线表示具有最大熵分布的值，使用代码 max_ent_priors 计算。可以看到，没有一个随机生成的分布的熵大于具有最大熵分布的熵，尽管这不是形式化的证明，但结果是令人放心的。

在以下约束下，对应的最大熵分布分别为 19：

  • 无约束时：均匀分布（连续的或离散的，取决于随机变量类型）

  • 具有正均值，值域为 \([0, \infty)\) 时：指数分布

  • 具有绝对值均值，值域为 \((-\infty, \infty)\) 时：拉普拉斯（也称为双指数）

  • 具有指定的均值和方差，值域为 \((-\infty, \infty)\) 时：高斯分布

  • 具有指定的均值和方差，值域为 \([-\pi, \pi]\) 时：冯·米塞斯分布（一种圆上的连续概率分布，也被称作循环正态分布）

  • 只存在两个可能的无序值，且均值为常数：二项分布，或者泊松分布（ 泊松可以看作存在罕见事件的二项分布 ）

有趣的是，在考虑到模型约束时，许多传统上的广义线性模型（ 如 第 3 章 中的模型 ）都是使用最大熵分布来定义的。与客观先验类似，MaxEnt 先验有可能并不存在或难以推导。

1.4.4 弱信息性先验与正则化先验

在前面部分中，我们使用一般性的过程来生成了无信息先验（此处指客观先验），旨在不将太多信息放入分析中。这些过程甚至还提供了“以某种方式”自动生成先验的方法。这两个特征听起来非常具有吸引力，而且在实际上被大量贝叶斯实践者和理论家所采用。

但在本书中，我们不会过分依赖这些先验。我们认为先验的选择应该取决于背景环境。这意味着特定问题的细节、给定科学领域的特性等，都可以为先验的选择提供信息。虽然 MaxEnt 先验能够包含其中一些约束，但我们似乎还可以更加靠近信息性先验频谱的信息端，这就是弱信息先验。

构造弱信息先验的方法通常在数学上没有 Jeffreys 先验 或 MaxEnt 先验 那样的良好定义。相反，弱信息先验更多是经验主义和模型驱动 的。也就是说，弱信息先验大多通过结合领域知识和模型本身来定义。对于很多问题，我们经常有关于参数可取值的信息，这些信息往往来自于参数的物理意义，例如身高必须是正数。我们甚至可以从之前的实验或观测中得到取值范围。我们或许有充分理由证明一个值应该接近零或高于某个预定义的下界。上述这些信息都能够为我们选择先验提供微弱的信息，同时保持一定程度的未知。

这里再次使用 Beta-Binomial 模型作为例子，Fig. 11 显示了四个可选的先验。前两个分别是 Jeffreys 先验 和最大熵先验；第三个是弱信息先验，它优先考虑 \(\theta=0.5\) ，同时对其他值保持很宽泛或相对模糊；最后一个是信息性先验，以 \(\theta=0.8\) 为中心 20 。如果从理论、之前的实验、观测数据中能够获得高质量的信息，则信息性先验是最有效的选择。信息性先验可以传达大量信息，因们通常需要比选择其他先验更强的理由。正如 Carl Sagan 说的 “非凡主张需要非凡的证据” [12]。

重要的：先验的信息量取决于模型及其上下文。一个在某种情境中的无信息先验，可能在另一个情境中变得非常有用 [13] 。例如，如果以米为单位对成年人的平均身高进行建模，则 \(\mathcal{N}(2,1)\) 的先验被认为是无信息的；但如果用于估计长颈鹿的高度，则该先验变得信息量非常大，因为现实中长颈鹿的高度与人类身高相差很大，该先验的取值范围对于人类的身高范围而言信息量几乎为 \(0\)，但对长颈鹿的高度而言，具有很好的解释性。

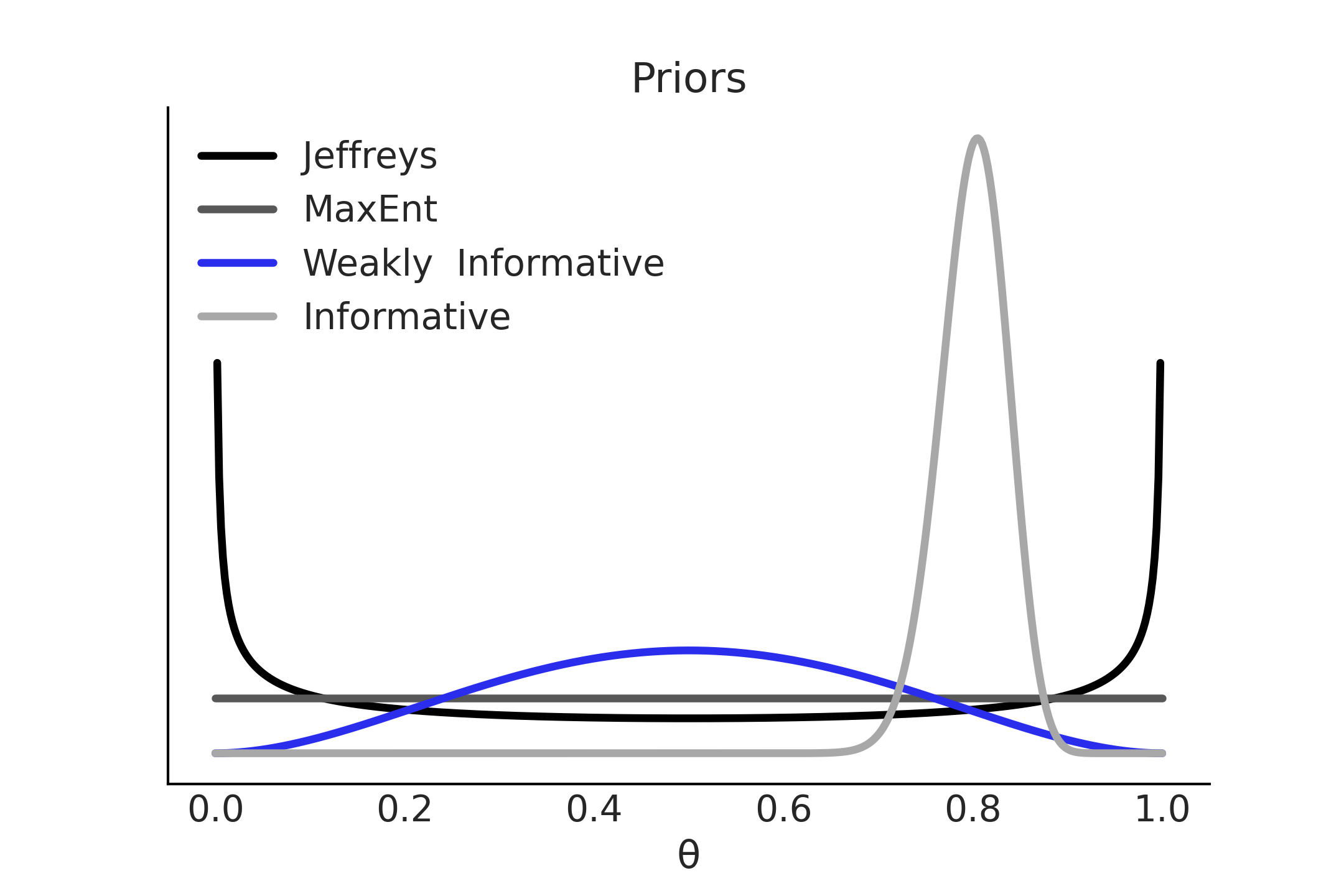
../_images/prior_informativeness_spectrum.png

Fig. 11 先验信息谱： Jeffrey 先验和 MaxEnt 先验是为二项似然唯一定义的，但弱信息先验和信息性先验不是，后者取决于之前的信息和实践者的建模决策。

弱信息先验可以将后验分布保持在一定的合理范围内，所以它们也被称为正则化先验。正则化是一种添加信息的过程，目的是解决不适定问题或减少过拟合的机会，先验提供了一种执行正则化的原则方法。在本书中，我们经常使用弱信息先验。

有时会在没有太多理由的情况下在模型中使用先验，仅仅是因为示例的重点可能与贝叶斯建模工作流程的其他方面有关。但我们也会展示一些使用先验预测检查来校准先验分布的例子。

过拟合（ Overfitting ）

当模型生成的预测非常接近用于拟合它的有限数据集时，往往会发生过拟合，但这样的模型无法拟合新数据和/或不能很好地预测未来的观测。也就是说，它未能将其预测推广到更广泛的可观测结果。过拟合的反义词是欠拟合，即模型未能充分捕捉数据的底层结构。我们会在 2.5 模型比较 和 11.4 信息准则 部分讨论此主题的更多信息。

1.4.5 先验预测分布用于评估先验选择

在评估先验选择时，1.3 人工建模与自动推断 中显示的先验预测分布是一个方便的工具。通过从先验预测分布中采样，计算机会将 在参数空间中的选择 转换为 在观测空间中的样本 。而考虑观测值通常会比考虑模型参数更直观，这使模型评估变得更容易。以 Beta-Binomial 模型为例，与判断 \(\theta\) 的特定值是否合理不同，先验预测分布允许我们判断特定的成功次数是否合理。这对于那些参数需要许多数学运算或多个先验相交互的复杂模型来说，更为有用。最后，计算先验预测分布可以帮助我们确保模型已经被正确地编码，并且能够在概率编程语言中运行，甚至可以帮助我们调试模型。

在接下来的章节中，我们将看到更具体的示例，说明如何推断先验预测样本并使用它们来选择合理的先验。

1.5 练习

Problems are labeled Easy (E), Medium (M), and Hard (H).

1E1. As we discussed, models are artificial representations used to help define and understand an object or process.

However, no model is able to perfectly replicate what it represents and thus is deficient in some way. In this book we focus on a particular type of models, statistical models. What are other types of models you can think of? How do they aid understanding of the thing that is being modeled? How are they deficient?

1E2. Match each of these verbal descriptions to their corresponding mathematical expression:

  1. The probability of a parameter given the observed data

  2. The distribution of parameters before seeing any data

  3. The plausibility of the observed data given a parameter value

  4. The probability of an unseen observation given the observed data

  5. The probability of an unseen observation before seeing any data

1E3. From the following expressions, which one corresponds to the sentence, The probability of being sunny given that it is July 9th of 1816?

  1. \(p(\text{sunny})\)

  2. \(p(\text{sunny} \mid \text{July})\)

  3. \(p(\text{sunny} \mid \text{July 9th of 1816})\)

  4. \(p(\text{July 9th of 1816} \mid \text{sunny})\)

  5. \(p(\text{sunny}, \text{July 9th of 1816}) / p(\text{July 9th of 1816})\)

1E4. Show that the probability of choosing a human at random and picking the Pope is not the same as the probability of the Pope being human. In the animated series Futurama, the (Space) Pope is a reptile. How does this change your previous calculations?

1E5. Sketch what the distribution of possible observed values could be for the following cases:

  1. The number of people visiting your local cafe assuming Poisson distribution

  2. The weight of adult dogs in kilograms assuming a Uniform distribution

  3. The weight of adult elephants in kilograms assuming Normal distribution

  4. The weight of adult humans in pounds assuming skew Normal distribution

1E6. For each example in the previous exercise, use SciPy to specify the distribution in Python. Pick parameters that you believe are reasonable, take a random sample of size 1000, and plot the resulting distribution. Does this distribution look reasonable given your domain knowledge? If not adjust the parameters and repeat the process until they seem reasonable.

1E7. Compare priors \(\text{Beta}(0.5, 0.5)\), \(\text{Beta}(1, 1)\), \(\text{Beta}(1, 4)\). How do the priors differ in terms of shape?

1E8. Rerun Code Block binomial_update but using two Beta-priors of your choice. Hint: you may what to try priors with \(\alpha \neq \beta\) like \(\text{Beta}(2, 5)\).

1E9. Try to come up with new constraints in order to obtain new Max-Ent distributions (Code Block max_ent_priors)

1E10. In Code Block metropolis_hastings, change the value of can_sd and run the Metropolis-Hastings sampler. Try values like 0.001 and 1.

  1. Compute the mean, SD, and HDI and compare the values with those in the book (computed using can_sd=0.05). How different are the estimates?

  2. Use the function az.plot_posterior.

1E11. You need to estimate the weights of blue whales, humans, and mice. You assume they are normally distributed, and you set the same prior \(\mathcal{HN}(200\text{kg})\) for the variance. What type of prior is this for adult blue whales? Strongly informative, weakly informative, or non-informative? What about for mice and for humans? How does informativeness of the prior correspond to our real world intuitions about these animals?

1E12. Use the following function to explore different combinations of priors (change the parameters a and b) and data (change heads and trials). Summarize your observations.

def posterior_grid(grid=10, a=1, b=1, heads=6, trials=9):
    grid = np.linspace(0, 1, grid)
    prior = stats.beta(a, b).pdf(grid)
    likelihood = stats.binom.pmf(heads, trials, grid)
    posterior = likelihood * prior
    posterior /= posterior.sum()
    _, ax = plt.subplots(1, 3, sharex=True, figsize=(16, 4))
    ax[0].set_title(f"heads = {heads}\ntrials = {trials}")
    for i, (e, e_n) in enumerate(zip(
            [prior, likelihood, posterior],
            ["prior", "likelihood", "posterior"])):
        ax[i].set_yticks([])
        ax[i].plot(grid, e, "o-", label=e_n)
        ax[i].legend(fontsize=14)


interact(posterior_grid,
    grid=ipyw.IntSlider(min=2, max=100, step=1, value=15),
    a=ipyw.FloatSlider(min=1, max=7, step=1, value=1),
    b=ipyw.FloatSlider(min=1, max=7, step=1, value=1),
    heads=ipyw.IntSlider(min=0, max=20, step=1, value=6),
    trials=ipyw.IntSlider(min=0, max=20, step=1, value=9))

1E13. Between the prior, prior predictive, posterior, and posterior predictive distributions which distribution would help answer each of these questions. Some items may have multiple answers.

  1. How do we think is the distribution of parameters values before seeing any data?

  2. What observed values do we think we could see before seeing any data?

  3. After estimating parameters using a model what do we predict we will observe next?

  4. What parameter values explain the observed data after conditioning on that data?

  5. Which can be used to calculate numerical summaries, such as the mean, of the parameters?

  6. Which can can be used to to visualize a Highest Density Interval?

1M14. Equation (1) contains the marginal likelihood in the denominator, which is difficult to calculate.

In Equation (3) we show that knowing the posterior up to a proportional constant is sufficient for inference.

Show why the marginal likelihood is not needed for the Metropolis-Hasting method to work. Hint: this is a pen and paper exercise, try by expanding Equation (7).

1M15. In the following definition of a probabilistic model, identify the prior, the likelihood, and the posterior:

\[\begin{split}\begin{split} Y \sim \mathcal{N}(\mu, \sigma)\\ \mu \sim \mathcal{N}(0, 1)\\ \sigma \sim \mathcal{HN}(1)\\ \end{split}\end{split}\]

1M16. In the previous model, how many parameters will the posterior have? Compare your answer with that from the model in the coin-flipping problem in Equation (8).

1M17. Suppose that we have two coins; when we toss the first coin, half of the time it lands tails and half of the time on heads. The other coin is a loaded coin that always lands on heads. If we choose one of the coins at random and observe a head, what is the probability that this coin is the loaded one?

1M18. Modify Code Block metropolis_hastings_sampler_rvs to generate random samples from a Poisson distribution with parameters of your choosing.

Then modify Code Blocks metropolis_hastings_sampler and metropolis_hastings to generate MCMC samples estimating your chosen parameters. Test how the number of samples, MCMC iterations, and initial starting point affect convergence to your true chosen parameter.

1M19. Assume we are building a model to estimate the mean and standard deviation of adult human heights in centimeters. Build a model that will make these estimation. Start with Code Block beta_binom and change the likelihood and priors as needed. After doing so then

  1. Sample from the prior predictive. Generate a visualization and numerical summary of the prior predictive distribution

  2. Using the outputs from (a) to justify your choices of priors and likelihoods

1M20. From domain knowledge you have that a given parameter can not be negative, and has a mean that is roughly between 3 and 10 units, and a standard deviation of around 2. Determine two prior distribution that satisfy these constraints using Python. This may require trial and error by drawing samples and verifying these criteria have been met using both plots and numerical summaries.

1M21. A store is visited by \(n\) customers on a given day.

The number of customers that make a purchase \(Y\) is distributed as \(\text{Bin}(n, \theta)\), where \(\theta\) is the probability that a customer makes a purchase. Assume we know \(\theta\) and the prior for \(n\) is \(\text{Pois}(4.5)\).

  1. Use PyMC3 to compute the posterior distribution of \(n\) for all combinations of \(Y \in {0, 5, 10}\) and \(\theta \in {0.2, 0.5}\). Use az.plot_posterior to plot the results in a single plot.

  2. Summarize the effect of \(Y\) and \(\theta\) on the posterior

1H22. Modify Code Block metropolis_hastings_sampler_rvs to generate samples from a Normal Distribution, noting your choice of parameters for the mean and standard deviation. Then modify Code Blocks metropolis_hastings_sampler and metropolis_hastings to sample from a Normal model and see if you can recover your chosen parameters.

1H23. Make a model that estimates the proportion of the number of sunny versus cloudy days in your area. Use the past 5 days of data from your personal observations. Think through the data collection process. How hard is it to remember the past 5 days. What if needed the past 30 days of data? Past year? Justify your choice of priors. Obtain a posterior distribution that estimates the proportion of sunny versus cloudy days. Generate predictions for the next 10 days of weather.

Communicate your answer using both numerical summaries and visualizations.

1H24. You planted 12 seedlings and 3 germinate. Let us call \(\theta\) the probability that a seedling germinates. Assuming \(\text{Beta}(1, 1)\) prior distribution for \(\theta\).

  1. Use pen and paper to compute the posterior mean and standard deviation. Verify your calculations using SciPy.

  2. Use SciPy to compute the equal-tailed and highest density \(94\%\) posterior intervals.

  3. Use SciPy to compute the posterior predictive probability that at least one seedling will germinate if you plant another 12 seedlings.

After obtaining your results with SciPy repeat this exercise using PyMC3 and ArviZ

1

If you want to be more general you can even say that everything is a probability distribution as a quantity you assume to know with arbitrary precision that can be described by a Dirac delta function.

2

Some authors call these quantities latent variables and reserve the name parameter to identify fixed, but unknown, quantities.

3

Alternatively you can think of this in terms of certainty or information, depending if you are a glass half empty or glass half full person.

4

Sometimes the word distribution will be implicit, this commonly occurs when discussing these topics.

5

Here we are using experiment in the broad sense of any procedure to collect or generate data.

6

https://xkcd.com/2117/

7

Technically we should talk about the expectation of a random variable. See Section 11.1.8 期望 for details.

8

See detailed balance at Sections 11.1.11 马尔可夫链 and 11.9.2 Metropolis-Hastings 采样器.

9

For a more extensive discussion about inference methods you should read Section 11.9 推断方法 and references therein.

10

This is sometimes referred to as a kernel in other Universal Inference Engines.

11

You can use ArviZ plot_trace function to get a similar plot. This is how we will do in the rest of the book.

12

Notice that in principle the number of possible intervals containing a given proportion of the total density is infinite.

14

Except, the ones happening in your brain.

15

For example, a regularized linear regression with a L2 regularization is the same as using a Gaussian prior on the coefficient.

16

For example, if we have samples from the posterior, then we can plug those samples of \(\theta\) into \(\kappa = \frac{\theta}{1-\theta}\).

17

https://en.wikipedia.org/wiki/Likelihood_principle

18

See Section 11.2 熵 for more details.

19

Wikipedia has a longer list at https://en.wikipedia.org/wiki/Maximum_entropy_probability_distribution#Other_examples

20

Even when the definition of such priors will require more context than the one provided, we still think the example conveys a useful intuition, that will be refined as we progress through this book.

previous

符号表

next

第二章：贝叶斯模型的探索性分析