第七章：贝叶斯加性回归树¶

在第 5 章中，我们看到了如何通过一系列基函数的求和来构造一个近似函数，同时展示了 B-样条 作为基函数时带来的一些不错的性质。在本章中，我们将讨论一种类似方法，但会使用决策树而不是 B-样条。

决策树是表示分段常数或阶跃函数的另外一种比较灵活方式。在这里，我们将重点关注贝叶斯加性回归树（ BART ） 。贝叶斯加性回归树是一种贝叶斯非参数模型，它通过对多个决策树求和来获得更灵活的模型 1。加性回归树通常以更接近机器学习的术语而不是统计术语来讨论 [69]。从某种意义上说，相较其他章节中的模型而言，BART 更像一个“一劳永逸的模型”。

在 BART 的文献中，人们通常不讨论基函数，而是讨论学习器，但总体思路非常相似。我们使用简单函数（也称为学习器）的组合来逼近复杂函数，并具备足够的正则化，这样就可以在模型不太复杂的情况下获得足够的灵活性。使用多个学习器来求解同一问题的方法被称为集成方法（ Ensemble Methods ），其中学习器可以是任何统计模型或数据算法。集成方法基于这样一个基本观测：组合多个弱学习器通常比使用单个强学习器效果更好。为了在准确度和泛化方面获得良好效果，一般认为基础学习器应该尽可能准确，并且尽可能多样化 [70] 。 BART 的主要贝叶斯思想是：决策树很容易过拟合，因此我们为每棵树添加一个正则化先验（或收缩先验），以使其表现为一个弱学习器。

为了将上述描述转化为可以理解和应用的东西，我们下面会首先讨论决策树。如果你已经熟悉这个板块的内容，可以跳过下一节。

7.1 决策树¶

7.1.1 什么是决策树？¶

假设有两个变量 $X_1$ 和 $X_2$，我们希望依据这些变量将对象分为两类： ⬤ 或 ▲ 。为了实现此目标，可以使用 Fig. 119 左图中所示的树结构。树是节点的集合，其中任何两个节点之间最多通过一条线或一条边相连。 Fig. 119 中的树被称为二叉树，因为每个节点最多可以有两个子节点。没有子节点的节点被称为叶子节点或终端节点。在此示例中，有 $2$ 个内部节点（表示为矩形）和 $3$ 个叶子节点（表示为圆角矩形）。所有内部节点都有一个与之相关联的决策规则，如果遵循这些决策规则，最终将到达其中一个叶子节点，而该节点将提供决策问题的答案。

例如，如果变量 $X_1$ 的实例 $x_{1i}$ 大于 $c_1$，决策树会将类 ⬤ 分配给该实例。如果 $x_{1i}$ 的值小于 $c_1$ 并且 $x_{2i}$ 的值小于 $c_2$，决策树会将类 ▲ 分配给该实例。

从算法上讲，可以将树概念化为一组 if-else 语句，程序遵循这些语句来执行分类等特定任务。也可以从几何角度理解二叉树，将其视为一种将样本空间划分为不同块的方式，如 Fig. 119 的右侧子图所示。每个块均由与某个预测变量轴相垂直的分割线定义，因此样本空间的每次分割都会与某个预测变量轴对齐。

在数学上，我们可以说决策树 $g$ 由两个集合完全地定义：

$\mathcal{T}$ ：边和节点的集合，即 Fig. 119 中的矩形、圆角矩形、连接它们的线，以及与内部节点相关联的决策规则。
$\mathcal{M} = \{\mu_1, \mu_2, \dots, \mu_b\}$ ：与 $\mathcal{T}$ 的每个叶子节点相关联的一组参数值。

也就是说，决策树 $g(X; \mathcal{T}, \mathcal{M})$ 就是将 $\mu_i \in M$ 分配给 $X$ 的那个函数。例如，在 Fig. 119 中，$\mu_{i}$ 的取值为（ ⬤ 、⬤ 、 ▲ ）。 $g$ 函数将 ⬤ 分配给 $X_1$ 大于 $c_1$ 的案例；将 ⬤ 分配给 $X_1$ 小于 $c_1$ 并且 $X_2$ 大于 $c_2$ 的案例；将 ▲ 分配给 $X_1$ 小于 $c_1$ 并且 $X_2$ 小于 $c_2$ 的案例。

当讨论树的先验时，将其抽象定义为两个集合构成的元组 $g(\mathcal{T}, \mathcal{M})$ 非常有用。

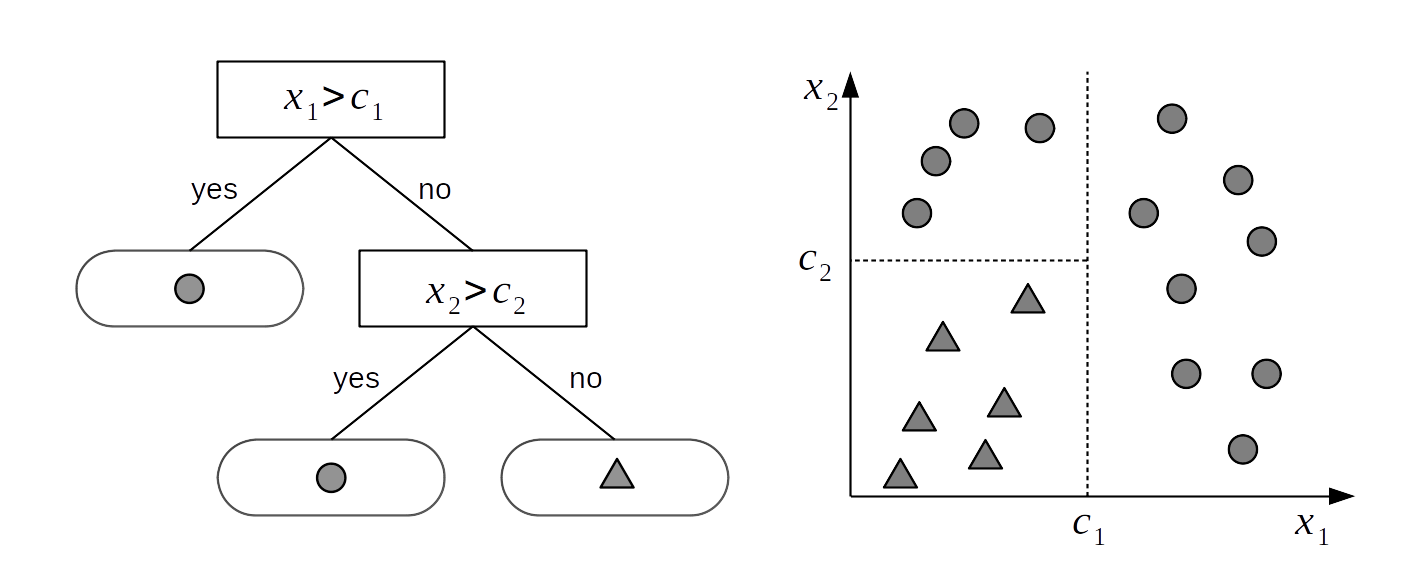
Fig. 119 二叉树（左）和相应的空间分区（右）。树的内部节点是那些有子节点的节点，它们有一个到下面节点的连接，内部节点具有与之相关联的划分规则。叶子节点是没有子节点的节点，它们包含要返回的值，在本例中取值为 ⬤ 或 ▲ 。决策树将样本空间划分为被垂直于轴的分割线分割的子空间块。这意味着样本空间的每次分割都将与某个预测变量轴对齐。¶

虽然 Fig. 119 展示了如何将决策树用于分类，其中 $\mathcal{M}_j$ 包含类或标签值，但其也可以用于回归。不过，回归时不是将叶子节点与类标签相关联，而是与实数相关联。例如某个子空间块内数据点的均值。

Fig. 120 显示了只有一个预测变量的回归问题。左边有一棵类似于 Fig. 119 的二叉树，主要区别在于 Fig. 120 中每个叶子节点返回一个实数值。将该树与右侧近似正弦波的数据做比较，注意回归树并没有采用连续函数来做近似，而是将数据划分成了三个块，并且估计了每个块的均值。

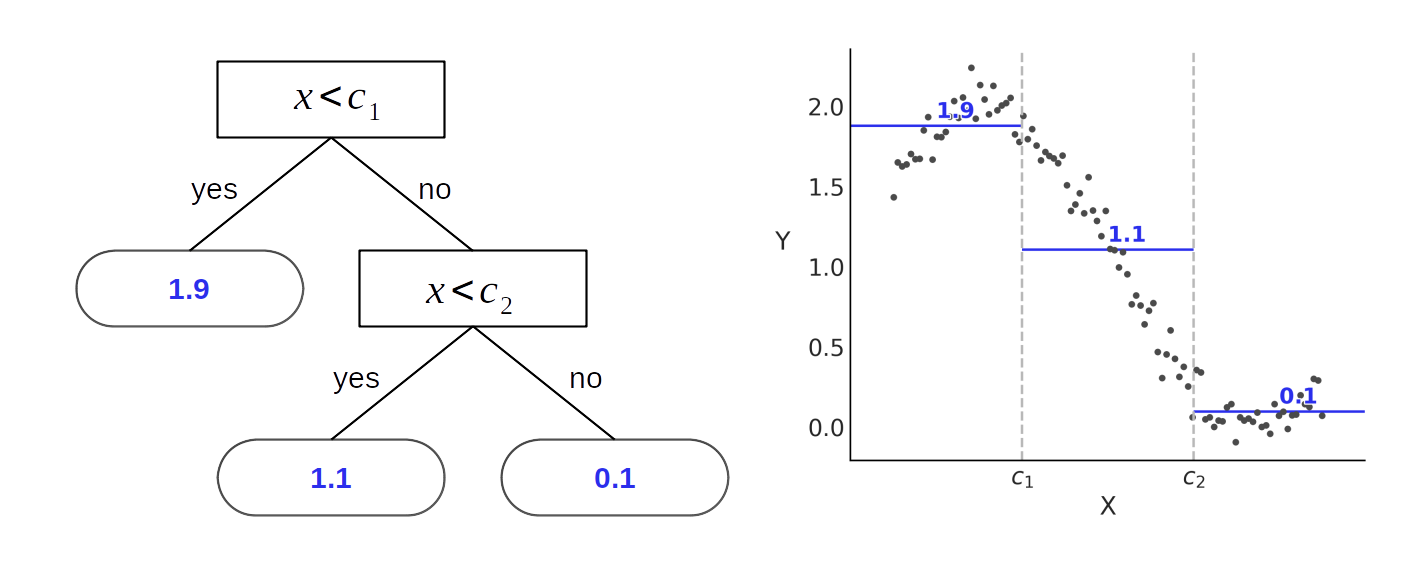
Fig. 120 二叉树（左）和相应的空间划分（右）。树的内部节点是那些有子节点的节点，内部节点有与之相关联的划分规则。叶子节点是那些没有子节点的节点，包含要返回的值（在本例中为 $1.1$、$1.9$ 和 $0.1$ ）。图中可以明显看出：树是表示分段函数的一种方式。¶

回归树不限于返回块内数据点的均值，还有其他选择。例如，可以将叶子节点与中值关联，或者与块内数据点的线性回归拟合关联，甚至与更复杂的函数关联。不过均值可能是回归树中最常见的选择之一。

需要特别注意：回归树的输出不是平滑函数，而是分段阶梯函数，但这并不意味着回归树不能用于拟合平滑函数。因为理论上，可以用阶梯函数逼近任何连续函数，而且在实践中这种逼近足够好。

决策树的一个吸引人的特性是其可解释性，你可以从字面上阅读决策树，并按照解决某个问题所需的步骤进行操作。因此，你可以清晰地了解该方法在做什么，为什么它会以这种方式执行，为什么某些类可能无法正确分类，或者为什么某些数据的近似度很差。此外，用简单术语向非技术型的观众解释结果也更为容易。

不幸的是，决策树的灵活性意味着它们很容易过拟合，因为你总能找到一个足够复杂的树，使得每个数据点都对应一个分区。关于过于复杂的分类解决方案，请参见 Fig. 121。拿来一张纸，绘制几个数据点，然后为每个数据点创建一个单独划分出来的分区，你可以很容易看到这种过拟合。在进行此练习时，你可能还会注意到，实际上有不止一棵树可以拟合该数据。

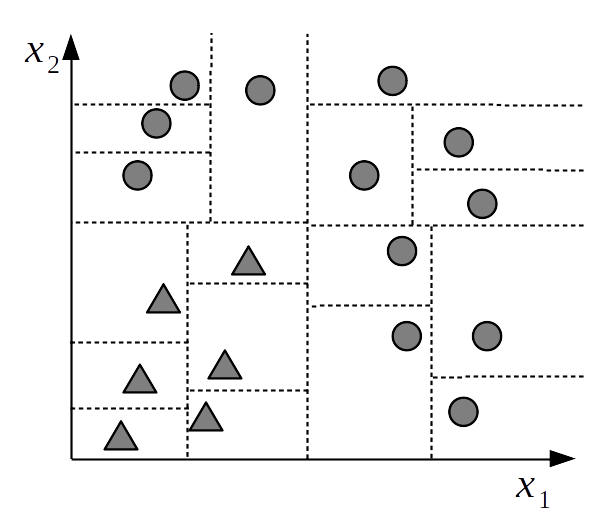
../_images/decision_tree_overfitting.png

Fig. 121 过于复杂的样本空间分区。每个数据点都分配了一个单独的块。之所以称之为过于复杂的分区，是因为我们完全可以使用更简单的分区方案（如 Fig. 119 中的分区），以相同的准确度来解释和预测数据。简单的分区方案比复杂方案更有可能泛化，更有可能预测和解释新数据。¶

当从主效应和交互作用的角度来考虑决策树时，就会出现一个树的有趣特性。注意 $\mathbb{E}(Y \mid \boldsymbol{X})$ 项等于所有叶子节点参数 $\mu_{ij}$ 的和，因此：

当一棵树仅依赖于某个单一变量时（如 Fig. 120 ），树中每个叶子节点的 $\mu_{ij}$ 就代表了一个主效应；
当一棵树依赖多个变量时（如 Fig. 119 ），树中叶子节点的 $\mu_{ij}$ 就代表了一种交互效应。例如，返回三角形需要 $X_1$ 和 $X_2$ 的交互，因为子节点的条件 ( $X_2 > c_2$ ) 基于父节点的条件 ( $X_1 > c_1$ ) 。

由于树的大小可变，因此可以用树来模拟不同阶的交互效果。随着树变得更深，更多变量进入树的机会增加，然后表示更高阶交互的潜力也在增加。此外，由于我们会使用树的集成方法，所以几乎可以构造主效果和交互效果的任意组合，详情见下一节。

7.1.2 决策树的集成¶

考虑到过于复杂的树可能会由于过拟合而不太擅长预测新数据，因此通常会引入一些工具来降低决策树的复杂性，并获得更能适应数据复杂性的拟合。其中一种解决方案依赖于拟合一组决策树，其中每棵树都被正则化为浅层树，因此，每棵树单独只能解释一小部分数据。只有通过组合许多这样的树，我们才能提供正确的答案。

贝叶斯加性回归树 等贝叶斯方法和 随机森林 等非贝叶斯方法都遵循此集成策略。一般来说，集成模型可以降低泛化误差，同时保持拟合给定数据集的足够灵活的能力。

使用集成方法也有助于减轻阶跃性，因为输出是树的组合，虽然它仍然是一个阶跃函数，但它是一个具有更多阶跃的函数，因此在某种程度上是更平滑的近似。只要我们确保树足够多样化，这就能成为事实。

使用树集成的缺点是失去了单个决策树的可解释性。现在要获得一个答案，我们不只是遵循一棵树，而是遵循许多树，这会混淆任何简单的解释。或者换句话说，我们用可解释性换取了灵活性和泛化能力。

7.2 贝叶斯加性回归树（ BART ）¶

如果假设公式 (43) 中的 $B_i$ 样条函数是决策树，则我们可以这样写：

(71)¶\[\mathbb{E}[Y] = \phi \left(\sum_{j=0}^m g_j(\boldsymbol{X}; \mathcal{T}_j, \mathcal{M}_j), \theta \right)\]

式中每个 $g_j$ 都是形式为 $g(\boldsymbol{X}; \mathcal{T}_j, \mathcal{M}_j)$ 的决策树，其中 $\mathcal{T}_j$ 表示二叉树，即所有内部节点及其相关决策规则和叶子节点一起构成的集合。而 $\mathcal{M}_j = \{\mu_{1,j}, \mu_{2,j}, \cdots, \mu_{b, j} \}$ 表示叶子节点 $b_j$ 的值，$\phi$ 是作为模型似然的任意概率分布，$\phi$ 中的 $\theta$ 表示未被建模为决策树之和的其他参数。

我们可以将 $\phi$ 设置为高斯，然后有：

\[Y = \mathcal{N}\left(\mu = \sum_{j=0}^m g_j(\boldsymbol{X}; \mathcal{T}_j, \mathcal{M}_j), \sigma \right)\]

或者我们可以像尝试其他分布。例如，如果 $\phi$ 是泊松分布，可以得到：

\[Y = \text{Pois}\left(\lambda = \sum_{j}^m g_j(\boldsymbol{X}; \mathcal{T}_j, \mathcal{M}_j)\right)\]

或者 $\phi$ 是学生 $t$ 分布，那么：

\[Y = \text{T}\left(\mu = \sum_{j}^m g_j(\boldsymbol{X}; \mathcal{T}_j, \mathcal{M}_j), \sigma, \nu \right)\]

像往常一样，要完全指定贝叶斯加性回归树模型，必须选择先验。我们已经熟悉高斯似然 $\sigma$ 参数的先验指定，或者学生 $t$ 似然的 $\sigma$ 和 $\nu$ 参数的先验指定，因此现在重点关注那些特定于贝叶斯加性回归树模型的先验。

7.3 贝叶斯加性回归树的先验¶

原始的贝叶斯加性回归树论文 [71]，以及大多数后续改进和实现都依赖于共轭先验。

PYMC3 中的贝叶斯加性回归树实现并未使用共轭先验，并且在其他方面也存在差异。本节中将专注于 PYMC3 实现，并将其用于我们的示例。

7.3.1 先验的独立性¶

为了简化先验的指定，我们假设树结构 $\mathcal{T}_j$ 和叶子节点值 $\mathcal{M}_j$ 是独立的。此外，这些先验独立于其他参数，即方程 (71) 中的 $\theta$。通过独立性假设，我们可以将先验的指定分成几部分。否则，我们需要发明一种方法来为整个树空间指定一个先验 2。

7.3.2 树结构 $\mathcal{T}_j$ 的先验¶

树结构 $\mathcal{T}_j$ 的先验由三个方面指定：

深度为 $d=(0, 1, 2, \dots)$ 的节点是非叶子结点的概率，由 $\alpha^{d}$ 给出。 $\alpha$ 建议为 $\in [0, 0.5)$ [72] 3。
切分变量的分布。也就是树中包含哪些预测变量（即 Fig. 119 中的 $X_i$ ）。最常见的是所有可用预测变量上的均匀分布。
切分规则的分布。也就是，一旦选择了一个切分用的预测变量，我们使用什么值做出决策（即 Fig. 119 中的 $c_i$ ）。这通常是可用值上的均匀分布。

7.3.3 叶子结点值 $\mu_{ij}$ 和树数量 $m$ 的先验¶

默认情况下，PYMC3 不会为叶子节点的值设置先验，而是在采样算法的每次迭代中返回残差的均值。

集成方法中决策树的数量 $m$ 通常也是用户预定义的。实践表明，设置 $m=200$ 甚至低至 $m=10$ 的值都能获得良好的结果。此外，推断对于 $m$ 的确切值来说可能非常稳健。因此，一般的经验法则是多尝试一些 $m$ 值，并执行交叉验证以选择最适合特定问题的值 4。

7.4 拟合贝叶斯加性回归树¶

到目前为止，我们讨论了如何使用决策树来编码分段函数，我们可以使用这些函数来建模回归或分类问题。我们还讨论了如何为决策树指定先验。现在我们将讨论如何有效地对树进行采样，以便找到给定数据集的树的后验分布。有很多策略可以实现这一点，而且细节对于本书来说过于具体。鉴于此，我们将只描述主要要素。

为了拟合贝叶斯加性回归树模型，我们不能使用类似 Hamiltonian Monte Carlo 的基于梯度的采样器，因为树空间是离散的，对梯度并不友好。出于此原因，研究人员开发了为树量身定制的 MCMC 和序贯蒙特卡洛 (SMC) 变体。 PYMC3 中实现的贝叶斯加性回归树采样器以顺序和迭代方式工作。简而言之，从一棵树开始并将其拟合到结果变量 $Y$ ，残差 $R$ 计算为 $R = Y - g_0(\boldsymbol{X}; \mathcal{T}_0, \mathcalf{M}_0)$ 。第二棵树拟合到 $R$，而不是$Y$。然后考虑目前为止已经拟合的所有树并更新残差 $R$， $R - g_1(\boldsymbol{X}; \mathcal{T}_0, \mathcal{M}_0) + g_0( \boldsymbol{X}; \mathcal{T}_1, \mathcal{M}_1)$ 。一直这样做，直到拟合了 $m$ 棵树。

此过程将产生后验分布的一个样本，一个拥有 $m$ 棵树的样本。第一次迭代很容易导致次优树，主要原因是：第一次拟合的树会比必要的更为复杂，并且可能会陷入局部最小值，最终，后面树的拟合会受到以前树的影响。当继续采样时，所有这些影响将趋于消失，因为采样方法会多次重复访问以前拟合过的树，并让它们有机会重新适应更新后的残差。事实上，在拟合贝叶斯加性回归树模型时，一个常见的观测结果是，第一轮中的树往往更深，然后它们会逐步塌陷成较浅的树。

在文献中，特定的贝叶斯加性回归树通常是为特定采样器量身定制的，因为它们依赖于共轭性。正因为如此，具有高斯似然的贝叶斯加性回归树与具有泊松似然的贝叶斯加性回归树不同。 PYMC3 使用了一个基于粒子 Gibbs 采样器 [73] 的采样器，该采样器专门用于处理树。 PYMC3 会自动将此采样器分配给 pm.BART 分布；如果模型中还存在其他随机变量，PyMC3 会为这些变量分配其他采样器（如 NUTS）。

7.5 示例：自行车数据的贝叶斯加性回归树¶

让我们看看贝叶斯加性回归树如何拟合之前在第 5 章中研究过的自行车数据集。该模型将是：

\[\begin{split}\begin{aligned} \begin{split} \mu \sim& \; \text{BART}(m=50) \\ \sigma \sim& \; \mathcal{HN}(1) \\ Y \sim& \; \mathcal{N}(\mu, \sigma) \end{split} \end{aligned}\end{split}\]

在 PYMC3 中构建贝叶斯加性回归树模型与构建其他类型的模型非常相似，不同之处在于为随机变量指定 pm.BART时，既需要知道预测变量，也需要知道结果变量。主要原因在于：用于拟合贝叶斯加性回归树模型的采样方法在残差方面提出了一个新树，如前节所述。

在做了所有这些澄清之后，PyMC3 中的模型如下所示：

Listing 102 bart_model_gauss¶

with pm.Model() as bart_g:
    σ = pm.HalfNormal("σ", Y.std())
    μ = pm.BART("μ", X, Y, m=50)
    y = pm.Normal("y", μ, σ, observed=Y)
    idata_bart_g = pm.sample(2000, return_inferencedata=True)

在展示拟合模型的最终结果之前，我们将稍微探索一下中间步骤。这会使我们更直观地了解贝叶斯加性回归树的工作原理。

Fig. 122 显示了从代码 bart_model_gauss 中模型计算的后验采样的树。在顶部，有 m=50 棵树中的三棵单独的树。树返回的实际值是实心点，线条是连接它们的辅助线。数据范围（每小时租用的自行车数量）大约在每小时租用 $0-800$ 辆自行车的范围内。因此，即便这些图省略了数据，我们也可以看到拟合相当粗糙，并且这些分段函数在数据的尺度上大多是平坦的。这符合对树是 弱学习者 的预期。鉴于我们使用了高斯似然，负计数值在模型中是被允许的。

在底部子图上，有来自后验的样本，每个样本都是 $m$ 棵树的和。

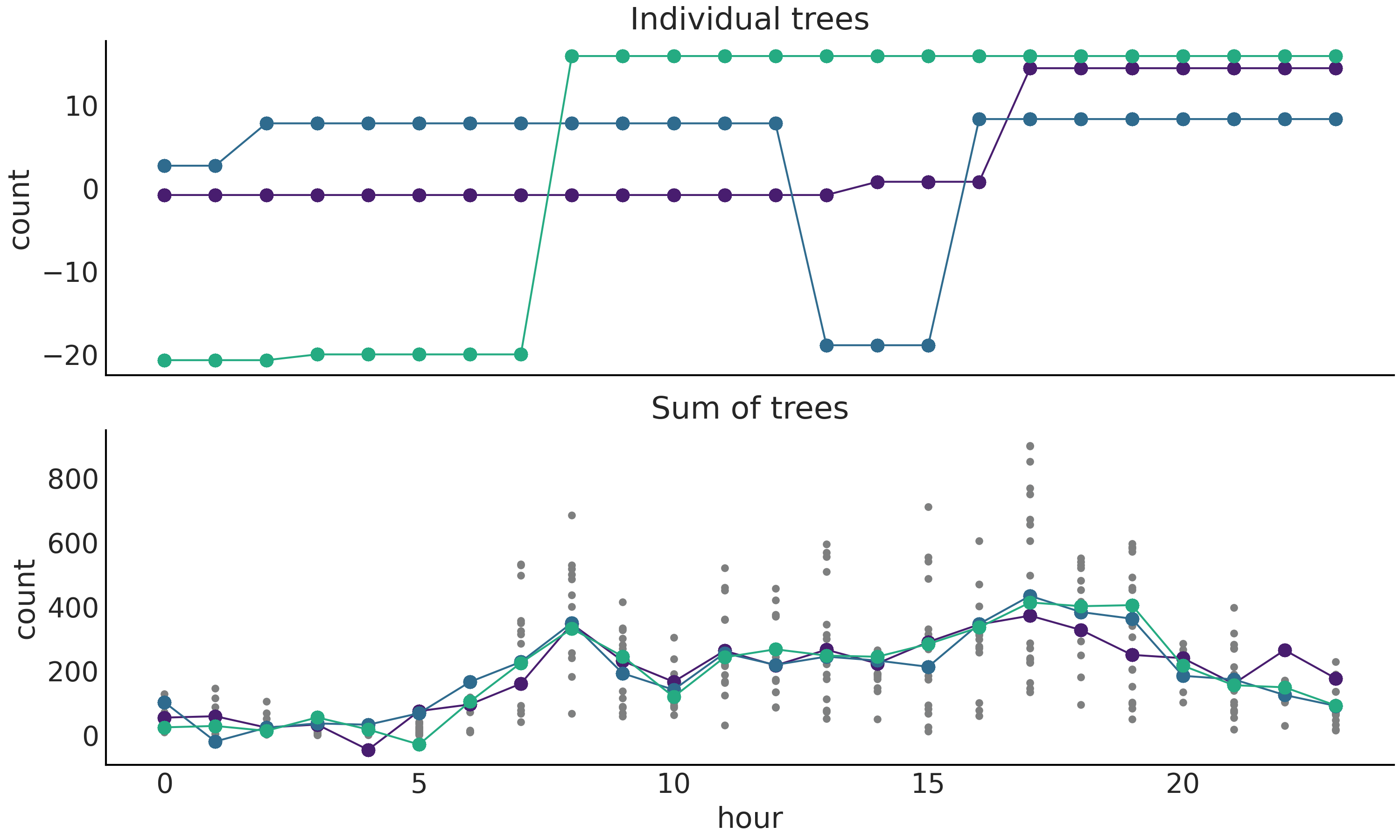
Fig. 122 后验树实现。顶部图为从后验中抽取的三棵树。底部图为三个后验样本，每个样本都是 $m$ 棵树的和。实际贝叶斯加性回归树的采样值由圆圈表示，虚线起视觉辅助作用。小圆点（仅在底部图中）表示观测到的自行车租用数量。¶

Fig. 123 显示了将贝叶斯加性回归树拟合到自行车数据集的结果（租用自行车的数量与一天中的小时数）。与使用样条线创建的 Fig. 93 相比，该图提供了类似的拟合。与使用样条曲线获得的拟合相比，贝叶斯加性回归树的拟合锯齿状特征更明显，差异更明显。这并不是说没有其他差异，例如 HDI 的宽度。

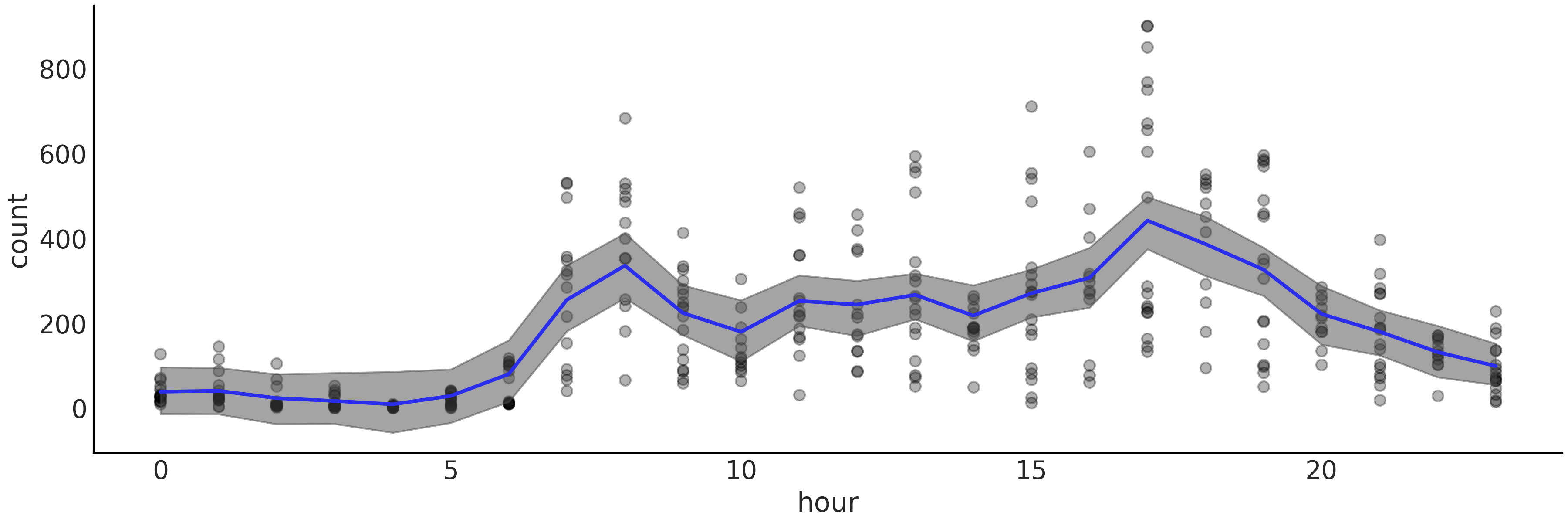
Fig. 123 使用 BART（特别是 bart_model ）拟合的自行车数据（黑点）。带阴影的曲线代表均值参数的 $94\%$ HDI 区间，蓝色曲线代表均值的趋势。与 Fig. 93 进行比较。¶

围绕贝叶斯加性回归树的文献倾向于强调其通常无需调整即可提供有竞争力的答案 5。例如，与拟合样条曲线相比，我们无需担心手动设置连接点或选择先验来调整连接点。当然，也有人可能会争辩说，对于某些问题，能够调整连接点对问题或许是有益的。

7.6 广义贝叶斯加性回归树¶

贝叶斯加性回归树的 PYMC3 实现试图让似然的调整变得更简单 6 ，类似于在第 3 章中的广义线性模型。让我们看看如何在贝叶斯加性回归树中使用伯努利似然。对于这个例子，我们将使用太空流感的疾病数据集，该流感主要影响年轻人和老年人，但不影响中年人。幸运的是，太空流感并不严重，因为它已经完全被控制了。在此数据集中，记录了接受太空流感检测的人及检测结果，如确诊 ( $1$ ) 还是健康 ( $0$ ) 、受检者年龄等。使用代码 bart_model_gauss 中具有高斯似然的贝叶斯加性回归树模型作为参考，可以看出伯努利似然模型与之差别不大：

Listing 103 bart_model_bern¶

with pm.Model() as model:
    μ = pm.BART("μ", X, Y, m=50,
                inv_link="logistic")
    y = pm.Bernoulli("y", p=μ, observed=Y)
    trace = pm.sample(2000, return_inferencedata=True)

首先，伯努利分布只有一个参数 p ，因此不再需要定义 $\sigma$ 参数。代码中对贝叶斯加性回归树的定义有一个新参数 inv_link，这是指反向链接函数。我们需要将 $\mu$ 值限制在区间 $[0, 1]$ 内。为此，将反向链接函数设置为逻辑斯谛函数，就像在第 3 章中对逻辑斯谛回归所做的那样。

Fig. 124 显示了代码 bart_model_bern 中的模型采用四种 $m$ 取值时的 LOO 模型比较结果，其中决策树的个数分别为 $m=\{2, 10, 20, 50\}$ 。 Fig. 125 显示了数据、拟合的函数和 $94\%$ HDI 区间。可以看到，根据 LOO ，$m=10$ 和 $m=20$ 提供了更好的拟合。这与目视检查的定性分析一致，因为 $m=2$ 明显欠拟合（ ELPD 值很低，但样本内和样本外 ELPD 之间的差异并不大），而 $m=50$ 似乎过拟合了（ ELPD 的值很低，样本内和样本外 ELPD 之间的差异很大）。

Fig. 124 代码 bart_model_bern 中的模型采用 $m = \{2、10、20、50\}$ 时的 LOO 模型比较。根据 LOO 结果，$m=10$ 时的贝叶斯加性回归树提供了最佳拟合。¶

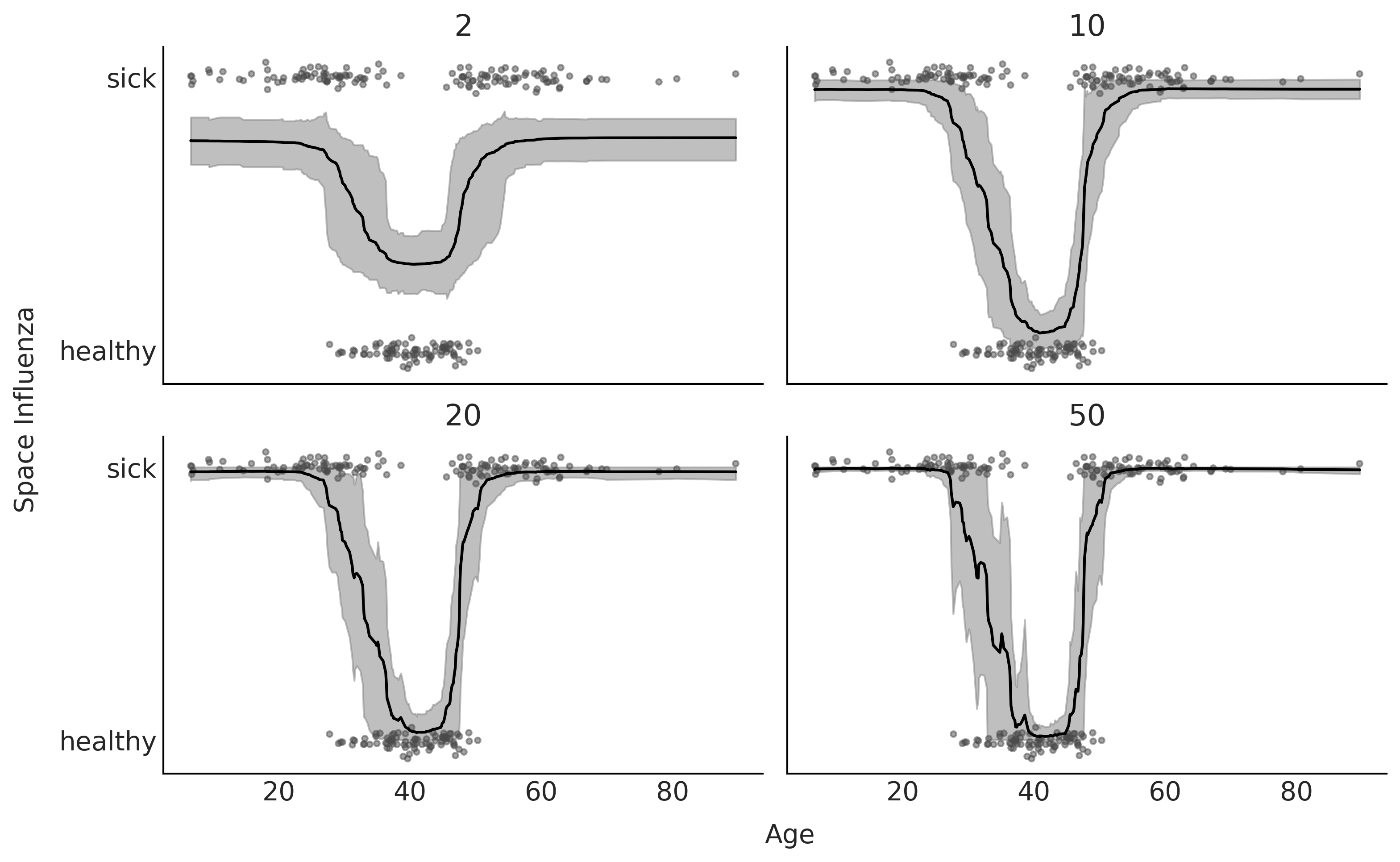
Fig. 125 $m=\{2、10、20、50\}$ 时，根据 Space Influenza 数据集拟合的贝叶斯加性回归树。结果与 LOO 一致， $m=2$ 的模型是欠拟合的，而 $m=50$ 的模型存在过拟合问题。¶

到目前为止，我们已经讨论了具有单个预测变量的回归。但可以使用更多预测变量来拟合数据集。从 PYMC3 的实现角度来看，这很容易，我们只需要传递一个包含超过 $1$ 个预测变量的二维数组 $X$ 即可。不过，多元预测变量带来了一些有趣的统计问题，例如：如何解释具有许多预测变量的贝叶斯加性回归树模型？如何找出每个预测变量对结果的贡献程度？

在接下来的章节中，我们将回答这些问题。

7.7 贝叶斯加性回归树的可解释性¶

单棵决策树通常比较容易解释，但是当将一堆树加在一起时，情况就不同了。有人可能认为，通过添加树我们得到了一些奇怪的、无法识别或难以表征的对象，但事实上树的总和也只是另一棵树。解释这种 组装树 的难点在于：对于复杂的问题，决策规则将很难掌握。这就像在钢琴上弹奏一首曲子，弹奏单个音符相当容易，但以悦耳的方式弹奏组合的音符，在带来丰富的声音同时，也带来了个性化解释的复杂性。

我们仍然可以通过直接检查树的和来获得一些有用信息（参见 7.7 预测变量的选择），但不如使用更简单的单棵树那样透明或有用。因此，为了解释贝叶斯加性回归树模型的结果，我们通常依赖模型诊断工具 [74, 75]，例如一些用于多元线性回归和其他非参数模型的工具。

我们将在下面讨论两个相关工具：部分依赖图（Partial Dependence Plots, PDP）[76] 和 单体条件期望图（ Individual Conditional Expectation Plots, ICEP) [77]。

7.7.1 部分依赖图¶

在贝叶斯加性回归树的文献中，常采用一种被称为部分依赖图 (PDP) 的方法 [76] ，参见 Fig. 126 。部分依赖图：在对其余预测变量的边缘分布求平均的情况下，更改某个预测变量时，结果变量的相应变化。也就是说，部分依赖图计算然后绘制：

(72)¶\[\tilde{Y}_{\boldsymbol{X}_i}= \mathbb{E}_{\boldsymbol{X}_{-i}}[\tilde{Y}(\boldsymbol{X}_i, \boldsymbol{X}_{-i})] \approx \frac{1}{n}\sum_{j=1}^{n} \tilde{Y}(\boldsymbol{X}_i, \boldsymbol{X}_{-ij})\]

其中 $\tilde{Y}_{\boldsymbol{X}_i}$ 是在边缘化 $\boldsymbol{X }_{-i}$ 基础上（即边缘化除 $\boldsymbol{X}_i$ 以外的其他预测变量），关于 $\boldsymbol{X}_i$ 的函数，表示结果变量的值。通常 $X_i$ 会是 $1$ 个或 $2$ 个预测变量构成的子集，因为在更高维度上绘图通常很困难。

如公式 (72) 所示，期望可以通过在（以观测数据 $\boldsymbol{X}_{-i}$ 为条件的）结果变量值上求平均来进行数值近似。但请注意，这意味着 $\boldsymbol{X}_i, \boldsymbol{X}_{-ij}$ 中的某些组合可能与实际观测到的组合并不对应，甚至可能压根儿无法观测到某些组合。这类似于我们在第 3 章中介绍的反事实图。事实上，部分依赖图本身就是一种反事实装置。

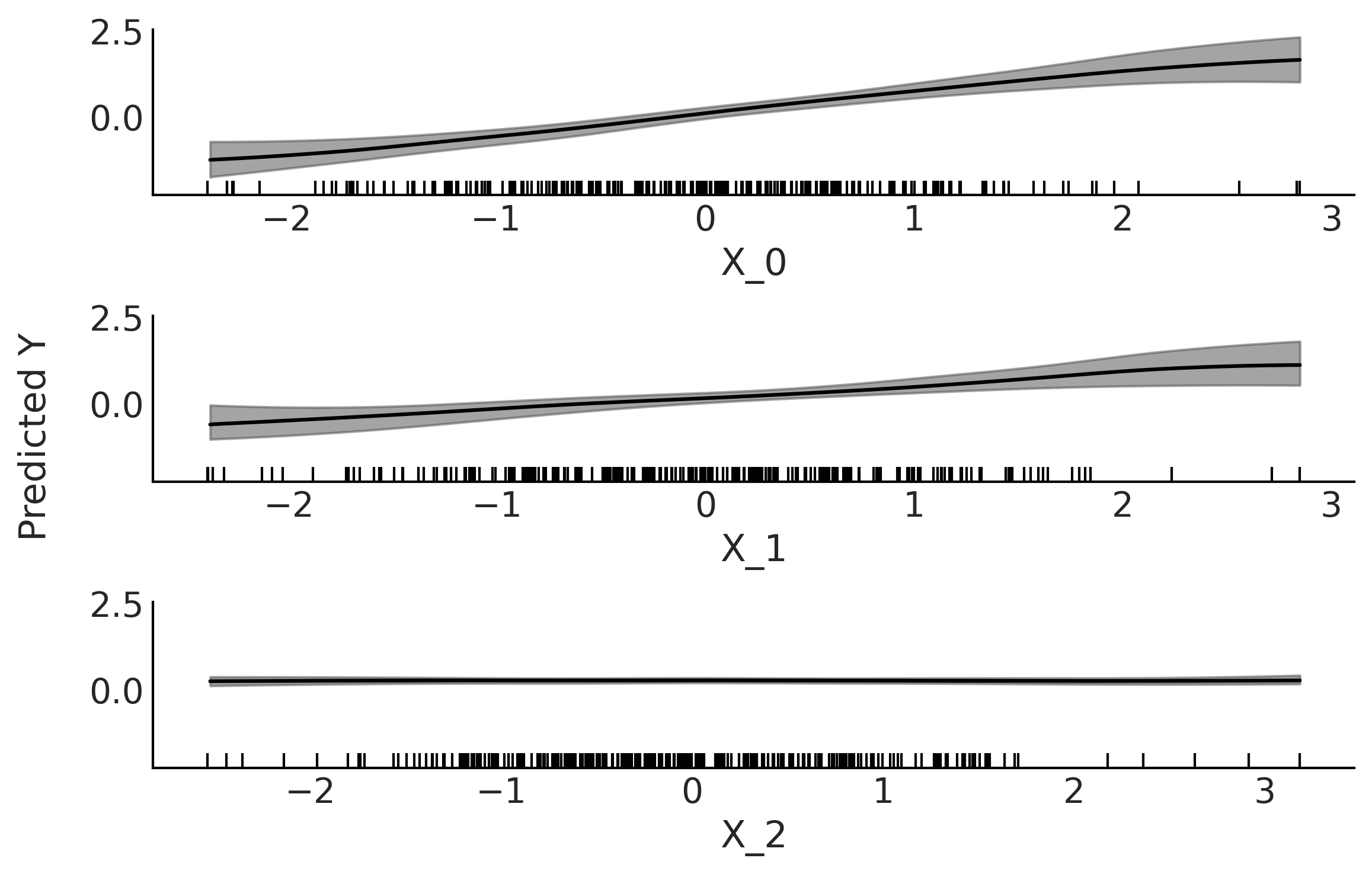
Fig. 126 部分依赖图。在边缘化其余变量 ($X_{-i}$) 的贡献的基础上，变量 $X_i$ 对 $Y$ 的部分贡献。灰色区域代表 HDI $94\%$。均值和 HDI 区域都已做平滑处理（参见 plot_ppd 函数）。底部的垂线表示各预测变量的观测值所在位置。¶

Fig. 126 显示了将贝叶斯加性回归树模型拟合到合成数据后的部分依赖图：$Y \sim \mathcal{N}(0, 1)$ 、 $X_{0} \sim \mathcal{N}(Y, 0.1)$ 和 $X_{1} \sim \mathcal{N}(Y, 0.2)$ 、 $X_{2} \sim \mathcal{N}(0, 1)$。可以看到 $X_{0}$ 和 $X_{1}$ 都与 $Y$ 呈现线性关系，与合成数据的生成过程一致。此外，与 $X_{1}$ 相比，$X_{0}$ 对 $Y$ 的影响更强，因为 $X_{0}$ 的斜率更陡峭。由于预测变量尾部的数据比较稀疏（它们服从高斯分布），因此这部分区域显示出了更高的不确定性，这也符合预期。最终，$X_{2}$ 的贡献在变量 $X_{2}$ 的整个定义区间内几乎可以忽略不计。

现在回到自行车数据集。这次我们使用四个预测变量对自行车的日租用数量（结果变量）进行建模，这四个预测变量分别是：当天的小时、温度、湿度和风速。

Fig. 127 显示了拟合模型后的部分依赖图。可以看到：

小时的部分依赖图看起来与 Fig. 123 非常相似（该图是在没有其他变量的情况下做拟合获得的）。
随着温度的升高，自行车的租用数量也增加了，但在某些点这种趋势趋于平稳。通过专业知识，我们可以推测这种模式大致是合理的，因为温度太低或太高时，人们不太会骑自行车。
湿度呈平缓趋势，随后出现负增长，我们可以再次想象为什么较高的湿度会降低人们骑自行车的意愿。
风速显示出更平坦的贡献，但我们仍然能够看到效果，似乎有意愿在大风条件下租用自行车的人更少。

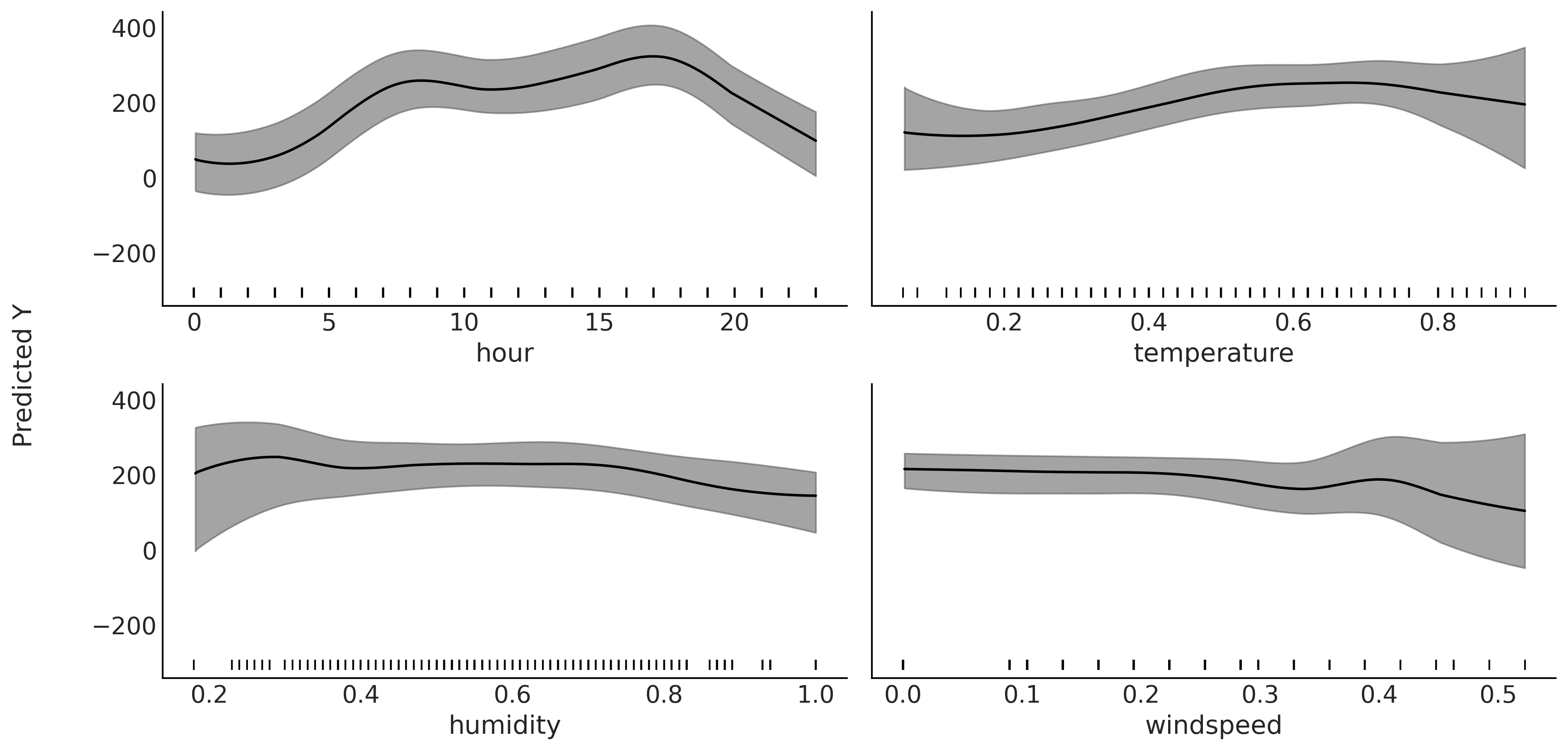
../_images/partial_dependence_plot_bikes.png

Fig. 127 部分依赖图。小时、温度、湿度和风速对自行车日租用数量的部分贡献图（分别边缘化了其余变量 $X_{-i}$ 的贡献）。灰色带状区域代表 HDI $94\%$ 。均值和 HDI 区域均已做平滑处理（请参阅 plot_ppd 函数）。图底部的垂线显示了每个预测变量的观测值位置。¶

计算部分依赖图的一个基本假设是变量 $X_i$ 和 $X_{-i}$ 之间不相关，因此可以基于边缘分布求均值。但在大多数实际问题中，情况并非如此简单，此时部分依赖图可能会隐藏了数据中的某些关系。不过当所选变量子集之间的依赖性不是太强时，部分依赖图还是有用的 [76]。

部分依赖的计算成本

部分依赖图的计算要求很高。因为在变量 $X_i$ 的每一点，我们都需要计算 $n$ 个预测结果（其中 $n$ 是样本量）。

为了使贝叶斯加性回归树能够获得预测 $\tilde Y$ ，我们需要首先对 $m$ 棵树求和，以获得 $Y$ 的点估计，然后还要对树的和的完整后验分布进行平均，以获得可信区间。这个过程需要相当多的计算！减少计算的一种方法是仅在 $p$ 个点处评估 $X_i$ （ $p << n$ ）。我们可以选择 $p$ 个等间距点，也可以选择一些分位数。或者，如果我们不做 $\boldsymbol{X}_{-ij}$ 的边缘化，而是将其固定在均值上，这样可以实现显著的加速。当然，这也意味着信息的丢失，而且均值有时并不能很好地代表分布。还有一个选择是对 $\boldsymbol{X}_{-ij}$ 进行二次采样，这对于大型数据集来说特别有用。

7.7.2 单体条件期望图¶

单体条件期望图与部分依赖图密切相关。不同之处在于，我们不绘制预测变量对结果变量的平均效应，而是绘制 $n$ 条估计出来的条件期望曲线。也就是说，单体条件期望图是一组曲线，其中每条曲线都反映了在固定了 $\boldsymbol{X}_{-ij}$ 的基础上，结果变量作为预测变量 $\boldsymbol{X}_{i}$ 的一个函数。有关示例，参见 Fig. 128 。如果在每个 $\boldsymbol{X}_{ij}$ 值处平均所有灰色曲线，我们可以得到一条蓝色曲线，该曲线与 partial_dependence_plot_bikes 中的部分依赖图相同。

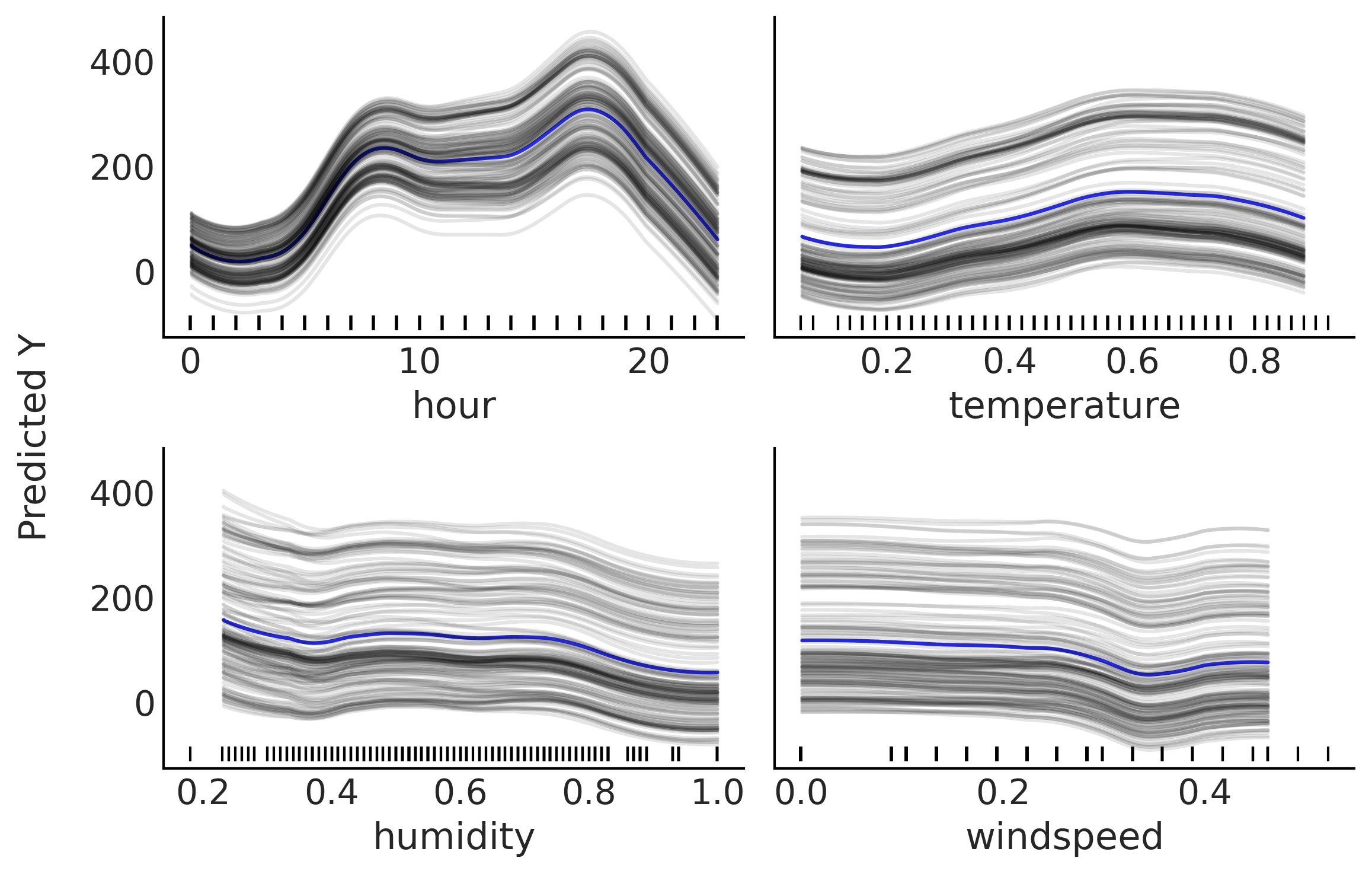
../_images/individual_conditional_expectation_plot_bikes.png

Fig. 128 单体条件期望图。小时、温度、湿度和风速四个预测变量对自行车日租数量的部分贡献，每条曲线均将其余预测变量 ($X_{-i}$) 固定在某个观测值处。蓝色曲线对应于灰色曲线的均值。图中所有曲线都经过了平滑处理（参见 plot_ice 函数）。图底部的垂线显示了每个预测变量的观测值位置。¶

单体条件期望图最适合变量具有强交互作用的场景，当情况并非如此时，部分依赖图和单体条件期望图传达的信息是一致的。 Fig. 129 显示了一个示例，其中部分依赖图隐藏了数据中的关系，但单体条件期望图能够更好地表现它。该图是通过将贝叶斯加性回归树模型拟合到合成数据集上生成的： $Y = 0.2X_0 - 5X_1 + 10X_1 \unicode{x1D7D9}_{X_2 \geq 0} + \epsilon$ ，其中 $X \sim \mathcal{U}( -1, 1)$\epsilon \sim \mathcal{N}(0, 0.5)$ 。注意 $X_1$ 取值依赖于 $X_2$ 的值。

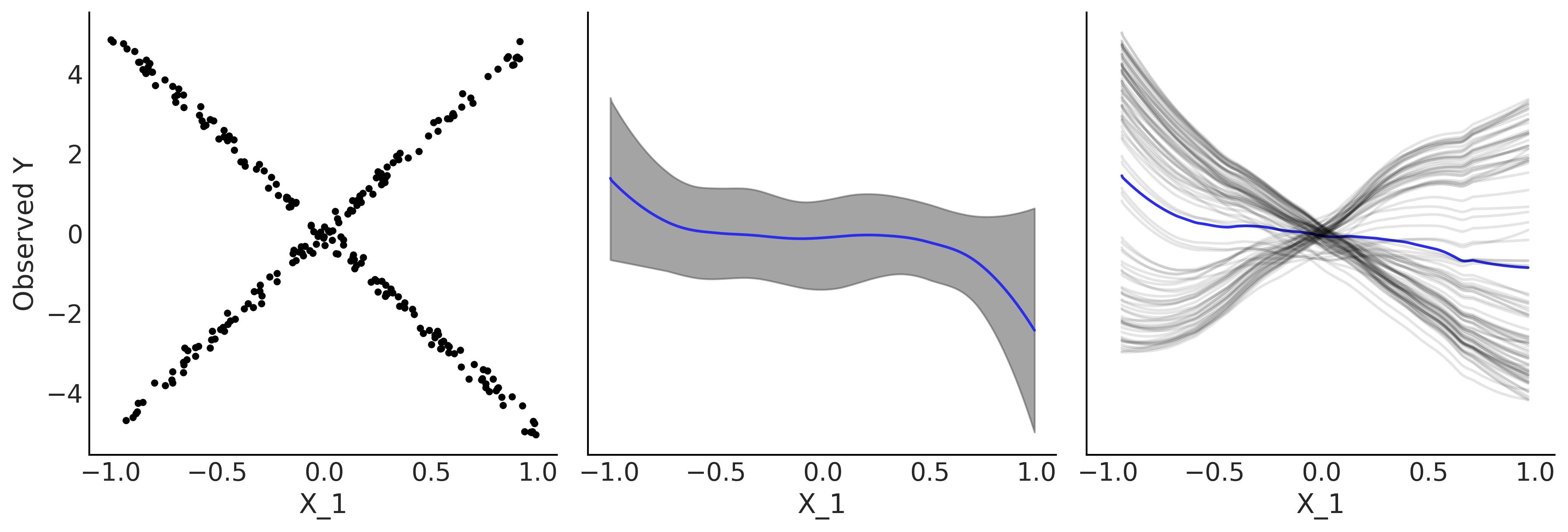
Fig. 129 部分依赖图与单体条件期望图。左图为 $X_1$ 和 $Y$ 之间的散点图，中图为部分依赖图，右图为单体条件期望图。¶

Fig. 129 的左图绘制了 $X_1$ 与 $Y$ 的散点图。考虑到 $X_1,X_2$ 之间存在交互效应， $Y$ 值随 $X_1$ 线性增加或减少的关系依赖于 $X_2$ 的值，该图表现出了 X 形 的模式。中图显示了一个部分依赖图，根据图可以看出关系是平坦的，这在平均时是正确的，但隐藏了交互作用。右图为个体条件期望图，更好地揭示这种关系，因为每条灰色曲线代表了一个 $X_{0,2}$ 的值 7 。图中蓝色曲线是灰色曲线的均值，虽然与部分依赖图不完全相同，但显示了相同的信息 8。

7.7 预测变量的选择¶

当用多个预测变量拟合回归时，了解哪些预测变量更重要通常很有价值。在某些情况下，我们真的有兴趣更好地了解不同变量如何促成了特定输出。例如，哪些饮食和环境因素会导致结肠癌。此外，有时候收集具有许多预测变量的数据集可能代价太大，在经济上无法负担，或需要花费太长时间，又或是在逻辑上过于复杂。例如，在医学研究中，测量来自人类的大量变量是昂贵、耗时或烦人的（甚至对患者来说是有风险的）。因此，我们最好在试点研究中测量很多变量，但在将此类分析扩展到更大人群时，主动减少变量的数量。在这种情况下，我们希望保留最小（最便宜、更方便获得）的变量集，但仍然能够提供合理的预测能力。

贝叶斯加性回归树模型提供了一种非常简单且几乎无需计算的启发式方法来估计变量的重要性，它通过跟踪预测变量被用于切分的次数来判断变量的重要性。例如，在 Fig. 119 中有两个切分节点，一个为变量 $X_1$ 和另一个为 $X_2$ ，因此对于这棵树而言，两个变量同等重要。如果 $X_1$ 为两次和 $X_2$ 为一次。则我们会说 $X_1$ 的重要性是 $X_2$ 的两倍。对于贝叶斯加性回归树模型，变量重要性是通过对 $m$ 棵树和所有后验样本平均来计算的。请注意，这个简单的启发式方法，只能以相对方式报告重要性。

为了进一步简化解释，我们可以报告归一化的值，因此每个值都在区间 $[0, 1]$ 内，总重要性为 $1$ 。很容易将这些数字解释为后验概率，但这只是一个简单的启发式方法，没有强大的理论支撑，用更细致的术语来说，它还没有被很好地理解 [78]。

Fig. 130 显示了已知生成过程的 $3$ 个不同数据集中相对的变量重要性。

$Y \sim \mathcal{N}(0, 1)$ 、 $X_{0} \sim \mathcal{N}(Y, 0.1)$ 、 $X_{1} \sim \mathcal{N}(Y, 0.2)$ 、 $\boldsymbol{X}_{2:9} \sim \mathcal{N}(0, 1)$ 。只有前 $2$ 个输入的变量变量与预测变量无关，而第一个比第二个更相关。
$Y = 10 \sin(\pi X_0 X_1 ) + 20(X_2 - 0.5)^2 + 10X_3 + 5X_4 + \epsilon$ ，其中 $\epsilon \sim \mathcal{N}(0, 1)$ 、 $\boldsymbol{X}_{0:9} \sim \mathcal{U}(0, 1)$ 这通常被称为弗里德曼的五维测试函数 [76]。请注意，虽然前 $5$ 个随机变量（不同程度地）与 $Y$ 相关，但后 $5$ 个则不相关。
$\boldsymbol{X}_{0:9} \sim \mathcal{N}(0, 1)$ 、 $Y \sim \mathcal{N}(0, 1)$ 。所有变量都与结果变量无关。

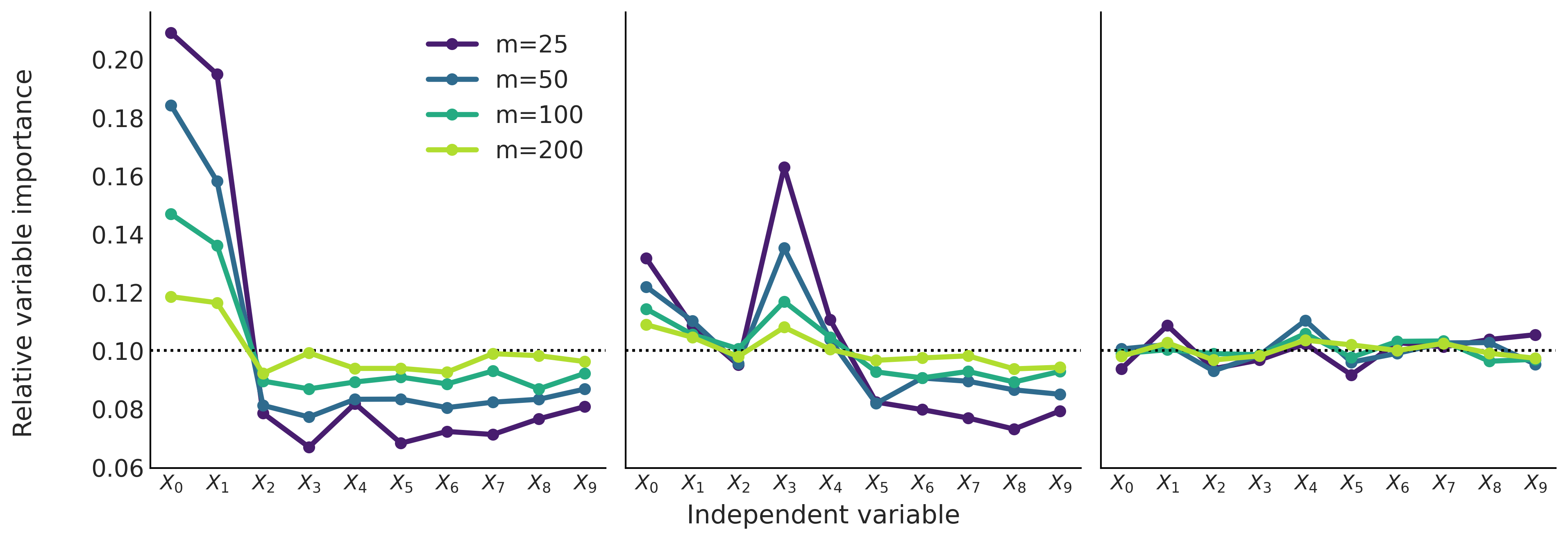
Fig. 130 相对的变量重要性。左图中，前 $2$ 个输入变量对预测变量有贡献，其余是噪声。中图中，前 $5$ 个变量与输出变量有关。右图中，$10$ 个输入的变量与预测变量完全无关。如果所有变量都同等重要，黑色虚线表示变量重要性的值。¶

我们可以从 Fig. 130 中看到增加树的数量 $m$ 的效果。一般来说，随着 $m$ 的增加，相对重要性的分布往往会变得平坦。这是一个众所周知的结果，且具有直观的解释。随着增加 $m$ 的值，我们要求每棵树的预测能力都降低，这意味着不太相关的特征更有可能成为给定树的一部分。相反，如果减少 $m$ 的值，我们对每棵树的要求会更高，这会导致变量之间更严格的竞争也成为树的组成部分，因此只有 真正重要的 变量才会包含在最终的树中。

Fig. 130 之类的图可用于帮助将更重要的变量与不太重要的变量分开 [71, 79]。我们可以查看 $m$ 从低值转移到高值的过程中会发生什么。如果相对重要性降低，则变量 更重要 ，如果变量重要性增加，则变量 不那么重要 。例如，在第一个图中，很明显对于不同的 $m$ 值，前两个变量比其他变量重要得多。对于前 $5$ 个变量，可以从第二个子图得出类似的结论。在最后一个子图上，所有变量都同样（不）重要。

这种评估变量重要性的方法可能很有用，但也很棘手。在某些情况下，为变量重要性设置信念区间会有所帮助，而不仅仅是点估计。我们可以通过使用相同的参数和数据多次运行贝叶斯加性回归树来实现这一点。然而，缺乏将重要变量与不重要变量分开的明确阈值，可能被视为问题。目前已经提出了一些替代方法 [79, 80]。其中一种方法可以总结如下：

使用较小的 $m$ 值（例如 $25$ ）多次拟合模型（大约 $50$ 次），记录均方根误差 9 。
剔除所有 $50$ 次运行中信息最少的变量。
重复 $1$ 和 $2$ ，每次在模型中剔除一个变量。一旦达到模型中指定数量的预测变量（不一定是 $1$ ），就停止迭代。
最后，选择平均均方根误差最小的模型。

但根据 Carlson [79] 的说法，此过程似乎总是返回与创建像 Fig. 130 图相同的结果。人们可以争辩说这是更自动的方法（具有自动决策的所有优点和缺点），没有什么理由能阻止我们运行自动化程序，并将其绘图结果用于可视化检查。

让我们转向具有小时、温度、湿度和风速四个预测变量的自行车租赁示例。从 Fig. 131 中，我们可以看到小时和温度与自行车租用数量之间的预测关系，比湿度或风速更相关。我们还可以看到，变量重要性的顺序与部分依赖图（ Fig. 127 ）和单体条件期望图（ Fig. 128 ）的结果一致。

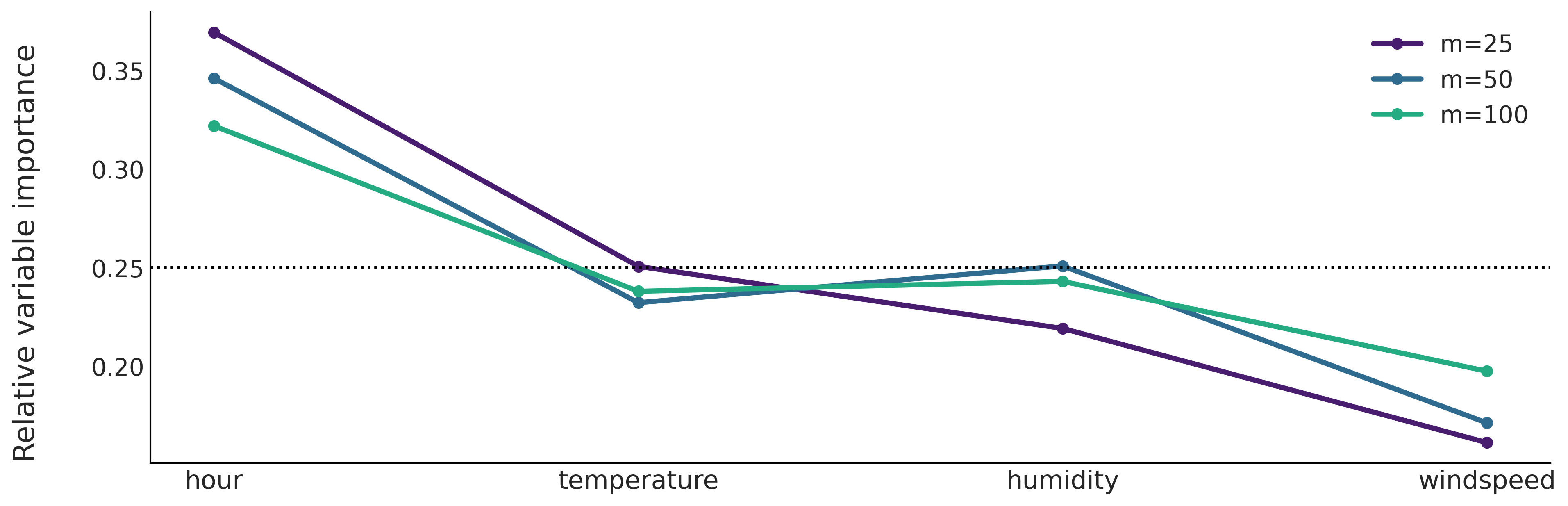
Fig. 131 具有不同树数量的贝叶斯加性回归树拟合后的相对变量重要性。小时是最重要的预测变量，其次是温度。湿度和风速似乎是不太相关的预测变量。¶

7.8 PYMC3 中的先验选择¶

与本书中的其他模型相比，BART 是最“黑盒”的。我们无法设置想要生成贝叶斯加性回归树模型的任何先验。相反，我们需要通过一些参数来控制预定义的先验。 PYMC3 允许使用 $3$ 个参数来控制贝叶斯加性回归树的先验：

树的数量 $m$
树的深度 $\alpha$
切分变量的分布

我们已经看到了改变树数量的效果，这被证明可以为 $50-200$ 区间内的值提供可靠的预测。还有很多例子表明使用交叉验证来确定这个数字可能是有益的。我们还可以看到，通过扫描 $m$ 来寻找相对较低的值，例如 $25-100$ 范围内的值，能够评估变量的重要性。我们没有费心去改变 $\alpha=0.25$ 的默认值，因为此调整似乎影响更小，尽管仍然需要研究来更好地理解这个先验 [72]。与 $m$ 一样，交叉验证也可用于调整它以提高效率。最后，PYMC3 提供了传递权重向量的选项，因此不同变量具有不同的被选中先验概率，当用户有证据表明某些变量可能比其他变量更重要时，这很有用，否则最好保持均匀分布。已经提出了更复杂的基于 Dirichlet 的先验来实现这一目标，并在需要归纳稀疏性时允许更好的推断 10 。这在我们有很多预测变量，但只有少数可能有贡献，且事先不知道哪些最相关的场景中非常有用。这种情况比较常见，例如，在基因研究中，测量数百或更多基因的活性相对容易，但它们之间的关系不仅未知，而且是科学家研究的目标。

大多数贝叶斯加性回归树的实现都是在单个软件包场景中完成的，在某些情况下甚至面向特定的子学科。它们通常不是概率编程语言的一部分，因此不希望用户过多地调整贝叶斯加性回归树模型。因此，即使可以直接为 $m$ 设置先验，在实践中通常也不建议这样做。相反，贝叶斯加性回归树相关的文献鼓励在默认参数下的良好性能，同时认识到可以使用交叉验证来获得额外的收益。 PYMC3 中的贝叶斯加性回归树实现稍微偏离了这一传统，允许了一些额外的灵活性，但与高斯、泊松分布，甚至像高斯过程这样的非参数分布相比，这种灵活性仍然非常有限。预计会很快出现更灵活的贝叶斯加性回归树的软件实现，以允许用户构建灵活和针对问题的模型。

习题¶

7E1. Explain each of the following

How is BART different from linear regression and splines.
When you may want to use linear regression over BART?
When you may want to use splines over BART?

7E2. Draw at least two more trees that could be used to explain the data in Fig. 119.

7E3. Draw a tree with one more internal node than the one in Fig. 119 that explains the data equally well.

7E4. Draw a decision tree of what you decide to wear each morning. Label the leaf nodes and the root nodes.

7E5. What are the priors required for BART? Explain what is the role of priors for BART models and how is this similar and how is this different from the role of priors in the models we have discussed in previous chapters.

7E6. In your own words explain why it can be the case that multiple small trees can fit patterns better than one single large tree. What is the difference in the two approaches? What are the tradeoffs?

7E7. Below we provide some data. To each data fit a BART model with m=50. Plot the fit, including the data. Describe the fit.

x = np.linspace(-1, 1., 200) and y = np.random.normal(2*x, 0.25)
x = np.linspace(-1, 1., 200) and y = np.random.normal(x**2, 0.25)
pick a function you like
compare the results with the exercise 5E4. from Chapter 5

7E8. Compute the PDPs For the dataset used to generate Fig. 130. Compare the information you get from the variable importance measure and the PDPs.

7M9. For the rental bike example we use a Gaussian as likelihood, this can be seen as a reasonable approximation when the number of counts is large, but still brings some problems, like predicting negative number of rented bikes (for example, at night when the observed number of rented bikes is close to zero). To fix this issue and improve our models we can try with other likelihoods:

use a Poisson likelihood (hint you will need to use an inverse link function, check pm.Bart docstring). How the fit differs from the example in the book. Is this a better fit? In what sense?
use a NegativeBinomial likelihood, how the fit differs from the previous two? Could you explain the result.
how this result is different from the one in Chapter 5? Could you explain the difference?

7M10. Use BART to redo the first penguin classification examples we performed in Section 3.4.2 结果变量为类别变量时 — 分类模型 (i.e. use “bill_length_mm” as covariate and the species “Adelie” and “Chistrap” as the response). Try different values of m like, 4, 10, 20 and 50 and pick a suitable value as we did in the book. Visually compare the results with the fit in Fig. 50. Which model do you think performs the best?

7M11. Use BART to redo the penguin classification we performed in Section 3.4.2 结果变量为类别变量时 — 分类模型. Set m=50 and use the covariates “bill_length_mm”, “bill_depth_mm”, “flipper_length_mm” and “body_mass_g”.

Use Partial Dependence Plots and Individual Conditional Expectation. To find out how the different covariates contribute the probability of identifying “Adelie”, and “Chinstrap” species.

Refit the model but this time using only 3 covariates “bill_depth_m”, “flipper_length_mm”, and “body_mass_g”. How results differ from using the four covariates? Justify.

7M12. Use BART to redo the penguin classification we performed in Section 3.4.2 结果变量为类别变量时 — 分类模型. Build a model with the covariates “bill_length_mm”, “bill_depth_mm”, “flipper_length_mm”, and “body_mass_g” and assess their relative variable importance. Compare the results with the PDPs from the previous exercise.

参考文献¶

1: Maybe you have heard about its non-Bayesian cousin: Random Forest [81]
2: for alternatives see [82, 83]
3: Node depth is defined as distance from the root. Thus, the root itself has depth 0, its first child node has depth 1, etc.
4: In principle we can go fully Bayesian and estimate the number of tree $m$ from the data, but there are reports showing this is not always the best approach. More research is likely needed in this area.
5: The same literature generally shows that using cross-validation to tune the number of trees and/or the prior over the depth of the tree can be further beneficial.
6: Other implementations are less flexible or require adjustments under the hood to make this work.
7: This notation means the variables ($X_0$, $X_2$), that is, excluding $X_1$
8: The mean of the ICE curves and the mean partial dependence curve are slightly different. This is due to internal details on how these plots were made including the order in which we average over the posterior samples or over the observations. What really matter is the general features, for instance in this case that both curves are essentially flat. Also, to speed up computation we evaluate $X_1$ over 10 equally separated points for partial dependence plots and we subsample $X_{0,2}$ for computing the individual conditional expectation plot
9: The original proposal suggests 10, but our experience with the BART implementation in PyMC3 is that values of $m$ below 20 or 25 could be problematic.
10: This is likely to be added in the future versions of PyMC3.

Bayesian Modeling and Computation in Python

第七章：贝叶斯加性回归树

Contents