repository open issue

Contents

第四章：扩展线性模型

在 第 3 章 中，我们展示了扩展线性回归的几种方法。但其实还可以用线性模型做更多的事情，从“对预测变量做变换”，到“支持可变的方差”，再到 “分层模型”。这些想法为为更广泛地使用线性回归提供了灵活性。

4.1 转换预测变量

在 第 3 章 中，通过最简单的线性模型和恒等链接函数，在任意 \(X_i\) 的取值处，\(x_i\) 的一个单位变化导致结果变量 \(Y\) 的 \(\beta_i\) 个单位的预期变化。然后，我们学习了如何通过改变似然函数（ 例如从高斯到伯努利 ）来创建广义线性模型，这通常需要改变链接函数。

本节介绍对简单线性模型的另一种改进方法，即对预测变量 \(\mathbf{X}\) 进行变换，使 \(\mathbf{X}\) 和 \(Y\) 之间产生一种非线性关系，进而为更复杂的情况建模。

例如，我们可以假设 \(x_i\) 平方根的单位变化（或者 \(x_i\) 对数的单位变化等），会导致结果变量 \(Y\) 中 \(\beta_i\) 个单位的预期变化。在数学形式上，可以通过对任一预测变量 \((X_i)\) 实施变换 \(f(.)\) ，来扩展方程 (25) ：

(31)\[\begin{split}\begin{split} \mu =& \beta_0 + \beta_1 f_1(X_1) + \dots + \beta_m f_m(X_m) \\ Y \sim& \mathcal{N}(\mu, \sigma) \end{split}\end{split}\]

实际上之前的示例都存在 \(f(.)\) ，只不过由于它表现为恒等函数而被习惯性省略了。另外，在前面示例中，我们曾经对预测变量做过中心化处理，以使系数更易于解释。本质上来说，中心化处理就是一种对预测变量的变换，只是更一般性地，\(f(.)\) 可以是任意变换。

为了说明此方法，这里借用 [41] 中的一个示例，为婴儿的身高创建一个模型。首先，在代码 babies_data 中加载数据， Fig. 57 中展示了月龄和身高之间关系的散点图。

Listing 44 婴儿数据

babies = pd.read_csv("../data/babies.csv")
# Add a constant term so we can use the dot product to express the intercept
babies["Intercept"] = 1

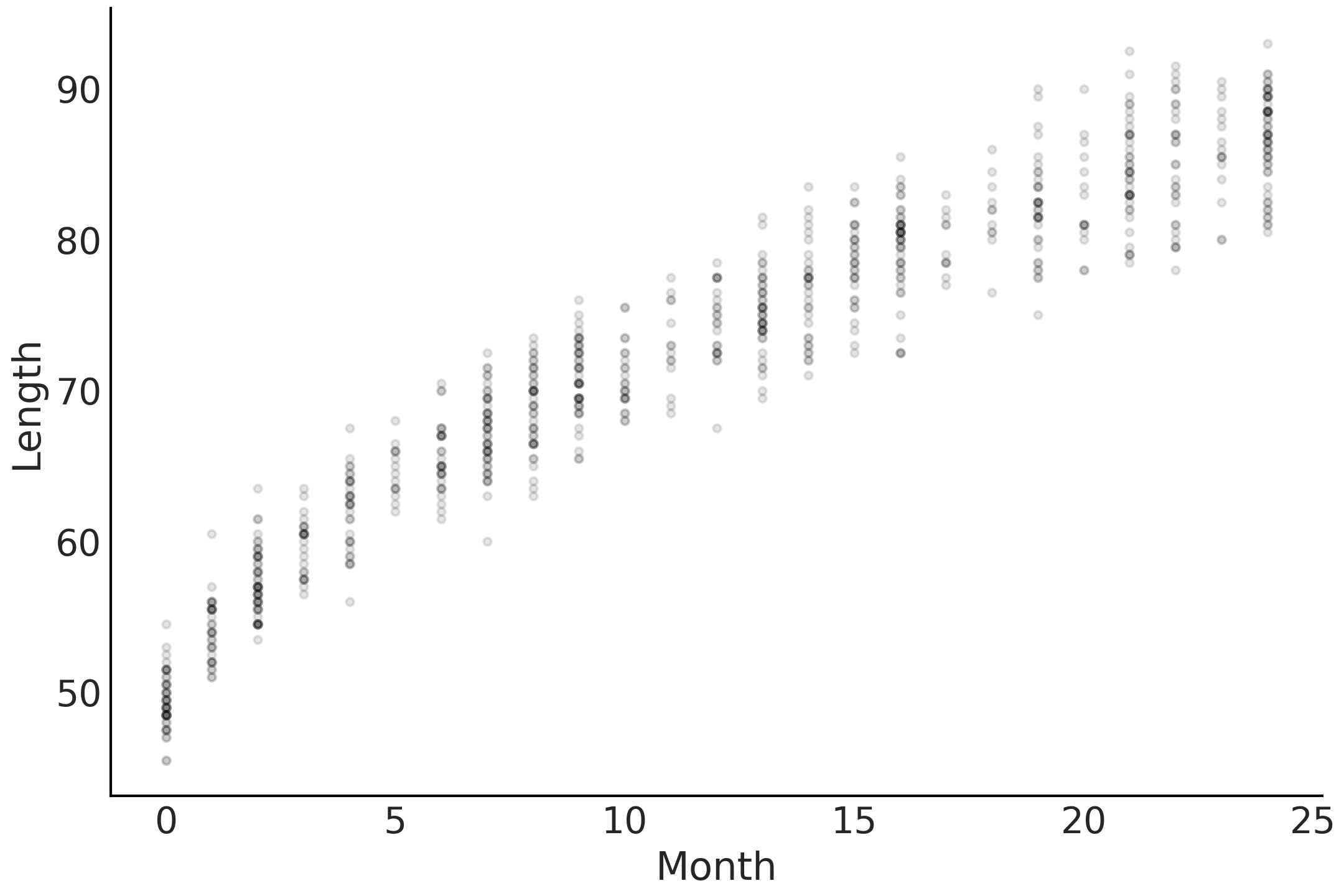
Fig. 57 婴儿的月龄与身高之间的非线性相关散点图。

我们在代码 babies_linear 中指定了一个模型，可以用它来预测婴儿每个月的身高，并确定孩子每个月的生长速度。请注意，该模型不包含任何对预测变量的变换，也没有第 3 章 的逆连接函数变换。

Listing 45 babies_linear

with pm.Model() as model_baby_linear:
    β = pm.Normal("β", sigma=10, shape=2)

    μ = pm.Deterministic("μ", pm.math.dot(babies[["Intercept", "Month"]], β))
    ϵ = pm.HalfNormal("ϵ", sigma=10)

    length = pm.Normal("length", mu=μ, sigma=ϵ, observed=babies["Length"])

    trace_linear = pm.sample(draws=2000, tune=4000)
    pcc_linear = pm.sample_posterior_predictive(trace_linear)
    inf_data_linear = az.from_pymc3(trace=trace_linear,
                                    posterior_predictive=pcc_linear)

model_linear 提供了如图 Fig. 58 所示的线性增长率。根据模型和数据，婴儿在观测期间，每个月都会以大约 \(1.4\) 厘米的稳定速度增长。但是，常识告诉我们，人在一生中的成长速度并不相同，而且在生命早期阶段往往长得更快。换句话说，年龄和身高之间的关系是非线性的。

仔细观测 Fig. 58，可以看到线性趋势和基础数据存在一些问题。该模型倾向于高估接近 \(0\) 月龄的婴儿身高、高估 \(10\) 月龄的婴儿身高，但低估 \(25\) 月龄的婴儿身高。

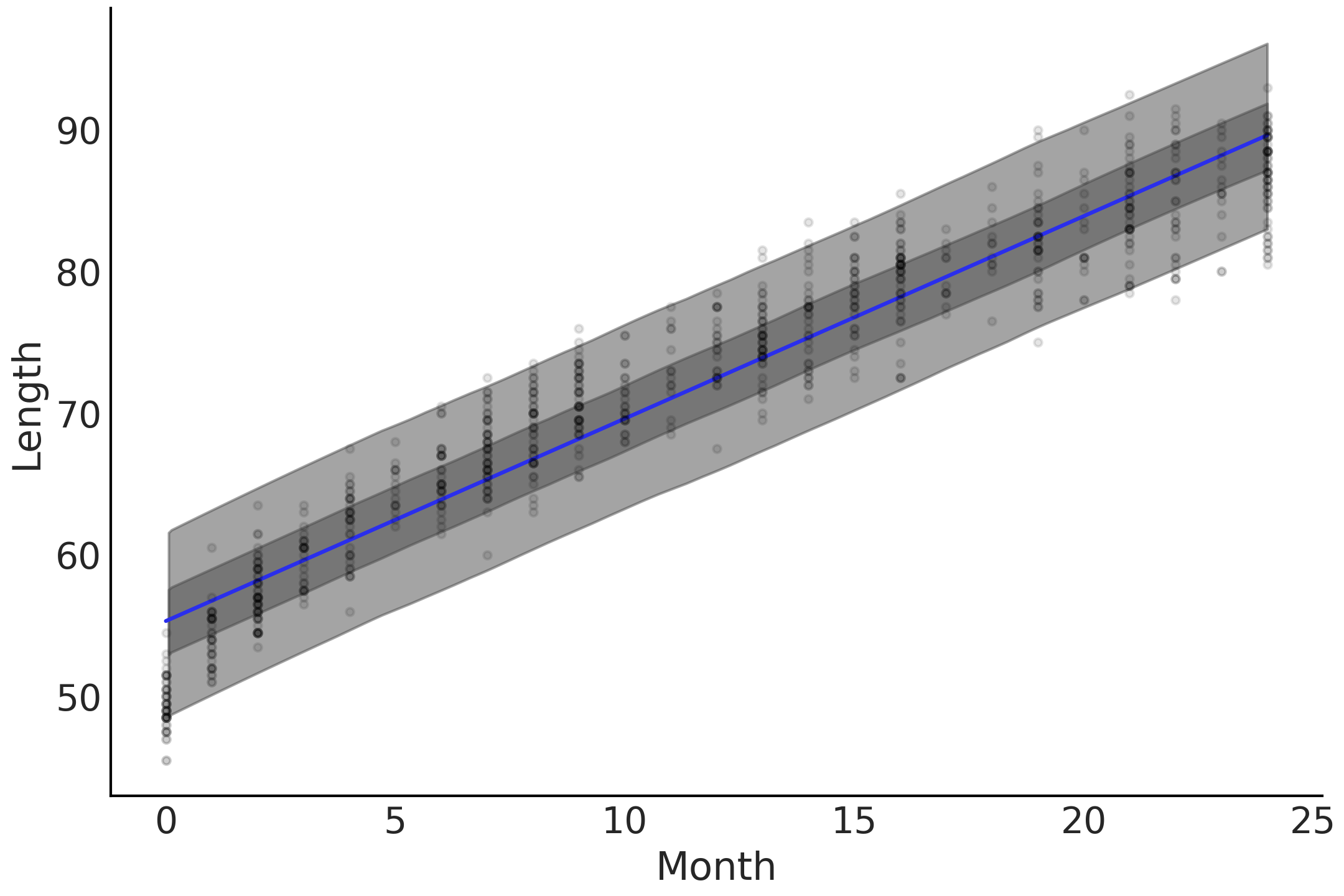
Fig. 58 婴儿身高的线性预测，其中均值为蓝线，后验预测的 \(50\%\) 最高密度区间为深灰色，后验预测的 \(94\%\) 最高密度区间为浅灰色。平均拟合线附近的最高密度区间覆盖了大部分数据点，可以明显看出在早期（ \(0\) 到 \(3\) 月）以及后期（ \(22\) 到 \(25\) 月）存在预测偏高的情况，而在中间（ \(10\) 到 \(15\) 月 ）则存在预测偏低的情况。

回顾一下模型的选择，我们仍然可以认为，在任何年龄的垂直切片中，婴儿身高的分布类似于高斯分布；但在水平方向上，月份和平均身高之间的关系似乎是非线性的。具体来说，我们决定让这种非线性体现为代码 babies_transformed 中的 model_sqrt ，即对月份预测变量实施平方根变换。

Listing 46 babies_transformed

with pm.Model() as model_baby_sqrt:
    β = pm.Normal("β", sigma=10, shape=2)

    μ = pm.Deterministic("μ", β[0] + β[1] * np.sqrt(babies["Month"]))
    σ = pm.HalfNormal("σ", sigma=10)

    length = pm.Normal("length", mu=μ, sigma=σ, observed=babies["Length"])
    inf_data_sqrt = pm.sample(draws=2000, tune=4000)

绘制均值的拟合结果以及预测身高的最高密度区间，可以生成 Fig. 59，其中均值倾向于拟合观测到的关系曲线。除了这种视觉检查，我们还可以使用 az.compare 来验证非线性模型的 ELPD 值。在你自己的分析中，可以使用任何想要的转换函数。与所有模型一样，重要的是能够证明你的选择是合理的，并使用视觉和数字检查来验证结果的合理性。

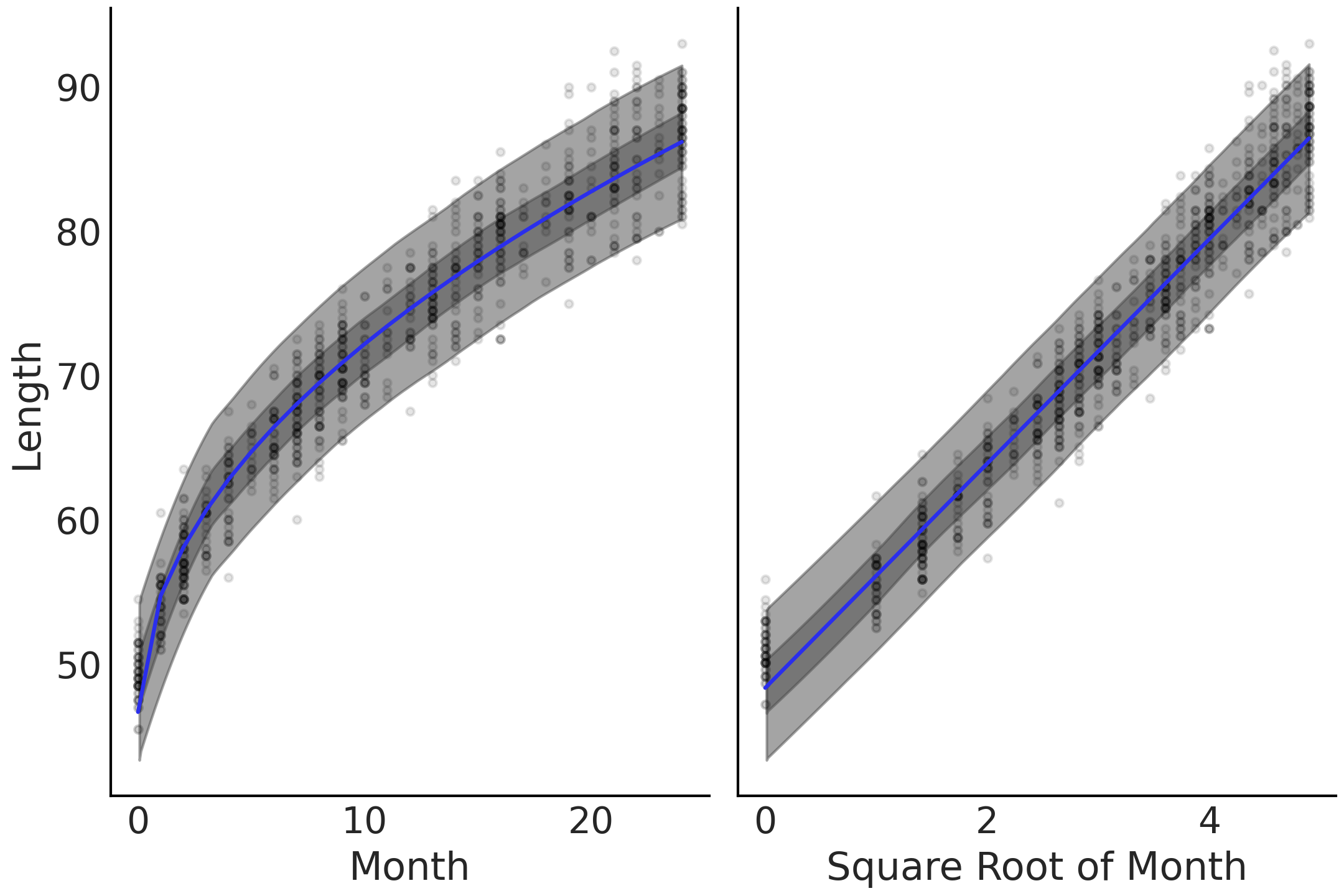
Fig. 59 对预测变量使用变换后的线性预测。左图的 \(x\) 轴未变换，右图的 \(x\) 轴已变换为平方根。非线性增长率的线性化在右图转换后的坐标轴上可以表现出来。

4.2 可变的方差

到目前为止，我们使用线性模型对 \(Y\) 的均值进行建模，同时假设残差具有在响应范围内恒定的方差。但这种恒定方差的假设可能是一种不够充分的建模选择。为了能够对不断变化的不确定性（一般指观测空间中的不确定性）做出解释，可以将公式 (31) 扩展为：

(32)\[\begin{split}\begin{split} \mu =& \beta_0 + \beta_1 f_1(X_1) + \dots + \beta_m f_m(X_m) \\ \sigma =& \delta_0 + \delta_1 g_1(X_1) + \dots + \delta_m g_m(X_m) \\ Y \sim& \mathcal{N}(\mu, \sigma) \end{split}\end{split}\]

估计 \(\sigma\) 的第二行代码与对均值建模的线性项非常相似。我们不仅可以使用线性模型对均值参数建模，还可以对其他参数进行建模。让我们扩展在代码 babies_transformed 中定义的 model_sqrt。现在假设当孩子们小的时候，身高更集中一些，但随着年龄增长，他们的身高变得越来越发散。

Listing 47 babies_varying_variance

with pm.Model() as model_baby_vv:
    β = pm.Normal("β", sigma=10, shape=2)
    
    # Additional variance terms
    δ = pm.HalfNormal("δ", sigma=10, shape=2)

    μ = pm.Deterministic("μ", β[0] + β[1] * np.sqrt(babies["Month"]))
    σ = pm.Deterministic("σ", δ[0] + δ[1] * babies["Month"])

    length = pm.Normal("length", mu=μ, sigma=σ, observed=babies["Length"])
    
    trace_baby_vv = pm.sample(2000, target_accept=.95)
    ppc_baby_vv = pm.sample_posterior_predictive(trace_baby_vv,
                                                 var_names=["length", "σ"])
    inf_data_baby_vv = az.from_pymc3(trace=trace_baby_vv,
                                     posterior_predictive=ppc_baby_vv)

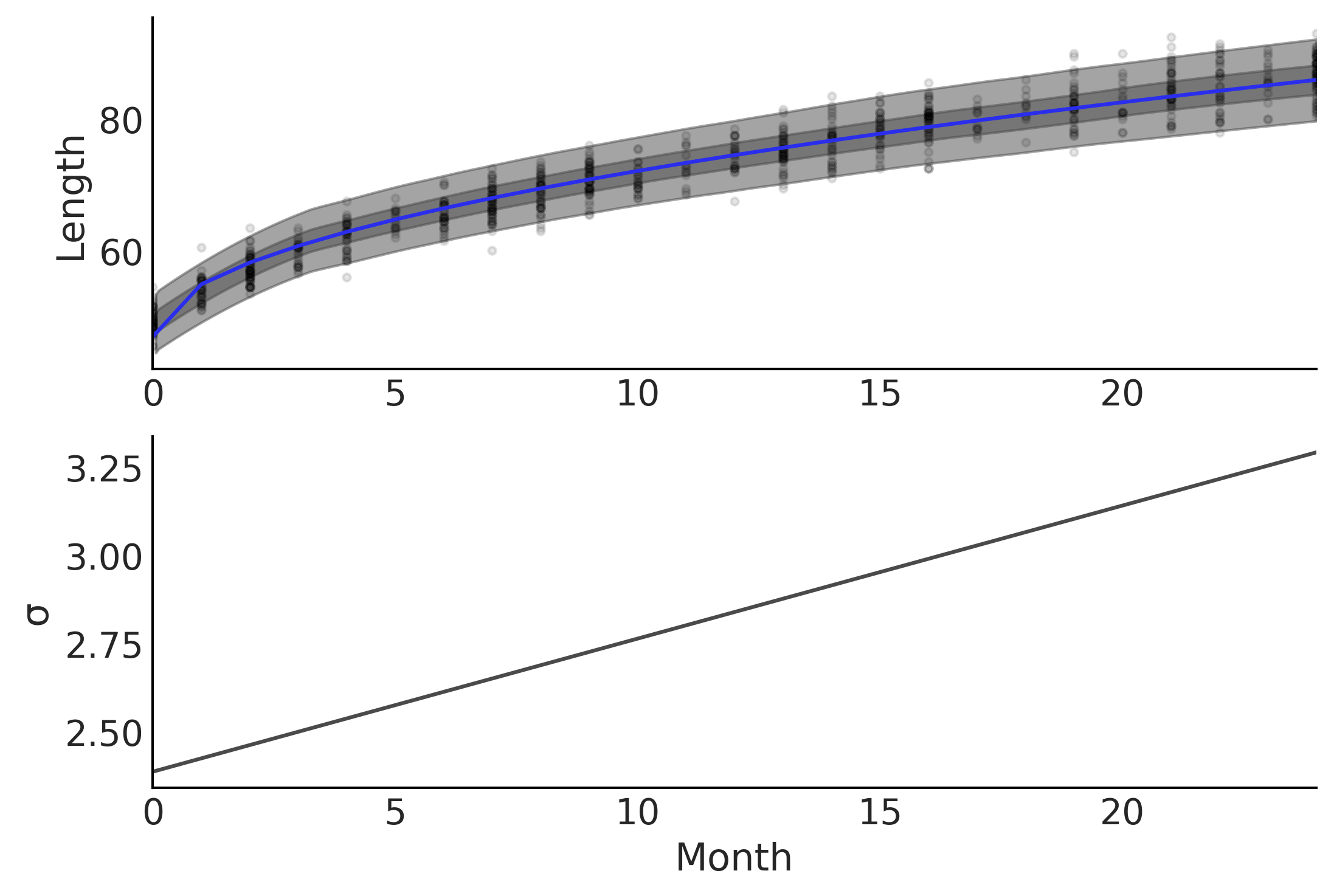
为了模拟随着儿童年龄增长而增加的身高离散度，我们将 \(\sigma\) 的定义从固定值更改为随年龄变化的值。换句话说，我们将模型假设从具有恒定方差的 同质性 更改为具有变化方差的 异质性。模型定义在代码 babies_varying_variance 中，我们需要做的就是更改定义 \(\sigma\) 的表达式，然后概率编程语言会自动处理后验估计。该模型的结果绘制在 Fig. 60 中。

Fig. 60 显示婴儿月龄与身高之间关系的拟合图。上图为身高均值与月龄之间关系的拟合图，蓝线表示均值预测的期望值，与 Fig. 59 中相同，但后验的 HDI 区间是非恒定的。下图绘制了误差估计的期望值与月龄之间关系的拟合图。请注意，随着月数增加，误差估计的期望在增加。

4.3 引入交互效应

到目前为止的所有模型中，都假设某个预测变量对结果变量的影响独立于任何其他预测变量，但实践中并非总是如此。考虑一种情形，我们想为特定城镇的冰淇淋销售情况建模。通常我们会自然而然想到：如果冰淇淋店比较多，有了更多的冰淇淋可供选择，则预计冰淇淋的销售业绩会更好；但如果这个城镇气候寒冷，日均气温为 \(-5\) 摄氏度，那么冰淇淋的销量应该会下降。在相反情况下，如果该城镇处于平均温度为 \(30\) 摄氏度的炎热沙漠中，但并没有太多冰淇淋店，则冰淇淋的销量也会很低。只有当天气炎热 和 冰淇淋销售点比较多时，才预计销量肯定会增加。对于这种联合现象进行建模，我们需要引入 交互效应 的概念，即某个预测变量对结果变量的影响，取决于其他预测变量的值。如果在建模时，我们假设预测变量均为独立的贡献，则无法完全解释这种现象。

我们可以将交互作用表示为：

(33)\[\begin{split}\begin{split} \mu =& \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_1X_2\\ Y \sim& \mathcal{N}(\mu, \sigma) \end{split}\end{split}\]

式中 \(\beta_3\) 是交互项 \(X_1X_2\) 的系数。其实还存在其他引入交互的方法，但采用原始预测变量乘积的形式应用比较广泛。

现在定义了交互效应是什么，我们就可以对比性地定义 主效应 ，即一个预测变量对结果变量的影响只与自身取值有关，与所有其他预测变量取值无关。

为了说明，我们使用一个消费模型的例子，代码 tips_no_interaction 对用餐者留下的小费金额进行了建模，将小费建模为总账单的函数。这听起来很合理，因为小费金额通常是按总账单的百分比来计算的。不过确切的百分比会因不同因素而异，例如餐厅类型、服务质量、所在国家等。在此示例中，我们重点关注吸烟者与非吸烟者的小费金额差异，重点研究吸烟与总账单金额之间是否存在交互作用 2。就像模型 penguin_mass_multi 一样，先将吸烟者作为独立的预测变量添加到回归模型中。

Listing 48 tips_no_interaction

tips_df = pd.read_csv("../data/tips.csv")
tips = tips_df["tip"]
total_bill_c = (tips_df["total_bill"] - tips_df["total_bill"].mean())  
smoker = pd.Categorical(tips_df["smoker"]).codes

with pm.Model() as model_no_interaction:
    β = pm.Normal("β", mu=0, sigma=1, shape=3)
    σ = pm.HalfNormal("σ", 1)

    μ = (β[0] +
         β[1] * total_bill_c + 
         β[2] * smoker)

    obs = pm.Normal("obs", μ, σ, observed=tips)
    trace_no_interaction = pm.sample(1000, tune=1000)

让我们另外创建一个包含交互项的模型，见代码 tips_interaction 。

Listing 49 tips_interaction

with pm.Model() as model_interaction:
    β = pm.Normal("β", mu=0, sigma=1, shape=4)
    σ = pm.HalfNormal("σ", 1)

    μ = (β[0]
       + β[1] * total_bill_c
       + β[2] * smoker
       + β[3] * smoker * total_bill_c
        )

    obs = pm.Normal("obs", μ, σ, observed=tips)
    trace_interaction = pm.sample(1000, tune=1000)

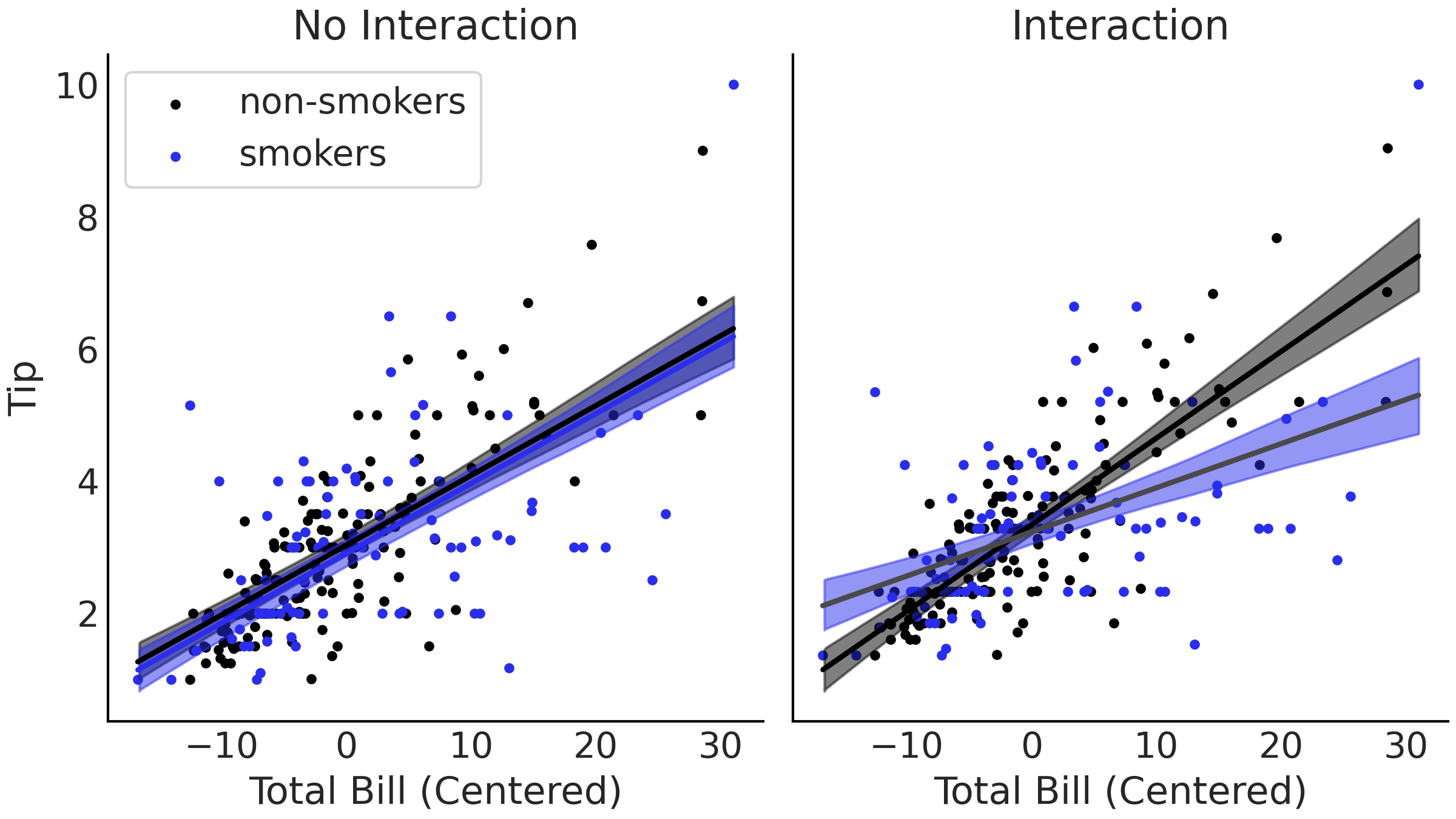
Fig. 61 两种小费模型的线性估计图。左图显示了代码 tips_no_interaction 的无交互估计，其中估计的线是平行的。右图展示了来自代码 tips_interaction 的有交互模型，其中包括吸烟者（或非吸烟者）与账单总金额之间的交互项。该图中不同组的斜率由于添加的交互项而允许变化。

两种模型的差异在 Fig. 61 中可以看到。比较左侧的无交互模型和右侧的交互模型，在交互模型中，平均拟合线不再平行，吸烟者和非吸烟者的斜率不同！

通过引入交互项，我们可以构建一个能拆分数据的模型。在本例中拆分为两类：吸烟者和非吸烟者。你可能会认为手动拆分数据并拟合两个单独的模型也是可以的。这没错，但使用交互的好处之一是：我们能够使用所有可用数据来拟合单个模型，从而提高参数估计的准确性。例如，如果我们假设方差 \(\sigma\) 不受变量 smoker 影响，则单个模型可以利用所有吸烟者和非吸烟者的数据来估计 \(\sigma\) ，进而获得更好的参数估计。

另一个好处是我们可以估计交互的效应强度。如果只是为了拆分数据，则其隐含假设交互作用的强度正好为 \(0\) 或 \(1\)。但通过对交互作用建模，我们其实还能够估计交互作用的强度。

最后，为同一数据构建分别一个有交互模型和一个无交互模型，可以更容易的使用 LOO 比较模型。如果数据被拆分了，我们最终做比较的是在不同数据上的不同模型，而不是在同一数据上评估的不同模型，而后者是 LOO 的必要条件。

总而言之，虽然交互效应模型的主要区别在于对每组不同斜率进行建模的灵活性，但将所有数据建模在一起会产生许多额外的好处。

4.4 更稳健的回归

异常值指位于 “合理预期” 范围之外的观测值。异常值通常不可取，因为其中的某个或几个异常值可能会显著改变模型的参数估计结果。存在多种异常值的处理方法 [42] ，但无论如何，如何处理异常值都是统计学家必须做出的主观选择。

一般来说，至少有两种方法可以解决异常值问题。一种是使用一些预定义规则删除异常值，例如 \(3\) 个标准差或四分位间距的 \(1.5\) 倍。另一种策略是选择一个可以处理异常值并仍然提供有用结果的模型。在回归问题中，后者通常被称为稳健（或鲁棒）回归模型，特别要注意：此类模型对远离大量数据的观测点不太敏感。

从技术上讲，稳健回归模型旨在减少基础数据生成过程那些有违假设的影响。在贝叶斯回归中，一个常见的例子，是将似然函数从高斯分布更改为学生 \(t\) 分布。高斯分布由位置参数 \(\mu\) 和尺度参数 \(\sigma\) 两个参数定义，这些参数控制着高斯分布的均值和标准差（离散度）。

学生 \(t\) 分布也有位置参数和尺度参数 3。但还有一个附加的参数，被称为自由度 \(\nu\)。自由度参数控制学生 \(t\) 分布尾部的权重，如 Fig. 62 所示。图中比较了 \(3\) 个学生 \(t\) 分布和一个高斯分布，其间的主要区别在于尾部密度在总概率质量中所占的比例。当\(\nu\) 较小时，分布主体处的质量比例减少，尾部分布的质量更多；随着\(\nu\) 值的增加，分布主体处的质量比例也增加，尾部分布的质量相应地减少，此时学生 \(t\) 分布越来越接近于一个高斯分布。这也意味着：当 \(\nu\) 较小时，更可能出现远离均值的值。因此，当用学生 \(t\) 分布替换高斯分布作为似然时，将会为异常值提供稳健性。

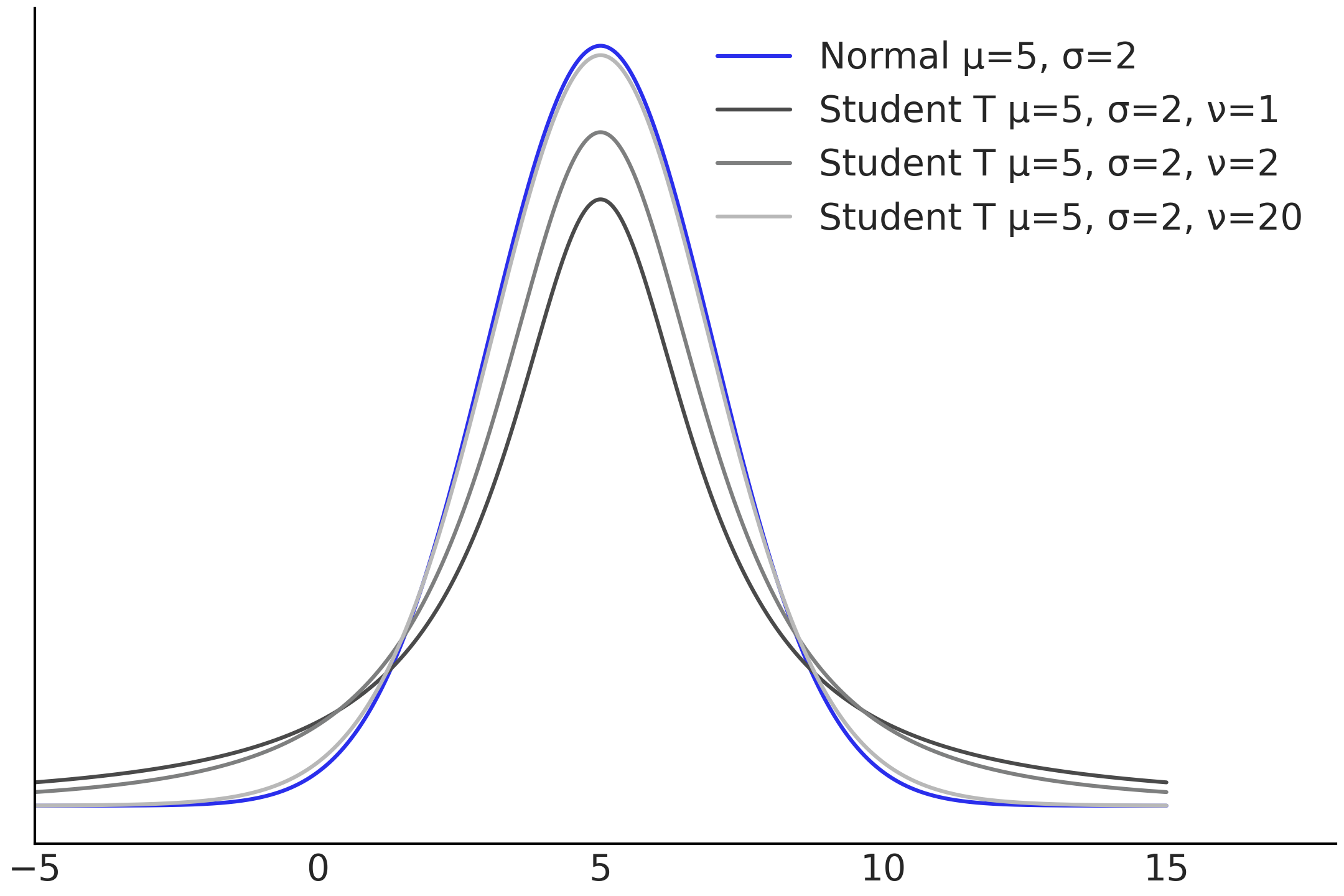
Fig. 62 高斯分布（蓝色），与 \(3\) 个具有不同 \(\nu\) 参数的学生 \(t\) 分布比较。位置和比例参数都是相同的，这可以分理出 \(\nu\) 对尾部的影响。 \(\nu\) 的值越小，分布尾部的密度越大。

稳健回归可以在下面的例子中体现。假设你在阿根廷拥有一家餐厅并出售肉馅馅饼 4。随着时间推移，你收集了每天顾客数量和餐厅收入总金额的数据，如 Fig. 63 所示。其中，大多数数据点沿着一条线排列，只是偶尔有几天，售出的单客馅饼数量远高于邻近数据点。这可能是因为在某些大型庆祝活动日 5，人们比平时吃的馅饼更多。

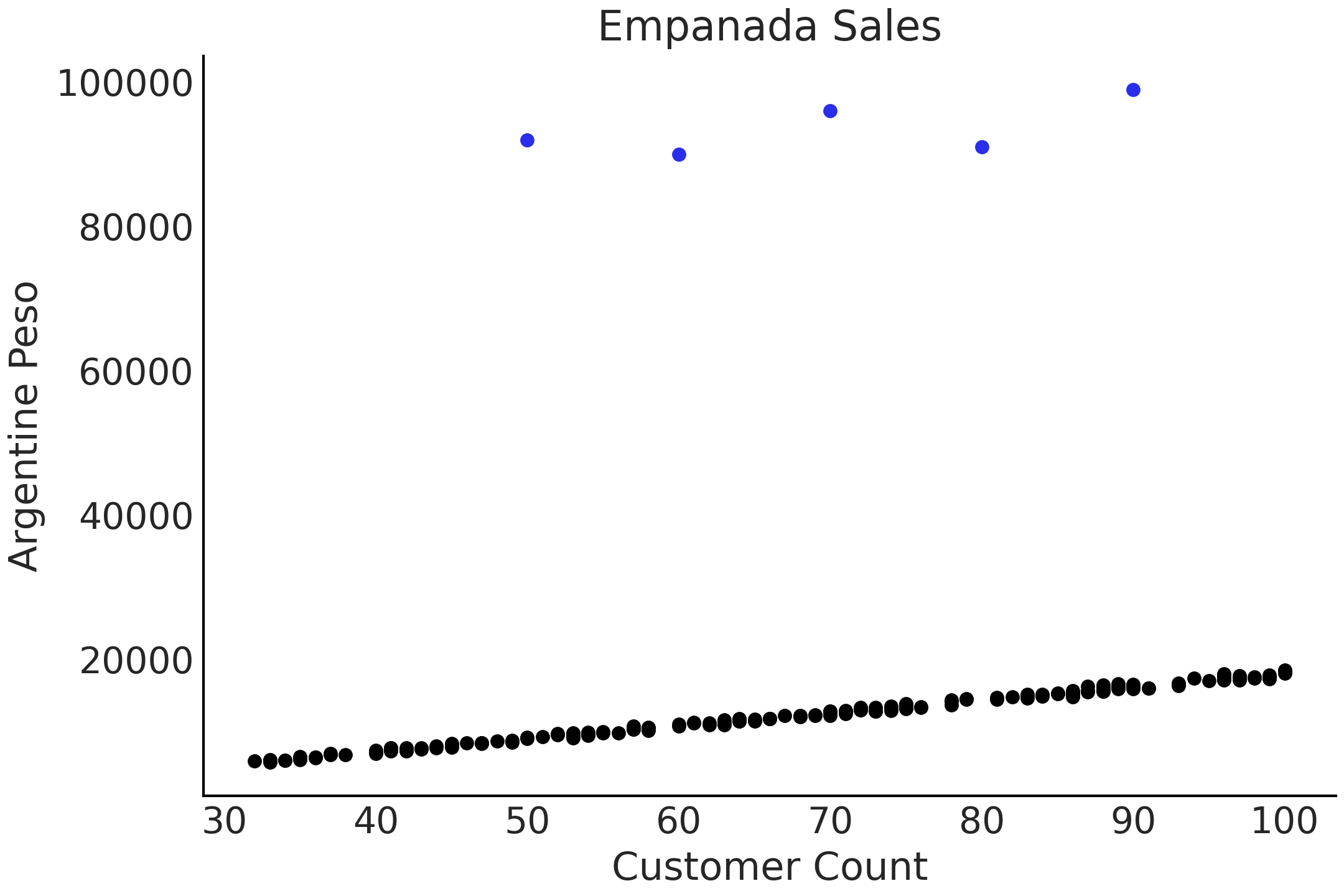
Fig. 63 根据顾客数量和收入绘制的模拟数据。图表顶部的 \(5\) 个点被视为异常值。

无论异常值如何，我们都希望能够估计顾客与餐厅收入之间的关系。通过图形绘制，我们发现线性回归似乎是合适的，例如在代码 non_robust_regression 中编写的使用高斯似然的线性回归。在完成参数估计后，我们在 Fig. 64 中以两个不同的尺度绘制了回归的均值。注意图中拟合回归线几乎位于所有可见数据点之上。在 Table 8 中，还可以看到各参数的估计值，注意 \(\sigma\) 的均值为 \(2951.1\) ，显著大于图中给人的感觉。对于高斯似然，后验分布必须在主体观测和 \(5\) 个异常值之间做“伸缩”，从而导致了上述估计结果。还要注意到，与 Fig. 64 中的主体数据相比，\(\sigma\) 的估计值过于宽泛。

Listing 50 non_robust_regression

with pm.Model() as model_non_robust:
    σ = pm.HalfNormal("σ", 50)
    β = pm.Normal("β", mu=150, sigma=20)

    μ = pm.Deterministic("μ", β * empanadas["customers"])

    sales = pm.Normal("sales", mu=μ, sigma=σ, observed=empanadas["sales"])
    
    inf_data_non_robust = pm.sample()

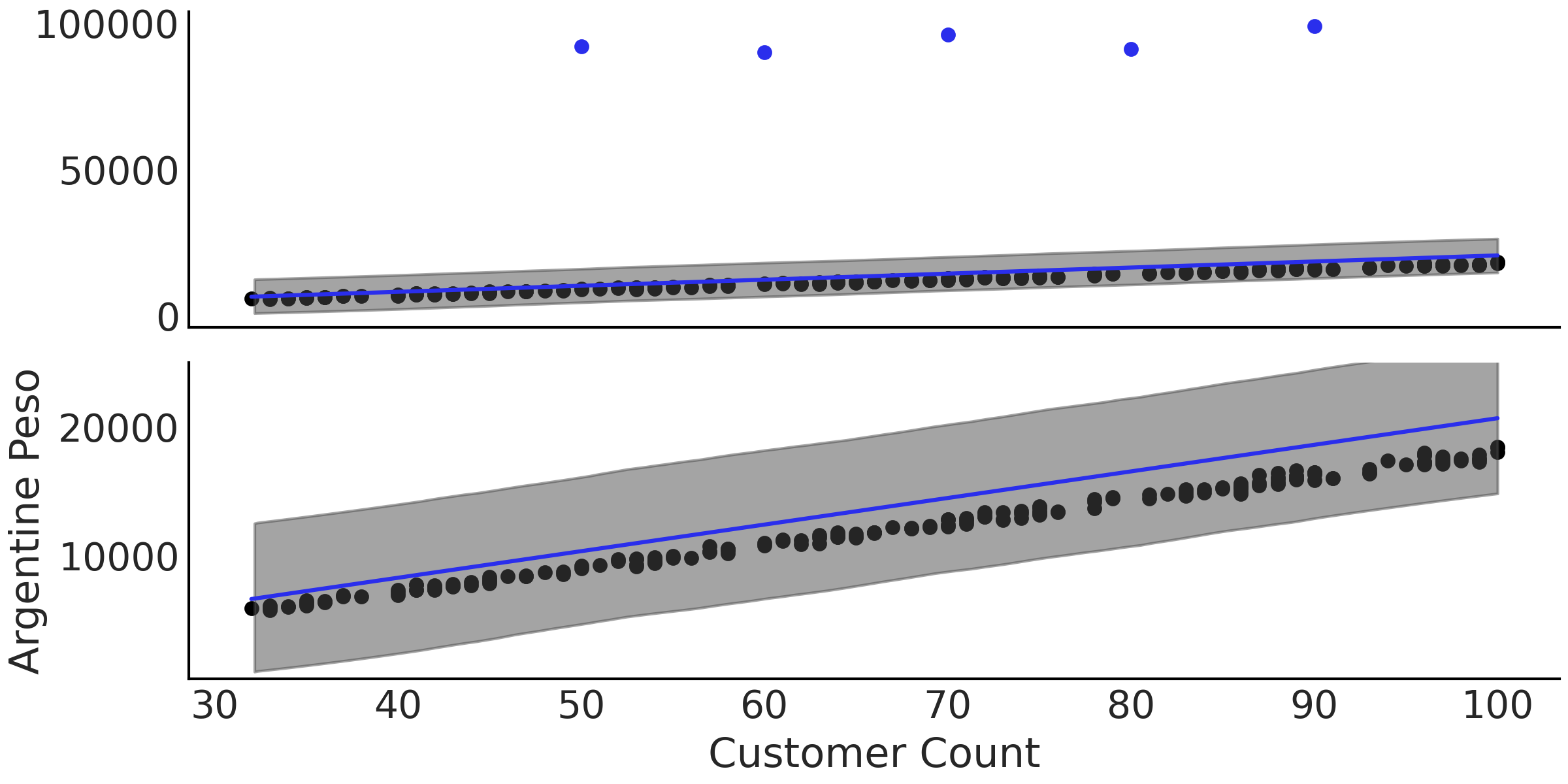
Fig. 64 来自代码 non_robust_regression 的数据、拟合回归线和 \(94\%\) HDI 区间。在上部子图中，顶部的点为异常值，底部的点为主体数据，蓝色线为回归线；在下部尺度被放大的子图中，可以明显看出拟合线存在系统偏差，估计的均值回归线高于大部分数据点。

Table 8 Estimate of parameters for model non_robust_regression.

	mean	sd	hdi_3%	hdi_97%
\(\beta\)	207.1	2.9	201.7	212.5
\(\sigma\)	2951.1	25.0	2904.5	2997.7

我们使用学生 \(t\) 分布作为似然，对同一数据建模，如代码 code_robust_regression 所示。请注意，数据集没有更改，仍然包含异常值。当检查 Fig. 65 中的拟合回归线时，可以看到拟合落在主体观测数据点之间，更接近预期的位置。查看 Table 9 中的参数估计值（ 注意增加了参数 \(\nu\) ），可以看到 \(\sigma\) 的估计值已从非稳健回归中的约 \(2951\) ，大幅下降到了稳健回归中的 约 \(152\) ，表明新模型对于数据而言似乎更合理。似然分布的变化表明，尽管数据中存在异常值，但学生 \(t\) 分布有足够灵活性来合理地对其进行建模。

Listing 51 code_robust_regression

with pm.Model() as model_robust:
    σ = pm.HalfNormal("σ", 50)
    β = pm.Normal("β", mu=150, sigma=20)
    ν = pm.HalfNormal("ν", 20)

    μ = pm.Deterministic("μ", β * empanadas["customers"])
    
    sales = pm.StudentT("sales", mu=μ, sigma=σ, nu=ν,
                        observed=empanadas["sales"])

    inf_data_robust = pm.sample()

Table 9 model robust_regression 模型的参数估计

	mean	sd	hdi_3%	hdi_97%
\(\beta\)	179.6	0.3	179.1	180.1
\(\sigma\)	152.3	13.9	127.1	179.5
\(\nu\)	1.3	0.2	1.0	1.6

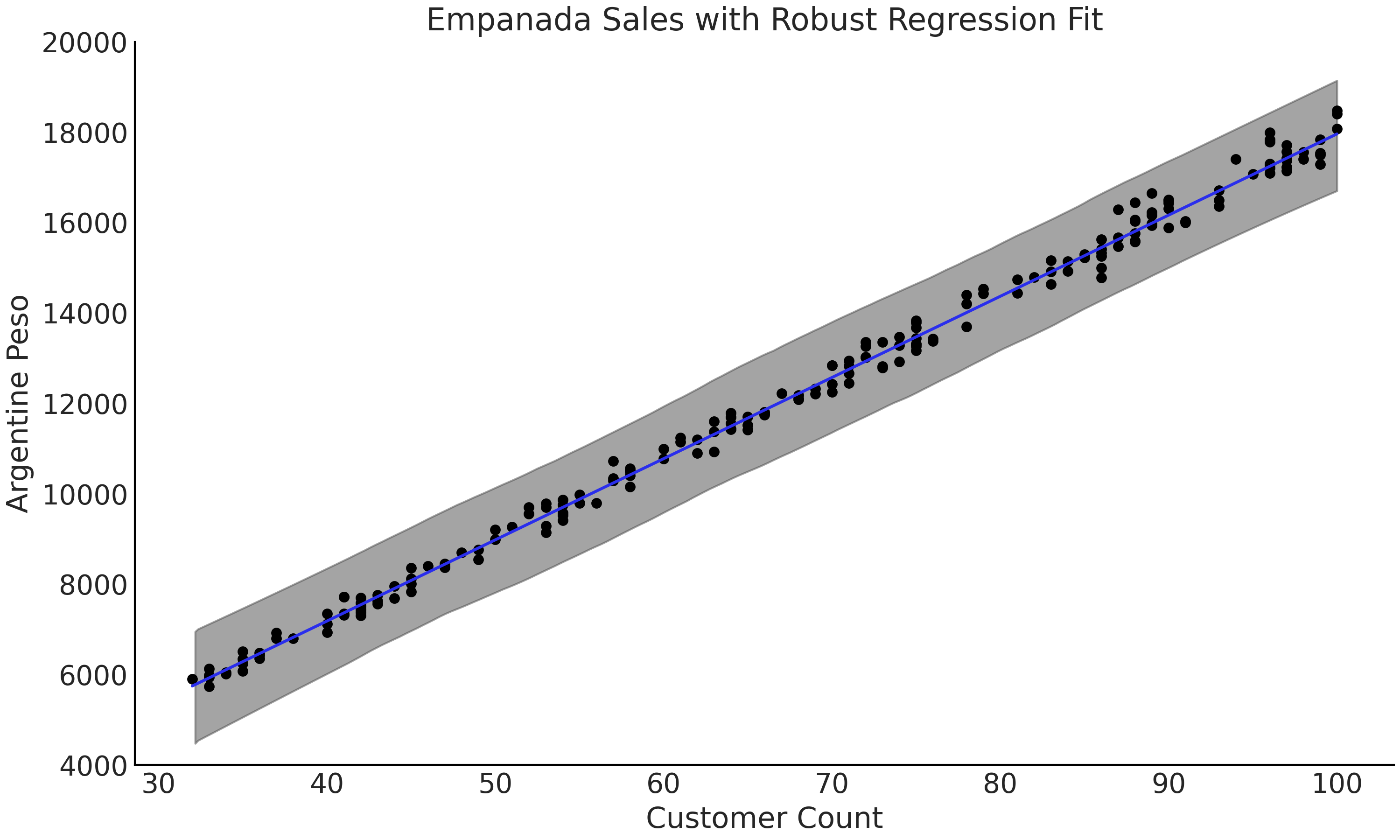
Fig. 65 模型 model_robust 对应的拟合回归线和 \(94\%\) HDI。图中未绘制异常值，但其仍然存在于数据中。与 Fig. 64 相比，新模型的拟合回归线基本落在了数据点范围内。

在本例中，异常值并不是测量误差、数据输入错误等，而是在某些条件下实际发生的真实观测结果，我们希望能够将其作为建模问题的组成部分。如果我们的目的仅仅是模拟常规时间的馅饼平均销售数量，那么确实可以将其视为真的异常值，但如果用其拟合的模型来确定下一个重大节日的馅饼数量，结果一定会很离谱。在此示例中，稳健线性回归模型避免了显式地为高销售日单独建模（ 所谓显式指将“常规时间”和“节假日”区分开建模 ）。除了进行稳健回归建模外，使用其他形式的模型（如本书后面将介绍到的混合模型或分层模型）也能实现对异常值的建模。

适应数据的模型调整

改变似然以实现稳健性，仅仅是通过修改模型以适应观测数据的一种方式，还有许多其他方法。例如，在检测放射性粒子发射时，由于传感器故障 [43]（或其他一些测量问题），或者实际上没有要记录的事件，因此可能会出现零计数。而这种情况会产生 夸大零计数 的效果。针对此类问题，部分学者开发了一种 零膨胀模型 用于估计一种组合的数据生成过程。例如，将泊松似然（通常用于建模时间发生的起点计数）扩展为零膨胀泊松似然。有了这种似然，我们可以更好地将正常的泊松过程计数与 异常零生成过程计数 区分开来。

零膨胀模型仅是处理混合数据的一种方法，其中观测来自两个或多个组，而且不知道哪个观测属于哪个组。实际上，我们完全可以使用此类混合似然来实现另一种稳健回归，它将为每个数据点分配一个隐标签（异常值或非异常值）。

贝叶斯模型的可定制性使建模者能够灵活地创建适合数据情况的模型，而不必强制将数据情况与预定义的模型做匹配。

4.5 池化、多级模型和混合效应

在实际问题中，有时候预测变量之间会包含一些嵌套结构，使得我们能够采用一些层次性方法对数据进行分组。我们可以考虑将这种分组视为不同的数据生成过程。下面用一个例子来说明。

假设你在一家销售沙拉的公司工作。这家公司在一些区域市场拥有悠久的业务，并且在一个新市场开设了办事处以响应顾客需求。出于财务规划目的，你需要预测这个新市场中的门店每天将赚取多少美元。你有两个数据集，\(3\) 天的沙拉销售数据，以及同一市场中一年的披萨和三明治的销售数据。数据（合成的）显示在 Fig. 66 中。

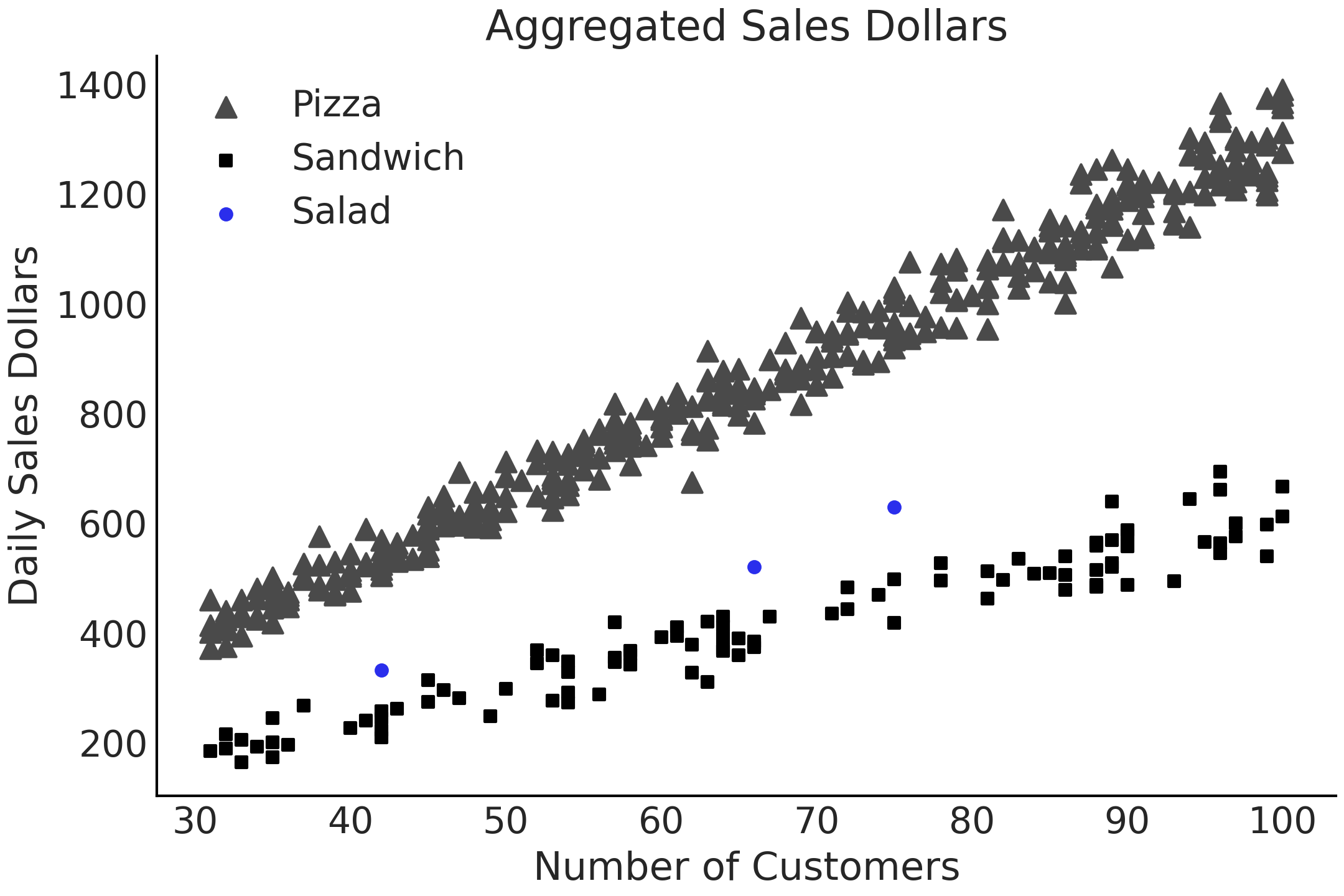
Fig. 66 面向真实世界场景的模拟数据集。在此案例中，一个企业仅有 \(3\) 条有关沙拉的日常销售数据，但有大量关于披萨和三明治的销售数据。

从专业知识和数据来看，一致认为这 \(3\) 种食品的销售额存在相似之处。因为它们都吸引相同类型的顾客，都是典型的 快销食品 类别，但它们又不完全相同。在接下来的部分中，我们将讨论如何对这种 相似但又不完全相似 的情况进行建模。让我们先从“所有组彼此无关”的最简单情况开始。

4.5.1 非池化的参数

我们可以创建一个能够将每个组与其他组完全分离的回归模型。这种模型等价于为每个类别运行单独的回归，这也是称其为非池化回归的原因。分离回归模型的唯一不同是同时估计所有组的系数。参数和组之间的关系在 Fig. 67 和公式 (34) 中以数学符号直观表示，其中 \(j\) 为每个分组的索引。

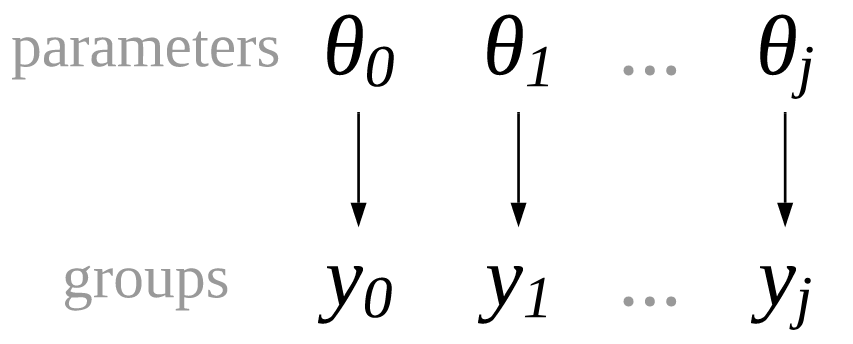
Fig. 67 一个非池化模型，其中每个组的观测 \(y_1, y_2, ..., y_j\) 都有独立于其他组的参数。

(34)\[\begin{split}\begin{split} \beta_{mj} \sim& \overbrace{\mathcal{N}(\mu_{\beta m}, \sigma_{\beta m})}^{\text{Group-specific}}\\ \sigma_{j} \sim& \overbrace{\mathcal{HN}(\sigma_{\sigma})}^{\text{Group-specific}}\\ \mu_{j} =& \beta_{1j} X_1 + \dots + \beta_{mj} X_m \\ Y \sim& \mathcal{N}(\mu_{j}, \sigma_{j}) \end{split}\end{split}\]

这些参数被标记为 group-specific 参数，表示每个组都有一个专用参数。非池化的 PYMC3 模型体现在代码 model_sales_unpooled 中，拟合结果见 Fig. 68 。此处所有组都没有截距参数，原因很简单，如果门店顾客为零，总销售额也将为零，因此没有必要为其建模。

Listing 52 非池化的销售模型

customers = sales_df.loc[:, "customers"].values
sales_observed = sales_df.loc[:, "sales"].values
food_category = pd.Categorical(sales_df["Food_Category"])

with pm.Model() as model_sales_unpooled:
    σ = pm.HalfNormal("σ", 20, shape=3)
    β = pm.Normal("β", mu=10, sigma=10, shape=3)
    
    μ = pm.Deterministic("μ", β[food_category.codes] *customers)
    
    sales = pm.Normal("sales", mu=μ, sigma=σ[food_category.codes],
                      observed=sales_observed)
    
    trace_sales_unpooled = pm.sample(target_accept=.9)
    inf_data_sales_unpooled = az.from_pymc3(
        trace=trace_sales_unpooled, 
        coords={"β_dim_0":food_category.categories,
                "σ_dim_0":food_category.categories})

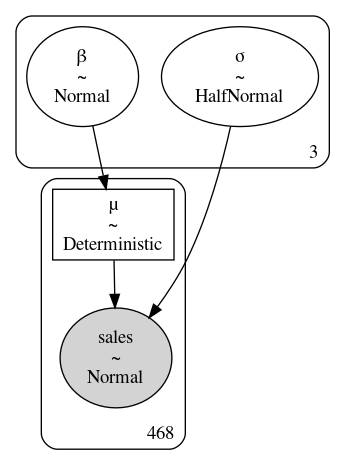
Fig. 68 model_sales_unpooled 模型的示意图。注意参数 \(\beta\) 和 \(\sigma\) 周围的框在右下角都有一个 \(3\) ，表明模型为 \(\beta\) 和 \(\sigma\) 分别估计了 \(3\) 个参数。

从 model_sales_unpooled 采样后，可以创建参数估计的森林图，如 Fig. 69 和 Fig. 70 所示。请注意，与三明治组和披萨组相比，沙拉组的 \(\sigma\) 后验估计相当广泛。当观测数据中某些组的样本少而其他组样本多时，非池化模型应当有此预期结果。

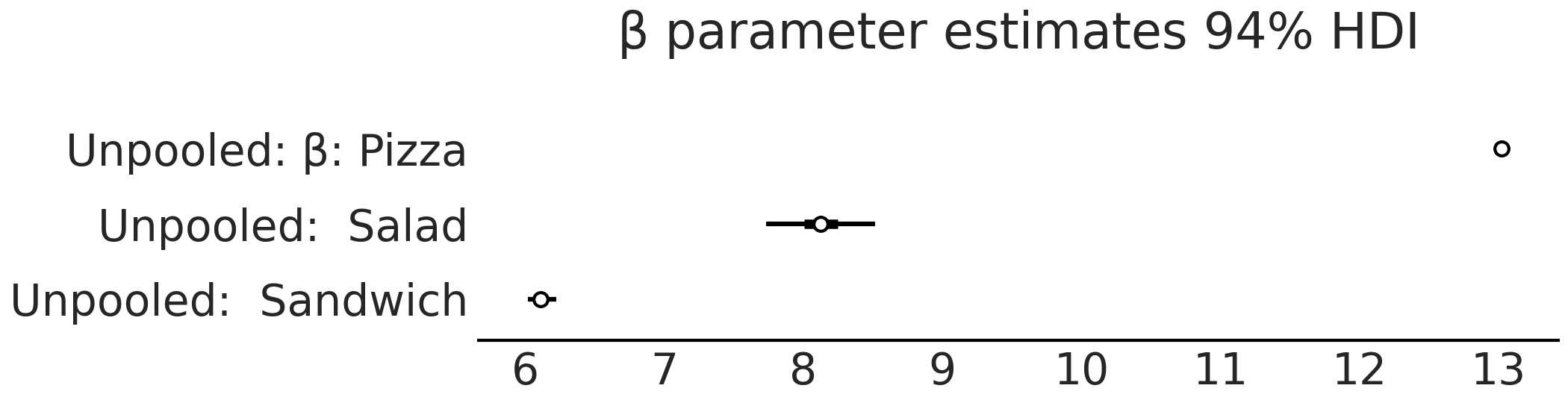
Fig. 69 model_sales_unpooled 模型的 \(\beta\) 参数估计对应的森林图。正如预期的那样，沙拉组的 \(\beta\) 系数估计是最宽泛的，因为该组数据量最少。

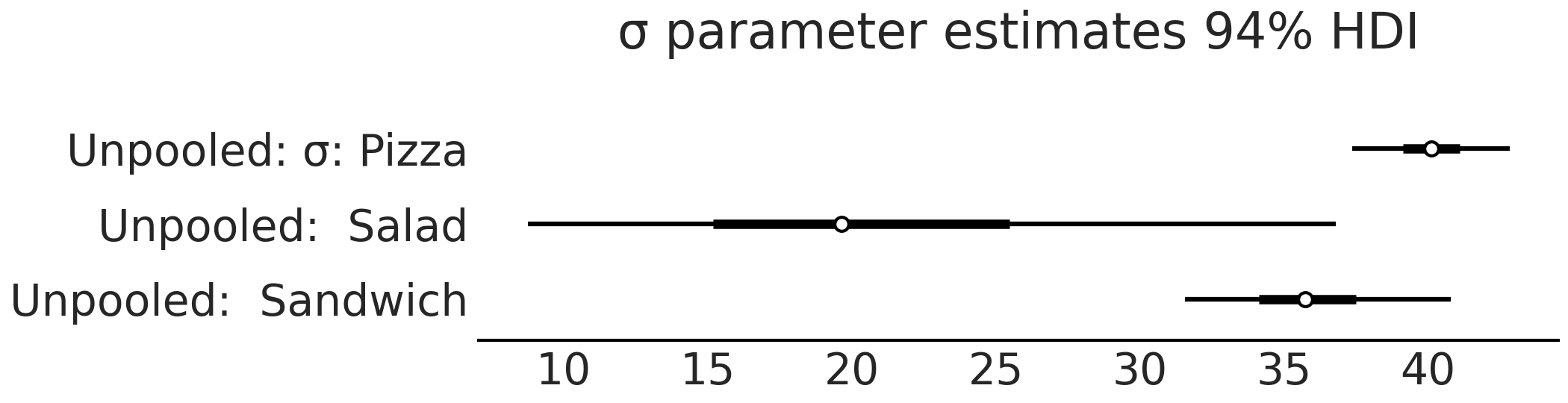
Fig. 70 model_sales_unpooled 模型的 \(\sigma\) 参数估计对应的森林图。与 Fig. 69 类似，沙拉组的销售额变化 \(\sigma\) 的估计值最大，因为相对于披萨组和三明治组而言，其数据点过少。

非池化模型与使用数据子集创建三个分离的模型本质上没有什么不同，就像 3.1 比较两个或多个组 中所做的那样，其中各组的参数都单独估计，因此可以考虑将非池化模型应用于对各组独立建模的线性回归模型。

现在可以将非池化模型及其参数估计作为基线，来比较本节后续的其他模型，特别是可以了解额外的复杂性是否具备合理性。

4.5.2 池化的参数

既然有非池化的参数，你可能会猜到也应该有池化的参数。没错！顾名思义，池化的参数是忽略了组间区别的参数。此类模型显示在 Fig. 71 中，从概念上讲，各组共享相同的参数，因此我们也将池化的参数称为公共参数。

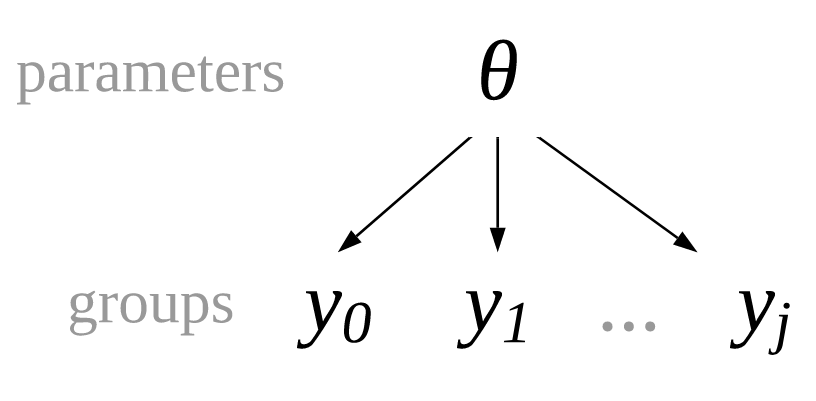
Fig. 71 一个池化模型，其中各组观测值 \(y_1, y_2, ..., y_j\) 共享参数。

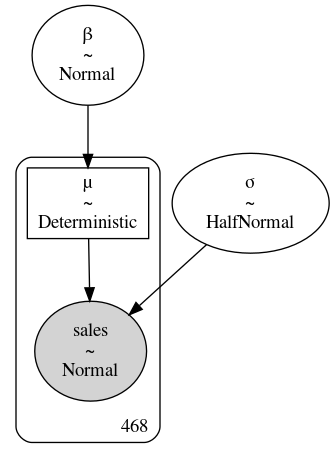
对于餐厅示例，池化的模型见公式 (35) 和代码 model_sales_pooled 。 该模型的 GraphViz 图表示见 Fig. 72 。

(35)\[\begin{split}\begin{split} \beta \sim& \overbrace{\mathcal{N}(\mu_{\beta}, \sigma_{\beta})}^{\text{Common}}\\ \sigma \sim& \overbrace{\mathcal{HN}(\sigma_{\sigma})}^{\text{Common}}\\ \mu =& \beta_{1} X_{1} + \dots + \beta_{m} X_{m} \\ Y \sim& \mathcal{N}(\mu, \sigma) \end{split}\end{split}\]

Listing 53 model_sales_pooled

with pm.Model() as model_sales_pooled:
    σ = pm.HalfNormal("σ", 20)
    β = pm.Normal("β", mu=10, sigma=10)

    μ = pm.Deterministic("μ", β * customers)
    
    sales = pm.Normal("sales", mu=μ, sigma=σ,
                      observed=sales_observed)
                        
    inf_data_sales_pooled = pm.sample()

Fig. 72 model_sales_pooled 模型示意图。与 Fig. 68 不同，\(\beta\) 和 \(\sigma\) 只有一个实例。

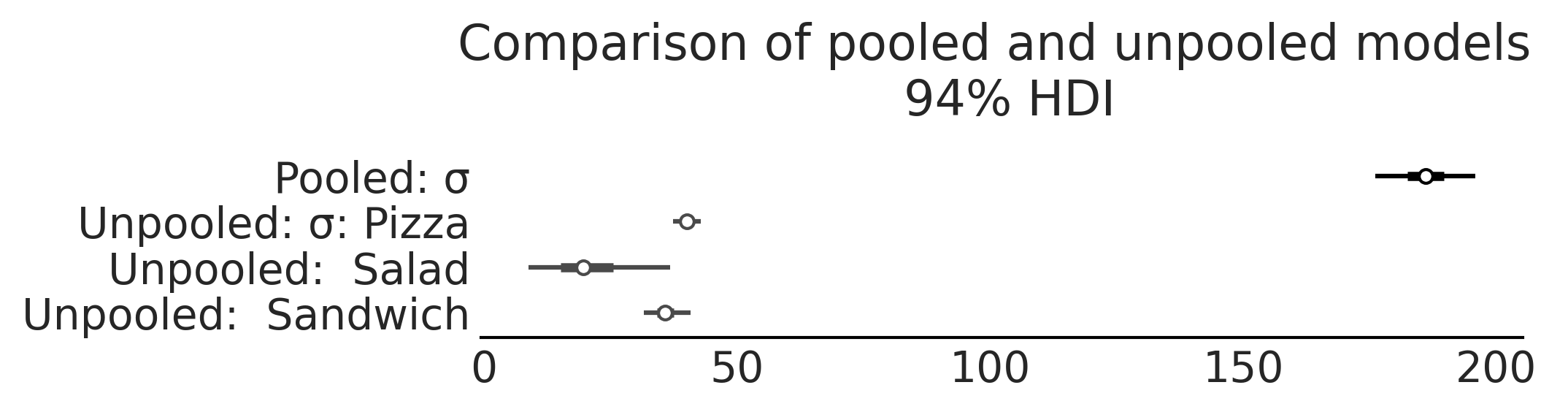
Fig. 73 model_pooled_sales 模型和 model_unpooled_sales 模型的 \(\sigma\) 参数估计值比较。请注意，与非池化模型相比，池化模型的 \(\sigma\) 估计值高很多，因为统一的线性拟合必须捕获所有池化数据中的方差。

池化方法的好处是有更多数据用于估计每个参数，但这同时意味着我们无法单独地了解每个组，而只能了解更高层次的整个食物类别。查看 Fig. 74， \(\beta\) 和 \(\sigma\) 的估计并不表示任何特定的食物组，因为模型将具有不同尺度的多组数据合并在了一个组里。将 \(\sigma\) 的值与 Fig. 73 中非池化模型的值进行比较。当在 Fig. 74 中绘制回归时，可以看到一条比任何单组都包含更多数据的回归线，但却无法很好地拟合任何一个组。该结果意味着组间差异太大而无法忽略，因此池化数据对于我们的预期目的，可能并不是特别有用。

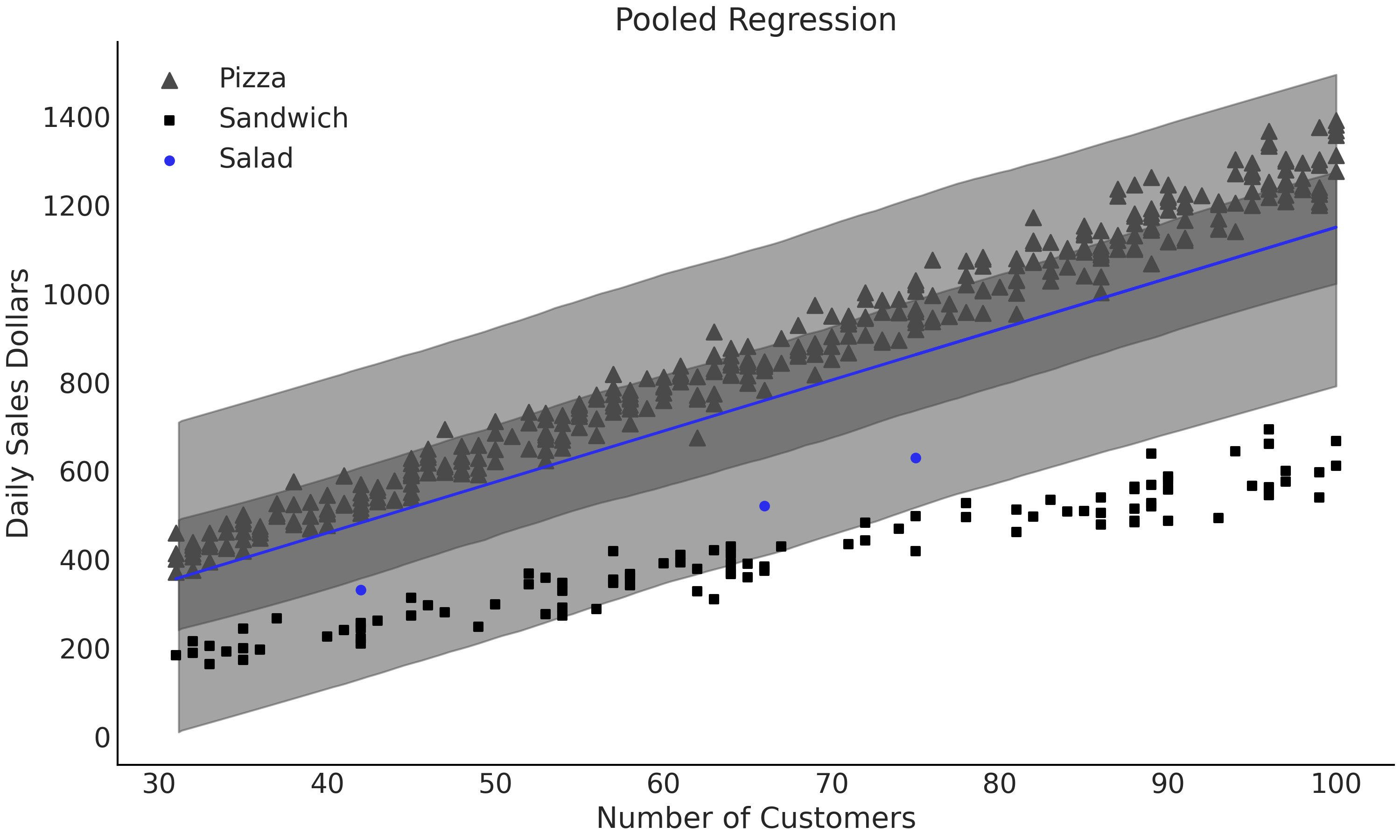
Fig. 74 池化的线性回归模型 model_sales_pooled，所有数据都汇集在一起​​。每一个参数都是使用所有数据估计的，但最终对各组的估计都非常差，因为一个仅有 \(2\) 个参数的模型，无法很好地泛化并捕获各组之间的细微差别。

4.5.3 组混合与多级模型

在非池化方法中，我们具有保留组间差异的优势，能够获得每个组的参数估计结果。在池化方法中，我们利用了所有数据来估计同一组参数，以得到更通用的估计。幸运的是，我们还可以将两种方法混合在一个模型中，如公式 (36) 所示。在该公式中，我们保持各组的 \(\beta\) 估计是非池化的，但 \(\sigma\) 估计是池化的。示例中依然没有考虑截距，但应当清楚有截距项的回归模型也是类似的。

(36)\[\begin{split}\begin{split} \beta_{mj} \sim& \overbrace{\mathcal{N}(\mu_{\beta m}, \sigma_{\beta m})}^{\text{Group-specific}}\\ \sigma \sim& \overbrace{\mathcal{HN}(\sigma_{\sigma})}^{\text{Common}}\\ \mu_{j} =& \beta_{1j} X_{1} + \dots + \beta_{m} X_{m} \\ Y \sim& \mathcal{N}(\mu_{j}, \sigma) \end{split}\end{split}\]

随机效应和固定效应以及为什么你应该忘记这些术语

特定于每个级别的参数和跨级别的通用参数有着不同的名称，前者被称为随机效应或变化效应，而后者被成为固定效应或恒定效应。经常令人困惑的是，不同的人可能会对这些术语赋予不同含义，尤其是在谈论固定效应和随机效应时 [44]。

如果必须有区别地标记这些术语，我们建议采用 组间通用的参数 和 组内专用的参数 [33, 36]。但是，由于所有这些术语都被广泛使用，我们建议你始终验证模型的细节，以避免混淆和误解。

重新审视食品销售模型，我们对采用池化数据来估计 \(\sigma\) 非常感兴趣，因为披萨组、三明治组和沙拉组的销售额可能存在相同的方差，但我们对各组的 \(\beta\) 参数并没池化，因为我们知道各组之间存在差异。有了这些想法，我们就可以编写 PYMC3 模型，如代码 model_sales_mixed_effect 所示，并生成 Fig. 75 所示的模型结构图。从模型中可以得到 Fig. 76 ，图中显示了叠加在数据上的拟合结果。此外还能够得到 Fig. 77 ，其中比较和展示了池化和非池化方法估计出来的 \(\sigma\) 参数。

这些结果令人鼓舞，对于所有三个组别来说，拟合结果看起来都是合理的，特别是对于沙拉组来说，该模型似乎能够对此新市场的沙拉销售产生合理的推论。

Listing 54 model_sales_mixed_effect

with pm.Model() as model_pooled_sigma_sales:
    σ = pm.HalfNormal("σ", 20)
    β = pm.Normal("β", mu=10, sigma=20, shape=3)
    
    μ = pm.Deterministic("μ", β[food_category.codes] * customers)
    
    sales = pm.Normal("sales", mu=μ, sigma=σ, observed=sales_observed)
    
    trace_pooled_sigma_sales = pm.sample()
    ppc_pooled_sigma_sales = pm.sample_posterior_predictive(
        trace_pooled_sigma_sales)

    inf_data_pooled_sigma_sales = az.from_pymc3(
        trace=trace_pooled_sigma_sales,
        posterior_predictive=ppc_pooled_sigma_sales,
        coords={"β_dim_0":food_category.categories})

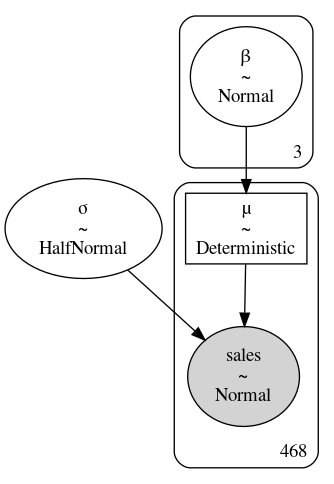
Fig. 75 model_pooled_sigma_sales 模型，其中 \(\beta\) 是非池化的，如右上角含 \(3\) 的框所示，\(\sigma\) 是池化的，不含数字框表示所有组具有相同的参数。

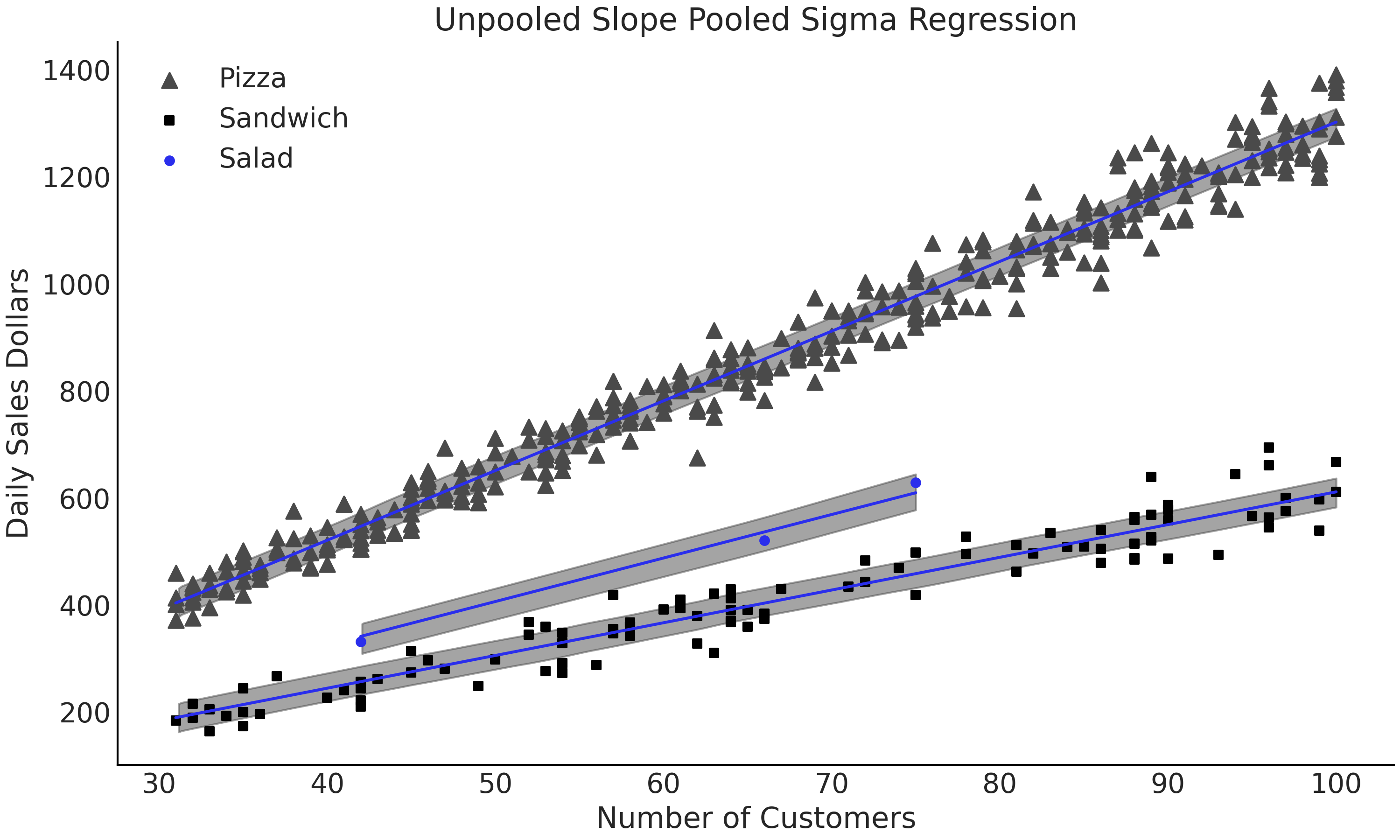
Fig. 76 model_pooled_sigma_sales 模型的拟合结果，叠加显示 \(50\%\) HDI 。此模型对于估计沙拉预计销售额的目的更有用，因为每个组的斜率独立，并且所有数据都用来估计相同的 \(\sigma\) 参数。

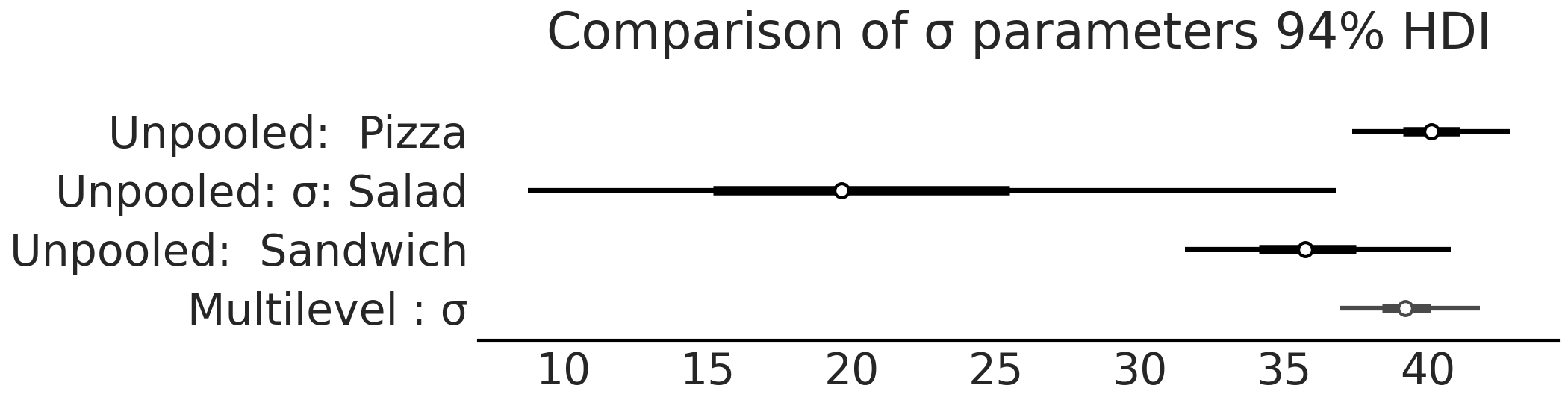
Fig. 77 比较来自 model_pooled_sigma_sales 模型和 model_pooled_sales 模型的 \(\sigma\)。请注意，多级模型 model_pooled_sigma_sales 中的 \(\sigma\) 估计值在全池化模型 model_pooled_sales 的估计值范围之内。

4.6 分层模型

根据上一节内容，我们建模时，对参数有两种可能的组选项：一是在参数在组之间没有区别时做池化，二是在组之间有区别的情况下不做池化。回想一下，在餐厅示例中，我们相信 \(3\) 种食物类别的 \(\sigma\) 参数相似，但有可能并不完全相同。此时该如何处理呢？

4.6.1 什么是分层模型

在贝叶斯建模中，有一种 分层模型（ Hierarchical Models ） 可以来表达这种情形。在分层模型中，参数是 部分池化的 。部分是指各组之间并不共享固定的参数值，而是共享用于生成该参数值的同一个概率分布。此想法的概念图见 Fig. 78 。图中各组都有自己的参数，但这些参数值都来自于同一个超先验分布。先验分布的建模对象是模型中的参数，而超先验的建模对象是模型参数所服从的概率分布的参数，因此被称为分层模型。

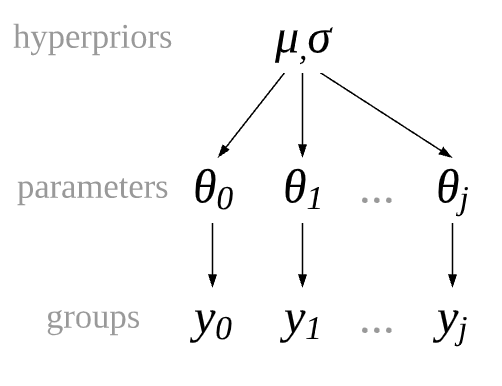
Fig. 78 一个部分池化的模型架构，其中每个组的观测 \(y_1, y_2, ..., y_k\) 都有自己的参数，但不同组的参数并非完全独立，而是来自于同一个概率分布。

使用统计符号，可以将分层模型写为公式 (37) ，代码 model_hierarchical_sales 中展示了相应源码，在 {numref}`fig:Salad_Sales_Hierarchial_Regression_Model 中绘制了其图形化表示。

(37)\[\begin{split}\begin{split} \beta_{mj} \sim& \mathcal{N}(\mu_{\beta m}, \sigma_{\beta m}) \\ \sigma_{h} \sim& \overbrace{\mathcal{HN}(\sigma)}^{\text{Hyperprior}} \\ \sigma_{j} \sim& \overbrace{\mathcal{HN}(\sigma_{h})}^{\substack{\text{Group-specific} \\ \text{pooled}}} \\ \mu_{j} =& \beta_{1j} X_1 + \dots + \beta_{mj} X_m \\ Y \sim& \mathcal{N}(\mu_{j},\sigma_{j}) \end{split}\end{split}\]

注意：与 Fig. 75 中的多级模型相比，添加了新的参数 \(\sigma_{h}\)。这是新的超先验分布，用于定义各组中参数的可能值。我们可以在代码 model_hierarchical_sales 中添加超先验。

你可能会问 “我们是否也可以为 \(\beta\) 项添加一个超先验？”，答案很简单：可以。只是针对当前问题，我们假设只有方差存在一定的相关性，而斜率则完全独立。

Listing 55 model_hierarchical_sales

with pm.Model() as model_hierarchical_sales:
    σ_hyperprior = pm.HalfNormal("σ_hyperprior", 20)
    σ = pm.HalfNormal("σ", σ_hyperprior, shape=3)
    
    β = pm.Normal("β", mu=10, sigma=20, shape=3)
    μ = pm.Deterministic("μ", β[food_category.codes] * customers)
    
    sales = pm.Normal("sales", mu=μ, sigma=σ[food_category.codes],
                      observed=sales_observed)
    
    trace_hierarchical_sales = pm.sample(target_accept=.9)
    
    inf_data_hierarchical_sales = az.from_pymc3(
        trace=trace_hierarchical_sales, 
        coords={"β_dim_0":food_category.categories,
                "σ_dim_0":food_category.categories})

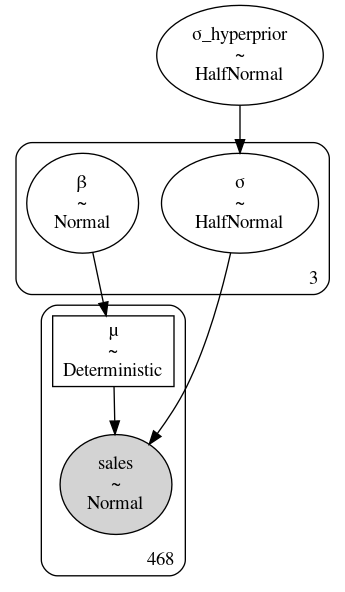
Fig. 79 model_hierarchical_sales 分层模型。其中超先验 \(\sigma_{hyperprior}\) 是一个用于获取三个分组 \(\sigma\) 参数的概率分布参数的上层分布（有点拗口）。

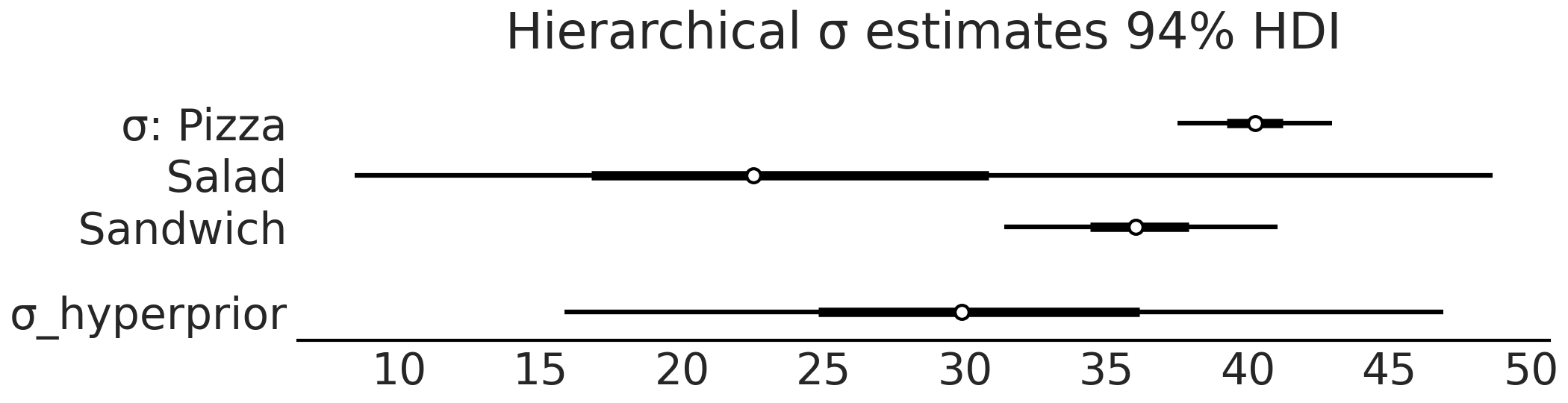
Fig. 80 model_hierarchical_sales 模型的 \(\sigma\) 参数估计的森林图。请注意其中超先验的 \(\sigma_hyperprorior\) 倾向于落在三个分组的 \(\sigma\) 范围中间。

完成分层模型的拟合后，可以检查 Fig. 80 中的 \(\sigma\) 参数估计值。注意模型添加了超先验参数 \(\sigma_{hyperprior}\) ，这是一个估计三个食物类别中 \(\sigma\) 参数分布的分布。如果比较 Table 10 中非池化模型和分层模型的汇总表，我们可以看到分层模型的效果。在非池化估计中，沙拉的 \(\sigma\) 估计的均值是 \(21.3\) ，而在分层模型的估计中，相同参数估计的均值现在是 \(25.5\)，并且被披萨组和三明治组的均值“拉升”。与此同时，在分层类别中，披萨组和沙拉组的估计值虽然略微向均值回归，但与非池化的估计值基本相同。

请注意各组的 \(\sigma\) 估计值明显不同。鉴于观测数据和模型在组之间并不共享参数，这也符合预期。

Table 10 非池化模型中各组别 σ 参数的估计

	mean	sd	hdi_3%	hdi_97%
\(\sigma\)Pizza	40.1	1.5	37.4	42.8
\(\sigma\)Salad	21.3	8.3	8.8	36.8
\(\sigma\)Sandwich	35.9	2.5	31.6	40.8

Table 11 分层模型中各组别 σ 参数的估计

	mean	sd	hdi_3%	hdi_97%
\(\sigma\)Pizza	40.3	1.5	37.5	43.0
\(\sigma\)Salad	25.5	12.4	8.4	48.7
\(\sigma\)Sandwich	36.2	2.6	31.4	41.0
\(\sigma_{hyperprior}\)	31.2	8.7	15.8	46.9

听说你喜欢超先验，所以我在超先验之上又为你设置了一个超先验

在代码 model_hierarchical_salad_sales_centered 中，各组的 \(\sigma_j\) 参数上放置了超先验。同样，我们也可以为参数 \(\beta_{mj}\) 添加超先验，来进一步扩展模型。不过由于 \(\beta_{mj}\) 是高斯先验，所以实际上可以设置两个超先验，其中每个超参数对应一个。

你可能会问：我们是否可以更进一步，将超-超先验添加到参数的超先验分布的参数中呢？是能更进一步，设置超-超-超先验，甚至超-超-超-超先验呢？

虽然设计这种很多层次的模型并从中采样是可行的，但必须要退一步思考超先验在做什么。直观地说，超先验是模型从数据的子组中 “借用” 信息的一种方式，以便为观测较少的其他子组提供估计所需的信息。具有更多观测的组将信息传递给超参数的后验，然后超参数的后验反过来调节具有较少观测值的子组参数。从这个视角看，将超先验放在 组间通用参数 上毫无意义。

分层模型不仅限于两个级别。例如，餐厅销售模型可以扩展为三层模型，顶层代表公司级别，中间层代表区域市场（纽约、芝加哥、洛杉矶），最低层代表具体门店。此时，我们可以拥有一个描述整个公司运行方式的超先验，一个指示某区域运行方式的超先验，以及描述各门店运行方式的先验。这样就可以轻松地比较均值和变化，并基于同一个模型以多种不同方式扩展应用。

4.6.2 分层模型的新问题 — 后验几何形态的复杂性带来的采样难题

到目前为止，我们主要关注模型背后的结构和数学，并假设采样器能够提供对后验的“准确”估计。对于相对简单的模型而言，这大体上是对的，最新版本的通用推断引擎大多能够“正常工作”，但要命的是它们并不总是能够工作。某些后验的几何形态对采样器而言具有较大挑战，一个常见例子是在 Fig. 81 中显示的 Neal 漏斗 [45]。正如名字暗示的那样，此类分布的几何形态中，有一端形状很宽，然后在另一端变窄形成瓶颈。回顾 1.2 一个自制的采样器 节，采样器的功能是从一组参数值转移到另一组参数值，其中一个关键设置是在探索后验时要采取多大步长。在复杂的几何形态中，例如 Neal 漏斗，某步长在一个区域运行良好，但在另一个区域却会惨遭失败。

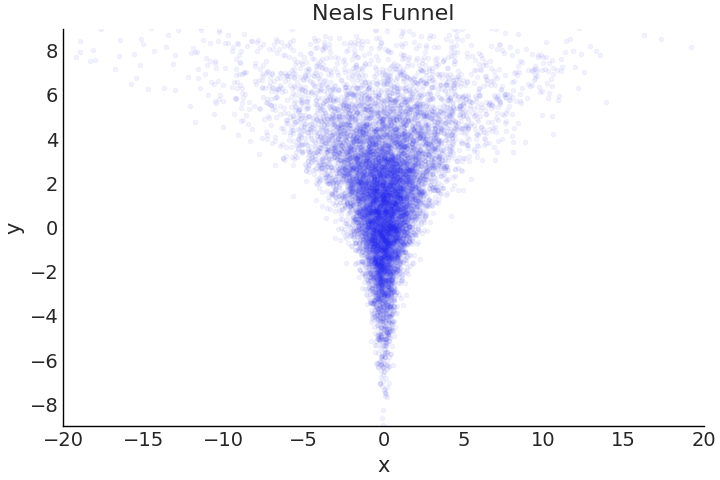
Fig. 81 被称为 Neal 漏斗 的特定几何形态的概率分布及其样本。当在 \(Y\) 值为 \(6\) 到 \(8\) 左右的漏斗顶部采样时，采样器使用 \(1\) 个单位的大步长进行转移，依然能够保持在后验的密集区域内。但是，如果在 \(Y\) 值约为 \(-6\) 到 \(-8\) 的漏斗底部附近进行采样，则几乎在任何方向上的 \(1\) 个单位步长，都会导致转移至低密度区域（图中蓝色点区域表示高密度区域，白色区域表示低密度区域）。后验几何形态造成的这种差异，会使采样器的后验估计性能变差。对于 HMC 采样器，散度会有助于诊断此类采样问题。

在分层模型中，后验的几何形态主要由超先验和其他参数之间的相关性定义，这种相关性会导致上述难以采样的漏斗形态。这并非一种理论上的可能，而是切实存在的问题。幸运的是，有一种被称为“非中心参数化”的建模技巧，有助于缓解此问题。

继续沙拉示例，假设我们开了 \(6\) 家沙拉餐厅，并且像以前一样，希望将销售额预测为顾客数量的某个函数。合成数据集已经由 Python 代码生成，并显示在 Fig. 82 中。由于餐厅销售完全相同的产品，因此分层模型适用于跨组共享信息。我们在公式 (38) 和代码 model_hierarchical_salad_sales 中以数学方式编写了中心化后的模型。我们将在本章剩余部分使用 TFP 和 tfd.JointDistributionCoroutine，这更容易突出参数化的改变。该模型遵循标准的分层格式，其中一个超先验参数被用于部分池化斜率参数 \(\beta_m\) 。

(38)\[\begin{split}\begin{split} \beta_{\mu h} \sim& \mathcal{N} \\ \beta_{\sigma h} \sim& \mathcal{HN} \\ \beta_m \sim& \overbrace{\mathcal{N}(\beta_{\mu h},\beta_{\sigma h})}^{\text{Centered}} \\ \sigma_{h} \sim& \mathcal{HN} \\ \sigma_{m} \sim& \mathcal{HN}(\sigma_{h}) \\ Y \sim& \mathcal{N}(\beta_{m} * X_m,\sigma_{m}) \end{split}\end{split}\]

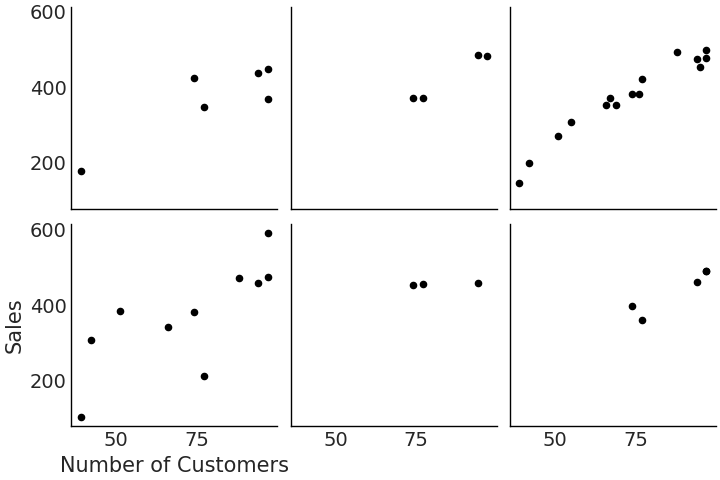
Fig. 82 在 \(6\) 个门店观测的沙拉销售情况。请注意，某些位置相对于其他位置的数据点非常少。

Listing 56 model_hierarchical_salad_sales

def gen_hierarchical_salad_sales(input_df, beta_prior_fn, dtype=tf.float32):
    customers = tf.constant(
        hierarchical_salad_df["customers"].values, dtype=dtype)
    location_category = hierarchical_salad_df["location"].values
    sales = tf.constant(hierarchical_salad_df["sales"].values, dtype=dtype)

    @tfd.JointDistributionCoroutine
    def model_hierarchical_salad_sales():
        β_μ_hyperprior = yield root(tfd.Normal(0, 10, name="beta_mu"))
        β_σ_hyperprior = yield root(tfd.HalfNormal(.1, name="beta_sigma"))
        β = yield from beta_prior_fn(β_μ_hyperprior, β_σ_hyperprior)

        σ_hyperprior = yield root(tfd.HalfNormal(30, name="sigma_prior"))
        σ = yield tfd.Sample(tfd.HalfNormal(σ_hyperprior), 6, name="sigma")

        loc = tf.gather(β, location_category, axis=-1) * customers
        scale = tf.gather(σ, location_category, axis=-1)
        sales = yield tfd.Independent(tfd.Normal(loc, scale),
                                      reinterpreted_batch_ndims=1,
                                      name="sales")

    return model_hierarchical_salad_sales, sales

与在 第 3 章 中使用的 TFP 模型类似，该模型被包装在一个函数中，因此可以更轻松地对任意输入进行条件化。除了输入数据，gen_hierarchical_salad_sales 还接受一个可调用的参数 beta_prior_fn，它用于定义斜率参数 \(\beta_m\) 的先验。在 Coroutine 模型中，我们使用 yield from 语句来调用 beta_prior_fn。这个描述在文字上过于抽象，在代码 model_hierarchical_salad_sales_centered 中可能更容易看到行为动作：

Listing 57 model_hierarchical_salad_sales_centered

def centered_beta_prior_fn(hyper_mu, hyper_sigma):
    β = yield tfd.Sample(tfd.Normal(hyper_mu, hyper_sigma), 6, name="beta")
    return β

# hierarchical_salad_df is the generated dataset as pandas.DataFrame
centered_model, observed = gen_hierarchical_salad_sales(
    hierarchical_salad_df, centered_beta_prior_fn)

如上所示，代码 model_hierarchical_salad_sales_centered 定义了中心化的斜率参数 \(\beta_m\) ，它服从具有超参数 hyper_mu 和 hyper_sigma 的高斯分布。centered_beta_prior_fn 是一个产生 tfp.distribution 的函数，类似于我们编写 tfd.JointDistributionCoroutine 模型的方式。

现在我们有了模型，可以在代码 model_hierarchical_salad_sales_centered_inference 中运行推断并检查结果。

Listing 58 model_hierarchical_salad_sales_centered_inference

mcmc_samples_centered, sampler_stats_centered = run_mcmc(
    1000, centered_model, n_chains=4, num_adaptation_steps=1000,
    sales=observed)

divergent_per_chain = np.sum(sampler_stats_centered["diverging"], axis=0)
print(f"""There were {divergent_per_chain} divergences after tuning per chain.""")

There were [37 31 17 37] divergences after tuning per chain.

我们重用之前在代码 tfp_posterior_inference 中显示的推断代码来运行模型。结果中的第一个问题是散度，我们在第 2.4.7 散度 中介绍过它。样本空间中的另外一个诊断工具展示在 Fig. 83 中。注意随着超先验 \(\beta_{\sigma h}\) 接近零，\(\beta_m\) 参数的后验估计的宽度趋于缩小。特别注意零附近没有样本。换句话说，当 \(\beta_{\sigma h}\) 接近零时，对参数 \(\beta_m\) 进行采样的区域会崩溃，并且采样器无法有效地表征这个后验空间。

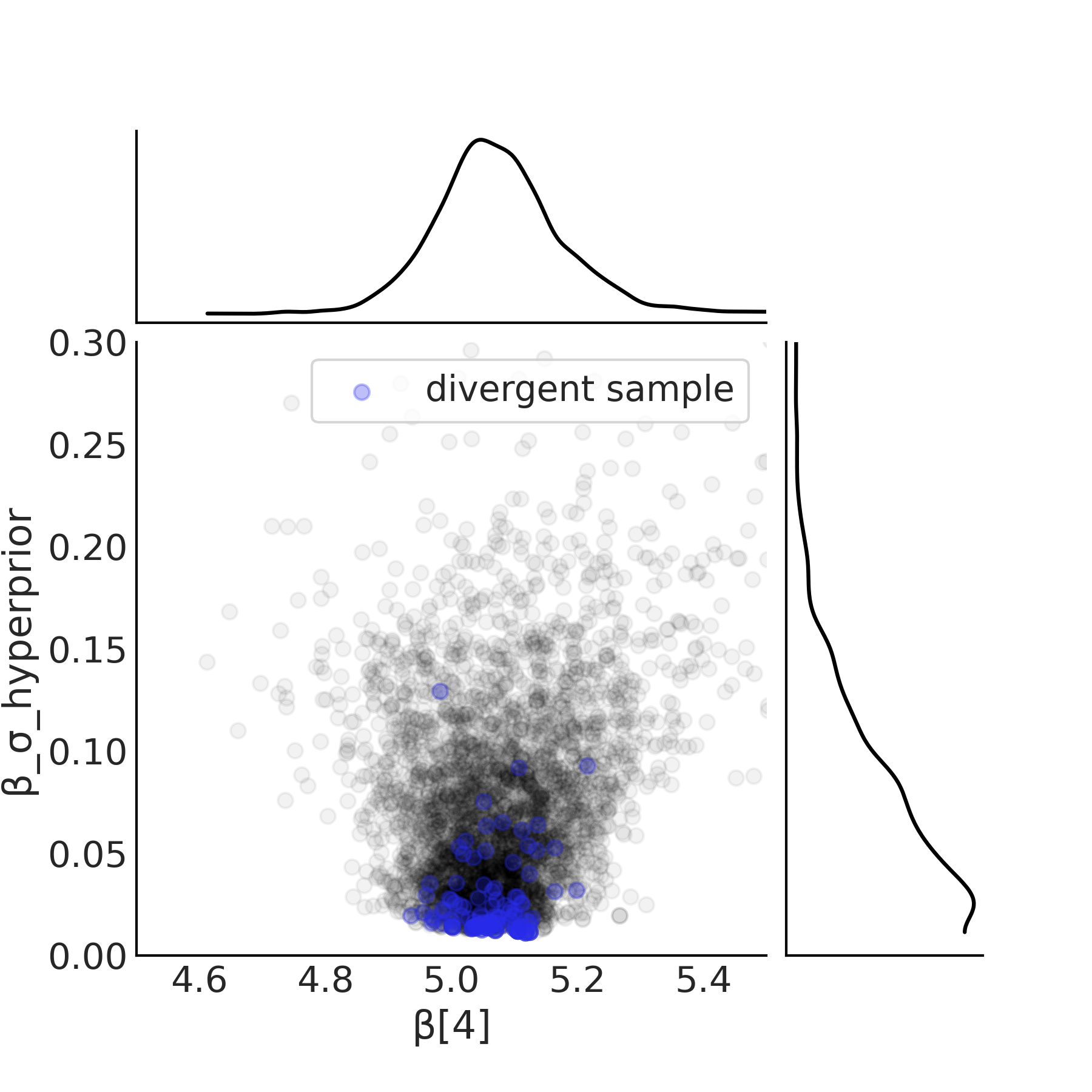
Fig. 83 来自代码 model_hierarchical_salad_sales_centered 中定义的 centered_model 的超先验和 \(\beta[4]\) 斜率的散点图。当超先验接近零时，斜率塌陷的后验空间导致以蓝色显示的散度。

为了缓解这个问题，可以将中心参数化转换为代码 model_hierarchical_salad_sales_non_centered 和公式 (39) 中所示的非中心参数化。关键区别在于，它不是直接估计斜率 \(\beta_m\) 的参数，而是建模为所有组之间共享的公共项和每个组的一个项，该项捕获了各组与公共项的偏差。这使采样器能够更容易地探索 \(\beta_{\sigma h}\) 的所有可能值，并修改后验几何形态。这种后验几何形态变化的影响如 Fig. 84 所示，其中 \(x\) 轴上有多个样本下降到了 \(0\) 值。

(39)\[\begin{split}\begin{split} \beta_{\mu h} \sim& \mathcal{N} \\ \beta_{\sigma h} \sim& \mathcal{HN} \\ \beta_\text{m\_offset} \sim& \mathcal{N}(0,1) \\ \beta_m =& \overbrace{\beta_{\mu h} + \beta_\text{m\_offset}*\beta_{\sigma h}}^{\text{Non-centered}} \\ \sigma_{h} \sim& \mathcal{HN} \\ \sigma_{m} \sim& \mathcal{HN}(\sigma_{h}) \\ Y \sim& \mathcal{N}(\beta_{m} * X_m,\sigma_{m}) \end{split}\end{split}\]

Listing 59 model_hierarchical_salad_sales_non_centered

def non_centered_beta_prior_fn(hyper_mu, hyper_sigma):
    β_offset = yield root(tfd.Sample(tfd.Normal(0, 1), 6, name="beta_offset"))
    return β_offset * hyper_sigma[..., None] + hyper_mu[..., None]

# hierarchical_salad_df is the generated dataset as pandas.DataFrame
non_centered_model, observed = gen_hierarchical_salad_sales(
    hierarchical_salad_df, non_centered_beta_prior_fn)

mcmc_samples_noncentered, sampler_stats_noncentered = run_mcmc(
    1000, non_centered_model, n_chains=4, num_adaptation_steps=1000,
    sales=observed)

divergent_per_chain = np.sum(sampler_stats_noncentered["diverging"], axis=0)
print(f"There were {divergent_per_chain} divergences after tuning per chain.")

There were [1 0 2 0] divergences after tuning per chain.

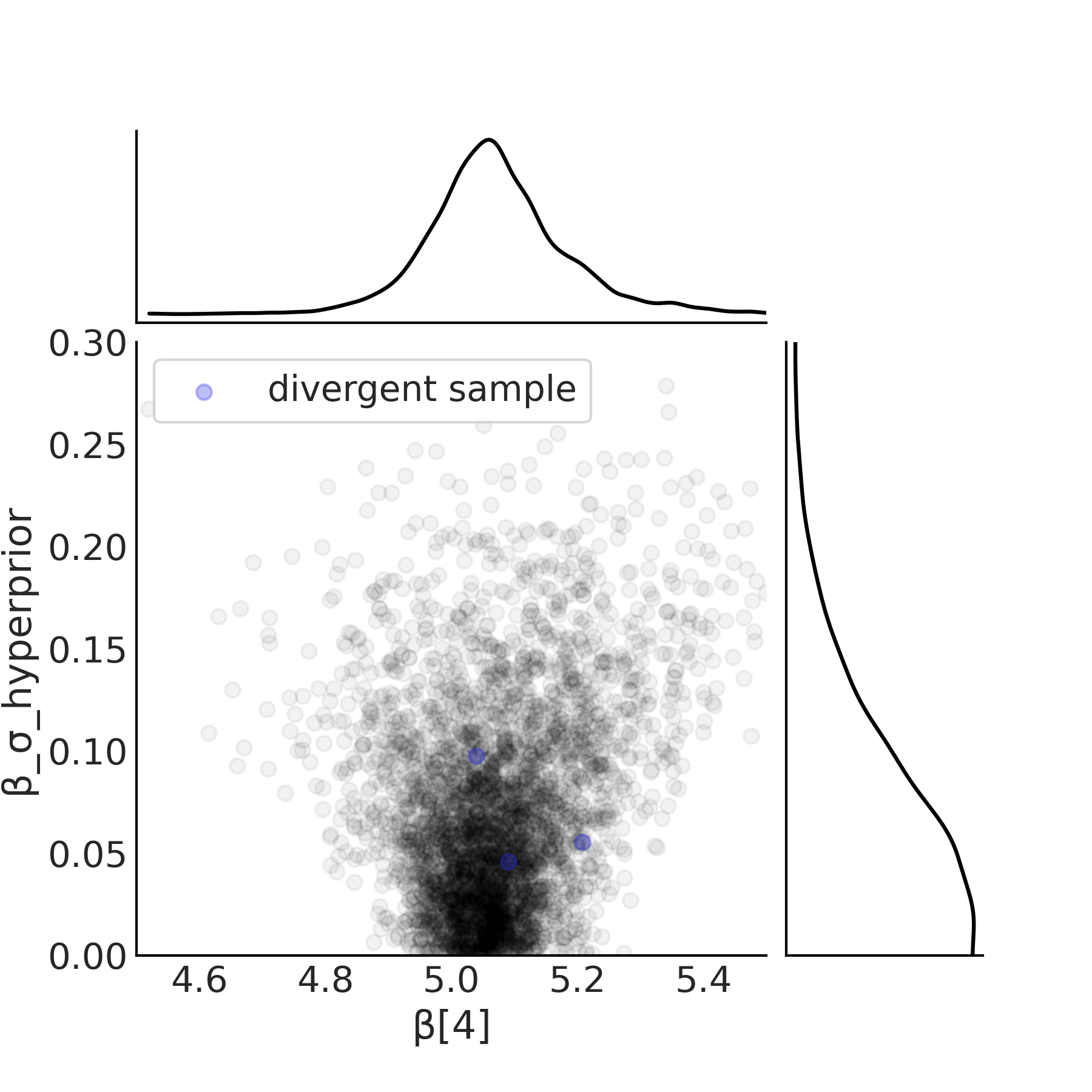
Fig. 84 代码 model_hierarchical_salad_sales_non_centered 中定义的 non_centered_model 中位置 4 的超先验和估计斜率 \(\beta[4]\) 的散点图。在非中心参数化中，采样器能够对接近零的参数进行采样。分歧的数量较少，并不集中在一个领域。

采样的改进对 Fig. 85 中显示的分布估计有重大影响。

虽然再次提醒这个事实可能会令人不快，但采样器只是估计后验分布，虽然在许多情况下它们做得很好，但不能保证永远很好！如果出现警告，请务必注意诊断并进行更深入的检查。

值得注意的是，对于中心或非中心参数化 [46] 方案，没有一种适合所有解决方案的通用方法。它是组级个体似然的信息量（通常对于特定组拥有的数据越多，似然函数的信息量越多）、组级先验的信息量和参数化之间的复杂交互。一般的启发式方法是，如果观测不多，则首选非中心参数化。然而实践中，你应该尝试使用指定了不同先验的中心化和非中心化参数的同组合。你甚至可能会发现，在单个模型中需要同时采用中心化和非中心化的情况。如果你怀疑模型的参数化导致了采样问题，建议你阅读 Michael Betancourt 的分层建模案例研究 [47]。

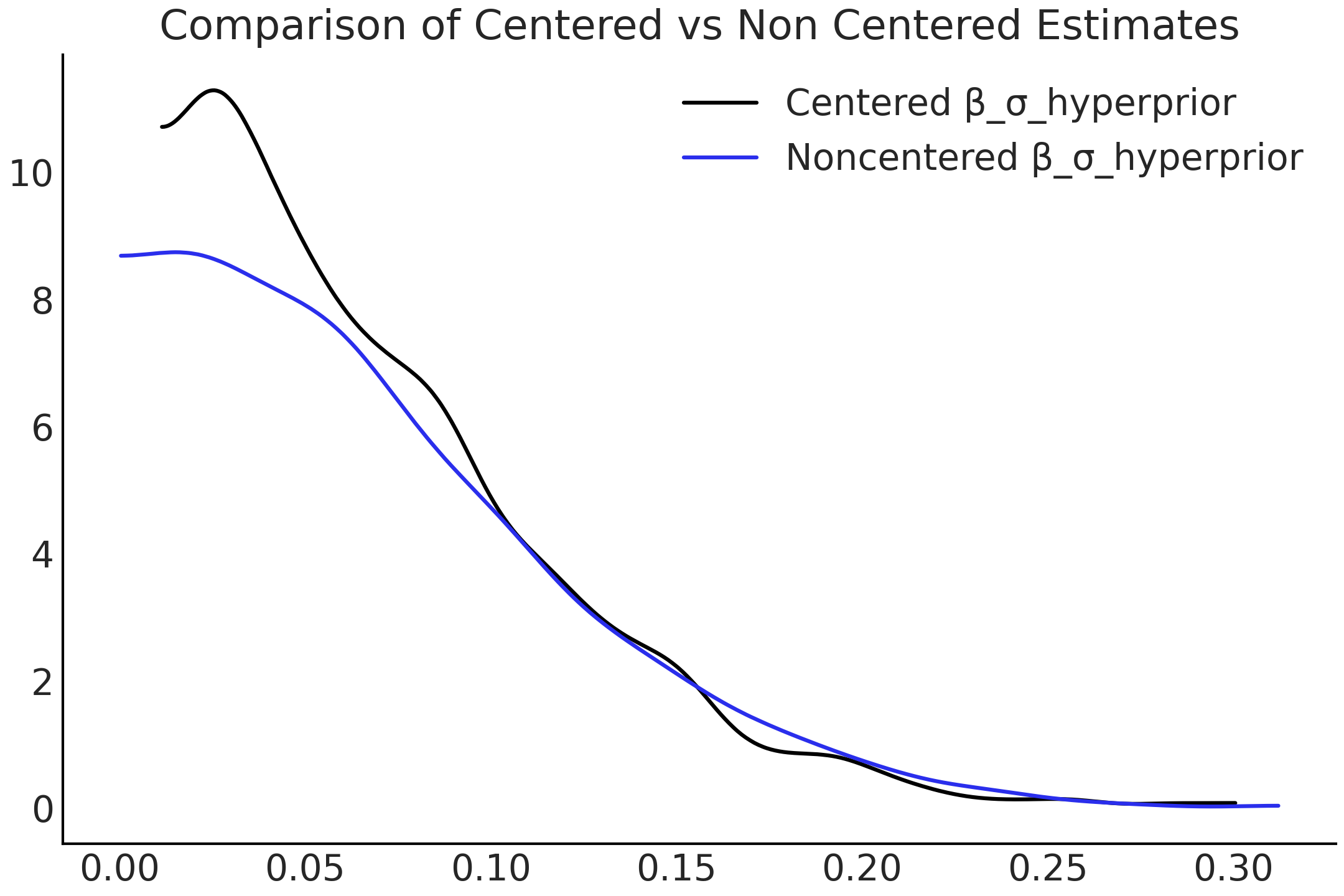
Fig. 85 \(\beta_{\sigma h}\) 在中心化和非中心化参数的概率分布（ KDE 处理）。这种变化源于采样器能够更充分地探索可能的参数空间。

4.6.3 分层模型的优势 — 支持在多个层次上的预测

分层模型的一个微妙特征是它们能够在多个层次上进行估计。虽然看起来很明显，但它非常有用，因为它让我们可以使用一个模型来回答比单层模型更多的问题。在 第 3 章 中，我们可以建立一个模型来估计单个物种的质量，或者建立一个单独的模型来估计任何企鹅的质量，而不考虑物种。使用分层模型，我们可以用一个模型同时估计所有企鹅和每个企鹅物种的质量。使用我们的沙拉销售模型，我们既可以对单个位置进行估计，也可以对整个整体进行估计。我们可以使用代码 model_hierarchical_salad_sales_non_centered 的 non_centered_model 模型来做到这一点，然后编写一个 out_of_sample_prediction_model 模型，如代码 model_hierarchical_salad_sales_predictions 所示。

这使用拟合参数同时对两个地点和和整个公司的 \(50\) 个顾客进行样本外预测。由于 non_centered_model 也是一个 TFP 分布，我们可以将它嵌套到另一个 tfd.JointDistribution 中，这样做构建了一个更大的贝叶斯图模型，该模型扩展了初始 non_centered_model 以包含用于样本 外预测的节点。估计值绘制在 Fig. 86 中。

Listing 60 model_hierarchical_salad_sales_predictions

out_of_sample_customers = 50.

@tfd.JointDistributionCoroutine
def out_of_sample_prediction_model():
    model = yield root(non_centered_model)
    β = model.beta_offset * model.beta_sigma[..., None] + model.beta_mu[..., None]
    
    β_group = yield tfd.Normal(
        model.beta_mu, model.beta_sigma, name="group_beta_prediction")
    group_level_prediction = yield tfd.Normal(
        β_group * out_of_sample_customers,
        model.sigma_prior,
        name="group_level_prediction")
    for l in [2, 4]:
        yield tfd.Normal(
            tf.gather(β, l, axis=-1) * out_of_sample_customers,
            tf.gather(model.sigma, l, axis=-1),
            name=f"location_{l}_prediction")

amended_posterior = tf.nest.pack_sequence_as(
    non_centered_model.sample(),
    list(mcmc_samples_noncentered) + [observed])

ppc = out_of_sample_prediction_model.sample(var0=amended_posterior)

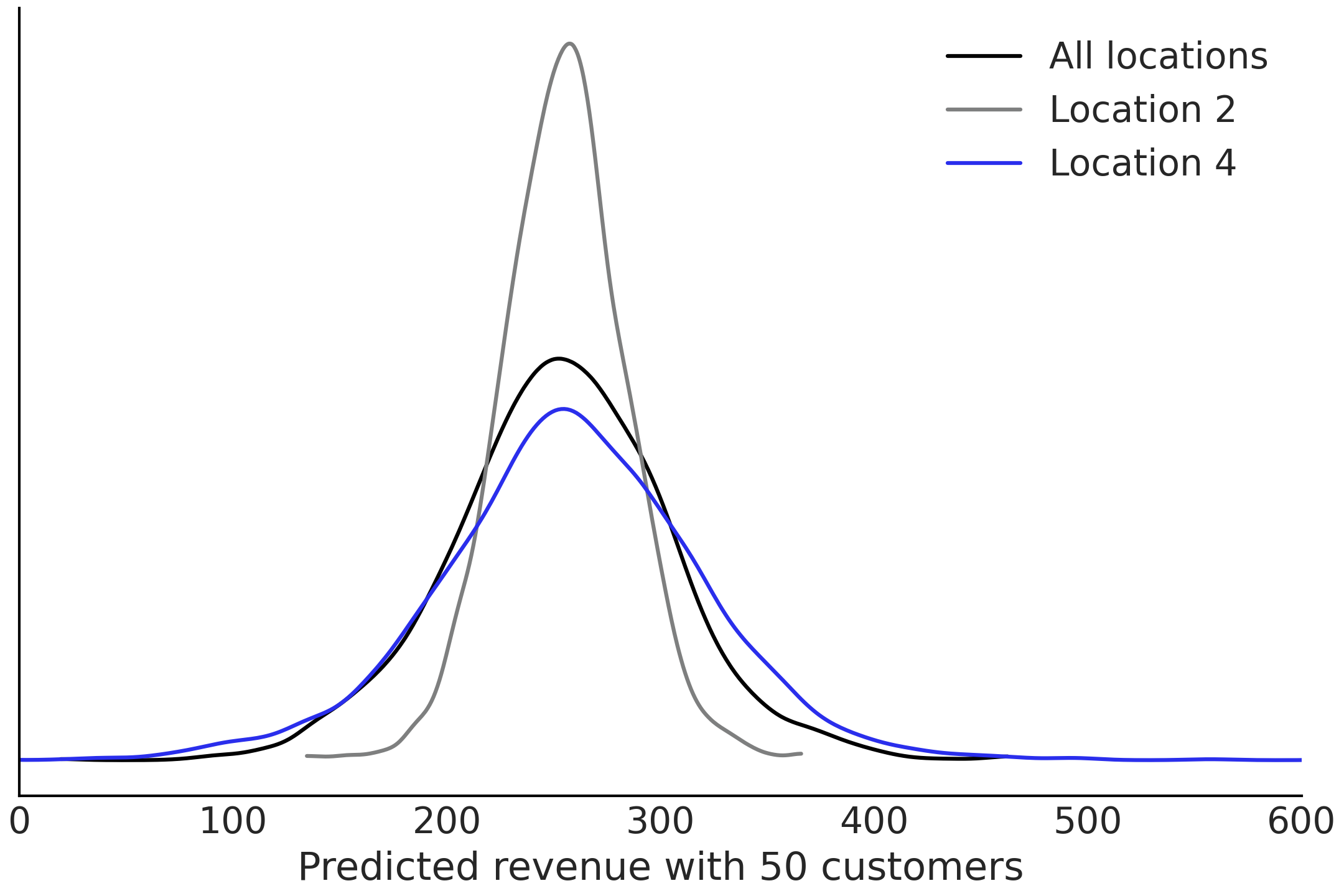
Fig. 86 model_hierarchical_salad_sales_non_centered 模型同时给出的两种后验预测：两个组的单独收入他预测和总体的收入预测。

使用具有超先验的分层模型进行预测的另一个优势是，我们可以对从未观测过的组进行预测。

在这种情况下，假设我们正在新地点开设另一家沙拉门店，就可以获得 \(\beta_{i+1}\) 和 \( \sigma_{i+1}\) 的后验估计，然后通过后验预测采样得到沙拉销售的预测数据，见代码 model_hierarchical_salad_sales_predictions_new_location 。

Listing 61 model_hierarchical_salad_sales_predictions_new_location

out_of_sample_customers2 = np.arange(50, 90)

@tfd.JointDistributionCoroutine
def out_of_sample_prediction_model2():
    model = yield root(non_centered_model)
    
    β_new_loc = yield tfd.Normal(
        model.beta_mu, model.beta_sigma, name="beta_new_loc")
    σ_new_loc = yield tfd.HalfNormal(model.sigma_prior, name="sigma_new_loc")
    group_level_prediction = yield tfd.Normal(
        β_new_loc[..., None] * out_of_sample_customers2,
        σ_new_loc[..., None],
        name="new_location_prediction")

ppc = out_of_sample_prediction_model2.sample(var0=amended_posterior)

除了分层建模的数学优势之外，从计算的角度来看还有一个好处，因为我们只需要构建和拟合单个模型。如果随着时间的推移多次重复使用模型，这会加快建模过程和后续的模型维护过程。

关于 LOO 验证

分层模型使我们可以对以前从未观测过的组进行后验预测。但其预测有效性如何？可以使用交叉验证来评估模型性能吗？

通常在统计中，答案是看这取决于什么。交叉验证（ 以及 LOO 和 WAIC 等方法）是否有效取决于要执行的预测任务以及数据生成机制。如果只是想使用 LOO 来评估模型预测某一个新观测值的能力，那么 LOO 可能就够了。现在，如果想要评估整个组的预测效果，则需要执行留一个组而不是一个数据点的交叉验证方法。但这种情况下，LOO 方法很可能不是太好，因为要一次删除了许多观测值，并且 LOO 近似中的重要性采样依赖于点/组/等的分布彼此是否接近。

4.6.4 分层模型的先验选择

先验选择对于分层模型来说更为重要，因为先验如何与似然的信息量相互作用，如上面第 4.6.2 分层模型的新问题 — 后验几何形态的复杂性带来的采样难题 部分所示。此外，不仅先验分布的形状很重要，我们还可以选择如何参数化它们。这并不仅限于高斯先验，还适用于位置尺度分布族 6 中的所有分布。

在分层模型中，先验分布不仅可以表征组内变化，还可以表征组间变化。从某种意义上说，超先验的选择是在定义“变化的变化”，这可能会使先验信息的表达和推断变得困难。此外，部分池化是超先验的信息量、组数量以及组中的观测数的组合效应。因此，如果你在相似数据集上使用相同的模型但使用较少的组执行推断，则相同的超先验可能不起作用。

因此，除了经验主义（例如，文章中发表的一般性推荐）或一般性建议 7，我们还可以进行敏感性研究，以更好地了解我们的先验选择。例如 Lemoine [48] 表明，当使用如下模型结构对生态数据进行建模时：

(40)\[\begin{split}\begin{split} \alpha_i \sim& \mathcal{N}(\mu_{\alpha},\sigma^2_{\alpha}) \\ \mu_{i} =& \alpha_i + \beta Day_i \\ Y \sim& \mathcal{N}(\mu_{j},\sigma^2) \end{split}\end{split}\]

在非池化截距的情况下，柯西先验在数据点稀少的地方提供了正则化，并且在模型拟合附加数据时不会影响后验。这是在先验参数化和不同的数据量基础上，通过先验敏感性分析来完成的。在你自己的分层模型中，请务必注意先验选择影响推断的多种方式，并使用你的领域专业知识、或先验预测分布之类的工具来做出明智的选择。

习题

4E1. What are examples of covariate-response relationships that are nonlinear in everyday life?

4E2. Assume you are studying the relationship between a covariate and an outcome and the data can be into 2 groups. You will be using a regression with a slope and intercept as your basic model structure.

\[\begin{split}\begin{split} \mu =& \beta_0 + \beta_1 X_1 \\ Y \sim& \mathcal{N}(\mu, \sigma) \end{split}\end{split}\]

Also assume you now need to extend the model structure in each of the ways listed below. For each item write the mathematical equations that specify the full model.

1. Pooled

2. Unpooled

3. Mixed Effect with pooled \(\beta_0\)

4. Hierarchical \(\beta_0\)

5. Hierarchical all parameters

6. Hierarchical all parameters with non-centered \(\beta\) parameters

4E3. Use statistical notation to write a robust linear regression model for the baby dataset.

4E4. Consider the plight of a bodybuilder who needs to lift weights, do cardiovascular exercise, and eat to build a physique that earns a high score at a contest. If we were to build a model where weightlifting, cardiovascular exercise, and eating were covariates do you think these covariates are independent or do they interact? From your domain knowledge justify your answer?

4E5. An interesting property of the Student’s t-distribution is that at values of \(\nu = 1\) and \(\nu = \infty\), the Student’s t-distribution becomes identical two other distributions the Cauchy distribution and the Normal distribution. Plot the Student’s t-distribution at both parameter values of \(\nu\) and match each parameterization to Cauchy or Normal.

4E6. Assume we are trying to predict the heights of individuals. If given a dataset of height and one of the following covariates explain which type of regression would be appropriate between unpooled, pooled, partially pooled, and interaction. Explain why

1. A vector of random noise

2. Gender

3. Familial relationship

4. Weight

4E7. Use LOO to compare the results of baby_model_linear and baby_model_sqrt. Using LOO justify why the transformed covariate is justified as a modeling choice.

4E8. Go back to the penguin dataset. Add an interaction term to estimate penguin mass between species and flipper length. How do the predictions differ? Is this model better? Justify your reasoning in words and using LOO.

4M9. Ancombe’s Quartet is a famous dataset highlighting the challenges with evaluating regressions solely on numerical summaries. The dataset is available at the GitHub repository. Perform a regression on the third case of Anscombe’s quartet with both robust and non-robust regression. Plot the results.

4M10. Revisit the penguin mass model defined in Code Block nocovariate_mass. Add a hierarchical term for \(\mu\). What is the estimated mean of the hyperprior? What is the average mass for all penguins? Compare the empirical mean to the estimated mean of the hyperprior. Do the values of the two estimates make sense to you, particularly when compared to each other? Why?

4M11. The compressive strength of concrete is dependent on the amount of water and cement used to produce it. In the GitHub repository we have provided a dataset of concrete compressive strength, as well the amount of water and cement included (kilograms per cubic meter). Create a linear model with an interaction term between water and cement. What is different about the inputs of this interaction model versus the smoker model we saw earlier? Plot the concrete compressive strength as function of concrete at various fixed values of water.

4M12. Rerun the pizza regression but this time do it with heteroskedastic regression. What are the results?

4H13. Radon is a radioactive gas that can cause lung cancer and thus it is something that would be undesirable in a domicile.

Unfortunately the presence of a basement may increase the radon levels in a household as radon may enter the household more easily through the ground. We have provided a dataset of the radon levels at homes in Minnesota, in the GitHub repository as well as the county of the home, and the presence of a basement.

1. Run an unpooled regression estimating the effect of basements on radon levels.

2. Create a hierarchical model grouping by county. Justify why this model would be useful for the given the data.

3. Create a non-centered regression. Using plots and diagnostics justify if the non-centered parameterization was needed.

4H14. Generate a synthetic dataset for each of the models below with your own choice of parameters. Then fit two models to each dataset, one model matching the data generating process, and one that does not. See how the diagnostic summaries and plots differ between the two.

For example, we may generate data that follows a linear pattern \(x=[1,2,3,4], y=[2,4,6,8]\). Then fit a model of the form \(y=bx\) and another of the form \(y=bx**2\)

1. Linear Model

2. Linear model with transformed covariate

3. Linear model with interaction effect

4. 4 group model with pooled intercept, and unpooled slope and noise

5. A Hierarchical Model

4H15. For the hierarchical salad regression model evaluate the posterior geometry for the slope parameter \(\beta_{\mu h}\).

Then create a version of the model where \(\beta_{\mu h}\) is non-centered. Plot the geometry now. Are there any differences? Evaluate the divergences and output as well. Does non-centering help in this case?

4H16. A colleague of yours, who now lives on an unknown planet, ran experiment to test the basic laws of physics. She dropped a ball of a cliff and registers the position for 20 seconds. The data is available in the Github repository in the file gravity_measurements.csv You know that from Newton’s Laws of physics if the acceleration is \(g\) and the time \(t\) then

\[\begin{split}\begin{split} \text{velocity} &= gt \\ \text{position} &= \frac{1}{2}gt^2 \\ \end{split}\end{split}\]

Your friend asks you to estimate the following quantities

1. The gravitational constant of the planet

2. A characterization of the noise of her measurement device

3. The velocity of the ball at each point during her measurements

4. The estimated position of the ball from time 20 to time 30

参考文献

---

2

Remember this is just a toy dataset, so the take-home message should be about modeling interactions and not about tips.

3

Although the mean is defined only for \(\nu > 1\), and the value of \(\sigma\) agrees with the standard deviation only when \(\nu \to \infty\).

4

A thin dough filled with a salty or sweet preparation and baked or fried. The filling can include red or white meat, fish, vegetables, or fruit. Empanadas are common in Southern European, Latin American, and the Filipino cultures.

5

The commemoration of the first Argentine government and the Argentine independence day respectively.

6

https://en.wikipedia.org/wiki/Location–scale_family

7

https://github.com/stan-dev/stan/wiki/Prior-Choice-Recommendations

previous

第三章：线性模型与概率编程语言

next

第五章: 样条