repository open issue

Contents

第九章: 端到端的贝叶斯工作流

一些餐厅提供一种被称为菜单式品尝的用餐方式。在这种用餐方式中，为客人提供一系列精选的菜肴，通常从前菜开始，然后是汤、沙拉、肉食，最后是甜点。要创造这种体验，单靠菜谱将无济于事。厨师负责使用良好的判断力来确定选择特定的菜谱，准备每一道菜，并将过程安排为一个整体，以无可挑剔的质量和呈现，为客人创造有深刻印象的体验。

同样的想法也适用于贝叶斯分析。仅有数学和代码的一本书可能什么也做不了。随意使用各种技术的统计学家也不会走得太远。成功的统计学家必须能够识别预期结果，确定所需技术，并通过一系列步骤来实现该结果。

9.1 工作流、上下文和问题

通常，所有烹饪菜谱都遵循类似结构：选择食材，通过一种或多种方法加工，然后组装出菜。具体如何做则取决于用餐者。如果他们想要三明治，那么食材包括西红柿和面包，同时还要准备加工用的刀具。如果他们想要番茄汤，则仍然需要番茄，但还需要一个炉子来加工。对周围环境的考虑也很重要，如果在野餐时准备饭菜，而且没有炉子，那么从头开始做汤似乎不太可能。

在较高层面中，执行贝叶斯分析与烹饪菜谱有一些相似之处，但只是表面的。贝叶斯数据分析过程通常是迭代的，并且以非线性方式执行各个步骤。此外，贝叶斯分析过程更难以提前知道获得良好结果所需的确切步骤。

贝叶斯数据分析过程也被称为贝叶斯工作流 [17]，其简化版本显示在 Fig. 150 中。贝叶斯工作流包括模型构建的三个步骤：推断、模型检查和改进、模型比较。在此场景下，模型比较的目的不仅限于选择最佳模型，更重要的是能够帮助我们更好地理解模型。贝叶斯工作流（ 而不仅仅是贝叶斯推断 ）非常重要。贝叶斯计算可能具有挑战性，通常需要对可选模型进行探索和迭代，以获得我们可以信任的推断结果。对于复杂问题，通常我们不会提前知道想要拟合什么模型，但即便如此，我们仍然想了解拟合的模型及其与数据的关系。所有贝叶斯分析所需的一些共同要素包括（ 反映在 Fig. 150 中）：对数据和先验（或领域）知识的需求、用于处理数据的技术、听众通常希望得到的某种体现我们所需内容的报告等等。

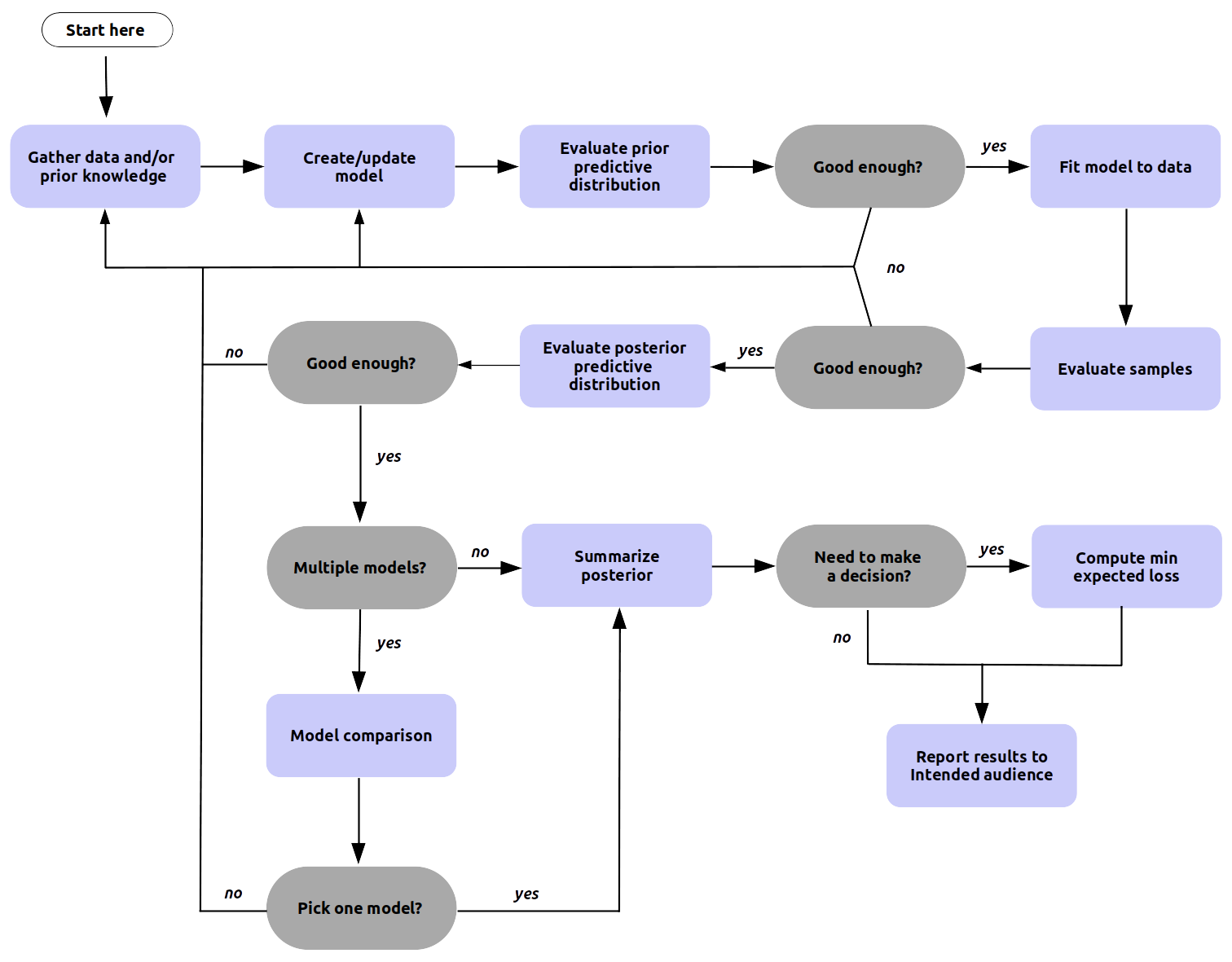
Fig. 150 体现主要步骤的高层次通用贝叶斯工作流。该工作流有许多需要决策的节点，其中有些步骤可能会完全省略，从业人员有责任在其所面临的问题中做出决定。例如，“选择一个模型” 可能意味着 “选择某个单一模型”、“对所有模型进行平均”、或者甚至是“展示所有模型并讨论其优缺点”。另请注意，所有 “评估” 步骤都可用于模型比较。我们可以根据模型的后验预测分布来比较和选择模型、或者选择具有更好收敛性诊断的模型、或者选择具有更接近领域知识的先验预测分布的模型。最后，必须清楚，有时我们需要放弃。即便我们对某些模型并不完全满意，它也可能是在可用资源情况下能够实现的最佳模型。

贝叶斯工作流的详细版本可以在 Gelman 等人的一篇题为贝叶斯工作流的论文 [17] 和 Betancourt 的论文 “Towards a Principled Bayesian Workflow” 中看到 [43] 。

在所使用的特定技术中，最有影响力的因素是所谓的驱动问题。这是对所有同事和涉众都有价值的问题，而我们正试图用分析来回答它，值得花时间和精力去寻找答案。将驱动问题与其他问题区分开也非常重要。

在我们的分析过程中，会遇到许多其他问题（ 例如数据问题、建模问题、推断问题等 ），主要涉及 “如何分析？”的工作方法。不应将这些问题与驱动问题混淆，因为驱动问题主要涉及“为什么要进行分析？”的根源。

因此，在开始任何统计分析之前，首要任务是明确定义要回答的问题。因为驱动问题会影响贝叶斯工作流下游各步骤中的所有选择。他会帮助我们确定应该收集哪些数据、需要哪些工具、模型是否合适、什么模型合适、如何制定模型、如何选择先验、从后验中期望什么、如何在模型之间进行选择、结果表明什么、如何总结结果、传达什么结论等。这里每个问题的答案都会影响分析的价值，以及在寻求答案方面值得付出多少时间和精力。

数据从业者常常在知道一个问题后，决定它需要一个答案，并立即使用最复杂、最细微的统计工具，几乎不花时间去了解需求。设想如果我们是厨师，当听说有人饿了，不去了解需求就为他们准备了一盘价值 \(10,000\) 美元的鱼子酱，结果却发现一碗简单的麦片就已经足够了，这是多么懊恼。这好比在实际情况下，当线性回归已经足够时，数据科学家在大型 GPU 机器上使用神经网络生成了 \(10,000\) 美元的云计算账单。所以，在真正了解需求之前，不要成为那个急着使用贝叶斯方法、神经网络、分布式计算集群或其他复杂工具的数据科学家和统计学家。

9.1.1 应用示例：航班延误问题

对于本章中的大多数部分，每个示例都将建立在上一节的基础上，我们将从这里开始。让我们想象一下，我们在美国威斯康星州麦迪逊机场工作，是一名统计学家。航班到达的延误导致了挫败感，我们的数学技能可以帮助量化这种情况。我们首先认识到涉及多个人，一个必须决定何时到达机场的旅行者，一个为机场工作的会计师，或者必须管理整个运营的机场首席执行官。

这些人中的每一个都有不同的担忧，这导致了不同的问题，其中一些可能是：

1. 我的航班出发延误的可能性有多大？

2. 我的航班到达延误的可能性有多大？

3. 上周有多少航班延误？

4. 航班延误给机场造成的损失是多少？

5. 给定两种业务选择，我应该选择哪一种？

6. 与航班起飞延误有什么关系？

7. 航班起飞延误的原因是什么？

这些问题中的每一个虽然都是相关的，但都存在微妙的不同。旅客担心他们的特定航班延误，但机场会计师和管理人员关心所有航班的延误。会计师并不担心航班延误的持续时间，而是对财务记录延误的成本感兴趣。这位高管不太关心历史，而更关心在未来航班延误的情况下做出什么样的战略决策。

在这一点上，读者可能会问，我来这里学习贝叶斯建模，我们什么时候开始？在我们到达那里之前考虑这个示例。如果驱动问题是*“上周晚些时候有多少飞机抵达？”*我们需要贝叶斯模型吗？不满意的答案是否定的，不需要推断，只是基本的计数。不要假设每个问题都需要贝叶斯统计。强烈考虑简单的计数、均值和图等统计量数据是否足以回答驱动问题。

现在，假设机场首席执行官来找你，机场统计员，他进退两难。每次到达时，机场必须让工作人员随时待命，引导飞机着陆，并设有一个可供乘客下机的登机口。

这意味着当飞机晚点到达时，工作人员和机场基础设施将闲置等待到达，最终将资金浪费在未使用的资源上。因此，机场和航空公司达成了一项协议，每迟到一分钟，航空公司将向机场支付每分钟 300 美元的费用。然而，航空公司现在要求更改该协议。他们建议所有 10 分钟以下的延误费用为 1000 美元，10 分钟到 100 分钟之间的延误费用为 5000 美元，超过 100 分钟的延误费用为 30,000 美元。你的 CEO 怀疑航空公司提出这种结构是为了省钱。机场 CEO 要求您使用您的数据能力来回答这个问题，“我们应该接受新的滞纳金结构还是保留旧的？\”。航空公司的 CEO 提到如果做出错误的决定可能会付出多大的代价，并要求您准备一份有关潜在财务影响的报告。作为经验丰富的统计学家，您决定量化延迟的潜在分布并使用决策分析来帮助选择基础设施投资。我们相信综合的端到端贝叶斯分析将提供对未来结果的更完整的理解。您可以证明模型开发的成本和复杂性是合理的，因为做出错误决策的财务风险远远超过了制作贝叶斯模型的时间和成本。如果您不确定我们是如何得出这个结论的，请不要担心，我们将在后续部分中逐步完成思考过程。我们在标题以 Applied Example 开头的小节中回到这个航班延误问题。

9.2 获取数据

对于没有食材的厨师来说，烹制出一道好菜是不可能的，而且用劣质的食材也很有挑战性。同样，如果没有数据，推断也是不可能的。质量差的数据具有挑战性，最好的统计学家会花费大量时间来了解其信息的细微差别和细节。不幸的是，对于哪些数据可用或如何为每个驾驶问题收集数据，没有一种适合所有策略的方法。考虑的主题涵盖从所需精度、成本、道德到收集速度等主题。但是，我们可以考虑一些广泛的数据收集类别，每种类别都有其优点和缺点。

9.2.1 样本调查

美国历史上有“向邻居要一杯糖”的民间说法，方便你用完的时候。对于统计学家来说，相当于采样调查，也称为民意调查。轮询的典型动机是使用有限数量的观察来估计总体参数 \(Y\)。采样调查还可以包括协变量，例如年龄、性别、国籍，以找到相关性。存在各种采样方法，例如随机采样、分层采样和整群采样。不同的方法在成本、可忽略性和其他因素之间进行权衡。

9.2.2 试验设计

如今，一个非常流行的用餐概念是从农场到餐桌。对于厨师来说，这可能很有吸引力，因为他们不受通常可用的限制，而是可以获得更广泛的成分，同时保持对各个方面的控制。对于统计学家来说，等效的过程称为实验设计。在实验中，统计学家能够决定他们想研究什么，然后设计数据生成过程，以帮助他们最好地理解他们感兴趣的主题。通常这涉及“治疗”，实验者可以改变部分过程，或者换句话说，改变协变量，以查看对 \(\boldsymbol{y}_{obs}\) 的影响。典型的例子是药物试验，其中测试新药的有效性，将药物从一组中扣留给另一组。实验设计中的处理模式示例包括随机化、区组和因子设计。数据收集方法的示例包括双盲研究等主题，其中受试者和数据收集者都不知道应用了哪种治疗方法。

实验设计通常是识别因果关系的最佳选择，但运行实验通常会付出高昂的代价。

9.2.3 可观测的研究

种植自己的原料可能很昂贵，因此更便宜的选择可能是寻找自己生长的原料。统计学家对此的看法是观察性研究。在观察性研究中，统计学家几乎无法控制治疗或数据收集。这使得推断具有挑战性，因为可用数据可能不足以实现分析工作的目标。然而，好处是，特别是在现代，观察性研究一直在进行。例如，在研究恶劣天气期间公共交通的使用时，随机选择下雨或不下雨是不可行的，但可以通过记录当天的天气以及当天的门票销售等其他测量值来估计效果。与实验设计一样，观察性研究可用于确定因果关系，但必须更加小心以确保数据收集是可忽略的（您将在下面看到一个定义）并且模型不排除任何隐藏的影响。

9.2.4 缺失数据

所有数据收集都容易受到丢失数据的影响。人们可能无法对民意调查做出回应，实验者可能会忘记写下来，或者在观察性研究中，一天的日志可能会被意外删除。

丢失数据也不总是二进制条件，它也可能意味着部分数据丢失。例如，未能记录小数点后的数字，例如缺少精度。

为了解决这个问题，我们可以扩展我们对贝叶斯定理的公式，通过添加如公式 (77) [18] 中所示的项来解释缺失。在这个公式中，\(\boldsymbol{I}\) 是包含向量，表示哪些数据点缺失或包含，\(\boldsymbol{\phi}\) 表示分布包含向量的参数。

(77)\[\begin{split}\begin{split} Y_{obs} &= {(i,j): \boldsymbol{I}_{ij}=1} \\ Y_{mis} &= {(i,j): \boldsymbol{I}_{ij}=0} \\ p(\boldsymbol{\theta}, \boldsymbol{\phi} \mid Y_{obs},I) &\propto p(Y_{obs}, I \mid \boldsymbol{\theta}, \boldsymbol{\phi})p(\boldsymbol{\theta}, \boldsymbol{\phi}) \end{split} \end{split}\]

即使丢失的数据没有被明确建模，谨慎的做法是保持注意你的观察数据是有偏差的，只是因为它已经被观察到了！收集数据时，请确保不仅要注意存在的内容，还要考虑可能不存在的内容。

9.2.5 应用示例：收集航班延误数据

在机场工作，您可以访问许多数据集，从当前温度到餐馆和商店的收入，再到机场营业时间、登机口数量，再到有关航班的数据。

回顾我们的驾驶问题，“基于飞机的晚到，我们更喜欢哪种滞纳金结构？\”。我们需要一个数据集来量化迟到的概念。如果滞纳金结构是二进制的，例如，每次迟到 100 美元，那么布尔值 True/False 就足够了。在这种情况下，当前滞纳金结构和以前的滞纳金结构都需要关于到达延迟的分钟级数据。

您意识到，作为一个小型机场，麦迪逊机场从未有航班从遥远的目的地（如伦敦盖特威克机场或新加坡樟宜机场）抵达，这在您观测数据集中存在很大差距。您向您的 CEO 询问此事，她提到该协议仅适用于来自明尼阿波利斯和底特律机场的航班。有了所有这些信息，您对了解建模相关航班延误所需的数据感到很自在。 从“数据生成过程”的知识中，您知道天气和航空公司对航班延误有影响。但是，出于三个原因，您决定不将这些包括在您的分析中。您的老板并没有问为什么航班延误，因此不需要分析协变量。您独立假设历史天气和航空公司行为将保持一致，这意味着您无需针对预期的未来情景执行任何反事实调整。最后，您知道您的老板的期限很短，因此您专门设计了一个可以相对快速完成的简单模型。

您的数据需求已缩小到航班到达延误的分钟级数据集。在这种情况下，使用观察数据的先前历史是实验设计或调查之上的明确选择。美国运输统计局保留了包括延误信息在内的航班数据的详细日志。这些信息保持在足以用于我们分析的精确度，并且考虑到航空公司旅行的监管程度，我们希望这些数据是可靠的。有了我们手中的数据，我们可以开始我们的第一个专门的贝叶斯任务。

9.3 设计不止一个模型

有了我们的问题和数据，我们就可以开始构建我们的模型了。请记住，模型构建是迭代的，您的第一个模型可能在某种程度上是错误的。虽然这看起来令人担忧，但实际上它可以释放出来，因为我们可以从良好的基础开始，然后使用我们从计算工具中获得的反馈来迭代一个模型来回答我们的驱动问题。

9.3.1 在构建贝叶斯模型前需要问的问题

在贝叶斯模型的构建中，一个自然的起点是贝叶斯公式。我们可以使用原始公式，但我们建议使用公式 (77) 并单独考虑每个参数

• \(p(Y)\)：（似然）什么分布描述了给定 X 的观察数据？

• \(p(X)\)：（协变量）潜在数据生成过程的结构是什么？

• \(p(\boldsymbol{I})\)：（可忽略性）我们需要对数据收集过程进行建模吗？

• \(p(\boldsymbol{\theta})\)：（先验）在看到任何数据之前，什么是合理的参数集？

此外，由于我们是计算贝叶斯主义者，我们还必须回答另一组问题

• 我可以在概率编程框架中表达我的模型吗？

• 我们可以在合理的时间内估计后验分布吗？

• 后验计算是否显示任何缺陷？

所有这些问题都不需要立即回答，几乎每个人在最初构建新模型时都会弄错。虽然最终模型的最终目标是回答驱动问题，但这通常不是第一个模型的目标。第一个模型的目标是表达最简单合理且可计算的模型。然后我们使用这个简单的模型来了解我们的理解，调整模型，然后重新运行，如 Fig. 150 所示。为此，我们使用了贯穿本书的大量工具、诊断和可视化。

统计模型的类型

如果我们参考 DR Cox [112]，有两种一般的方式来考虑构建统计模型，一种基于模型的方法，其中“感兴趣的参数旨在捕获该生成过程的重要且可解释的特征，分开来自特定数据的偶然特征。或者基于设计的方法，其中“对现有人群进行采样和实验设计有一种不同的方法，其中概率计算基于调查人员在调查计划阶段使用的随机化\ “。贝叶斯公式的基本原理对使用哪种方法没有意见，贝叶斯方法可以用于两种方法。我们的航空公司示例是基于模型的方法，而本章末尾的实验模型是基于设计的方法。例如，可以说大多数基于频率论的分析都遵循基于设计的方法。

这并不意味着他们是对还是错，只是针对不同情况采取不同的方法。

9.3.2 应用示例：选择航班延误的似然

对于我们的航班延误困境，我们决定通过选择观察到的航班延误的可能性来开始建模之旅。我们花一点时间来收集我们现有领域知识的详细信息。在我们的数据集中，延迟可以是负值或正值。正值表示航班晚，负值表示航班早。我们可以在这里选择只模拟延误并忽略所有提前到达。但是，我们将选择对所有到达进行建模，以便我们可以为所有航班到达建立生成模型。这对于我们稍后将要进行的决策分析可能会派上用场。

我们的驱动问题没有提出任何有关相关性或因果关系的问题，因此为了简单起见，我们将在没有任何协变量的情况下对观察到的分布进行建模。这样我们就可以只关注可能性和先验。添加协变量可能有助于对观察到的分布进行建模，即使它们本身对个人没有兴趣，但我们不想超越自己。让我们使用代码块 plot_flight_data 绘制观测数据以了解其分布，结果显示在 Fig. 151 中。

Listing 112 plot_flight_data

df = pd.read_csv("../data/948363589_T_ONTIME_MARKETING.zip")
fig, ax = plt.subplots(figsize=(10,4))

msn_arrivals = df[(df["DEST"] == "MSN") & df["ORIGIN"].isin(["MSP", "DTW"])]["ARR_DELAY"]

az.plot_kde(msn_arrivals.values, ax=ax)
ax.set_yticks([])
ax.set_xlabel("Minutes late")

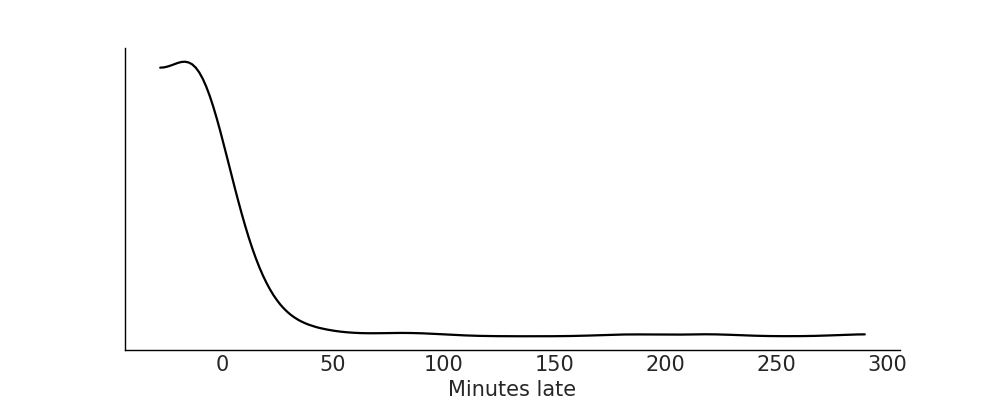
Fig. 151 观察到的到达延迟数据的核密度估计图。请注意几个有趣的功能。所有航班到达的大部分都在 -20 到 40 之间，并且在该地区有一个普遍的钟形图案。然而，大值的长尾表明虽然相对较少的航班晚点，但其中一些航班在抵达麦迪逊机场时可能真的晚了。

考虑可能性，我们有几个选择。我们可以将其建模为离散的分类分布，其中每一分钟都被分配一个概率。但这可能会带来一些挑战：从统计角度来看，我们需要选择桶的数量。虽然有非参数技术可以改变桶的数量，但这意味着我们还必须创建一个可以估计桶数量的模型，除了估计每个桶的每个概率。

根据领域专业知识，我们知道每一分钟并不是完全独立的。如果很多飞机晚点 5 分钟，直观的感觉就是很多飞机也会晚点 4 分钟或 6 分钟。因此，连续分布似乎更自然。我们希望对早到和晚到都进行建模，因此分布必须支持负数和正数。结合统计和领域知识，我们知道大多数飞机准点，而且航班通常会早一点或晚一点到达，但如果晚点，他们可能真的会晚点。

用尽我们的领域专业知识，我们现在可以绘制数据，检查与我们的领域专业知识的一致性以及帮助形成我们的模型的进一步线索。从 Fig. 151，我们有几个合理的似然分布选择：高斯分布、偏斜高斯分布和 Gumbel 分布。普通高斯分布是对称的，与分布的偏度不一致，但它是一种直观的分布，可用于基线比较。顾名思义，Skew-Normal 有一个附加参数 \(\alpha\) 控制分布的偏度。最后，Gumbel 分布专门用于描述一组值的最大值。

如果我们想象飞机延误是由行李装载、乘客装载和其他潜在因素的最大值引起的，那么这种分布的想法就符合航班到达过程的现实。

由于航空公司流程受到严格监管，我们认为目前不需要对缺失数据进行建模。此外，我们选择忽略协变量以简化我们的贝叶斯工作流。通常建议从一个简单的模型开始，让完整的贝叶斯工作流通知您根据需要添加复杂性的决定，而不是从一个复杂的模型开始，在以后的步骤中调试变得更具挑战性。 通常，我们会选择一种可能性，并在尝试另一种可能性之前一直使用贝叶斯工作流。但是为了避免回溯这个例子，我们将继续并行处理两个。现在我们将继续使用代码块 plane_likelihoods 中的 Normal 和 Gumbel 似然，将 Skew-Normal 似然模型留给读者作为练习。

Listing 113 plane_likelihoods

with pm.Model() as normal_model:
    normal_alpha = ...
    normal_sd = ...
    
    normal_delay = pm.Normal("delays", mu=mu, sigma=sd,  
                             observed=delays_obs)

with pm.Model() as gumbel_model:
    gumbel_beta = ...
    gumbel_mu = ...
    
    gumbel_delays = pm.Gumbel("delays", mu=mu, beta=beta, 
                              observed=delays_obs)

现在所有的先验都有占位符省略运算符 (…)。

选择先验将是下一节的主题。

9.4 选择先验和预测先验分布

现在我们已经确定了我们需要选择先验的可能性。与之前类似，有一些一般性问题可以帮助指导先验的选择。

1. 先验在数学背景下有意义吗？

2. 先验在领域的上下文中是否有意义？

3. 我们的推断引擎能否产生具有所选先验的后验？

我们在前面的部分中广泛地介绍了先验。在 1.4 先验分布的选择方法 部分中，我们展示了先验选择的多个原则选项，例如 Jeffrey 的先验或弱信息先验。在 2.2 先验预测检查 节中，我们展示了如何通过计算评估先验选择。作为快速复习，应根据可能性、模型目标（例如参数估计还是预测）来证明先前的选择是合理的。

我们还可以使用先验分布来编码我们关于数据生成过程的先验领域知识。我们也可以使用先验作为工具来集中推断过程，以避免花费时间和计算来探索“明显错误”的参数空间，至少正如我们使用我们的领域专业知识所期望的那样。

在工作流中，采样和绘制先验和先验预测分布为我们提供了两个关键信息。第一个是我们可以在我们选择的概率编程语言中表达我们的模型，第二个是了解我们选择的模型的特征，以及对我们先验的敏感性。如果我们的模型在先前的预测采样中失败，或者我们意识到在没有数据的情况下我们不了解模型的响应，我们可能需要在继续之前重复前面的步骤。幸运的是，使用概率编程语言，我们可以更改先验的参数化或模型的结构，以了解其影响并最终了解所选规范的信息性。

不应该有先验分布或似然分布是预先确定的错觉，本书中印出的是无数试验和调整的结果，以找到提供合理的先验预测分布的参数。在编写自己的模型时，您还应该在进行下一步推断之前迭代先验和可能性。

9.4.1 应用示例：选择航班延误模型的先验

在做出任何具体的数字选择之前，我们会评估我们关于航班到达的领域知识。航空公司的航班到达时间可能早或晚（分别为负或正），但有一定的界限。例如，航班迟到 3 小时以上似乎不太可能，但也不太可能提前 3 小时以上。让我们指定参数化并绘制先验预测以确保与我们的领域知识的一致性，如代码块 airline_model_definition 所示。

Listing 114 airline_model_definition

with pm.Model() as normal_model:
    normal_sd = pm.HalfStudentT("sd",sigma=60, nu=5)
    normal_mu = pm.Normal("mu", 0, 30) 

    normal_delay = pm.Normal("delays",mu=normal_mu,
                             sigma=normal_sd, observed=msn_arrivals)
    normal_prior_predictive = pm.sample_prior_predictive()
    
with pm.Model() as gumbel_model:
    gumbel_beta = pm.HalfStudentT("beta", sigma=60, nu=5)
    gumbel_mu = pm.Normal("mu", 0, 40)
    
    gumbel_delays = pm.Gumbel("delays",
                              mu=gumbel_mu,
                              beta=gumbel_beta,
                              observed=msn_arrivals)
    gumbel_prior_predictive = pm.sample_prior_predictive()

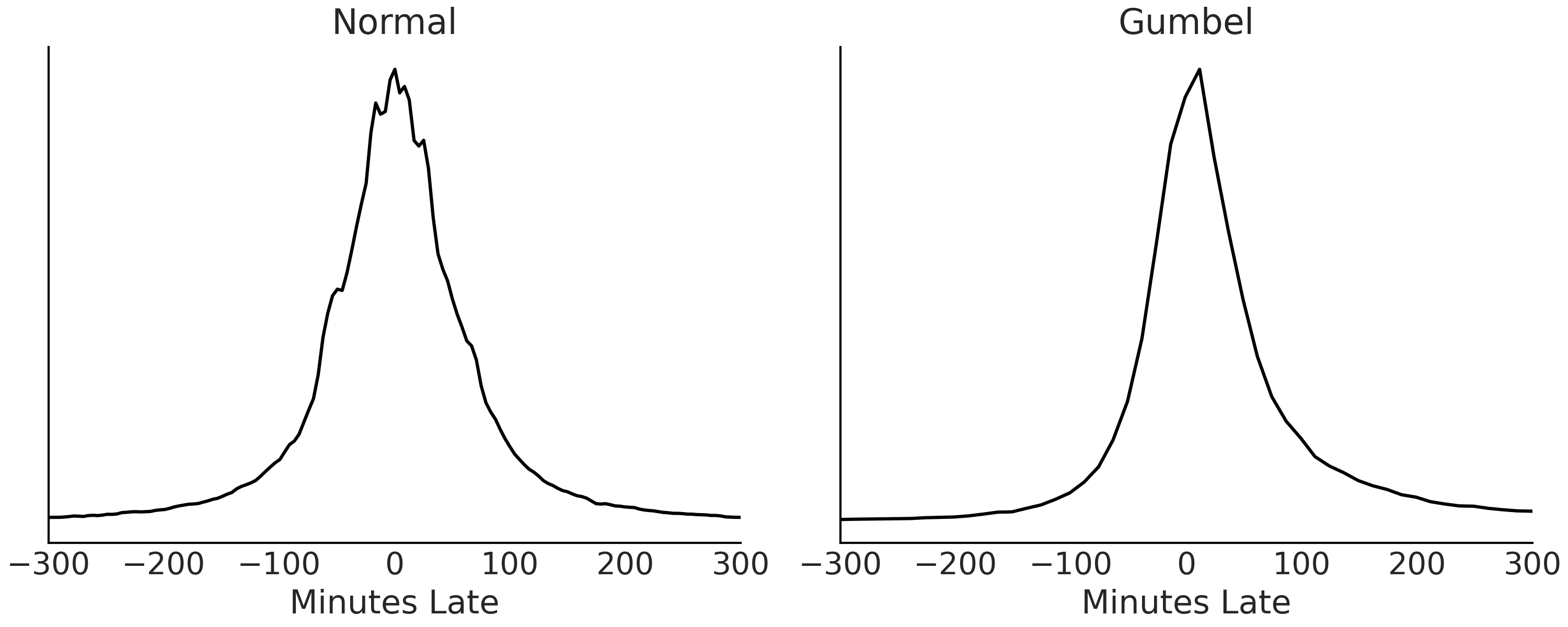
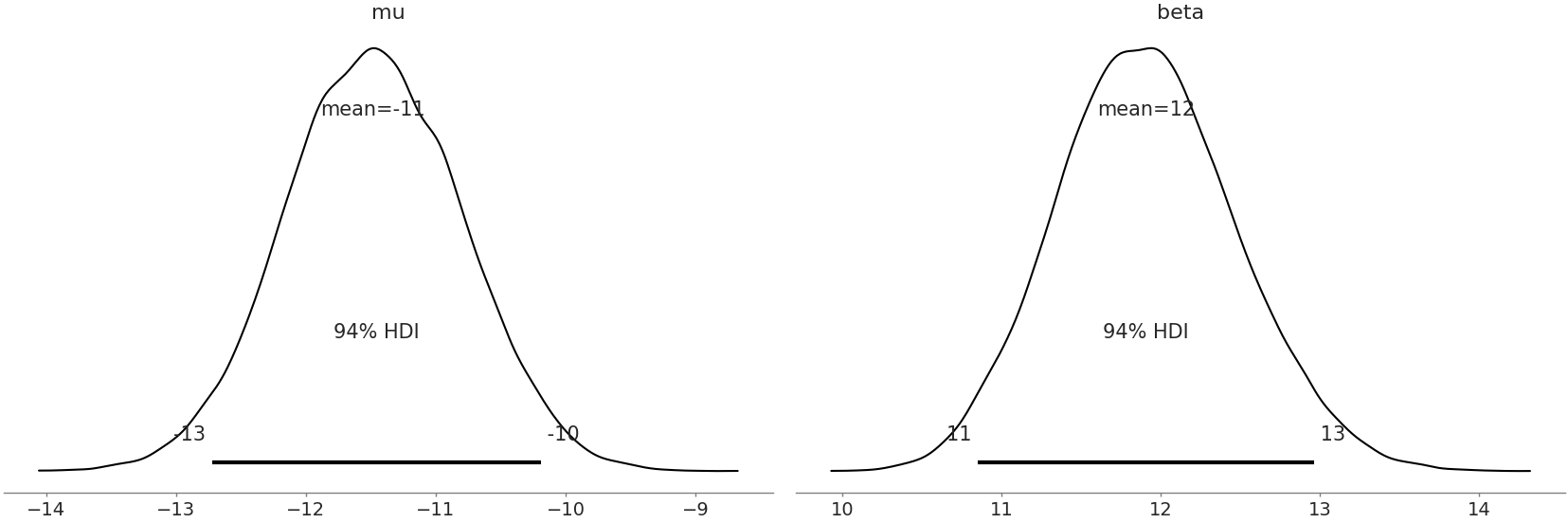
Fig. 152 每个模型的先验预测分布。在对数据进行调节之前，两种分布对于我们的领域问题看起来都是合理的，并且彼此相似。

在概率编程语言报告的先前预测模拟中没有错误并且在 Fig. 152 中具有合理的先验预测分布，我们决定我们选择的先验足以继续我们的下一步。

9.5 推断和推断的诊断

亲爱的读者，我们希望您没有直接跳到本节。

推断是“最有趣”的部分，一切都聚集在一起，计算机给了我们“答案”。但是，如果没有很好地理解问题、数据和模型（包括先验），推断可能是无用的，并且会产生误导。在贝叶斯工作流中，推断建立在前面的步骤之上。一个常见的错误是尝试通过首先调整采样器参数或运行超长链来修复分歧，而实际上，先验或可能性的选择才是问题的根本原因。统计计算的民间定理说：“当你有计算问题时，你的模型 [113] 经常有问题。

话虽如此，我们有一个强大的先验，如果你做到了这一点，那么你就是一个勤奋的读者，并且了解我们迄今为止的所有选择，所以让我们深入推断。

9.5.1 应用示例： 运行航班延误模型上的推断

我们选择使用 PYMC3 中默认的 HMC 采样器从后验分布中采样。

让我们运行我们的采样器并使用典型的诊断评估我们的 MCMC 链。我们对采样挑战的第一个迹象是 MCMC 采样期间的分歧。有了这些数据和模型，没有人提出来。但是，如果提出了一些问题，则表明应该进行进一步的探索，例如我们在 4.6.2 分层模型的新问题 — 后验几何形态的复杂性带来的采样难题 部分中执行的步骤。

Listing 115 airline_model_inference

with normal_model:
    normal_delay_trace = pm.sample(random_seed=0, chains=2)
az.plot_rank(normal_delay_trace)

with gumbel_model:
    gumbel_delay_trace = pm.sample(chains=2)
az.plot_rank(gumbel_delay_trace)

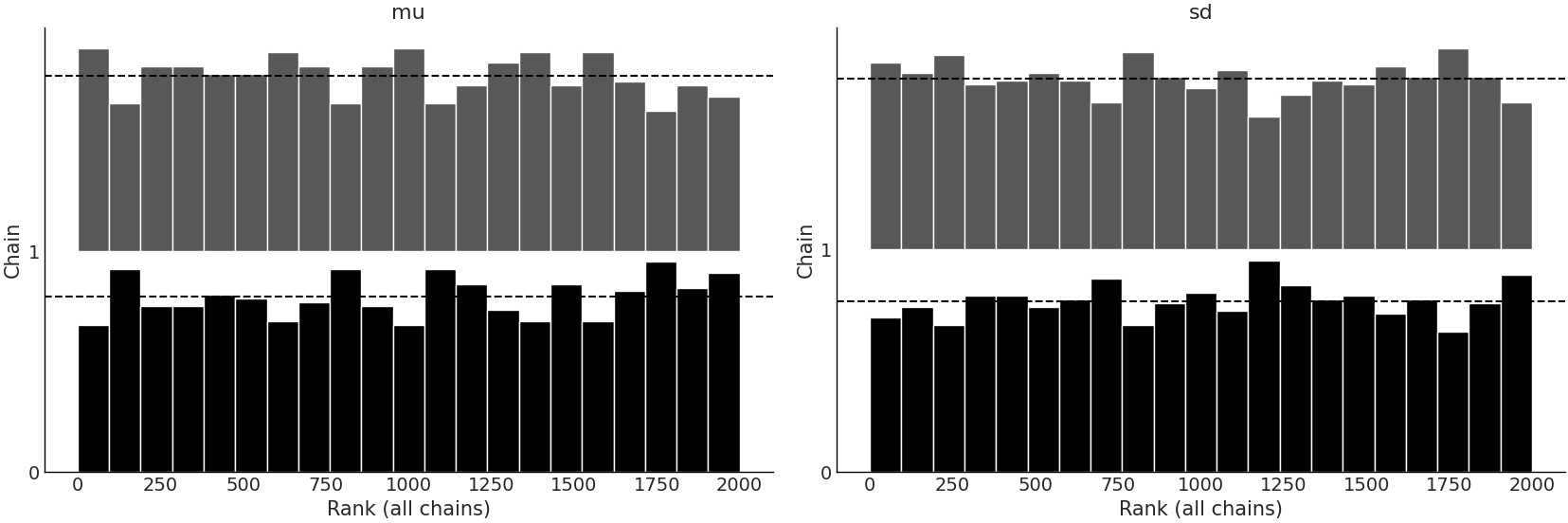
Fig. 153 来自具有高斯似然的模型的后验样本的秩图。

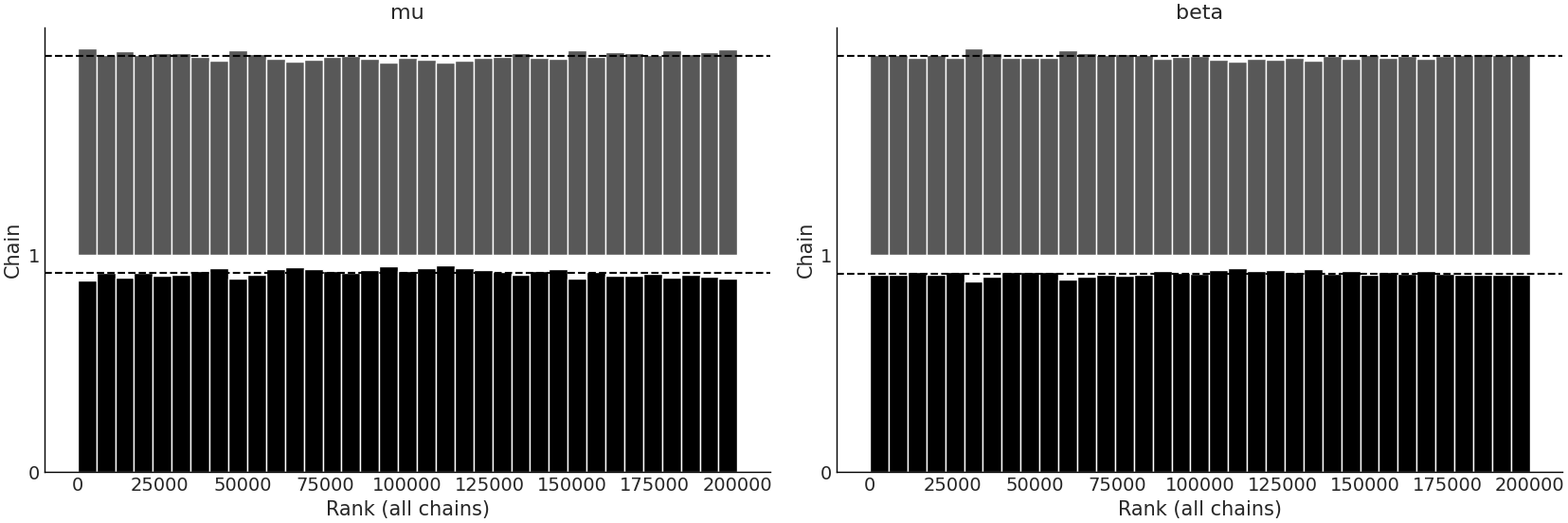
Fig. 154 具有 Gumbel 似然的模型的后验样本的秩图。

对于这两个模型，秩图（如图 Fig. 153 和 Fig. 154 所示）在所有秩中看起来都相当一致，这表明跨链的偏差很小。由于此示例中缺乏挑战，推断似乎就像“按下按钮并获得结果”一样简单。

然而，这很容易，因为我们已经花时间预先了解数据，思考好的模型架构，并设置好的先验。在练习中，您将被要求故意做出“错误”的选择，然后进行推断以查看采样期间会发生什么。

对 NUTS 采样器生成的后验样本感到满意，我们将进入下一步，生成估计延迟的后验预测样本。

9.6 后验绘图

正如我们所讨论的，后验图主要用于可视化后验分布。有时后验图是分析的最终目标，请参阅 9.11 实验性示例: 在两个组之间比较 示例。在其他一些情况下，对后验分布的直接检查几乎没有意义。我们的航空公司示例就是这种情况，我们将在下面进一步详细说明。

9.6.1 应用示例：航班延误模型的后验

在确保我们的模型中没有推断错误后，我们快速检查图 Fig. 155 和 Fig. 156 中 Normal 和 Gumbel 模型的后验图。乍一看，它们看起来形状良好，没有意外的异常。在这两种分布中，从领域的角度来看，\(\mu\) 的均值估计低于零是合理的，这表明大多数飞机准时。除了这两个观察值之外，参数本身并不是很有意义。

毕竟，您的老板需要决定是保持当前的收费结构还是接受航空公司提出的新收费结构的建议。

鉴于决策是我们分析的目标，在快速健全性检查后，我们继续工作流程。

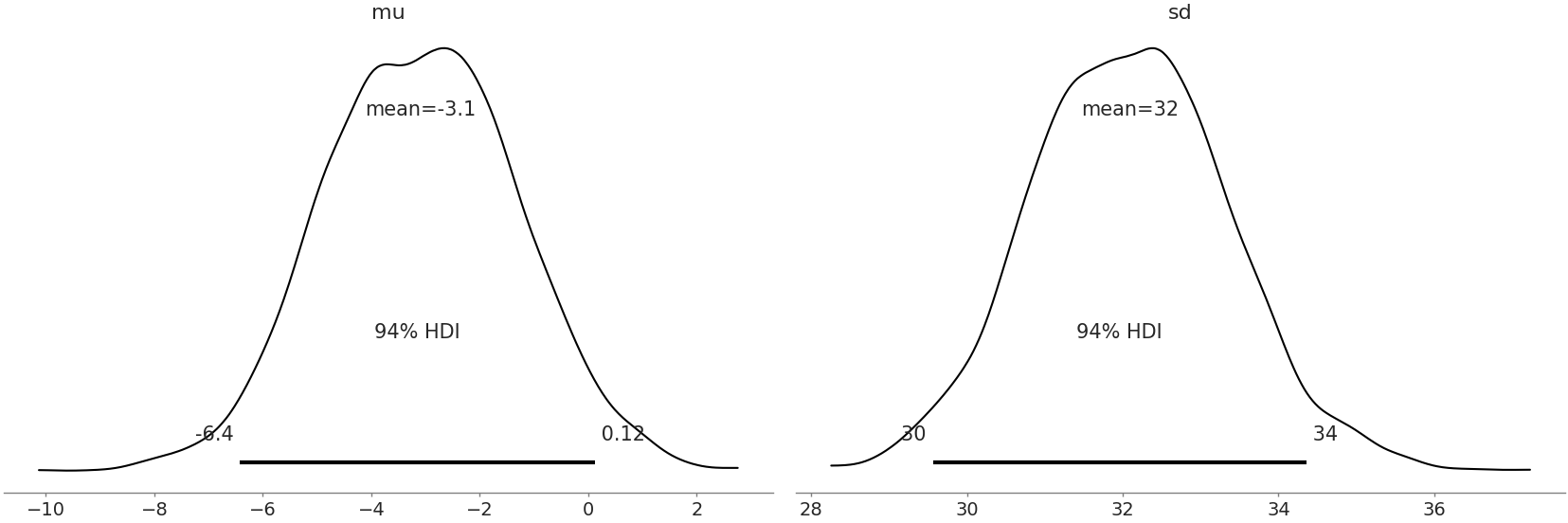
Fig. 155 高斯模型的后验图。两种分布看起来都是合理的，并且没有分歧增加了更多证据表明我们的采样器已经合理地估计了参数。

Fig. 156 Gumbel 模型参数的后验图。与 Fig. 155 类似，这些估计看起来格式正确，让我们对参数估计充满信心。

9.7 评估后验预测分布

如 Fig. 150 中的工作流所示，一旦获得后验估计，贝叶斯分析就不会结束。

我们可以采取许多额外的步骤，例如，如果需要以下任何一项，则生成后验预测分布。

• 我们想使用后验预测检查来评估我们的模型校准。

• 我们希望获得预测或执行反事实分析

• 我们希望能够以观测数据为单位传达我们的结果，而不是根据我们模型的参数。

我们在方程 (6) 中指定了后验预测分布的数学定义。 使用来自后验预测分布的现代概率编程语言采样很容易，只需添加代码块 posterior_predictive_airlines 中所示的几行代码。

9.7.1 应用示例：航班延误的后验预测分布

在我们的航空公司示例中，我们被要求根据未见的未来航班延误做出决定。为此，我们需要估计未来航班延误的分布。然而，目前我们有两种模型，需要在两者之间进行选择。我们可以使用后验预测检查来直观地评估与观察数据的拟合度，也可以使用测试统计数据来比较某些特定特征。

让我们为代码块 postterior_predictive_airlines 中所示的 Normal 似然模型生成后验预测样本。

Listing 116 posterior_predictive_airlines

with normal_model:
    normal_delay_trace = pm.sample(random_seed=0)
    normal_ppc = pm.sample_posterior_predictive(normal_delay_trace)
    normal_data = az.from_pymc3(trace=normal_delay_trace,
                            posterior_predictive=normal_ppc)

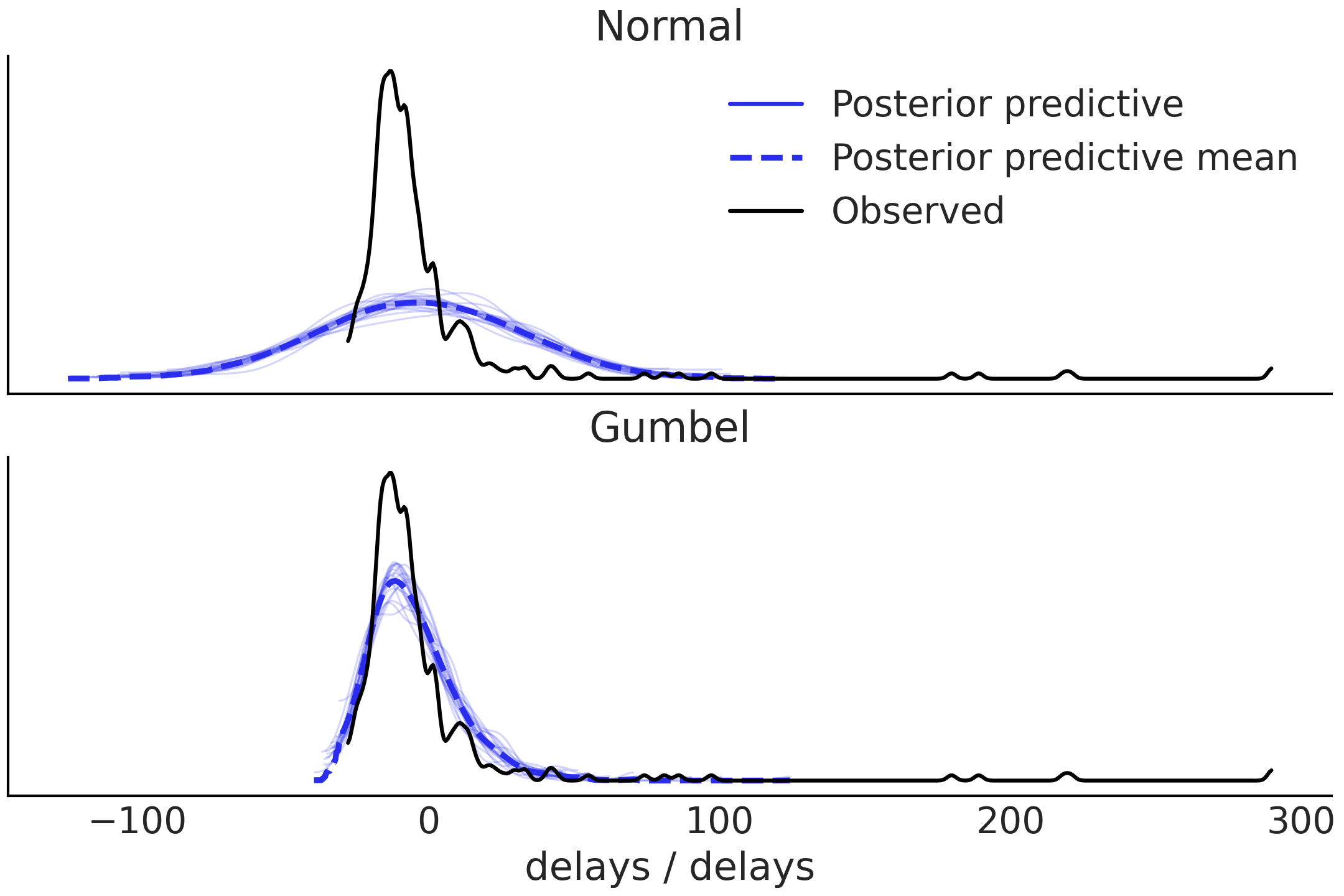
Fig. 157 Normal 和 Gumbel 模型的后验预测检查。高斯模型不能很好地捕捉长尾，并且还会返回更多低于观察数据界限的预测。 Gumbel 模型拟合更好，但对于低于 0 的值和尾部仍然存在相当多的不匹配。

从 Fig. 157 我们可以看到 Normal 模型无法捕获到达时间的分布。

转到 Gumbel 模型，我们可以看到后验预测样本似乎在预测早到的航班方面做得很差，但在模拟晚到的航班方面做得更好。我们可以使用两个测试统计数据运行后验预测检查来确认。第一个是检查航班迟到的比例，第二个是检查后验预测分布和观测数据之间的航班延误中位数（以分钟为单位）。

Fig. 158 表明 Gumbel 模型在拟合航班延误中位数方面比 Normal 模型做得更好，但在拟合准时到达比例方面做得很差。 Gumbel 模型在拟合航班延误的中位数方面也做得更好。

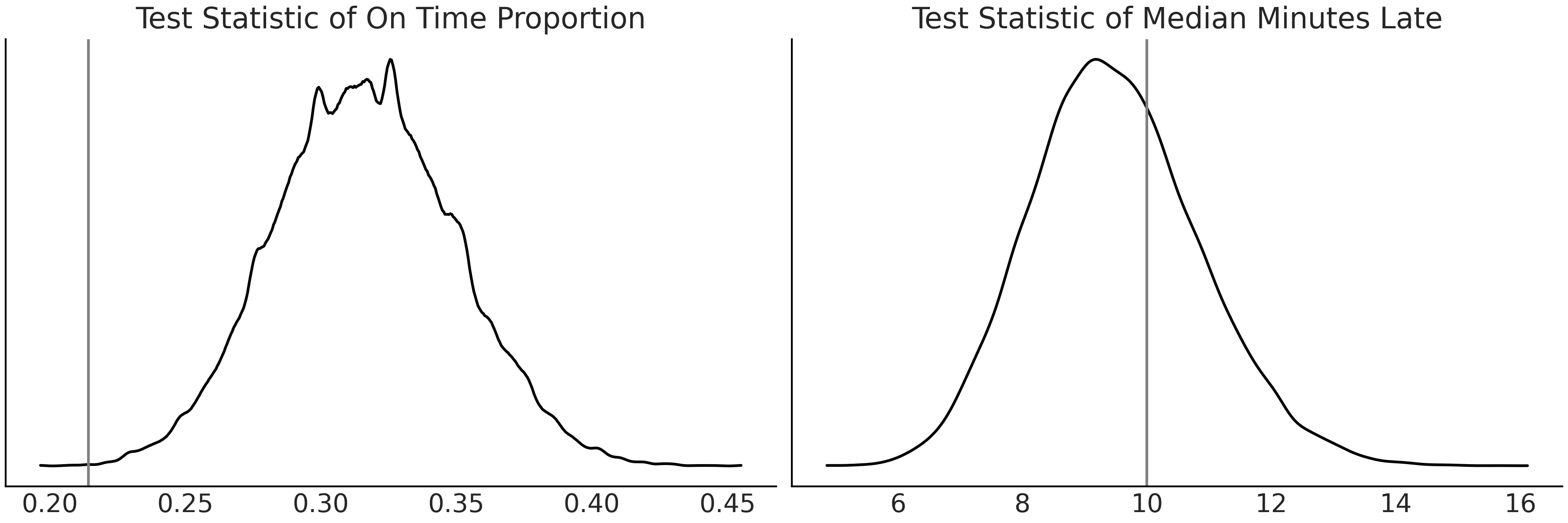
Fig. 158 使用 Gumbel 模型的检验统计量进行后验预测检查。在左侧，我们看到与观察到的比例相比，准时比例的估计分布。右侧是延迟中位数分钟的测试统计量。似乎 Gumbel 模型更适合估计航班迟到的时间与航班迟到的比例。

9.8 模型比较

到目前为止，我们已经使用后验预测检查来独立评估每个模型。这种类型的评估对于单独理解每个模型很有用。然而，当我们有多个模型时，这就引出了模型相对于彼此的性能如何的问题。模型比较可以进一步帮助我们了解一个模型在哪些区域可能表现良好，另一个模型在哪里挣扎，或者哪些数据点特别难以拟合。

9.8.1 应用示例： 用 LOO 做航班延误模型的比较

对于我们的航班延误模型，我们有两个候选模型。从我们之前的视觉后验预测检查来看，高斯似然似乎不能很好地拟合航班延误的偏态分布，特别是与 Gumbel 分布相比。我们可以使用 ArviZ 中的比较方法来验证这一观察结果：

Listing 117 delays_comparison

compare_dict = {"normal": normal_data,"gumbel": gumbel_data}
comp = az.compare(compare_dict, ic="loo")
comp

Table 17 Summary of model comparison for the gumbel and normal models

	rank	loo	p_loo	d_loo	weight	se	dse	warning	loo_scale
gumbel	0	-1410.39	5.85324	0	1	67.4823	0	False	log
normal	1	-1654.16	21.8291	243.767	0	46.1046	27.5559	True	log

Table 17，使用代码块 delays_comparison 生成，显示按其 ELPD 秩的模型。毫不奇怪，Gumbel 模型在对观测数据进行建模方面做得更好。

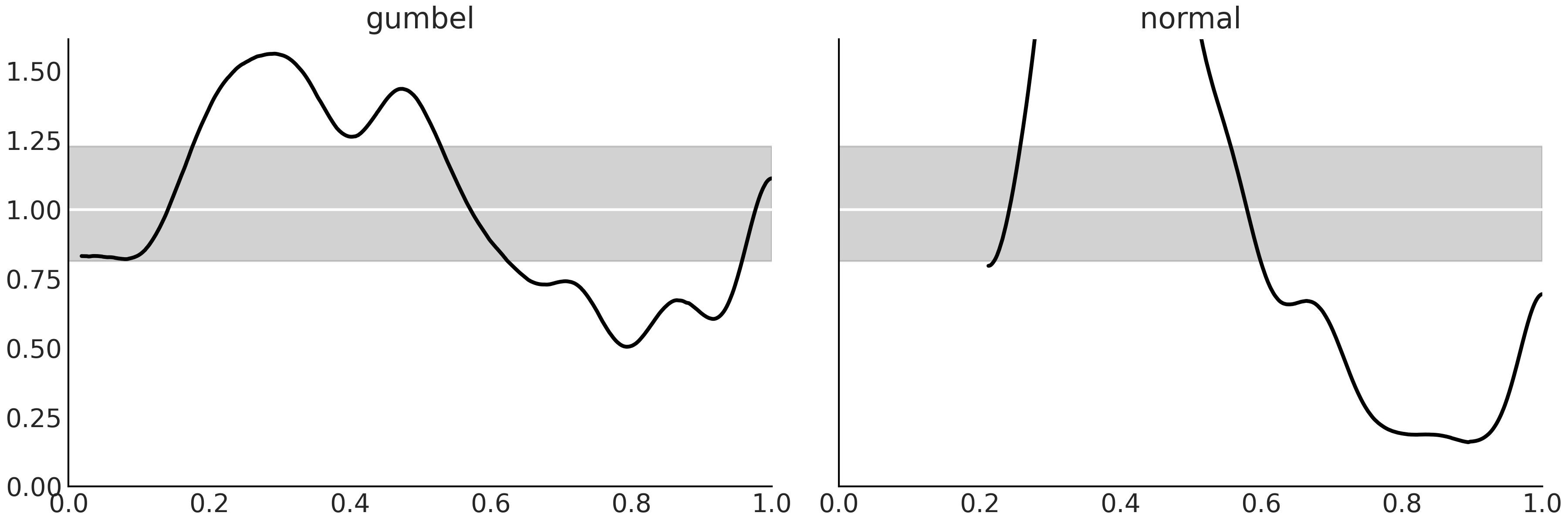
Fig. 159 使用 LOO-PIT 进行模型校准。我们可以看到，这两个模型在捕获数据的相同部分时都存在问题。这些模型低估了最大的观测值（最大的延迟）并高估了较早的到达。这些观察结果符合 Fig. 157。即使两个模型都出现问题，Gumbel 模型与预期的均匀分布的偏差也较小。

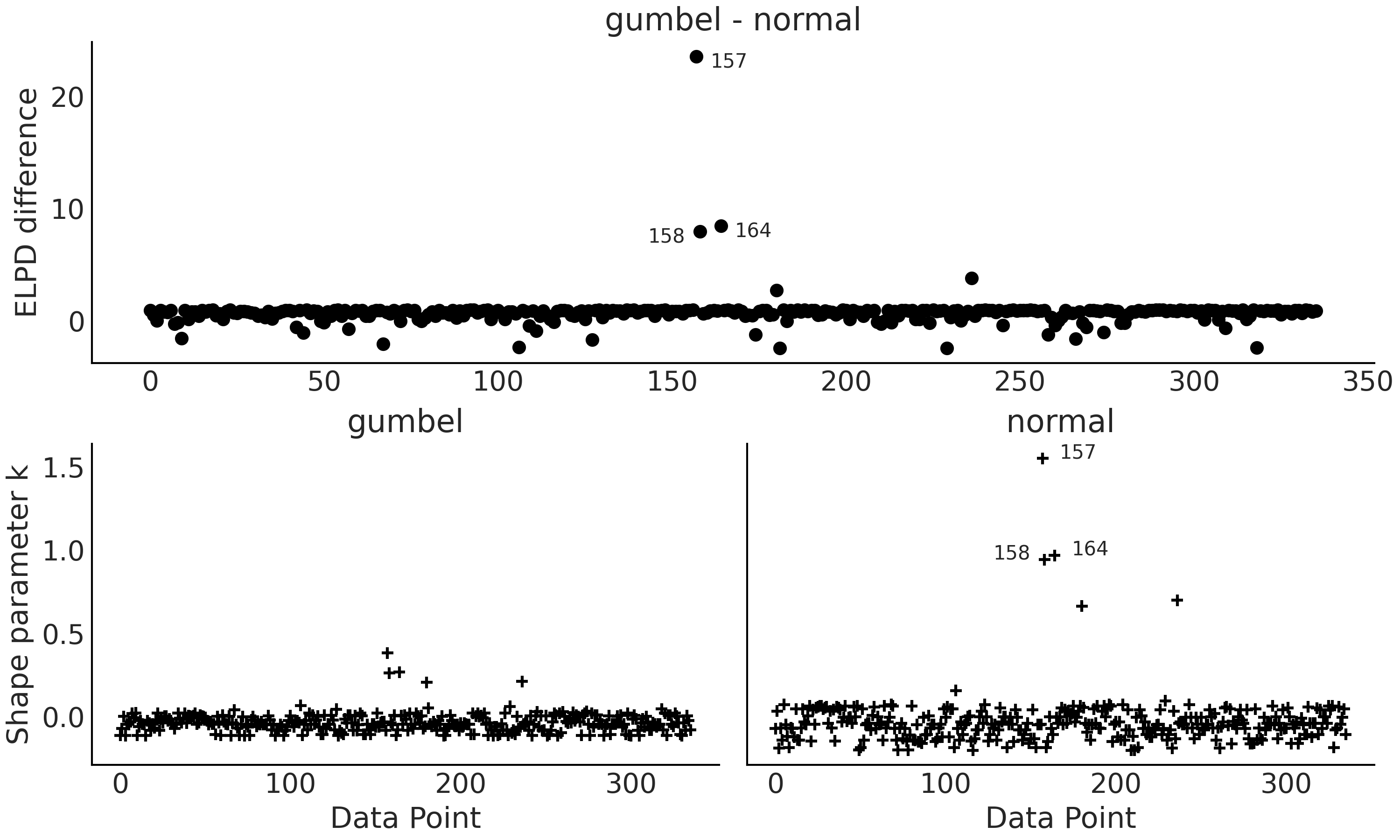
Fig. 160 Gumbel 和 Normal 模型之间的顶部面板 ELPD 差异。对偏差最大的 3 个观测值进行了注释（157、158 和 164）。底部面板，来自 Pareto 平滑重要性采样的 \(\hat \kappa\) 值的图。观测值 157、158 和 164 的值大于 0.7

从 Table 17 我们可以看到，Normal 模型给出的 p_loo 值远高于模型中的参数数量，表明模型指定错误。此外，我们收到一条警告，表明我们至少有一个 \(\hat \kappa\) 的高值。从 Fig. 160（右下图）我们可以看到违规观察是数据点 157。从上图我们还可以看到（图 Fig. 160 上图）Normal 模型很难将这一观测与观测 158 和 164 一起捕获。对数据的检查表明，这 3 个观测是延迟最大的观测。

我们还可以使用代码块 delays_comparison_plot 生成视觉检查，结果是 Fig. 161。我们看到，即使考虑 LOO 中的不确定性，Gumbel 模型也比 Normal 模型更好地表示数据。

Listing 118 delays_comparison_plot

az.plot_compare(comp)

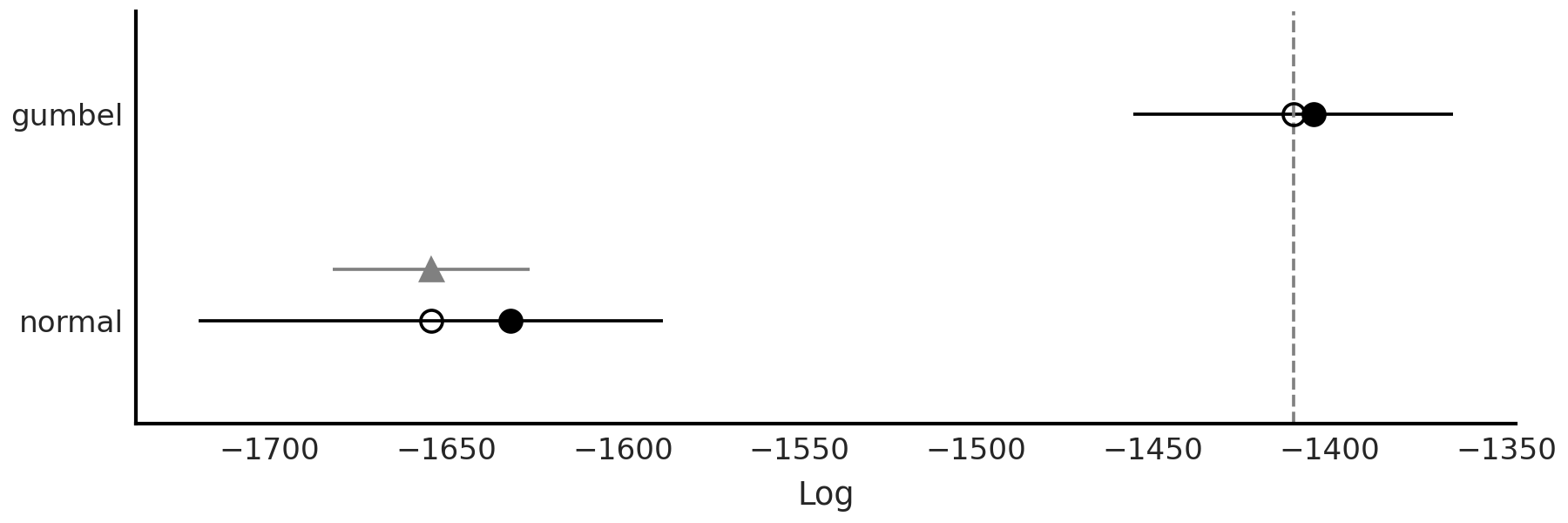
Fig. 161 使用代码块 delays_comparison_plot 中的两个航班延误模型的 LOO 进行模型比较。我们证实了我们的观点，即 Gumbel 数据在估计观察到的分布方面比高斯模型更好。

根据我们之前对后验预测检查的比较，以及我们直接的 LOO 比较，我们可以做出明智的选择，只使用 Gumbel 模型。这并不意味着我们的 Normal 模型没有用，事实上恰恰相反。开发多个模型有助于建立对我们选择一个模型或模型子集的信心。这也不意味着 Gumbel 模型是真实的甚至是最好的模型，事实上我们有证据证明它的缺点。因此，如果我们探索不同的可能性、收集更多数据或进行一些其他修改，仍有改进的空间。在这一步重要的是，我们充分确信 Gumbel 模型是我们评估过的所有合理模型中最“充分”的模型。

9.9 奖励函数和决策

在本书中，我们已经看到如何将一个空间中的一组数量转换为另一个空间，从而使我们的计算变得更简单或改变我们的思维方式。例如，在上一节中，我们使用后验预测采样从参数空间移动到观察量空间。奖励函数，有时也称为成本、损失或效用函数，是从观察量空间到从结果（或决策空间）派生的奖励的另一种转换。回想 7.5 示例：自行车数据的贝叶斯加性回归树 节中的示例，我们有每小时租用自行车数量的后验估计（参见例如

Fig. 123。如果我们对每天的收入感兴趣，我们可以使用奖励函数来计算每次租金的收入并将总计数相加，从而有效地将计数转换为收入。另一个例子是估计一个人在下雨和干燥时的幸福程度。如果我们有一个模型和对是否会下雨的估计（基于天气数据），并且我们有一个函数可以将一个人的衣服的干湿程度映射到幸福值，我们可以将天气估计映射到预期幸福估计。

奖励函数变得特别有用的地方是存在决策。通过能够估计所有未来结果，并将这些结果映射到预期回报，您可以做出可能产生最大回报的选择。一个直观的例子是决定在早上收拾雨伞。带伞很烦人，这可以被认为是一种负面的奖励，但被雨淋湿是更糟糕的结果。是否带雨伞的选择取决于下雨的可能性。

我们可以进一步扩展这个例子来揭示一个关键思想。假设您想建立一个模型，帮助您的家人决定何时收拾雨伞。你建立一个贝叶斯模型来估计下雨的概率，这是推断部分。然而，当你建立模型后，你发现你的兄弟非常讨厌带伞，除非已经下雨了，否则他永远不会带伞，而你的母亲非常讨厌被淋湿，即使没有云，她也会抢先带伞天空。在这种情况下，估计的数量，即下雨的概率，完全相同，但由于奖励不同，采取的行动也不同。更具体地说，模型的贝叶斯部分是一致的，但奖励的差异会产生不同的动作。

奖励和行动都不需要是二元的，两者都可以是连续的。供应链中的一个典型例子是报刊供应商模型 1，其中报刊供应商必须在需求不确定时决定每天早上购买多少份报纸。如果他们买得太少，他们就有失去销售的风险，如果他们买太多，他们就会在未售出的库存上赔钱。

因为贝叶斯统计提供了完整的分布，我们能够提供比提供点估计的方法更好的未来奖励估计 2。当我们考虑到贝叶斯定理包括尾部风险等特征时，我们可以直观地理解这一点，而点估计则不会。

使用生成贝叶斯模型，特别是计算模型，可以将模型参数的后验分布转换为观察单位域中的后验预测分布，转换为奖励的分布估计（以财务单位为单位），最可能结果的点估计。使用这个框架，我们可以测试各种可能决策的结果。

9.9.1 应用示例：基于航班延误建模结果做出决策

回想一下，延误对机场来说是相当昂贵的。在准备航班抵达时，机场必须准备好登机口，在飞机降落时有工作人员在场指挥飞机，而且由于容量有限，迟到的航班最终意味着更少的航班到达。我们还回顾了晚班罚款结构。航班每晚一分钟，航空公司就必须向机场支付 300 美元的费用。我们可以将此语句转换为代码块 current_revenue 中的奖励函数。

Listing 119 current_revenue

def current_revenue(delay):
    if delay >= 0:
        return 300 * delay
    return np.nan

现在，给定任何个别晚点航班，我们可以计算我们将从航班延误中获得的收入。由于我们有一个模型可以生成延迟的后验预测分布，因此我们可以将其转换为预期收入的估计值，如代码块 reward_calculator 中所示，它提供每个延迟航班的收入数组和平均收入估计。

Listing 120 reward_calculator

def revenue_calculator(posterior_pred, revenue_func):    
    revenue_per_flight = revenue_func(posterior_pred)
    average_revenue = np.nanmean(revenue_per_flight)
    return revenue_per_flight, average_revenue

revenue_per_flight, average_revenue = revenue_calculator(posterior_pred,
current_revenue)
average_revenue

3930.88

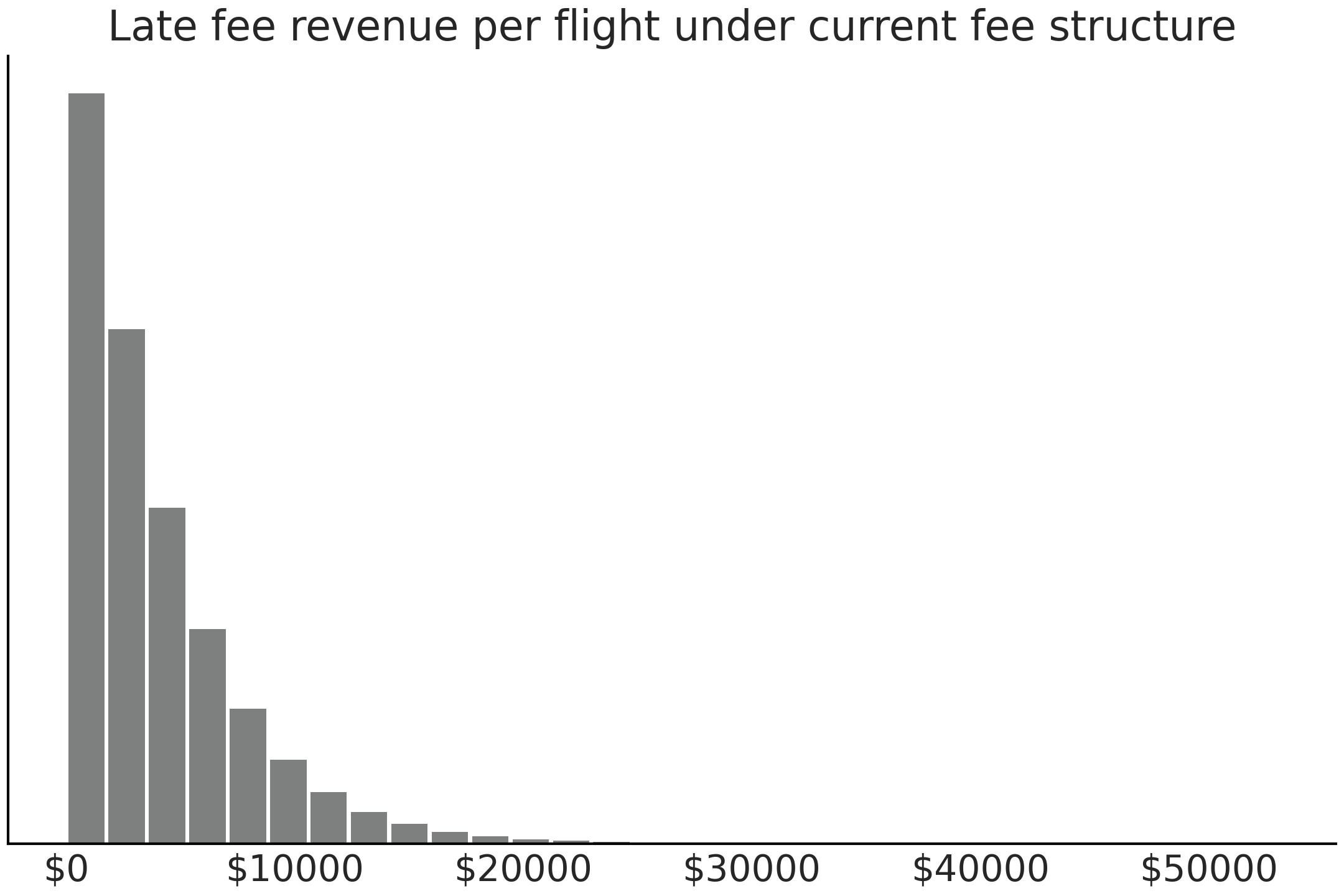
Fig. 162 使用奖励函数和后验预测分布计算的当前滞纳金结构的预期延迟航班收入。很少有非常晚的航班，因此情节的右侧部分看似空旷。

从后验预测分布和当前的滞纳金结构来看，我们预计每个延迟航班平均可提供 3930 美元的收入。我们还可以在 Fig. 162 中绘制每个航班晚点航班收入的分布。

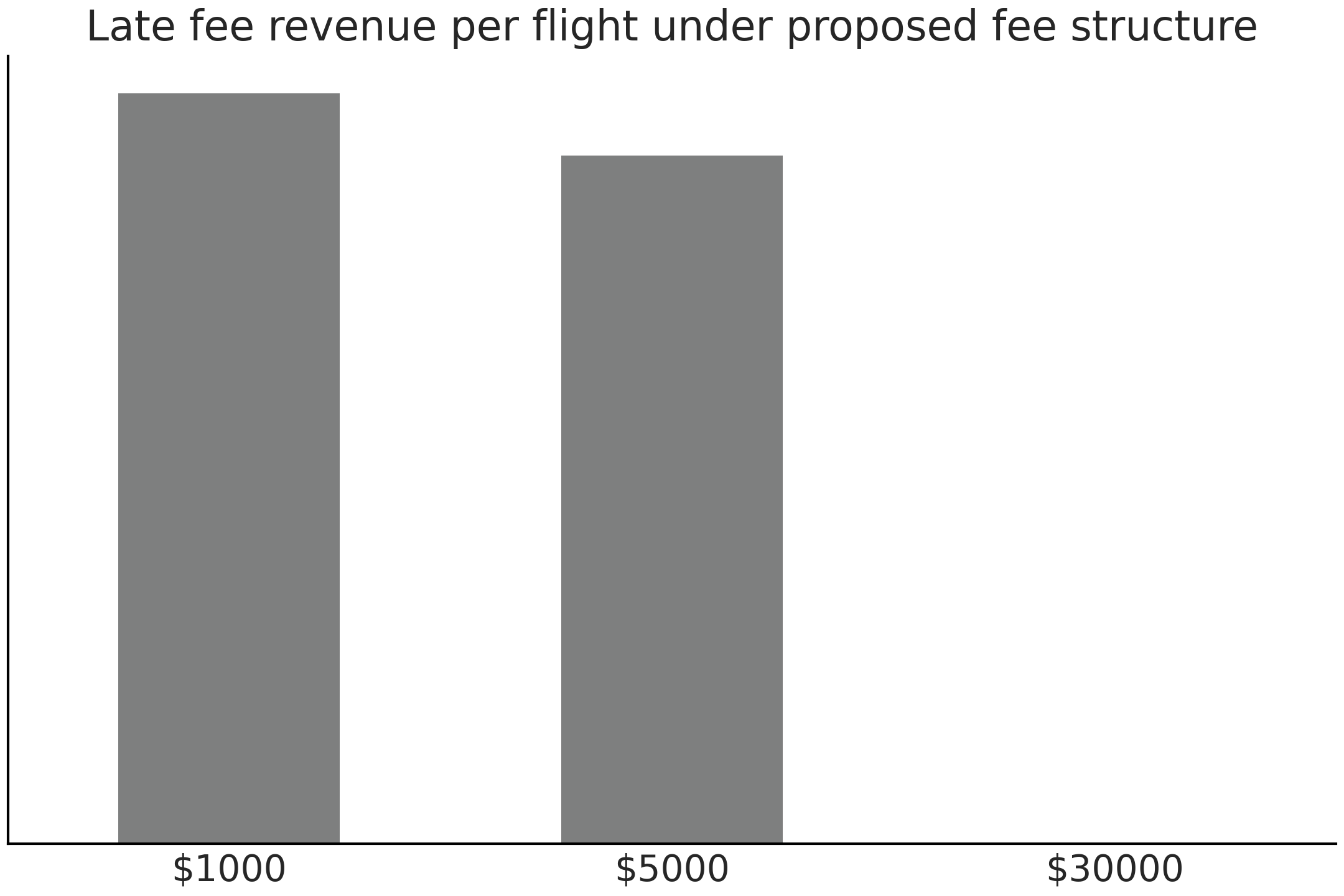
回顾航空公司提出的成本结构，如果航班晚点 0 到 10 分钟，费用为 1000 美元。如果航班迟到 10 到 300 分钟，费用为 5,000 美元，如果迟到 100 分钟以上，费用为 30,000 美元。假设成本结构对飞机的准时或迟到没有影响，您可以通过编写新的成本函数并重用先前计算的后验预测分布来估计新提案下的收入。

@np.vectorize
def proposed_revenue(delay):
    """Calculate proposed revenue for each delay """
    if delay >= 100:
        return 30000
    elif delay >= 10:
        return 5000
    elif delay >= 0:
        return 1000
    else:
        return np.nan
revenue_per_flight_proposed, average_revenue_proposed = revenue_calculator(posterior_pred, proposed_revenue)

2921.97

Fig. 163 使用建议的奖励函数和后验预测分布计算的预期延迟航班收入。请注意，后验预测分布与 Fig. 162 中的完全相同。只是奖励函数的变化使该图有所不同。

在新的成本结构中，您估计机场平均每晚航班将赚取 2921.97 美元，低于当前的罚款定价结构。我们再次可以在 Fig. 163 中绘制估计的迟到航班收入的分布。

9.10 与特定受众分享结果

贝叶斯工作流中最重要的步骤之一是将您的结果传达给他人。在纸上或屏幕上投掷数字和图表，无济于事。推断的结论部分仅在它间接或直接地改变或通知决策时才重要。这将需要一些准备工作，所需要的努力不容小觑。在某些情况下，此步骤花费的时间比前一个步骤的总和还要多。这里没有具体的表述，需要做什么很大程度上取决于具体情况和受众，但我们将在高层次上涵盖这些概念以调查景观。

9.10.1 分析流程的可重复性

分析工作流程的可重复性是指另一个个人或团体能够完成所有步骤并获得与先前报告的相同或相似的结论。 可重复性使包括您自己在内的人们能够了解执行了哪些工作、做出了哪些假设以及导致结果的原因。如果忽略可重复性，那么理解结论背后的推断或在未来某个日期扩展结果将是具有挑战性或不可能的。通常情况下，结果充其量是浪费资源重新创建相同的工作流程步骤，最坏的情况是原始结论无效，还可能失去声誉。再现性的理想是完全再现性，这意味着结论可以“从头开始”自动重新创建。相反，我们将专注于分析的可重复性，这意味着给出一个结论，从原始数据到贝叶斯工作流，到最终结果的所有步骤都是可重现的。分析重现性由四个主要支柱组成，我们将依次详细说明

• 源数据的管理

• 建模和分析代码

• 计算环境规范

• 文档

在执行分析时，重要的是要注意或保留作为分析基础的原始数据。这就是为什么您会一遍又一遍地看到相同的数据集，例如 Palmer Penguins、Radon 和 Eight Schools。这些数据很容易理解并且很容易获得，这使其成为那些希望共享方法的人的简单参考。标记、识别、存储和访问特定数据的具体方法因情况、规模、组织以及道德和合法性而异，但重要的是要注意这一点。一些示例包括在代码版本控制中包含数据或引用存储在服务器上的数据集的链接。

接下来是建模和分析代码，例如贯穿本书的所有代码。理想情况下，此代码将使用版本控制系统（例如 git）进行版本控制，并存储在可访问的位置，例如开源存储库。我们想强调版本控制是有用的，即使你是一个单独的从业者而不是在一个团队中工作。使用版本控制将允许您在代码版本之间跳转，它使您能够轻松地测试想法，减少知识丢失或丢失结果的风险。这极大地有助于提高工作流程中步骤之间的迭代速度并比较结果。 在计算统计中，任何结果的关键部分都是计算机本身。虽然计算机制在很大程度上没有改变，但用于计算的库变化很快。正如我们所见，现代贝叶斯方法至少依赖于概率编程语言，但这只是冰山一角。操作系统版本以及结合使用的数百个其他软件库都在提供结果方面发挥了作用。当环境无法复制时，一个结果是代码正在运行，现在抛出异常或错误并失败。

这个结果虽然令人沮丧，但至少是有帮助的，因为失败状态是显而易见的。一个更危险但微妙的问题是代码仍然运行但结果不同。这可能是因为库可能会更改，或者算法本身可能会发生变化。例如，TFP 可能会改变调整样本的数量，或者 PYMC3 可能会在一个版本和下一个版本之间重构采样器。不管是什么原因，即使数据和分析代码相同，在没有完整的计算环境规范的情况下，仅靠两者都不足以在计算上完全重现分析。指定环境的一种常见方法是通过显式的依赖项列表，在 Python 包中常见为 requirements.txt 或 environment.yml 文件。

另一种方法是通过计算环境虚拟化，例如虚拟机或容器化。

播种伪随机数生成器

创建可重现的贝叶斯工作流的一个挑战是算法中使用的伪随机数生成器的随机性。一般来说，您的工作流程应该是稳健的，将种子更改为伪随机数生成器不会改变您的结论，但在某些情况下，您可能希望修复种子以获得完全可重现的结果。这很棘手，因为单独修复种子并不意味着您将始终获得完全可重现的结果，因为不同操作系统中使用的实际伪随机数生成器可能会有所不同。如果您的推断算法和结论对种子的选择很敏感，这通常是您工作流程的危险信号。

借助数据、代码和计算环境，计算机只能再现分析的一部分。最后一个支柱，文档，也是为了让人类理解分析。正如我们通过本书所见，统计从业者需要在整个建模过程中做出许多选择，从先验的选择到过滤数据，再到模型架构。随着时间的推移，很容易忘记为什么做出某个选择，这就是为什么存在如此多的工具只是为了帮助键盘后面的人。最简单的是代码文档，它是代码中的注释。应用科学家的另一种流行方法是将代码块与包含文本、代码和图像的文档块混合使用的笔记本格式。本书使用的 Jupyter 笔记本就是一个例子。对于贝叶斯从业者来说，ArviZ 等专用工具也有助于使分析具有可重复性。

在这一点上，值得重申的是，再现性的主要受益者是你自己。没有什么比被要求扩展分析或发现错误更糟糕的了，只是意识到您的代码将不再运行。次要受益人是您的同龄人。他们复制您的工作的能力是分享您的工作流程和结果的最身临其境的方式。简而言之，可重复的分析既可以帮助您和其他人对您之前的结果建立信心，也可以帮助未来的工作扩展工作。

9.10.2 理解听众

在内容和交付方式方面，了解您的受众是谁以及如何与他们交流非常重要。

当您获得最终结果集时，您最终会得到许多想法、可视化和沿途产生的结果，这些都是实现结果所必需的，但除此之外没有任何意义。

回想一下我们的烹饪类比，用餐者希望得到一道菜，但不希望在此过程中产生的脏锅和食物垃圾。同样的想法也适用于统计分析。

花点时间考虑一下：

• 你的观众想要什么，不想要什么？

• 你可以通过什么方式交付它？

• 他们需要吃多长时间？

将您的结果提炼成最易消化的版本需要齐心协力和思考。这意味着回顾分析的原始问题和动机，谁想要结果以及他们为什么想要它。这也意味着要考虑观众的背景和能力。例如，更多的统计受众可能更喜欢查看有关模型和假设的详细信息。更多面向领域的受众可能仍然对模型中的假设感兴趣，但主要是在领域问题的上下文中。 通过演示格式思考，是口头的还是视觉的？如果它是视觉的，它是静态的，比如这本书，还是一个 pdf 或论文，或者是一个潜在的动态格式，比如网页或视频？还要考虑时间安排，您的听众是否有几分钟的时间来聆听重点，或者是否有专门的时间段专注于了解细节？所有这些问题的答案将告诉你分享什么，但你也分享它

数字汇总

顾名思义，数字汇总是总结您的结果的数字。在本书中，我们看到了很多，从总结分布位置的均值和中位数，到总结离差的方差或 HDI，或总结概率的 PDF。例如 Table 4，它总结了企鹅的质量。数字摘要具有很大的优势，因为它们将大量信息压缩成一个小的表示，可以很容易地记住，容易比较，并以多种格式呈现。它们在口头对话中特别有效，因为不需要其他助手来传播它们。在商业对话中，奖励函数，如第 9.9 奖励函数和决策 部分所述，可以将分析的全部不确定性捕获到一个数字中，也可以用最通用的商业语言金钱来构建。

不幸的是，数字摘要可能会掩盖分布的细微差别并且可能会被误解。许多人在听到均值时往往会过度期望该值，即使实际上平均结果的概率可能很少。为了帮助共享一组数值摘要，一次可以帮助观众了解分布的各个方面，例如获得模式感的最大可能性和获得分散感的 HDI。但是，共享过多的数字摘要会变得有害。如果一次共享许多数字，既难以背诵数字表，又难以让听众记住所有信息。

9.10.3 静态可视化辅助

有句谚语说一张照片值一千字。对于贝叶斯统计数据尤其如此，其中后验图传达了一个不容易用文字描述的细节水平。 ArviZ 预先打包了许多常见的可视化，例如后验图。但是，我们也建议制作定制图形。本文中的示例包括后验估计，例如 Fig. 123，它显示了一天所有时间的观察数据、平均趋势和不确定性。静态视觉辅助工具就像数字摘要，如今它们也很容易共享。

随着笔记本电脑和手机以及互联网连接设备的广泛使用，共享图片变得比以前更容易。

但是，缺点是它们确实需要纸张或屏幕来共享，并且需要准备好或在需要时快速找到它们。

另一个风险是他们可能与您的听众交流太多，他们有时可能只想要平均或最大似然值。

动画

任何看过图片和电影之间区别的人，即使是无声电影，都知道运动在交流中的强大力量。

通常情况下，动画比其他格式 3 更容易理解的想法，例如 MCMC 采样 4。现在可以在许多可视化包中生成动画，包括 ArviZ 用于动画后验预测检查的 Matplotlib。不确定性交流中使用动画的著名例子是纽约时报选举针5，它使用摇动的针规来突出显示。另一个选举例子是马修凯的总统普林科 6。这两种可视化都使用运动来显示各种美国选举结果的估计结果以及它是如何产生的。最重要的是，这两个使用的动画都给人一种不确定性的感觉，来自纽约时报可视化中的摇动针，或马蒂凯示例中的 plinko 下降的随机性。

动画能够显示许多图像以显示不断变化的状态，从而传达运动、进展和迭代的感觉。与静态图像一样，数字屏幕的广泛使用意味着它们可以更容易地观看，但它们需要观众更多的时间来暂停并观看完整的动画。它们还需要开发人员的更多工作，因为它们比简单的图片更难以生成和共享。

交互式辅助

交互式辅助工具让观众可以控制正在显示的内容。

在静态可视化和动画中，观众都被讲述了一个他们无法控制的故事。交互式辅助翻转脚本，用户可以创建自己的故事。一个简单的示例可能包括更改显示内容的滑块，例如轴的限制或数据点的不透明度。它还可能包括一个工具提示，向用户显示特定点的值。用户还可以控制计算。例如，在我们对企鹅的后验预测中，它选择了平均鳍状肢长度并绘制了 Fig. 42 的结果。

不同的人可能对不同值的后验预测分布感兴趣，因此具有交互性。示例包括各种 MCMC 技术的可视化 7，其中允许用户选择不同的采样器、分布和参数，允许用户进行他们想要的特定比较。

与静态绘图和动画类似，许多软件库都支持动画，例如 Matplotlib 或 Bokeh，另一个 Python 可视化库是专门为这种类型的交互而设计的。交互性的缺点是它们通常需要实时计算环境和某种软件部署。它不像共享静态图像或视频那么容易。

9.10.4 可重复的计算环境

回想上面的可再现性，共享结果的黄金标准是完全可再现的计算环境，其中包含复制结果所需的一切。这在历史上是一个很大的障碍，需要时间和专业知识才能在自己的设备上设置本地计算环境，但通过容器化等虚拟化技术变得更加容易。如今，计算环境和代码可以打包并在互联网上轻松分发。对于像 Binder 这样的项目，让同事只需单击一下即可在浏览器中访问定制环境，无需本地安装。大多数人只想要结果，而不是每个说的所有原材料。但是在某些人绝对需要运行代码的情况下，例如教程或深入审查，能够轻松共享实时环境非常有帮助。

9.10.5 应用示例：展示航班延误模型和结论

对您在模型构建、推断运行和成本函数正确性方面的严谨性充满信心，您现在需要将结果传达给组织中的其他人，以向数据同行证明您的分析方法的合理性，并帮助您的老板在当前费用结构之间做出决定，以及拟议的费用结构。你意识到你有两组不同的观众，并为每一组准备不同的内容。

在接近你的老板之前，你需要与你的同事完成一次同行评审。由于您的同行精通统计和计算，您可以为他们提供 Jupyter Notebook 的分析，其中混合了叙述、代码和结果。这本笔记本包含了你以前为老板推荐的所有模型、假设和情节。由于笔记本包含所有细节并且可重现，因此您的同事能够自信地评估您的工作是否正确。

您的一些同事询问他们是否可以使用不同的先验运行模型来检查先验敏感性。您提供 Dockerfile8，它完全指定了环境。这样他们就可以运行 Jupyter notebook 并重新创建部分工作流程。

现在专注于通知老板的初始任务，您开始思考如何与她沟通的策略。你知道你最多有 30 分钟，而且会在她的办公室。您将使用笔记本电脑来展示视觉辅助工具，但您知道您的老板也需要能够在她没有视觉辅助工具的情况下将这个想法传达给她的同事。您还知道您的老板可能想测试不同的收费结构，以了解她可以安全谈判的地方。

换句话说，她想看看不同奖励函数的效果。您设置了一个简单的笔记本，将奖励函数作为输入并生成收入直方图和表格。你与你的老板开会并迅速解释说“我花了一些时间利用过去的晚班航班延误来创建一个未来航班延误的模型。使用我估计在当前费用结构中的模型，我们每次晚班可以赚 3930 美元平均航班，在航空公司提议的费用结构中，我们将平均每晚航班赚 2921 美元。”您向老板展示底部图 Fig. 157，解释这是预期和建模的晚班航班的分布，Fig. 162 显示预计将在未来产生的收入.然后，您向老板展示 Table 18，显示新范式下的预期收入。您选择了一个表格而不是一个数字，因为 100 分钟以上延迟类别中的航班比例在图中并不明显。您使用该表来解释可能晚点超过 100 分钟的航班非常少，从收入的角度来看，该类别在您的模拟中可以忽略不计。您建议您的老板要么拒绝该提议，要么就 0 到 100 分钟范围内的延误协商更高的滞纳金。然后你的老板问你是否可以测试她选择的几种不同的费用结构，以便她看到效果。随着你老板的理解，推断的目标已经实现，你的老板拥有在她的谈判中做出明智决定所需的所有信息。

Table 18 Percentages of expected revenue from each fee category. There are so few late flights in the $30000 fee category that it is essentially negligible.

Late Fee	Revenue
$1000	52%
$5000	47%
$30000	.03%

9.11 实验性示例: 在两个组之间比较

对于我们的第二个应用示例，将展示贝叶斯统计在更具实验性的环境中的使用，其中两组之间的差异很重要。在处理统计数据之前，我们将解释动机。

机械工程师在设计产品时，首要考虑的是所使用材料的特性。毕竟，没有人希望他们的飞机在飞行途中分崩离析。机械工程师有关于陶瓷、金属、木材等材料的重量、强度和刚度的参考书，这些材料已经存在了很长时间。

最近，塑料和纤维增强复合材料变得可用并且更常用。纤维增强复合材料通常由塑料和编织布的组合制成，赋予它们独特的性能。

为了量化材料的强度特性，物理测试机械工程师运行称为拉伸测试的程序，其中将材料试样固定在两个夹具中，拉伸试验机拉动试样直至其断裂。许多数据点和物理特性可以从这一测试中估计出来。在这个实验中，重点是极限强度，或者换句话说，是材料完全失效前的最大载荷。作为研究项目的一部分 9，其中一位作者制造了 2 套，每套 8 个样品，除了增强纤维的编织外，其他所有方面都是相同的。其中一种纤维是平铺在彼此顶部的，称为单向编织。在另一种中，纤维被编织在一起形成称为双向编织的互锁图案。 对每个样品独立进行一系列拉伸试验，结果以磅力 10 记录。对于机械工程来说，力除以面积来量化每单位面积的力，在这种情况下是磅力/平方英寸。例如，第一个双向试样在 3774 lbf (1532 kg) 的截面面积为 0.504 英寸 (12.8 mm) x 0.057 英寸 (1.27 mm) 时失效，产生的极限强度为 131.393 ksi（千磅每平方英寸） .作为参考，这意味着横截面积为 USB A 连接器 1/3 的试样理论上能够提升小型汽车的重量 11。

Bidirectional Ultimate Strength (ksi)	Unidirectional Ultimate Strength (ksi)
131.394	127.839
125.503	132.76
112.323	133.662
116.288	136.401
122.13	138.242
107.711	138.507
129.246	138.988
124.756	139.441

在最初的实验中，进行了频率论假设检验，在拒绝中得出最终拉伸等效的无效假设。然而，这种类型的统计测试不能单独表征每种材料的极限强度分布或强度差异的大小。

虽然这代表了一个有趣的研究结果，但它产生了一个无用的实际结果，因为打算在实际环境中选择一种材料而不是另一种材料的工程师需要知道*一种材料比另一种材料“更好”多少，而不仅仅是有一个显着的结果。虽然可以执行额外的统计测试来回答这些问题，但在本文中，我们将关注如何使用单个贝叶斯模型回答所有这些问题，并进一步扩展结果。

让我们在代码块 uni_model 中为单向样本定义一个模型。先前的参数已经使用领域知识进行了评估。在这种情况下，先验知识来自于报告的类似类型的其他复合材料试样的强度特性。这是一个很好的示例，来自其他实验数据和经验证据的知识可以帮助减少得出结论所需的数据量。当每个数据点都需要大量时间和成本才能获得时，这一点尤其重要，就像在这个实验中一样。

Listing 121 uni_model

with pm.Model() as unidirectional_model:
    sd = pm.HalfStudentT("sd_uni", 20)
    mu = pm.Normal("mu_uni", 120, 30)
    
    uni_ksi = pm.Normal("uni_ksi", mu=mu, sigma=sd, 
                        observed=unidirectional)
    
    uni_trace = pm.sample(draws=5000)

我们在 Fig. 164 中绘制后验结果。正如贝叶斯建模方法多次看到的那样，我们得到了平均极限强度和标准偏差参数的分布估计，这对于理解这种特定材料的可靠性非常有帮助。

az.plot_posterior(uni_data)

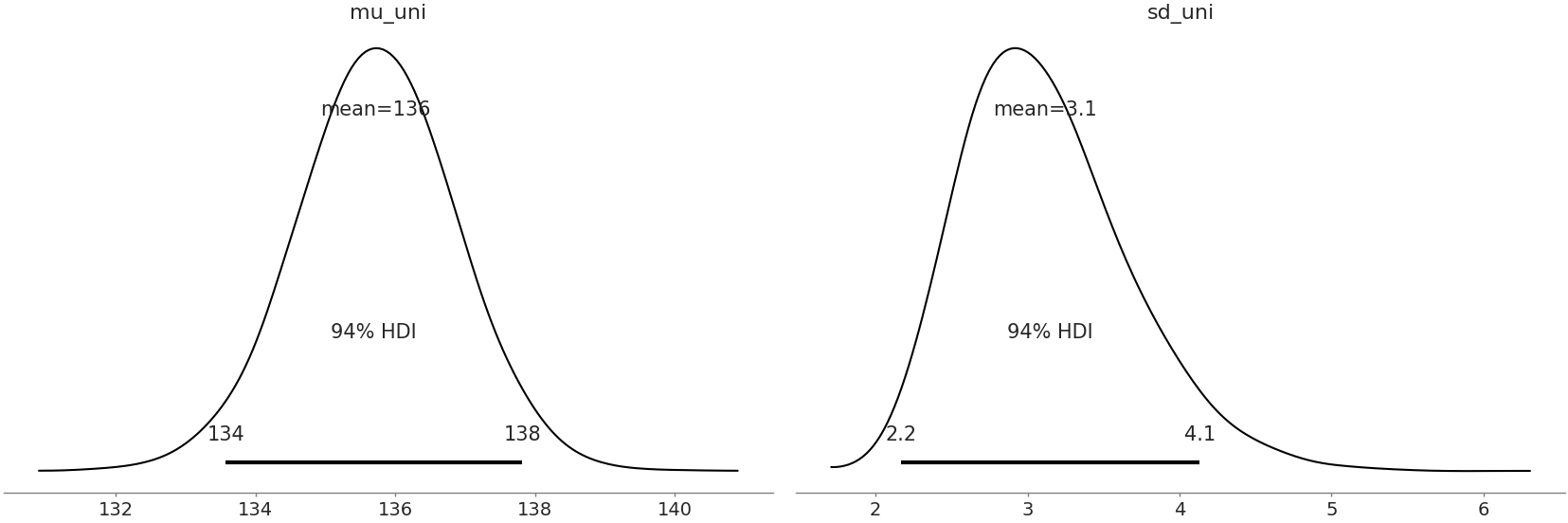
Fig. 164 具有 \(94\%\) HDI 和点统计量的所有参数的后验图

然而，我们的研究问题是关于单向和双向复合材料之间极限强度的差异。虽然我们可以为双向样本运行另一个模型并比较估计值，但更方便的选择是在单个模型中比较两者。我们可以利用“贝叶斯估计取代 t 检验”中定义的 John Kruschke 的模型框架{引用：p}kruschke_2013 来获得这种“一劳永逸”的比较，如代码块 comparison_model 中所示。

Listing 122 comparison_model

μ_m = 120
μ_s = 30

σ_low = 1
σ_high = 100

with pm.Model() as model:
    uni_mean = pm.Normal("uni_mean", mu=μ_m, sigma=μ_s)
    bi_mean = pm.Normal("bi_mean", mu=μ_m, sigma=μ_s)
    
    uni_std = pm.Uniform("uni_std", lower=σ_low, upper=σ_high)
    bi_std = pm.Uniform("bi_std", lower=σ_low, upper=σ_high)
    
    ν = pm.Exponential("ν_minus_one", 1/29.) + 1
    
    λ1 = uni_std**-2
    λ2 = bi_std**-2

    group1 = pm.StudentT("uni", nu=ν, mu=uni_mean, lam=λ1,
        observed=unidirectional)
    group2 = pm.StudentT("bi", nu=ν, mu=bi_mean, lam=λ2, 
        observed=bidirectional)
    
    diff_of_means = pm.Deterministic("difference of means", 
                                     uni_mean - bi_mean)
    diff_of_stds = pm.Deterministic("difference of stds",
                                    uni_std - bi_std)
    pooled_std = ((uni_std**2 + bi_std**2) / 2)**0.5
    effect_size = pm.Deterministic("effect size",
                                   diff_of_means / pooled_std)
    
    t_trace = pm.sample(draws=10000)

compare_data = az.from_pymc3(t_trace)

拟合模型后，我们可以使用 Fig. 165 中的 Forest Plot 可视化均值的差异，两种样本的均值之间似乎没有太多重叠，表明它们的最终强度确实不同，单向更强，甚至更可靠。

az.plot_forest(t_trace, var_names=["uni_mean","bi_mean"]) 

Fig. 165 每组均值的森林图。 \(94\%\) HDI 是分开的，表明均值不同。

Kruschke 的公式还有一个额外的好处，以及我们的概率编程语言中的一个技巧。我们可以让模型直接自动计算差异，在这种情况下，其中之一是均值差异的后验分布。

az.plot_posterior(trace, 
                  var_names=["difference of means","effectsize"],
                  hdi_prob=.95, ref_val=0)

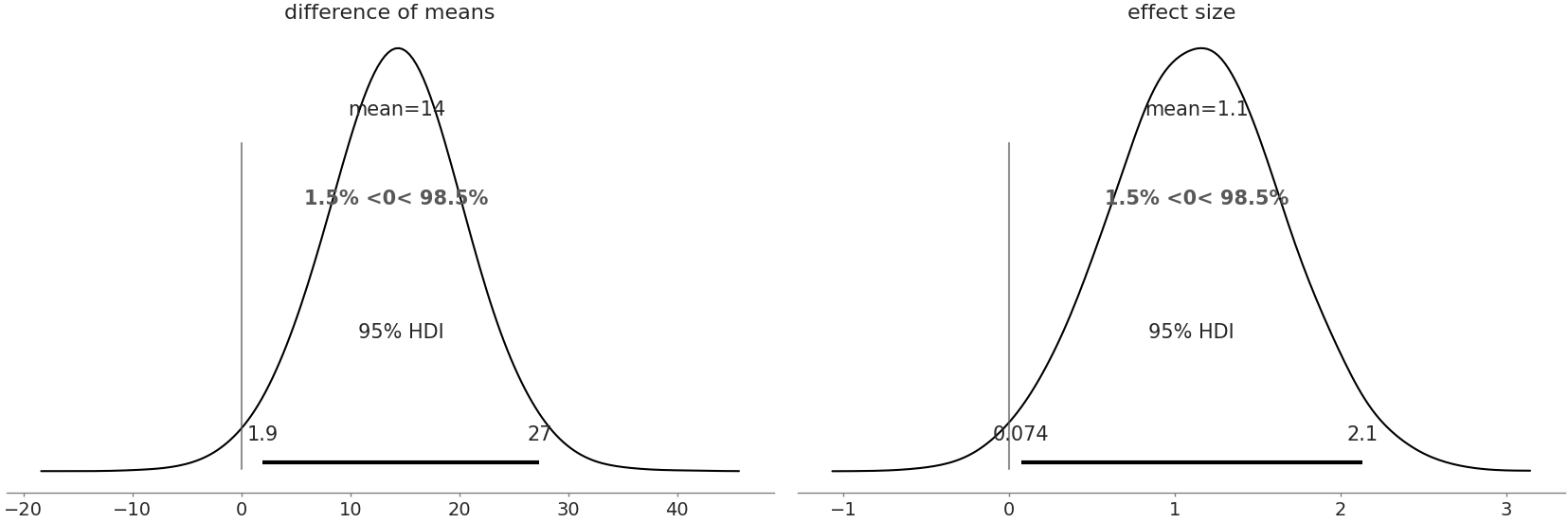
Fig. 166 均值和效应大小差异的后验图，包括 0 处的参考值。在这两个图中，0 值似乎相对不太可能表明既有效应又有差异。

我们也可以比较每个参数的数值摘要。

az.summary(t_trace, kind="stats")

	mean	sd	hpd_3%	hpd_97%
uni_mean	135.816	1.912	132.247	139.341
bi_mean	121.307	3.777	114.108	128.431
uni_std	4.801	1.859	2.161	8.133
bi_std	9.953	3.452	4.715	16.369
\(\boldsymbol{\nu}\)_minus_one	33.196	30.085	0.005	87.806
difference of means	14.508	4.227	6.556	22.517
difference of stds	-5.152	3.904	-13.145	1.550
effect size	1.964	0.727	0.615	3.346

从这些数字总结和后验图中，我们可以更确定两种复合材料的平均强度存在差异，这有助于在两种材料类型之间进行选择。我们还获得了强度的具体估计值及其分散性，帮助工程师了解材料在现实世界应用中的安全使用位置和方式。一个模型可以帮助我们得出多个结论是非常方便的。

习题

9E1. What kind of data collection scheme would be most appropriate for these situations scenarios. Justify your choices by asking questions such as “How important is it that the information is reliable?” or “Can we collect the data in a reason time?” Explain how you would collect the data

1. A medical trial for for a new drug treatment for cancer patients

2. An estimate of the most popular ice cream flavors for a local newspaper article

3. An estimate of which parts needed for a factory have the longest delivery lead times

9E2. What kind likelihood is suited for these types of data? Justify your choice. What other information would be useful to pick a likelihood?

1. Count of customers that visit a shop each day

2. Proportion of parts that fail in a high volume manufacturing line

3. Weekly revenue of a restaurant

9E3. For our airline model provide a justification, or lack thereof, for each of these priors of the mean of a Gumbel likelihood, using your domain knowledge and a prior predictive check. Do these seem reasonable to use in a model? Why or why not?

1. \(\mathcal{U}(-200, 200)\)

2. \(\mathcal{N}(10, .01)\)

3. \(\text(Pois)(20)\)

9E4. For each of the priors in the exercise above perform an inference run using the Gumbel model in Code Block airline_model_definition

1. Are any errors raised by the sampler?

2. For the completed inference run generate post sampling diagnostics such as autocorrelation plots. What are the results? Would you consider the run to be a successful inference run?

9E5. For our airline delays model we initially included arrivals from the MSP and DTW airports. We are now asked to include another arrival airport, ORD, into the analysis. Which steps of the Bayesian Workflow do we need to reconsider? Why is that the case? What if instead we are asked to include SNA? What steps would we need to reconsider?

9E6. In Chapter 6 we forecasted the CO~2~ concentration. Using the figures and models in the chapter what conclusions can we reach about CO~2~? Communicate your understanding of projected CO~2~ levels, including an explanation of the uncertainty, in the following ways. Be sure to include specific numbers. You may need to run the examples to obtain them. Justify which model you chose and why

1. A 1 minute verbal explanation without visual aid to data scientist colleague

2. A 3 slide presentation for an non-statistician executive.

3. Use a Jupyter notebook for a software engineering colleague who wants to productionize the model as well.

4. Write a half page document for a general internet audience. Be sure to include at least one figure.

9E7. As the airport statistician your boss asks you to rerun the fee revenue analysis with a different cost function than the one specified in Code Block current_revenue. She asks that any minute delay that is even costs 1.5 dollars per minute of delay, any that minute delay that is odd costs 1 dollar a minute of delay. What will the average revenue per late flight be the airport be with this fee model?

9M8. Read the workflow article and paper from Betancourt[43] and Gelman[17]. From each list a step which is the same? Which steps are different? Explain why these examples workflows may be different. Do all practitioners follow the same workflow? Why would they differ if not?

9M9. In our bike rental model from Code Block splines we used splines to estimate bike rentals per hour. The bike rental company wants to know how much money they will make from rentals. Assume each rental costs 3 dollars. Now assume that the rental company is proposing that from the hours of 0 to 5 bike rentals are reduced to 1.5 dollars, but it is projected rentals will increase 20% due to the reduced cost. What is the expected revenue per hour?

Write a reward function specifically to estimate both situations above.

1. What is the mean projected revenue per day? What would be reasonable upper and lower estimates?

2. Does the estimated mean and revenue seem reasonable? Note any issues you see and explain you may fix them? (Don’t actually make any changes)

3. Now assume that the rental company is proposing that from the hours of 0 to 5 bike rentals are reduced to 1.5 dollars, but it is projected rentals will increase 20% due to the reduced cost. What is the expected revenue per day?

9M10. For the airline delay model replace the likelihood in Code Block airline_model_definition with a Skew Normal likelihood. Prior to refitting explain why this likelihood is, or is not, a reasonable choice for the airline flight delay problem.

After refitting make the same assessment. In particular justify if the Skew Normal is “better” than the Gumbel model for the airline delays problem.

9H11. Clark and Westerberg[114] ran an experiment with their students to see if coin flips can be biased through tosser skill. The data from this experiment is in the repository under CoinFlips.csv. Fit a model that estimates the proportion of coin tosses that will come up heads from each student.

1. Generate 5000 posterior predictive samples for each student. What is the expected distribution of heads for each student?

2. From the posterior predictive samples which student is the worst at biasing coin towards heads?

3. The bet is changed to 1.5 dollars for you if heads comes up, and 1 dollar of tails comes up. Assuming the students don’t change their behavior, which student do you play against and what is your expected earnings?

9H12. Make an interactive plot of the posterior airline flights using Jupyter Notebook and Bokeh. You will need to install Bokeh into your environment and using external documentation as needed.

1. Compare this to the static Matplotlib in terms of understanding the plotted values, and in terms of story telling.

2. Craft a 1 minute explanation posterior for general audience that isn’t familiar statistics using Matplotlib static visualization.

3. Craft a 1 minute explanation to the same audience using the Bokeh plot, incorporating the additional interactivity allowed by Bokeh.

参考文献

---

1

https://en.wikipedia.org/wiki/Newsvendor_model

2

<www.ee.columbia.edu/~vittorio/BayesProof.pdf>

3

See https://bost.ocks.org/mike/algorithms/

4

See https://elevanth.org/blog/2017/11/28/build-a-better-markov-chain/

5

See https://www.nytimes.com/interactive/2020/11/03/us/elections/forecast-president.html

6

See http://presidential-plinko.com/

7

https://chi-feng.github.io/mcmc-demo/app.html

8

Docker is one method to create fully reproducible environments that has become quite popular

9

Much gratitude to Dr. Mehrdad Haghi and Dr. Winny Dong for funding and facilitating this research

10

A recordings of the tests are available https://www.youtube.com/watch?v=u_XDUWgzs_Y

11

This is in an ideal situation. Factors other than ultimate strength can limit the true load bearing capacity in real world situations.

previous

第八章：近似贝叶斯计算

next

第十章: 概率编程语言