Contents

第二章：贝叶斯模型的探索性分析

第二章：贝叶斯模型的探索性分析

正如 第 1 章 所述，贝叶斯推断 使用观测数据对模型（即先验和似然）进行条件化并获得后验分布。我们可以使用纸笔、计算机或其他设备来实现推断 1 。此外，推断过程通常还包括一些其他量的计算，例如先验预测分布和后验预测分布。但 贝叶斯建模 相对于贝叶斯推断而言内容更为广泛。我们通常希望贝叶斯建模能够靠简单指定模型和计算后验就能实现，但通常情况下并非如此。现实情况是，成功的贝叶斯数据分析需要完成许多其他同等重要的任务。

在本章中，我们将讨论其中一些任务，包括：

  • 模型假设的检查

  • 模型推断结果的诊断

  • 模型的比较

2.1 “贝叶斯建模” 大于 “贝叶斯推断”

成功的贝叶斯建模方法除了贝叶斯推断之外，还需要执行很多其他额外的任务 2。

典型如：

  • 模型诊断，对使用数值方法获得的推断结果进行诊断，评估其质量。

  • 模型评判，包括对模型假设和模型预测的评估。

  • 模型比较，包括模型选择或模型平均。

  • 模型沟通，为特定受众准备结果。

实现上述任务需要一些数字汇总和可视化手段来帮助从业者对模型进行分析，我们称此类方法为 贝叶斯模型的探索性分析（ Exploratory Analysis of Bayesian Models ）。此名称源于统计方法中的探索性数据分析 ( Exploratory Data Analysis, EDA ) [14] 。该分析方法旨在汇总数据集的主要特征，并且通常使用可视化方法。用 Persi Diaconis 的话来说 [15] ：

探索性数据分析 （探索性数据分析） 旨在揭示数据中的结构或简单描述。人们查看数字或图表并尝试找到其中蕴含的模式（ Patterns ），寻求由背景信息、想象力、感知到的模式和其他数据分析经验提供的前瞻性线索。

探索性数据分析 通常在推断之前执行，有时甚至可以代替推断。我们以及之前许多研究者 [16, 17] 认为，探索性数据分析 中的许多想法都可以被使用、重新解释，并扩展为强大的贝叶斯建模方法。

在本书中将主要使用 Python 的 ArviZ 库 3 来对贝叶斯模型进行探索性分析。

在现实生活中，贝叶斯推断步骤和模型的探索性分析步骤经常交织在一个迭代的工作流中，其中可能还包括编码错误、计算问题、对模型充分性的怀疑、对我们当前对数据的理解的怀疑、非线性模型构建、模型检查等很多方面。

试图在一本书中描述这种复杂的工作流非常具有挑战性，而且也不是本书的重点。因此，我们会省略部分甚至全部探索性分析步骤，或者将其留作练习。这并非因为探索性分析没有必要或不重要；相反，它非常地重要，在编写本书过程中，我们实际上在 “幕后” 进行了大量地迭代工作。但也确实在某些地方省略了它们，以便将重点放在其他注意力方面，例如模型细节、计算特征或基础数学。

2.2 先验预测检查

正如在 1.4 先验分布的选择方法 节中讨论的，“什么是最好的先验？” 是一个很吸引人的话题。但除了 “这取决于 ？” 之外，很难给出一个令人满意的答案。我们可以尝试寻找给定模型或模型族的默认先验，将其推广到更广泛的数据集，并产生良好结果。但如果能够为特定问题生成具有更多信息的先验，那么一定也能够找到在特定问题上优于它们的方法。事实上，好的缺省先验不仅可以作为快速分析的基础，当我们深入迭代式探索的贝叶斯建模工作流时，它还可以作为更优先验的一个占位符。

选择先验时的一个问题在于：当先验按照模型传导到数据中时，有时候很难直观理解其产生的结果。我们在参数空间中做出的选择，在观测数据空间中可能会引发一些意想不到的结果。因此，为了更好地理解假设，我们需要一种能够查看其效果的工具，这就是 先验预测检查（ Prior Predictive Checks ），我们曾经在 1.1.2 贝叶斯推断 （ Bayesian Inference ） 和公式 (5) 中提到过它。

在实际工作中，当做出先验假设（可能是不合适的）后，无需以观测数据为条件，就可以通过从模型中采样来获得先验预测分布（ Prior Predictive Distribution ）。 这些先验预测分布的样本，将我们在参数空间中所做的选择，转换成了观测数据空间中的预测结果，从而让我们有机会更直接得理解假设。这种利用先验和模型生成样本，并用样本来评估先验的过程，被称为先验预测检查。

2.2.1 有助于发现先验设置产生的问题

假设我们希望建立一个足球模型。具体来说，我们对踢点球的进球概率感兴趣。经过思考，我们决定使用几何模型来建模 4。根据 Fig. 12 中的草图和三角函数知识，可以得出以下计算进球概率的公式：

(16)\[p\left(|\alpha| < \tan^{-1}\left(\frac{L}{x}\right)\right) = 2\Phi\left(\frac{\tan^{-1}\left(\frac{L}{x}\right)}{\sigma}\right) - 1\]

公式 (16) 的直觉印象是：（1）假设进球结果由 \(|\alpha|\) 是否小于某个角度阈值 \(\tan^{-1}\left(\frac{L}{x}\right)\) 决定；(2) 假设球员努力将球踢直（即射门角度为 \(0\) ），但存在某些因素导致足球的轨迹出现了大小为 \(\sigma\) 的偏差。

../_images/football_sketch.png

Fig. 12 罚球的示意草图。虚线表示进球得分所必须的角度 \(\alpha\) 。 \(x\) 代表罚球距离（ \(11\) 米），\(L\) 代表球门长度的一半（ \(3.66\) 米）。

公式 (16) 中唯一的未知量是偏差参数 \(\sigma\) ，\(L\) 和 \(x\) 的值都可以从足球规则中得到。作为贝叶斯工作者，当我们不知道一个量时，通常会为其分配先验，然后尝试建立贝叶斯模型去估计它。例如，可以这样写：

(17)\[\begin{split}\begin{split} \sigma &= \mathcal{HN}(\sigma_{\sigma}) \\ \text{p_goal} &= 2\Phi\left(\frac{\tan^{-1}\left(\frac{L}{x}\right)}{\sigma}\right) - 1 \\ Y &= \text{Bin}(n=1, p=\text{p_goal}) \end{split}\end{split}\]

其中 \(\phi\) 为累积正态分布函数。

现在我们尚不完全确定模型对足球领域知识的表达程度如何，因此可以尝试从先验预测中采样以获得一些直观的感觉。Fig. 13 显示了三个先验样本（分别用 \(\sigma_{\sigma}\) 的三个值 \(5\)、\(20\) 和 \(60\) 来表示）对应的预测结果。灰色的扇形区域代表罚球未受其他因素（如：风、摩擦等）影响时，应该进球的一组角度。可以看到，当前的模型假设在射门角度比灰色区域更大时，也是有可能进球的。更为有趣的是，如果存在较大的 \(\sigma_{\sigma}\) 值，当前模型会认为朝球门相反的方向射门也是有可能进球的（ 虽然可能性很小 ），这样的假设显然存在一些缺陷。

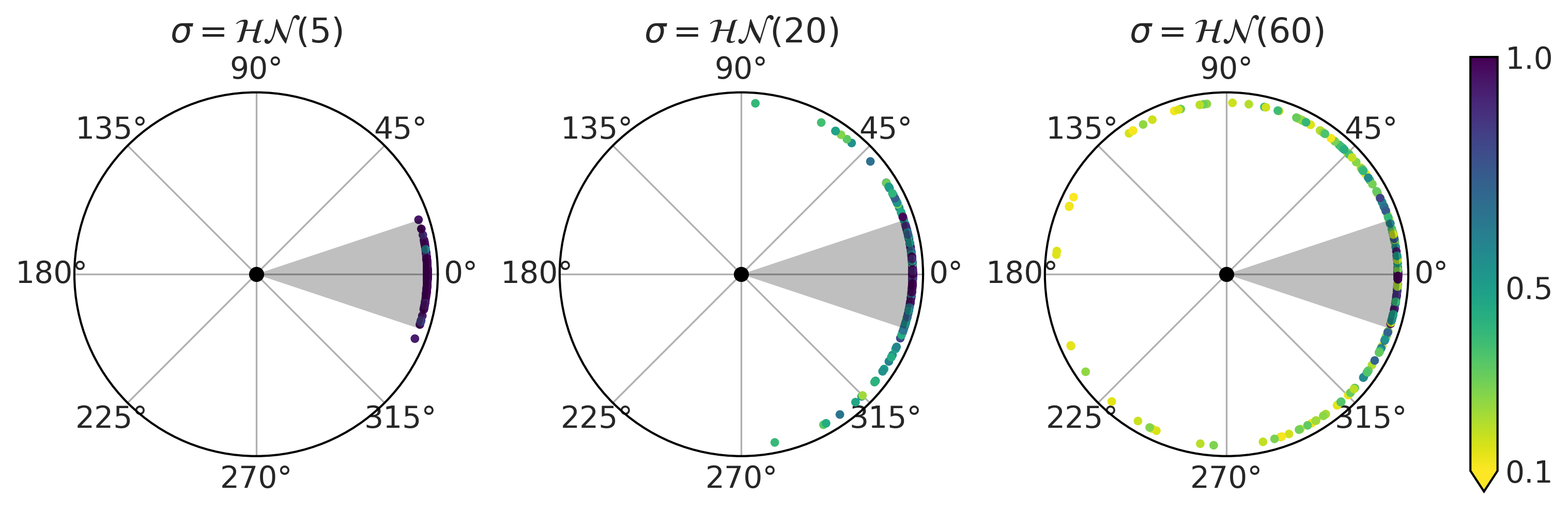
../_images/prior_predictive_distributions_00.png

Fig. 13 公式 (17) 中模型的先验预测检查。每个图对应于 \(\sigma\) 参数的不同先验样本。每个圆形图中心的黑点代表罚球点，边缘处的点代表射门位置，由角度 \(\alpha\) 的值刻画（ 参见 Fig. 12 ），不同颜色代表了有区别的进球概率。

针对上述问题，我们现在有几个选择：一是重新设计模型以结合更多的几何性质；二是调整先验以减少无意义结果发生的机会（即便我们并没有完全排除它们）；三是将错就错，直接用当前先验拟合数据，然后查看数据是否具备足够信息（充分到能够排除无意义的参数值）来得出后验。

2.2.2 有助于发现模型设置产生的问题

Fig. 14 显示了另一个我们可能觉得意外的例子 5 。该示例显示了一个具有两个预测变量的逻辑斯蒂回归 6 ，其回归系数上的先验为 \(\mathcal{N}(0, 1)\) 。

当我们增加预测变量的数量时，先验预测分布的均值参数从聚集在 \(0.5\) 左右（左侧子图）变为均匀分布（中间子图），更进一步变得支持极值 \(0\) 或 \(1\)（右侧子图）。

这个例子提示我们：随着预测变量数量的增加，先验预测分布会将更多质量放在极值上。因此，我们可能需要一个更强的正则化先验，以使模型远离那些不太可能发生的极值。

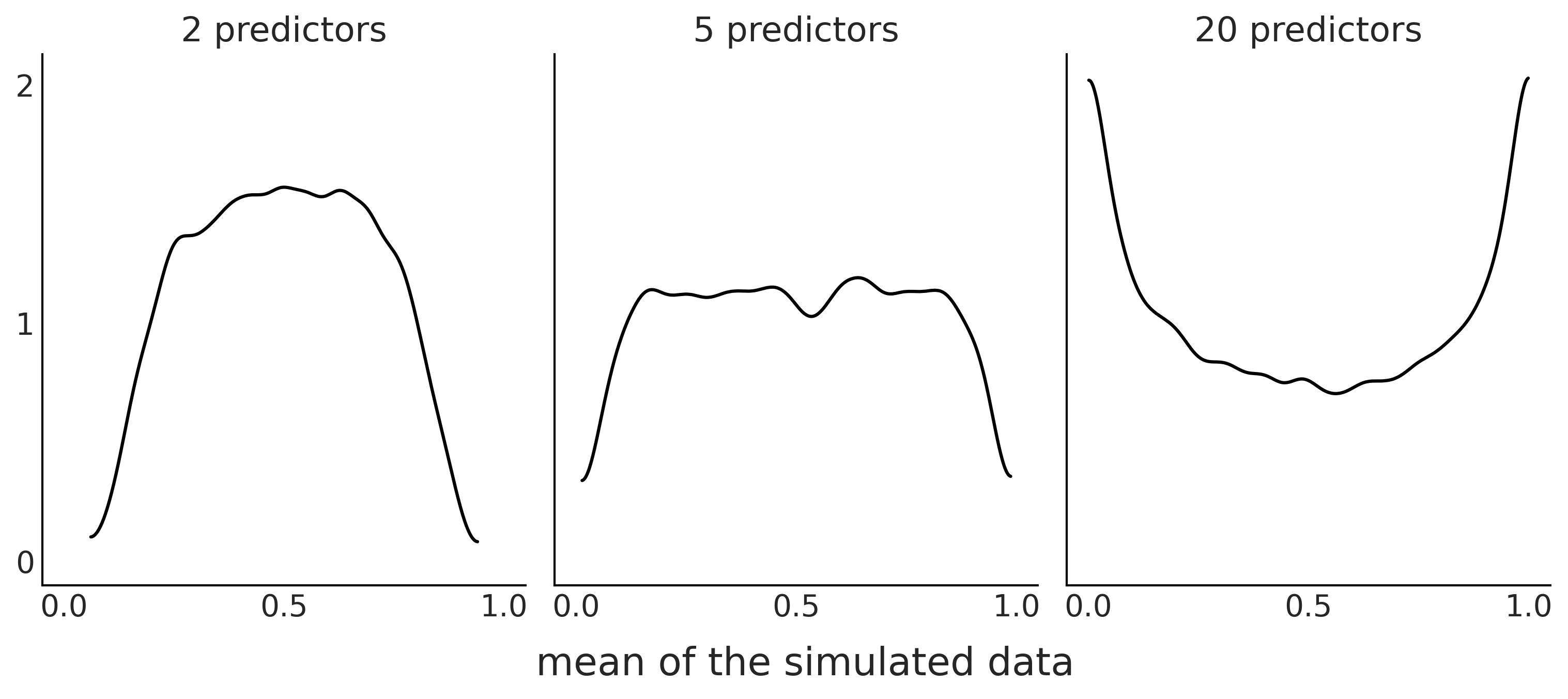
../_images/prior_predictive_distributions_01.png

Fig. 14 对具有 \(2\) 个、\(5\) 个、 \(15\) 个预测变量和 \(100\) 个数据点的逻辑斯蒂回归模型做出的先验预测分布。核密度估计曲线表示了 \(10000\) 条模拟数据的均值呈现出的分布特点。三个图中的系数均采用了 \(\mathcal{N}(0, 1)\) 先验，但预测变量数量的增加在实际上等价于使用了一个偏爱极值的先验。

2.2.3 其他好处

上述两个例子都表明，不能孤立地理解先验，我们必须将其放在特定模型的语境中。通常直接根据观测值进行思考，会比直接根据模型参数进行思考更容易，因此先验预测分布有助于降低模型评估的难度。在参数经过多次转换或多个先验存在交互的复杂模型场景中，先验预测分布的这种作用更为明显。

此外，先验预测分布也可用于直观向广大涉众展示结果或讨论模型。当领域专家不熟悉统计符号或代码时，沟通很难富有成效，但如果你展示的是一个或多个模型的直观涵义，那就可以为他们提供更多讨论材料，进而为你和合作伙伴提供有价值的见解。

计算先验预测还具有其他优势，例如辅助调试模型、确保模型编写正确、保证模型能够在计算环境中正确运行等。

2.3 后验预测检查

既然可以使用来自先验预测分布的合成数据来帮助我们检查模型，那么也可以使用 后验预测分布 进行类似的分析，这个概念在 1.1.2 贝叶斯推断 （ Bayesian Inference ） 和公式 (6) 中曾经提到过。

2.3.1 什么是后验预测检查？

生成后验预测样本并基于样本做模型评估的过程，通常被称为 后验预测检查（ Posterior Predictive Checks ）。其基本思想是评估生成数据与实际观测数据的接近程度。

理论上，评估接近程度的方法取决于研究问题本身，但也存在一些通用规则。我们甚至可能想要使用多种测度来评估不同模型匹配数据（或错配数据）的方式。

Fig. 15 显示了一个非常简单的 Beta-Binomial 模型 和数据示例。在左图中，我们将数据中观测到的成功次数（蓝线）与后验预测分布中超过 \(1000\) 个样本的预测成功次数进行了比较。右图是另一种表示结果的方式，显示了观测数据（蓝线）与来自后验分布的 \(1000\) 个样本中的成功/失败比。正如我们所见，在当前设置下，模型在捕获均值方面做得非常好，即使模型认识到存在很多不确定性。不过，我们不应该对此感到惊讶，因为我们直接对二项分布的均值进行了建模。在后续章节中，我们还将看到一些后验预测检查为模型拟合数据提供有价值信息的示例。

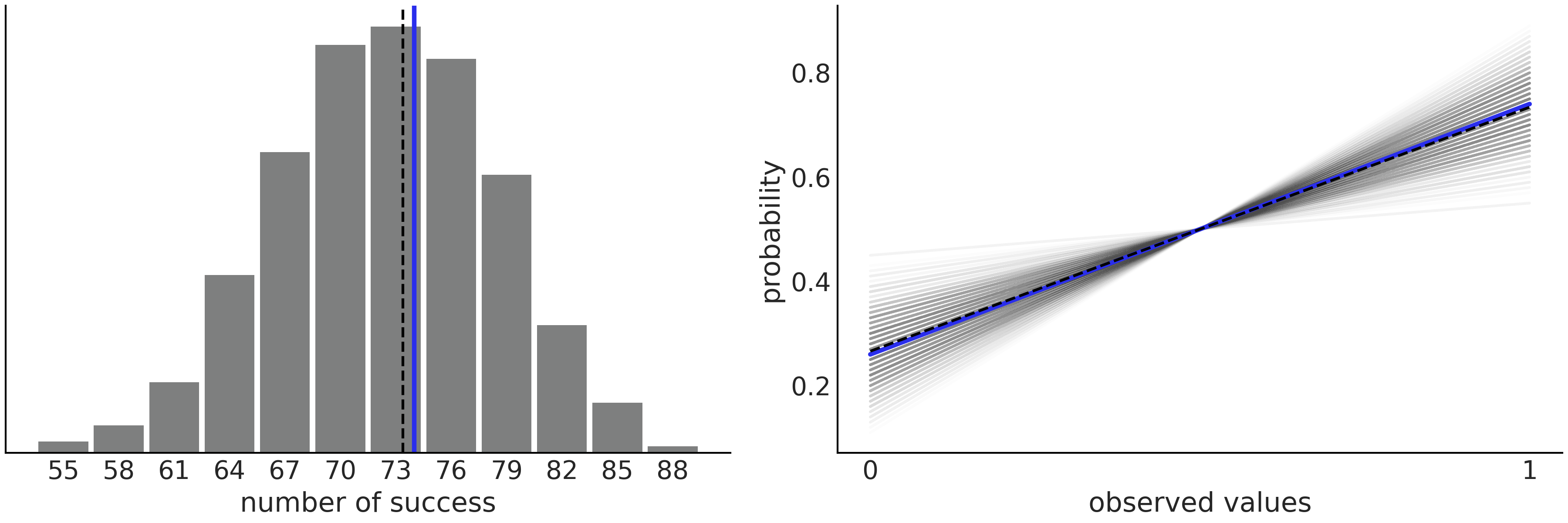
../_images/posterior_predictive_check.png

Fig. 15 Beta-Binomial 模型的后验预测检查。左图中有预测成功的数量（灰色直方图），黑色虚线表示预测成功的均值，蓝线是根据观测数据计算的均值。右图用另外一种形式表达了相同的信息，该图中绘制的是获得 \(0\) （或 \(1\) ）的概率，而不是成功的数量。我们用一条直线来表示 \(p(y=0) = 1-p(y=1)\) 的概率，其中黑虚线代表预测概率的均值，蓝线则是从观测数据中计算出的概率均值。

2.3.2 贝叶斯 \(p\) 值

后验预测检查不仅限于绘图，还可以用于执行数值检验 [18]。计算贝叶斯 \(p\) 值就是其中一种：

(18)\[p_{B} = p(T_{sim} \leq T_{obs} \mid \tilde Y)\]

其中 \(p_{B}\) 是贝叶斯 \(p\) 值，定义为模拟的统计量 \(T_{sim}\) 小于或等于观测统计量 \(T_{obs}\) 的概率。统计量 \(T\) 可以是任何 “用于评估模型是否拟合数据的” 指标。

对于上述二项模型的示例，我们可以选择成功率作为统计量，其中观测到的成功率作为 \(T_{obs}\) ，然后将其与后验预测分布的成功率 \(T_{sim}\) 进行比较。如果 \(p_{B}=0.5\) ，表明我们模拟生成的统计量 \(T_{sim}\) ，有一半时间低于观测统计量 \(T_{obs}\)，另外一半时间高于观测统计量 \(T_{obs}\)，而这恰恰是一个我们期望的正确拟合结果。

因为绘图更加直观一些，所以也可以使用贝叶斯 \(p\) 值来制图。

Fig. 16 的左图以黑色实线显示了贝叶斯 \(p\) 值的分布，虚线表示了相同大小数据集期望的分布。 我们使用 ArviZ 的 az.plot_bpv(., kind="p_value") 函数获得此图。右图在概念上相似，不同之处在于评估了有多少模拟数据低于（或高于）观测数据。对于一个校准良好的模型，所有观测值都应该得到同样好的预测，即预测高于或低于期望的数量应该相同，因此应该得到一个均匀分布。对于任何有限数据集，即使完美校准的模型也会显示出与均匀分布的偏差，我们绘制了一个条带，期望看到类均匀曲线的 \(94\%\) 区间。

贝叶斯 \(p\) 值

我们将 \(p_{B}\) 称为贝叶斯 \(p\) 值，因为公式 (18) 中的量，实质上是 \(p\) 值的定义，之所以称其为贝叶斯的，是因为我们并没有使用零假设条件下统计量 \(T\) 的分布作为采样分布，而是使用了后验预测分布。请注意，我们没有以任何零假设为条件；也没有使用任何预定义的阈值来声明统计显著性或执行假设检验。

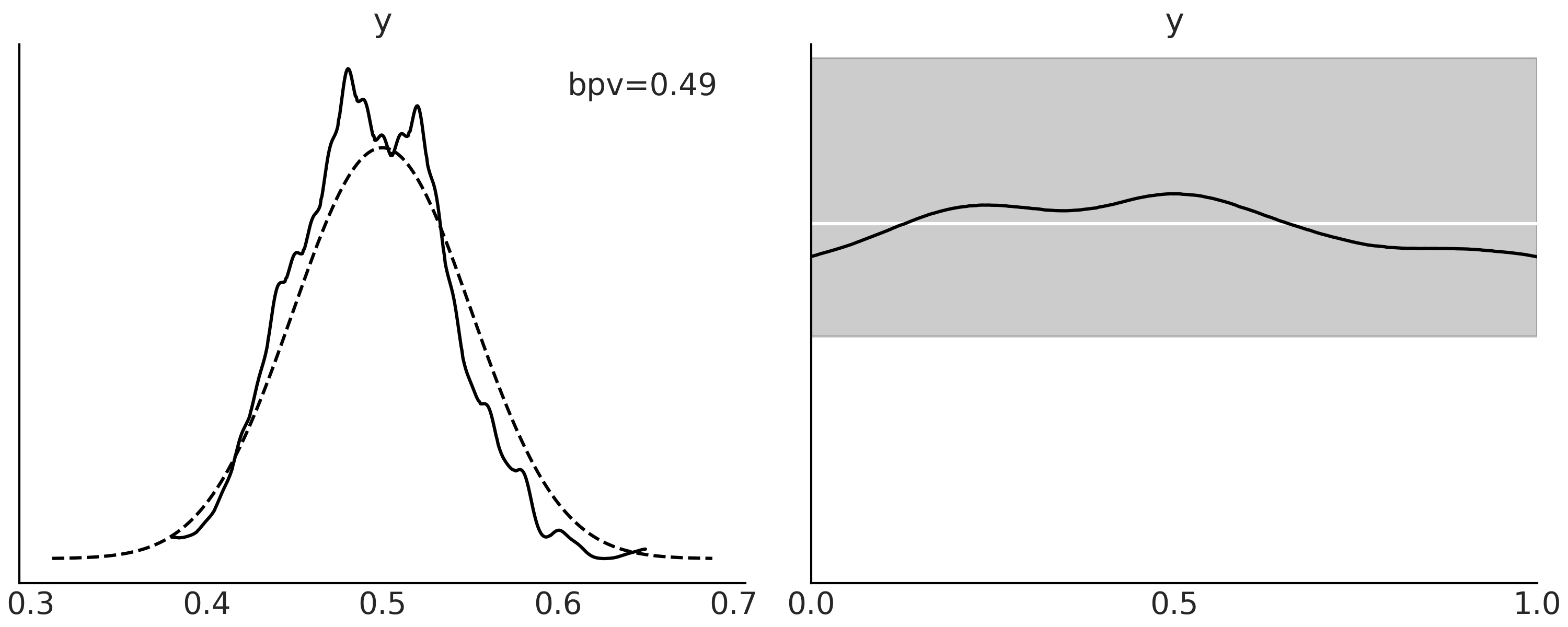
../_images/posterior_predictive_check_pu_values.png

Fig. 16 Beta-Binomial 模型的后验预测分布。在左图中，实曲线表示小于等于实际观测值的预测值比例（采用了核密度估计）。虚线表示当预测数据集与观测数据大小相同时，我们期望的分布。在右图中，黑线同样表示了小于等于观测值的预测值比例 （采用了核密度估计），但与左图中在每个模拟上做计算不同，右图是在每个观测上做计算。白线代表了一个标准均匀分布的理想情况，灰色区域表示在相同大小数据集上，我们期望看到的该均匀分布的偏差（\(94\%\) 区间）。

正如之前所述，我们可以在许多 \(T\) 统计量中做出选择，来汇总观测数据和预测结果。

Fig. 17 显示了其中两个示例，左图中的 \(T\) 为均值，右图中的 \(T\) 为标准差。曲线表示基于后验预测分布的 \(T\) 统计量的分布（采用了核密度估计），底部的黑点是实际观测数据的值。

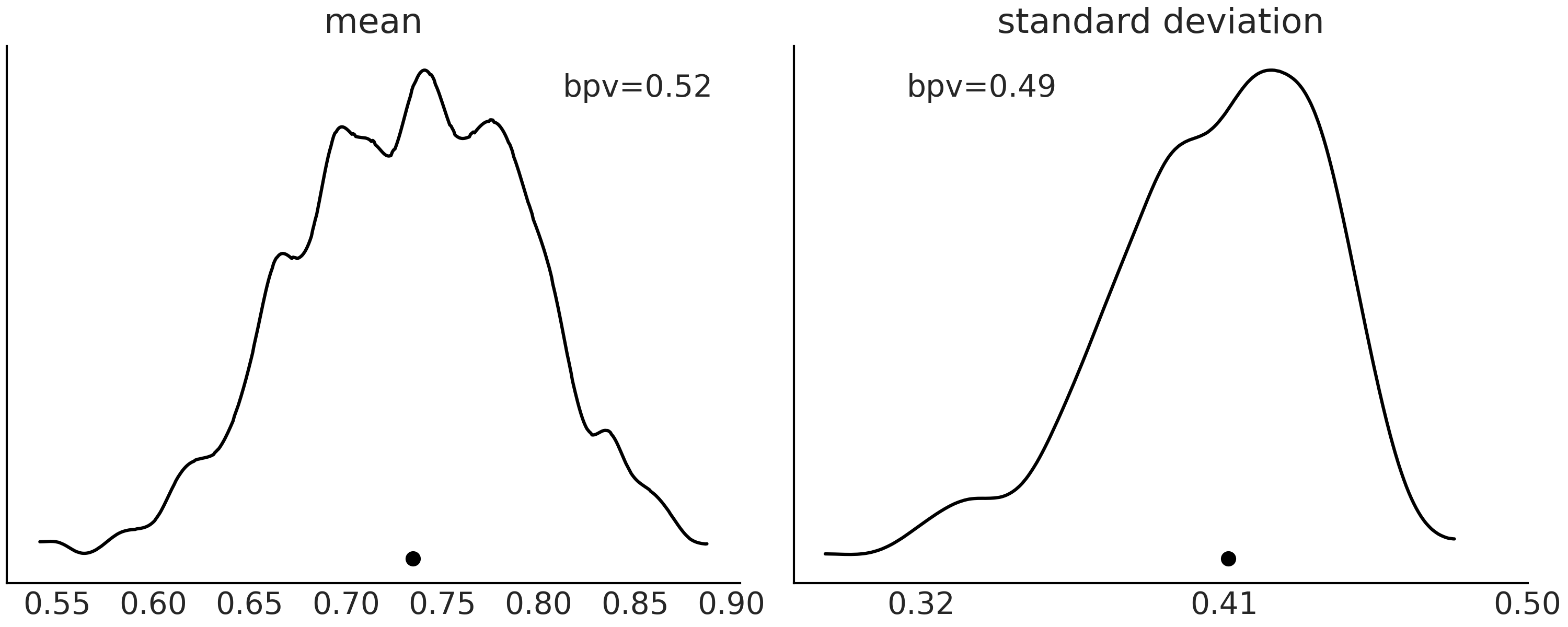
../_images/posterior_predictive_check_tstat.png

Fig. 17 Beta-Binomial 模型的后验预测分布。在左图中，实曲线表示均值小于等于实际观测数据的模拟预测结果的比例（采用了核密度估计）。在右图中，形式相同，只是统计量变成了标准差。黑点代表从观测数据计算的均值（左图）或标准差（右图）。

2.3.3 图表的分析与理解

在继续阅读之前，你应该花点时间仔细检查 Fig. 18 ，并自己尝试着理解这些图为什么会有如此表现。在此图中，有一系列简单例子来帮助我们获得用于解释后验预测检查图的直观感觉7。在所有这些示例中，观测数据（蓝色）都遵循高斯分布。

  1. 在第一行，模型预测相对于观测数据系统地转移到更高值的观测值。

  2. 在第二行，模型做出的预测比观测数据更广泛。

  3. 在第三行，我们有相反的情况，模型没有在尾部生成足够的预测。

  4. 最后一行显示了一个模型在混合高斯后进行预测。

现在注意 Fig. 18 的第三列。此列中的图表非常有用，但同时可能会令人困惑。

从上到下，你可以将它们阅读为：

  1. 模型左尾缺少观测值（而右尾观测值更多）。

  2. 模型在中间做出更少的预测（而在尾部做出更多的预测）。

  3. 模型在尾部的预测较少。

  4. 该模型正在或多或少地做出经过良好校准的预测，但我是一个持怀疑态度的人，所以我应该运行另一个后验预测检查来确认。

如果这种阅读图表的方式仍然让你感到困惑，可以从完全等效的不同角度尝试，但它可能更直观，只要你记住你可以更改模型，而不是观测结果 8。从上到下，你可以将它们阅读为：

  1. 左侧观测较多

  2. 中间观测较多

  3. 尾部观测较多。

  4. 观测结果似乎分布良好（至少在预期范围内），但你不应该相信我。我只是柏拉图世界中的柏拉图模型。

我们希望 Fig. 18 和随附的讨论为你提供了足够的直觉，以便更好地在实际场景中执行模型检查。

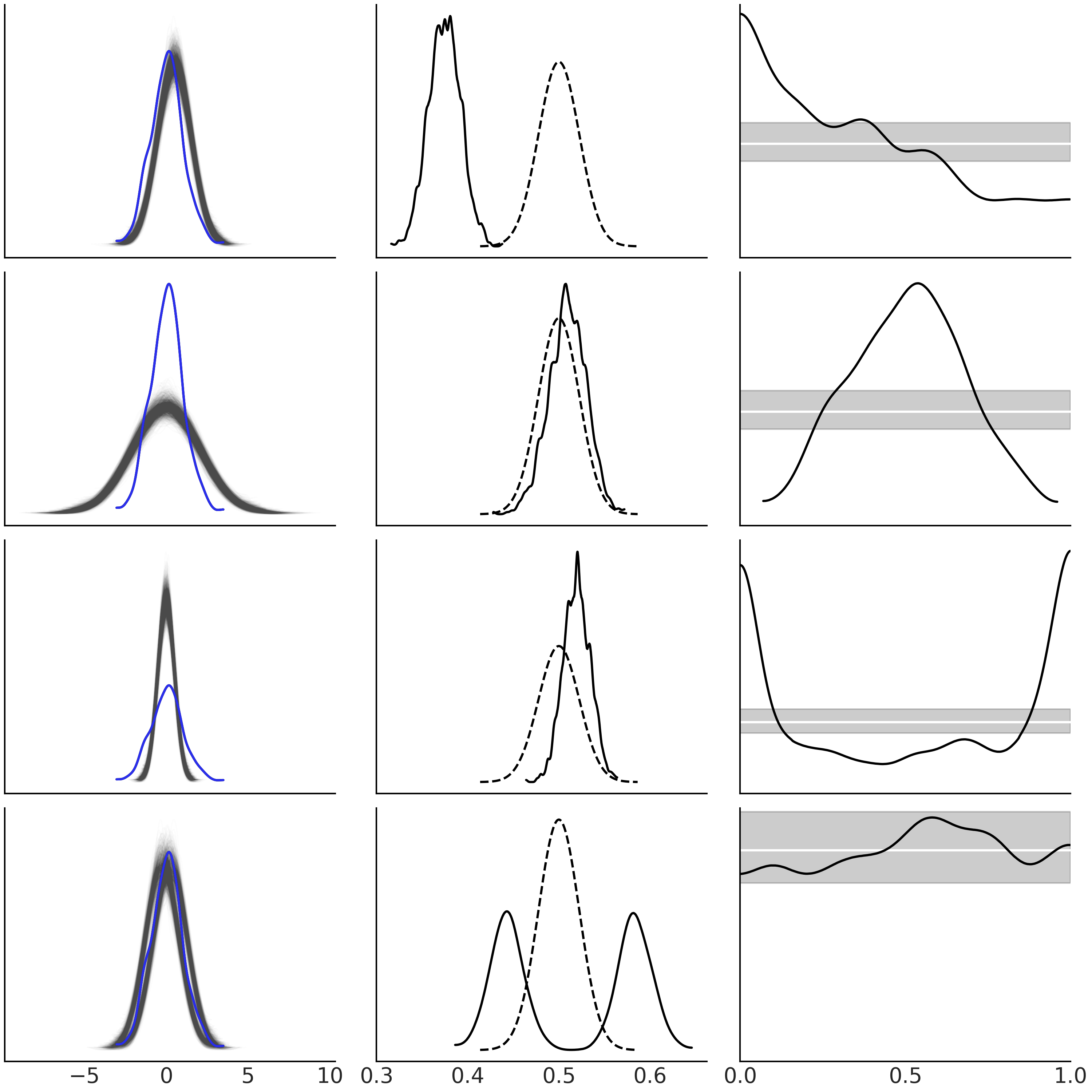
../_images/posterior_predictive_many_examples.png

Fig. 18 一组简单模型的后验预测检查。在第一列中，蓝色实线代表观测数据和来自模型的浅灰色预测结果。在第二列中，实线是小于等于观测数据的预测结果比例（采用了核密度估计），而虚线表示采用与观测数据集大小相同的数据集时预期的分布。在第三列中，黑色曲线指在每个观测处，小于等于观测数据的预测结果比例。白线代表预期的均匀分布，灰色区域表示采用与观测数据集大小相同的数据集时预期的偏差。该图使用 ArviZ 的函数 az.plot_ppc(.)、az.plot_bpv(., kind="p_values") 和 az.plot_bpv(., kind="u_values") 绘制。

无论是采用绘图、数字汇总信息还是两者结合的方式，后验预测检查都是一个足够灵活的思想。这个概念足以让从业者发挥他们的想象力，通过自己的后验预测来探索、评估和理解不同的途径和模型，进一步在面向特定问题时，掌握这些模型工作的优劣程度。

2.4 常用的数值化诊断方法

对于某些模型，用笔和纸求解后验可能很乏味，有些甚至在数学上可能是无解的，此时采用数值方法来近似计算后验分布，能够让我们求解贝叶斯模型。不幸的是，这些数值方法并不总是按照预期工作。出于此原因，必须人工参与评估其结果的可用性。目前，有一系列数值和可视化诊断工具用于辅助诊断。在本节中，我们将面向 MCMC 方法，讨论其最常见和最有用的诊断工具。

为了理解这些诊断工具，我们先创建三个 合成后验 ：

第一个为来自 \(\text{Beta}(2, 5)\) 的样本。我们使用 SciPy 生成它，并称之为 good_chains，表示这是一个好样本，因为这是在理想情况下，我们想要的独立同分布样本。

第二个合成后验被称为 bad_chains0，表示来自后验的不良样本。它是在对 good_chains 排序后，通过添加一个小的高斯误差生成的。 bad_chains0 是一个糟糕的样本，原因有两个：一是这些值不独立。相反，它们是高度自相关的，这意味着如果给定序列中任何位置的任何数字，都可以高精度地计算出其前后的值。二是这些值并非同分布的，因为我们正在将之前展平并排序的数组整形为二维数组，代表了两条链。

第三个合成后验被称为 bad_chains1，它也是从 good_chains 生成的，我们随机地引入彼此高度相关的连续样本片段，来生成后验的不良样本表示。 bad_chains1 代表了一种很常见的场景，即采样器可以很好处理参数空间的大部分区域，但同时存在一个或多个很难采样的区域。

good_chains = stats.beta.rvs(2, 5,size=(2, 2000))
bad_chains0 = np.random.normal(np.sort(good_chains, axis=None), 0.05,
                               size=4000).reshape(2, -1)

bad_chains1 = good_chains.copy()
for i in np.random.randint(1900, size=4):
    bad_chains1[i%2:,i:i+100] = np.random.beta(i, 950, size=100)

chains = {"good_chains":good_chains,
          "bad_chains0":bad_chains0,
          "bad_chains1":bad_chains1}

请注意，\(3\) 个合成后验都是标量（单参数或一元随机变量）的后验分布样本，不过这对于当前讨论来说已经足够了，因为后面的诊断都是逐模型参数计算的。

2.4.1 有效样本数量 （ ESS ）

使用 MCMC 采样方法时，有理由怀疑样本是否足够大，是否能够可靠地支撑计算感兴趣的量，如均值或 HDI。这个问题无法仅通过查看样本数量直接回答，因为来自 MCMC 方法的样本具有一定程度的自相关，因此其中包含的实际 信息量 会比从相同大小的独立同分布样本要少。一系列数值的自相关是指，我们可以观测到这些值之间的相似性是其时间滞后的函数。例如，如果今天的日出时间是早上 6:03，那么你知道明天的日出时间大约是同一时间。事实上，在知道今天的值后，你离赤道越近预测未来日落时间的时间滞后就越长。也就是说，赤道处的自相关比靠近两极的地方大 9。

从上述分析出发，我们可以将有效样本数 ( Effective Sample Size, ESS ) 视为一个考虑了自相关的估计量，能够提供当样本为独立同分布时应该具备的抽样次数。此解释很吸引人，但小心不要过度解读，我们将在后面看到这一点。

我们可以使用 ArviZ 的 az.ess() 函数计算均值参数的有效样本大小：

az.ess(chains)

<xarray.Dataset>
Dimensions:      ()
Data variables:
    good_chains  float64 4.389e+03
    bad_chains0  float64 2.436
    bad_chains1  float64 111.1

可以看到，当合成后验中的真实样本数为 \(4000\) 时，bad_chains0 的有效样本数量仅相当于 \(\approx 2\) 个独立同分布样本。这个数字过低，表明采样器存在问题。不过考虑到我们创建 bad_chains0 的方法，此结果完全可以预期。bad_chains0 为双峰分布，每条链都被卡在了两个峰值之间。此时，有效样本数将大约等于 MCMC 链所探索的峰值数量。 bad_chains1 也得到了一个较低的数字 \(\approx 111\)，只有 good_chains 的有效样本数接近实际样本数。

关于有效样本的有效性

如果使用不同的随机种子重新生成合成后验的样本，你会看到每次的有效样本数都不同，这是由于每次的样本不会完全相同。对于 good_chains ，平均而言有效样本数的值将低于样本数。但请注意，有效样本数实际上可能更大！当使用 NUTS 采样器（ 参见 11.9 推断方法 ）时，如果存在某些参数的后验分布接近高斯分布但几乎独立于模型中其他参数，则可能会出现大于样本实际数的有效样本数。

马尔可夫链的收敛性在参数空间上并不均匀 [19] ，直观地说，从分布主体中获得良好近似值比从尾部更容易，因为尾部由罕见的事件主导。 az.ess() 返回的默认值为 bulk-ESS，它主要评估分布中心的情况。如果你对后验区间或者罕见事件感兴趣，可以检查 tail-ESS 的值，它对应于百分位数 \(5\) 和 \(95\) 处的最小有效样本数。如果你对特定分位数感兴趣，可以使用 az.ess(., method='quantile') 函数对特定值进行查询。

由于有效样本数在参数空间中存在变化，因此在一个图中可视化这种变化会很有用。目前至少有两种方法可以做到这一点：一是用 az.plot_ess(., kind="quantiles") 函数绘制有效样本数的具体分位数，二是用 az.plot_ess(., kind="local") 函数绘制两个分位数之间定义的区间，如 Fig. 19。

_, axes = plt.subplots(2, 3, sharey=True, sharex=True)
az.plot_ess(chains, kind="local", ax=axes[0]);
az.plot_ess(chains, kind="quantile", ax=axes[1]);
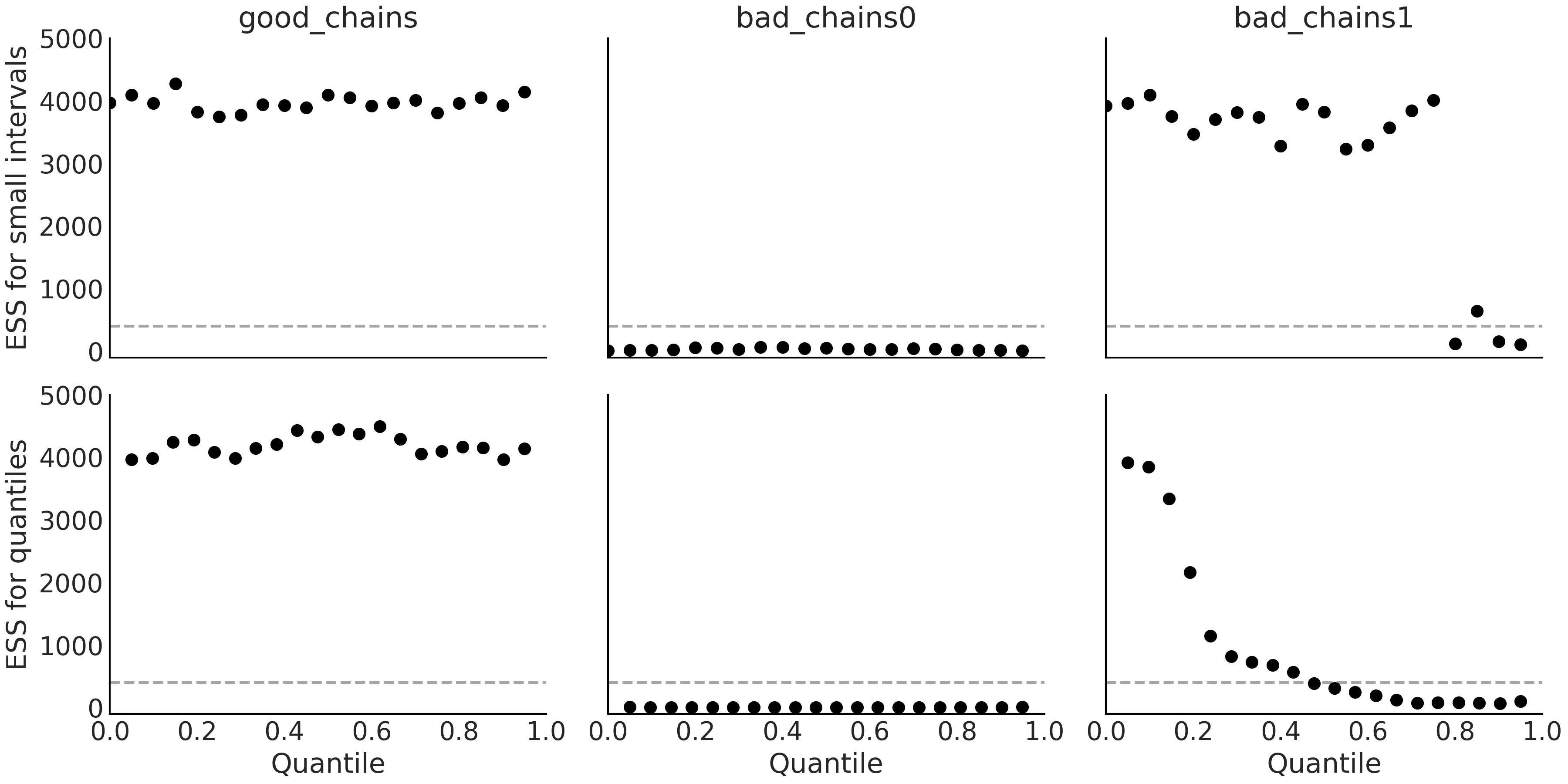
../_images/plot_ess.png

Fig. 19 上图：小区间概率估计的局部有效样本数。底部：分位数有效样本数估计。虚线为人为设定的有效样本数最小建议值 \(400\)。理想情况下，我们希望局部和分位数有效样本数在参数空间的所有区域都很高。

作为一般经验，我们建议有效样本数大于 \(400\)，否则，对有效样本数自身的估计和对其他量（ 如下面将看到的 \(\hat R\) ）的估计，基本上不可靠 [19] 。最后再次强调，我们讨论的有效样本数是指当样本为独立同分布时的样本数量，但必须非常小心地做出这种解释，因为参数空间不同区域的实际有效样本数可能并不相同。

2.4.2 潜在尺度缩减因子（ \(\hat R\) ）

在一般条件下，MCMC 方法有理论上的保证，无论该链的起点在哪儿，最终都会得到正确答案，但这仅对无限样本有效。在实践中，需要一些估计有限样本收敛性的方法。其中一个普遍做法是运行多个链，各自从不同的点开始，然后检查这些生成的链是否彼此看起来足够相似。

这个直观的概念可以被形式化为指标潜在尺度缩减因子（ Potential Scale Reduction Factor, PSRF），记为 \(\hat R\) 。该指标的计算公式有很多版本，因为多年来它一直在改进 [19]。最初，\(\hat R\) 被解释为对样本方差的一种估计方法。理论上如果进行无限地采样，样本的估计方差应当逐步缩小，而 \(\hat R\) 正是对此缩小程度的量化，通常计算为 所有样本的方差 和 链内样本的均方差 之比。 \(\hat R\) 的目标值为 \(1\) ，也就是说，当 \(\hat R\) 达到 \(1\) 时，采样就进入了理想状态，继续增加样本已经无助于减少估计方差了。

在实践中，通常将 \(\hat R\) 视为一种诊断工具，用于判断 MCMC 链是否已经达到了可接受的收敛状态。例如，一种常见的 \(\hat R\) 计算公式为：

\[\hat R = \frac{\text{sd}_{All-Samples}}{\sqrt{\frac{1}{N}\sum_{i=1}^N \text{sd}^2_{samples-of-Chain_i}}}\]

实际计算时涉及的内容会更多一点，但总体思路仍然不变 [19]。当链达到收敛的理想情况下，我们应该得到值 \(1\)，即链间方差应该与链内方差一致。但从实用角度来看，\(\hat R \lessapprox 1.01\) 通常也被认为是安全的。

使用 ArviZ，可以调用 az.rhat() 函数来计算 \(\hat R\) ：

az.rhat(chains)

<xarray.Dataset>
Dimensions:      ()
Data variables:
    good_chains  float64 1.000
    bad_chains0  float64 2.408
    bad_chains1  float64 1.033

从此结果可以看出 \(\hat R\) 准确地将 good_chains 识别为好样本，将 bad_chains0 和 bad_chains1 正确识别为具有不同程度问题的样本。虽然 bad_chains0 完全是一场灾难，但 bad_chains1 似乎更接近于达到良好链的状态，但其值 \(\hat R = 1.033 > 1.01\) 依然有点大。

2.4.3 蒙特卡洛标准误差

MCMC 方法用有限数量的样本来近似整个后验分布，进而引入了额外的不确定性。这种不确定性可以使用基于 马尔可夫链中心极限定理 的 蒙特卡洛标准误差 (MCSE) 来量化（参见 11.1.11 马尔可夫链 ）。 考虑到样本并非真正相互独立，蒙特卡洛标准误差实际上是从有效样本数（ ESS ） 计算得出的 [19] 。有效样本数 ESS 和缩减因子 \(\hat R\) 的取值独立于参数自身的尺度，因此对 MCSE 大小的解释需要在参数的尺度空间中进行，无法给出一个类似 \(\hat R < 1.01\) 的指示阈值，往往需要分析人员具有领域专业知识。如果想要将估计的参数值取到小数点后两位，就需要确保 MCSE 低于小数点后两位，否则将错误地取得比实际精度更高的精度。此外，只有当我们确定有效样本数 ESS 足够大并且缩减因子 \(\hat R\) 足够小时，检查 MCSE 才有意义；否则，计算 MCSE 是没有用的。

使用 ArviZ，可以调用函数 az.mcse() 计算 MCSE ：

az.mcse(chains)

<xarray.Dataset>
Dimensions:      ()
Data variables:
    good_chains  float64 0.002381
    bad_chains0  float64 0.1077
    bad_chains1  float64 0.01781

与有效样本数 ESS 一样，MCSE 在参数空间中也存在变化，因此有时可能想进一步评估不同区域的 MCSE，例如特定分位数附近。此外，有时会需要像 Fig. 20 一样，同时可视化多个值。

az.plot_mcse(chains)
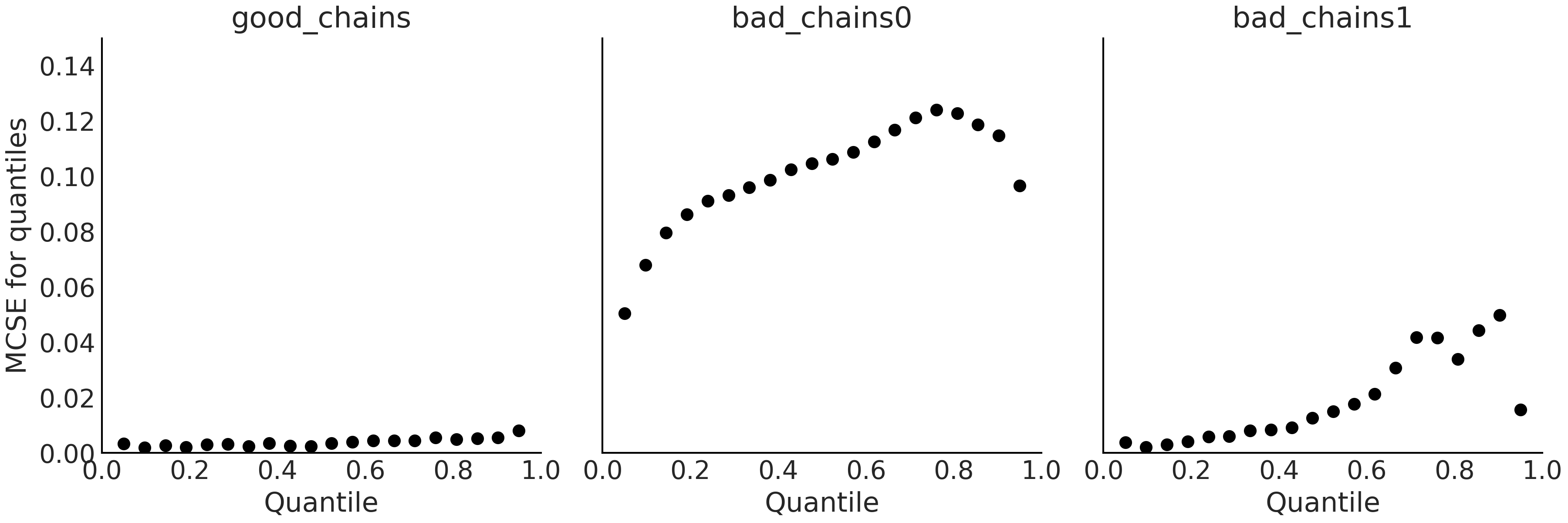
../_images/plot_mcse.png

Fig. 20 分位数的局部 MCSE。图中 \(y\) 轴共享相同的尺度以方便对比。理想情况下，我们希望 MCSE 在参数空间的所有区域中都很小。请注意，与两条不良链的 MCSE 相比，good_chains 的 MCSE 值在参数空间的所有值处都相对较低。

最后，ESS、\(\hat R\) 和 MCSE 可以通过一次性调用 az.summary(.) 函数一起计算。

az.summary(chains, kind="diagnostics")

mcse_mean*

mcse_sd

ess_bulk

ess_tail

r_hat

good_chains

0.002

0.002

4389.0

3966.0

1.00

bad_chains0

0.108

0.088

2.0

11.0

2.41

bad_chains1

0.018

0.013

111.0

105.0

1.03

表中第一列是均值参数的 MCSE ，第二列是标准差参数的 MCSE 10 。然后依次是参数空间的主体区域和尾部区域的有效样本数，最后是 \(\hat R\) 的收敛性诊断。

2.4.4 轨迹图

轨迹图可能是贝叶斯领域中最流行的图。它通常是贝叶斯推断完成后制作的第一张图，可以非常直观地检查 我们得到了什么。

轨迹图利用在每个迭代步骤中抽取得到的样本值来绘制。在轨迹图中，能够看到不同的链是否收敛到了同一分布、可以得到自相关程度的 直觉 …… 。使用 ArviZ ，只需调用函数 az.plot_trace(.) 即可方便地获得模型参数的轨迹图（右）和样本值的概率分布图（左），对于概率分布图，连续型随机变量采用核密度估计曲线来绘制，而离散型随机变量采用直方图来表示。

az.plot_trace(chains)
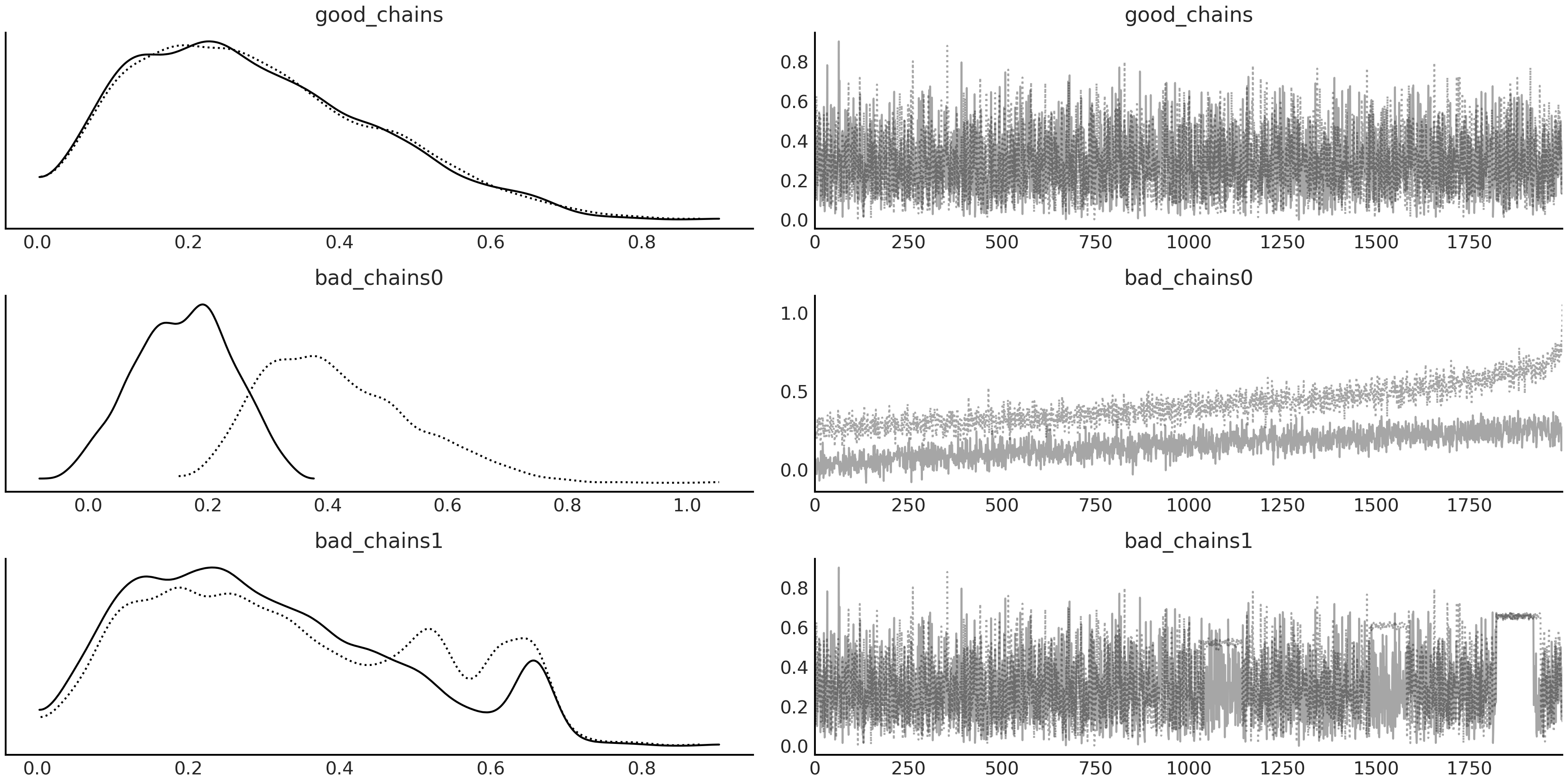
../_images/trace_plots.png

Fig. 21 在左侧中，可以看到每条链的样本概率分布图（经过核密度估计）。在右图中，可以看到每条链每一步的采样值情况。注意三条链之间样本概率分布图和轨迹图的差异，特别是 good_chains 中具有毛毛虫似的外观，而其他两条链中则多多少少存在不规整性。

Fig. 21 显示了三种情况下的双链轨迹图（即将两条独立链的轨迹绘制在一张图上）。从中可以看到：

在 good_chains 中，两条独立链的抽取几乎来自于同一分布，因为它们的分布图之间（随机）差异很小。当我们按照迭代顺序查看抽取的样本时，可以发现两条链都相当 杂乱 且不存在明显趋势或模式，而且通过肉眼很难将两条链区分开来。

bad_chains0 的情况与之形成了鲜明对比，可以通过样本概率分布图和轨迹图清楚地看到两个不同的分布，其间只有少量重叠区，这表明两条链正在探索参数空间的不同区域且无法收敛。

bad_chains1 的情况有点微妙。其样本概率分布图似乎与 good_chains 中的分布相似，但两条独立链之间存在更加明显的差异。我们真的有 \(2\) 个或 \(3\) 个峰吗？分布似乎也不一致，也许真实分布只有一个峰，而另外一个是伪影！多峰形态通常看起来是比较可疑的，除非有确切理由让我们确信存在多峰分布，例如，数据来自多个群组。其轨迹图似乎也与 good_chains 中的轨迹有些相似，但仔细检查会发现其中存在部分单调性区域（图中平行于 \(x\) 轴的线）。这清楚地表明采样器卡在了参数空间的某些区域中，这或许因为后验存在多峰，且在峰之间存在低概率的障碍区，又或许是因为参数空间中存在一些区域的曲率与其他区域存在明显不同。

2.4.5 自相关图

正如在讨论有效样本数时所述，自相关减少了样本中包含的实际信息量，因此希望尽量将其控制在最低限度，此时可以使用 az.plot_autocorr 函数直接可视化地检查自相关性。

az.plot_autocorr(chains, combined=True)
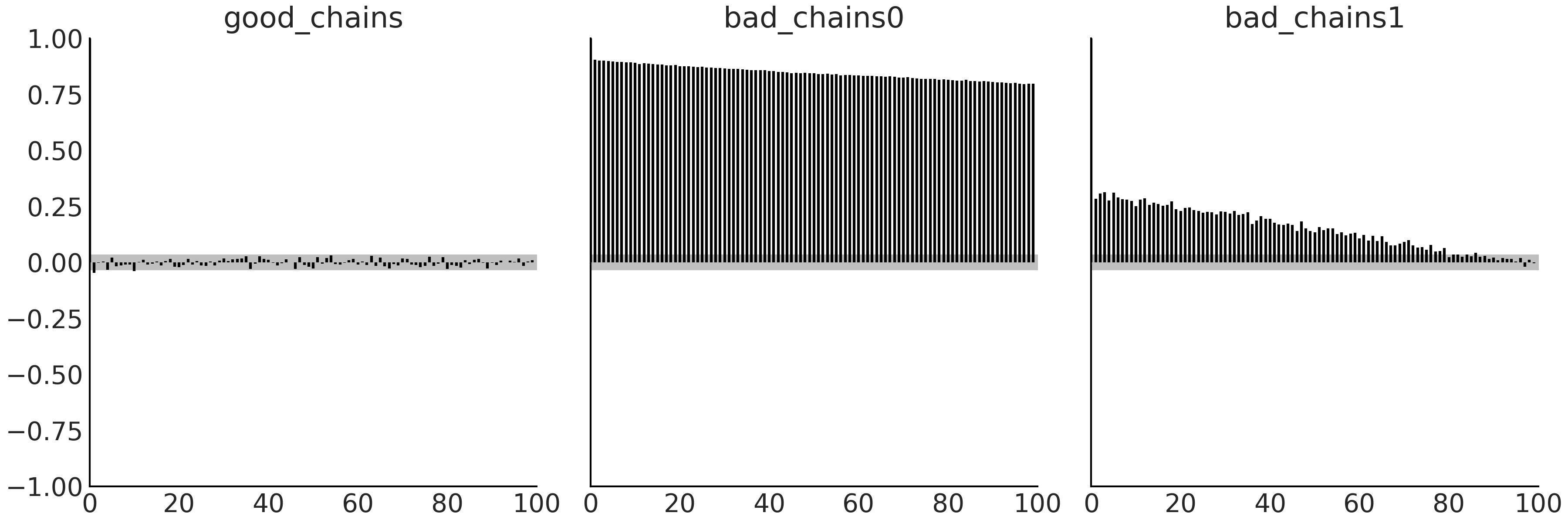
../_images/autocorrelation_plot.png

Fig. 22 在 \(100\) 步窗口上的自相关函数柱状图。对于整个图，good_chains 的柱高度接近于零（并且大部分在灰色带内），这表明自相关非常低。 bad_chains0 和 bad_chains1 中较高的柱状图表明自相关值较大，这是不可取的。灰色区域代表 \(95\%\) 信念区间。

fig:autocorrelation_plot 中的内容在看到的 az.ess 结果后，至少是可定性预见的。good_chains 显示出基本上为零的自相关；bad_chains0 高度相关；而 bad_chains1 并没有那么糟糕，但自相关仍然很明显并且不会迅速下降。

2.4.6 秩图

秩图是另一种可视化诊断工具，可以用它来比较链内和链间的采样行为。秩图是排序后样本的直方图，它先组合所有链后统一计算秩，然后再分别为每条链绘制排序结果。如果所有链都针对同一分布，则秩应当服从均匀分布。此外，如果所有链的秩图看起来相似，通常表明链的混合良好 [19]。

az.plot_rank(chains, ax=ax[0], kind="bars")
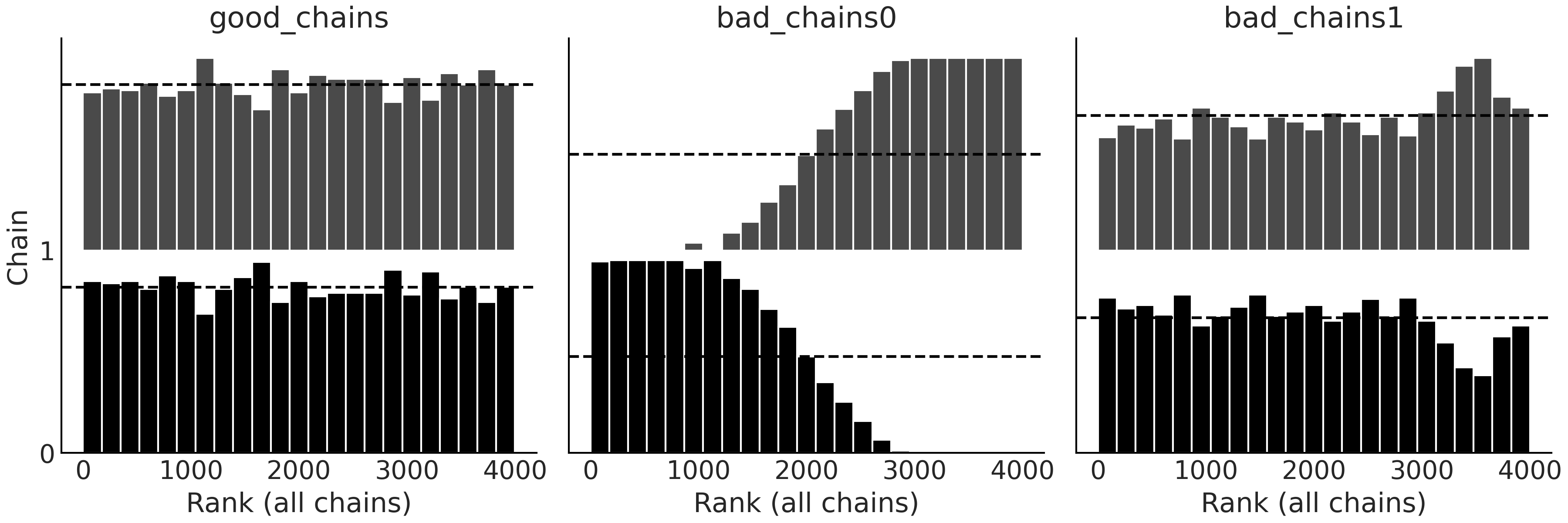
../_images/rank_plot_bars.png

Fig. 23 使用柱状图表示的两条链的秩图。特别将柱高度与表示均匀分布的虚线进行比较。理想情况下，柱图应遵循均匀分布。

柱图表示法的一种替代方法是垂线，缩写为“vlines”。

az.plot_rank(chains, kind="vlines")
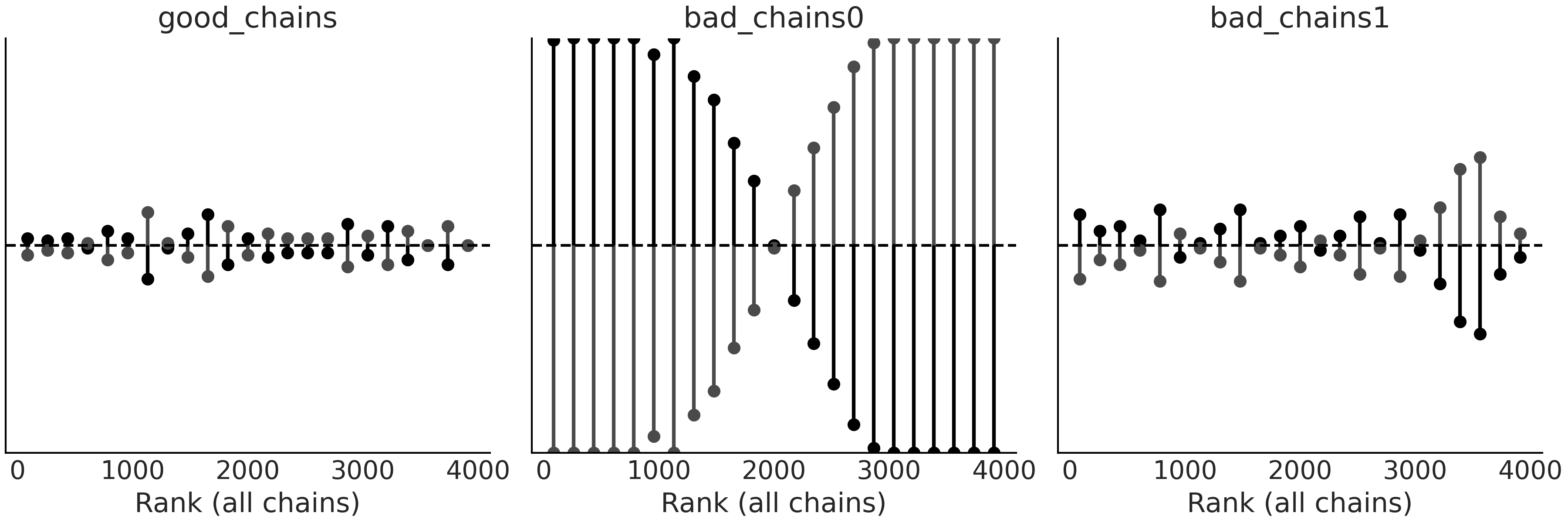
../_images/rank_plot_vlines.png

Fig. 24 使用垂线表示的秩图。垂线越短越好，虚线上方的垂线表示特定秩处的采样量过多，而下方的垂线表示采样量不足。

在 Fig. 23 和 Fig. 24 中可以看到，good_chains 的秩非常接近均匀分布，并且两条链彼此相似，不存在明显的模式。而 bad_chains0 与之形成了鲜明对比，其结果偏离了均匀分布，并且两条链在分别探索不同的区域，只是在中间的秩附近有一些重叠。这个现象与 bad_chains0 的创建方式以及轨迹图显示的内容是一致的。 bad_chains1 在某种程度上是均匀的，但随处都存在较大的偏离，反映出问题比 bad_chains0 更局部。

秩图比轨迹图更敏感，因此我们推荐多使用秩图。你可以使用 az.plot_trace(., kind="rank_bars") 函数或 az.plot_trace(., kind="rank_vlines") 函数绘制上面的两种秩图。这些函数不仅可以绘制秩图，还能绘制后验的边缘分布。这有助于快速了解后验 看起来像什么 ，并帮助我们发现采样或模型定义中存在的问题。尤其是在建模早期阶段，我们不太确定真正想做的事情时，需要探索许多不同的选择。随着进展，待模型变得更有意义后，我们再检查 ESS 、\(\hat R\) 和 MCSE 等指标是否正常，如果不正常我们也可以知道模型下一步需要改进的方向。

2.4.7 散度

到目前为止，我们一直在研究 MCMC 方法生成的样本，以诊断采样器的工作状况。本节将介绍另外一种通过监视采样器内部工作行为做诊断的方法。此类诊断方法的一个突出例子是 Hamiltonian Monte Carlo ( HMC ) 采样器中涉及的 散度（ Divergences ） 概念 11。散度是一种强大而灵敏的样本诊断方法，可作为前几节中诊断方法的补充。

向量场的梯度、散度和旋度

梯度是一个向量，代表在协变量空间中的某点处，响应函数变化的大小和方向。协变量空间中所有点的梯度构成一个向量场，也被成为梯度场。

旋度也是一个向量，代表给定一个向量场，旋度代表在该场中的某点处，环流量强度。

给定一个向量场 \(f\)，设闭合曲线 \(L\) 包围形成面积 \(\Delta S\) ，当 \(\Delta S \rightarrow 0\) 时， \(f\) 对 \(L\) 的环量与 \(\Delta S\) 之比的极限被称为 \(f\) 的旋度沿着该面法线的分量，即 \(rot f = \lim_{\Delta S \rightarrow 0} \frac{\oint f \cdot dl}{\Delta S}\) 。

给定一个向量场 \(f\)，散度代表在该场的某点处，是否存在逸出现象以及逸出的大小。散度是一个标量。严格的数学定义如下：

给定一个向量场 \(f\)，假设一个闭合曲面 \(S\) 包围形成体积 \(\Delta V\) ，当 \(\Delta V \rightarrow 0\) 时， \(f\) 对 \(S\) 的通量与 \(\Delta V\) 之比的极限被称为 \(f\) 的散度，即 \(div f = \lim_{\Delta V \rightarrow 0} \frac{\oint f \cdot ds}{\Delta V}\).

< 此处一定要注意和 KL 散度 是两个完全不相干的概念 >

让我们在一个简单模型背景下讨论散度，本书后面还能找到更现实的例子。模型由一个参数 \(\theta_2\) 组成，该参数服从区间 \([-\theta_1, + \theta_1]\) 内的均匀分布，并且 \(\theta_1\) 采样自高斯分布。当\(\theta_1\) 很大时，\(\theta_2\) 将服从一个跨越很大范围的均匀分布，当\(\theta_1\) 接近于零时，\(\theta_2\) 的分布宽度也将接近于零。使用 PyMC3，可以将此模型编写为：

Listing 9 divm0
with pm.Model() as model_0:
    θ1 = pm.Normal("θ1", 0, 1, testval=0.1)
    θ2 = pm.Uniform("θ2", -θ1, θ1)
    idata_0 = pm.sample(return_inferencedata=True)

ArviZ 支持的推断数据格式 – InferenceData Format

az.InferenceData 是一种专门为 MCMC 的贝叶斯用户设计的数据格式。

它以一个 \(N\) 维数组的软件包 xarray [20] 为基础。 InferenceData 对象的主要目的是提供一种方便的方法来存储和操作贝叶斯工作流程中生成的信息，包括来自分布的样本，如后验、先验、后验预测、先验预测以及采样期间生成的其他信息和诊断数据。 InferenceData 对象使用组的概念来组织这些信息。

在本书中，我们会大量使用az.InferenceData。用它来存储贝叶斯推断结果、计算诊断、生成绘图以及从磁盘读取和写入。有关完整的技术说明和 API，请参阅 ArviZ 文档。

请注意代码 divm0 中的模型不以任何观测为条件，这意味着 model_0 指定了由两个未知数（ \(\theta_1\) 和 \(\theta_2\) ）参数化的后验分布。

你可能注意到代码中包含了参数 testval=0.1。这样做是为了指示 PyMC3 从特定值（ 本例中为 \(0.1\) ）开始采样，而不是从其默认值 \(\theta_1 = 0\) 开始采样。因为对于 \(\theta_1 = 0\) ，\(\theta_2\) 的概率密度函数将对应狄拉克函数 12，这会产生错误。使用 testval=0.1 可以调整采样的初始位置，避免出现上述错误。

在 Fig. 25 中，可以在 model0 的核密度估计曲线底部看到很多竖线。每条竖线都代表一个散度，表明在采样过程中出现了问题。我们可以在其他图看到类似的东西，例如 Fig. 26 中所示的 az.plot_pair(.,divergences=True)，其中散度表示为无处不在的蓝点！

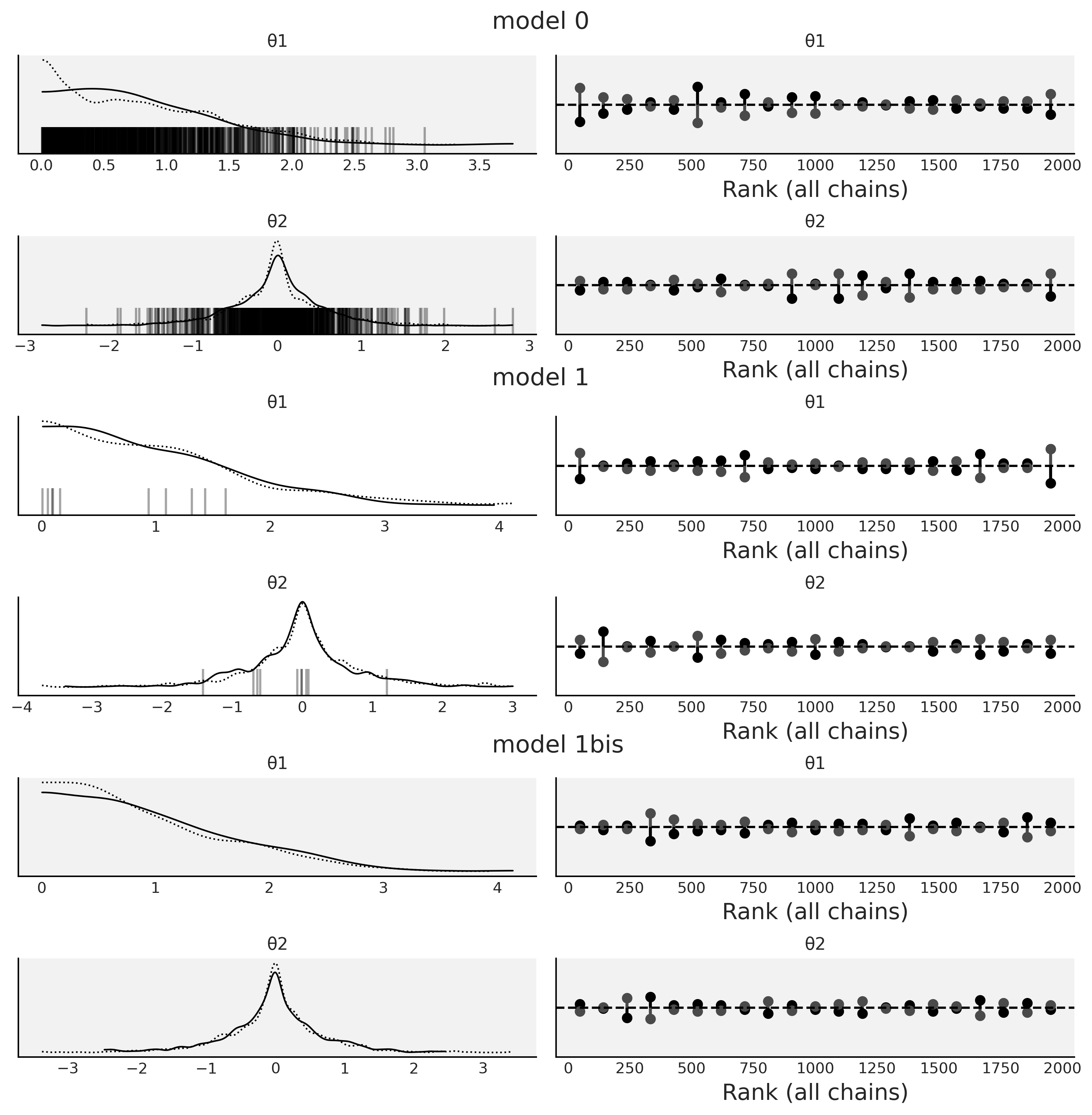
../_images/divergences_trace.png

Fig. 25 模型 \(0\) divm0、模型 \(1\) divm1 、模型 \(1bis\) （ 与模型 \(1\) 相同，但带有 pm.sample(., target_accept =0.95) ）的核密度估计图和秩图。黑色竖条代表散度。

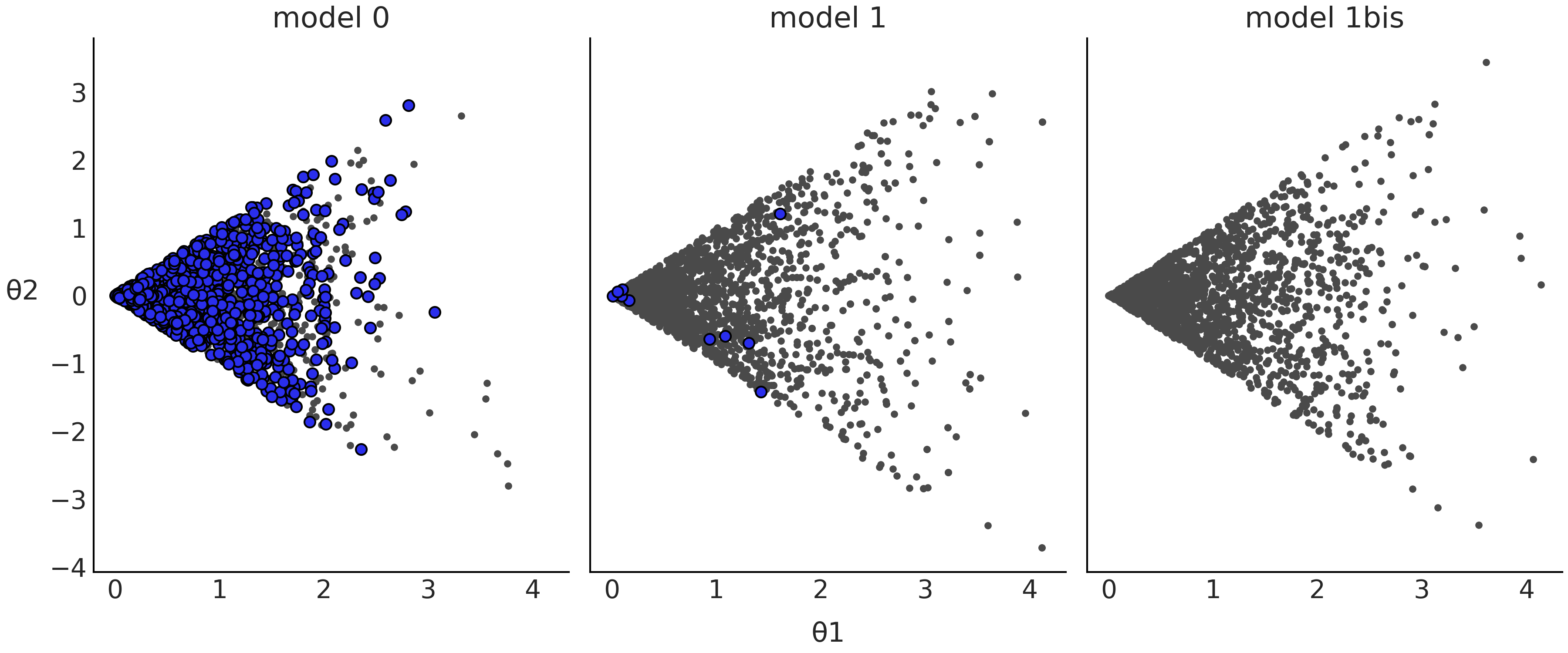
../_images/divergences_pair.png

Fig. 26 模型 \(0\) divm0、模型 \(1\) divm1 、模型 \(1bis\) （ 与模型 \(1\) 相同但使用了 pm.sample(., target_accept=0.95) ）的后验分布样本的散点图。蓝点代表散度。

model0 肯定有问题。通过检查代码 divm0 中的模型定义，你可能会意识到我们以一种奇怪方式定义了它。\(\theta_1\) 是一个以 \(0\) 为中心的高斯分布，因此预期有一半的值是负数，但是对于负值， \(\theta_2\) 将定义在区间 \([+\theta_1, -\theta_1]\) 内，这多少有点奇怪。

因此，让我们尝试 重参数化 该模型，即采用数学上等效但参数化不同的形式来表达模型。例如，可以这样做：

Listing 10 divm1
with pm.Model() as model_1:
    θ1 = pm.HalfNormal("θ1", 1 / (1-2/np.pi)**0.5)
    θ2 = pm.Uniform("θ2", -θ1, θ1)
    idata_1 = pm.sample(return_inferencedata=True)

现在 \(\theta_1\) 将始终提供合理的值，可以将其输入到 \(\theta_2\) 的定义中。请注意，我们将 \(\theta_1\) 的标准差定义为 \(\frac{1}{\sqrt{(1-\frac{2}{\pi})}}\) 而不是 \(1\)。这是因为半高斯分布的标准差是 \(\sigma \sqrt{(1-\frac{2}{\pi})}\) ，其中 \(\sigma\) 是半高斯分布的尺度参数。换句话说，\(\sigma\) 是 展开了的 高斯分布的标准差，而不是半高斯分布的标准差。

无论如何，让我们观察一下重参数化的模型是如何处理散度的。 Fig. 25 和 Fig. 26 表明，model1 的散度数量已大大减少，但仍然可以看到一部分。尝试减少散度的一个简单选择是增加 target_accept 的值，如代码 divm2 所示，默认情况下此值为 \(0.8\)，最大有效值为 \(1\)（ 请参阅 11.9.3 哈密顿蒙特卡洛采样器（ HMC ） 了解详情 ）。

Listing 11 divm2
with pm.Model() as model_1bis:
    θ1 = pm.HalfNormal("θ1", 1 / (1-2/np.pi)**0.5)
    θ2 = pm.Uniform("θ2", -θ1, θ1)
    idata_1bis = pm.sample(target_accept=.95, return_inferencedata=True)

Fig. 25 和 Fig. 26 中的model1bis 与 model1 相同，但更改了一个采样参数的默认值 pm.sample(., target_accept =0.95) 。可以看到最终消除了所有散度。这是个好消息，但为了信任这些样本，仍然需要像前几节一样，检查 \(\hat R\) 和 ESS 的值，。

重参数化

重参数化有助于将难以采样的后验几何形态转换为更容易采样的几何形态。这有助于消除散度，但即使不存在散度时，重参数化也会有所帮助。例如，可以在无需增加计算成本的条件下，使用它加快采样速度或增加有效样本数。此外，重参数化还有助于更好地解释或沟通模型及其结果（ 参见第 1.4.1 共轭先验 节中的 Alice 和 Bob 的示例 ）。

2.4.8 采样器的参数和其他诊断方法

大多数采样器方法都有影响自身性能的超参数。虽然大多数概率编程语言尝试使用合理的默认值，但实践中并不适用于所有的数据和模型。

有时可以通过增加参数target_accept 来消除部分散度，例如，当散度源于数值不精确的时候。

另外还有其他参数能够帮助解决采样问题，例如，我们可能希望增加 MCMC 采样器的迭代次数。在 PYMC3 中，有默认的采样参数 pm.sample(.,tune=1000)。在调整阶段，采样器参数会自动调整。而有些模型更复杂，需要更多交互才能让采样器学习到更好的参数。因此增加调整步数有助于增加 ESS 或降低 \(\hat R\)。增加抽样次数也有助于收敛，但总的来说其他途径更有效。如果一个模型在数千次抽取后都未能收敛，那么通常它在 \(10\) 倍以上的抽取中仍然会失败，或者稍有改进但其额外计算成本并不合理。此时，重参数化、改进模型结构、提供信息更多的先验，甚至更改模型通常会更有效 13。

需要注意的是，在建模早期，我们可以使用较少的抽取次数来测试模型是否能够运行、是否已经编写了期望的模型、是否大致得到了合理结果等。这种初始检查大约只需要 \(200\) 或 \(300\) 次抽样就足够达到目的了。然后，当我们对模型更有信心时，可以将抽取次数增加到几千次，大约可以设置为 \(2000\) 或 \(4000\) 次。

除了本章中介绍的诊断之外，还存在其他诊断方法，例如平行图和分离图。所有这些诊断方法都是有自己的用途。但是为了简洁性，本节中没有介绍它们。建议你访问包含更多示例的 ArviZ 文档和绘图库。

2.5 模型比较

通常，我们希望模型既不太简单以至于错过了数据中有价值的信息，也不会太复杂从而过拟合了数据中的噪声。找到这个 甜蜜点 是一项复杂的任务，一方面没有单一的标准来定义最佳解决方案，二是可能压根儿不存在最佳解决方案，三是在实践中需要对同一数据集支撑下的有限个模型进行选择。

2.5.1 评分法与对数评分规则（ ELPD ）

尽管没有最佳解决方案，我们仍然可以尝试寻找一些好的通用策略。一种解决方案是计算模型的泛化误差，也被称为样本外预测精度，这是对新数据进行预测时，模型表现情况的一种估计。理想情况下，任何预测准确性的度量都应该考虑到问题本身，包括与模型预测有关的收益和成本。也就是说，应该应用一些决策论方法。不过我们也可以依赖一些适用于广泛模型和问题的通用手段，这种手段有时被称为评分规则，因为它们有助于对模型进行评分和排序。

在众多评分规则中，对数评分规则具有非常好的理论性质 [21]，因此被广泛使用。对数评分规则的计算公式为：

(19)\[\text{ELPD} = \sum_{i=1}^{n} \int p_t(\tilde y_i) \; \log p(\tilde y_i \mid y_i) \; d\tilde y_i\]

其中 \(p_t(\tilde y_i)\) 为生成数据 \(\tilde y_i\) 的真实分布（即理想中的数据生成分布），而 \(p(\tilde y_i \mid y_i)\) 为模型对应的后验预测分布。

公式 (19) 中定义的量被称为 逐点对数预测密度的期望（Expected Log Pointwise Predict Density, ELPD）。之所以称为 “期望”，是因为我们是在真实数据生成过程上做 积分运算，即在可能由该过程生成的所有数据上做积分；之所以称为 “逐点”，是因为我们是在 \(n\) 个观测点上执行 逐点计算；术语“密度”，则是为了简化表述而同时被用于表示连续和离散模型 14。

在实践中，我们并不知道真实的数据分布 \(p_t(\tilde y_i)\) ，因此公式 (19) 中定义的 ELPD 没法直接计算，只能用观测数据集做经验主义的近似，即用下式计算：

(20)\[\sum_{i=1}^{n} \log \int \ p(y_i \mid \boldsymbol{\theta}) \; p(\boldsymbol{\theta} \mid y) d\boldsymbol{\theta}\]

公式 (20) 定义的量（或乘以某个常数的量）通常称为离差，它在贝叶斯和非贝叶斯场景中都有使用 15。当似然为高斯时，公式 (20) 与均方误差成正比。

离差（ Deviance ）及相关容易混淆的概念

离差（又称“偏差”）是关于某个统计模型拟合优劣的统计量。

离差在英文中与偏差（ Deviate ）、偏差值（ Deviation ）、离散度（ Discrepancy ）、散度（ Divergence ）等术语近似，所以比较容易产生混淆。

  • 偏差（ Deviate ）：是一个形式化的概念，用于泛指随机变量的输出值与该随机变量的中心（如均值）之间差。

  • 偏差值（ Deviation ）：是随机变量的输出值与某个参考值（常见如均值） 之间差异的具体度量，是偏离概念的一次具体实现。偏离值的符号代表了差异的方向，偏离值的大小代表了偏离的程度。常见的偏差术语有：

    • 误差（ Error ）：某个感兴趣量的观测值与真实值（期望值）之间的偏差值。例如，如果 \(21\) 岁男性人口的平均高度为\(1.75\) 米，某个随机选择的人身高为 \(1.80\) 米，那么误差为 \(0.05\) 米；如果随机选择的人高 \(1.70\) 米，那么误差为 \(-0.05\) 米。期望值是整体的均值，通常不可观测，因此误差也无法观测。

    • 残差（ Residual ）：某个感兴趣量的观测值与真实值的估计值之间的偏差值。针对身高的例子，假设我们有 \(n\) 个人的随机样本，则可以用样本作为总体的近似估计，例如用样本的均值作为总体均值的估计。进而样本中每个人每个人的身高与不可观测的期望值之差是误差，而样本中每个人的身高与可观测样本的均值之间的差是残差。这些偏差值的概念适用于测量间隔和比率水平的数据。通常会用一组偏离值的统计量来定量地刻画总体的偏离情况，其中常见的有标准差。

  • 散度（ Divergence ）：在统计和信息几何中，泛指一个概率分布到另一个概率分布的统计距离，参见 11.3 KL 散度 中关于 \(KL\) 散度的定义。

为了计算公式 (20)，我们使用了用于拟合模型的相同数据，因此平均而言，会高估 ELPD（ 公式 (19) ），并导致最终选择的模型容易过拟合。幸运的是，还有几种方法可以更好地估计 ELPD 。其中之一是下面将看到的交叉验证法（ Cross Validation, CV ）。

2.5.2 交叉验证和留一法

（1）交叉验证的原理

交叉验证 (CV) 是一种估计样本外预测准确性的方法。该方法需要在留出部分数据的情况下重复多次拟合模型（每次留出不同的数据），每次拟合后都使用被留出的数据来测量一次模型的准确性。此过程重复多次后，将所有精度测量结果的均值视为模型的预测精度。此后用完整数据集再拟合一次模型，此模型才是用于进一步分析和/或预测的最终模型。我们可以将 CV 视为一种在使用所有样本点的情况下（或者说无需投入新观测点的情况下），仍然能够模拟（或近似）样本外统计量的方法。

（2）留一法交叉验证

当被留出的数据仅包含一个数据点时，就是非常著名的留一法交叉验证 (LOO-CV) 。使用 LOO-CV 计算的 ELPD 为 \(\text{ELPD}_\text{LOO-CV}\) ：

(21)\[\text{ELPD}_\text{LOO-CV} = \sum_{i=1}^{n} \log \int \ p(y_i \mid \boldsymbol{\theta}) \; p(\boldsymbol{\theta} \mid y_{-i}) d\boldsymbol{\theta}\]

计算公式 (21) 成本很高，因为在实践中，\(\boldsymbol{\theta}\) 并不确定，因此我们每次运行都需要计算一次后验，也就是说，需要计算 \(n\) 次后验 zhi， \(n\) 为数据集中观测点数量。

（3）帕雷托平滑重要性采样留一交叉验证

幸运的是，可以使用一种被称为 帕雷托平滑重要性采样留一交叉验证（ Pareto Smoothed Importance Sampling Leave-One-Out Cross Validation, PSIS-LOO-CV ） 的方法，仅通过一次拟合就可以得到 \(\text{ELPD}_\text{LOO-CV}\) 的近似值，详情参阅 11.5 深入理解留一交叉验证法 。

为了与 ArviZ 保持一致，本书后面章节中所指的留一交叉验证（ LOO ），均为 PSIS-LOO-CV 。而且除非另有说明，否则本书中提到 ELPD 时，也均指采用 PSIS-LOO-CV 方法估计的 ELPD 。

ArviZ 提供了许多与 LOO 相关的函数，使用起来也非常简单，但理解其结果时可能需要仔细一点。为了说明如何解释这些函数的输出，我们将使用代码 pymc3_models_for_loo 中定义的 \(3\) 个模型。

Listing 12 pymc3_models_for_loo
y_obs = np.random.normal(0, 1, size=100)
idatas_cmp = {}

# Generate data from Skewnormal likelihood model
# with fixed mean and skewness and random standard deviation
with pm.Model() as mA:
    σ = pm.HalfNormal("σ", 1)
    y = pm.SkewNormal("y", 0, σ, alpha=1, observed=y_obs)
    idataA = pm.sample(return_inferencedata=True)

# add_groups modifies an existing az.InferenceData
idataA.add_groups({"posterior_predictive":
                  {"y":pm.sample_posterior_predictive(idataA)["y"][None,:]}})
idatas_cmp["mA"] = idataA

# Generate data from Normal likelihood model
# with fixed mean with random standard deviation
with pm.Model() as mB:
    σ = pm.HalfNormal("σ", 1)
    y = pm.Normal("y", 0, σ, observed=y_obs)
    idataB = pm.sample(return_inferencedata=True)

idataB.add_groups({"posterior_predictive":
                  {"y":pm.sample_posterior_predictive(idataB)["y"][None,:]}})
idatas_cmp["mB"] = idataB

# Generate data from Normal likelihood model
# with random mean and random standard deviation
with pm.Model() as mC:
    μ = pm.Normal("μ", 0, 1)
    σ = pm.HalfNormal("σ", 1)
    y = pm.Normal("y", μ, σ, observed=y_obs)
    idataC = pm.sample(return_inferencedata=True)

idataC.add_groups({"posterior_predictive":
                  {"y":pm.sample_posterior_predictive(idataC)["y"][None,:]}})
idatas_cmp["mC"] = idataC

计算 LOO 只需要抽自后验的样本 16 ，然后调用 az.loo(.) 函数计算模型的 LOO 。

在实践中，常常需要为多个模型计算 LOO ，Arviz 提供了 az.compare(.) 函数来进行多个模型之间 LOO 的比较。 Table 2 就是通过 az.compare(idatas_cmp) 生成的。

Table 2 模型比较的汇总数据。模型按照 loo 列的 ELPD 值自低至高排序。

rank

loo

p_loo

d_loo

weight

se

dse

warning

loo_scale

mB

0

-137.87

0.96

0.00

1.0

7.06

0.00

False

log

mC

1

-138.61

2.03

0.74

0.0

7.05

0.85

False

logde qi wang

mA

2

-168.06

1.35

30.19

0.0

10.32

6.54

False

log

Table 2 中有很多列，让我们一一说明其含义：

  1. 第一列为索引，它列出了传递给 az.compare(.) 的模型名称。

  2. rank 列：按照预测精度做的排名，值从 \(0\) 依次到模型总数，其中 \(0\) 代表最高精度。

  3. loo 列：各模型 ELPD 值的列表，总是按照 ELPD 值从最好到最差排序。

  4. p_loo 列：惩罚项的值列表，可以将其粗略地视为有效参数数量的估计值（但不要太认真）。此值可能低于 具有更多结构的模型 （如分层模型）中的实际参数数量，或者高于那些预测能力非常弱或严重错误指定的模型的实际参数数量。

  5. d_loo 列：每个模型与排名第一的模型之间的 LOO 相对差。因此第一个模型始终取值为 \(0\) 。

  6. weight 列：分配给每个模型的权重。权重可以粗略地解释为在指定数据的条件下，是（参与比较的各模型中）该模型的概率。详细信息参阅 2.6 模型平均 。

  7. se 列：ELPD 的标准误差。

  8. dse 列：ELPD 相对差的标准误差。 dse 与 se 不一定相同，因为 ELPD 的不确定性在模型之间可能存在相关性。排名第一的模型 dse 值始终为 \(0\) 。

  9. warning 列：如果为True，表示这是一个警告，LOO 的近似估计不可靠，详见 2.5.4 帕累托形状参数 \hat \kappa。

  10. loo_scale 列：估计值所用的尺度（或量纲）。默认为对数尺度。其他选项还包括：离差值尺度，即对数分值乘以 \(-2\) ，这会颠倒排序，较低的 ELPD 会更好；负对数尺度，即对数分值乘以 \(-1\)，与离差值尺度一样，值越低越好。

我们还可以在 Fig. 27 中以图形方式表示 Table 2 中的部分信息。图中模型的预测精度也是从高到低排列。空心点代表 loo 值，黑点是没有 p_loo 惩罚项时的预测精度。黑色部分代表计算 LOO 的 se 标准误差 。以三角形为中心的灰色区域表示每个模型与最佳模型之间的 dse 标准误差。可以看到 mB \(\approx\) mC \(>\) mA。

从 Table 2 和 Fig. 27 可以看到模型 mA 的排名最低，并且与其他两个明显分开。我们现在讨论另外两个模型，因为其间的区别更加微妙。 mB 是预测精度最高的模型，但与 mC 相比差异几乎可以忽略不计。根据经验，低于 \(4\) 的 d_loo 被认为很小。这两个模型之间的主要区别在于：对于 mB ，均值固定为 \(0\) ，而对于 mC ，均值具有先验分布。 LOO 会对添加此先验做出惩罚，由 p_loo 的值表示，可以看出 mC 大于 mB；黑点（未惩罚的 ELPD）和开放点（ \(\text{ELPD}_ \text{LOO-CV}\) ）之间的距离表现出， mC 比 mB 大。我们还可以看到，两个模型之间的 dse 远低于各自的 se，表明两者的预测结果高度相关。

鉴于 mB 和 mC 之间的微小差异，在稍微不同的数据集下，这些模型的排名就可能会交替， mC 可能会成为最佳模型。此外，权重的值也会发生变化，参见 2.6 模型平均 。我们可以更改随机种子并重新拟合模型几次来检查这种现象。

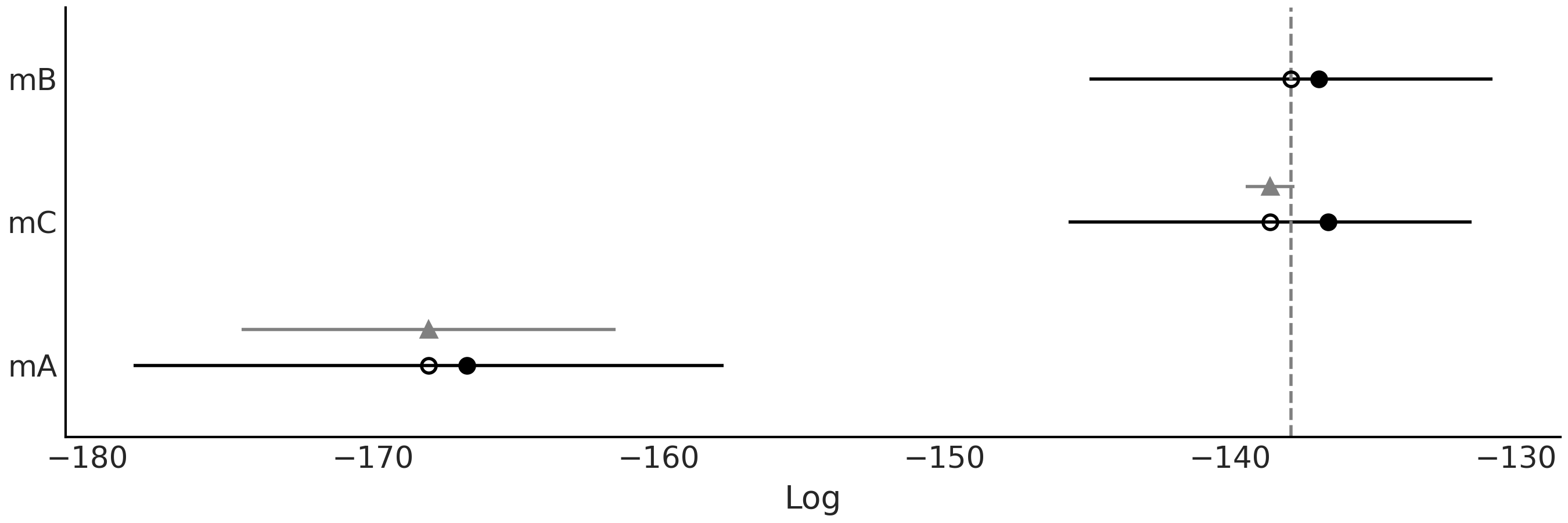
../_images/compare_dummy.png

Fig. 27 使用 LOO 进行模型比较。空心点代表 loo 的值，黑点是不含惩罚项 p_loo 的预测精度。黑色部分代表 LOO 计算 se 的标准误差。以三角形为中心的灰色部分表示每个模型的相对差 dse 的标准误差。

2.5.3 对数预测密度的期望

在上一节中，我们计算了每个模型的 ELPD 值。这是一个有关模型 全局 的比较，它会将模型和数据简化为一个数字。但是从公式 (20) 和 (21) 可以看到， LOO 是对逐点值求和得到的，每个观测值对应一个。因此，我们还可以执行 局部的 比较，可以将 ELPD 的每个值视为一个模型在预测特定观测值时的 难度指示器。

为了利用逐观测点的 ELPD 值来比较模型，ArviZ 提供了 az.plot_elpd(.) 函数。 Fig. 28 以成对方式显示了模型 mA、mB 和 mC 之间的比较情况。

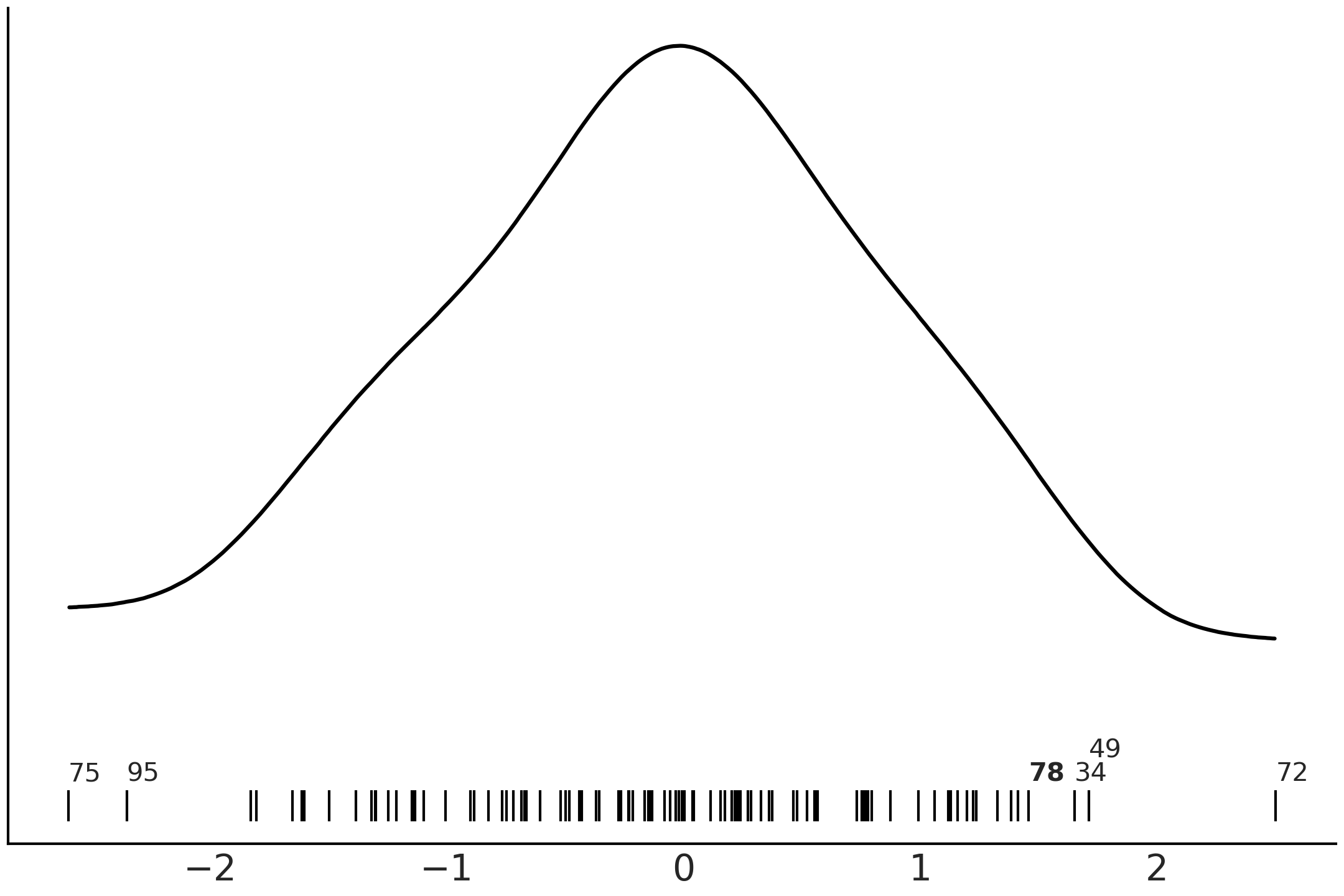
正值表示第一个模型比第二个模型更好地解释了观测结果。例如，如果观察第一个图（mA-mB），模型 mA 比模型 mB 更好地解释了观测 \(49\) 和 \(72\)，而观测 \(75\) 和 \(95\) 则相反。可以看到 mA-mB 和 mA-mC 这两个图非常相似，原因是模型 mB 和模型 mC 实际上彼此非常相似。 Fig. 30 表明观测 \(34\)、 \(49\)、 \(72\)、 \(75\) 和 \(82\) 实际上是五个最极端的观测。

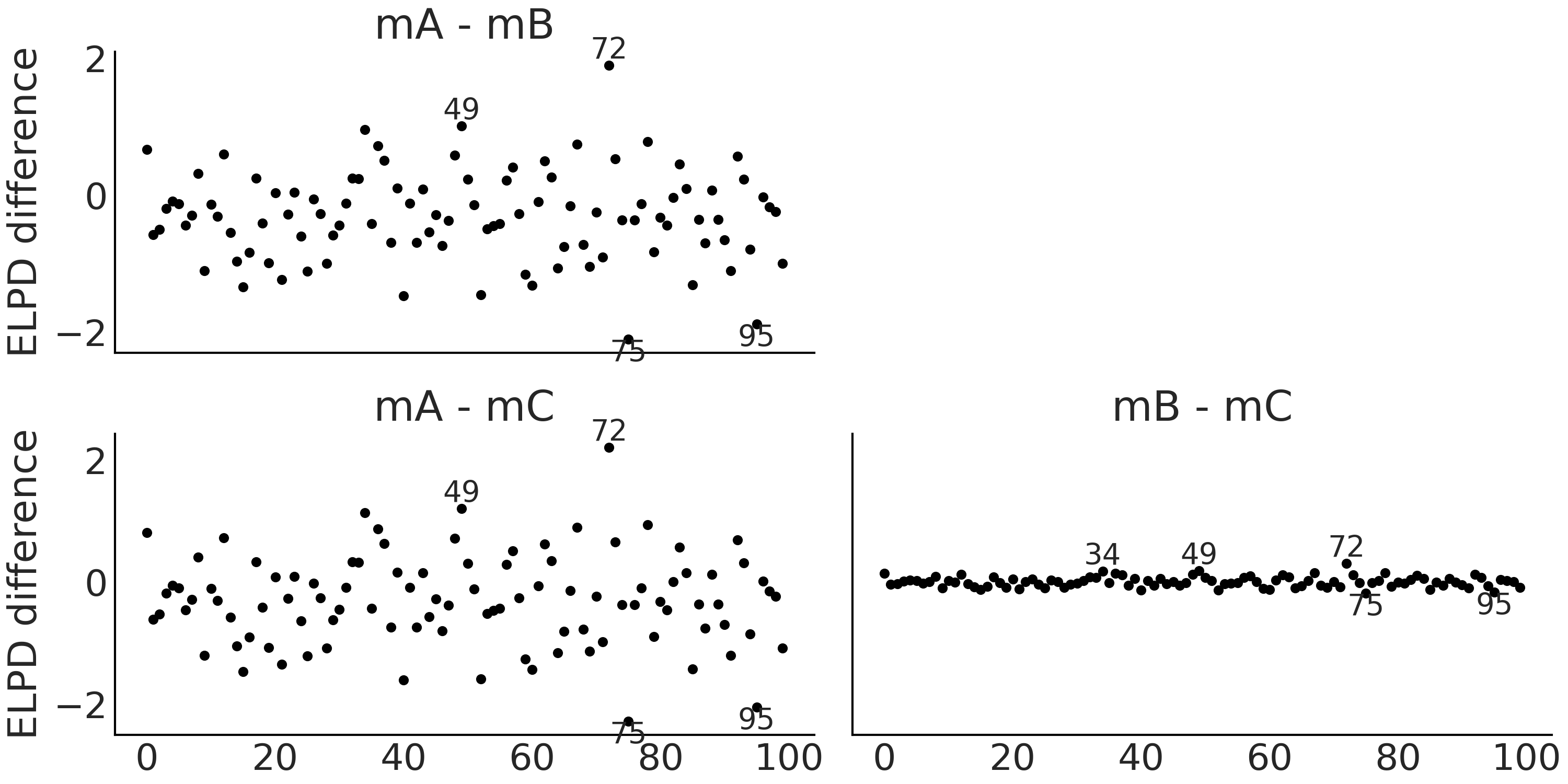
../_images/elpd_dummy.png

Fig. 28 逐观测点的 ELPD 差。被标记的点对应于 ELPD 差为两倍标准差的观测值。所有 \(3\) 个示例中的差都很小，尤其是在 mB 和 mC 之间。正值表示第一个模型比第二个模型更好地解释了观测结果。

2.5.4 帕累托形状参数 \(\hat \kappa\)

用 LOO 近似计算 \(\text{ELPD}_\text{LOO-CV}\) 涉及帕累托分布的计算（ 参见 11.5 深入理解留一交叉验证法 ），其主要目的是获得更稳健的估计，衍生效应是帕累托分布的 \(\hat \kappa\) 参数还可以用于检测影响力较大的观测点，即能够指示出那些 如果不参与拟合就会严重影响预测分布的 观测值。通常较高的 \(\hat \kappa\) 值可能表明数据或模型存在问题，尤其是当 \(\hat \kappa > 0.7\) 时 [16, 22] 。此时建议 [23]：

  • 使用匹配矩方法 [24] 17。通过一些额外的计算，有可能通过对后验分布样本进行变换，获得更可靠的重要性采样估计。

  • 对存在问题的观测点执行精确的留一交叉验证或使用 \(k\) 折交叉验证。

  • 使用对异常观测更稳健的模型。

当计算结果中存在至少一个 \(\hat \kappa > 0.7\) 的值时，az.loo(.) 或 az.compare(.) 就会输出警告。 Table 2 中的 warning 列的值均是 False，是因为 \(\hat \kappa\) 的所有值都 \(< 0.7\)，你可以通过 Fig. 29 自行验证。

我们在 Fig. 29 中对 \(\hat \kappa > 0.09\) 观测进行了标记，\(0.09\) 是随意选择的值，没有特定含义。比较 Fig. 28 和 Fig. 29 ，可以看到 \(\hat \kappa\) 的最大值和 ELPD 的最大值并不对应，反之亦然。

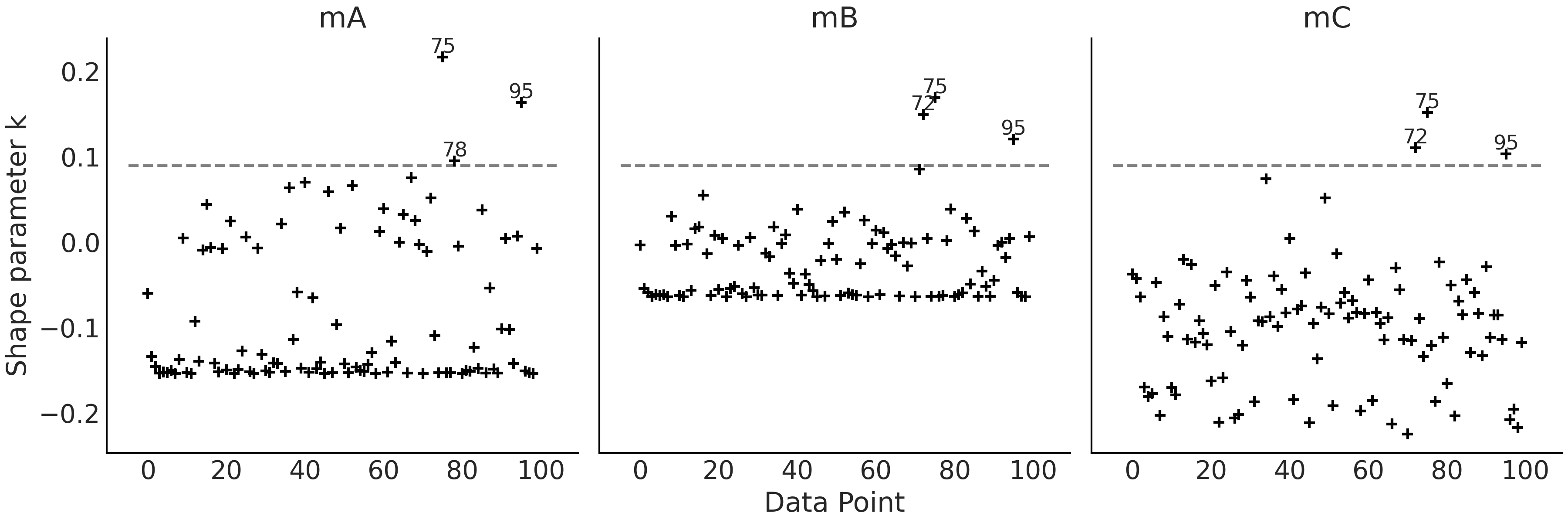
../_images/loo_k_dummy.png

Fig. 29 逐观测点的 \(\hat \kappa\) 值。标记点对应于 \(\hat \kappa > 0.09\) 的观测值，这是随意选取的一个阈值。

../_images/elpd_and_khat.png

Fig. 30 被模型 mA 、mB 和 mC 拟合的观测值的核密度估计曲线。底部每条黑色竖线代表一个观测点。被标记的观测点与 Fig. 28 中突出显示的观测点相同，但观测 \(78\) 以粗体标记，仅在 Fig. 29 中突出显示。

2.5.5 当帕累托参数 \(\hat \kappa\) 较大时解读 p_loo

p_loo 可以粗略地解释为模型中被估计的有效参数数量。然而，对于 \(\hat\kappa\) 值较大的模型，可以获得一些额外的信息。如果 \(\hat \kappa > 0.7\)，那么将 p_loo 与参数数量 \(p\) 进行比较可以提供一些额外信息 [23]：

  • 如果 \(p\_loo << p\)，那么模型很可能被错误指定。你通常还会在后验预测检查中观察到后验预测样本与观测结果匹配不佳的现象。

  • 如果 \(p\_loo < p\) ，并且与观测次数 \(N\) 相比 \(p\) 相对较大（ 例如，\(p > \frac{N}{5}\) ），这通常表明模型过于灵活或先验信息太少。因此，模型很难预测被留出的观测。

  • 如果 \(p\_loo > p\)，模型也很可能被严重错误指定。如果参数数量 \(p << N\)，那么后验预测检查也可能已经揭示了一些问题 18。但是，如果 \(p\) 与观测次数相比相对较大，例如 \(p > \frac{N}{5}\)，则你可能在后验预测检查中观察不到任何问题。

你可以尝试修复模型错误指定的一些启发式方法：为模型添加更多结构。例如，添加非线性组件、使用不同的似然（例如，用 NegativeBinomial 这种过度分散的似然代替 Poisson ）、使用混合似然等。

2.5.6 LOO – 概率积分变换（ LOO-PIT ）

前面 2.5.3 对数预测密度的期望 、 2.5.4 帕累托形状参数 \hat \kappa 等关于模型比较的内容中， LOO 除了声明某个模型的优劣外，还可以被用于实现其他目的，事实上可以将 模型比较 作为深入理解模型的一种途径。随着模型复杂性的增加，仅通过查看其数学定义或实现代码来理解模型会变得越加困难，此时使用 LOO 或其他工具（如后验预测检查）来进行模型比较，可以帮助我们更好地理解它们。

对后验预测检查的一种评判机制是使用两次数据，一次是为了拟合模型，一次是为了评判模型。 LOO-PIT 图为此提供了解决答案，其思想是直接将 LOO 作为交叉验证的一个快速而可靠近似，从而避免两次使用数据。 其中 PIT 部分表示概率积分变换 11.1.7 概率积分变换 (PIT)，使得我们能够通过 CDF 获得任何连续随机变量的均匀分布 \(\mathcal{U}(0, 1)\) （ 详情参阅 11.5 深入理解留一交叉验证法 ）。在 LOO-PIT 中，我们不知道真正的 CDF，但可以用经验 CDF 来近似它。

暂时搁置这些数学细节，权且认为它是柯计算的。那么对于一个经过良好校准的模型，我们应该期望 LOO-PIT 表现为一个近似均匀的分布。你可能会有似曾相识的感觉，因为这与在 2.3 后验预测检查 中使用函数 az.plot_bpv(idata, kind="u_value") 绘制贝叶斯 \(p\) 值时有过类似讨论。

LOO-PIT 通过将观测数据 \(y\) 与后验预测数据 \(\tilde y\) 比较获得，该比较是逐点进行的。有：

\[p_i = P(\tilde y_i \leq y_i \mid y_{-i})\]

从公式中可以直观地看到：当留出第 \(i\) 个观测点时，LOO-PIT 计算的是后验预测数据 \(\tilde y_i < y_i\) 的概率。

因此，az.plot_bpv(idata, kind="u_value") 和 LOO-PIT 之间的区别在于，后者避免了两次使用数据，不过两者对图的总体解释大致相同。

Fig. 31 展示了模型 mA、mB 和 mC 的 LOO-PIT。可以观察到，从模型 mA 的角度来看，低值的观测数据比预期的多，高值的数据少，即模型存在偏差（ Bias ）。相反，模型 mB 和 mC 似乎校准得较好。

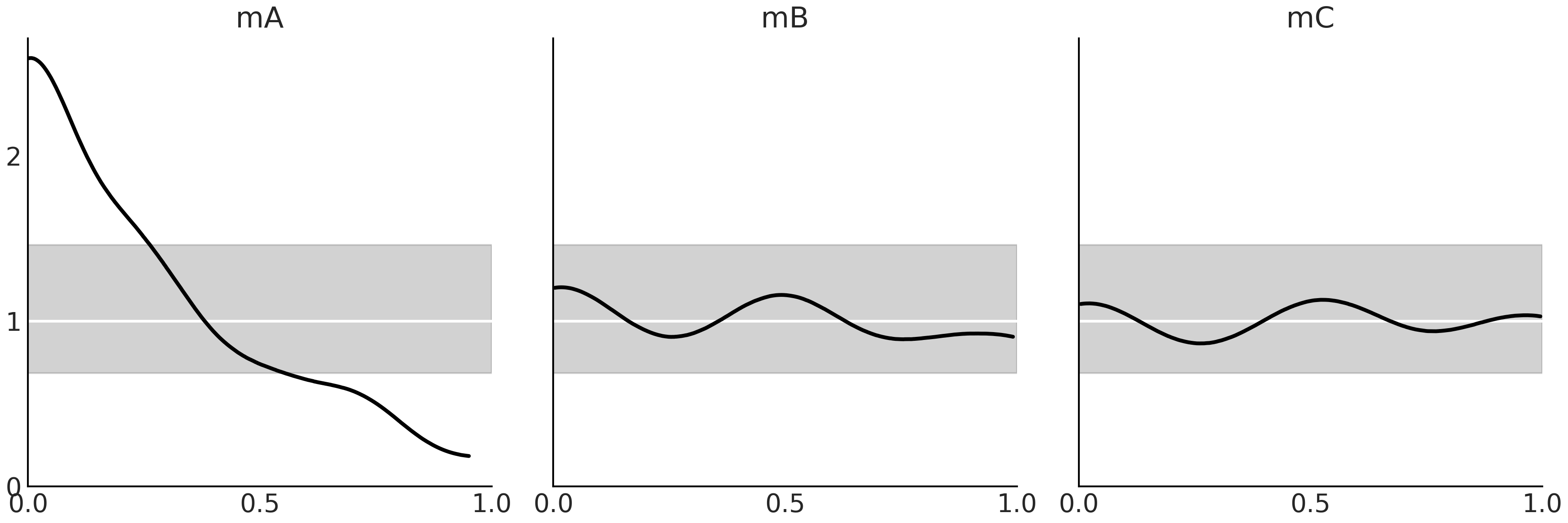
../_images/loo_pit_dummy.png

Fig. 31 黑线是 LOO-PIT 的核密度估计曲线，即小于或等于观测数据的预测值的比例，根据每次观测计算。白线表示预期的均匀分布，灰带表示数据集（大小与所用数据集相同）的预期偏差。

2.6 模型平均

模型平均可以被视为针对模型不确定性的贝叶斯，因为模型也和参数一样具有不确定性。如果我们不能确切地认定 a 模型就是那个想要的模型（通常不能），那么就应该以某种方式将这种不确定性考虑到模型分析中。处理模型不确定性的方法之一是对所有模型进行加权平均，将更大的权重赋予似乎能更好解释或预测数据的模型。

（1）贝叶斯模型平均

对贝叶斯模型进行赋权的一种自然而然的想法是利用边缘似然值（即贝叶斯公式的分母项），这也被称为贝叶斯模型平均 [25]。 虽然其思想在理论上很有吸引力，但在实践中却存在很多问题，因为边缘似然的计算非常棘手（ 详情参阅 11.7 边缘似然 ）。

（2）伪贝叶斯模型平均

直接计算边缘似然存在困难，因此有人提出了另外一种赋权方法，即使用 LOO 来估计模型的权重。可以使用以下公式：

(22)\[w_i = \frac {e^{-\Delta_i }} {\sum_j^k e^{-\Delta_j }}\]

其中 \(\Delta_i\) 是排序后的第 \(i\) 个 LOO 值与最大 LOO 值之差。此处假设使用对数尺度，这也是 ArviZ 的默认值。

此方法被称为 伪贝叶斯模型平均 或 类 Akaike 加权 20 ，是一种从 LOO 计算（若干指定）模型相对概率的启发式方法21。注意分母只是一个归一化项，以确保权重总和为 \(1\) 。公式 (22) 提供的权重计算方案简单且好用，但需要注意它没有考虑 LOO 计算本身的不确定性。对此，可以假设高斯近似来计算标准误差，并相应地修改公式 (22)；或者可以做一些更稳健的事情，比如使用贝叶斯自举法。

（3）预测分布的堆叠

模型平均的另一个选择是堆叠多个预测分布 [26]。其主要思想是将多个模型组合在一个 元模型（ Meta-Model ） 中，使元模型和 真实 生成模型之间的散度最小化。当使用对数评分规则时，这等效于计算：

(23)\[\max_{n} \frac{1}{n} \sum_{i=1}^{n}log\sum_{j=1}^{k} w_j p(y_i \mid y_{-i}, M_j)\]

其中 \(n\) 是数据点数量，\(k\) 是模型数量。为了能够强制求解，我们将 \(w\) 限制为 \(w_j \ge 0\) 和 \(\sum_{j=1}^{k} w_j = 1\)。 \(p(y_i \mid y_{-i}, M_j)\) 是 \(M_j\) 模型的留一法预测分布。前面已经谈到过，该预测分布的计算成本过高，在实践中可以使用 LOO 来近似。

预测分布堆叠法具有比伪贝叶斯模型平均法更有趣的特性。我们可以从其定义中看出：公式 (22) 只是对每个模型权重的归一化，而且这些权重独立于其他模型计算得出。相反，在等式 (23) 中，权重通过最大化组合对数评分来计算，即：即便在伪贝叶斯模型平均中独立地拟合模型，权重的计算也会同时考虑所有模型。这有助于解释为什么模型 mB 的权重为 \(1\) ，而 mC 的权重为 \(0\)（ 参见 Table 2 ），虽然它们非常相似。为什么权重没有都在 \(0.5\) 左右呢？原因是根据堆叠过程，一旦 mB 包含在比较模型集合中，加入模型 mC 不会再提供新信息。也就是说，包含它是多余的。

函数 pm.sample_posterior_predictive_w(.) 输入参数为轨迹列表和权重列表，从而能够让我们轻松生成加权的后验预测样本。权重可以采用多种方式获取，但使用 az.compare(., method="stacking") 计算的权重，可能更有意义。

习题

2E1. Using your own words, what are the main differences between prior predictive checks and posterior predictive checks? How are these empirical evaluations related to Equations (5) and (6).

2E2. Using your own words explain: ESS, \(\hat R\) and MCSE. Focus your explanation on what these quantities are measuring and what potential issue with MCMC they are identifying.

2E3. ArviZ includes precomputed InferenceData objects for a few models. We are going to load an InferenceData object generated from a classical example in Bayesian statistic, the eight schools model [27]. The InferenceData object includes prior samples, prior predictive samples and posterior samples. We can load the InferenceData object using the command az.load_arviz_data("centered_eight"). Use ArviZ to:

  1. List all the groups available on the InferenceData object.

  2. Identify the number of chains and the total number of posterior samples.

  3. Plot the posterior.

  4. Plot the posterior predictive distribution.

  5. Calculate the estimated mean of the parameters, and the Highest Density Intervals.

If necessary check the ArviZ documentation to help you do these tasks https://arviz-devs.github.io/arviz/

2E4. Load az.load_arviz_data("non_centered_eight"), which is a reparametrized version of the “centered_eight” model in the previous exercise. Use ArviZ to assess the MCMC sampling convergence for both models by using:

  1. Autocorrelation plots

  2. Rank plots.

  3. \(\hat R\) values.

Focus on the plots for the mu and tau parameters. What do these three different diagnostics show? Compare these to the InferenceData results loaded from az.load_arviz_data("centered_eight"). Do all three diagnostics tend to agree on which model is preferred? Which one of the models has better convergence diagnostics?

2E5. InferenceData object can store statistics related to the sampling algorithm. You will find them in the sample_stats group, including divergences (diverging):

  1. Count the number of divergences for “centered_eight” and “non_centered_eight” models.

  2. Use az.plot_parallel to identify where the divergences tend to concentrate in the parameter space.

2E6. In the GitHub repository we have included an InferenceData object with a Poisson model and one with a NegativeBinomial, both models are fitted to the same dataset. Use az.load_arviz_data(.) to load them, and then use ArviZ functions to answer the following questions:

  1. Which model provides a better fit to the data? Use the functions az.compare(.) and az.plot_compare(.)

  2. Explain why one model provides a better fit than the other. Use az.plot_ppc(.) and az.plot_loo_pit(.)

  3. Compare both models in terms of their pointwise ELPD values.

Identify the 5 observations with the largest (absolute) difference.

Which model is predicting them better? For which model p_loo is closer to the actual number of parameters? Could you explain why? Hint: the Poisson model has a single parameter that controls both the variance and mean. Instead, the NegativeBinomial has two parameters.

  1. Diagnose LOO using the \(\hat \kappa\) values. Is there any reason to be concerned about the accuracy of LOO for this particular case?

2E7. Reproduce Fig. 18, but using az.plot_loo(ecdf=True) in place of az.plot_bpv(.). Interpret the results. Hint: when using the option ecdf=True, instead of the LOO-PIT KDE you will get a plot of the difference between the LOO-PIT Empirical Cumulative Distribution Function (ECDF) and the Uniform CDF. The ideal plot will be one with a difference of zero.

2E8. In your own words explain why MCMC posterior estimation techniques need convergence diagnostics. In particular contrast these to the conjugate methods described in Section 1.4.1 共轭先验 which do not need those diagnostics. What is different about the two inference methods?

2E9. Visit the ArviZ plot gallery at https://arviz-devs.github.io/arviz/examples/index.html. What diagnoses can you find there that are not covered in this chapter? From the documentation what is this diagnostic assessing?

2E10. List some plots and numerical quantities that are useful at each step during the Bayesian workflow (shown visually in Fig. 150). Explain how they work and what they are assessing. Feel free to use anything you have seen in this chapter or in the ArviZ documentation.

  1. Prior selection.

  2. MCMC sampling.

  3. Posterior predictions.

2M11. We want to model a football league with \(N\) teams. As usual, we start with a simpler version of the model in mind, just a single team. We assume the scores are Poisson distributed according to a scoring rate \(\mu\). We choose the prior \(\text{Gamma}(0.5, 0.00001)\) because this is sometimes recommend as an objective prior.

Listing 13 poisson_football
with pm.Model() as model:
    μ = pm.Gamma("μ", 0.5, 0.00001)
    score = pm.Poisson("score", μ)
    trace = pm.sample_prior_predictive()

  1. Generate and plot the prior predictive distribution. How reasonable it looks to you?

  2. Use your knowledge of sports in order to refine the prior choice.

  3. Instead of soccer you now want to model basketball. Could you come with a reasonable prior for that instance? Define the prior in a model and generate a prior predictive distribution to validate your intuition.

Hint: You can parameterize the Gamma distribution using the rate and shape parameters as in Code Block poisson_football or alternatively using the mean and standard deviation.

2M12. In Code Block metropolis_hastings from Chapter 1, change the value of can_sd and run the Metropolis sampler. Try values like 0.2 and 1.

  1. Use ArviZ to compare the sampled values using diagnostics such as the autocorrelation plot, trace plot and the ESS. Explain the observed differences.

  2. Modify Code Block metropolis_hastings so you get more than one independent chain. Use ArviZ to compute rank plots and \(\hat R\).

2M13. Generate a random sample using np.random.binomial(n=1, p=0.5, size=200) and fit it using a Beta-Binomial model.

Use pm.sample(., step=pm.Metropolis()) (Metropolis-Hastings sampler) and pm.sample(.) (the standard sampler). Compare the results in terms of the ESS, \(\hat R\), autocorrelation, trace plots and rank plots.

Reading the PyMC3 logging statements what sampler is autoassigned? What is your conclusion about this sampler performance compared to Metropolis-Hastings?

2M14. Generate your own example of a synthetic posterior with convergence issues, let us call it bad_chains3.

  1. Explain why the synthetic posterior you generated is “bad”. What about it would we not want to see in an actual modeling scenario?

  2. Run the same diagnostics we run in the book for bad_chains0 and bad_chains1. Compare your results with those in the book and explain the differences and similarities.

  3. Did the results of the diagnostics from the previous point made you reconsider why bad_chains3 is a “bad chain”?

2H15. Generate a random sample using np.random.binomial(n=1, p=0.5, size=200) and fit it using a Beta-Binomial model.

  1. Check that LOO-PIT is approximately Uniform.

  2. Tweak the prior to make the model a bad fit and get a LOO-PIT that is low for values closer to zero and high for values closer to one.

Justify your prior choice.

  1. Tweak the prior to make the model a bad fit and get a LOO-PIT that is high for values closer to zero and low for values closer to one.

Justify your prior choice.

  1. Tweak the prior to make the model a bad fit and get a LOO-PIT that is high for values close to 0.5 and low for values closer to zero and one. Could you do it? Explain why.

2H16. Use PyMC3 to write a model with Normal likelihood. Use the following random samples as data and the following priors for the mean. Fix the standard deviation parameter in the likelihood at 1.

  1. A random sample of size 200 from a \(\mathcal{N}(0,1)\) and prior distribution \(\mathcal{N}(0,20)\)

  2. A random sample of size 2 from a \(\mathcal{N}(0,1)\) and prior distribution \(\mathcal{N}(0,20)\)

  3. A random sample of size 200 from a \(\mathcal{N}(0,1)\) and prior distribution \(\mathcal{N}(20 1)\)

  4. A random sample of size 200 from a \(\mathcal{U}(0,1)\) and prior distribution \(\mathcal{N}(10, 20)\)

  5. A random sample of size 200 from a \(\mathcal{HN}(0,1)\) and a prior distribution \(\mathcal{N}(10,20)\)

Assess convergence by running the same diagnostics we run in the book for bad_chains0 and bad_chains1. Compare your results with those in the book and explain the differences and similarities.

2H17. Each of the four sections in this chapter, prior predictive checks, posterior predictive checks, numerical inference diagnostics, and model comparison, detail a specific step in the Bayesian workflow. In your own words explain what the purpose of each step is, and conversely what is lacking if the step is omitted. What does each tell us about our statistical models?

参考文献

1

https://www.countbayesie.com/blog/2015/2/18/bayes-theorem-with-lego

2

We are omitting tasks related to obtaining the data in the first place, but experimental design can be as critical if not more than other aspects in the statistical analysis, see Chapter 9.

3

https://arviz-devs.github.io/arviz/

4

This example has been adapted from https://mc-stan.org/users/documentation/case-studies/golf.html and https://docs.pymc.io/notebooks/putting_workflow.html

5

The example has been adapted from [17].

6

See Chapter 3 for details of the logistic regression model.

7

Posterior predictive checks are a very general idea. These figures do not try to show the only available choices, just some of the options offered by ArviZ.

8

Unless you realize you need to collect data again, but that is another story.

9

Try https://www.timeanddate.com/sun/ecuador/quito

10

Do not confuse with the standard deviation of the MCSE for the mean.

11

Most useful and commonly used sampling methods for Bayesian inference are variants of HMC, including for example, the default method for continuous variables in PyMC3. For more details of this method, see Section 11.9.3 哈密顿蒙特卡洛采样器（ HMC ）).

12

A function which is zero everywhere and infinite at zero.

13

For a sampler like Sequential Monte Carlo, increasing the number of draws also increases the number of particles, and thus it could actually provide better convergence. See Section 11.9.4 序贯蒙塔卡洛采样器.

14

Strictly speaking we should use probabilities for discrete models, but that distinction rapidly becomes annoying in practice.

15

In non-Bayesians contexts \(\boldsymbol{\theta}\) is a point estimate obtained, for example, by maximizing the likelihood.

16

We are also computing samples from the posterior predictive distribution to use them to compute LOO-PIT.

17

At time of writing this book the method has not been yet implemented in ArviZ, but it may be already available by the time you are reading this.

18

See the case study https://avehtari.github.io/modelselection/roaches.html for an example.

20

The Akaike information criterion (AIC) is an estimator of the generalization error, it is commonly used in frequentists statistics, but their assumptions are generally not adequate enough for general use with Bayesians models.

21

This formula also works for WAIC [^22] and other information criteria

previous

第一章：贝叶斯推断

next

第三章：线性模型与概率编程语言