2.4 统计判别理论

2.4 统计判别理论

这一节我们讨论一些理论，这些理论提供了构建模型的一个框架。先考虑定量输出的情形，并且从随机变量和概率空间的角度来考虑。

记 \(X\in \mathbb{R}^p\) 为实值随机输入向量，\(Y\in \mathbb{R}\) 为实值随机输出变量，联合概率分布为 \(\mathrm{Pr}(X,Y)\)。给定输入 \(X\)，我们寻找一个函数 \(f(X)\) 来预测 \(Y\)。这个理论需要一个损失函数 \(L(Y,f(X))\) 用来度量预测中的错误，到目前为止最常用并且最方便的是 平方误差损失： \(L(Y,f(X))=(Y-f(X))^2\)。这促使我们得到了一个关于 \(f\) 好坏的度量，即预测误差的期望（Expected Value of Predictive Error）。

\[ \mathrm{EPE}(f)=E(Y-f(X))^2\qquad\qquad\tag{2.9} \]
\[ =\int[y-f(x)]^2\mathrm{Pr}(dx,dy)\tag{2.10} \]

在 \(X\) 的条件下，可以把 \(\mathrm{EPE}\) 写成 ：

\[ \mathrm{EPE}(f) = \mathbb{E}_X\mathbb{E}_{Y\mid X}([Y-f(X)]^2\mid X)\tag{2.11} \]

而且我们看到使 \(\mathrm{EPE}\) 逐点最小就足够了：

\[ f(x) = \argmin_c\mathbb{E}_{Y\mid X}([Y-c]^2\mid X=x)\tag{2.12} \]

解为条件期望：

\[ f(x) = \mathbb{E}(Y\mid X=x)\tag{2.13}\,, \]

也被称作 回归 (regression) 函数。因此 \(Y\) 在任意点 \(X=x\) 处的最优预测为条件均值，“最优”是在均方误差意义下的。

注解：此处条件是指对联合概率密度分解 \(\mathrm{Pr}(X, Y ) = \mathrm{Pr}(Y \mid X)\mathrm{Pr}(X)\)，其中 \(\mathrm{Pr}(Y \mid X) = \mathrm{Pr}(Y, X)/\mathrm{Pr}(X)\)，因此分解成了双变量的积分。

最近邻方法试图直接利用训练数据完成任务。在每一点 \(x\) 处，需要输入 \(x_i=x\) 附近的所有 \(y_i\) 的均值。因为在任一点 \(x\)，一般至多有一个观测值，我们令：

\[ \hat{f}(x)=\mathrm{Ave}(y_i\mid x_i\in N_k(x))\tag{2.14} \]

其中 \(\text{Ave}\) 表示平均，\(N_k(x)\) 是集合 \(\mathcal{T}\) 中离 \(x\) 最近的 \(k\) 个点的邻域。这里有两个近似:

  • 用样本数据的平均来近似期望值；

  • 在每一点的条件（期望）松弛为在离该目标点近的某个区域上的条件（期望）。

对于规模为 \(N\) 的大规模训练数据，邻域中的点更可能接近 \(x\)，而且当 \(k\) 越大，平均值会更加稳定。事实上，在联合概率分布 \(\mathrm{Pr}(X,Y)\) 温和正则条件下，可以证明当 \(N,k \longrightarrow \infty\) 使得 \(k/N \longrightarrow 0\) 时，\(\hat{f}(x) \longrightarrow \mathbb{E}(Y \mid X = x)\)。根据这个，为什么看得更远，因为似乎我们有个一般的近似量吗？我们经常没有非常大的样本。如果线性或者其它更多结构化的模型是合适的，那么我们经常可以得到比 \(k\)-最近邻更稳定的估计，尽管这些知识必须也要从数据中学习。然而还有其它的问题，有时是致命的。在下一个部分我们看到当维数 \(p\) 变大，\(k\)-最近邻的度量大小也随之变大。所以最近邻代替条件会让我们非常失望。收敛仍然保持，但是当维数增长后收敛 速率 (rate) 变小。

线性回归怎样适应这个框架？最简单的解释是假设回归函数 \(f(x)\) 近似线性

\[ f(x)\approx x^T\beta\tag{2.15} \]

这是个基于模型的方式——我们明确用于回归函数的模型。将 \(f(x)\) 的线性模型插入 \(\mathrm{EPE} (2.9)\) 然后微分，可以理论上解出 \(\beta\)

\[ \beta = [\mathbb{E}(XX^T)]^{-1}\mathbb{E}(XY)\tag{2.16} \]

注意到我们在 \(X\) 上没有条件；而是已经用了我们对函数关系的理解 整合 \(X\) 的值 (pool over values of \(X\))。最小二乘的解 \((2.6)\) 相当于用训练数据的平均值替换掉 \((2.16)\) 中的期望。

所以 \(k\)-最邻近和最小二乘最终都是根据平均来近似条件期望。但是它们在模型上显著不同。

  • 最小二乘假设 \(f(x)\) 是某个整体线性函数的良好近似。

  • \(k\)-最近邻假设 \(f(x)\) 是局部常值函数的良好近似。

尽管后者似乎更容易被接受，但我们已经看到我们需要为这种灵活性付出代价。

这本书中描述的很多技巧都是基于模型的，尽管比严格的线性模型更加灵活。举个例子，可加性模型假设

\[ f(X) = \sum\limits_{j=1}^{p} f_j(X_j) \tag{2.17} \]

这保留着线性模型的可加性，但是每个并列的函数 \(f_j\) 是任意的。结果表明可加模型的最优估计是对于每个并列的函数 同时 (simultaneously) 用 \(k\)-最邻近去近似 单变量 (univariate) 的条件期望。因此在可加性的情况下，通过加上某些（通常不现实）的模型假设在高维中估计条件期望的问题被扫除了。

是否为 \((2.11)\) 的标准而高兴？如果我们用 \(L_1\) 损失函数 \(\mathbb{E} \mid Y-f(X)\mid \) 来替换 \(L_2\) 损失函数会怎么样。这种情况下解是条件中位数，

\[ \hat{f}(x) = \mathrm{median}(Y \mid X = x)\tag{2.18} \]

条件中位数是另一种定位的方式，而且它的估计比条件均值更加鲁棒。 \(L_1\) 准则的导数不连续，阻碍了它们的广泛应用。其它更多耐抵抗 (resistant) 的损失函数会在后面章节中介绍，但是平方误差是分析方便而且是最受欢迎的。

当输出为类变量 \(G\) 时，我们应该怎样处理？同样的范例在这里也是可行的，除了我们需要一个不同的损失函数来惩罚预测错误。预测值 \(\hat{G}\) 在 \(\mathbb{G}\) 中取值， \(\mathbb{G}\) 是可能类别的集合。我们的损失函数可以用 \(K\times K\) 的矩阵 \(\mathbf{L}\) 来表示，其中 \(K=\mathrm{card}(\mathcal {G})\)。矩阵 \(\mathbf{L}\) 对角元为 \(0\) 且其它地方值非负，其中 \(L(k,\ell)\) 为把属于 \(\mathbb{G}_k\) 的类分到 \(\mathbb{G}_\ell\) 的代价。大多数情况下我们用 \(0\)-\(1\) (zero-one) 损失函数，其中所有的错误分类都被要求一个单位的惩罚。预测错误的期望为

\[ \mathrm{EPE} = \mathbb{E}[L(G,\hat{G}(X))]\tag{2.19} \]

同样关于联合分布 \(\mathrm{Pr}(G,X)\) 取期望。再一次考虑条件分布，我们可以写出如下的 \(\mathrm{EPE}\)

\[ \mathrm{EPE} = \mathbb{E}_X\sum\limits_{k=1}^KL[{\mathbb{G}}_k,\hat{G}(X)]\mathrm{Pr}({\mathbb{G}}_k\mid X)\tag{2.20} \]

同样逐点最小化 \(\mathrm{EPE}\) 就足够了:

\[ \hat{G}(x) = \argmin_{g\in \mathbb{G}}\sum\limits_{k=1}^KL({\mathbb{G}}_k,g)\mathrm{Pr}(\mathcal {G}_k\mid X = x)\tag{2.21} \]

结合 0-1 损失函数上式简化为

\[ \hat{G}(x) = \argmin_{g\in \mathbb{G}}[1 − \mathrm{Pr}(g\mid X = x)]\tag{2.22}\, \]

note “weiya 注：推导 式（ 2.22 ）” 注意到，对于 0-1 损失，

\[\begin{split} L(G_k, g) = \begin{cases} 0 & \text{if } \ g=G_k\\ 1 & \text{if} \ g\neq G_k \end{cases} \end{split}\]

则我们有

\[ \sum_{k=1}^KL({\mathbb{G}}_k,g) \ \mathrm{Pr}(G=\mathcal {G}_k\mid X = x) = \sum_{G_k\neq g}\mathrm{Pr}(G=G_k \mid X=x)=1-\mathrm{Pr}(G=g \mid X=x) \]

或者简单地

\[ \hat{G}(X) = {\mathbb{G}}_k \text{ if } \mathrm{Pr}({\mathbb{G}}_k\mid X = x) = \underset{g\in{\mathbb{G}}}{\max } \mathrm{Pr}(g\mid X = x)\tag{2.23} \]

合理的解决方法被称作 贝叶斯分类 (Bayes classifier)，利用条件（离散）分布 \(\mathrm{Pr}(G\mid X)\) 分到最合适的类别。对于我们模拟的例子图 2.5 显示了最优的贝叶斯判别边界。贝叶斯分类的误差阶被称作 贝叶斯阶 (Bayes rate)。

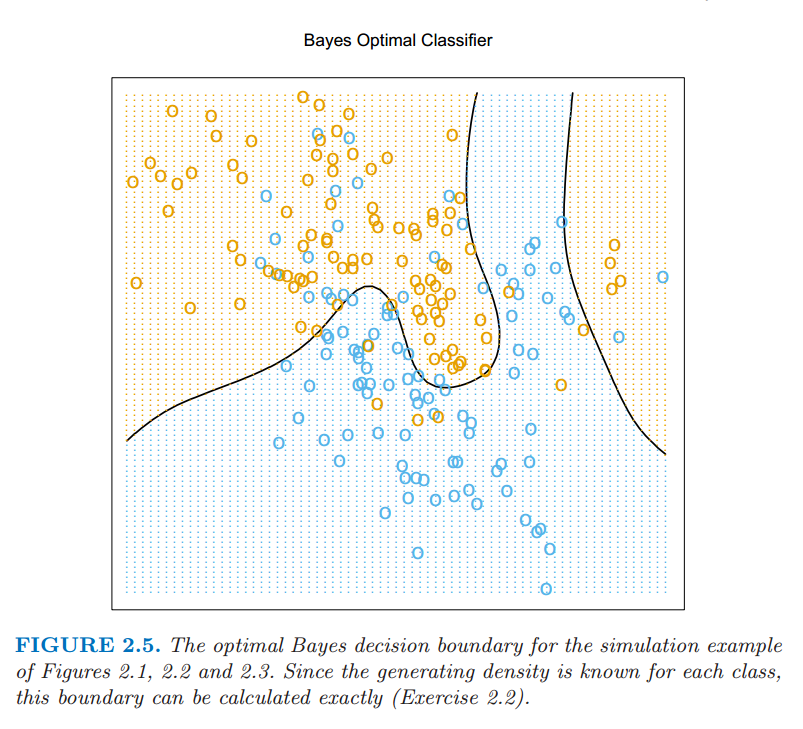
图 2.5：在图 2.1，2.2，和 2.3 中模拟的例子的最优贝叶斯判别边界。因为每个类别的产生密度已知，则判别边界可以准确地计算出来。

再一次我们看到 \(k\)-最近邻分类直接近似这个解决方法——在最近邻内占绝大多数恰好意味着这个，除了某一点的条件概率松弛为该点的邻域内的条件概率，而且概率是通过训练样本的比例来估计的。

假设对于一个二分类的问题，我们采用虚拟变量的方法并且通过二进制变量 \(Y\) 编码 \(G\)，然后进行平方误差损失估计。当 \({\mathbb{G}}_1\) 对应 \(Y=1\)，有 \(\hat{f}(X)=\mathbb{E}(Y\mid X)=\mathrm{Pr}(G={\mathbb{G}}_1\mid X)\)。同样对于 \(K\) 个类别的问题 \(\mathbb{E}(Y_k\mid X)=\mathrm{Pr}(G={\mathbb{G}}_k\mid X)\)。这显示了我们虚拟变量回归的过程，然后根据最大的拟合值来分类，这是表示贝叶斯分类器的另一种方式。尽管这个理论是确定的，在实现中问题也会随着采用的回归模型不同而出现。举个例子，当采用线性回归模型，\(\hat{f}(X)\) 不必要为正值，而且我们可能会怀疑用这个作为概率的一个估计。我们将在第四章中讨论构建模型 \(\mathrm{Pr}(G\mid X)\) 的各种不同的方式。

previous

2.3 两种简单的预测方式：最小二乘和最近邻

next

2.5 高维问题的局部方法