15.2 随机森林的定义
15.2 随机森林的定义¶
Bagging 的核心思想是对许多有噪声但近似无偏的模型进行平均,也因此降低了方差。树是用于 bagging 的理想模型,因为它们可以捕捉数据中复杂的交互项,而且如果树长得足够深的话,会有相对较低的偏差。因为树是充满噪声的,所以通过平均可以很大程度地改善它们。而且,因为 bagging 中产生的每棵树是同分布的,\(B\) 棵这样的树的平均的期望与它们中的任一个是相同的。这意味着经过 bagged 的树的偏差与单个(bootstrap)树的偏差是一样的,而且唯一改善的希望是通过降低方差。这与 boosting 是相反的,在 boosting 中树以一种自适应的方式减小偏差,因此不是同分布的。
\(B\) 棵独立同分布、方差为 \(\sigma^2\) 的随机变量的平均方差为 \(\frac{1}{B}\sigma^2\)。如果变量是简单的同分布(不一定独立),有着正的成对相关系数 \(\rho\),则平均的方差为(练习 15.1)
info “weiya 注:Ex. 15.1” 已解决,详见 Issue 23: Ex. 15.1。
当 \(B\) 增大时,第二项消失,但是第一项还在,而且成对 bagged 的树的相关系数的大小限制了平均的好处。随机森林的想法(算法 15.1)是通过降低树之间的相关系数来改善方差的降低,而不使方差增长过大。这可以通过在生成树的过程中对输入变量进行随机选择来实现。

特别地,当在一个 bootstrapped 数据集中生成树时:
在每次分割时,随机选择 \(m\le p\) 个输入变量作为候选变量用来分割
一般地,\(m\) 取为 \(\sqrt{p}\),或者甚至小到取 1。
生成 \(B\) 棵这样的树 \(\\{T(x;\Theta_b)\\}_1^B\),随机森林(回归)预测变量为
如 10.9 节一样,\(\Theta_b\) 根据分离变量、每个结点的分离值以及终止结点的值来表征第 \(b\) 个随机森林树。直观上,降低 \(m\) 会降低任意两棵树之间的相关系数,也因此通过 式( 15.1 ) 来降低平均的方差。
并非所有的估计都可以通过像这样震荡数据来改善。似乎强非线性估计,比如树,改善最大。对于其 bootstrapped 树,\(\rho\)一般很小(一般是 0.05 或更小;见图 15.9),而 \(\sigma^2\) 不比原树的方差要大。另一方面,bagging 不会改变线性估计,比如样本均值(因此也不会改变方差);其bootstrapped 均值之间的成对相关系数大约为 50%(练习 15.4)。
note “weiya 注:” Bagging 可以看成是特殊的随机森林,即 \(m=p\) 的随机森林。
随机森林很流行。Leo Breiman 的合作者 Adele Cutler 维护一个随机森林的网站 http://www.math.usu.edu/~adele/forests/。R 语言中有一个 randomForest 的包,由 Andy Liaw 维护,可以从 CRAN 网站上下载。
note “原书脚注:” 令人悲伤的是,Leo Breiman 逝世于 2005 年 7 月。
这些作者们声称随机森林取得了巨大的成功:“更精确”,“更有解释性”,以及类似这样的。在我们的经验中,随机森林确实做得很好,只需要非常少的调参。随机森林在 spam 测试集上取得了 4.88% 的误分类率,与其他方法相比表现得很好,没有显著性地比 gradient boosting (4.5%) 差。Bagging 达到 5.4%,显著地比其他方法要差,所以这个例子中额外的随机会有帮助。
图 15.1 展示了这三个方法在 2500 棵树上测试误差的变化。在这种情形下,尽管 10 折交互验证选择了所有的 2500 棵树,但有证据表明 gradient boosting 开始过拟合。
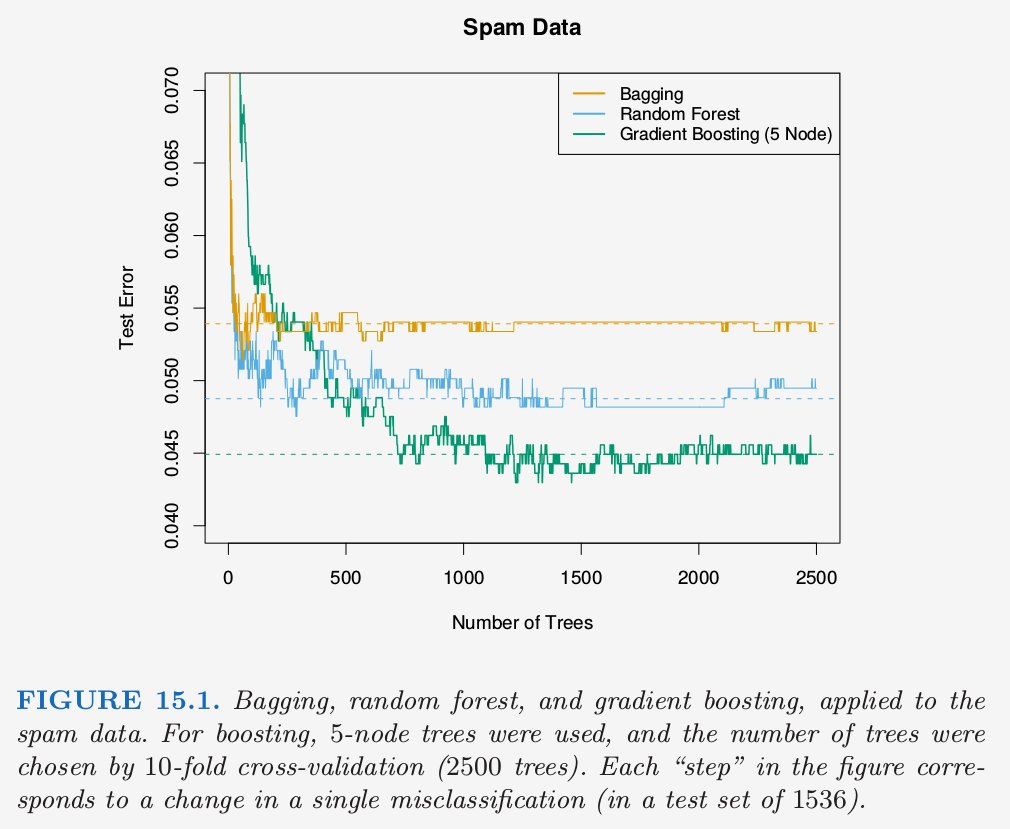
图 15.2 展现了在 nested spheres 问题上随机森林与 gradient boosting 模拟的结果。这里 boosting 很容易地比随机森林表现要好。注意到这里较小的 \(m\) 会更好,尽管部分原因是因为真实的判别边界是可加的。
note “weiya注” nested spheres问题在 10.1 boosting方法中定义,即 特征 \(X_1,\ldots,X_{10}\) 是标准独立高斯分布,目标 \(Y\) 定义如下
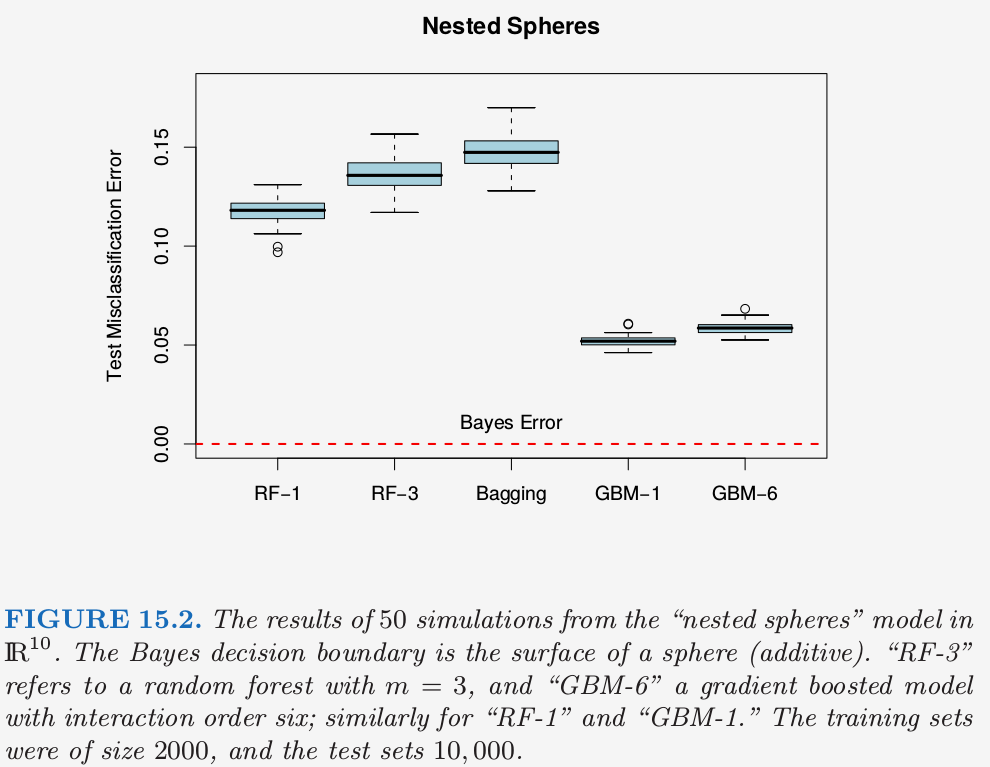
图 15.3 比较了在一个回归问题中随机森林与(带收缩的)boosting,该问题采用加利福利亚住房数据(10.14.1 节)。
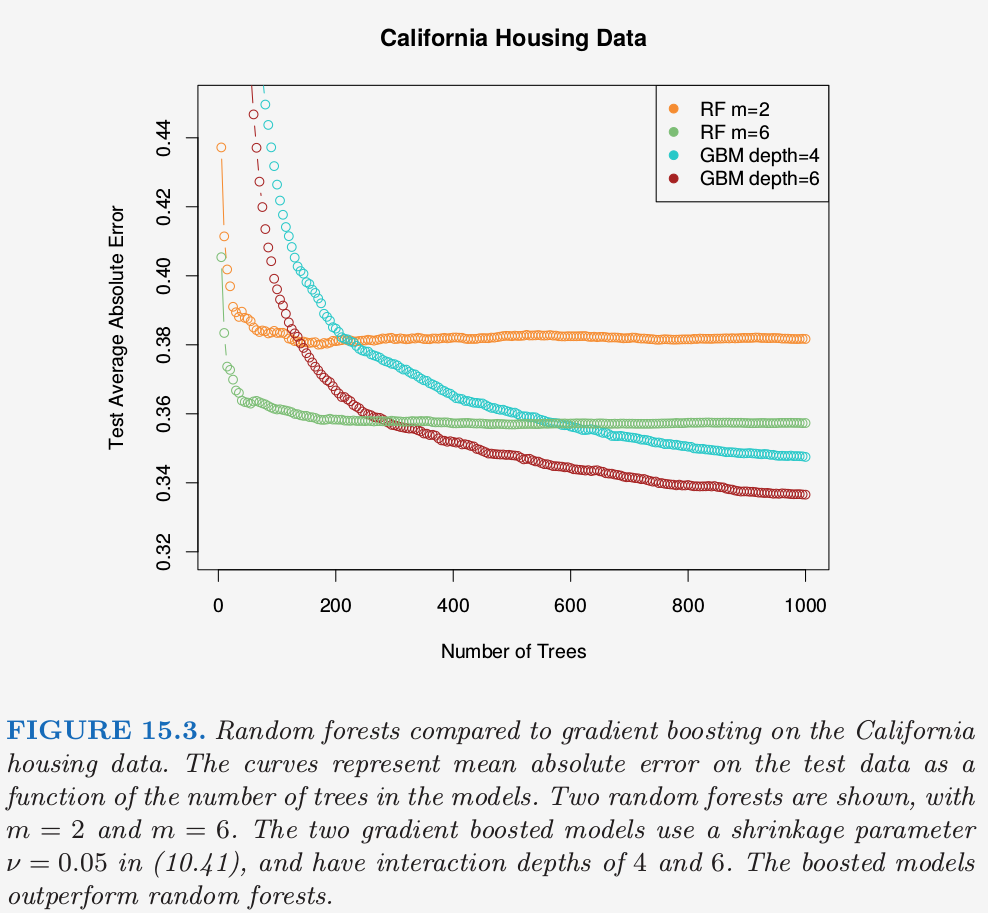
表现出的两个很强的特点是
随机森林在大概 200 棵树时稳定了,而在 1000 棵树的时候 boosting 仍然在改善。boosting 被收缩放慢了,同时也因为树更小的事实。
这里 boosting 比随机森林更好。在 1000 项的时候,弱 boosting 模型(深度为 4 的 GBM)比更强的随机森林(RF \(m=6\))有更小的误差;对均值绝对误差进行 Wilcoxon 检验得到 \(p\) 值为 0.007。对于较大的 \(m\),随机森林不会表现得更好。
