8.7 Bagging
Contents
8.7 Bagging¶
前面我们已经介绍了自助法可用来评估参数估计或预测的正确性。这里我们展示怎么使用自助法去改善估计或者预测本身。在 8.4 节中,我们研究了自助法和贝叶斯方法之间的关系,发现自助法均值近似于一个后验平均,Bagging 进一步探索这之间的联系。
首先考虑一个回归问题。假设我们根据我们的训练数据 \(\mathbf Z=\\{(x_1,y_1),(x_2,y_2),\ldots,(x_N,y_N)\\}\) 拟合一个模型,得到在输入 \(x\) 处的预测值 \(\hat f(x)\)。**自助法整合 (Bootstrap aggregation)**或者 bagging 在自助法样本的集合中平均了这个预测值,因此降低了它的方差。对于每个自助法样本 \(\mathbf Z^{*b},b=1,2,\ldots,B\),拟合我们的模型得到预测值 \(\hat f^{*b}(x)\)。bagging 估计定义为
记 \(\hat{\mathcal P}\) 为在每个数据点 \((x_i,y_i)\) 上赋予相同概率 \(1/N\) 的经验分布。实际上,“真正”的 bagging 估计由 \(\mathbb{E}_{\hat{\mathcal P}}\hat f^*(x)\) 定义,其中 \(\mathbf Z^*=\\{(x_1^*,y_1^*),(x_2^*,y_2^*),\ldots,(x_N^*,y_N^*)\\}\),并且每个 \((x_i^*,y_i^*)\in \hat{\mathcal P}\)。当\(B\rightarrow \infty\),表达式( 8.51 ) 是真实 bagging 估计的蒙特卡洛估计。
bagged 估计 式( 8.51 ) 与原始估计 \(\hat f(x)\) 仅仅当后者是数据的非线性或者数据的自适应函数才有区别。举个例子,为了 打包 (bag) 8.2.1 节的 B 样条光滑器,我们对图 8.2 的左下图中的曲线在每个 \(x\) 处进行平均。
note “Recall”
note “Recall”
\[ y_i^*=\hat\mu(x_i)+\varepsilon_i^*;\qquad \varepsilon_i^*\sim N(0,\hat\sigma^2);\qquad i=1,2,\ldots,N\tag{8.6} >\]
如果我们固定输入则 \(B\) 样条光滑器关于数据是线性的,因此如果我们采用式( 8.6 ) 给出的参数自助法,则当 \(B\rightarrow \infty\) 时,\(\hat f_{bag}(x)\rightarrow \hat f(x)\)(练习 8.4)。因此 bagging 刚好重现了图 8.2 的左上图中的原光滑曲线。如果我们使用非参自助法来 bagging 结论也近似正确。
一个更有趣的例子是回归树,其中 \(\hat f(x)\) 记为在每个输入向量 \(x\) 处树的预测(回归树在第九章中讨论)。每个自助法树跟比原始特征相比,涉及不同的特征,而且可能会有不同的终止结点。bagged 估计是在 \(x\) 处这 \(B\) 棵树的平均预测值。
现在假设我们的树产生一个用于 \(K\) 个类别响应变量的分类器 \(\hat G(x)\)。这里考虑一个潜在的指示向量函数 \(\hat f(x)\)(\(K\) 维向量,其中有一个 \(1\) 和 \(K-1\) 个 \(0\))使得 \(\hat G(x)=\mathrm{arg \; max}\_k\;\hat f(x)\) 是很有用的。则袋装估计 \(\hat f_{bag}(x)\) 式( 8.51 ) 是一个 \(K\) 维向量 \([p_1(x),p_2(x),\ldots,p_K(x)]\),其中 \(p_k(x)\) 等于在 \(x\) 处预测为类别 \(k\) 的树的比例。bagged 分类器从 \(B\) 棵树中选择得“票”最多的类别,也就是 \(\hat G_{bag}(x)=\mathrm{arg \; max}\_k\; \hat f_{bag}(x)\)。
经常我们需要在 \(x\) 的估计类别概率,而不是分类自身。将投票比例 \(p_k(x)\) 看成是这些概率的估计是很吸引人的。一个简单的二分类的例子显示了它们在这种情形下的失败。假设在 \(x\) 处类别 \(1\) 的真实概率为 \(0.75\),而且每个 bagging 分类器准确地预测了 \(1\)。于是 \(p_1(x)=1\),这是不正确的。然而,对于许多分类器 \(\hat G(x)\),已经有一个估计了 \(x\) 处类别概率的潜在函数 \(\hat f(x)\)(对于树而言,类别的比例即为末结点处的类别比例)。另一种 bagging 策略是对这些结点处的比例取平均而不是对得分指示向量取平均。这个过程不仅仅改善了类别概率的估计,而且趋向于产生低方差的 bagging 分类器,特别是对于小 \(B\)(见下一个例子的图 8.10)
例子: 树与模拟数据¶
我们生成规模为 \(N=30\),两个类别,以及有 \(p=5\) 个特征的样本,每个样本服从标准高斯分布,并且成对相关系数为 \(0.95\)。根据 \(\mathrm{Pr}(Y=1\mid x_1\le 0.5)=0.2\),\(\mathrm{Pr}(Y=1\mid x_1> 0.5)=0.8\) 生成响应变量 \(Y\)。贝叶斯误差率为 \(0.2\)。同时从相同的总体中生成大小为 \(2000\) 的测试集合。我们对训练样本和 \(200\) 个自助样本拟合分类树(分类树在第九章中有描述)。不使用剪枝技巧。图 8.9 显示了原始的树和 \(11\) 个自助树。
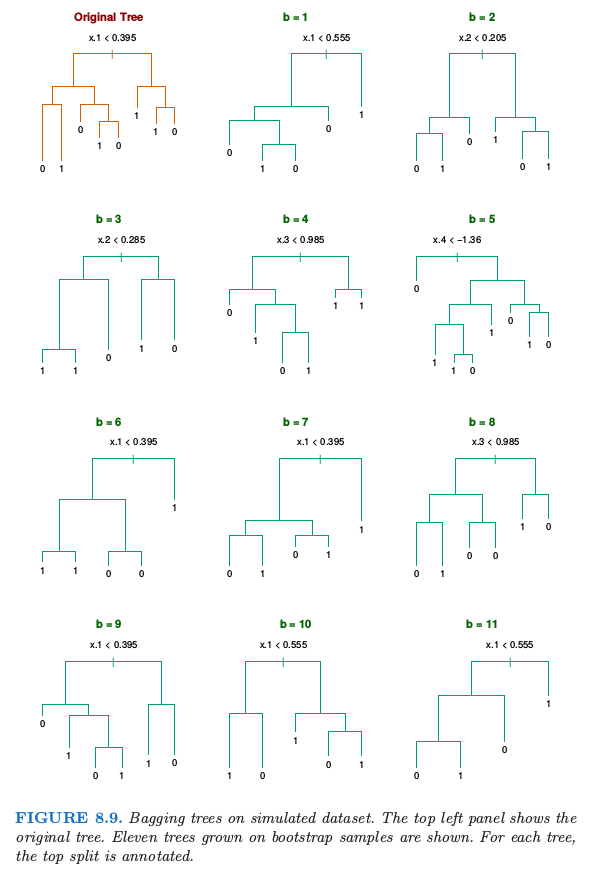
注意到这些树是怎样完全不同的,既有不同的分割特征,也有不同的截断点。原始分类树和 bagged 树的测试误差展现在图 8.10。
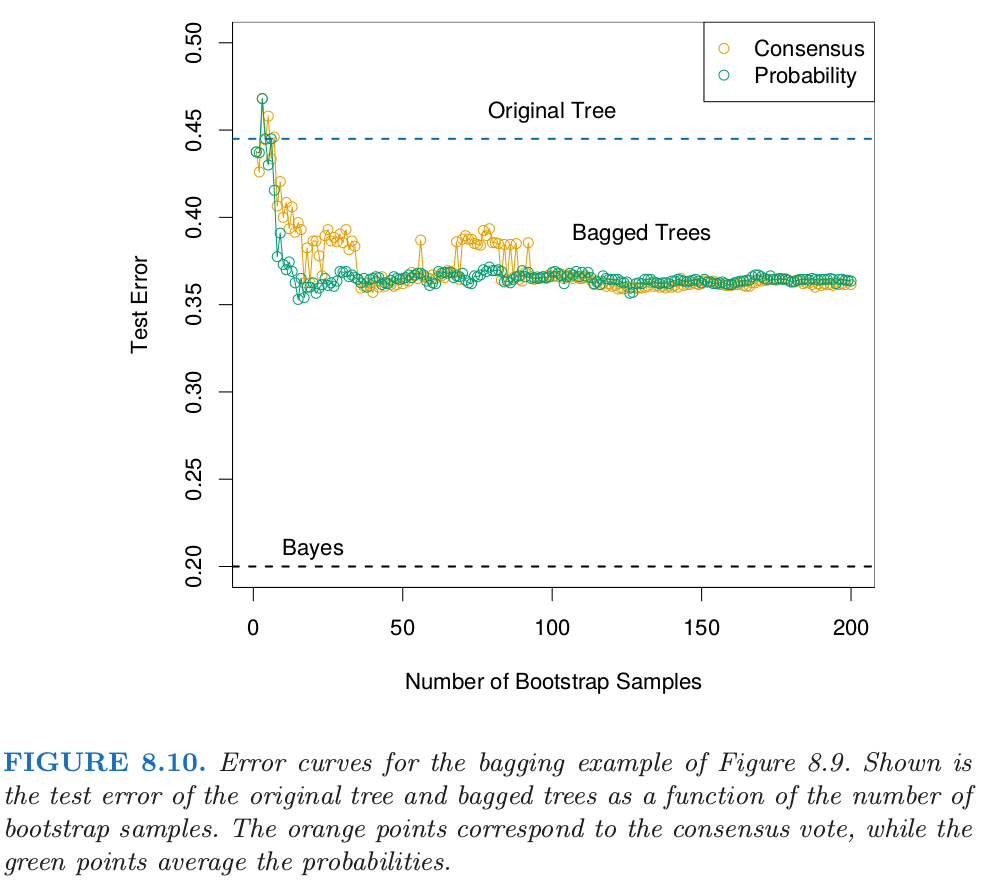
在这个例子中,由于预测变量间的相关性,树有很高的方差。Bagging 成功光滑掉方差,也因此降低了测试误差。
Bagging 可以显著降低不稳定的过程的方差得到更好的预测,比如说树。一个简单的论据说明了为什么 bagging 在平方误差损失下有效果,简单来说是因为它保持偏差不变降低了方差。
假设我们的训练样本 \((x_i, y_i),i=1,\ldots,N\) 是从分布 \(\mathcal P\) 中独立采样的,并且考虑理想的整合估计器 \(f_{ag}(x)=\mathbb{E}_{\mathcal P}\hat f^* (x)\)。这里 \(x\) 是固定的,并且自助数据集 \(\mathbf Z^*\) 包含从 \(\mathcal P\) 中采样的的观测 \(x_i^*, y_i^*, i=1,2,\ldots, N\)。注意到 \(f_{ag}(x)\) 是从实际总体 \(\mathcal P\) 中而不是数据中采样得到一个 bagging 估计。实际中这并不是我们可以用的估计,但是用于分析这是很方便的。我们可以写出如下关系
右侧额外的误差来自 \(\hat f^*(x)\) 在 \(f_{ag}(x)\) 附近的方差。因此真实的总体整合不会增加 均方误差 (mean squared error)。这表明从训练样本中采样的 bagging 将会经常降低均方误差。
上面的论据对于 0-1 损失下的分类并不能保证,因为偏差和方差的不可加性。在那种情形下,对一个较好的分类器进行 bagging 会变得更好,但是 bagging 一个差的分类器会变得更差。举个简单采用随机化规则的例子。假设对于所有的 \(x\) 我们都有 \(Y=1\),并且分类器 \(\hat G(x)\) 以概率 \(0.4\) 预测 \(Y=1\)(对所有 \(x\)),并且以 \(0.6\) 的概率预测\( Y=0\)(对所有 \(x\))。则 \(\hat G(x)\) 的误分类率为 \(0.6\),但是 bagged 分类器的误差率为 \(1.0\)。
question “weiya 注:” 所以这个例子失败的原因还是因为对 voting label 进行
bagging?如果像上文所说的对 class probability 进行bagging,是不是应该就没有这个问题了?
对于分类,我们可以就一个独立 弱学习器 (weak learners) 的共识来理解 bagging 的效应 (Dietterich, 2000a1)。令在两类别例子中 \(x\) 处的贝叶斯最优边界为 \(G(x)=1\)。假设每个弱分类器 \(G_b^*\) 的误差率为 \(e_b=e<0.5\),并令 \(S_1(x)=\sum_{b=1}^BI(G_b^*=1)\) 是类别 \(1\) 的 共识投票 (consensus vote)。因为弱分类器假设是独立的,则 \(S_1(x)\sim B(B, 1-e)\),并且当 \(B\) 变大时,\(\mathrm{Pr}(S_1>B/2)\rightarrow 1\)。这个概念已经作为“Wisdom of Crowds”流行于统计学之外了 (Surowiecki, 20042) ——多样且独立的人们的群体知识一般会超出任何单个的个体,而且可以用于投票。当然,最主要的警告是“独立”,但 bagged 树不是。图 8.11 说明了在模拟例子中 投票共识 (consensus vote) 的力量,其中只有 \(30\%\) 的投票者对候选者有一些了解。
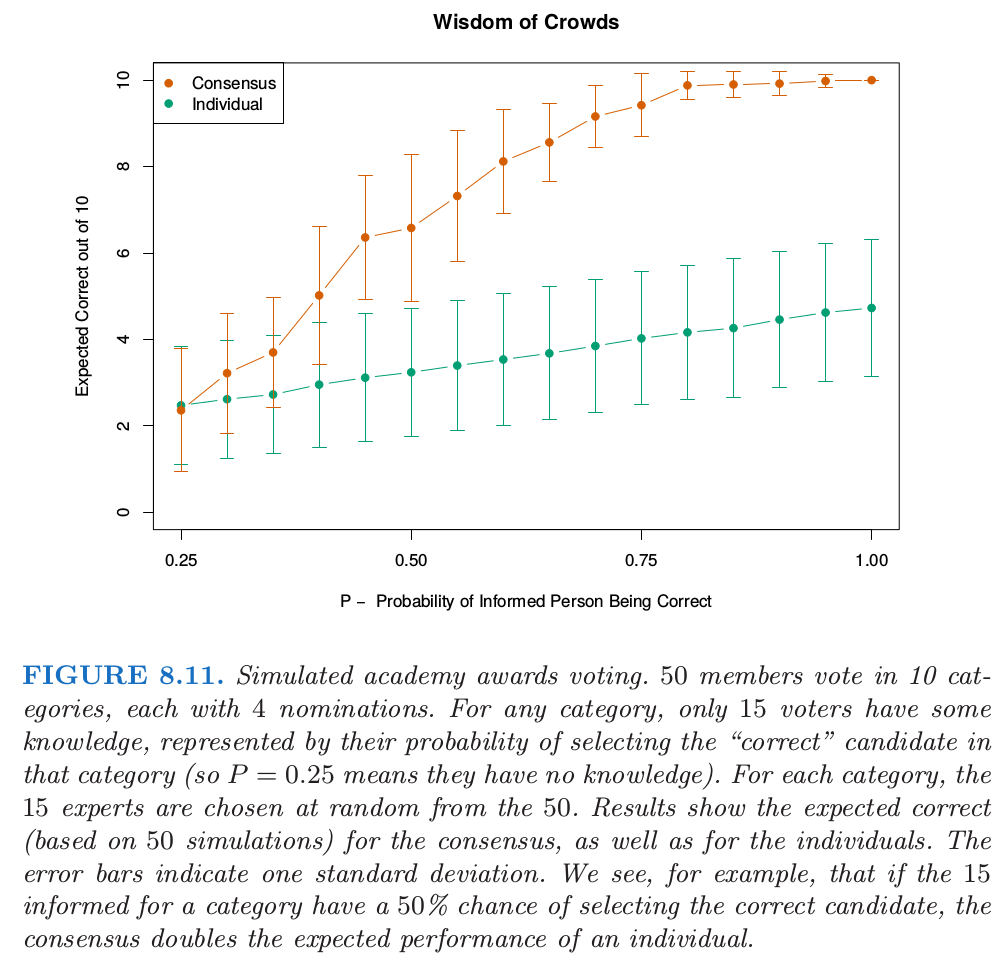
第 15 章中我们将看到随机森林通过降低被采样的树的相关性来改善bagging。
注意到当我们 bag 一个模型时,模型中任何简单的结构都会丢失。举个例子,bagged 树不再是一棵树。对于模型的解释性来说,这显然是一个缺点。更稳定的过程,如最近邻,一般不会被 bagging 所影响。不幸的是,大都被 bagging 改善的不稳定的模型其实是不稳定的,因为对解释性的重视,而且这在 bagging 过程中会丧失掉。
图 8.12 展示了一个 bagging 不起作用的例子。这 100 个数据点有两个特征和两个类别,被灰色线性边界 \(x_1+x_2=1\) 分隔开。我们选择单个坐标轴定向的分隔作为我们的分类器 \(\hat{\mathbb{G}(x)}\),选择沿着 \(x_1\) 或 \(x_2\) 那个使得训练误分类误差有最大下降的分割点。
在 50 个自助样本上的 0-1 判别规则进行 bagging 得到的判别边界用蓝色曲线显示在图 8.12 的左面板。在捕捉真实的边界方面做得很差。从训练数据中得到的单个判别规则,分割点在 0 附近(\(x_1\) 或 \(x_2\) 中间的值),因此对于远离中心有很小的贡献。对概率进行平均而不是对分类平均在这里并没有帮助。bagging 从单个分隔规则估计类别的期望概率,也就是,对许多重复实验进行平均。注意到通过 bagging 计算得到的期望类别概率不能被任意单个的实验所重现,这跟一个妇女不能有 2.4 个孩子的道理是一样的。在这个意义下,bagging 以某种方式增加了单个基分类器的模型空间。然而,在这里并没有帮助,而许多其它的例子是需要更大程度地扩大模型类。“boosting”是这样一种方式,这将在第 10 章讨论。图中右面板的判别边界是 boosting 过程的判别边界,而且其大致捕捉到了对角边界。