14.6 非负矩阵分解
Contents
14.6 非负矩阵分解¶
非负矩阵分解 (Lee and Seung, 1999)1是最近提出来的一个用来替代主成分分析的方法,在这个方法中数据以及成分假定为非负的。这对于建立非负数据的模型很有用,比如图象数据。
\(N\times p\) 数据矩阵 \(\mathbf X\) 由下式近似
其中 \(\mathbf W\) 阶为 \(N\times r\),\(\mathbf H\) 阶为 \(r\times p, r\le \max(N,p)\)。我们假设 \(x_{ij}, w_{ik}, h_{kj}\ge 0\)。
通过最大化下式来确定 \(\mathbf W\) 和 \(\mathbf H\)
这是模型的对数似然,模型中 \(x_{ij}\) 服从均值为 \((\mathbf{WH})_{ij}\) 的 Poisson 分布——这对于正值数据是很合理的。
下面的轮换 (alternating) 算法 (Lee and Seung, 2001)2 收敛到 \(L(\mathbf W, \mathbf H)\) 的局部最大值:
这个算法可以由最大化 \(L(\mathbf W, \mathbf H)\) 的 minorization 过程来导出(练习14.23)
info “weiya 注:Ex. 14.23” 练习 14.23 已解答,详细过程参见 Issue 86: Ex. 14.23
note “weiya 注:minorization” 练习 14.23中介绍了 minorization 的概念。对于函数\(g(x, y)\)和\(f(x)\),若对于定义域中所有的 \(x\) 和 \(y\),若满足
则称$g(x,y)$ minorize $f(x)$。
并且与对数线性模型的 迭代比例缩放算法 (iterative-proportional-scaling algorithm) 相关(练习 14.24)。
info “weiya 注:Ex. 14.24” 练习 14.24 已解答,详细过程参见 Issue 87: Ex. 14.24

图 14.33 展示了从 Lee and Seung (1999)1 中选取的例子,其中比较了非负矩阵分解 (NMF),向量量化(VQ,等价于 \(k\) 均值聚类)以及主成分分析 (PCA)。将这三种学习方法应用到大小为 \(N=2429\) 的人脸数据库中,每个包含 \(19\times 19\)的像素点,得到一个 \(2429\times 381\) 的矩阵 \(X\)。如 \(7\times 7\) 个蒙太奇画(每个都是 \(19\times 19\) 的图象)所示,每种方法学习 \(r=49\) 张基图象集。正值用黑色像素表示,而负值用红色像素点表示。对于一张特定的脸,如右上角所示,用基图象的线性叠加来近似。线性叠加的系数在 \(7\times 7\) 数组中的每个蒙太奇画的右边,最终得到的叠加图像显示在等式右边。作者指出,与 VQ 和 PCA 不同,NMF 是用表示脸的不同部位的基图象来学习去表征脸。
Donoho and Stodden (2004)3 指出非负矩阵分解的一个潜在的严重问题。即使在 \(X=W\H\)严格成立的情形下,分解可能不是唯一的。图 14.34 说明了这个问题。
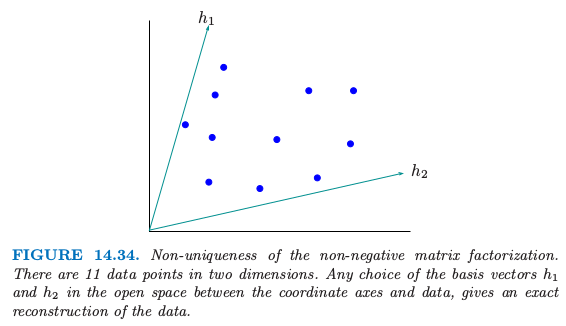
数据点落在 \(p=2\) 维空间中,并且数据与坐标轴之间存在开放的区域 (open space)。我们可以在这个开放区域中选择基向量 \(h_1\) 和 \(h_2\),并且用这些向量的非负线性组合来精确表示每个数据点。这个不唯一性表明上述的算法得到的解会依赖初始值,并且似乎阻碍了因子分解的解释性。尽管这个解释性方面的不足,非负矩阵分解及其应用吸引力许多研究者的兴趣。
()原型分析¶
归功于 Cutler and Breiman (1994)4,这个方法通过原型(数据点的线性组合)来近似数据点。在这个意义上,与 \(K\) 均值聚类有相似的地方。然而,不是用单个附近的原型来近似每个数据点,原型分析通过一系列原型的凸组合来近似每个数据点。凸组合的使用强制原型位于数据云的 凸包 (convex hull) 上。在这个意义下,原型是纯的 (pure),或典型的 (archetypal)。
如 式( 14.72 ) 一样,\(N\times p\) 的数据矩阵 \(X\) 建模为
其中 \(W\) 阶为 \(N\times r\),且 \(\H\) 为 \(r\times p\)。我们假设 \(w_{ik}\ge 0\),且 \(\sum_{k=1}^rw_{ik}=1\;\forall i\)。因此 \(p\) 维空间中的 \(N\) 个数据点(\(X\) 的行)用 \(r\) 个原型(\(\H\) 的行)的凸组合来表示。我们还假设
其中 \(\B\) 阶为 \(r\times N\),其中 \(b_{ki}\ge 0\),且 \(\sum_{i=1}^Nb_{ki}=1\forall k\)。因此原型本身是数据点的凸组合。使用 式( 14.75 ) 和 式( 14.76 ),我们对下式关于权重 \(W\) 和 \(\B\) 最小化
我们采用轮换的模式对函数进行最小化,其中每个单独的最小化都涉及到凸优化。然而整个问题不是凸的,所以算法收敛到准则的一个局部最小值点。
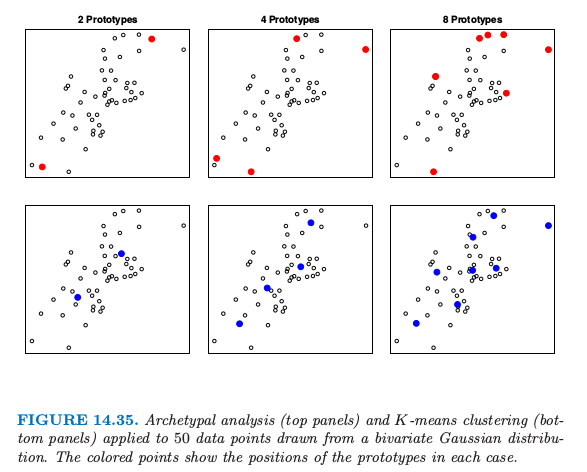
图 14.35 展示了二维中模拟数据的例子。上面板展示了 \(K\) 均值聚类的结果。为了从原型的凸组合中重构出数据,需要在数据的凸包上定位原型。可以在图 14.35 的上图中看到,并且一般地是这种情形,如 Cutler and Breiman (1994)4 所证明的那样。如图中下面板所示,\(K\) 均值聚类在数据云的中间选择原型。
我们可以把 \(K\) 均值聚类看成原型模型的特殊情形,其中 \(W\) 的每一行有一个元素取 1,其余取 0。
注意到原型模型 式( 14.75 ) 与非负矩阵分解模型 式( 14.72 ) 有相同的一般形式。然而,这两个模型应用在不同的条件中,并且目标也不太相同。非负矩阵分解目的是近似数据矩阵 \(X\) 的列,并且主要感兴趣的是 \(W\) 的列,它表示了数据中主要的非负组分。原型分析而是关注用 \(\H\) 的行(表示了原型数据点)来近似 \(X\) 的行。非负矩阵分解还假设 \(r\le p\)。当 \(r=p\),简单将 \(W\) 选为列经过缩放(所以加起来和为1)的 \(X\),可以得到精确的重构。相反,原型分析要求 \(r\le N\),但允许 \(r>p\)。举个例子,在图 14.35 中,\(p=2,N=50\),而 \(r=2,4,8\)。额外的约束 式( 14.76 ) 表明典型分析不是完美的,即使 \(r>p\)。

图 14.36 展示了将典型分析应用于图 14.22 中的 3 的数据集的结果。 图 14.36 中的三行是取自三次原型分析的结果,分别是 2 个原型、3 个原型和 4 个原型。和预想一样,该算法得到了大小和形状上都极端的 3。
- 1(1,2)
Lee, D. and Seung, H. (1999). Learning the parts of objects by non-negative matrix factorization, Nature 401: 788.
- 2
Lee, D. and Seung, H. (2001). Algorithms for non-negative matrix factorization, Advances in Neural Information Processing Systems, (NIPS 2001), Vol. 13, Morgan Kaufman, Denver., pp. 556–562.
- 3
Donoho, D. and Stodden, V. (2004). When does non-negative matrix factorization give a correct decomposition into parts?, in S. Thrun, L. Saul and B. Sch¨olkopf (eds), Advances in Neural Information Processing Systems 16, MIT Press, Cambridge, MA.
- 4(1,2)
Cutler, A. and Breiman, L. (1994). Archetypal analysis, Technometrics 36(4): 338–347.
