11.6 例子:模拟数据
11.6 例子:模拟数据¶
note “更新笔记” @2017-12-28 挺惭愧的!直到今天才认真地从零开始写了个简单的神经网络代码,具体代码详见Notebook for Simple Neural Network。对于本节的例子,我也写了份代码试图重现书中的结果,代码详见Notebook for this Section
我们从两个可加误差模型 \(Y=f(X)+\varepsilon\) 中产生数据:
这里 \(X^T=(X_1,X_2,\ldots,X_p)\),每个 \(X_j\) 是标准高斯变量,第一个模型中 \(p=2\),第二个模型中 \(p=10\).
对于sigmoid模型,\(a_1=(3,3),a_2=(3,-3)\);对于径向模型,\(\phi(t)=(1/2\pi)^{1/2}exp(-t^2/2)\).\(\varepsilon_1\)和\(\varepsilon_2\)都是高斯误差,选择方差使得两个模型的信噪比都为4。
我们取大小为100的训练集和大小为10000的测试集。我们采用权重系数衰减和不同的隐藏单元来拟合神经网络,然后记录10个随机初始权重系数值情形下的平均测试误差\(E_{Test}(Y-\hat f(X))^2\)。虽然只产生了一个训练集,但是结果是“平均”的训练集的典型。测试误差展示在图11.6中。注意到0个隐藏层单元指的是线性最小二乘回归。神经网络对于sigmoid函数之和的模型拟合效果很好,而且当有两个神经元时效果最好,非常接近贝叶斯误差率。(回忆一下,回归的平方误差的贝叶斯误差率是误差的方差;这张图中是测试误差相对于贝叶斯误差的比例)然而,注意到更多的隐藏层单元,很快便出现了过拟合,而且有些权重系数的初始值比线性模型(0个隐藏单元)拟合得还差。即便是2个隐藏单元的情形,10个权重系数的初始值中有两个的结果不好于线性模型,证实了多重初始值的重要性。
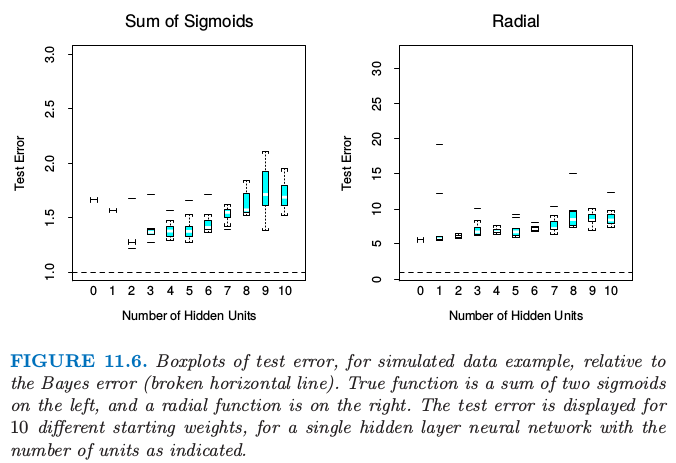
图11.6 模拟数据例子的测试误差相对于贝叶斯误差(水平虚线)的箱线图。左图的真实函数是两个sigmoid函数之和,右图是径向函数。对于具有所指示单元数目的单个隐藏层神经网络,显示10个不同起始权重的测量误差。
在某种程度上径向函数对于神经网络是最困难的,因为它是球对称且没有偏好的方向。我们可以从图11.6的右图中看出在这种情形下缺失效果很差,测试误差远远超出贝叶斯误差(注意与左图不同的垂直刻度)。事实上,因为常值拟合(比如样本均值)的相对误差率达到5(当SNR为4),我们看到神经网络比均值表现得越来越差。
这个例子中我们采用一个固定的系数衰减参数0.0005,表现一个温和的正则化。图11.6的左图的结果表明在更多隐藏单元的情形下需要更多的正则化。
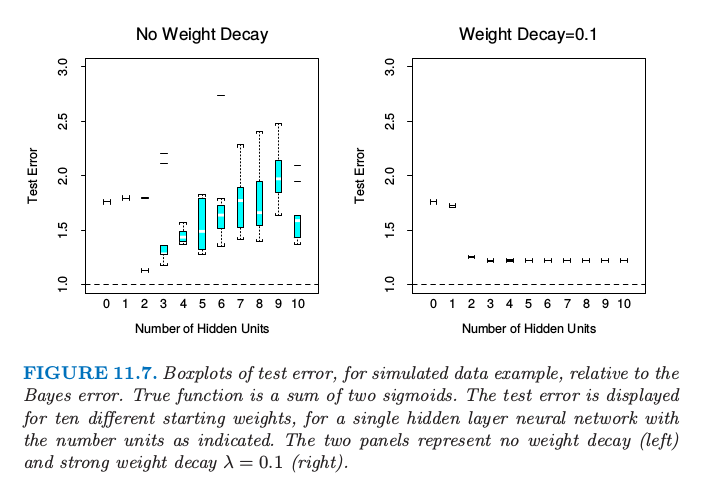
图11.7. 模拟数据例子的测试误差相对于贝叶斯误差的箱线图。真实函数是两个sigmoid函数之和。对于具有所指示单元数目的单个隐藏层神经网络,显示10个不同起始权重的测量误差。两个图分别表示无系数衰减(左边)和强误差衰减\(\lambda=0.1\)(右图)
图11.7中,我们对两sigmoids和的模型重复实验,左边图没有系数衰减,右边图为更强的系数衰减(\(\lambda=0.1\)).没有系数衰减时,越多的隐藏单元,过拟合变得越严重。系数衰减值\(\lambda=0.1\)在所有隐藏神经元个数的情形下都能得到好结果,当隐藏单元的个数增加并不表现出过拟合的现象。最后,图11.8显示了含10个隐藏单元神经网络的测试误差随着不同衰减参数的变化。值为0.1时近似是最优的。
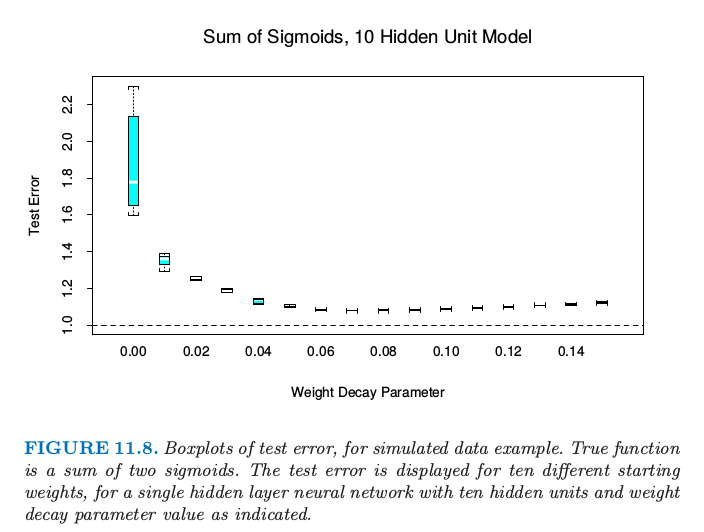
图11.8. 对于模拟数据例子的测试误差的箱线图。真实函数为两个sigmoid函数之和。对于具有所指示单元数目的单个隐藏层神经网络,显示10个不同起始权重的测量误差。
总的来说,有两个自由参数需要选择:权重衰减参数\(\lambda\)和隐藏层的数目\(M\)。作为一个学习的策略,可以在对应的最小约束模型下固定任一个参数,来确保模型足够丰富,并且运用交互验证来选择另一个参数。这里最少约束值为0权重衰减和10个隐藏层单元。将图11.7的左图与图11.8相比,我们可以看到测试误差对于系数衰减更不敏感,因此此参数的交互验证会更好。
