12.7 混合判别分析
Contents
12.7 混合判别分析¶
线性判别分析可以看成是 原型 (prototype) 分类器。每个类别都由其形心表示,并且使用某种合适的度量,将其分到最近的形心处。在许多情形下,单个原型不足以表示不均匀的类别,而混合模型是更合适的。在这节中,我们回顾高斯混合模型,并且展示怎么从之前讨论的 FDA 和 PDA 中推广得到。第 \(k\) 类别的高斯混合模型密度为
\( P(X\mid G=k)=\sum\limits_{r=1}^{R_k}\pi_{kr}\phi(X;\mu_{kr},\mathbf\Sigma),\tag{12.59} \)$
其中 混合比例 (mixing proportions) \(\pi_{kr}\) 的和为 \(1\)。第 \(k\) 类有 \(R_k\) 个原型,并且在我们的情形中,始终采用相等的协方差作为度量。对每个类别给定这样一个模型,类别后验概率由下式给出
\( P(G=k\mid X=x)=\frac{\sum_{r=1}^{R_k}\pi_{kr}\phi(X;\mu_{kr},\mathbf \Sigma)\Pi_k}{\sum_{\ell=1}^K\sum_{r=1}^{R_\ell}\pi_{\ell r}\phi(X;\mu_{\ell r},\mathbf \Sigma)\Pi_\ell}\tag{12.60} \)$
其中 \(\Pi_k\) 表示类别的先验概率。
我们在第 8 章看到两个组分的特殊情形的计算。如 LDA 中一样,我们通过极大似然估计参数,采用如下基于 \(P(G,X)\) 的联合对数似然:
如果直接处理对数中的和,会变成很复杂的优化问题。计算混合分布的极大似然估计的经典的、自然的方法是 EM 算法 (Dempster et al., 19771),它具有良好的收敛性质。EM 在下面两步间轮换:
E-step:给定当前的参数,对类别 \(k\) 的每个观测 (\(g_i=k\)) 计算其子类 \(c_{kr}\) 的 responsibility:
\( W(c_{kr}\mid x_i, g_i)=\frac{\pi_{kr}\phi(x_i;\mu_{kr},\mathbf \Sigma)}{\sum\limits_{\ell=1}^{R_k}\pi_{k\ell}\phi(x_i;\mu_{k\ell},\mathbf \Sigma)}.\tag{12.62} \)$
M-step: 采用 E-step 的权重,计算每个类别中每个高斯组分的参数的加权 MLE。
在 E-step,算法将类别 \(k\) 中的观测的单位权重赋给属于该类的不同子类。如果观测点离某个子类的形心很近,且离其它形心很远,则它会收到该更近的子类更大的权重。另一方面,如果观测点在两个子类中间则它会得到两个子类近似相等的权重。
在 M-step,类别 \(k\) 的观测使用 \(R_k\) 次,来估计 \(R_k\) 个组分密度中每一个的参数,对于每个组分有不同的权重。EM 算法在第 8 章中有详细介绍。算法要求初始化,这可能有影响,因为混合模型一般都是多种模型。我们的软件(后面计算上的考虑一节中有提到)允许多种策略;这里我们描述默认的策略。用户提供每个类中子类的个数 \(R_k\)。在类别 \(k\) 中,用多重随机起始点的 \(k\) 均值聚类模型对数据进行拟合。根据元素为 \(0\) 和 \(1\) 的初始权重矩阵,将观测值划分到 \(R_k\) 个不相交的群中。
我们对始终相等的组分协方差矩阵 \(\mathbf\Sigma\) 的假设带来额外的简化;我们可以像 LDA 中一样在混合形式中结合秩的约束。为了理解这一点,回顾下 LDA 的一些事实(4.3.3 节)。rank-\(L\) 的 LDA 拟合等价于高斯模型的极大似然拟合,其中每个类别中不同的均值向量约束到 \(\mathbb{R}^p\) 的 rank-\(L\) 子空间(练习 4.8)。
info “weiya 注:Ex. 4.8” 结合作者的原论文,目前看懂其中一种情形的证明,详见 Issue 143: Ex. 4.8。
我们可以在混合模型中继承这条性质,并且在满足所有 \(\sum_kR_k\) 个形心上的秩约束的条件(\(\mathrm{rank}\\{\mu_{k\ell}\\}=L\))下最大化对数似然 式( 12.61 )。
又一次可以用 EM 算法,并且 M-step 事实上是加权版本的 LDA,其中有 \(R=\sum_{k=1}^KR_k\) 个“类别”。而且,我们可以采用之前一样的最优得分来解决加权 LDA 问题,使得我们在这一步可以使用 FDA 或者 PDA。可以预料,除了“类别”数可以增加,第 \(k\) 类中的观测数也会类似增加 \(R_k\) 倍。事实证明如果线性算子用于最优得分回归,则不是这种情形。增广的响应变量矩阵 \(\mathbf Y\) 变成 模糊的 (blurred) 响应矩阵 \(\mathbf Z\),直觉上令人愉快。举个例子,假设有 \(K=3\) 个类别,并且每个类中有 \(R_k=3\) 个子类。则 \(\mathbf Z\) 可能是
其中类别 \(k\) 行的元素对应 \(W(c_{kr}\mid x,g_i)\)。
剩下的步骤是一样的:
这些简单的改进大大增加了模型的灵活性:
LDA,FDA 或者 PDA 中的降维那一步被类别数限制;特别地,对于 \(K=2\) 个类别,不可能有降维。MDA 用子类代替了类别,并且允许从这些子类形心张成的子空间的低维视角中观测数据。这个子空间经常是用于判别时重要的一个。
通过在 M-step 使用 FDA 或者 PDA,我们可以适应更具体的情形。举个例子,我们可以对数字模拟信号及图像拟合 MDA 模型,其中要求光滑的约束。
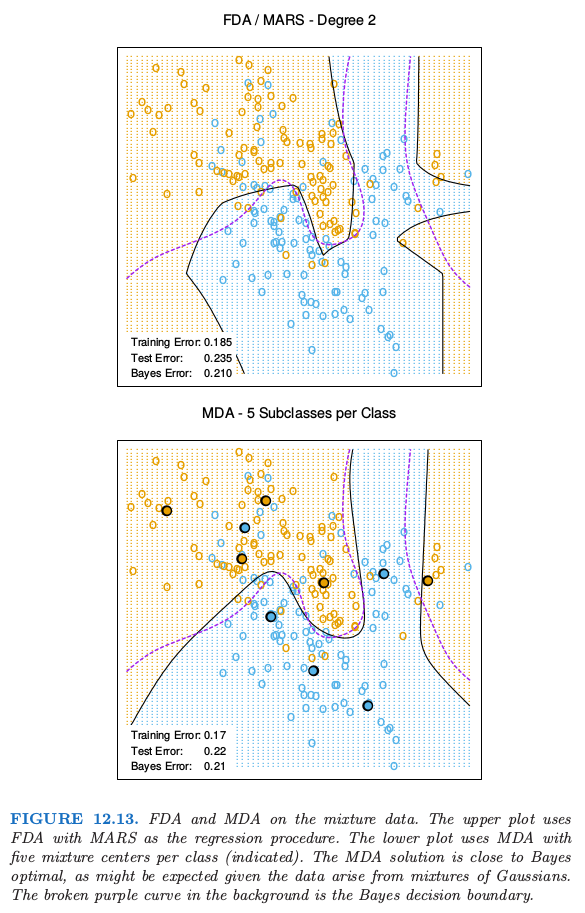
图 12.13 在混合例子中比较了 FDA 和 MDA。
()例子:波形数据¶
现在我们在一个流行的模拟数据中说明这些想法,这个模拟数据取自 Breiman et al. (1984, pages 49–55)2,并且用在了 Hastie and Tibshirani (1996b)3 和其它地方。这是有着 21 个变量的三类别问题,并且被认为是复杂的模型识别问题。预测变量由下式定义
其中 \(j=1,2,\ldots,21\),\(U\) 是 \((0,1)\) 上的均匀分布,\(\epsilon_j\) 是标准的正态分布,并且 \(h_\ell\) 是平移的三角波形:\(h_1(j)=\max (6-\vert j-11\vert,0)\),\(h_2(j)=h_1(j-4)\) 以及 \(h_3(j)=h_1(j+4)\)。图 12.14 展示了每个类的一些波形的例子。
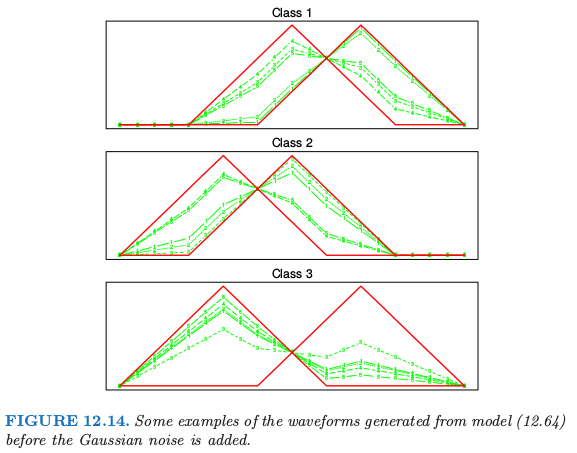
表 12.4 展示了 MDA 应用到波形数据上的结果,以及本章和其他章的一些其它方法。每个训练样本有 300 个观测,并且使用相同的先验概率,所以每个类大概有 100 个观测。我们采用大小为 500 的测试样本。这两个 MDA 模型在说明文字中有描述。
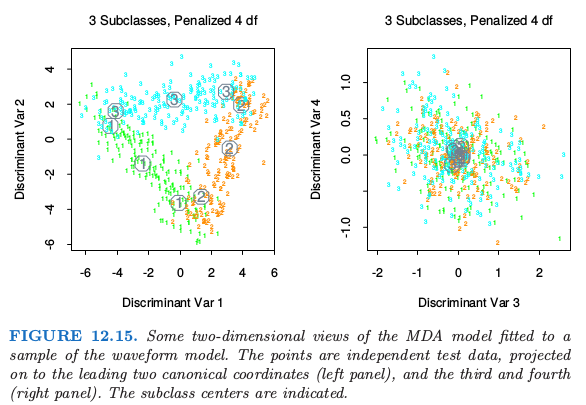
图 12.15 展示了在测试数据上取值的带惩罚的 MDA 模型的第一个典则变量。如我们可能猜测的一样,类别看上去位于三角形的三边。这是因为 \(h_j(i)\) 用 21 维空间中的三个点来表示,因此构成了三角形的顶点,并且每个类别用成对顶点的凸组合来表示,因此位于一条边上。也清楚地看出所有的信息都在前两个维度中;前两个维度解释的方差的比例是 \(99.8\%\),所以在这里截断解不会有损失。这个问题的贝叶斯风险已经估计大约为 0.14 (Breiman et al., 19842)。MDA 接近最优的比例,这个结果也不是很惊奇,因为 MDA 模型的结构类似生成模型。
- 1
Dempster, A., Laird, N. and Rubin, D. (1977). Maximum likelihood from incomplete data via the EM algorithm (with discussion), Journal of the Royal Statistical Society Series B 39: 1–38.
- 2(1,2)
Breiman, L. and Ihaka, R. (1984). Nonlinear discriminant analysis via scaling and ACE, Technical report, University of California, Berkeley.
- 3
Hastie, T. and Tibshirani, R. (1996b). Discriminant analysis by Gaussian mixtures, Journal of the Royal Statistical Society Series B. 58: 155–176.
