8.9 随机搜索: Bumping
8.9 随机搜索: Bumping¶
这章描述的最后一个方法不涉及平均或者结合模型,但是是寻找一个更好单模型的方法。Bumping 采用 bootstrap 采样在模型空间中随机移动。对于拟合方法经常会找到许多局部最小值的问题,bumping 可以帮助这些方法避免陷入坏的解。
像在 bagging 中一样,我们抽取自助样本并且对每个样本拟合模型。但是不是对这些预测值进行平均,我们而是选择拟合训练数据最好的自助样本的模型。具体地,我们抽取自助样本 \(Z^{*1}, \ldots, Z^{*B}\) 并对每个样本拟合我们的模型,然后给出在输入点 \(x\) 处的预测 \(\hat f^{*b},n=1,2,\ldots,B\)。我们在原始训练集上平均选择产生最小预测误差的模型。举个例子,对于平方误差,我们选择从自助样本 \(\hat b\) 中得到的模型,其中
对应的模型预测为 \(\hat f^{*\hat b}(x)\)。按照约定,我们也把原始训练样本包含进自助样本的集合中,所以如果原始模型有更低的训练误差,这种方法也能选择原始模型。
通过打乱数据,bumping 试图将拟合过程移动到模型空间的好区域中。举个例子,如果只有少数的数据点会导致这个过程找到差的解,则任意删除掉这些数据点的自助样本应该会产生更好的解。
举另一个例子,考虑图 8.13 中的分类数据,臭名昭著的异或(exclusive or)(XOR)问题。其中有两个类别(蓝色和橘黄色)以及两个输入特征,并且特征间存在单纯的交互。
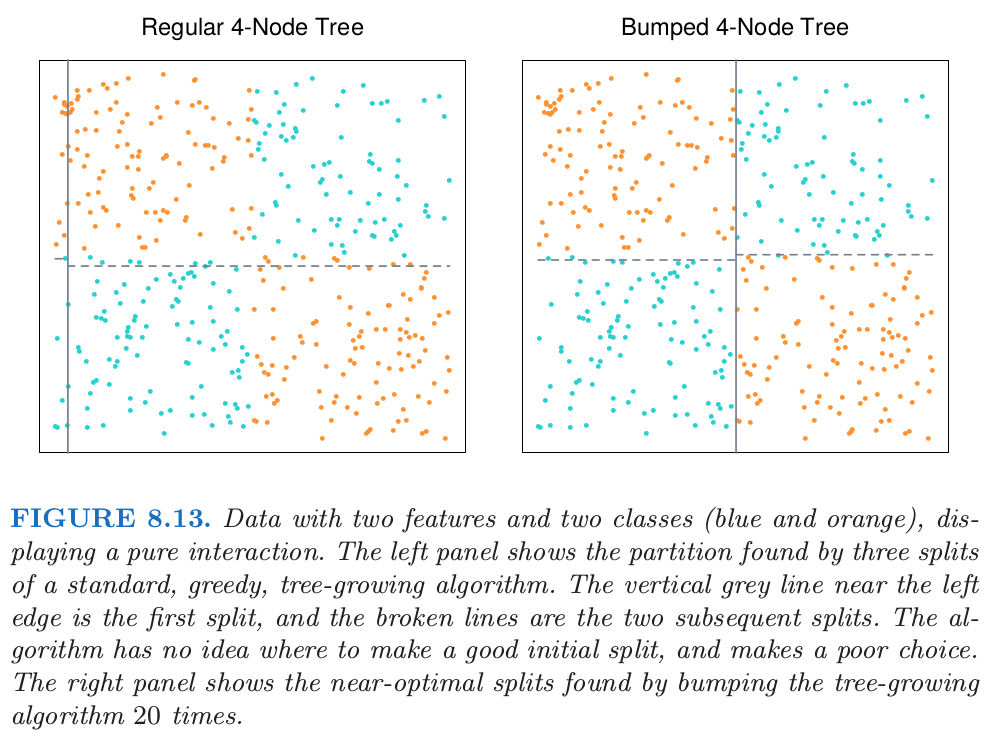
通过先在 \(x_1=0\) 处分离数据,然后在每个分层的 \(x_2=0\) 处分离数据(或者反过来),一个基于树的分类器可以达到完美的判别。然而,贪婪的、见识短的 CART 算法(9.2节)试图寻找任意一个特征上的最优分割,接着再对得到的分层进行分割。由于数据的平衡特性,所有在 \(x_1\) 或 \(x_2\) 上的初始分割似乎无用,而且这个过程本质上在第一层产生随机的分割。对于这些数据找到的实际分割展示在图 8.13 的左图。通过对数据 bootstrap 采样,bumping 打破了类别之间的平衡,以一个合理大小的自助样本(这里是20),这至少会随机产生一个初始分割点在 \(x_1=0\) 或 \(x_2=0\) 附近的树。仅仅使用 20 个自助样本,bumping 找到了图 8.13 的右图中展示的接近最优的分割。如果我们添加一系列独立于类别标签的噪声特征,贪婪的生成树的算法的缺点会被加重。则生成树的算法不能区分 \(x_1\) 或 \(x_2\),并且将会更加迷路。
因为 bumping 在训练数据上比较了不同的模型,必须保证模型近似有相同的复杂度。在树的情形下,这意味着在每个自助样本上生成终止结点个数相同的树。bumping 在很难最优化拟合准则的问题中也有帮助,或许是因为缺少光滑性。技巧是在自助样本上优化一个不同的、但更方便的准则,接着选择在训练样本上产生原始准则达到最优的模型。
