7.5 样本内误差的估计¶

样本内误差估计的一般形式为：

\[ \widehat{\text{Err}}_{in}=\overline{\text{err}}+\hat\omega \tag{7.25} \]

其中 $\hat\omega$ 是乐观值期望的估计。

当在平方误差损失下拟合 $d$ 个参数后，是可以应用式（ 7.24 ）的；利用表达式（ 7.24 ）可以导出被称作 $C_p$ 的统计量：

\[ F_p=\overline{\text{err}}+2\cdot\frac{d}{N}\hat \sigma^2_\varepsilon\tag{7.26} \]

这里 $\hat\sigma_\varepsilon^2$ 是噪声方差的估计，由低偏差模型的均方误差得到。使用这个准则，我们用一个与使用的基函数个数成比例的因子来调节训练误差。

当采用对数似然损失函数时，Akaike 信息准则 (Akaike information criterion) 是类似的但使用更普遍的 $\text{err}_{in}$ 的估计。它依赖于与式（ 7.24 ）类似的关系式，在 $N\rightarrow \infty$ 渐近地有下式成立：

\[-2\cdot \mathbf{E}[\mathrm{log}\Pr\nolimits_{\hat \theta}(Y)]\approx -\frac{2}{N}\cdot \mathbf{E}[\mathrm{loglik}]+2\cdot\frac{d}{N}\tag{7.27} \]

这里 $\Pr_{\theta}(Y)$ 是 $Y$ 密度函数族（包含“真正的”密度），$\hat\theta$ 是 $\theta$ 的极大似然估计，并且“loglik”是最大化的对数似然：

\[ \mathrm{loglik}=\sum\limits_{i=1}^N\log \Pr\nolimits_{\hat\theta}(y_i)\tag{7.28} \]

举个例子，对于逻辑斯蒂回归模型，采用二项对数似然，我们有：

\[ \mathrm{AIC}=-\frac{2}{N}\cdot \mathrm{loglik}+2\cdot \frac{d}N\tag{7.29} \]

对于高斯模型（假设方差 $\sigma_\varepsilon^2=\hat\sigma_\varepsilon^2$ 已知），AIC 统计量等于 $C_p$，因此我们称它们一起称为 AIC。

Note

注意此处假设 $\sigma_\varepsilon^2$ 已知，如果也将其看成是未知的，并通过 MLE 求解，则 AIC 准则（忽略常数）为:

\[ \mathrm{AIC} = N\log\mathrm{RSS} + 2d\]

详见 Wiki: AIC

采用 AIC 来进行模型选择时，我们在考虑的模型中选择具有最小 AIC 的模型。对于非线性或者其他复杂模型，我们需要将 $d$ 换成其它衡量模型复杂度的量。我们将在 7.6 节讨论这点。

给定由调整参数 $\alpha$ 编号的一系列模型，用 $\overline{\text{err}}(\alpha)$ 和 $d(\alpha)$ 记为每个模型的训练误差和参数的个数。接着对于模型序列我们定义:

\[ \mathrm{AIC}(\alpha)=\overline{\text{err}}(\alpha)+2\cdot\frac{d(\alpha)}{N}\hat\sigma_\varepsilon^2\tag{7.30} \]

函数 $\mathrm{AIC}(\alpha)$ 给出了测试误差曲线的一个估计，而且我们找到最小化它的调整参数 $\hat \alpha$。我们最终选择的模型是 $f_{\hat\alpha}(x)$。注意到如果我们基函数是自适应地选择，式（ 7.23 ）不再成立。举个例子，如果我们总共有 $p$ 个输入，选择含有 $d < p$ 个输入的最优线性拟合模型，optimism 将会超过 $(2d/N)\sigma_\varepsilon^2$。换句话说，通过选择含有 $d$ 个输入的最优拟合模型，有效参数的个数将会超过 $d$。

图 7.4 显示了将 AIC 用于 5.2.3 节的音素识别的例子的效果。输入向量是口语元音的对数周期图，在 256 个均匀间隔的频率上取值。采用线性逻辑斯蒂回归模型来预测音素的类别，参数函数为 $\beta(f)=\sum_{m=1}^Mh_m(f)\theta_m$，是 $M$ 个样条基函数的展开。对于给定的 $M$，对 $h_m$ 应用自然三次样条，在频率范围内均匀选取结点（因此 $d(\alpha)=d(M)=M$）。使用 AIC 来选择基函数的个数会近似最小化损失函数为熵损失和 0-1 损失时的 $\text{err}(M)$。

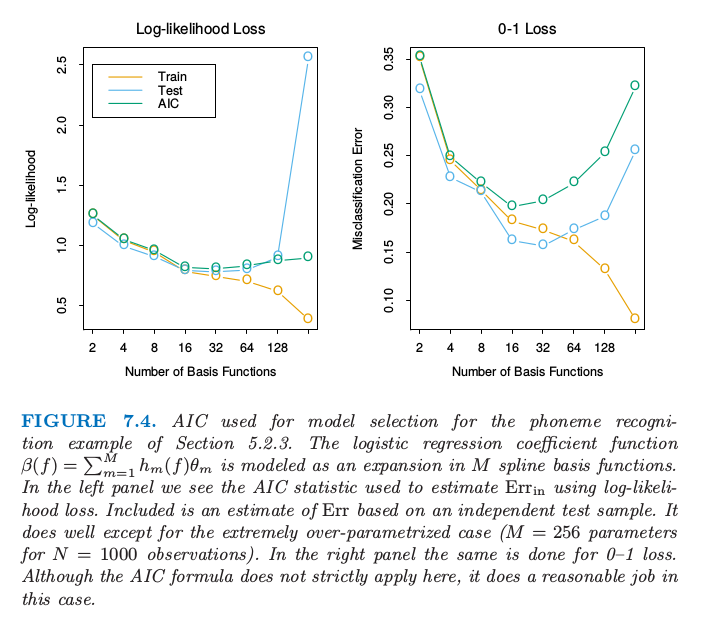
图 7.4. 对 5.2.3 节的音素识别的例子应用 AIC 来做模型选择。

逻辑斯蒂回归参数函数 $\beta(f)=\sum_{m=1}^Mh_m(f)\theta_m$ 建模成 $M$ 个样条基函数的展开。在左图中我们看到采用对数似然损失时用来估计 $\text{err}_{in}$ 的 AIC 统计量。也画出了基于独立的测试样本的 $\text{err}$ 估计。除了极端过参数化的情形（ $N=1000$ 个观测时含有 $M=256$ 个参数）都估计得很好。右图是在 0-1 损失下重复左图的工作。尽管这里 AIC 准则严格上不能应用，但是在这种情形下估计也是合理的。

下式这一简单的法则

$$ F/N\sum\limits_{i=1}^N\mathrm{Cov}(\hat y_i,y_i)=(2d/N)\sigma_\varepsilon^2 $

对于含有加性误差的线性模型在平方误差损失下是精确成立的，在对数似然损失下是近似成立的。特别地，这个法则一般地对于 0-1 损失是不成立的（Efron，19861），尽管许多作者仍然在这种情形下使用它（图 7.4 的右图）.

1: Efron, B. (1986). How biased is the apparent error rate of a prediction rule?, Journal of the American Statistical Association 81: 461–70.

统计学习精要(中文)

7.5 样本内误差的估计

7.5 样本内误差的估计¶