4.1 导言
4.1 导言¶
这章我们重新回到分类问题,并且集中讨论分类的线性方法。因为我们的预测变量 \(G(x)\) 是在离散集 \(\mathbb{G}\) 中取值,所以我们总是可以根据类别把输入空间分成一些区域的集合。在第 2 章中,我们看到这些区域之间的边界会随着预测函数不同而变得粗糙或者光滑。其中有一种很重要的边界形式为 线性判别边界 (decision boundaries) 。
可以通过许多不同方式找到线性判别边界。在第二章中,我们根据类别指示变量拟合线性回归模型,并将观测点分到拟合值最大的类别。假设有 \(K\) 个类别,为了方便分别标记为 \(1,2,\ldots,K\)。则第 \(k\) 个响应对应的指示变量拟合的线性模型为 \(\hat f_k(x)=\hat\beta_{k0}+\hat\beta_k^Tx\)。第 \(k\) 类和第 \(l\) 类之间的判别边界应当满足 \(\hat f_k(x)=\hat f_\ell(x)\) ,或者说边界上所有的点均具备上述等值特性,形式化为集合 \(\{x:(\hat\beta_{k0}-\hat\beta_{\ell 0})+(\hat\beta_k-\hat\beta_\ell)^Tx=0\}\),可以看出这是一个仿射集或者超平面。
注解: 严格来说,超平面需要通过原点,而仿射集不需要。我们有时忽略它们之间的区别并且统称为超平面。
因为对于任意两个类别这也成立,输入空间被分块超平面判别边界分成了若干个类别区域。回归方法对每个类别建立 判别函数 (discriminant functions) \(\delta_k(x)\),然后将 \(x\) 分到取最大值的判别函数所在类别中。建立后验概率 \(\mathrm{Pr}(G=k\mid X=x)\) 也是属于这种类别。说的更清楚点,只要 \(\delta_k(x)\) 或者 \(\mathrm{Pr}(G=k\mid X=x)\) 关于 \(x\) 是线性的,则判别边界将也是线性的。
实际上,我们仅要求 \(\delta_k\) 或者 \(\mathrm{Pr}(G=k\mid X=x)\) 的单调变换关于判别边界要是线性的。举个例子,如果这里有两个类,一个关于后验概率很流行的模型是
这里单调变换是 logit 变换:\(\log[p/(1-p)]\),事实上我们看到
判别边界是 log-odds 等于 \(0\) 的点的集合,这是由 \(\\{x\mid\beta_0+\beta^Tx=0\\}\) 定义的超平面。我们讨论两种非常流行但是不同的方法,最后都得到线性的 log-odds 或者 logits:线性判别分析和线性 logistic 回归。尽管它们的推导不相同,但是他们关键的区别在于用线性函数拟合训练数据的方式。
一种更直接的方式是在类别之间显性地建立线性边界。对于在 \(p\) 维输入空间的两个类别的问题,这意味着将判别边界建模为超平面——换句话说,一个 法向量 (normal vector) 和一个 分隔点 (cut-point)。我们将看到两种方法都是显式寻找“分隔超平面”。第一个是著名的 Rosenblatt (1958)1 的 感知器 (perceptron) 模型,以及一个从训练数据中寻找分离超平面的算法(如果存在超平面的话)。第二个方法要归功于 Vapnik(1996)2,如果超平面存在的话寻找一个最优分离超平面,不存在的话则寻找一个超平面使得训练数据中的重叠最小。我们这里处理可分的情形,不可分的情形将推到第 12 章讨论。
尽管整个章节都在谈论线性判别边界,但对于一般情形还有相当大的讨论余地。
note “weiya 注:翻译” 此处原文为,“While this entire chapter is devoted to linear decision boundaries, there is considerable scope for generalization.”
举个例子,我们可以对变量集 \(X_1,X_2,\ldots,X_p\) 加上他们的交互积 \(X_1^2,X_2^2,\ldots,X_1X_2,\ldots,\) (因此加入了 \(p(p+1)/2\) 个额外的变量)进行推广。当增广空间的线性函数投影到原空间的二次函数,则线性判别边界转换为二次判别边界。图 4.1 解释了这个想法。数据集是一样的,左边是在二维空间中用线性判别函数,而右图在增广的五维空间中用线性判别函数。这种方式可以跟任意基变换 \(h(X)\) 一起使用,其中 \(h:\mathbb{R}^p\rightarrow \mathbb{R}^q,q > p\),这将在后面章节中讨论。
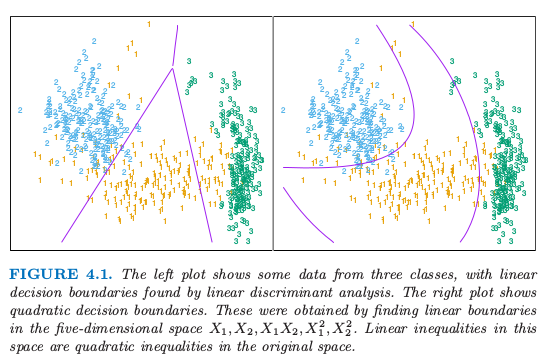
图 4.1:左图显示了三个类别的一些数据,以及通过线性判别分析得到的线性判别边界。右图显示了二次判别边界。这是通过在五维空间 \(X_1,X_2,X_1X_2,X_1^2,X_2^2\) 找到线性边界得到。这个空间里面的线性不等式是原空间的二次不等式。
