12.6 惩罚判别分析
12.6 惩罚判别分析¶
尽管 FDA 的动机是推广最优得分,但是它也可以直接看成是正则化判别分析的形式。假设 FDA 中的回归过程意味着在基展开 \(h(X)\) 上的、并且系数有二次惩罚的线性回归:
\( ASR(\{\theta_\ell,\beta_\ell\}^L_{\ell=1})=\frac 1N\sum\limits_{\ell=1}^L\Big[\sum\limits_{i=1}^N(\theta_\ell(g_i)-h^T(x_i)\beta_\ell)^2+\lambda\beta_\ell^T\mathbf \Omega\beta_\ell\Big].\tag{12.57} \)$
\(\mathbf \Omega\) 的选择取决于具体问题。如果 \(\eta_\ell(x)=h(x)\beta_\ell\) 是样条基函数的展开,则 \(\mathbf\Omega\) 可能约束 \(\eta_\ell\) 要在 \(\mathbb{R}^p\) 上光滑。在可加样条的情形下,每个坐标有 \(N\) 个样条基函数,则 \(h(x)\) 总共包含 \(Np\) 个基函数;在这种情形下,\(\mathbf\Omega\) 是 \(Np\times Np\) 的,并且是分块对角的。
然后 FDA 中的步骤就可以看成是 LDA 的推广形式,我们称之为 带惩罚的判别分析 (penalized discriminant analysis),或者 PDA:
通过基展开 \(h(X)\) 扩充预测变量 \(X\) 的集合;
在增广空间中采用(带惩罚的)LDA,其中带惩罚的 马氏距离 (Mahalanobis distance) 由下式给出
其中 \(\mathbf \Sigma_W\) 是导出变量 \(h(x_i)\) 的类别内协方差矩阵。
采用惩罚度量分解分类子空间:
$\( \max\; u^T\mathbf \Sigma_{\mathrm{Bet}}u\;\text{subject to }u^T(\mathbf\Sigma_W+\lambda\mathbf\Omega)u=1 \)
不严谨地说,带惩罚的麦哈顿距离趋向于给“粗糙”的坐标更少的权重,而给“光滑”的坐标更多的权重;因为惩罚不是对角的,同样的方式会应用到粗糙或光滑的线性组合中。
对于某些类的问题,第一步的基展开不是必须的;我们已经有太多(相关的)预测变量了。一个突出的例子是当分类的对象是 数字化模拟信号 (digitized analog signals) :
语音片段的对数周期图,在 256 个频率的集合上进行采样;见图 5.5。
手写数字的数字图像中的灰度像素值。
在这些情形中直观上很清楚为什么需要正则化。以数字图像为例。相邻像素值趋向于相关,通常几乎是一样的。这意味着这些像素的对应 LDA 系数对可能会很不一样并且符号相反,因此当作用到类似的像素值时系数会被抵消掉。正相关的预测变量导致噪声的、负相关的系数估计,并且这个噪声导致多余的采样方差。一个合理的策略是在空间中对系数正则化使之光滑,,图像也一样。这就是 PDA 做的事。计算步骤和 FDA 一样,除了需要使用合适的带惩罚的回归方法。这里 \(h^T(X)\beta_\ell=X\beta_\ell\),并且选择 \(\mathbf \Omega\) 使得 \(\beta_\ell^T\mathbf\Omega\beta_\ell\) 惩罚关于 \(\beta_\ell\) 的粗糙程度(将其看成图像时)。图 1.2 展示了一些手写字母的例子。图 12.11 显示了采用 LDA 和 PDA 的判别变量。
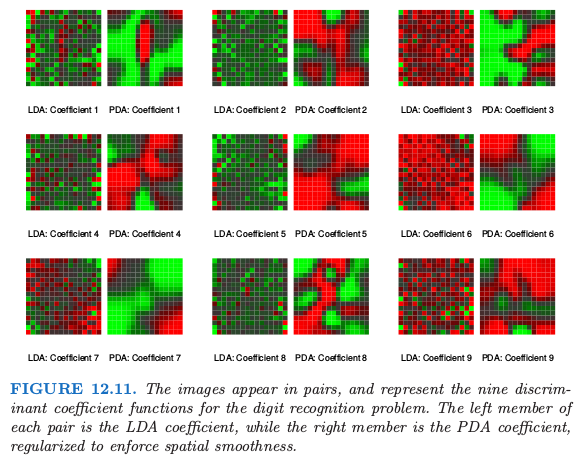
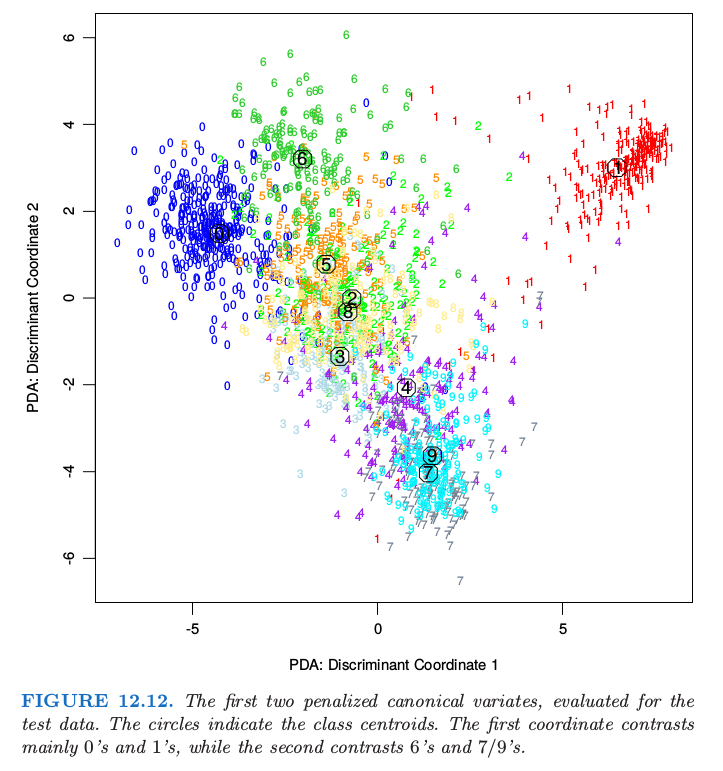
由 LDA 生成的判别变量系数看起来像 椒盐 (salt and pepper) 图像,而由 PDA 得到了光滑图像。第一张光滑图像可以看成是线性对比度函数的系数,用于从中间为中空的图像中(可能是 0 或 4)分离具有暗中心垂直条带的图像(可能是 1 或 7)。图 12.12 佐证了这个解释,第二个坐标的解释更加困难。这个以及其他例子在 Hastie et al. (1995) 中有更详细的讨论,其中也展示了在他们试过的情形中,在独立的测试数据中,正则化将 LDA 的分类效果约提高了 \(25\%\)。