5.8 正则化和再生核希尔伯特空间理论
Contents
5.8 正则化和再生核希尔伯特空间理论¶
这一节我们将样条放进更大的正规方法框架下以及 再生核希尔伯特空间 (reproducing kernel Hilbert spaces) 中。这部分非常专业 (quite technical),因此不感兴趣或者有些畏惧的读者可以跳过。
一般的正则化问题形式如下
其中 \(L(y,f(x))\) 是损失函数,\(J(f)\) 是惩罚函数,\(\mathcal H\) 是 \(J(f)\) 有定义的函数空间。Girosi et al. (1995)1 描述了形如下式的非常一般的惩罚函数
其中 \(\tilde f\) 记为 \(f\) 的 Fourier 变换,并且 \(\tilde G\) 是当 \(\Vert s\Vert\rightarrow \infty\) 趋于 \(0\) 的正函数。上式想法是 \(1/\tilde G\) 加大对 \(f\) 的高频组分的惩罚。在一些额外的假设下,他们证明解有如下形式
其中 \(\phi_k\) 张成惩罚函数 \(J\) 的零空间,并且 \(G\) 是 \(\tilde G\) 的逆 Fourier 变换。平滑样条和 thin-plate 样条都属于这个框架。这个解的显著特点是当准则 式( 5.42 ) 定义在无限维空间,解是有限维。在下一节我们考虑一些具体的例子。
5.8.1 核产生的函数空间¶
形如 式( 5.42 ) 的问题的一个重要子类是由正定核 \(K(x,y)\) 产生的,对应的函数空间 \({\mathcal H}_K\) 被称为 再生核希尔伯特空间 (reproducing kernel Hilbert space),简称为 RKHS。惩罚函数也是用核来定义的。我们对这个模型类进行一个简短的介绍,这取自 Wahba (1990)2 和 Girosi et al. (1995)1,并且在 Evgeniou et al. (2000)3 中有很好的总结。
令 \(x,y\in \mathbb{R}^p\)。我们考虑由 \(\\{K(\cdot, y), y\in \mathbb{R}^p\\}\) 线性张成的函数空间;也就是,形如 \(f(x)=\sum_m\alpha_mK(x, y_m)\) 的任意线性组合,其中每个核可以看成第一个变量的函数,并且由第二个变量索引。假设 \(K\) 有 特征展开 (eigen-expansion)
其中 \(\gamma_i\ge 0,\sum_{i=1}^\infty \gamma_i^2 < \infty\)。
note “weiya 注:Mercer’s theorem” 式( 5.45 ) 的分解由 Mercer’s theorem 保证,Mercer’s theorem 将半正定矩阵的特征分解推广到半正定核函数的特征分解,具体地,
图片来源: Wiki: Mercer’s theorem。
\({\mathcal H}_K\) 的元素是关于这些 特征函数 (eigen-functions) 的展开,即
并且约束条件为
其中 \(\Vert f\Vert_{{\mathcal H}\_K}\) 由 \(K\) 导出的范数。
note “weiya 注:Induced Norm”
希尔伯特空间是完备内积空间,对于一般的希尔伯特空间 \(\mathcal H\),其 导出范数 (induced norm) 为
\[ \Vert f\Vert_{{\mathcal H}} := \sqrt{\langle f,f\rangle_{{\mathcal H}}}\,. >\]note “weiya 注:两种构造 RKHS 的方法” 一般地,有两种构造 RKHS 的方法:
第一种,给定一个半正定核 \(K\),定义映射 \(\Phi:\mathcal{X}\mapsto \mathbb{R}^\mathcal{X}\) 为 \(\Phi(x) = K(\cdot, x)\),然后考虑向量空间
\[ \mathrm{span}(\{\Phi(x):x\in\mathcal{X}\}) = \left\{f(\cdot) = \sum_{i=1}^N\alpha_iK(\cdot, x_i)\right\}\,, >\]并对 \(f = \sum_{i=1}^N\alpha_iK(\cdot, u_i), g = \sum_{i=1}^N\beta_iK(\cdot, v_i)\) 定义内积
\[ \langle f, g\rangle = \sum_{i=1}^N\sum_{j=1}^N\alpha_i\beta_jK(u_i,v_j)\,, >\]则 \(K\) 满足核再生性质,并且 \(\overline{\mathrm{span}(\{\Phi(x)\})}\) 定义了 RKHS.
另外一种,则是用 Mercer 定理,定义内积
\[ \langle f, g\rangle_{\mathcal{H}} = \sum_{j=1}^{\infty}\frac{\langle f,\phi_j\rangle\langle g,\phi_j\rangle}{\mu_j} >\]则
\[ \left\{f=\sum_{j=1}^\infty c_j\phi_j\mid \sum_{j=1}^\infty c_j^2/\mu_j < \infty\right\} >\]为 RKHS.
式( 5.42 ) 中空间 \({\mathcal H}\_K\) 的惩罚函数定义为二次范数 \(J(f)=\Vert f\Vert_{{\mathcal H}\_K}^2\)。\(J(f)\) 的值可以解释为广义岭惩罚,其中在展开式( 5.45 ) 中,大的特征值惩罚较小,反之亦然。
重写 式( 5.42 ),我们有
或者等价地,
可以证明(Wahba, 19902, 另见 练习 5.15),式( 5.48 ) 的解是有限的,并且如下形式
基函数 \(h_i(x)=K(x,x_i)\)(关于第一个变量的函数)被称作 \({\mathcal H}\_K\) 中 \(x_i\) 处的 representer of evaluation,因为对于 \(f\in {\mathcal H}\_K\),容易看到 \(\langle K(\cdot, x_i),f\rangle_{{\mathcal H}\_K} = f(x_i)\)。类似地,\(\langle K(\cdot, x_i), K(\cdot,x_j)\rangle_{{\mathcal H}\_K}=K(x_i, x_j)\)(\({\mathcal H}\_K\) 的再生性质),
note “weiya 注: 核再生性质 (kernel reproducing property)” 对于任意的 \(x\in {\mathcal X}\), \(K(\cdot, x) \in \mathcal H\),并且满足
\[ \langle f, K(\cdot, x)\rangle_{\mathcal H} = f(x)\qquad \text{for all }f\in \mathcal H\,. >\]这称为 核再生性质 (kernel reproducing property)。另外,对于任意半正定核 \(K\),存在唯一的希尔伯特空间 \(\mathcal H\) 满足核再生性质,此时 \(\mathcal H\) 也被称之为 再生核希尔伯特空间 (RKHS).
也因此对于 \(f(x)=\sum_{i=1}^N\alpha_iK(x,x_i)\)
根据 式( 5.50 ) 和 式( 5.51 ),式( 5.48 ) 退化为有限维准则
我们正在使用向量记号,其中 \(K\) 是第 \(ij\) 个元素为 \(K(x_i,x_j)\) 的 \(N\times N\) 的矩阵。简单的数值算法可以用来优化 式( 5.52 )。无限维问题 式( 5.48 ) 或 式( 5.49 ) 退化为有限维优化问题的现象在支持向量机(见第 12 章)中被称为 核性质 (kernel property)。
这类模型有一个贝叶斯解释,其中 \(f\) 被解释为零均值平稳高斯过程的实现,其中先验协方差函数为 \(K\)。特征值分解得到一系列方差为 \(\gamma_j\) 的正交特征函数 \(\phi_j(x)\)。一般的情形是,“平滑”函数 \(\phi_j\) 有更大的先验方差,而“粗糙”的 \(\phi_j\) 有较小的先验方差。式( 5.48 ) 中的惩罚是先验对联合概率的贡献度,并且方差越小惩罚越大(与 式( 5.43 ) 相比)。
为了简便,我们这里处理所有 \(\mathcal H\) 中的成员都被惩罚的情形,如 式( 5.48 )。更一般地,\(\mathcal H\) 中可能有些组分我们希望单独留下来,比如 5.4 节 中的三次平滑样条的线性函数。5.7 节 的多维 thin-plate 样条以及张量积样条也都属于这类。在这些情形下,有个更方便的表示 \(\mathcal H=\mathcal H_0\oplus\mathcal H_1\),举个例子,其中零空间 \(\mathcal H_0\) 由没有被惩罚的 \(x\) 的低阶多项式组成。惩罚项变为 \(J(f)=\Vert P_1f\Vert\),其中 \(P_1\) 是 \(f\) 在 \(\mathcal H_1\) 上的正交投影。这个解形式为 \(f(x)=\sum_{j=1}^M\beta_jh_j(x)+\sum_{i=1}^N\alpha_iK(x,x_i)\),其中第一项表示 \(\mathcal H_0\) 中的展开。从贝叶斯的观点看,\(\mathcal H_0\) 中组分的系数的先验的方差无穷大。
5.8.2 RKHS 的例子¶
上述的机理是由核 \(K\) 和损失函数 \(L\) 的选择 驱动 (driven) 的 。我们首先考虑采用平方误差损失的回归。将 式( 5.48 ) 中的惩罚特定为最小二乘,则解可以用对应 式( 5.49 ) 或 式( 5.52 ) 的两个等价方式进行描述:
对于无穷维的广义岭回归问题
或者写成
易得 \(\alpha\) 的解
且
\(N\) 个拟合值的向量为
估计值 式( 5.57 ) 也是稀疏统计 (Cressie, 1993)4 中高斯随机域的 kriging 估计。另外 式( 5.58 ) 可以与平滑样条拟合 式( 5.17 ) 进行比较。
( 1 )带惩罚的多项式回归¶
核 \(K(x,y)=(\langle x, y\rangle+1)^d\) (Vapnik, 1996)5,对于 \(x,y\in \mathbb{R}^p\),有 \(M=\binom{p+d}{d}\) 个特征函数,它张成了 \(\mathbb{R}^p\) 中总阶数为 \(d\) 的多项式空间。举个例子,当 \(p=2, d=2,M=6\),有
其中
可以用 \(M\) 个 \(K\) 的特征函数和特征值来表示 \(h\)
其中 \(D_\gamma=\mathrm{diag}(\gamma_1,\gamma_2,\ldots, \gamma_M)\),并且 \(V\) 是 \(M\times M\) 的,且为正交。
假设我们希望求解带惩罚的多项式回归问题
将 式( 5.62 ) 代入 式( 5.63 ),我们得到 式( 5.53 ) 的展开来进行优化(练习 5.16)。
基函数的个数 \(M=\binom{p+d}{d}\) 可以非常大,通常大于 \(N\)。等式( 5.55 ) 告诉我们如果采用解函数的核表示,我们仅仅需要对核进行 \(N^2\) 次赋值,而且可以以 \(O(N^3)\) 的计算量得到解。
This simplicity is not without implications. 式( 5.61 ) 中的每个多项式 \(h_m\) 从 \(K\) 的特定形式继承了缩放因子,这对 式( 5.63 ) 的惩罚有影响。我们将在下一节详细讨论。
( 2 )高斯径向基函数¶
在前面的例子中,选择核是因为能表示成多项式的展开,这样可以方便地计算高维内积。在这个例子中,选择核是因为 式( 5.50 ) 中的函数形式。
举个例子,在平方误差损失下,高斯核 \(K(x,y)=e^{-\nu \Vert x-y\Vert^2}\) 能得到展开式为高斯径向基函数的回归模型,
每个点都在训练特征向量 \(x_m\) 处中心化了。可以采用 式( 5.54 ) 来估计参数。
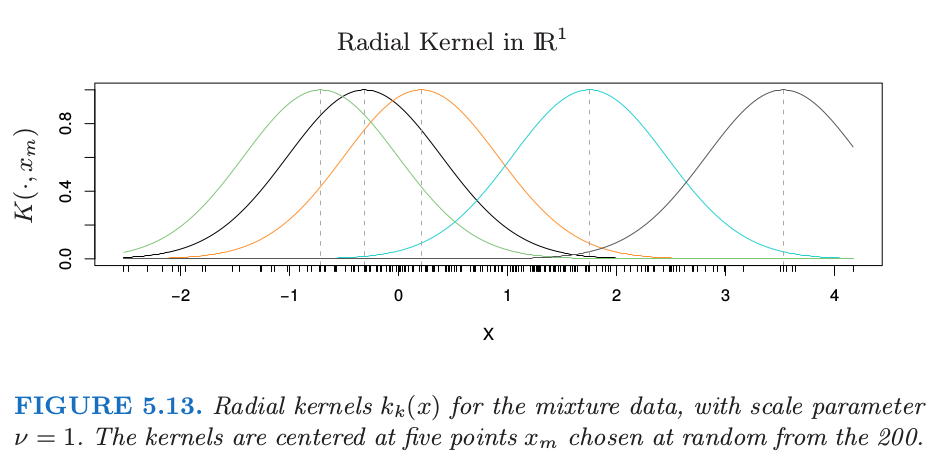
图 5.13 采用第二章混合例子中的第一个坐标展示了 \(\mathbb{R}^1\) 中的径向核。我们展示了 \(200\) 个核基函数 \(k_m(x)=K(x,x_m)\) 中的五个。
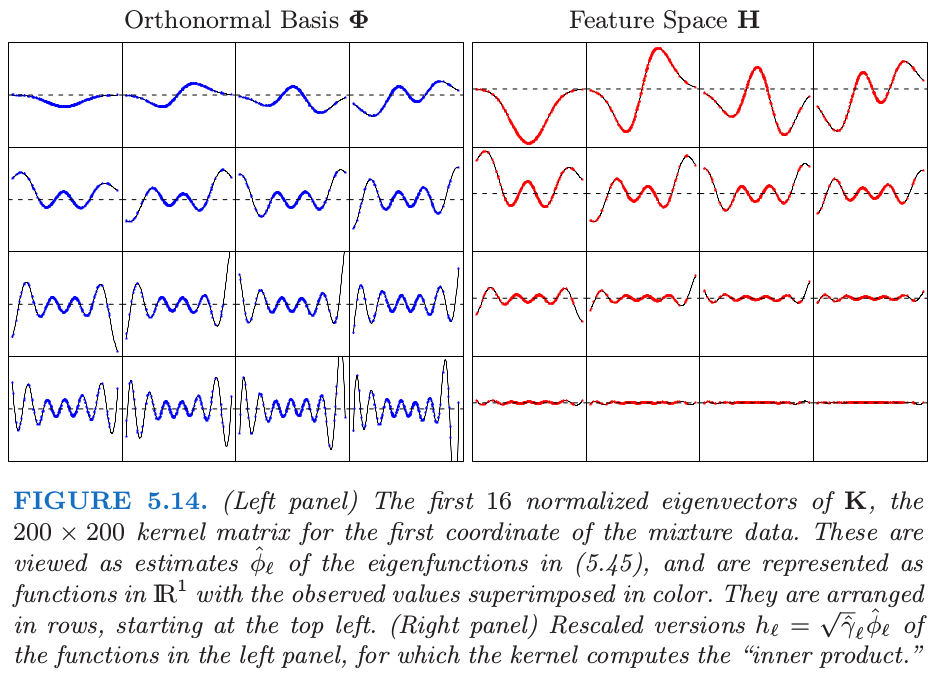
图 5.14 展示了 \(x\in \mathbb{R}^1\) 的径向核的隐式特征空间。我们计算 \(200\times 200\) 的核矩阵 \(K\),以及其特征分解 \(\Phi D_\gamma\Phi^T\)。我们可以认为 \(\Phi\) 的列和 \(D_\gamma\) 中对应的特征值是特征展开 式( 5.45 ) 中的经验估计。
note “原书脚注:” \(\Phi\) 的第 \(\ell\) 列是 \(\phi_\ell\) 的一个估计,这是对 \(N\) 个观测中的每一个进行赋值。另外,\(\Phi\) 的第 \(i\) 行是基函数 \(\phi(x_i)\)(在 \(x_i\) 处取值)的估计向量。尽管原则上,\(\phi\) 可以有无穷多的元素,但我们的估计至多有 \(N\) 个元素。
尽管特征向量是离散的,但我们还是可以将它们表示成 \(\mathbb{R}^1\) 中的函数(练习 5.17)。
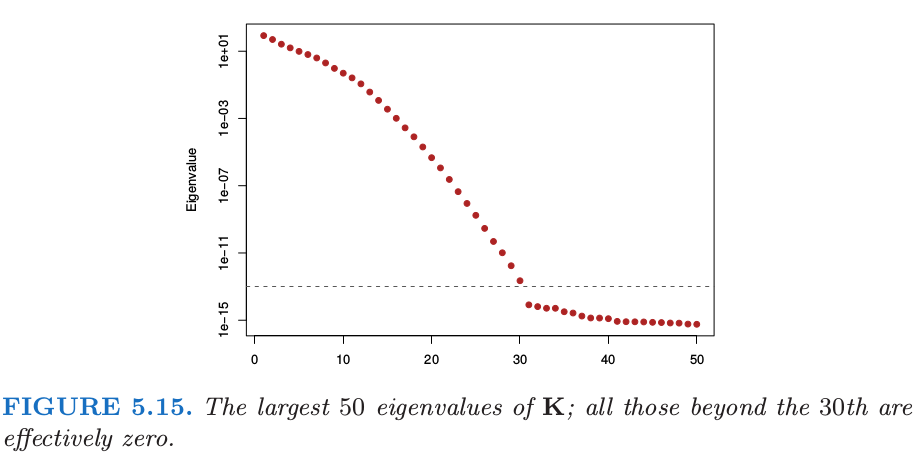
图 5.15 展示了 \(K\) 的最大的 \(50\) 个特征值。最大特征值对应的特征函数是平滑的,并且它们随着 order 增加变得更加弯曲。这使得 式( 5.49 ) 中的惩罚变成了可能,其中我们看到高阶函数的系数比低阶函数惩罚更多。图 5.14 中的右面板显示了下面特征函数对应的特征空间的表示
注意到 \(\langle h(x_i), h(x_{i'})\rangle=K(x_i, x_{i'})\)。通过特征值来缩放快速将大部分的函数降为 \(0\),在这种情形下留下大约 \(12\) 个有效维度。对应的优化问题是如 式( 5.63 ) 中标准的岭回归。所以尽管原则上隐式的特征空间是无穷维的,但有效维度还是非常小的,因为对每个基函数应用相对大小的收缩。核缩放参数 \(\nu\) 在这里也起一定作用;更大的 \(\nu\) 意味着更多局部的 \(k_m\) 函数,并且也增加了特征空间的有效维度。更多细节参见 Hastie and Zhu (2006)6。
我们知道被称为 thin-plate 样条 (5.7 节)是关于径向基函数的展开 (Girosi et al., 1995)1,它由下列核产生
径向基函数将在 6.7 节详细讨论。
()支持向量机¶
第 12 章中用于两个类别分类的支持向量机有形式 \(f(x)=\alpha_0+\sum_{i=1}^N\alpha_iK(x,x_i)\),选择参数使下式最小化
其中 \(y_i\in \\{-1, 1\\}\),并且 \([z]_+\) 记做 \(z\) 的正值部分。这可以看成是带线性约束的二次优化问题,并要求该解的二次规划算法。支持向量 (support vector) 的名字来自这样一个事实: 一般有许多的\(\hat\alpha_i=0\)【因为 式( 5.67 ) 中损失函数的 piecewise-zero 特性】,也因此 \(\hat f\) 是 \(K(\cdot, x_i)\) 的子集的展开。更多细节见 12.3.3节。
- 1(1,2,3)
Girosi, F., Jones, M. and Poggio, T. (1995). Regularization theory and neural network architectures, Neural Computation 7: 219–269.
- 2(1,2)
Wahba, G. (1990). Spline Models for Observational Data, SIAM, Philadelphia.
- 3
Evgeniou, T., Pontil, M. and Poggio, T. (2000). Regularization networks and support vector machines, Advances in Computational Mathematics 13(1): 1–50.
- 4
Cressie, N. (1993). Statistics for Spatial Data (Revised Edition), Wiley-Interscience, New York.
- 5
Vapnik, V. (1996). The Nature of Statistical Learning Theory, Springer, New York.
- 6
Hastie, T. and Zhu, J. (2006). Discussion of “Support vector machines with applications” by Javier Moguerza and Alberto Munoz, Statistical Science 21(3): 352–357.
