7.12 “条件测试误差”还是“测试误差的期望”?
7.12 “条件测试误差”还是“测试误差的期望”?¶
图 7.14 和 7.15 检验了交互验证是否能很好地估计 \(\mathbb{Err}_{\mathcal{T}}\) 的问题,其中 \(\mathbb{Err}_{\mathcal{T}}\) 表示给定训练集 \(\mathcal{T}\) 上的误差,它与期望预测误差相对。
Note
$$
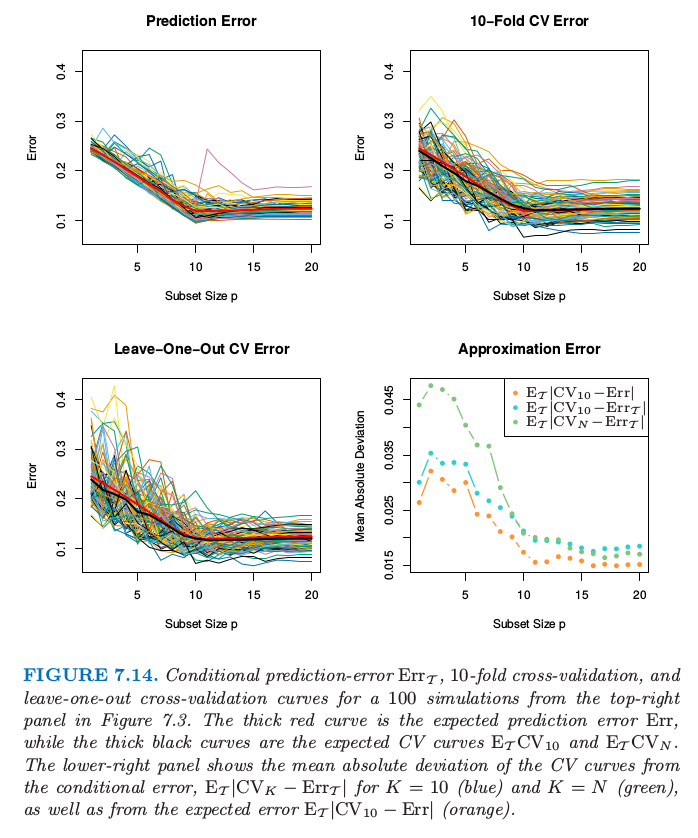
图 7.14. 从图 7.3 的右上图得到的 100 个模拟值的条件预测误差 \(\mathbb{Err}_{\mathcal{T}}\),10 折交互验证,以及舍一交互验证的曲线。红色粗线为期望预测误差 \(\mathbb{Err}\),而黑色粗线为期望 CV 曲线 \(\mathbb{E}_{\mathcal{T}}CV_{10}\) 和 \(\mathbb{E}_{\mathcal{T}}CV_N\)。右下图显示了 CV 曲线与条件误差的绝对偏差的期望 \(\mathbb{E}_{\mathcal{T}}\vert CV_k-\mathbb{Err}_{\mathcal{T}}\vert\),\(K=10\)(蓝色)以及 \(K=N\)(绿色),并且也显示了 CV 曲线与期望误差之间绝对偏差的期望 \(\mathbb{E}_{\mathcal{T}}\vert CV_{10}-\mathbb{Err}\vert\)(橘黄色)。
对于图 7.3 中右上图的 “reg/linear” 的设定中产生的 100 个训练集中的每一个训练集,图 7.14 展示了条件误差 \(\mathbb{Err}_{\mathcal{T}}\) 作为子集大小的函数图象(左上图)。接下来两张图显示了 \(10\) 折交互验证和 \(N\) 折交互验证,后者也称作留一法 (LOO)。每张图的红色粗线表示期望(预测)误差 \(\mathbb{Err}\),而黑色粗线表示期望交互验证。右下图则显示了交互验证近似条件误差和期望误差的程度。
可能会认为 \(N\) 折交互验证能很好地近似 \(\mathbb{Err}_{\mathcal{T}}\),因为它几乎用了整个训练样本来拟合新的测试点。另一方面,可能会期望 \(10\) 折交互验证会很好地估计 \(\mathbb{Err}\),因为它平均了不同的训练集。从图中看到估计 \(\mathbb{Err}_{\mathcal{T}}\) 时 \(10\) 折交互验证比 \(N\) 折做得更好,对 \(\mathbb{Err}\) 的估计甚至更好。确实如此,两条黑色曲线与红色曲线的相似性表明两个 CV 曲线对 \(\mathbb{Err}\) 近似无偏,且 \(10\) 折有更小的方差。类似的趋势由 Efron (1983)1 给出。
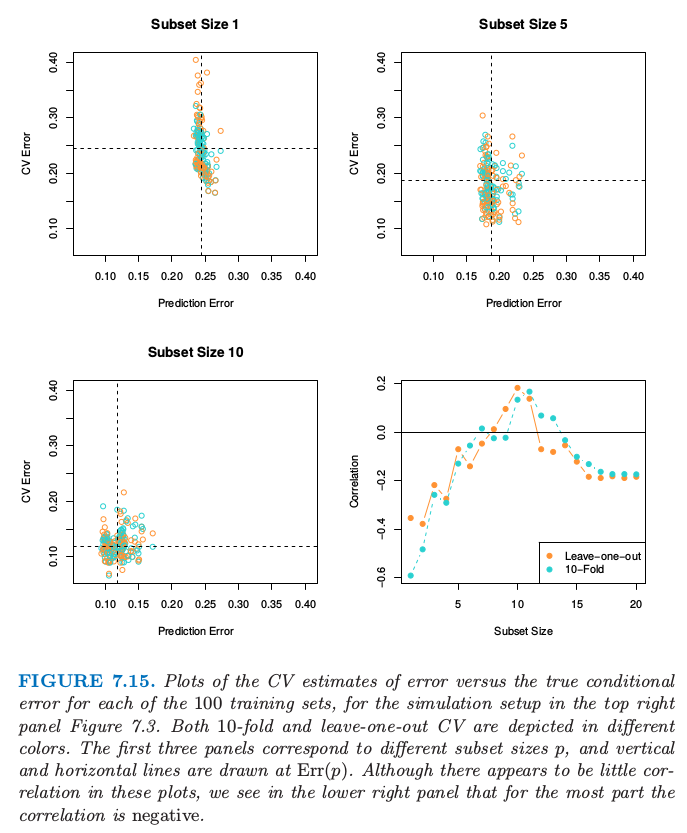
图 7.15. 对 100 个训练集的每个 CV 估计误差关于真实条件误差的图象,模拟的设定与图 7.3 的右上图相同。前三张图对应不同的子集大小 \(p\),且水平直线和垂直直线是在 \(\mathbb{Err}(p)\) 处画的。尽管看起来这些图象没有多大的关联,但是我们从右下图看到大部分是负相关的。
图 7.15 显示了 100 次模拟中,10 折交互验证和 \(N\) 折交互验证对误差的估计关于真实条件误差的散点图。尽管散点图没有表明太多的相关性,但右下图表明对于大部分来说是呈负相关的,这正是之前已经观察到的神奇现象。这种负相关解释了为什么任意形式的 CV 都不能很好地估计 \(\mathbb{Err}_{\mathcal{T}}\)。每张图的虚线是在 \(\mathbb{Err}(p)\) 处画的,\(\mathbb{Err}(p)\) 是最优子集大小 \(p\) 时的期望误差。我们再一次看到两种形式的 CV 对于期望误差是近似无偏的,但是对于不同训练集的测试误差的方差是相当不同的。
在 7.3 的四种实验条件下,“reg/linear” 条件表现出实际测试误差与预测测试误差最高的相关性。这个现象也发生在误差的自助法估计中,而且我们猜测,对条件预测误差的其他估计都成立。
我们得出结论,仅仅给出从与训练集相同的数据时,一般情况下得到特定训练集的测试误差的估计不是很容易的。相反地,交互验证和相关的方法可能可以对期望误差 \(\mathbb{Err}\) 给出合理的估计。
- 1
Efron, B. (1983). Estimating the error rate of a prediction rule: some improvements on cross-validation, Journal of the American Statistical Association 78: 316–331.
