8.3 贝叶斯方法¶

贝叶斯推断中，需要确定一个在给定参数 $\theta$ 时数据的采样模型 $\mathrm{Pr}(\mathbf Z | \theta)$ ，以及在得到数据之前对于参数 $\theta$ 认知的先验分布 $\mathrm{Pr}(\theta)$ 。然后计算后验分布：

\[ \mathrm{Pr}(\theta\mid\mathbf Z)=\frac{\mathrm{Pr}(\mathbf Z\mid\theta)\cdot \mathrm{Pr}(\theta)}{\int \mathrm{Pr}(\mathbf Z\mid \theta)\cdot \mathrm{Pr}(\theta)d\theta}\tag{8.23} \]

它表示当我们知道数据后更新了对 $\theta$ 的认知。为了理解后验分布，可以从中抽采样本或者通过计算均值或众数来描述它。

贝叶斯方法与一般推断方法的不同之处在于：用先验分布来表达知道数据之前的不确定性，而且在知道数据之后允许不确定性继续存在，并将不确定性表示成后验分布。

后验分布提供了预测未来观测 $z^{new}$ 的基础，可以通过计算预测分布 (predictive distribution) 来表达预测的不确定性，注意预测值是一个随机变量，存在概率分布：

\[ \mathrm{Pr}(z^{new}\mid \mathbf Z)=\int \mathrm{Pr}(z^{new}\mid \theta)\cdot \mathrm{Pr}(\theta\mid \mathbf Z)d\theta\tag{8.24} \]

在上述贝叶斯框架内，最大似然方法会使用上式分布中概率值最大那个点的密度 $\mathrm{Pr}(z^{new}\mid \hat\theta)$ 来预测未来的数据。不同于式（ 8.24 ）的预测分布，它不能说明 $\theta$ 估计的不确定性。

让我们在光滑化的例子中使用贝叶斯方法。

首先，从由式 8.5 给出的参数模型开始，假设 $\sigma^2$ 已知。

回顾 $$

\[\begin{align*} Y&=\mu(X)+\varepsilon;\; \varepsilon\sim N(0,\sigma^2),\\ \mu(X)&=\sum\limits_{j=1}^7\beta_jh_j(x) \tag{8.5} \end{align*}\]

$$

假设观测的特征 $x_1,x_2,\ldots,x_N$ 固定，因此数据的随机性仅仅来源于 $y$ 与均值 $\mu(x)$ 之间的偏差。

第二步，设置先验分布。为函数设置先验分布相当复杂。最常用的方式是使用高斯过程分布，需指定均值函数和协方差函数（Wahba,19901; Neal, 19962）。这里采取一个简单的方法：考虑 $\mu(x)$ 的有限 $B$ 样条基函数，并给出系数 $\beta$ 的先验分布，这隐式地定义了 $\mu(x)$ 的先验分布。我们选取中心化的先验高斯分布：

\[ \beta\sim N(0,\tau\mathbf \Sigma) \tag{8.25} \]

先验协方差矩阵 $\mathbf \Sigma$ 和方差 $\tau$ 将在下面讨论。$\mu(x)$ 隐式的先验过程因此是高斯的，其中协方差核为：

\[\begin{split} \begin{align*} K(x,x')&= \mathrm{cov}[\mu(x),\mu(x')]\\ &=\tau\cdot h(x)^T\mathbf\Sigma h(x') \tag{8.26} \end{align*} \end{split}\]

$\beta$ 的后验分布也是高斯的，均值和方差分别为：

\[\begin{split} \begin{align*} \mathbb{E}(\beta\mid \mathbf Z)&=(\mathbf{H^TH}+\frac{\sigma^2}{\tau}\mathbf\Sigma^{-1})^{-1}\mathbf{H^Ty}\\ \mathrm{Cov}(\beta\mid\mathbf Z)&=(\mathbf{H^TH}+\frac{\sigma^2}{\tau}\mathbf \Sigma^{-1})^{-1}\sigma^2 \tag{8.27} \end{align*} \end{split}\]

后验 $\mu(x)$ 对应的值为：

\[\begin{split} \begin{align*} \mathbb{E}(\mu(x)\mid\mathbf Z)&=h(x)^T(\mathbf{H^TH}+\frac{\sigma^2}{\tau}\mathbf\Sigma^{-1})^{-1}\mathbf{H^Ty}\\ \mathrm{cov}[\mu(x),\mu(x')\mid\mathbf Z]&=h(x)^T(\mathbf{H^TH}+\frac{\sigma^2}{\tau}\mathbf\Sigma^{-1})^{-1}h(x')\sigma^2 \tag{8.28} \end{align*} \end{split}\]

我们应该怎样选取先验协方差矩阵 $\mathbf \Sigma$ 呢？在某些设定下先验可以从对参数的主观感受来选择。这里我们想说函数 $\mu(x)$ 应该为光滑的，而且已经通过将 $\mu$ 表示成低维度的 $B$-样条的基来保证。因此可以选取先验协方差阵为单位矩阵 $\mathbf {\Sigma=I}$。当基函数个数很多，这或许不是充分的，通过对 $\mathbf\Sigma$ 上施加限制条件来保证更多的光滑；这恰巧是光滑样条的情形（ 5.8.1 节）。

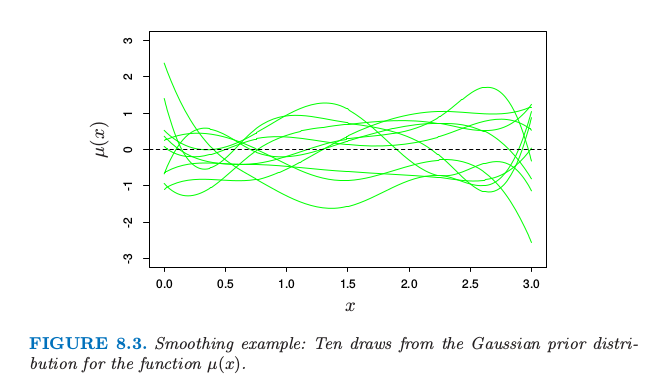
图 8.3. 光滑例子：十条函数 $\mu(x)$ 高斯先验分布的曲线。

图 8.3 显示了 10 个 $\mu(x)$ 对应的先验分布。为了产生函数 $\mu(x)$ 后验的值，我们从后验式（ 8.27 ）得到 $\beta'$，给出对应后验的值 $\mu'(x)=\sum_1^7\beta_j'h_j(x)$。十条这样的后验曲线如图 8.4 所示。取了两个不同的先验方差 $\tau$ 的值，1 和 1000。注意到右图与图 8.2 的左下图的相似度。这种相似性不是偶然的。当 $\tau\longrightarrow \infty$，后验分布式（ 8.27 ）和自助法分布式（ 8.7 ）相同。

另一方面，对于$\tau=1$，图 8.4 左图的后验曲线 $\mu(x)$ 比自助法曲线更加光滑，因为在光滑性上面强加了更多先验权重。

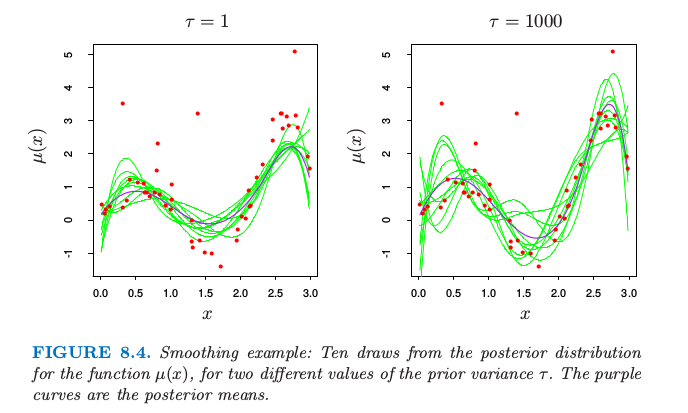
图 8.4. 光滑例子：对于两个不同的先验方差 $\tau$，十条函数 $\mu(x)$ 后验分布的曲线。紫色的曲线是后验均值。

当 $\tau\rightarrow \infty$ 时的分布式（ 8.25 ）称为 $\theta$ 的 无信息先验 (noninformative prior)，在高斯模型中，极大似然和参数自助法趋向于与对自由参数使用了无信息先验的贝叶斯保持一致。因为在常值先验情况下，后验分布与似然函数成比例，所以这些方法趋向于一致。这种对应也可以推广到非参的情形。其中非参自助法近似于一个无信息先验的贝叶斯分析，8.4 节将详细介绍。

然而，我们已经做了一些从贝叶斯观点来看不是很恰当的事情。我们已经用了 $\sigma^2$ 的无信息（常值）先验，而且在后验中换成了最大似然估计 $\hat\sigma^2$。一个更加标准的贝叶斯分析也会在 $\sigma$ 上加先验（一般地，$g(\sigma)\propto 1/\sigma$ ），计算 $\mu(x)$ 和 $\sigma$ 的联合后验分布，然后把 $\sigma$ 积分出来，而不是仅仅提取后验分布的最大值做 MAP 估计）

1: Wahba, G. (1990). Spline Models for Observational Data, SIAM, Philadelphia.
2: Neal, R. (1996). Bayesian Learning for Neural Networks, Springer, New York.

统计学习精要(中文)

8.3 贝叶斯方法

8.3 贝叶斯方法¶