7.8 最小描述长度
7.8 最小描述长度¶
**最小描述长度 (MDL) **方法给出与 BIC 形式上等价的选择准则,但是它是从最优编码角度出发的。我们首先回忆数据压缩的编码理论,接着将其应用到模型选择中。
我们将数据 \(z\) 看成是想要编码并且发给其他人(接受者)的信息。我们将模型看成是对数据编码的一种方式,然后选择最简模型,也就是传输的最短编码。
首先假设我们可能想要传送的信息为 \(z_1,z_2,\ldots,z_m\)。我们的编码采用长度为 \(A\) 的有限字母表:举个例子,我们可能采用长度为 \(A=2\) 的二进制编码 \(\\{0,1\\}\)。这里是 4 个可能信息以及二值编码的例子:
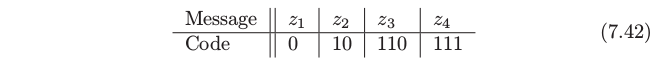
这个编码也被称作 瞬时前缀码 (instantaneous prefix code):没有编码是其它任意码的前缀,并且接受者(知道所有可能编码的人)当信息完全发送后知道精确的信息。我们将接下来的讨论限制在瞬时前缀码上。
可以采用 (7.42) 的编码或者交换编码,举个例子,对于 \(z_1,z_2,z_3,z_4\) 编码为 \(110,10,111,0\)。我们怎么决定采用哪一个?这取决于我们发送每条信息的次数。举个例子,如果我们发送 \(z_1\) 最多,对 \(z_1\) 采用最短编码 \(0\) 是有意义的。采用这种策略——最频繁的信息采用最短的编码——平均信息长度将会缩短。
一般地,如果以概率 \(\mathrm{Pr}(z_i),z_i=1,2,\ldots,4\) 来发送信息, Shannon 的著名定理说我们应该采用长度为 \(l_i=-\mathrm{log}_2 \mathrm{Pr}(z_i)\) 的编码,并且平均信息长度满足
上面的右侧项也被称作 \(\mathrm{Pr}(z_i)\) 分布的熵。当 \(p_i=A^{-l_i}\) 时上面不等式等号成立。在我们例子中,如果 \(\mathrm{Pr}(z_i)=1/2,1/4,1/8,1/8\),则 (7.42) 的编码是最优的而且达到了熵的下界。
一般地下界不能达到,但是像 Huffman 编码模型的过程可以接近下界。注意到对于无限的信息集合,熵替换成 \(-\int \mathrm{Pr}(z)\log_2\mathrm{Pr}(z)dz\)。
从这个结果我们得到以下结论:
为了传送概率密度函数为 \(\mathrm{Pr}(z)\) 的随机变量 \(z\),我们需要 \(-\log_2\mathrm{Pr}(z)\) 位信息。
从现在开始我们将记号 \(\log_2\mathrm{Pr}(z)\) 换成 \(\log\mathrm{Pr}(z)=\log_e \mathrm{Pr}(z)\);这是很方便的,因为仅仅引入了不重要的常数因子。
现在我们将这个问题的结果应用到模型选择。我们有参数为 \(\theta\) 的模型 \(M\),以及包含输入和输出的数据 \(\mathbf{Z=(X,y)}\)。令在模型条件下的输出的(条件)概率为 \(\mathrm{Pr}(\mathbf y\mid\theta,M,\mathbf X)\),假设接受者知道所有的输入,而且我们希望传送输出值。传送输出要求的信息长度为
这是在给定输入的情况下目标值的对数似然。
Note
这里我理解为其实就是 :
其中 \(y\) 和 \(\theta\) 是目标值,而 \(X\) 和 \(M\) 都是输入。
第二项是传递模型参数 \(\theta\) 的平均编码长度,而第一项是传递模型与真实目标值之间差异的平均编码长度。举个例子假设我们有单目标 \(y\sim N(\theta,\sigma^2)\),参数为 \(\theta\sim N(0,1)\),并且没有输入(为了简单)。则模型长度为
注意到 \(\sigma\) 越小,平均信息长度越短,因为 \(y\) 更集中在 \(\theta\) 附近。
MDL 准则说我们应该选择最小化公式(7.44) 的模型。我们将公式(7.44)看成(负)对数后验分布,因此最小化描述长度等价于最大化后验概率。因此,作为近似对数后验概率导出的 BIC 准则,也可以看成是通过最小描述长度来(近似)模型选择的工具。
注意到我们忽略随机变量 \(z\) 编码的精确性。我们不可能使用有限的编码长度对连续变量进行精确地编码。然而,如果我们对编码 \(z\) 有容忍度 \(\delta z\),需要的信息长度是在区间 \([z,z+\delta z]\) 中概率的对数,如果 \(\delta z\) 很小,可以用 \(\delta z\mathrm{Pr}(z)\) 来近似。因为 \(\log\delta z\mathrm{Pr}(z)=\mathrm{log}\delta z + \mathrm{log}\;\mathrm{Pr}(z)\),这意味着我们可以仅仅忽略掉常数 \(\mathrm{log}\;\delta z\),并且使用 \(\mathrm{log\; \Pr}(z)\) 来作为我们信息长度的衡量,就像我们上面做的那样。
用于模型选择的 MDL 的上述观点表明我们应该选择后验概率达到最大的模型。然而,许多贝叶斯学家倾向于通过从后验分布中采样来做推断。
